Matrix multiplication with MapReduce

If A is an m × p matrix and B is an p × n matrix, then the product of A and B is the m × n matrix C = AB, where the (i, j)^th element of C is computed as the inner product of the i^th row of A with the j^th column of B:

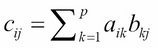
This is a dot product—simple arithmetic if m, p, and n are small. But not so simple if we're working with big data.

The formula for c_ij requires p multiplications and p – 1 additions, and there are m· n of these to do. So, that implementation runs in O(mnp) time. That is slow. Furthermore, if A and B are dense matrices (that is, most elements are nonzero), then storage requirements can also be overwhelming. This looks like a job for MapReduce.

For MapReduce, think key-value pairs. We assume that each matrix is stored as a sequence of key-value pairs, one for each non-zero element of the matrix. The key is the subscript pair (i, j), and the value is the (i, j)^th element of the matrix. For example, this matrix

would be represented by the list shown in Figure 11-4. This is sometimes called sparse matrix format.

Figure 11-4. Key-value pairs

By list, we don't necessarily mean a Java List object. In practice, it could be a file or more general input stream. In the following coding, we will assume that each is a text file, represented by a Java File object.

To implement matrix multiplication within the MapReduce framework, we will assume that we are given a file containing the elements of two matrices, organized as shown in Figure 11-4. These 12 values are the elements of a 3 × 2 matrix named A followed by a 2 × 3 matrix named B. For example, a₁₂ = 3.21 and b₂₃ = 1.94. Notice that these two matrices are full—no zero elements.

The map() and reduce() methods for multiplying two matrices that are input this way are shown in Listing 11-4.

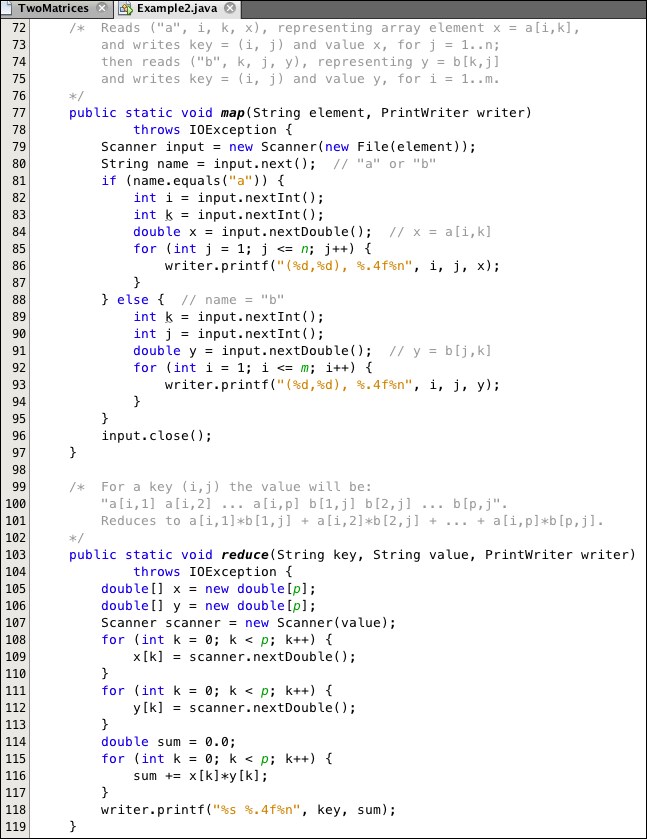
Listing 11-4. The map and reduce methods for matrix multiplication

The complete MapReduce program for this application is similar to the WordCount implementation shown in Listing 11-1.

As the comment at lines 72-76 indicates, the map() method reads the input file, one line at a time. For example, the first line from the file shown in Figure 11-5 would be:

a 1 1 4.26

Figure 11-5. Two matrices

The numeric values would be stored as i = 1, k = 1, and x = 4.26 (at lines 82-84). Then the for loop at lines 85-87 would write these three outputs to whatever context is assigned to the writer object:

(1,1)   4.26
(1,2)   4.26
(1,3)   4.26

Note that, for this example, the program has set the global constants m = 3, p = 2, and n = 3 for the dimensions of the matrices.

The map() method writes each value three times because each one will be used in three different sums.

The grouping process that follows the map() calls will reassemble the data like this:

(1,1) a₁₁ a₁₂ b₁₁ b₂₁

(1,2) a₁₁ a₁₂ b₁₂ b₂₂

(1,3) a₁₁ a₁₂ b₁₃ b₂₃

(2,1) a₂₁ a₂₂ b₁₁ b₂₁

(2,2) a₂₁ a₂₂ b₁₂ b₂₂

Then for each key (i, j), the reduce() method computes the inner product of the two vectors that are listed for that key's value:

(1,1) a₁₁b₁₁ + a₁₂b₂₁

(1,2) a₁₁b₁₂ + a₁₂b₂₂

(1,3) a₁₁b₁₃ + a₁₂b₂₃

(2,1) a₂₁b₁₁ + a₂₂b₂₁

(2,2) a₂₁b₁₂ + a₂₂b₂₂

Those are the correct values for the elements c₁₁, c₁₂, c₁₃, and so on of the product matrix C = AB.

Note

Note that for this to work correctly, the order in which the map() method emits the key-values must be maintained by the grouping process. If it doesn't, then some additional indexing scheme may have to be included so that the reduce() method can do the a_ik b_kj pairing correctly.