
The law of constant composition states that all samples of a given compound will contain the same elements in identical mass ratios. For instance, every sample of H2O will contain two atoms of hydrogen for every atom of oxygen and therefore one gram of hydrogen for every eight grams of oxygen.
There are two ways to express a formula for a compound. The empirical formula gives the simplest whole number ratio of the elements in the compound. The molecular formula gives the exact number of atoms of each element in the compound and is a multiple of the empirical formula. For example, the empirical formula for benzene is CH, whereas the molecular formula is C6H6. For some compounds, the empirical and molecular formulas are the same, as in the case of H2O. An ionic compound, such as NaCl or CaCO3, will have only an empirical formula.
Note that, given a molecular formula, the empirical formula for that molecule can be calculated by simplifying the ratio of the subscripts next to each component. However, given only an empirical formula, the molecular formula of a specific molecule cannot be determined without more information since several different molecules could share the same empirical formula. For example, the empirical formula CH2 is shared by ethylene (C2H4), butane (C4H8), and cyclohexane (C6H12)
The percent composition by mass of an element is the mass percent of the element in a specific compound. To determine the percent composition of an element X in a compound, the following formula is used:

The percent composition of an element may be determined using either the empirical or molecular formula. If the percent compositions are known, the empirical formula can be derived. It is possible to determine the molecular formula if both the percent compositions and molecular mass of the compound are known.
Example:
What is the percent composition of chromium in K2Cr2O7 (potassium’s molecular mass is 39 g/mol, chromium’s is 52 g/mol, and oxygen’s is 16 g/mol)?
Solution:
The formula mass of K2Cr2O7 is: 2(39 g/mol) + 2(52 g/mol) + 7(16 g/mol) = 294 g/mol
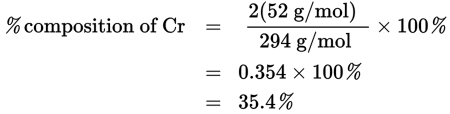
Example:
What are the empirical and molecular formulas of a compound that contains 40.9% carbon, 4.58% hydrogen, and 54.52% oxygen by mass and has a molecular mass of 264 g/mol (carbon’s molar mass is 12 g/mol, hydrogen’s is 1 g/mol, and oxygen’s is 16 g/mol)?
Method One:
First, determine the number of moles of each element in the compound by assuming a 100-gram sample; this converts the percentage of each element present directly into grams of that element. Then convert grams to moles:
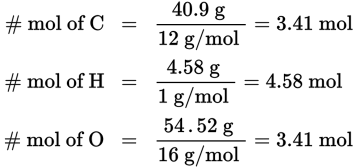
Next, find the simplest whole number ratio of the elements by dividing the number of moles of each element by the smallest number obtained in the previous step:
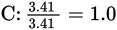 |
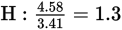 |
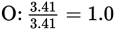 |
Finally, the empirical formula is obtained by converting the numbers obtained into whole numbers (multiplying them by an integer value).
Multiplying all the subscripts by 3 to obtain all whole numbers for the subscripts shows that C3H4O3 is the empirical formula.
To determine the molecular formula, divide the molecular mass by the mass represented by the empirical formula. The resulting value is the number of empirical formula units in the molecular formula.
The empirical formula mass of C3H4O3 is:
3(12 g/mol) + 4(1 g/mol) + 3(16 g/mol) = 88 g/mol
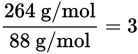
C3H4O3 × 3 = C9H12O9 is the molecular formula.
Method Two:
When the molecular mass is given, it can be faster to find the molecular formula first. This is accomplished by multiplying the molecular mass by the given percentages to find the grams of each element present in one mole of compound, then dividing by the respective atomic masses to find the mole ratio of the elements:

Thus, the molecular formula, C9H12O9, is the direct result.
The empirical formula can now be found by reducing the subscript ratio to the simplest integral values.