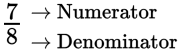
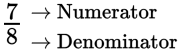
Multiplying fractions: Multiply numerators by each other and denominators by each other.
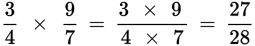
Dividing fractions: Flip the numerator and denominator of the fraction you’re dividing by, then multiply.
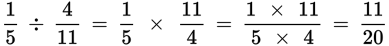
Adding fractions: You can add fractions only when they have the same denominator. When you add, add only the numerators, NOT the denominators.
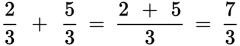
If you don’t have a common denominator, you have to find one. The fastest way to get a common denominator is to multiply each fraction by a fraction whose numerator and denominator are the same as the denominator of the other fraction. (You can do this because any fraction with the same numerator and denominator is equal to 1, and multiplying any number by 1 doesn’t change the value of the number.)
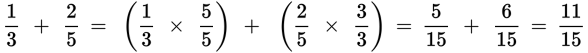
Subtracting fractions: This works the same way as adding fractions, except you subtract the numerators instead of adding them.
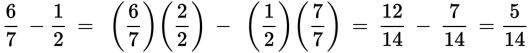
Remember, parentheses can be used to indicate multiplication instead of the “×” sign.
Reducing fractions: Whenever there is a common factor in the numerator and denominator, you can reduce the fraction by removing the factor from both parts of the fraction. You can do this because dividing the numerator and denominator by the same number doesn’t change the value of the fraction as a whole. This will often make working with the fraction much easier because you’ll be using smaller numbers.
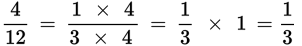
On Test Day, you don’t actually have to write out all this math. For example, you might work like this:
Or, even more simply, you might keep track of the multiplication operations mentally,
only writing down the results. For example, if attempting to reduce
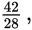you might write your work by cancelling like this:
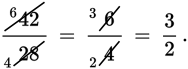
Because both 42 and 28 are divisible by 7, you can divide both the numerator (42)
and the denominator (28) by 7. Thus,
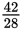reduces to
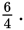Because both 6 and 4 are divisible by 2, you can divide both the numerator (6) and
the denominator (4) by 2. Thus,
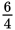reduces to
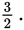
Canceling: Whenever you have to multiply two or more fractions, you should cancel common factors
before you multiply. This is a lot like reducing and has the same advantages.
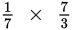can be canceled like this:
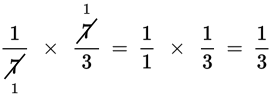
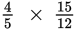can be canceled like this:
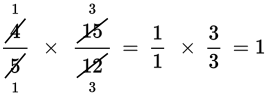
Notice that both the 5 in the denominator of the first fraction and the 15 in the numerator of the second fraction are divisible by 5. Similarly, the 4 in the numerator of the first fraction and the 12 in the denominator of the second fraction are both divisible by 4. Simplifying fractions requires identifying these types of relationships and dividing accordingly.
One way to compare fractions is to re-express them with a common denominator.
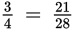and
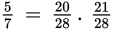is greater than
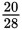so
is greater than
Another way to compare fractions is to convert them both to decimals.
converts to 0.75, and
converts to approximately 0.714.
A mixed number consists of an integer and a fraction. For example,
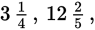and
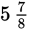are all mixed numbers.
To convert an improper fraction (a fraction whose numerator is greater than its denominator) to a mixed number, divide the numerator by the denominator. The number of “whole” times that the denominator goes into the numerator will be the integer portion of the mixed number; the remainder will be the numerator of the fractional portion.
Example:
Convert
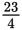to a mixed number.
Solution:
Dividing 23 by 4 gives you 5 with a remainder of 3, so
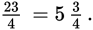
To change a mixed number to a fraction, keep the denominator of the fraction. To figure out the numerator, multiply the integer portion of the mixed number by the number in the denominator. Then add this result to the numerator of the mixed number.
Example:
Convert
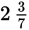to a fraction.
Solution:
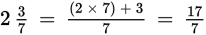
Example:
Convert
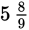to a fraction.
Solution:
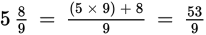
Adding or subtracting mixed numbers whose fractional parts have the same denominator will probably be on the test.
Example:
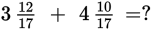
Solution:
First, add the integer parts: 3 + 4 = 7.
Next, add the fractional parts:
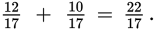
Now,
Therefore,
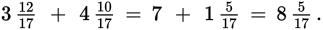
Example:
Solution:
The wrinkle here is that the fractional part of the first number is smaller than the
fractional part of the second number (i.e.,
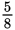is smaller then
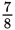). What you need to do, therefore, is borrow from the integer part of the first number
to make the fractional part of the first number bigger. Borrow 1 from the integer
part and add it to the fractional part (remembering that 1 can be rewritten as
).
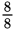So
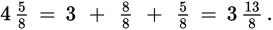So the problem of finding
has been replaced with the problem of finding
which is easier because the fractional part of the first number is greater than the
fractional part of the second number.
Notice that all you need to do is replace
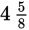with
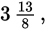which is equal to
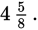To find
first subtract the integer parts: 3 − 2 = 1. Next subtract the fractional parts:
So
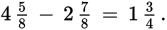
Example:
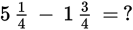
Solution:
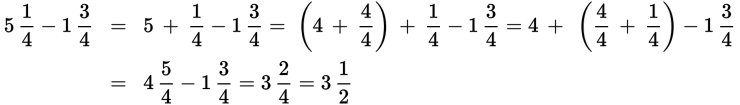
When you gain experience with this, you’ll be able to skip some of the steps and do this type of problem more quickly.
Example:
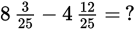
Solution:
