You can get numerical solutions for more than one unknown if you are given more than one equation. Simultaneous Equations questions take a little thought to answer. Solving simultaneous equations almost always involves combining equations, but you have to figure out the best way to combine each unique set of equations.
You can solve for two variables only if you have two distinct equations. Two forms of the same equation will not be adequate. Combine the equations in such a way that one of the variables cancels out. For example, to solve the two equations 4x + 3y = 8 and x + y = 3, multiply both sides of the second equation by −3 to get −3x − 3y = −9. Now add the two equations; the 3y and the −3y cancel out, leaving x = −1. Plug that back into either one of the original equations and you’ll find that y = 4.
Example:
If 2x − 9y = 11 and x + 12y = −8, what is the value of x + y ?
Solution:
If you just plow ahead without thinking, you might try to answer this question by solving for one variable at a time. That would work, but it would take a lot more time than this question needs. As usual, the key to this Simultaneous Equations question is to combine the equations, but combining the equations doesn’t necessarily mean losing a variable. Look what happens here if you just add the equations as presented:
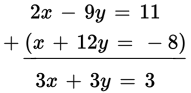
Suddenly you’re almost there! Just divide both sides by 3 and you get x + y = 1.