Solutions to Review Problems

1. B

   Substitute −2 for y into the equation x = 3 − y²:

   x = 3 − y² = 3 − (−2)² = 3 − 4 = −1
2. A

   The sum of 4 identical quantities is 4 times one of those quantities, so the sum of the four terms 2^x is 4 times 2^x:

   2^x + 2^x + 2^x + 2^x = 4(2^x) = 2²(2^x) = 2^{x + 2}
3. D

   Factor the top and the bottom and cancel the factors they have in common:

   
4. B

   Use long division. Watch out: The expression that goes under the division sign needs a place-holding 0x² term:

   

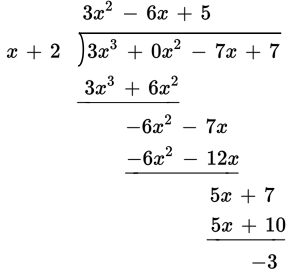
   The remainder is −3.

5. B

   To undo the fourth-root symbol, raise both sides to the exponent 4:

   

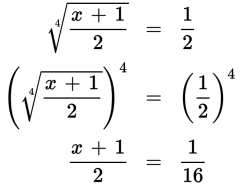
   Now cross multiply:

   
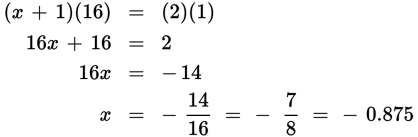
6. C

   This might look at first glance like a candidate for cross multiplication, but that would just make things more complicated. Notice that the fractions on both sides have the same numerator, 19. If the two fractions are equal and they have the same numerator, then they must have the same denominator, so just write an equation that says that one denominator is equal to the other denominator:

   
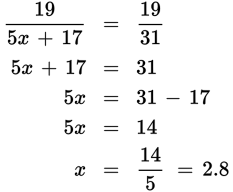
7. C

   Watch what happens when you express everything as powers with a base of 3:

   

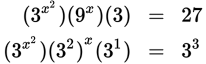
   When you raise a power to an exponent, multiply the exponents, and keep the same base. So (3^2)x = 3^2x:

   

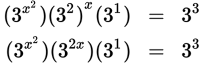
   The left side of the equation is the product of powers with the same base, so just add the exponents:

   

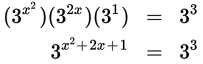
   Now the two sides of the equation are powers with the same base, so you can just set the exponents equal:

   

   The positive value is 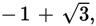which is approximately 0.732.

8. D

   First multiply both sides by y − 4a to clear the denominator:

   

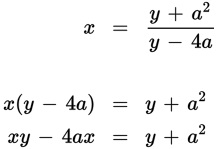
   Now move all terms with y to the left and all terms without y to the right:

   

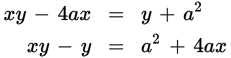
   Now factor the left side and divide to isolate y:

   
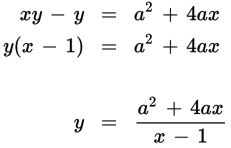
9. B

   With only two equations, you won’t be able to get numerical solutions for three unknowns. But apparently you can get far enough to rule out three of the four answer choices. How? Look for a way to combine the equations that leads somewhere useful. Notice that the first equation contains +ky and the second equation contains −ky, so if you add the equations as they are, you’ll lose those terms:

   

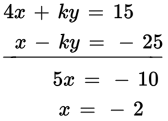
   There’s not enough information to get numerical solutions for k or y, but you do know that x = −2, so the correct answer is the only choice that has an x-value of −2.

10. D

    If the absolute value of something is less than 8, then that something is between −8 and 8:

    

    There are four integers in that range: −2, −1, 0, and 1.