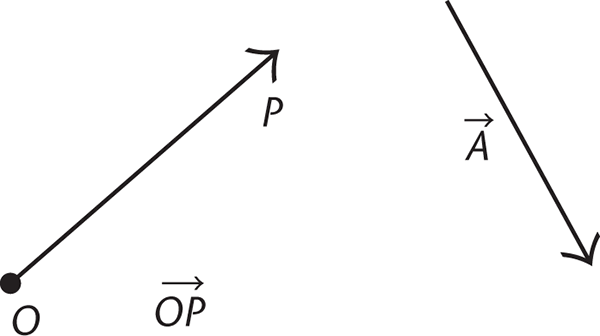
While complex numbers define a point, vectors define a line. This is important to remember because now you have to keep in mind both the magnitude and the direction of the line when dealing with vectors. Vectors start at one point and end at another point. It is convenient to describe vectors that start at the origin (denoted O) and end at a point (denoted P). The point that has the arrow defines the direction.


Vectors can be denoted as  or
or  Typically, vectors are denoted simply as a single variable, such as
Typically, vectors are denoted simply as a single variable, such as  or A.
or A.
Vectors that start at the origin and end at another point can be described simply as coordinates. This is known as the rectangular form. An example is 4i + 3j. The “i” in vectors is not the same “i” from complex numbers, but vectors in this form are graphed in the same way. In this case, the i part is a unit vector in the positive x direction, and the j part is a unit vector in the positive y direction. The origin of the axes also serves as the origin for the vector. You may also see them defined as a magnitude and an angle only, like 5, 45°. This is known as the polar form and tells you the magnitude (or length) of the vector is 5 units at an angle of 45°. Get used to seeing vectors in both the rectangular form and the polar form because both of these forms are prevalent.
Similar to complex numbers, you can perform mathematical operations on vectors.
The sum or difference of vectors is called a resultant because it’s the vector that is the result of adding or subtracting vectors. To be able to find the resultant:
Example:
Find the resultant  in both rectangular and polar form, of the following two vectors:
in both rectangular and polar form, of the following two vectors: 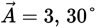 and
and  given that
given that  and that sin 60° = 0.87.
and that sin 60° = 0.87.
Solution:

Ax + Bx = 2.61 + 2.5 = 5.11
Ay + By = 1.5 + 4.35 = 5.85
In rectangular form, the resultant is 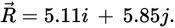

In polar form, the resultant is 
Vector multiplication has many meanings. Conceptually, it is not very straightforward, and you need to understand what the vectors represent to understand what type of multiplication you will want to use. The two most common types of multiplication of vectors are briefly covered below.
Dot Product: Let  and
and  be vectors and let θ be the angle between these vectors. The dot product of the vectors
be vectors and let θ be the angle between these vectors. The dot product of the vectors  and
and  is found using the following equation:
is found using the following equation:

Because the dot product results in a number, or a magnitude, it is often referred
to as the scalar product. Let  be a nonzero vector. Then
be a nonzero vector. Then  is a unit vector in the direction of
is a unit vector in the direction of  The dot product of
The dot product of  and
and  is the magnitude of the component of the vector
is the magnitude of the component of the vector  In the direction of the vector
In the direction of the vector  Therefore:
Therefore:

Example:
Find the dot product of the two vectors  and
and  from the previous example.
from the previous example.
Solution:

Cross Product: The cross product allows you to find a new vector that is perpendicular to the plane of the two vectors being multiplied. Because you are finding a vector, this is also referred to as the vector product. Use the following equation to find the cross product:

Here, θ represents the smaller angle between the two vectors and n is a unit vector perpendicular to the plane formed by the vectors 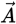 and
and  The magnitude of
The magnitude of  is
is  sin θ. The direction of
sin θ. The direction of  is determined by the right hand rule. The right hand rule says that when you rotate
the right hand from
is determined by the right hand rule. The right hand rule says that when you rotate
the right hand from  to
to 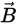 through the smaller angle between
through the smaller angle between  and
and 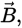 then your thumb points in the direction of
then your thumb points in the direction of 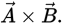 This is the direction of the unit vector n.
This is the direction of the unit vector n.
Example:
Given the vectors  and
and  from the previous two examples, find the cross product.
from the previous two examples, find the cross product.
Solution:

The magnitude of  is 7.5. Here, n represents the unit vector in the positive z direction. Remember,
is 7.5. Here, n represents the unit vector in the positive z direction. Remember,  is a vector in the plane perpendicular to the plane of vectors
is a vector in the plane perpendicular to the plane of vectors  and
and 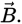 The right hand rule says that
The right hand rule says that  is in the positive z direction. So
is in the positive z direction. So  is 7.5 units long in the positive z direction.
is 7.5 units long in the positive z direction.