I. DYNAMIC EQUILIBRIUM AND EQUILIBRIUM CONSTANTS
A. ESTABLISHING A DYNAMIC EQUILIBRIUM
1. A dynamic equilibrium is established when, in a reversible reaction, the rate of the forward reaction is equal to the rate of the backward reaction.
2. Because the reactants are used up equally as fast as the products are produced, the concentrations of each substance are constant.
All concentrations being constant (not changing) is not the same thing as concentrations being equal (all having the same value). This is a common misconception and one that you must not have.
B. A GENERIC EQUILIBRIUM CONSTANT
1. All equilibrium constants show the ratio of products to reactants present in an equilibrium mixture.
2. Depending on the reaction, one of three equilibrium constants may be calculated—Kc, Kp, or Ksp (also see Ka, Kb, and Kw in Chapter 19). In each case, the K expression has the following characteristics:
i. Some aspects of the products are multiplied together in the numerator.
ii. Some aspects of the reactants are multiplied together in the denominator.
iii. All aspects of products and reactants are raised to the powers of the stoichiometric numbers found in the balanced chemical equation.
iv. It has a numerical value that is constant at constant temperature.
v. It does not include any values for pure solids or pure liquids.
C. SPECIFIC EQUILIBRIUM CONSTANTS
1. Kc—using equilibrium concentrations. Consider the following equilibrium where a, b, c, and d are the stoichiometric coefficients of substances A, B, C, and D, respectively.
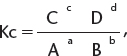where [ ] represents concentration.
2. Kp—using equilibrium partial pressures, i.e., in gaseous equilibria. Consider the following equilibrium where a, b, c, and d are the stoichiometric coefficients of substances A, B, C, and D, respectively.
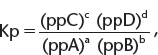where pp represents partial pressure.
3. Ksp—using equilibrium concentrations in the specific case of sparingly soluble solids. Consider the following equilibrium that is set up when a sparingly soluble solid is placed into water and an equilibrium is set up between the undissolved solid and its aqueous ions.
An expression for Ksp can be written as follows:
Ksp = [Ab+]a [Ba−]b, where [ ] represents concentration.
A. KC CALCULATIONS WHERE EQUILIBRIUM HAS ALREADY BEEN ESTABLISHED
1. Consider the following gaseous phase reaction, where gaseous butanoic acid (C3H7CO2H(g)) reacts with gaseous ethanol (C2H5OH(g)) to produce the gaseous ester, ethyl butanoate (C3H7CO2C2H5(g)), and steam, H2O(g).
Equilibrium was achieved and then the following data were collected. Moles of butanoic acid = 10.0, moles of ethanol = 10.0, moles of ethyl butanoate = 20.0, and moles of steam = 20.0. Calculate the equilibrium constant Kc, at this temperature.
Because the equilibrium has been established, the moles of each substance can be converted to concentrations and go straight into the K expression. V is the volume and conveniently it cancels (if it did not cancel we would have to know its value). Each component of the mixture is raised to the stoichiometric number in the chemical equation.
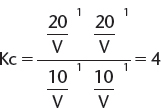
B. KC CALCULATIONS WHERE INITIAL AMOUNTS ARE KNOWN BEFORE EQUILIBRIUM IS ESTABLISHED—THE USE OF ICE TABLES
1. Using the same reaction and the same Kc calculated in A. earlier (i.e., same reaction at the same temperature), calculate the number of moles of each substance present at equilibrium, when 1.00 mole of gaseous butanoic acid and 2.00 moles of gaseous ethanol are mixed.
Set up an ICE table to find the moles of each substance present at equilibrium.
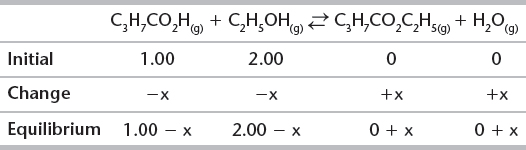
Because this is same reaction as in A at the same temperature, we can use the same value for K.
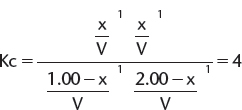
Again, volumes cancel and this leads to a quadratic equation and a value for x = 0.845.
It is not at all likely that you would be asked to solve a quadratic on the test; however, you should understand the chemistry of the preceding example, even if you ignore the math.
C. THE USE OF KP IN CALCULATIONS
1. Dinitrogen tetroxide dissociates into nitrogen dioxide according to the following equation.
When 1 mole of N2O4, at an equilibrium pressure of 3.0 atm, is 50.% dissociated, what is the value of Kp?
Set up an ICE table to find the moles of each substance present at equilibrium.
If we know the gas is 50.% dissociated, then half of it will be converted to NO2 and x = 0.5. Converting to mole fractions, we find mole fraction of 
fraction of 
Then, partial pressure of N2O4 = (0.333)(3.0 atm) = 1.0 atm and partial pressure of NO2 = (0.666)(3.0 atm) = 2.00 atm.
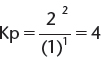
D. THE USE OF KSP IN CALCULATIONS
1. Given that Ksp for Ag2SO4 = 1.41 x 10−5, calculate the molar solubility of Ag2SO4. The dissociation of Ag2SO4 in water is summarized in the following equation.
Because Ag2SO4 is a solid, it is omitted from the Ksp expression to give 
Set up an ICE table to find the moles of each substance present at equilibrium.
ICE Table
III. THE RELATIONSHIP BETWEEN KC AND KP
A. HOMOGENEOUS, GASEOUS EQUILIBRIA
1. When a homogeneous gaseous equilibria is established, it is possible to express the equilibrium constant for the reaction in terms of concentration (Kc) or in terms of pressure (Kp).
i. The relationship is summarized by the equation Kp = Kc(RT)Δn, where Δn = (sum of the stoichiometric numbers of gaseous products − sum of the stoichiometric numbers gaseous reactants), T = temperature in K, and R = 0.0821 atm L K−1 mol−1.
When n = 0—i.e., the sums of the stoichiometric numbers of the gases on each side of the equation are the same—then (RT)Δn = 1, and Kp = Kc.
IV. RELATIONSHIP BETWEEN EQUILIBRIUM CONSTANT WHEN EQUATIONS ARE REARRANGED
A. CONSIDER THE REACTION, 
1. The Kc expression is 
2. If the chemical equation in (1) is reversed, 
the new Kc expression is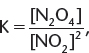 
which is the reciprocal of the K expression in (1).
3. If the chemical equation in (1) is halved, 
the new Kc expression is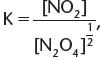 
which is the square root of the K expression in (1).
4. If the chemical equation in (1) is doubled, 
the new Kc expression is 
which is the square of the K expression in (1).
A. PRINCIPLE
1. Format of Q. The format of Q is exactly the same as the format of any given K, but the difference is that K is used when equilibrium has been established, and Q is used at any other (nonequilibrium) point.
B. USING Q TO MAKE PREDICTIONS ABOUT THE PROCEDURE OF AN EQUILIBRIUM REACTION
1. A calculated value of Q can be used to determine which way a reaction will proceed at any given point.
i. if Q > K, then too many products are currently present and the reaction must proceed backwards (toward the reactants) to achieve equilibrium.
ii. If Q < K, then insufficient products are currently present and the reaction must proceed forward (toward the products) to achieve equilibrium.
iii. If Q = K, then equilibrium has been established and no shift is required.
2. See the following examples.
i. This section shows how to use Q to predict the procedure of an equilibrium reaction.
Consider the reaction, 
At a certain temperature, the reaction has a value of K = 24.0. If N2 at a pressure of 0.20 atm, H2 at a pressure of 0.40 atm, and NH3 at a pressure of 2.00 atm are brought together, in which direction will the reaction proceed?
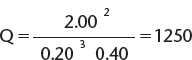
Because Q > K, then too many products are present under these conditions and the reaction must proceed in the reverse direction in order to reach equilibrium.
ii. This section shows how to use Q to predict the formation of precipitates.
If 750. mL of 0.010 M BaCl2 and 150. mL of 0.010 M K2SO4 are mixed, will a precipitate form? (Ksp for barium sulfate = 1.1 × 10−10.)
a) Calculate the moles of the ions that may form the precipitate by multiplying concentration by volume.
Moles of Ba2+ = (0.010) (0.750) = 0.00750 mols
Moles of SO42− = (0.010) (0.150) = 0.00150 mols
b) Calculate the concentrations of these ions by remembering that when the solutions are mixed, the total volume = 750. mL + 150. mL = 900. mL = 0.900 L.
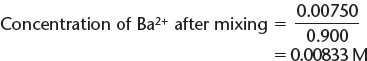
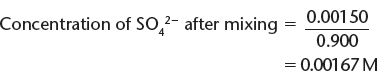
c) Calculate Q, knowing the dissociation of BaSO4 in water is summarized by 
and because BaSO4 is a solid, it is omitted from the Ksp expression to give the following equation.
and
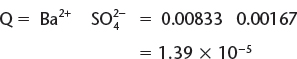
Because Q > K, then too many products are present under these conditions and the reaction must proceed in the reverse direction in order to reach equilibrium. Because the solid is on the left-hand side of the equation when the reaction proceeds in the reverse direction, it will cause the precipitate to form.
A. WHAT IS IT?
1. Attempting to dissolve a sparingly soluble, solid salt in pure water will yield different results than when attempting to dissolve the salt in a solvent that is not pure water.
2. When the solvent already contains some ions that are common to the solid salt, the common ion effect is observed.
B. WHAT IS ITS EFFECT?
1. Here’s an example to illustrate its effect: silver chloride will dissolve more readily in pure water than it will in a solution that already contains either silver or chloride ions.
2. If there are already silver or chloride ions present, the following reaction will be shifted to the reactant side (see Le Chatelier’s principle in Chapter 30), the solid will form more readily, and less will dissolve.
