I. RATES OF REACTION AND COLLISION THEORY—
Different chemical reactions can occur at significantly different rates. The basis for the study of the rate of chemical reactions (kinetics) is collision theory.
A. COLLISION THEORY
1. Successful collisions (ones that lead to a reaction) only occur if three criteria are met.
i. The reactants come into contact (i.e., they collide).
ii. The collision occurs with a certain minimum energy, known as the activation energy (Eact).
iii. The collision has the correct collision geometry. This means that the reactants must collide in a certain physical orientation for a reaction to take place.
2. Any collision that does not fulfill all of these criteria will be unsuccessful—i.e., it will not lead to a reaction.
B. MEASURING RATES
1. A rate is some aspect of a reaction monitored as a function of time. Following are the two options when measuring rates. The choice is motivated by practical considerations for any given reaction and will be different for each unique situation.
i. Monitor the speed at which products are produced.
ii. Monitor the speed at which reactants are used up.
II. FACTORS CONTROLLING RATE OF REACTION
A. CONCENTRATION
1. Increasing the concentration of reactants (by putting more reactants into the same space) increases the collision frequency, leading to a faster rate of reaction.
2. The concentrations of the reactants in a gaseous reaction can be increased by increasing their pressure. Increases in pressure can be achieved by reducing the volume while leaving the amount of gas the same.
B. TEMPERATURE
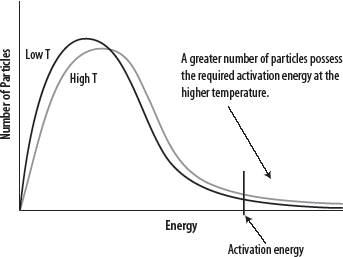
1. An increase in temperature will result in an increased rate of reaction.
2. At higher temperatures, the average energy of the particles is greater and a greater number of particles will have energies > Eact. See the following diagram.
3. In addition, as the temperature increases so will the frequency of collisions, leading to more, successful collisions.
C. SOLID PARTICLE SIZE
1. When a solid reacts, only the particles on the surface of the solid are available for reaction.
2. If the solid is broken up into smaller pieces, its surface area increases and more particles are available for collision; therefore, the reaction rate increases.
1. Catalysts are substances that increase the rate of a reaction while remaining chemically unchanged.
2. Catalysts work by providing an alternative reaction pathway that requires a lower activation energy.
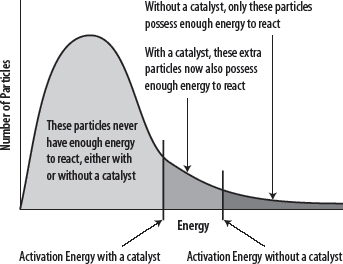
3. With a lower activation energy, a greater number of particles will possess the required, minimum energy (Eact) and a greater number of collisions will be successful. See the following diagrams.
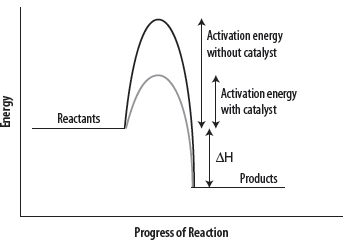
Note carefully that the addition of a catalyst does not change the ΔH value for the reaction (see Chapter 33), and that both the rate of the forward and the backward reaction will be increased when using a catalyst.
III. THE RATE LAW AND ORDERS OF REACTION
A. THE RATE LAW
1. Rate law format. The rate law (or rate equation) for a chemical reaction is used to express rates in a quantitative manner.
It takes the following format: rate = k [A]x [B]y [C]z....... and so on. In this format, k is the rate constant, [ ] represents concentration, and x, y, and z are the orders with respect to the reactants A, B, and C.
2. Orders of reaction. The order with respect to a given reactant is the power to which the concentration of that reactant is raised in the rate law.
i. The overall order of the reaction is the sum of the individual orders.
ii. It is not possible to deduce anything about the order of a reaction from the balanced chemical equation. Orders must be found experimentally.
iii. Orders can be fractional.
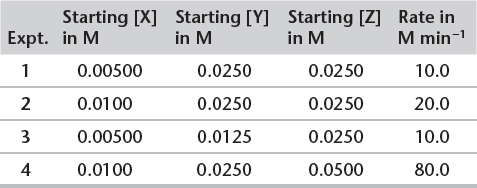
3. Example of using initial rate data to find the rate law. Consider the following data for the reaction between X, Y, and Z. Deduce the orders of reaction with respect to each reactant, the overall order, the rate equation, and a value and units for the rate constant.
Using Initial Rate Data to Determine Orders
i. The first method is inspection.
a) Compare the results from experiment 1 and 2.
Doubling [X] doubles the rate.
Other concentrations are kept constant to ensure a fair test.
Therefore, the rate ∝ [X] and the rate are said to be first order with respect to [X].
b) Compare the results from experiments (3) and (1).
Doubling [Y] does nothing to the rate.
Other concentrations are kept constant to ensure a fair test.
Therefore, the rate does not depend upon [Y] and the rate is said to be zero-order with respect to [Y].
c) Compare the results from experiments (2) and (4).
Doubling [Z] quadruples the rate.
Other concentrations are kept constant to ensure a fair test.
Therefore, the rate ∝[Z]2 and the rate are said to be second order with respect to [Z].
ii. The second method is the mathematical treatment of initial rate data.
a) By comparing experiments 2 and 1, we find the following.
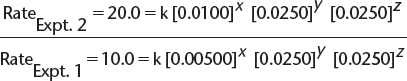
In this equation, x, y, and z are the orders with respect to [X], [Y], and [Z], respectively, and k is the rate constant.
This allows the simplification of the expression to read as follows:
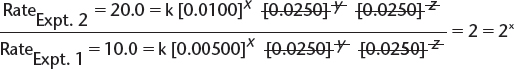
Therefore, x = 1—i.e., the order with respect to
b) By comparing experiments 1 and 3, we find the following.
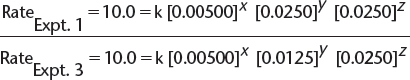
In this equation, x, y, and z are the orders with respect to [X], [Y], and [Z], respectively, and k is the rate constant.
This allows the simplification of the expression to read as follows:
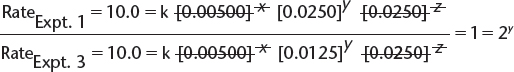
Therefore, y = 0—i.e., the order with respect to [Y] is 0.
c) By comparing experiments 2 and 4, we find the following.
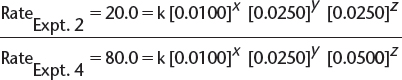
In this equation, x, y, and z are the orders with respect to [X], [Y], and [Z], respectively, and k is the rate constant.
This allows the simplification of the expression to read as follows:
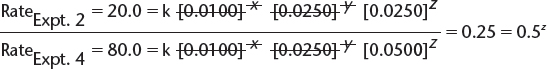
Therefore, z = 2—i.e., the order with respect to
iii. Combining the results from either the first or second method, gives rate ∝ [X]1 [Y]0 [Z]2 and by introducing the rate constant (k) and mathematically “tidying,” the equation becomes rate = k [X]1[Z]2. So the overall order is 1 + 2 = 3.
iv. Using this rate law, plug in data from experiment 1 to find k and its units.
10.0 M min−1 = k (0.00500 M)1 (0.0250 M)2
k = 3.20 × 106 M−2 min−1
The units of rate constants can vary dramatically and should always be considered carefully on a case-by-case, question-by-question basis.