Introduction
Marx’s reproduction schemes are thought to represent one of the first-ever two-sector macroeconomic models, and the first-ever model of balanced economic growth. Marx models the interaction between two great departments of production—each specialized in making capital and consumption goods—showing the conditions required for reproduction and balanced growth. The fundamentals of how a capitalist system functions are captured in this simple but sophisticated framework.
The problem, however, is that Marx’s reproduction schemes are contained in notes that after Marx’s death formed the basis for the second volume of Capital, as assembled and published by Engels. These notes were far from being finished, comprising disparate tables and models, with no summary available from Marx of the purpose of the reproduction schemes. And this has left the field wide open for scholars to make their own interpretations. As commented by Joan Robinson, “The waters are dark and it may be that whoever peers in them sees their own face” (Robinson 1968, 111).
This openness also has some advantages. The reproduction schemes can be seen as providing a framework in which different ideas and theories can be organized. This chapter will show how ideas from the pantheon of political economy—Leontief, Keynes, Kalecki, Luxemburg, Graziani, Minsky—can be integrated into the reproduction schemes. The chapter will start by using Marx’s schemes of simple and reproduction to piece together different strands of political economy—not, that is, in a crude attempt at tight synthesis, but in a spirit of critical appraisal. In the last part, the monetary theories of Graziani and Minsky will be shown to overestimate the amount of borrowing required for reproduction, which has implications for how we might theorize financial fragility.
The Reproduction Schemes
The starting point for understanding the reproduction schemes is to set them in the context of Marx’s method of abstraction. Although economists tend to be drawn towards concrete phenomena, in the Grundrisse Marx proposes a method of empirical enquiry that seeks through abstraction to capture the most important elements.
The economists of the seventeenth century, e.g., always begin with the living whole, with population, nation, state, several states, etc.; but they always conclude by discovering through analysis a small number of determinant, abstract, general relations such as division of labor, money, value, etc.
(Marx 1973, 100)
A method of successive approximations is required that starts as an abstraction of the most important relations, before moving towards concrete reality. Levels of analysis “approach step by step the form in which they appear on the surface of society” (Marx 1981, 117).
The first most abstract stage of Marx’s method of abstraction is to start with simple circulation, where commodities circulate for commodities—as formulated by Marx in the opening chapters of Capital, volume 1. This abstract starting point allows Marx to introduce the division of labor between simple commodity producers. A baker, for example, may exchange bread that is exchanged for shoes produced by the shoemaker. Ratios of exchange are determined by the labor embodied in these commodities, a starting point for Marx’s labor theory of value. A rudimentary role for money as a means of circulation and unit of account is also established in this approach. But, sophisticated as this is, there is no macroeconomic surplus produced by the system as a whole. Individual producers may produce more than they consume, for exchange with other producers, but for the system as a whole there is no surplus.
Enter simple reproduction: stage 2 in Marx’s successive approximations, moving with great speed from the start of volume 1 to its later chapters and through to volume 2 of Capital. Here we abandon simple circulation, with its independent producers working hard to exchange their wares. Production is transformed into two great industrial agglomerations: the first produces capital goods, such as machinery and raw materials; the second produces consumption goods. Any pretence of connection between producers and their outputs is abandoned in this production structure. The producers in these departments are a pool of wage labor, employed by capitalists who control their outputs and harness the use value of these outputs for mass production. Workers in the capital goods department produce outputs that are used in the consumption goods sector. They do not have any control over these outputs. Similarly, workers in the consumption goods department, though producing goods for their own subsistence consumption, also produce goods that are appropriated by capitalists for their own luxurious consumption (see Olsen 2015 for an empirical treatment of unproductive expenditures in the reproduction schemes)
The elements of these two departments are organized according to Marx’s value categories. For each department i = 1,2; means of production (produced by department 1) are used up as constant capital, Ci; consumption goods are used up as variable capital, Vi. The remaining surplus value (Si) is all used up as capitalist consumption. Hence for each department the total value produced (Wi) is:
For the reproduction schemes it is assumed throughout that commodities are exchanged at these values; labor values are assumed equal to money prices. I also assume here that all capital inputs are used up during the period of production (see Carchedi and de Haahn 1995 for an attempt to consider fixed capital). On this basis the simple reproduction scheme takes the form of Table 1 (see Marx 1978, 473).
Table 1 Marx’s Scheme of Simple Reproduction
| Ci | Vi | Si | Wi | |
|---|---|---|---|---|
| Dept. 1 | 4,000 | 1,000 | 1,000 | 6,000 |
| Dept. 2 | 2,000 | 500 | 500 | 3,000 |
| Total | 6,000 | 1,500 | 1,500 | 9,000 |
A key additional assumption is that the rate of surplus value (Si/Vi) is uniform between the two sectors at 100 per cent. For department 1, we can see that at this rate of exploitation 1,000 units of variable capital generate 1,000 units of surplus value. Combined with 4,000 units of constant capital, a total value of 6,000 is produced by department 1.
Under the social division of labor, the two departments exchange capital goods for consumption goods. Department 1 sells 2,000 units of capital goods, which are used up as C2 for department 2. These are exchanged for 2,000 units of consumption goods produced by department 2. For these outputs to be sold, they have to be required by the capitalists in the other sectors. Like two drunken men holding each other up, the capitalists in the two departments, sodden with surplus value, are mutually dependent.
The total surplus value of 1,500 is realized in the expenditure of capitalists in both departments on 1,500 units of surplus consumption goods. This means that the system is static, with none of the surplus directed to expansion: a situation that is somewhat unrealistic but not irrelevant to the study of capitalism. This is an abstract starting point for unravelling the complexities of capitalism. For Marx even under capital accumulation “simple reproduction still remains a part of this” (Marx 1978, 471).
To capture the expansion of capital out of surplus value we have to move to a third more concrete level of abstraction: the scheme of expanded reproduction (Marx 1978, 586–89). As shown in Table 2, an examination of department 1 shows how this differs from the simple reproduction scheme of Table 1. Department 1 still produces 6,000 units of value, but only requires 5,500 to be used up to replace constant capital. There is a surplus of 500 units of constant capital that can be used to expand the stock of capital in the next production period. This represents both a solution and a problem for the capitalist juggernaut. It shows how it can expand, but it also requires a solution as to how the surplus capital goods are demanded. Whereas simple reproduction is directed to a basic goal, the satisfaction of capitalist consumption, under expanded reproduction the goal is one of expansion of capital and the successful intertwining of outputs with consumption.
Table 2 Marx’s Scheme of Simple Reproduction
| Ci | Vi | Si | Wi | |
|---|---|---|---|---|
| Dept. 1 | 4,000 | 1,000 | 1,000 | 6,000 |
| Dept. 2 | 1,500 | 750 | 750 | 3,000 |
| Total | 5,500 | 1,750 | 1,750 | 9,000 |
The Structure of Demand
Showing how outputs and consumption can be intertwined under expanded reproduction requires a focus on the structure of demand. This requires a synthesis between three key strands of modern economics. The first of these is classical input-output analysis, as developed by Wassily Leontief, which has its roots in the Marxian reproduction schemes (see Gilibert 1998).
The expanded scheme of Table 2 can easily be transformed into input-output form, as shown in Table 3. In this format, the rows represent outputs and the columns inputs. Department 1, for example, produces 4,000 units for itself, 1,500 units for consumption by department 2 and 500 units for additional constant capital, dC. Reading down the first column, department 1 uses up 4,000 inputs from itself and 1,000 inputs from department 2, together with a surplus value element of 1,000 units viewed as value added. The surplus produced by department 2 is directed to new variable capital (dV) and capitalist consumption (u).
Table 3 Expanded Reproduction in an Input-Output Table
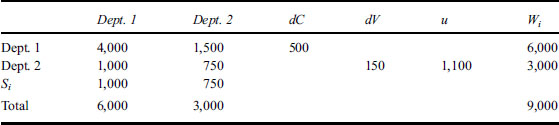
Following the procedure developed in Trigg (2006, 17–19), this input-output scheme can be formalized using matrix algebra. This involves specifying the underlying physical structure of the scheme using the Leontief equation
where X is a vector of gross physical outputs, A is a square matrix of interindustry coefficients, h is a column vector of worker consumption coefficients, l is a row vector of labor coefficients and F is a column vector of final demands. By specifying a net output vector Q = (I – A)X in which I is the identity matrix
where v = l(I – A)-1 is a row vector of labor values, i.e., the vertically integrated labor coefficients defined by Pasinetti (1981). Pre-multiplying (2) by v, we have
which rearranges to
This equation relates a second strand of modern economics to the Marxian reproduction schemes: the multiplier analysis of Keynesian economics. From this demand-side perspective, final demand (vF = dC + dV + u) consists of additions to constant and variable capital together with capitalist consumption—as represented in Table 3 by dC of 500, dV of 150 and u of 1,100, a total final demand of 1,750. This final demand generates a total value (vQ) of output, as represented by the 9,000 units of value produced in Table 3. The term 1/1 – vh is a scalar Keynesian multiplier that in Marx’s example takes a value of . Locating the Keynesian multiplier in Marx’s reproduction schemes can be traced back to the work of Lianos (1979).
Following an insight originally made by Olgin (1992), a term representing surplus value can also be identified in the Keynesian multiplier. Marx’s category, the value of labor power, is represented in the denominator of the multiplier by the term vh, the labor embodied (v) in worker consumption per unit of labor (h). Hence the denominator of the multiplier represents the share of surplus value produced per unit of labor, e = 1 – vh.
Under Marx’s assumption throughout the first two volumes of Capital that money prices (p) are equal to values (v), we can specify net money output as y = vQ = pQ and final demand as f = vF = pF. The Keynesian multiplier therefore takes the form
The final stage in our synthesis is to consider the insights of Michal Kalecki, who engaged directly with the reproduction schemes. Kalecki identified the key role of capitalist spending in determining the level of profits: according to the Kalecki principle, capitalists earn what they spend. If we denote capital accumulation by the term I = dC + dV, then by rearranging (5), total surplus value (S = ey) is determined by the relationship
Total surplus value is determined by the expenditure of capitalists either on their own consumption or on investment. And, under the assumption that prices are equal to values, this total surplus value is also equal to total profits (P):
Furthermore, Kalecki breaks down capitalist consumption into a constant component (B0) and a part dependent on profits according to the proportion λ, such that
Substituting (8) into (7)
and hence
Here the Kalecki multiplier (1/1 – λ) captures the determination of profits by investment. Since profits are identical to final demand (f), equation (10) can be substituted into (5) to give
This multiplier relationship demonstrates the synthetic potential of the reproduction schemes. It combines Keynesian and Kalecki multipliers with a structure based on Marx’s category of surplus value, all derived from a representation of the reproduction schema using Leontief’s input-output analysis. This provides a genuinely post-Keynesian contribution, in the sense that it moves the project beyond the limited one-good world inhabited by the Samuelson textbook Keynesians of the neoclassical synthesis. By drawing on Marx, Leontief and Kalecki, our adaptation of the reproduction schemes pulls Keynes’s legacy towards a classical tradition, based on industrial interdependence and structure. It also helps develop Kalecki’s legacy in response to the critique of Steedman (1992) that Kalecki failed to take into account input-output relations. A limitation of this interpretation, however, as shown by Brennan (2014), is that even Kalecki himself struggled in his empirical analysis to maintain Marxian class-based categories when transferring the reproduction schemes to a national accounting context.
This location of the multiplier in the reproduction schemes also relates Marx’s system to the model of economic growth developed by Domar (Trigg 2006, 53–7). It does not prove that balanced growth must take place, only that certain conditions are required for this growth, however unlikely they are to be established. The key demand requirement is that investment must grow at the required rate, and its impact must be provided by the correct multiplier mechanism. Furthermore, this opens up a problem of how the money can be found for growth to be financed. A hoard of gold money, which would be sufficient under simple reproduction to finance capital outlays, will soon become exhausted under expanded reproduction.
This opens up two questions raised by Rosa Luxemburg: “Where does the demand come from?” and “Where does the money come from?” Her Accumulation of Capital, published in 1913, is considered to be the first major work on political economy to explore the reproduction schemes. In it she seems to adopt something close to the Kalecki principle: “If the capitalists themselves have set in motion all the money which circulates in society, they must also advance the money needed for the realization of their own surplus value” (Luxemburg 1951, 71). As shown by Bellofiore (2014), Rosa Luxemburg was not an underconsumptionist. The problem of demand relates to the demand of capitalists realizing their surplus value, not the consumption of the masses.
But Luxemburg also views money as something of a distraction. “It is not the source of money that constitutes the problem of accumulation, but the source of the demand for the additional goods produced by the capitalized surplus value” (Luxemburg 1951, 147). Following Kotz (1991, 73), however, in a contribution to Rethinking Marxism, it can be argued that questions of money and demand are related issues “since the monetary problem seems to be an aspect of the demand problem.” In the analysis that follows we shall see that the Kalecki principle can also be invoked to look at money related issues.
The Circuit of Money
The Kalecki principle allows a sharp focus on the circulation of money in the reproduction schemes. As shown by Sardoni (1989), in the second volume of Capital Marx is explicit about how capitalists cast money into circulation: “The capitalist class itself casts into circulation the money that serves towards the realization of the surplus value contained in its commodities” (Marx 1978, 409). In expanded reproduction, the money cast into circulation consists of both unproductive capitalist consumption and expenditure on investment. For Sardoni (1989, 214): “Capitalists’ profits therefore now depend on their consumption and investment expenditure, just as in Kalecki’s analysis.”
The field of Marxian economics, as taught in universities, has been so influenced by orthodox economic techniques that it has tended to ignore Marx’s writings on money. It was only in the 1970s that something of a revival of Marx-based monetary theory took place, as exemplified by de Brunhoff’s Marx on Money (1973). Subsequently, the theory of monetary circuits, pioneered by Graziani (1989), has been used to model Marx in a modern setting, moving away from metallic money to a focus on the issuing of loans by banks. This has been regarded as a significant contribution to Marxian economics (Bellofiore and Realfonzo 1997), with its incorporation of Marx’s distinction in the reproduction schemes between investment and consumption goods.
For Nell (1998), however, the structure of reproduction is regarded as incomplete in Graziani’s circuit. The failure to identify a multiplier relationship overestimates the amount of money that is required for reproduction to take place. A multiplier such as that defined in (11), derived from a fully interconnected reproduction scheme, offers a precise specification of the monetary requirements of reproduction. Under the Kalecki principle, the outlay on capitalist consumption and investment (B0 + I) creates a greater volume of income (y), depending on the size of the multiplier. The initial outlay can be viewed as money that is borrowed from banks by the capitalists, which is then injected into the departments of production. The multiplier then becomes the velocity of circulation, the amount of time in which each unit of money injected turns over in the economy. In Marx’s example of expanded reproduction (Table 3), the size of the velocity of circulation (multiplier) is ; hence the initial outlay of 1,750 circulates times around the economy to create a total value of 9,000.
Since the 2008 global financial crisis, issues relating to money and finance have become prominent, in particular the prophetic insights of Hyman Minsky. It is not so well known that Minsky based his financial instability hypothesis on the Kalecki principle (Minsky 1978). With aggregate profits driven by capitalist expenditure, financed by loans, any faltering of this expenditure can have disastrous consequences, leading to a constraint on profits, making capitalists unable to pay off their debts.
There is, however, a problem raised by Toporowski (2008) concerning the ability of capitalists to pay off loans out of profits. He argues that Minsky fails to take into account the difference between debts of individual capitalists and those of the capitalist class as a whole. Minsky overestimates the debts incurred by capitalists—towards those producing capital goods there is an immediate flow of money that allows them to incur no further financial or business liabilities (Toporowski 2008, 734). These capitalists may gain assets while others carrying out the capital investment may incur liabilities—with assets and liabilities cancelling out at the aggregate level.
This critique is extended by Trigg (2014), using Marx’s empirical example (Table 3) of an expanded reproduction scheme. As shown in Table 4, more detail can be specified about the destination of new capital and capitalist consumption. Part of the new constant capital is earmarked for use in department 1 in the next period (dC1 = 400); the other part (dC2 = 100) is earmarked for use in department 2. Similarly, new variable capital is earmarked for use in department 1, as specified by dV1 = 100, with dV2 = 50 sent to department 2. Capitalist consumption is split into two parts, u1 and u2, expenditure by capitalists in each department.
Table 4 Expanded Reproduction and the Destination of Surplus Outputs

Now assuming that there is no borrowing within departments, we can examine the reproduction scheme to see if liabilities arise between departments. To do this the outlays and receipts of each department are put in a balance sheet (Table 5). The outcome is that no liabilities are incurred by either department; all outlays are balanced by receipts. Department 2, for example, has outlays of 3,000 balanced by receipts of 3,000. The Kalecki principle, that capitalists earn what they spend, applies in this case to both departments, and not just to the economy as a whole. This further extends the critique of Minsky, by casting doubt on how debts and financial fragility can originate in the structure of production. This is of course a specific two-sector numerical example, but it provides just a hint that Marx’s reproduction schemes provide a starting point for exploring the conditions under which Minsky’s hypothesis might hold.
Table 5 Outlays and Receipts under Expanded Reproduction
| Department 1 Outlays | Receipts | Department 2 Outlays | Receipts |
|---|---|---|---|
| 4,000 (C1) | 4,000 (C1) | 1,500 (C2) | 1,000 (V1) |
| 1,000 (V1) | 1,500 (C2) | 750 (V2) | 750 (V2) |
| 400 (dC1) | 400 (dC1) | 100 (dC2) | 100 (dV1) |
| 100 (dV1) | 100 (dC2) | 50 (dV2) | 50 (dV2) |
| 500 (u1) | 600 (u2) | 500 (u1) | |
| 600 (u2) | |||
| 6,000 | 6,000 | 3,000 | 3,000 |
Conclusions
Marxian reproduction schemes have been shown to provide an organizing framework for different components of political economy: from the multiplier to the Kalecki principle, money circuits and Minsky’s financial instability hypothesis. The reproduction schemes formalize the precise conditions in which money circuits and finance can function in a sustainable capitalist system. And they offer a basis for critical engagement with theories that are at times not defined with the degree of rigor offered by the reproduction schemes.
These analytical tools are available to Marxists and post-Keynesians at a time when political economy is starting to recover some of its roots in the early part of the twentieth century. The bright flame of Marxism was almost cut off at birth by the age of extremes under Hitler and Stalin. And many of those socialists that survived, such as Kalecki, were subject to much repression. But as shown in the recent first translation into English of the book Rosa Luxemburg: Theory of Accumulation and Imperialism (2014) authored by Kalecki’s Polish colleague, Tadeusz Kowalik, the reproduction schemes are central to the history of Marxism. Kowalik “found the roots of twentieth-century political economy in the discussions of Marx’s schemes of capitalist reproduction . . . .” (Toporowski 2014, xi). Moreover, Kowalik’s important book opens up the importance of a socialist critique of political economy. For him, followers of Kalecki should not scramble to prove that he was a precursor of Keynes; instead, they should highlight the advantages of Kalecki’s grounding in the reproduction schemes. Furthermore, following Luxemburg and the subsequent Marxist tradition, the reproduction schemes can be interpreted as a tool for socialist planning, beyond the confines of our analysis of capitalist reproduction.
References
Bellofiore, R. 2014. “Luxemburg and Kalecki: The Actuality of Tadeusz Kowalik’s Reading of Accumulation of Capital.” In The Legacy of Rosa Luxemburg, Oskar Lange and Michal Kalecki, vol. 1, R. Bellofiore, E. Karwowski, and J. Toporowski, eds., 78–103. Basingstoke: Palgrave Macmillan.
Bellofiore, R. and R. Realfonzo. 1997. “Finance and the Labor Theory of Value.” International Journal of Political Economy 27(2): 97–118.
Brennan, D. 2014. “‘Too Bright for Comfort’: A Kaleckian View of Profit Realization in the USA, 1964–2009.” Cambridge Journal of Economics 38: 239–255.
Carchedi, G. and W. de Haan. 1995. “On the Replacement of Fixed Capital in Marx’s Simple Reproduction.” History of Political Economy 27(3): 599–604.
de Brunhoff, S. 1973. Marx on Money. New York: Urizen Books.
Gilibert, B. 1998. “Wassily Leontief.” In The Elgar Companion to Classical Economics, H.D. Kurz and N. Salvadori, eds., 40–45. Cheltenham: Edward Elgar.
Graziani, A. 1989. “The Theory of the Monetary Circuit.” Thames Papers in Political Economy. London: Thames Polytechnic.
Kotz, D. M. 1991. “Accumulation, Money and Credit in the Circuit of Capital.” Rethinking Marxism 4: 119–133.
Kowalik, T. 2014. Rosa Luxemburg: Theory of Accumulation and Imperialism. Trans. and edited by J. Toporowski and H. Szymborska. Basingstoke: Palgrave Macmillan.
Lianos, T. P. 1979. “Domar’s Growth Model and Marx’s Reproduction Scheme.” Journal of Macroeconomics 1(4): 405–412.
Luxemburg, R. 1951 [1913]. The Accumulation of Capital. London: Routledge & Kegan Paul.
Marx, K. 1973. Grundrisse. Harmondsworth: Penguin.
Marx, K. 1976. Capital, Volume 1. Harmondsworth: Penguin.
Marx, K. 1978. Capital, Volume 2. Harmondsworth: Penguin.
Marx, K. 1981. Capital, Volume 3. Harmondsworth: Penguin.
Minsky, H. 1978. “The Financial Instability Hypothesis: A Restatement.” Thames Papers in Political Economy. London: Thames Polytechnic.
Nell, E. J. 1998. The General Theory of Transformational Growth. Cambridge: Cambridge University Press.
Olgin, D. S. 1992. “On an Accidental Proof to the ‘Fundamental Marxian Theorem.’” History of Political Economy 24(2): 471–475.
Olsen, E. 2015. “Unproductive and Endogenous Technological Change in a Marxian Model of Economic Reproduction and Growth.” Review of Radical Political Economics 47(1): 34–55.
Pasinetti, L. L. 1981. Structural Change and Economic Growth. Cambridge: Cambridge University Press.
Robinson, J. 1968. “Marx and Keynes.” In Marx and Modern Economics, D. Horowitz, ed., 103–116. London: MacGibbon and Kee.
Sardoni, C. 1989. “Some Aspects of Kalecki’s Theory of Profits: Its Relationship to Marx’s Schemes of Reproduction.” In Kalecki’s Relevance Today, M. Sebastiani, ed., 206–219. Basingstoke: Macmillan.
Steedman, I. 1992. “Questions for Kaleckians.” Review of Political Economy 4: 125–151.
Toporowski, J. 2008. “Minsky’s Induced Investment and Business Cycles.” Cambridge Journal of Economics 32: 725–737.
Toporowski, J. 2014. “Preface.” In T. Kowalik, Rosa Luxemburg: Theory of Accumulation and Imperialism, J. Toporowski and H. Szymborska, trans. and eds., vii–xiii. Basingstoke: Palgrave Macmillan.
Trigg, A. B. 2006. Marxian Reproduction Schema: Money and Aggregate Demand in a Capitalist Economy. London: Routledge.
Trigg, A. 2014. “Financial Fragility and the Kalecki Principle under Expanded Reproduction”. In The Legacy of Rosa Luxemburg, Oskar Lange and Michal Kalecki, Volume 1, R. Bellofiore, E. Karwoski, and J. Toporowski, eds., 205–214. Basingstoke: Palgrave Macmillan.