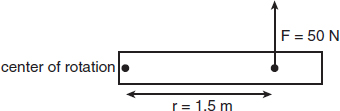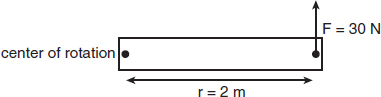Common Types of Forces

Gravity and Weight

As seen previously, weight is different from mass. Mass is an intrinsic property of matter, whereas weight is the force exerted on an object due to gravity. The downward pull that the Earth exerts on bodies outside of itself is a specific case of gravity at work. Weight can be easily measured using a spring scale like that found in many people’s bathrooms, and the direction of weight for all objects on Earth is the same: straight down toward the center of the Earth.

The general formula for Newton’s Law of Universal Gravitation was given in chapter 9: General Science. It can be used to explain why the same person will weigh less on planets of different sizes and masses (for example, when astronauts walked on the moon, their weight was only of what it was while on Earth). However, unless you are told otherwise, it is safe to assume that for the purposes of everyday mechanical work the location is here on Earth.

For bodies free-falling near the Earth’s surface, the acceleration due to gravity (g) is calculated to be about 9.8 m/s², ignoring air resistance. (Note that “near the Earth’s surface” really means anywhere on Earth, including on top of Mount Everest or parachuting from a plane thousands of meters in the air. The value of g doesn’t change significantly at the top of a stair ladder.)

Applying Newton’s second law, F = ma, for the specific case of weight, the more general symbol for force, F, is replaced with the more specific force of weight, W, and acceleration, a, is replaced with the constant value of acceleration due to gravity, g. This results in the modified version of the formula

W = mg

where W is weight in newtons (N), m is mass in kilograms (kg), and g is acceleration due to gravity (either m/s² or N/kg). To determine an object’s weight in N, therefore, simply multiply its mass in kg by 9.8.

Study the example that follows, which does not have answer choices, to help you practice predicting an answer to this type of question.

Question	Analysis
How many newtons of force due to gravity will act on an 80 kg man while in a plane flying over Denver, Colorado?	The question asks for the amount of force due to gravity.
	The man is not an astronaut (or if he is an astronaut, he’s not currently in outer space or on the moon), so his weight will be pretty much the same as any other 80 kg man on Earth. This weight will be basically unchanged whether he’s at sea level, in the United States’ highest-altitude large city, or in a plane flying above that same city.
	The phrase “newtons of force due to gravity” is just another way of saying weight. Weight W = (80 kg)(9.8 m/s²) = 784 N. The answer is 784 N.

Friction

There are several responsive forces which act to resist movement. When you move an object across a surface, the rubbing of the two surfaces results in kinetic friction, which always acts in a direction opposite to the motion of the object. Because it always opposes motion, kinetic friction will eventually slow any moving object to a stop. Ice is polished to minimize kinetic friction, but unless it is constantly being pushed, a hockey puck will eventually slide to a stop in even the most slippery of rinks.

When an object is not moving, a force that attempts to slide it across a surface will encounter a different type of friction. Attempting to push a stationary box across a concrete floor will require a person to overcome the static friction that opposes any attempted movement.

Both kinds of friction are based on two factors: the coefficient of friction, µ (the Greek letter mu), which represents how much two materials resist sliding against each other; and the normal force, F_N, which represents the equal and opposite force a surface exerts when an object presses against it. The formulas for kinetic and static friction, respectively, are

F_f = µ_kF_N

F_f = µ_sF_N

where F_f stands for the force of friction and µ_k and µ_s stand for the coefficients of kinetic and static friction. The coefficients of friction are constant for any two surfaces in contact. The coefficients of friction are dimensionless quantities, with no units of their own. Therefore, whatever force unit is used to measure F_N (N or lbs, for example), will also be used to measure F_f.

Slippery surfaces like ice or wet asphalt have low coefficients of both kinetic and static friction with most objects. Friction is directly proportional to these coefficients. That’s why it’s important for drivers of cars to understand that weather conditions can make braking to a stop (which relies on the friction of the wheels with the road surface) less effective.

Free Body Diagram of Forces Acting on a Sliding Object

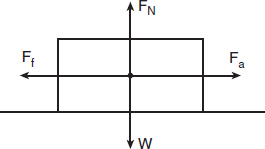
For any given surface, the coefficient of static friction is higher than the coefficient of kinetic friction. This means that more force is required to initially get a stationary object moving than to keep it moving afterwards. Once the large static friction force has been overcome and the object is in motion, the smaller coefficient of kinetic friction takes over, and the resistant force of friction decreases. This is why moving heavy objects usually involves one extra big push at the beginning, but then a somewhat smaller force for the rest of the trip.

One more important difference between static and kinetic friction is that static friction only arises in response to an attempt to move an object along a surface. Like the normal force that holds up objects with weight, it responds to an applied force by matching and counteracting it. The formula is actually used to determine the maximum of a variable value for static friction, beyond which it breaks and an object will begin to move.

Both kinds of friction forces are directly proportional to the normal force of the surface. As an experiment, try laying your palm flat and sliding your hand along a nearby surface like a table or desk. Feel the resistance of the movement due to kinetic friction. Now, with your palm still flat, try pushing harder against the same surface, while still trying to slide your hand along it.

Is it more difficult? If you push very hard against the surface, you may find you are not even able to overcome the force of static friction and slide your hand without decreasing the normal force first. When a person leans against a wall, she allows a portion of the weight to push against the wall, which pushes back with an equal and opposite normal force. This normal force contributes to a corresponding static friction force that prevents the person from sliding down the wall to the floor.

Most frequently, the normal force arises on flat horizontal surfaces as a response to the weight of an object pressing it down. As a result, the normal force is equal to an object’s weight much of the time, so that the forces of friction are equal to the coefficients of friction multiplied by the object’s weight. This assumption is false only on non-horizontal surfaces (for example, slopes), or when additional forces are acting to push an object down or hold it up.

Question	Analysis
A 15 kg object rests on a concrete floor, and the coefficients of static and kinetic friction are 0.3 and 0.2, respectively. If a continuous force of 35 N is applied to the object in a direction parallel with the floor, what will happen?	Step 1: The question asks for a prediction as to whether an object will move given an applied force and taking into account friction.
	Step 2: Comparing the applied force to the frictional forces should make it obvious whether the object will move or not. The weight of the object will be equal to the normal force holding the object up. Then the force of friction can be determined. F_N = W = (15 kg)(9.8 m/s²) = 147 N F_f = µ_kF_N = (147 N)(0.2) = 29.4 N F_f = µ_sF_N = (147 N)(0.3) = 44.1 N
	Step 3: The applied force of 35 N is less than the maximum value for the force of static friction. Since the object is already at rest, and the applied force is not enough to “break” the force of static friction, the net force will be zero and the object will stay put. The lesser force of kinetic friction is irrelevant since the object will not slide to begin with.
(A) The object will be bounced back due to friction. (B) The object will remain at rest as the applied force is unable to overcome the static friction. (C) The object will initially move but then stop as kinetic friction overcomes the applied force. (D) The object will accelerate continuously.	Step 4: Answer choice (B) is correct. (The key is that an object at rest must experience a large enough applied force to overcome static friction before kinetic friction becomes relevant.)

Now you try one:

Four objects of the same material and dimensions, but different weights, are placed on four different tabletops. When a force is applied that causes the boxes to move, which one generates the greatest amount of kinetic friction?

Explanation

Answer choice (C) is correct. According to the formula for kinetic friction, the box with the greater weight will have the greater normal force and thus greater frictional force compared to one of less weight. The oily surface will have a lower coefficient of friction than the dry surface. Therefore, the heaviest box on the driest surface will experience the most friction.

Another responsive force comes from air resistance, sometimes known as air friction but more commonly known as drag. Drag opposes movement not across a solid surface but through a fluid, like water or air. The two main variables that affect drag are cross-sectional area and speed. High-performance cars, boats, and aircraft are designed to be sleek and pointy, to minimize the area of the side that is plowing through the air or water. Parachutes work by intentionally increasing area for a skydiver, so that drag is increased and the person can be slowed down to a safe speed before hitting the ground.

Tension

When cables are used to pull an object, an applied force exerted on one end results in the attached object receiving the same pulling force from the other end. When force is transmitted through rope or other pullable materials, the internal stretch force of the material is called tension. Tension can be measured in N or lbs, or any other force unit measurement.

As a simplification, tension is often assumed to be equal in all parts of the material. This assumes, however, that the mass of the material under tension is either zero or negligible. In reality, tension is greatest where the force is being applied. To understand why this is, imagine a 100-pound weight suspended from a 10-pound chain. The bottommost link in the chain has an important job: it’s holding up the 100-pound weight. The tension at this point in the chain, therefore, is 100 pounds.

But the chain link just above it also has an important job. It’s holding up the link that’s holding up the 100-pound weight, which means it must have a tension equal to 100 pounds, plus the weight of one chain link. If you continue to the top of the chain, where the applied force is holding it in place, the topmost link is responsible for not only the 100-pound weight, but for another 10 pounds from the chain itself. At this section of the chain, the tension is 110 pounds.

The takeaway from this is that, barring imperfections or weaknesses in the material under tension, the most likely place for a rope or cable to snap is not near the object it is holding or pulling, but near the place where the rope or cable is itself being pulled. When a winch (a mechanical device used to wind a rope) draws in a heavy-duty cable and the tension exceeds the material’s tensile strength, it will likely snap very close to the winch, rather than close to the load.

Question	Analysis
A concrete block is suspended by two steel cables, spaced equidistant from the edges. What best describes the value of T1?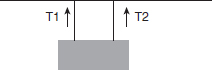	Step 1: The question asks for the tension of one of two cables from which a weight is suspended.
	Step 2: The system is in static equilibrium. Since the block is remaining in one place without accelerating, the net force is zero and the downward force due to gravity must be exactly balanced by the tension in the two cables. Each cable must contribute half of the upward force (tension). T1 + T2 = 50 N T1 = T2 = 25 N
	Step 3: The tension in the first cable must be equal to half of the downward force on the block.
(A) 5 N (B) 25 N (C) 50 N (D) 100 N	Step 4: Choice (B) is correct.

Now try one on your own.

Using a cable attached at one end, a force is applied to a slab of metal. At which point along the cable is the cable most likely to snap?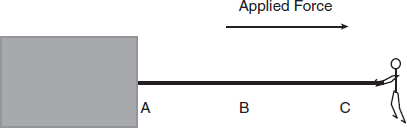
1. A
2. B
3. C
4. It is equally likely to break at any point along the rope.

Explanation

Choice (C) is correct. The force applied to the cable will result in acceleration of the metal slab. However, the metal slab by itself requires less force than the slab and cable combination. Thus, more force is applied at the end of the cable where the force is applied compared to what is actually acting on the metal slab itself. This corresponds to a greater tension near point C compared to points B and A. If the cable were to snap, it would likely happen where there is higher tension.

Hydraulic Pressure

Fluid power can also be used to gain mechanical advantage. Hydraulics is the transmission of force through the use of liquids. While the classic simple machines are effective and reliable for many purposes, hydraulics is a little more versatile at redirecting and multiplying forces in complex systems. In order to understand how hydraulics works, it is first necessary to have a grasp of the concept of pressure. If force is applied evenly over a certain area, then pressure is applied to that area. Pressure is calculated using the formula

P =

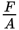
where F is force in pounds (lb), A is area in square inches (in²), and P is pressure in pounds per square inch (psi). While other applications of pressure in physics and chemistry use standard units of newtons and square meters, the above units are more common in hydraulics. Keep in mind that F is divided by A. A force of 100 pounds applied over an area of 10 square inches results in a pressure of 10 psi being developed.

Using the formula for pressure, you can derive F = PA, which is useful for calculating the amount of force that is developed when pressure P is applied to area A.

Even when extremely high pressure is applied to a liquid, the volume of the liquid will decrease only a very small amount. This property of near-incompressibility makes liquids very effective at transmitting force, as no force (or very little) is used up in compressing the liquids into a smaller space. Liquids also tend to take the shape of their container, filling up any available space (given enough of the liquid). According to Pascal’s law (discovered by French mathematician and physicist Blaise Pascal in the seventeenth century), the pressure in any part of an enclosed fluid is the same and points in all directions.

Putting it all together, applying force to one end of a hydraulic system will increase the pressure everywhere, which, when applied to an area of the same size, produces the same force at a different location and in a different direction. Changing the area over which force acts can also change the magnitude of the force. A smaller force applied over a greater distance produces a greater force over a smaller distance in a hydraulic system.

Hydraulic Lift

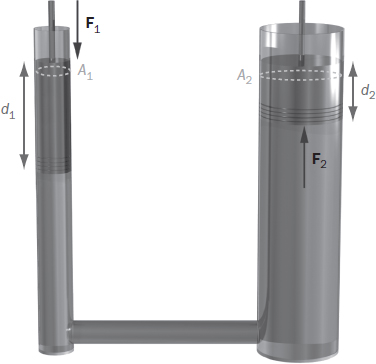
Try your hand at a problem about pressure.

Pressure is equal to force acting over
1. a distance
2. a period of time
3. a volume
4. an area

Explanation

Choice (D) is correct. Pressure is equal to force acting over an area.

Torque

Torque measures how much a force is able to cause an object to rotate. Torque, like pressure, cannot be properly called a force itself. The formula for torque is

τ = rF

where torque (τ, the Greek letter tau) is the product of an applied force (F) perpendicular to the lever arm of the rotated object, and the length of the lever arm (r), measured from the pivot point (center of rotation) or fulcrum, to the point where the force is being is applied. Force is normally measured in either N or lb and the length of the lever arm in m or ft. Torque may therefore be measured in standard N-m (newton-meters) or the ft-lb (foot-pound) unit.

However, remember this length measurement is perpendicular to the force applied in rotating the object, not parallel, so torque is not equivalent to work, whose N-m units (more often expressed as joules, J) represent a force applied through a distance. (Nor is torque equivalent to energy, also measured in J.)

Torque Applied via a Wrench

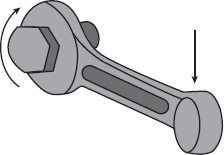
Torque is directly proportional to the force applied to rotation, and is also proportional to the distance from the center of rotation where the force acts. Applying a force at the farthest end of a lever arm is advisable in getting the greatest possible torque. When a mechanic applies his maximum force but is unable to turn a difficult bolt, a longer wrench may do the trick. This doesn’t increase the force he is able to apply, but the use of a longer lever arm for the same force does result in increased torque and therefore, hopefully, better success in loosening the bolt. Unlike work, an object does not have to be successfully rotated before a torque is said to have been applied.

Question	Analysis
How much force is needed to apply 50 ft-lb of torque to a bolt using a 2 ft long wrench?	Step 1: The question asks for the amount of force applied to a lever arm for a certain torque.
	Step 2: The torque formula relates length, force, and torque. To solve this question, isolate force and plug in values. Based on the units in this question, force is measured in pounds (since pounds multiplied by feet is the only way to get foot-pound units for torque). τ = rF F = τ/r = (50 ft-lb)/(2 ft) = 25 lbs
	Step 3: The force must be 25 lbs, not 25 N.
(A) 100 lbs (B) 50 N (C) 25 lbs (D) 25 N	Step 4: There is only one perfect match: choice (C).

Now try a question about torque on your own.

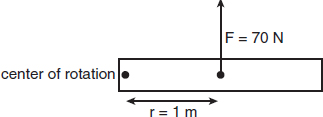
Which of the following applied forces will result in the greatest torque?

Explanation

Choice (A) is correct. The product of the force and the length of the lever arm, where the two quantities are perpendicular to each other, produces torque. For (A), τ = (1.5 m)(50 N)=75 N-m, compared to 60 N-m in (B) and 70 N-m in (C). (D) provides no torque at all. Although there is a large applied force, it is pushing along the lever arm toward the fulcrum, and cannot result in any rotation.