Part 2: Arithmetic Reasoning (AR): Answers and Explanations

D

The ratios of apples to pears and pears to oranges for a given cost are provided. What’s needed to solve this problem, however, is the ratio of apples to oranges. To merge these into one ratio relating all three fruits, you need to express both ratios using the same number of pears. In one ratio it’s 4, and in the other it’s 3. Since the least common multiple of 3 and 4 is 12, you can multiply both individual ratios so that the number of pears comes to equal 12:

apples:pears = 3:4 = 9:12 (multiply both sides of the ratio by 3)

pears:oranges = 3:2 = 12:8 (multiply both sides of the ratio by 4)

Now you can combine the ratios:

apples : pears : oranges

9:12:8

Now you can also state the ratio of apples to oranges:

apples:oranges = 9:8

Given a value for the number of oranges as 72, you can now set up a proportion:

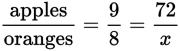
Cross-multiply and solve for x:

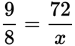= . Cross-multiply, getting 8x = (9)(72). Divide both sides by 8 to get 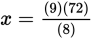. To make the arithmetic easier, divide 72 by 8 first, which equals 9, then multiply this answer by 9, getting 9 × 9 = 81.

C

If 48 of 60 seats are occupied, then 12 of 60 seats are unoccupied (since 60 − 48 = 12). What percent of the seats are unoccupied?

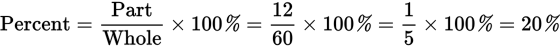, choice (C).

B

Break this question down into pieces. Before midnight, Effin gets paid $1,000 an hour. If she starts singing at 8:30 p.m., then she sings for hours before midnight. Her earnings for that time are 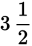× $1,000 = $3,500. After midnight, her rate increases 50%, so her hourly rate after becomes $1,000 + $1,000(50%) = $1,000 + $500 = $1,500. She works one hour after midnight, earning $1,500. Add the amount she earns before midnight and the amount she earns after midnight, so her total pay is $3,500 + $1,500 = $5,000.

B

The probability of an event occurring is a fraction: the number of possible outcomes in which the event can occur divided by the total number of possible outcomes. Fran is going to pick one shirt and the question asks for the probability that it will not be orange. In other words, you need to find the probability of picking a black or blue shirt. There are 4 black shirts and 5 blue shirts, so altogether there are 9 possible successful outcomes. The total number of shirts to choose from, including the orange shirts, is 12, so there are 12 possible outcomes. The probability of Fran picking a non-orange shirt is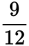

. Since

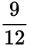is not available in the answer choices, reduce the fraction by dividing the top and bottom by 3 to get

.

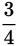B

Newark is two hours later than Denver, so if the time in Denver when Harry arrives is 2:30 p.m., then the time in Newark when he arrives is 4:30 p.m. The flight takes 5 hours, so the time he began in Newark is 5 hours earlier than 4:30 p.m., or 11:30 a.m.

B

How many times does 24 go into 198? 198 ÷ 24 = 8 with a remainder of 6, so Doris will have 6 pieces of chocolate left over.

C

If 75% of x is 150, then 0.75(x) = 150 or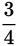

(x) = 150. Multiply both sides by

and x = 200. You could also Backsolve. Only choice (C), 200, works. If x = 200, then 0.75(x) = 150 since 0.75(200) = 150.

A

The formula for finding the average is:

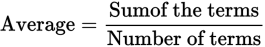
Don’t just average the old average and the last test score—that would give the last score as much weight as all the other scores combined. The best way to deal with changing averages is to use the sums. Use the old average to figure out the total of the first 6 scores:

Sum of first 6 scores = (83)(6) = 498

Then add the 7th score and divide:

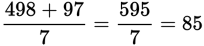
B

If the charge for one pound is $25.00, then the charge for 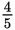of a pound would be 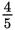× 25.00 = $20.00 plus 8% sales tax. 8% of $20.00 = 0.08($20.00) = $1.60. $20.00 + $1.60 = $21.60.

D

To answer this question, determine how many times 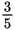goes into 60. It will be more than 60, so right away you can eliminate (A). 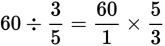. This is easier to multiply if you cancel first. 3 goes into 60 twenty times, so replace the 3 with a 1, and replace the 60 with a 20 to get .

B

Set up equations based on the information given in the problem. The question asks for the amount of money Robert has.

Ed has 100 more dollars than Robert:

E = R + 100.

Ed then spends 20 dollars and has five times as much money as Robert:

E – 20 = 5R.

Solve a question like this using algebra if it’s a strong area for you. Substitute R + 100 for E and solve:

R + 100 – 20 = 5R

R + 80 = 5R

80 = 4R

R = $20

You could also Backsolve, starting with choice (B) or (C) for Robert’s money. If you started with (C) 24, you would plug 24 into both equations and see if you got the same value for E.

In the first equation:

E = R + 100

E = 24 + 100

E = 124

In the second equation:

E – 20 = 5R

E – 20 = 5(24)

E – 20 = 120

E = 140

The numbers don’t match, so eliminate (C) and try (B) 20.

In the first equation:

E = R + 100

E = 20 + 100

E = 120

In the second equation:

E – 20 = 5R

E – 20 = 5(20)

E – 20 = 120

E = 120

The value for E is the same in both equations, which tells you that 20 is the correct answer.

D

This question is actually a remainder question in disguise. If 587 people are to be divided among buses that each seat 48 people, divide 587 by 48 to see how many buses would be filled completely. The remainder is the number of people in the unfilled bus. 587 ÷ 48 = 12 with a remainder of 11.

C

Riley brought 100 cookies, and 25 are left over. That means that Riley and her classmates ate 75 cookies.

C

This is a proportion question:

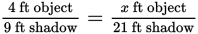
Cross-multiply to solve:

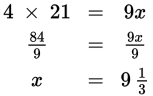
D

Percent times whole equals part:

Percent × 25 = 16

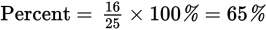
A

First find how long the trip takes him at each of the two different rates, using the formula

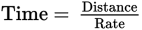
He travels the first 10 km at 30 km per hour, so he takes hour = 20 minutes for this portion of the journey. He travels the remaining 30 km at 15 km per hour, so he takes hours for this portion of the journey.

The whole journey takes him 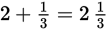hours = 2 hours 20 minutes.

Now calculate the amount of time it would take to make the same trip at a constant rate of 20 km per hour. If he traveled the whole 40 km at 20 km per hour, it would take =2 hours. Now 3 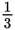hours is more than 2 hours by 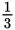hour, or 20 minutes.

B

Since 3 out of 24 students are in student organizations, the remaining 24 – 3 = 21 students are not in student organizations. Therefore, the ratio of students in organizations to students not in organizations is: = .

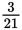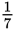A

By midseason, team A had won 60 and team B had won 49 games. Over the remaining 80 games, team A won 40 and lost 40. That means that team A wound up with 60 + 40 = 100 wins. To win 100 games, team B would have to win 100 – 49 = 51 games over the remainder of the season.

C

A vendor bought 10 crates for a total cost of $80. He wants to make a total profit of 25% over the total cost. So the total sale would have to equal $80 + (0.25)($80) = $80 + $20 = $100. He lost 2 crates, so he would need to sell the remaining 10 – 2 = 8 crates for $100 to make the required profit. 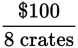= $12.50 per crate.

D

Set up a proportion on questions that give rates:

Before you cross-multiply, reduce the first fraction as much as possible to make the calculations easier. Divide the numerator and denominator by 10:

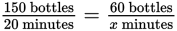
Cross-multiply:

15x = 120

Divide both sides by 15:

x = 8

C

To figure out whether the product is positive or negative, count the number of negatives given. If there are an odd number of negatives, the product is negative. That eliminates (A) and (B). Multiplying the two numbers gives: 15 × (-5) = -75.

B

The ratio of baseball cards to baseball figurines is 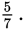You are given the number of cards, so you can set up a proportion: 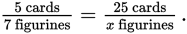Cross-multiply to get 5x = 175 and divide both sides by 5 so x = 35.

C

Set up equations to represent the relationships given in the problem:

2ℎ + 1s = $3.25

3ℎ + 1s = $4.50

The difference between the two totals is the price of a single hot dog. Thus, a single hot dog costs: $4.50 − $3.25 = $1.25. Plug the price of a single hot dog into the first equation to get the price of a soda:

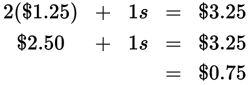
The question asks for the cost of two sodas: 2 × $0.75 = $1.50. Always double-check to be sure you are solving for the value the question asks for. In this case, choice (A) is a trap answer because it is the price of one soda.

A

When you are given two rates, you cannot simply take the average of the two. Thus, answer choice (B) 50 is a trap answer here. Because it takes more time to travel at a slower speed, the average for the entire trip will be closer to the slower speed. To solve this problem, pick a number for the distance of the entire trip. Since 40 and 60 are the rates, use the least common multiple, 120, for the number of miles. First, find the time spent traveling at each speed:

120 miles at 40 mph = 3 hours

120 miles at 60 mph = 2 hours

Total distance = 240 miles. Total time = 5 hours.

The average for the entire trip will be the total distance divided by the total time.

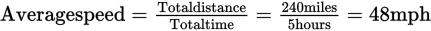
B

Call the number of teachers n. Then the number of students is 10n. The total number of teachers and students is n + 10n = 11n.

Since you can’t have a fraction of a person, n must be an integer, which means the total number of teachers and students must be a multiple of 11. Scan the answer choices and locate (B), 11 × 11, as the correct answer. None of the other answer choices are multiples of 11.

C

Use Backsolving for this one, beginning with choice (C). If the smaller number is 21 (and the larger number is 35), does the math from the question work?

The average of 21 and

The positive difference between 21 and 35 is 14. Twice the positive difference would be 2 × 14 = 28.

Thus, 21 is the smaller number and the correct answer.

You can also solve this question algebraically. Set the smaller number equal to y. Then, the average of the two numbers is: . Twice the positive difference of the two numbers is: 2(35 – y). The average is equal to twice the positive difference, so 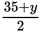= 2(35 – y). Solve:

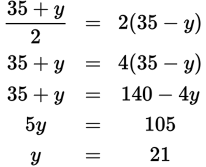
C

If a question uses the word “approximately” you can approximate the answer. If each of seven runners is running a little less than 1.3 kilometers, the total distance run would be a little less than 7 × 1.3 = 9.1, which is approximately 9 kilometers.

C

Set up a proportion:

Now cross-multiply and solve: 12x = 60, so .

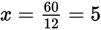A

This is a pure arithmetic computation question. First, add up all of the deductions:

218.99 + 107.05 + 25.03 + 68.65 + 42.75 = 462.47

Now subtract total deductions from gross pay:

1,769.23 – 462.47 = 1,306.76.

C

This is a standard average problem. Take the sum of all the terms and divide by the number of terms. 94 + 72 + 84 + 98 = 348. 348 ÷ 4 = 87. If dividing 348 by 4 was time consuming for you, you could have used Backsolving. Once you found the sum was 348, you could multiply the answer choices by 4, starting with (B) or (C), to see which answer choice gives 348. 87 × 4 = 348.