Answers and Explanations

Part 5: Mathematics Knowledge (MK)

  1. B
    In order to make this equation manageable, first turn the mixed number into an improper fraction, and then multiply both sides of the equation by 12 to clear the denominators:
  2. C

    Use FOIL:

    (3a + 4)(4a − 3)

    (3a × 4a) + [3a × (−3)] + (4 × 4a) + [4 × (−3)]

    = 12a2−9a + 16a − 12

    = 12a2 + 7a − 12

  3. D

    If 2m > 24, then m > 12. But so are all the answer choices, so check out the other inequality. If 3m < 48, then m < 16. thus, (d), 16, is not a possible value for m.

  4. A

    (D) is out because when you add square roots, you can’t simply combine the sums under the radical sign, as (D) does. But what you can do is factor out perfect squares from the number under the radical signs:

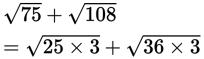
    You can then separate the terms under the radicals because they are connected by multiplication:

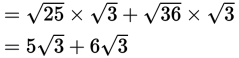
    Because the number under the radical is the same in both terms, you can add the terms together by adding the coefficients:

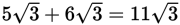
  5. B

    Since the lengths of each side of a square are the same, PQ = PS. Therefore:

    3a + 2 = 2a + 7

    a = 5

  6. B

    The three interior angles of any triangle add up to 180°, and the parts of the ratio here add up to 1 + 2 + 3 = 6. To get the amount of one part, divide 180 by 6, which gives you 30. Now you know that the three angles have degree measures of 1 × 30 = 30, 2 × 30 = 60, and 3 × 30 = 90. The difference in the degree measures between the largest and the smallest angles is:

    90 − 30 = 60

  7. A

    The Pythagorean theorem states that in a right triangle, a2 + b2 = c2, where a and b are the two perpendicular side lengths, called the legs, and c is the length of the hypotenuse. To figure out the perimeter of this triangle, first find the length of the hypotenuse using the Pythagorean theorem:

    Now add together the sides to get the perimeter:

  8. D

    Since AE is a line segment, all the lengths are additive, so AE = AD + DE. The question states that AD = 6 and AE = 8. So DE = AE − AD = 8 − 6 = 2. The question also states that BE = 6. So BD = BE − DE = 6 − 2 = 4. The question asks for the length of BC. Since CD = 3(BC ), the relationship can be written like this:

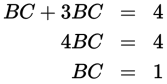
  9. B

    The central rectangle shares a side with each of the four squares, and the four squares form the legs of the four right triangles. Two of the rectangle’s sides have a length of 4, so the two squares that share these sides must also have sides of length 4. The other two sides of the rectangle have a length of 3, so the other two squares, which share these sides, must also have sides of length 3. Each triangle shares a side with a small square and a side with a large square, so the legs of each triangle have lengths of 3 and 4, respectively. Since the legs are of length 3 and 4, the hypotenuse of each triangle must have a length of 5.

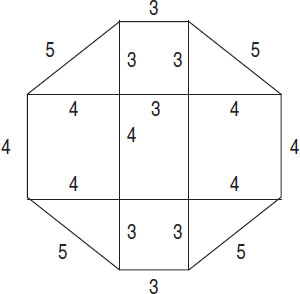
    image

    The perimeter is the sum of the hypotenuses of the triangles and a side from each square:

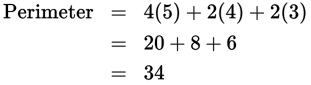
  10. D

    If 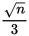is an even integer, then 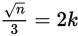, where k is an integer because any even integer is equal to 2 multiplied by an integer. Since 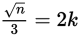, 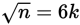. Squaring both sides of 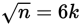gives: , and n = 36k2. So n must be a multiple of 36. Only choice (D), 144, is a multiple of 36. 144 = 4 × 36. Checking choice (D), 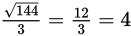and 4 is an even integer.

    If all that math seems too time consuming, you could use a combination of logic and Backsolving to get the correct answer. Since the problem deals with integers, then n must be a perfect square; only 81 and 144 among the answer choices are perfect squares. You could then Backsolve by plugging one of those choices into the equation to determine that choice (D) 144 is correct.

  11. D

    This is a good opportunity to Pick Numbers. For instance, you could pick 10 for n, so that Gheri is 10 years old. In that case, Carl is 4 years old and Jean is 2 years old. Then the sum of their ages is: 10 + 4 + 2 = 16. Now, plug 10 in for n into the answer choices, to see which gives you the target number of 16:

    3n + 4 = 3 × 10 + 4 = 34   Too big

    3n − 4 = 3 × 10 − 4 = 26   No good

    3n − 8 = 3 × 10 − 8 = 22   Still too big

    3n − 14 = 3 × 10 − 14 = 16  That’s correct!

  12. C

    2, 37, and 67 are all prime. 51 = 3×17, so it is not prime. Knowing the rules of divisibility can help you when dealing with problems involving prime numbers, multiples, or factors. For instance, 51 is divisible by 3, because its digits—5 and 1—add up to 6, which is a multiple of 3.

  13. B

    The circumference of a circle = 2π (radius), so a circle with a circumference of 2π has a radius of 1. The area of a circle = π(radius)2 so the area of a circle with a radius of 1 is π(1)2 = π.

  14. D

    To figure out the probability that a band member chosen at random will be a sophomore, apply the probability formula:

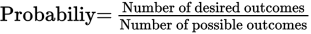
    In this case:

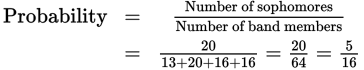
  15. D

    You could use an insight about math to solve this problem:

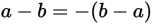    . So if 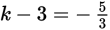, then .

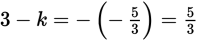    You could also have simply done the calculations:

    Now substitute that value into the second equation:

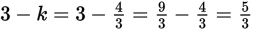
  16. A

    Solve the equation for x. Since x ≠ 0, you can divide both sides by x. Then 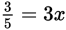. Dividing both sides by 3: .

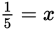  17. B

    You can Pick Numbers or use substitution for this problem. The best place to start Picking Numbers is with c and d. The question states that 4c = 3d, so make c = 3 and d = 4. If c = 3 and 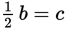, then b = 6. If b = 6 and a = 2b, then a = 12. Therefore, using the numbers picked: .

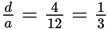  18. B

    Begin by converting the dimensions of the rectangular area to be covered to inches: 2 feet by 3 feet = 24 inches by 36 inches. 3 inches goes into 24 inches 8 times, and 4 inches go into 36 inches 9 times, so to cover the area, 8 × 9 = 72 tiles are needed.

    Alternatively, you could determine that each tile has an area of 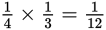square foot. So you need 12 tiles to cover one square foot. The area to be covered is 6 square feet, so 6 × 12 = 72 tiles needed.

  19. B

    If 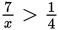, then multiply both terms by 4x and the result is x < 28. (when multiplying inequalities the sign must be flipped when multiplying by a negative number. you will remember that that means, in most cases, that you can’t multiply both sides of an inequality by a variable, since you don’t know whether a variable is negative or positive. however, in this case, you know from the construction of the problem that x must be positive.) Similarly, if 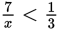 ,  then x > 21. Therefore, 22, 23, 24, 25, 26, and 27 (a total of 6 numbers) are the allowable integer values of x.

  20. B

    The hole cover has a diameter of 14 inches, so its radius is 7 inches and its area is π(7)2 = 49π square inches. The diameter of the hole is 12 square inches, so its radius is 6 inches and its area is π(6)2 = 36π square inches. Thus, the cover is 49π − 36π = 13π square inches greater than the area of the hole.

  21. B
    Some answer choices you can eliminate right away. 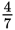is greater than 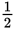, so that’s out, as is 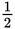. You’re left with 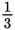, which is about 0.333, and 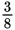, which is 0.375 and is the closest in value to 0.40.
  22. B

    Since the question asks for the answer in dollars, start by converting cents to dollars. There are 100 cents in a dollar, so 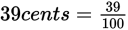dollars. Since each peach costs dollars, y peaches cost 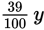dollars. If x oranges cost as much as y peaches, x oranges also cost 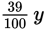dollars or 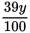dollars. Then one orange costs 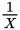as much: 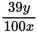dollars.

    Alternatively, this is an ideal problem to solve by Picking Numbers. Say that 5 oranges and 10 peaches cost the same; that is x = 5 and y = 10. If peaches are 39 cents each, 10 of them will cost $3.90 and that would equal the cost of 5 oranges. That means each orange costs 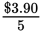or $0.78. Try the numbers in each answer choice, looking for the target number:

    Choice (A): 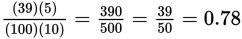  This may be the answer; hold onto it for now.

    Choice (B):                              Discard.

    Choice (C): 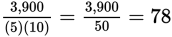                    This is 78 dollars, not 78 cents, so discard.

    Choice (D): 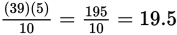                   Discard.

  23. C

    To come up with the largest number of groups, you should minimize the number of students in each group. Each group must contain at least three students, so that means you could have a total of 12 groups with 3 students in them, and one final group with 4 students in it, for a total of 13 groups.

  24. C

    The altitude at the base of the triangle is the same thing as the height of the triangle, and the area of a triangle = (base)(height). If the area of the triangle is 36 and its base is 9, the altitude is found as follows:

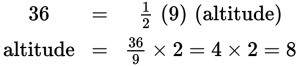
  25. C

    Plug in −5 for x into the equation and solve:

    2(−5)2 − 6(−5) + 5

    = 2(25) + 30 + 5

    = 85