
17

COMPUTERS: HOW TO TURN MENTAL LABOR INTO PHYSICAL LABOR, SO THEN YOU DON’T HAVE TO THINK SO HARD BUT CAN INSTEAD JUST TURN A CRANK OR WHATEVER

And yes, they may eventually try to take over the world, but you’ve got tons of time before that happens!

 The dream of (large segments of) humanity has always been not to work, and the fact you’re reading this guide (instead of just running out into your new world and figuring everything out from scratch as you go along) shows that even when trapped in the most dire and deadly circumstances it’s possible for a human being to be in, you are still interested in minimizing the amount of work you have to do. Most of the inventions we’ve shown you so far work on reducing physical labor, specifically by:
The dream of (large segments of) humanity has always been not to work, and the fact you’re reading this guide (instead of just running out into your new world and figuring everything out from scratch as you go along) shows that even when trapped in the most dire and deadly circumstances it’s possible for a human being to be in, you are still interested in minimizing the amount of work you have to do. Most of the inventions we’ve shown you so far work on reducing physical labor, specifically by:
-
getting animals to do it (plows, harnesses, etc.)
-
getting machines to do it (windmills and waterwheels, steam engines, flywheels, batteries, generators, and turbines)
-
giving you the information needed to avoid or minimize it (compasses, longitude and latitude)
-
and, if labor absolutely can’t be avoided, then at least feeding you better so it’s less of an imposition and you can do it for longer without dying (farming, preserved foods, bread and beer, etc.).
But physical labor is only one way humans work, and if you’ve ever taken a break from studying to relax, play a game, stare at a wall, go for a run, or do literally anything else but study, you know that mental labor can be exhausting too. You haven’t yet invented anything you can offload that work on . . . but you’re about to.*
It’s going to take a lot of work to duplicate a complete human brain (and this “artificial intelligence” you might one day create may not even be perfect, and when managing the internal workings of FC3000™ rental-market time machines, could in fact be prone to catastrophic failures for which no legal liability can be assigned), but even a machine that can perform the basics of calculation will provide the foundation required for you to build everything else. And while true AI may be generations off, the machines you build in the meantime that can calculate without error will still transform society, especially when you get those machines reasoning hundreds of thousands of times faster than humans can. We don’t need to tell you this, because you’ve seen computers. You know how useful, productive, entertaining, and completely awesome they are.
Here’s how you build them from scratch.
WHAT KIND OF NUMBERS YOUR COMPUTER WILL USE, AND WHAT IT WILL DO WITH THEM
You’re going to use binary as the basis for your computers, for two reasons: you already invented it back in Section 3.3: Non-Sucky Numbers, and it’ll make things easier by reducing the numbers you have to worry about to two: 0 and 1.* Now all you need to figure out is what your computer will do with those numbers. Ideally, we’d like a machine that can add, subtract, divide, and multiply. But do we actually need to be able to do all of that? In other words, what’s the minimum viable product for any computing machine?
It turns out that a computer doesn’t technically need to know how to multiply. You can emulate multiplication—that is, get the same result through different means—by repeated addition. 10 times 5 is the same as just adding 10 to itself 5 times. So addition emulates multiplication:
x × y = x added to itself y times
Subtraction works the same: 10 minus 5 gives the same result as adding a negative number, –5, to 10. So addition emulates subtraction too:
x – y = x + (–y)
And yes, you can also emulate division with adding. If you’re dividing 10 by 2, you’re trying to figure out how many times 2 goes into 10. You can calculate that by adding two to itself (like we did with multiplication), but this time, keep track how many 2s you add until you reach or exceed your goal. 2 + 2 + 2 + 2 + 2 = 10, which is five 2s, so 10 divided by 2 must equal 5. It even works for numbers that don’t divide evenly! You just keep adding until one more addition would make you go over the number you’re interested in, with whatever’s left over as your remainder.* So:
x/y = x added to itself until it reaches y, counting the number of additions it took
The four basic operations of math—addition, subtraction, multiplication, and division—can all be emulated by just one of them: addition. So to build a computer, all you need to do is build a machine that can add.
No sweat, right?
WHAT EVEN IS ADDING THOUGH, AND HOW CAN WE TALK ABOUT ADDING WHEN I DON’T EVEN KNOW HOW A COMPUTER WORKS YET?
Before you try to build an adding machine, let’s take a step back and remember the propositional calculus you invented in Section 10.13.1: Logic. There you defined an operation named “not” that meant “the opposite of whatever the proposition is.” So if you had a proposition p that was true, then “not p” (or ¬p for short) would therefore be false. What happens when you replace “true” with “1” and “false” with “0”? Well, you just take the truth table for p and ¬p, which looks like this . . .
|
p |
¬p |
|
False |
True |
|
True |
False |
Table 19: The truth table for p and ¬p.
. . . and convert it into a list of the expected inputs and outputs of a binary machine—we call these “gates”—that looks like this:
|
Input |
Output |
|
0 |
1 |
|
1 |
0 |
Table 20: Behold, the design for the world’s first NOT gate!
Any machine you build that given this input produces this output—no matter how it’s produced or what goes on inside it—will function as a NOT gate: you put a 1 in, you’ll get a 0 out, and vice versa. You can even draw it schematically:
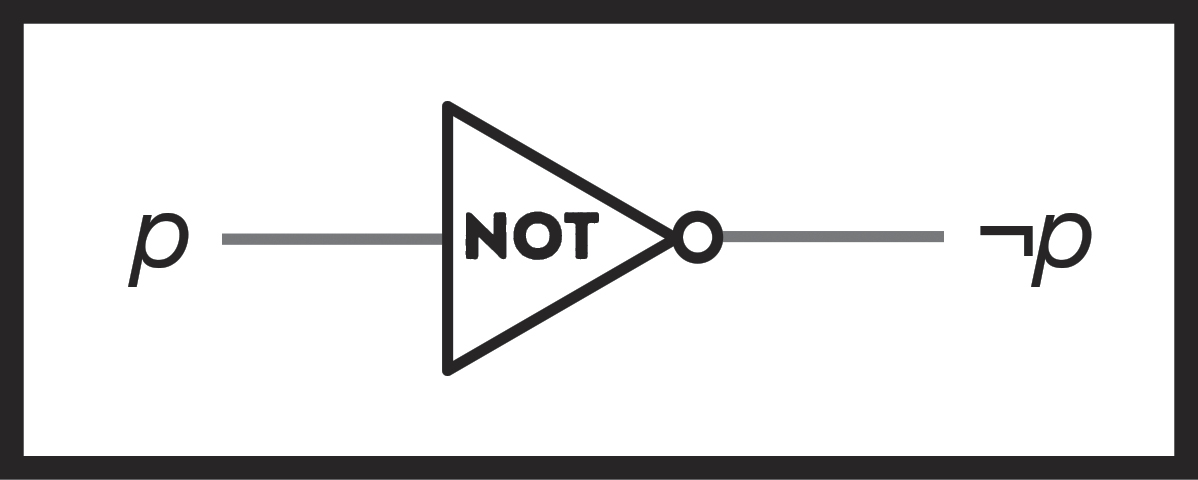
Figure 62: A representation of a NOT gate, drawn graphically.
At this point you still have no idea how to build this NOT machine, but at least you know what it’s supposed to do. And freed as you temporarily are from the restraint of “actually having to build these dang things,” you can come up with other operations too!
Remember how in propositional logic you defined “and” (or ∧) to mean that both arguments had to be true for a statement to be true? In other words, “(p ∧ q)” is only true if both p and q are true, and it’s false in every other condition. Here’s a truth table showing the only possible ways that can go:
|
p |
q |
(p ∧ q) |
|
False |
False |
False |
|
False |
True |
False |
|
True |
False |
False |
|
True |
True |
True |
Table 21: The truth table for (p ∧ q).
And just like with “not,” all you need to do is transform true and false into 1s and 0s to define the world’s first AND gate, which we’ll give a symbol to also:
|
Input p |
Input q |
Output: (p ∧ q) |
|
0 |
0 |
0 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
Table 22: The inputs and outputs of an AND gate.
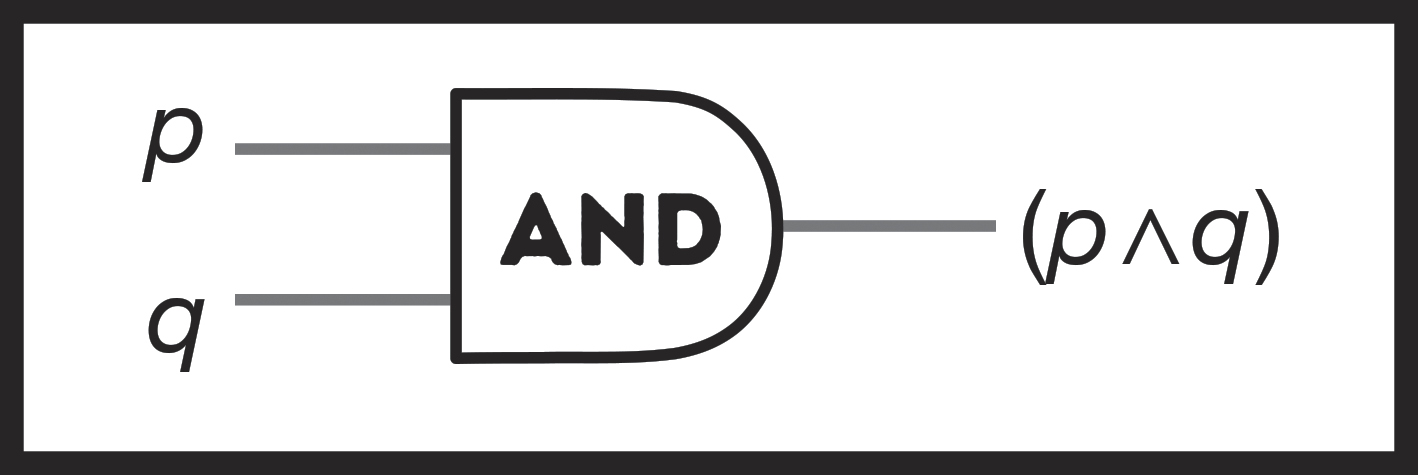
Figure 63: An AND gate.
The only piece you’re missing now is “or”: the opposite of “and.” An “or” operation between p and q, symbolized as “(p ∨ q)” will be true if either p or q are true. That makes an OR gate’s truth table look like this:
|
Input p |
Input q |
Output: (p ∨ q) |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
1 |
Table 23: The inputs and outputs of an OR gate.
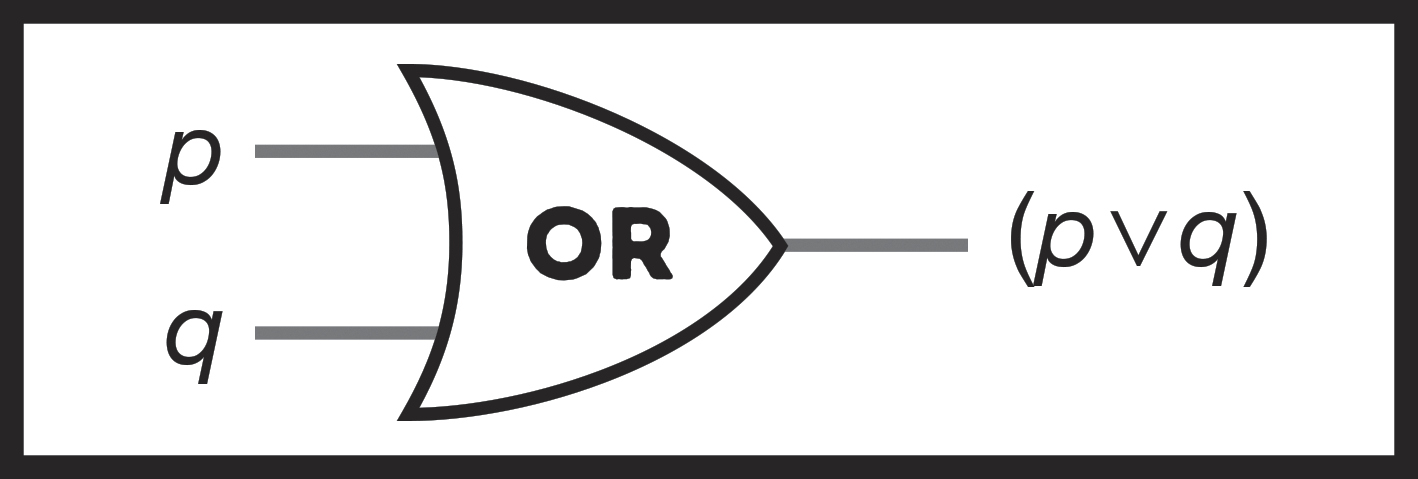
Figure 64: An OR gate.
You can use these three basic gates to build up new ones. For example, attach a NOT gate after an AND gate, and you’ve invented a “NOT AND” gate, or NAND for short. They look like this:
|
Input p |
Input q |
(p ∧ q) |
Output: ¬(p ∧ q) |
|
0 |
0 |
0 |
1 |
|
0 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
|
1 |
1 |
1 |
0 |
Table 24: The inputs and outputs of a NAND gate.
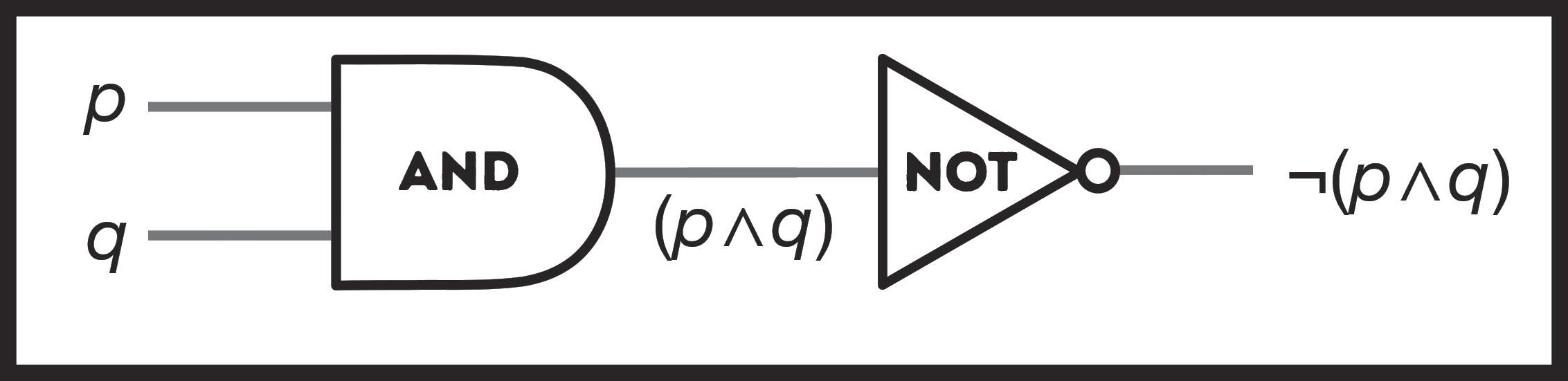
Figure 65: An expanded NAND gate.
As a time-saver, rather than drawing out a NOT and an AND gate separately, we’ll just merge them as a single gate, NAND, which we’ll draw like this:
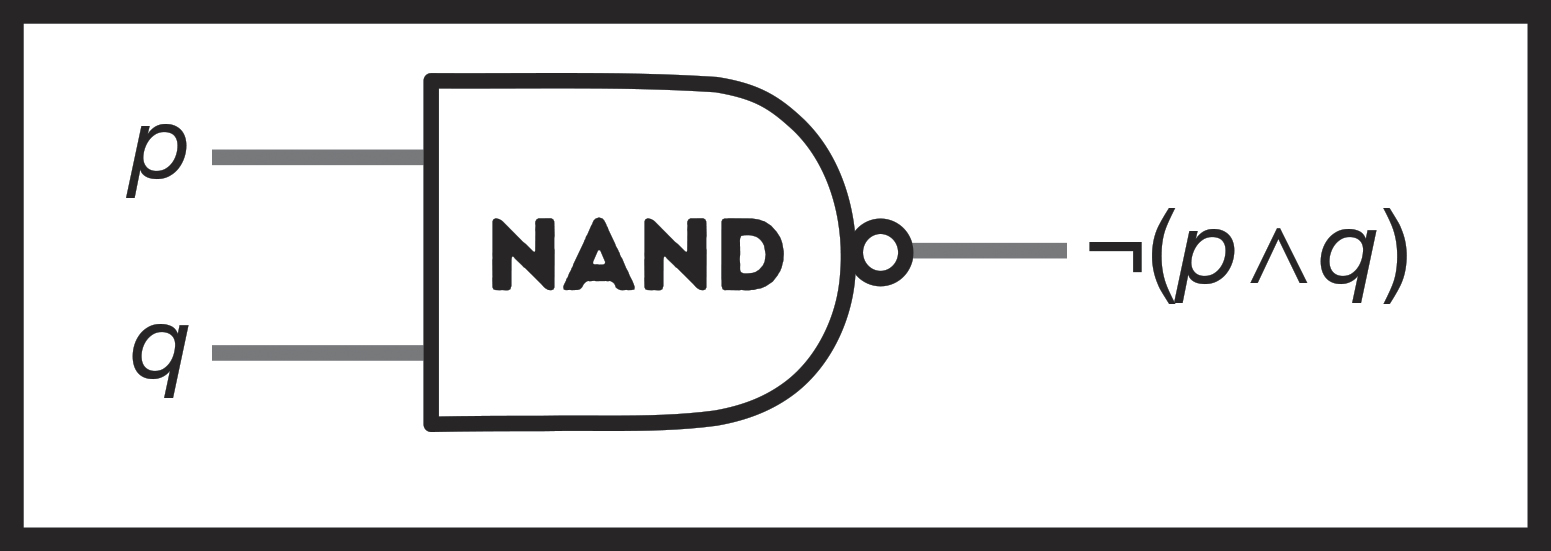
Figure 66: A simplified NAND gate.
That NAND gate is functionally identical to the NOT AND gate we first made, but easier to draw. And we can continue to combine gates, using a NAND gate, an OR gate, and an AND gate to make a new gate that outputs 1 if and only if one of its inputs is 1. Anything else, and it’ll return 0. We call this gate “exclusive or,” or XOR, and here’s how you build it:

Figure 67: An expanded XOR gate.
|
Input p |
Input q |
¬(p ∧ q) aka p NAND q |
(p ∨ q) aka p OR q |
Output: (¬(p ∧ q) ∧ (p ∨ q)) aka p XOR q |
|
0 |
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
1 |
|
1 |
0 |
1 |
1 |
1 |
|
1 |
1 |
0 |
1 |
0 |
Table 25: A truth table proving that you can make an XOR gate out of a NAND, an OR, and an AND gate.
And just like NAND, we can give this collection of gates its own symbol: the XOR symbol.
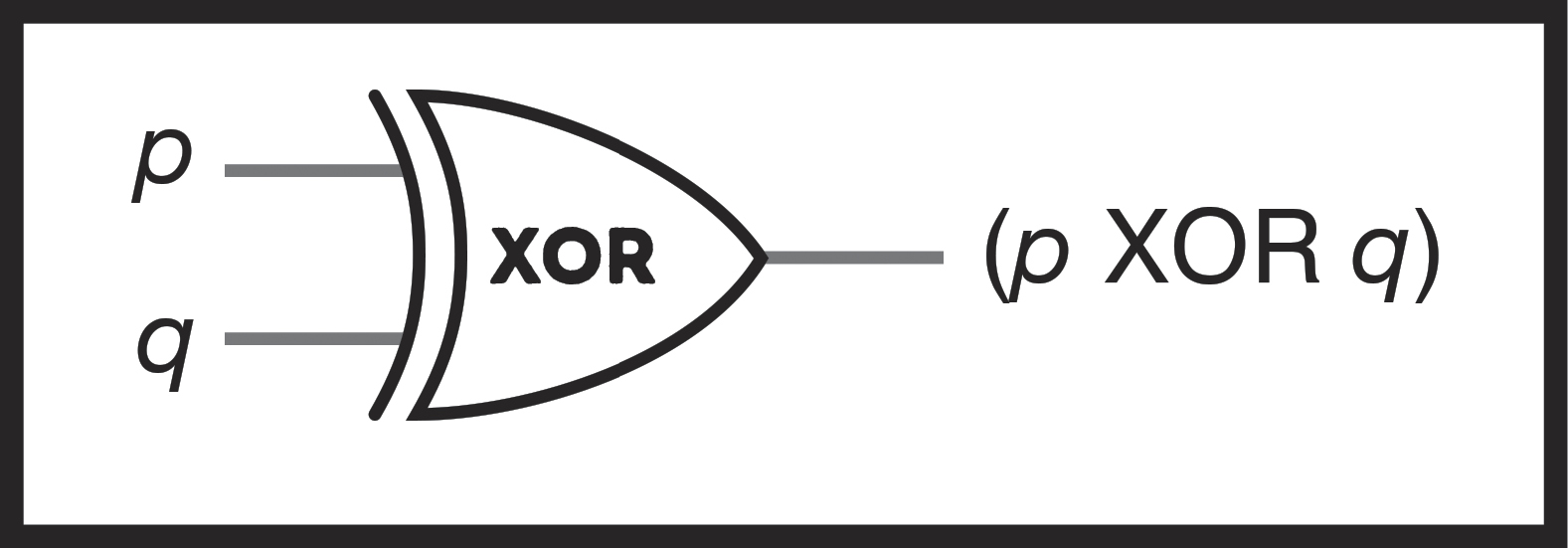
Figure 68: A simplified XOR gate.
Fun fact: besides the NAND and XOR you just invented, you can actually construct a gate that produces any pattern of output you can imagine just from the AND, OR, and NOT gates you started with.*
OKAY, SO, GREAT I’VE INVENTED ALL THESE GATES, BUT NONE OF THEM ADD ANYTHING YET, SO WHAT THE HECK?
Right. Well, let’s define what an addition gate should look like. Let’s start with the basics, adding two single-digit binary numbers. That gives us a manageable-looking truth table of all possible outcomes:
|
Input p |
Input q |
Output: (p + q) in decimal |
Output: (p + q) in binary |
|
0 |
0 |
0 |
0 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
2 |
10 |
Table 26: Incredibly, not the first time in this book we’ve explained that 1 + 1 = 2.
The catch is, binary deals in 1s and 0s, and you’ve got a binary “10”—that’s a two—there in your output. So let’s break our output out into two different channels, each representing a single binary digit, like so:
|
Input p |
Input q |
Output a |
Output b |
|
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
|
1 |
1 |
1 |
0 |
Table 27: How to add to two in binary.
Now, two inputs (representing the two single-digit binary numbers you want to add) go in, and two outputs (representing the two-digit solution, again in binary) come out. We’ve labeled those a and b here, and together they encode what the input digits add up to. All we need to do is figure out how to construct this from the gates we’ve already got: AND, OR, NOT, NAND, and XOR.*
If you look at the patterns of 1s and 0s produced by a and b, you’ll notice they look familiar: a’s output is identical to an AND gate (p ∧ q), and b corresponds perfectly with an XOR gate. That makes building it really simple! All you have to do is connect the inputs to an AND gate and to a separate XOR gate, like so, and your adding machine is invented:

Figure 69: An adding machine.
With that, you’ve defined the operation of a machine that can add 1 and 1 together! Now, since you already know what 1 + 1 equals,* this machine—called a “half adder”—probably seems pretty useless. But let’s look at how addition works one more time.
In the decimal number system you’re used to, 7 + 1 equals 8, 8 + 1 equals 9, but 9 + 1 gives you a two-digit answer: 10. Since we only have digits that go from 0 to 9, when numbers get larger, we have to “carry the one” and start a new column: a double-digit 10 instead of a single-digit 9. The exact same thing happens in binary, but instead of carrying the one to start a new column at 10, we start a new column at 2. Given that, we can re-label our a and b outputs with more accurate names: let’s call them s (for “sum”) and c (for “carry”). If c is 1, we need to carry that 1 over into a new binary digit.
And something really interesting happens if you take a half adder and connect it to another half adder with an XOR gate. This new machine, which we’ll call a “full adder,” looks like this:
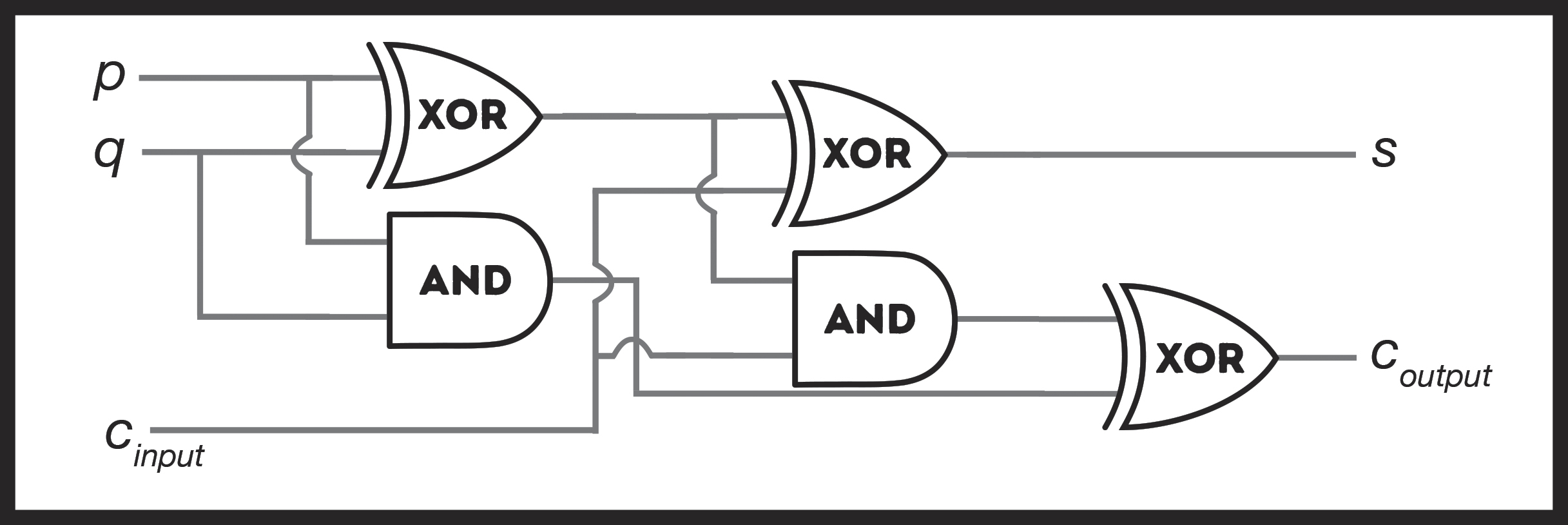
Figure 70: A full adder.
This new machine still outputs your solution as s and c (which, remember, represent “sum” and “carry”) like before, but now it can take a different c as an input. This c lets you “carry the one” from another full adder’s result and feed it into this one. You can therefore chain full adders together!
This is where the magic happens. With each full adder you include in your machine, you double the maximum number that machine can handle. One full adder outputs two binary digits, which gives you 4 numbers you can output, from zero to three. Two full adders give you three binary digits, so now you can count 8 different numbers. Three full adders get you to 16, four gets you to 32, and from there you reach 128, 256, 512, 1,024, 2,048, 4,096, 8,192, 16,384, and so on, doubling with each new full adder you include. By the time you have forty-two full adders chained together, you have built a machine that can count high enough to give every star in the visible universe its own unique number. That’s pretty good for a bunch of weird imaginary gates you just made up.
These adders are the heart of your calculation engine. All you need for multiplication, subtraction, and division is addition.* All you need for addition is to build full adders. And all you need for full adders is to build actual real-life versions of the logic gates you’ve invented. If you can build these gates, you’ve solved computers.
SO LET’S ACTUALLY BUILD SOME LOGIC GATES AND SOLVE COMPUTERS
Eventually your civilization will build computers that run on electricity, but to start, you’re going to build a computer that runs on something easier to manage than invisible electron flow. You’re going to build a computer that runs on water.
This may sound difficult (and indeed, building a NOT gate that turns 0 into 1, or in other words, a machine that when no water is going into it somehow summons water as output can be tricky), but your full adder used only AND and XOR gates. And you’re about to invent both of those at the same time with a single piece of technology. Here it is:

Figure 71: An apparatus that functions as both a fluidic AND gate and a fluidic XOR gate—at the same time.
If one or the other input is on, the water slooshes in from the top, whips around the sides, and comes out the bottom. But if both are on, they impact in the middle, and water comes out there instead. The output from the bottom is the XOR of the inputs, and the output from the middle is the AND of the inputs. This combination XOR-and-AND gate is all you need to build a full adder, and therefore it’s also all you need to make a computer that runs on water. In other words, properly configured water is all that’s needed to perform computational tasks.*
Done.
That said, a water-based computer will obviously be slower than the speed-of-electricity-itself ones you remember, and it won’t act as a replacement for the latest mass-market portable music players for a very long time, if ever. But it’s the foundation of computation that humans normally don’t even start glancing at until the late 1600s CE, and miniaturization, electronics, semiconductors, and everything that comes afterward will be built upon what you’ve just invented. You’ve not only figured out the basics of mechanical computation, you’ve built a machine that actually solves mathematical problems using these principles.
And you don’t need to stick with water! Remember: any machine that produces the output you want works as a gate, and besides the water gates you have and the electrical gates you’ll someday construct, you can explore other mediums: marbles running through grooves, ropes and pulleys,* and even living crabs* have been used to construct logic gates. It’s worth noting that most of these gates were invented after we invented electronic computers: once humans have the basics of binary logic, they start seeing ways to invent computers out of all sorts of things.
The next major innovation will be general-purpose computing machines. The computers you just invented are built to do a single thing, but as soon as you can program your machines with numbers rather than programming them by physically moving gates, you begin to blur the line between numbers that mean things and numbers that do things. This gives computers the ability to alter their own programming as they run, and once you have that, the potential of computation explodes, and the world is never the same.
It’s gonna be great!