APPENDIX E
TRIGONOMETRY TABLES, INCLUDED BECAUSE YOU’LL NEED THEM WHEN YOU INVENT SUNDIALS, BUT THEY’LL ALSO BE USEFUL IF YOU EVER DECIDE TO INVENT TRIGONOMETRY
This book is a guide to reinventing civilization from scratch, and while your civilization will eventually want to invent trigonometry, in an era where you don’t know where your next meal is coming from because you’re still figuring out what farming is, you probably don’t need it right away. We therefore won’t cover the entirety of trig here, but in this appendix we do give you some of the most useful low-hanging fruit: enough for practical purposes, and to point the way to future discoveries.
Trigonometry lets you use some known quantities about a triangle to determine its unknown quantities, we will interrupt ourselves right now because we can already hear you muttering, “Come on, when am I ever gonna use this?” Here is when you are going to use this: in navigation, astronomy, music, number theory, engineering, electronics, physics, architecture, optics, statistics, cartography, and more. You already need it just to build a proper sundial (Section 10.7.1), hence the unofficial slogan of trigonometry: “Okay, fine, I guess this is actually pretty important after all.”
Trigonometry deals only with right triangles (triangles with two edges that meet at 90 degrees, and we mark that angle with a little square), but since any non-right triangle can be divided into two right triangles (try it; it’s true), that’s not going to be a problem. A right triangle looks like this:
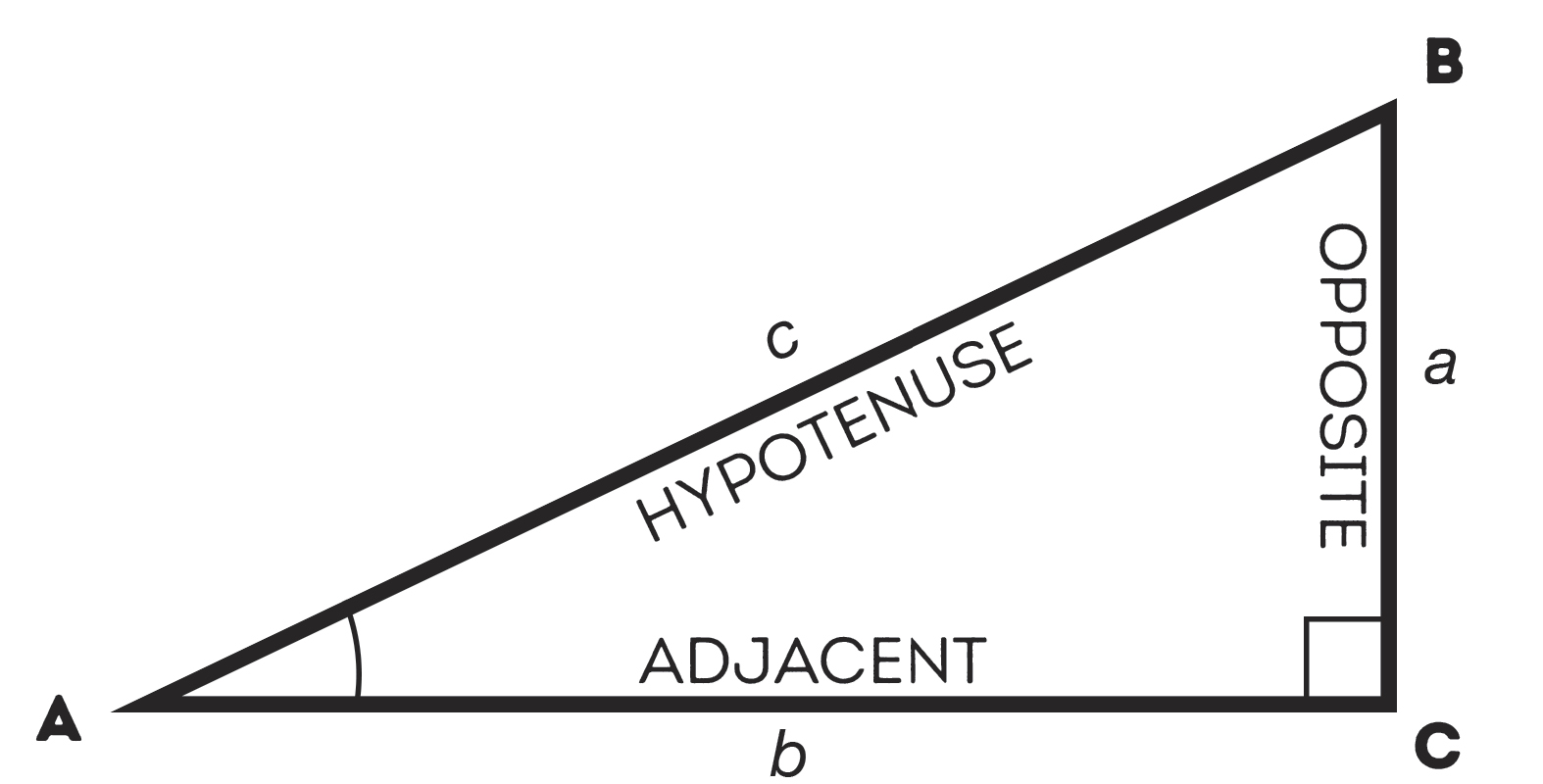
Figure 73: This is what a right triangle looks like.
We’ll call the longest side (c, which is always opposite the right angle) the “hypotenuse.” If we pick an angle (in this case we used the one at A) then we can label the side opposite A as the “opposite” side, and the side beside it “adjacent.” Incidentally, the three angles of any triangle add up to 180 degrees, so since we know in a right triangle one of them is 90, all it takes is knowing one of the other angles to determine the remaining one. Here’s a useful theorem about right triangles:
a2 + b2 = c2
That’s what we call the “Pythagorean theorem,” after a guy named Pythagoras who lived in ancient Greece around 500 BCE, but even he admitted he wasn’t the first to come up with the idea—and it’s been independently discovered before and since all over the world. It says that the sum of the square of the length of the two shortest sides of a right triangle is equal to the square of the length of the longest side. This lets you calculate all measurements of a right triangle from only partial data, which, as we already said, is something that trigonometry is all about.
If you know the angles in a right triangle, that means you’ve also described its shape, because there’s only one way those angles can fit together to make a triangle. And that means the opposite is true too: if you know the length of the sides of a right triangle, then you also know the angles involved. This lets us define some useful operations. The ratio of the length of the opposite side to the length of the hypotenuse we’ll call “the sine function,” or “sin” for short.* The ratio of the adjacent side to the hypotenuse we’ll call “cosine” (“cos” for short), and the ratio of the opposite to the adjacent we’ll call “tangent,” or “tan.” Given an angle we can determine what the sin, cos, and tan values for that angle are. Going the other way, if we know the sin, cos, or tan value, we can determine which angle that requires. We’ll mark these inverse functions with a tiny -1, so that’s sin−1, cos−1, and tan−1.
As you explore trigonometry you’ll discover proofs that relate this study of triangles to circles (draw a circle around your triangle and you’ll see connections between pi and your cos, sin, and tan functions); periodic functions (graph the values of cos, sin, and tan and you’ll notice how their patterns repeat); and even your trig functions to one another (as an example: the tangent of an angle is equal to its sine divided by its cosine). All of this is to say: if this interests you, there’s lots to explore, and many have dedicated their lives to much smaller and less noble subjects.*
The catch is, however, that calculating the values of sin, cos, and tan is complicated, and only really needs to be done once. So instead of making you do it yourself, we, your friends here at Chronotix Solutions, have provided full trigonometry tables on the following pages. Given an angle a, you can find the values of sin(a), cos(a), and tan(a). And to run the inverse functions (sin−1, cos−1, and tan−1), just look for the angle that matches the value you have.
The following is information you need to explore trigonometry, invent new theorems and trigonometric equations, and, most important, finish your sundial in Section 10.7.1.
|
Angle a |
sin(a) |
cos(a) |
tan(a) |
|
0 |
.0000 |
1.0000 |
.0000 |
|
1 |
.0175 |
.9998 |
.0175 |
|
2 |
.0349 |
.9994 |
.0349 |
|
3 |
.0523 |
.9986 |
.0524 |
|
4 |
.0698 |
.9976 |
.0699 |
|
5 |
.0872 |
.9962 |
.0875 |
|
6 |
.1045 |
.9945 |
.1051 |
|
7 |
.1219 |
.9925 |
.1228 |
|
8 |
.1392 |
.9903 |
.1405 |
|
9 |
.1564 |
.9877 |
.1584 |
|
10 |
.1736 |
.9848 |
.1763 |
|
11 |
.1908 |
.9816 |
.1944 |
|
12 |
.2079 |
.9781 |
.2126 |
|
13 |
.2250 |
.9744 |
.2309 |
|
14 |
.2419 |
.9703 |
.2493 |
|
15 |
.2588 |
.9659 |
.2679 |
|
16 |
.2756 |
.9613 |
.2867 |
|
17 |
.2924 |
.9563 |
.3057 |
|
18 |
.3090 |
.9511 |
.3249 |
|
19 |
.3256 |
.9455 |
.3443 |
|
20 |
.3420 |
.9397 |
.3640 |
|
21 |
.3584 |
.9336 |
.3839 |
|
22 |
.3746 |
.9272 |
.4040 |
|
23 |
.3907 |
.9205 |
.4245 |
|
24 |
.4067 |
.9135 |
.4452 |
|
25 |
.4226 |
.9063 |
.4663 |
|
26 |
.4384 |
.8988 |
.4877 |
|
27 |
.4540 |
.8910 |
.5095 |
|
28 |
.4695 |
.8829 |
.5317 |
|
29 |
.4848 |
.8746 |
.5543 |
|
30 |
.5000 |
.8660 |
.5774 |
|
31 |
.5150 |
.8572 |
.6009 |
|
32 |
.5299 |
.8480 |
.6249 |
|
33 |
.5446 |
.8387 |
.6494 |
|
34 |
.5592 |
.8290 |
.6745 |
|
35 |
.5736 |
.8192 |
.7002 |
|
36 |
.5878 |
.8090 |
.7265 |
|
37 |
.6018 |
.7986 |
.7536 |
|
38 |
.6157 |
.7880 |
.7813 |
|
39 |
.6293 |
.7771 |
.8098 |
|
40 |
.6428 |
.7660 |
.8391 |
|
41 |
.6561 |
.7547 |
.8693 |
|
42 |
.6691 |
.7431 |
.9004 |
|
43 |
.6820 |
.7314 |
.9325 |
|
44 |
.6947 |
.7193 |
.9657 |
|
45 |
.7071 |
.7071 |
1.0000 |
|
46 |
.7193 |
.6947 |
1.0355 |
|
47 |
.7314 |
.6820 |
1.0723 |
|
48 |
.7431 |
.6691 |
1.1106 |
|
49 |
.7547 |
.6561 |
1.1504 |
|
50 |
.7660 |
.6428 |
1.1918 |
|
51 |
.7771 |
.6293 |
1.2349 |
|
52 |
.7880 |
.6157 |
1.2799 |
|
53 |
.7986 |
.6018 |
1.3270 |
|
54 |
.8090 |
.5878 |
1.3764 |
|
55 |
.8192 |
.5736 |
1.4281 |
|
56 |
.8290 |
.5592 |
1.4826 |
|
57 |
.8387 |
.5446 |
1.5399 |
|
58 |
.8480 |
.5299 |
1.6003 |
|
59 |
.8572 |
.5150 |
1.6643 |
|
60 |
.8660 |
.5000 |
1.7321 |
|
61 |
.8746 |
.4848 |
1.8040 |
|
62 |
.8829 |
.4695 |
1.8807 |
|
63 |
.8910 |
.4540 |
1.9626 |
|
64 |
.8988 |
.4384 |
2.0503 |
|
65 |
.9063 |
.4226 |
2.1445 |
|
66 |
.9135 |
.4067 |
2.2460 |
|
67 |
.9205 |
.3907 |
2.3559 |
|
68 |
.9279 |
.3746 |
2.4751 |
|
69 |
.9336 |
.3584 |
2.6051 |
|
70 |
.9397 |
.3420 |
2.7475 |
|
71 |
.9456 |
.3256 |
2.9042 |
|
72 |
.9511 |
.3090 |
3.0779 |
|
73 |
.9563 |
.2924 |
3.2709 |
|
74 |
.9613 |
.2756 |
3.4874 |
|
75 |
.9659 |
.2588 |
3.7321 |
|
76 |
.9703 |
.2419 |
4.0108 |
|
77 |
.9744 |
.2250 |
4.3315 |
|
78 |
.9781 |
.2079 |
4.7046 |
|
79 |
.9816 |
.1908 |
5.1446 |
|
80 |
.9848 |
.1736 |
5.6713 |
|
81 |
.9877 |
.1564 |
6.3138 |
|
82 |
.9903 |
.1391 |
7.1154 |
|
83 |
.9925 |
.1219 |
8.1443 |
|
84 |
.9945 |
.1045 |
9.5144 |
|
85 |
.9962 |
.0872 |
11.4301 |
|
86 |
.9976 |
.0698 |
14.3007 |
|
87 |
.9986 |
.0523 |
19.0811 |
|
88 |
.9994 |
.0349 |
28.6363 |
|
89 |
.9998 |
.0175 |
57.2900 |
|
90 |
1.0000 |
.0000 |
infinity |
Table 29: Here are the numbers you need to make triangles work.