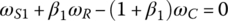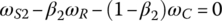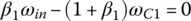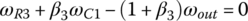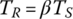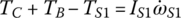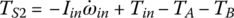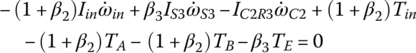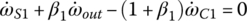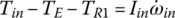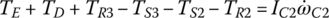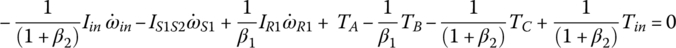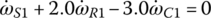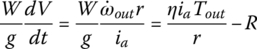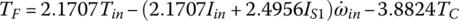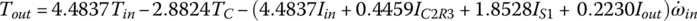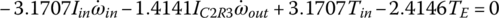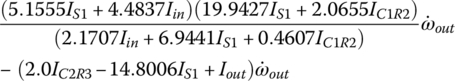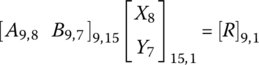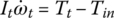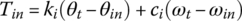5
Automatic Transmissions: Design, Analysis, and Dynamics
5.1 Introduction
Automatic transmissions (AT) that use planetary gear trains (PGT) and clutches for power transmission and ratio changes are the dominating transmission type in the automotive industry. This type of transmission dates back to the late 1930s [1,2], and they are conventionally termed automatic transmissions since they were the only production type for many decades before other types of automatic transmission, such as CVT and DCT, were applied in scale in the automotive industry. Early automatic transmissions [3] for rear wheel drive (RWD) vehicles provided three forward and one reverse gears, and were designed on an architecture that consisted of a torque converter, planetary gear train sets, and hydraulically controlled clutches, as illustrated in Figure 5.1. This design architecture or its variations stayed almost unchanged for more than three decades. Before the 1970s, passenger vehicles were almost exclusively RWD, and the vast majority of automatic transmissions had three forward speeds. Only a few high end models were equipped with four‐speed automatic transmissions, with the fourth gear as a direct drive [4]. The oil crisis in the 1970s called for the development of more fuel efficient passenger vehicles that are lighter and front wheel driven (FWD). An early type of FWD AT that provided three forward and one reverse gears is illustrated in Figure 5.2. As shown in the figure, in an FWD transmission, the final drive and differential assembly is integrated with the transmission, but the ratio change portion of the transmission is similar to that in RWD transmissions illustrated in Figure 5.1.
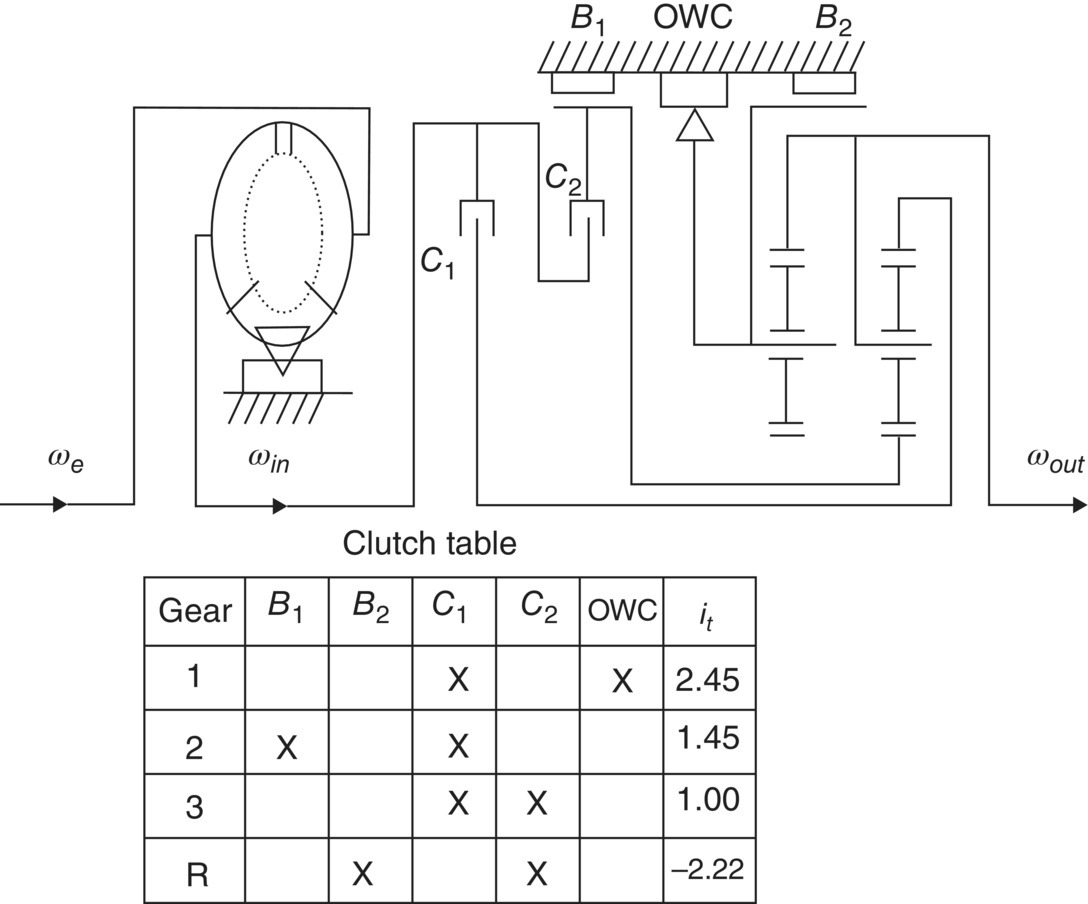
Figure 5.1 Structure of an early three‐speed automatic transmission.
Figure 5.2 Structure of an early three‐speed FWD automatic transmission.
As discussed in Chapter 1, the number of speeds in a transmission affects directly how well it can be matched to the engine in terms of performance and fuel economy. In general, automatic transmissions with more speeds provide better vehicle performance, improved fuel economy and enhanced drivability. To achieve the best trade‐off between performance and fuel economy for passenger vehicles, the automotive industry started to develop four‐speed automatic transmissions with the top gear as an overdrive in the middle of 1970s. Since then, both four‐speed and three‐speed automatic transmissions have been used across the product lines, and by 1990, three‐speed automatics had been phased out from the industry. Four‐speed ATs were the mainstream for the industry until the turn of the century, with five‐speed types also taking up a significant market share. Today, six‐speed ATs are the standard equipment across the industry and transmissions with eight or more speeds are already applied in high end passenger cars and SUVs. It can be predicted that transmissions with around ten speeds will be developed and applied in the industry in the next few years. By then, the benefits of more speeds shall diminish and the pursuit for more speeds will probably come to a halt.
This chapter will cover the design, kinematics, and dynamics of automatic transmissions. Section 5.2 will present the architectural configurations of automatic transmissions with various speeds, from the three‐speed of the early types to current generation of transmissions with eight or nine speeds. Standard stick diagrams drawn in conventional symbols are used in the chapter to illustrate transmission structures and layouts. Although automatic transmissions are primarily based on planetary gear train structure, this section will include examples of lay‐shaft transmission designs for a complete overview.
Section 5.3 will cover the kinematics of automatic transmissions based on the characteristics of planetary gear trains discussed in Chapter 3. The section focuses on how multiple gear ratios are achieved by a combination of clutches and planetary gear trains. A systematic method will be presented in the section for the design and analysis on the gear ratios of automatic transmissions. Case studies on production transmissions will be included to demonstrate the principles for design and analysis. The chapter then presents the analysis on the dynamics of automatic transmissions in Section 5.4. As a continuation of the case studies, this section starts with the free‐body diagrams of the assemblies that form the transmission system, and then derives the equations of motion for each of the assemblies. These equations are then transformed by eliminating the internal torques on planetary gear train members to form the state variable equation system. Static clutch torques in each gear are then determined as a special case of the state variable equation system.
In Section 5.5, a qualitative analysis on shift processes will be provided to demonstrate how transmission control and state variables affect shift quality. The concept of torque phase and inertia phase during transmission shifts will be introduced and transmission shift dynamics during the two shift phases will be discussed in this section. After the qualitative analysis in Section 5.5, Section 5.6 will present general vehicle powertrain dynamics in a systematic approach, using an eight‐speed automatic transmission as the example. System formulation and modeling will be presented in this section for the simulation, analysis and control of vehicles equipped with automatic transmissions. Finally, Section 5.7 will discuss model simulations and applications for vehicle powertrain systems under various operation conditions, such as fixed gear operation, shifting processes, and operations on specified drive ranges.
5.2 Structure of Automatic Transmissions
Automatic transmissions based on planetary gear train designs have evolved over the past seven decades from the first generation with three speeds to the current generation with eight or more speeds. In terms of mechanical structure, however, these transmissions are still built from the same components, which include a torque converter, planetary gear trains, and clutches. The differences between a first generation three‐speed AT and a current generation eight‐speed AT mainly lie in the number of planetary gear trains and their layouts, as well as the combination of clutches that realize multiple gear ratios. Stick diagrams of production transmissions are provided in this section as examples to illustrate the PGT layout and clutch combination for transmissions from three speeds to nine speeds.
A three‐speed RWD automatic transmission of the early type and the clutch table are shown in Figure 5.1. This transmission was developed by Chrysler in the mid 1950s based on the Simpson‐type planetary gear set and had been applied across the Chrysler product line. This transmission was representative of similar products in the automotive industry until the 1970s. As illustrated in Figure 5.1, the Simpson‐type planetary gear set consists of two simple planetary gear trains, with the two sun gears structurally connected and the ring gear of the front train structurally connected to the carrier of the rear train. The transmission output is from the ring‐carrier assembly. The transmission uses two multiple disk hydraulic clutches, C1 and C2, two band clutches, B1 and B2, and a one‐way clutch to realize three forward speeds and one reverse. The two band clutches are reaction clutches that ground the sun gear assembly and the carrier of the front PGT respectively when applied. As can be noticed from the clutch table, the off‐going clutch for the 1–2 upshift is the one‐way clutch. This makes the 1–2 shift control less challenging and is an important factor in achieving shift smoothness in the absence of advanced control technology at the time when the transmission was developed. The other upshift, i.e. the 2–3 shift, is clutch to clutch, which is generally more difficult to control, but in this case, the shift would occur at higher vehicle speed and is less sensible to the driver. Here it is worthwhile to introduce some terminologies commonly used in the transmission area: clutch to one‐way clutch shift, clutch to clutch shift, reaction clutch and coupling clutch. In a clutch to one‐way clutch shift, the off‐going clutch is a one‐way clutch, and in a clutch to clutch shift, the off‐going clutch is a regular hydraulically actuated clutch. A reaction clutch grounds a component and a coupling clutch couples two components when applied. A band clutch can only be applied as reaction clutch due to its structure.
An early type three‐speed FWD automatic transmission with its clutch table is shown in Figure 5.2. This transmission was developed by General Motors for FWD passenger cars in the 1970s and was applied across the GM product line for almost two decades. It uses two planetary gear trains for ratio change and a third PGT for the final drive. The transmission uses three multiple‐disk clutches and one band clutch. The one‐way clutch serves as the reaction clutch in first gear and makes the 1–2 upshift as a clutch to one‐way clutch shift. Clutch C3 serves as the reaction clutch for the reverse gear and also for the first gear when the driver selects the manual range for engine braking in downhill operations. To accommodate the assembly condition for transversely mounted engine, a chain is used to transfer power from the converter turbine to the transmission input.
It was in the 1980s that the four‐speed automatic transmissions started to enter the market in large scale, due to the ever more stringent demand for fuel economy. A four‐speed FWD automatic transmission developed by Ford is illustrated in Figure 5.3. This transmission and its variations were applied in Ford passenger vehicles for more than two decades until the introduction of the current generation of six‐speed automatics. Unlike the Simpson‐type, the planetary gear train set features two structural connections: front ring and rear carrier assembly, and front carrier and rear ring assembly. The latter is the output assembly, with a chain connecting it to the final drive input. The ATF pump is driven by the engine via a shaft passing through the center line of the transmission main structure. As shown in the clutch table, one‐way clutches are used to facilitate 1–2 and 3–4 upshifts. Clutch C3 is only applied in manual ranges in mountainous areas or in snowy conditions.
Figure 5.3 Structure of an early four‐speed FWD automatic transmission.
As discussed in Chapter 3, the Ravigneaux planetary gear train is structurally the combination of a dual‐planet PGT and a simple PGT with a shared ring gear and a shared carrier, as shown in Figure 3.22. Transmission designs based on Ravigneaux PGTs are more compact in comparison with those based on Simpson‐type PGTs. Figure 5.4 shows a four‐speed RWD transmission based on a Ravigneaux planetary gear train. This transmission was developed by Ford in the 1980s and was used in Ford pickup trucks for almost two decades. The transmission uses a total of eight clutches: four multiple disk clutches, two band clutches, and two one‐way clutches. As shown in Figure 5.4, the 1–2 and 2–3 upshifts are clutch to one‐way clutches. In manual ranges, band clutch B1 is applied in first gear and the band clutch B2 is applied in second gear.
Figure 5.4 A Ford four‐speed RWD Ravigneaux PGT automatic transmission.
Many different layouts for four‐speed ATs existed for production transmissions between 1980s and the beginning of the 21st century. Among the many AT structural designs, the FWD four‐speed AT named as Hydra‐matic 4 T80‐E and developed by General Motors in the early 1990s, stands out in terms of its seamless shift smoothness. As shown in Figure 5.5, the transmission uses two simple planetary gear trains, with the front ring gear and the rear carrier structurally connected as the output assembly. The front carrier and the rear ring gear are not structurally connected but coupled through four clutches, C4, C5, R2, and R3, in different gears. A chain with a ratio of 1 connects the turbine with the transmission input. With a total of 10 clutches: five multiple disk clutches, two band clutches and three one‐way clutches; this is the transmission that uses the highest number of clutches. Clutch C5 is a coast clutch that is only applied to enable engine braking in manual ranges. As can be seen in the clutch table, all upshifts, 1–2, 2–3, and 3–4, are clutch to one‐way clutches. This simplifies the upshift control and results in excellent shift quality. Clearly, there is a price to be paid for the enhanced shift smoothness since the ten clutches used in the transmission definitely increase hardware costs. This transmission and its variations were used across the product line of General Motors until around 2005, by which time the current generation of six‐speed FWD automatic transmissions had started to be the mainstream transmissions.
Figure 5.5 A four‐speed FWD AT with all clutch to one‐way clutch upshifts.
Unlike General Motor’s four‐speed AT discussed earlier, the four‐speed FWD AT developed by Chrysler in the late 1980s uses a lower number of clutches. As shown in Figure 5.6, the Chrysler transmission uses only five clutches to realize four forward speeds and one reverse. All shifts are clutch to clutch since no one‐way clutch is used in this transmission. In addition, this is the first transmission that uses only multiple disk clutches. In the absence of one‐way clutches during shifts, this transmission was the first that relied solely on advanced electronic control technology to realize shift smoothness. Note that the design of this transmission reflects the trend in the current generation of six‐speed and eight‐speed ATs, that use only multiple disk clutches in the minimum number possible, to reduce hardware cost and rely on control technology to guarantee shift quality.
Figure 5.6 Structure of a five‐clutch four‐speed FWD automatic transmission.
In addition to planetary gear train designs, four‐speed automatic transmissions had also been developed based on lay‐shaft gear designs. Lay‐shaft transmissions differ from planetary gear train transmissions mainly in structural layouts, the control systems for both types are similar in nature. Honda and the Saturn division of General Motors are the two major brand names that had developed and used lay‐shaft automatics for various passenger cars and SUVs. Figure 5.7 shows the layout of a Honda four‐speed lay‐shaft AT developed in the 1980s. The transmission is equipped with a torque converter, and gear shifts are realized by hydraulically actuated multiple disk clutches. As shown in the stick diagram and the clutch table, a hydraulically actuated shifter, called the “servo” in the stick diagram, engages forward gears in the D range and the reverse gear in the R range. A one‐way clutch is attached to the first gear on the counter shaft which enables the 1–2 upshift to be a clutch to one‐way clutch. The 2–3 and 3–4 upshifts are clutch to clutch. The first gear holding clutch is applied in manual ranges to enable engine braking when driving conditions deems it necessary. In comparison with planetary gear train automatic transmissions, lay‐shaft automatics have the advantage that many of the mechanical components are similar to those in manual transmissions that have similar lay‐shaft designs. It was more cost effective to develop a lay‐shaft automatic transmission based on existing manual transmission technology and technical resources than to develop a planetary gear train automatic transmission from scratch. However, lay‐shaft automatic transmissions are not as compact as their planetary gear train counterparts. In a lay‐shaft transmission, as shown in Figure 5.7, gear shafts are laid out parallel instead of coaxial, and multiple disk clutches are assembled separately on the lay‐shafts instead of nested in planetary gear train automatics. This makes lay‐shaft automatic transmissions bigger than planetary gear train counterparts. For transmissions with four, five, or even six forward speeds, it is still technically feasible to pack all the components, including, clutches, gears, and shafts into the limited volume allowed by a transversely mounted engine. Due to the intrinsic structural limitations, it would be very difficult to design an eight‐speed lay‐shaft automatic transmission that could be fitted to an FWD passenger car.
Figure 5.7 Honda lay‐shaft four‐speed FWD automatic transmission.
Improved versions were developed by Honda based the lay‐shaft automatic transmission shown in Figure 5.7. The one‐way clutch and the first gear holding clutch were eliminated in a later version, as shown in Figure 5.8. This version is smaller in overall dimensions due to the elimination of redundant components, and gear shifts are all clutch to clutch. Lay‐shaft transmissions was used across the Honda product line and were eventually replaced by other types of automatic transmissions with six or more speeds.
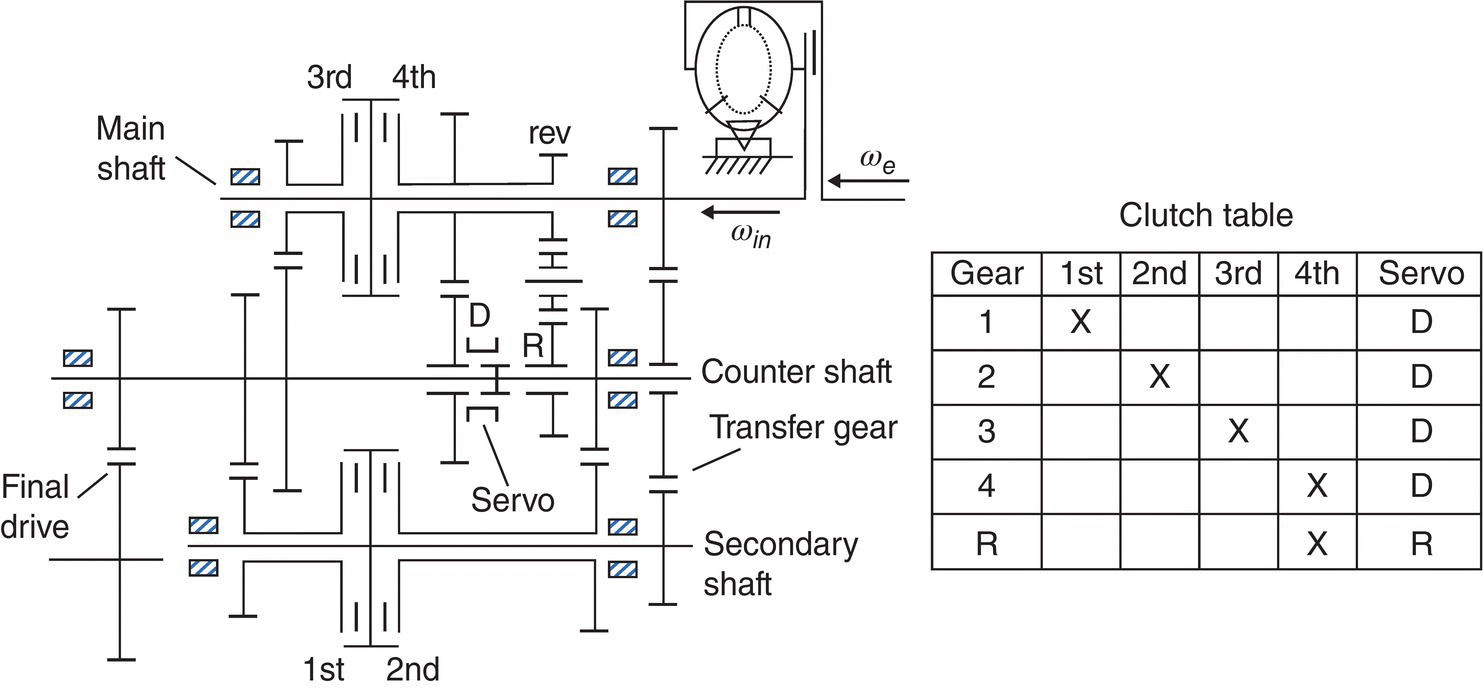
Figure 5.8 Honda lay‐shaft four‐speed FWD automatic transmission without one‐way clutch.
Automatic transmissions with four speeds had been the mainstream for FWD passenger cars or SUVs with 4WD extended from FWD layouts until around 2005. Five‐speed transmissions were also developed and used for various vehicles during the transition. Figure 5.9 shows a five‐speed RWD transmission developed by Ford. In this transmission, a third simple PGT is added in front a Simpson PGT set. Clutch C1 is only applied in manual ranges for engine braking. The fourth gear is a direct drive and the fifth gear provides an overdrive ratio of 0.69.
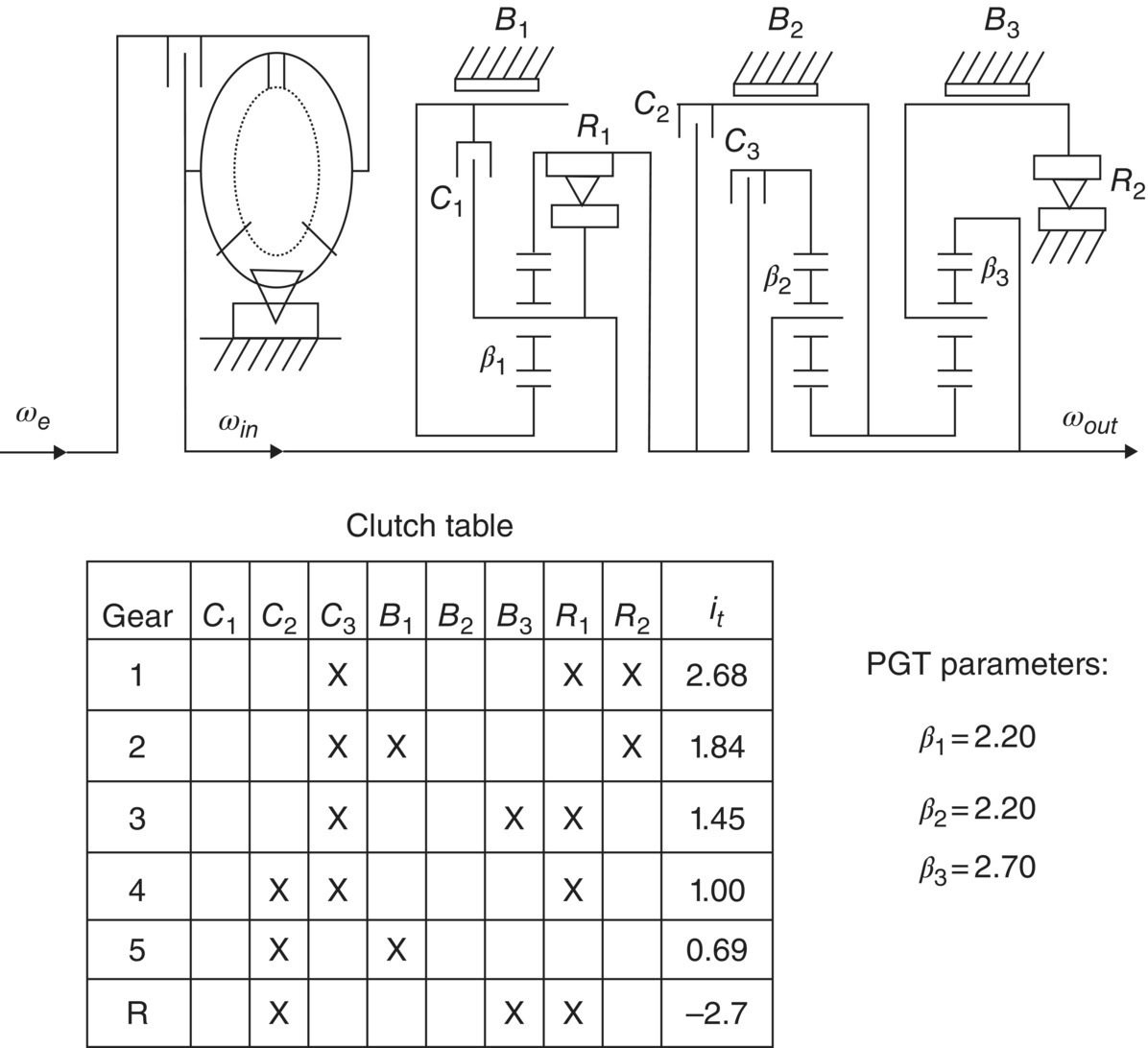
Figure 5.9 A five‐speed RWD automatic transmission.
A six‐speed FWD automatic transmission of the current generation is shown in Figure 5.10. This transmission was jointly developed by Ford and General Motors and is currently applied across the product lines of both companies in different versions. The transmission uses three simple planetary gear trains in parallel and six clutches: five multiple disk clutches and one one‐way clutch. The transmission output assembly consists of the first ring gear and the third carrier, and is connected to the differential carrier through two gear pairs via a transfer shaft. As shown in the clutch table, the one‐way clutch is only applied in first gear so that the 1–2 upshift is a clutch to one‐way clutch. Technically, the one‐way clutch F is redundant in kinematics and can be eliminated since it can be replaced by clutch D in first gear. The transmission would then have only five multiple disk clutches with all shifts clutch to clutch. Structurally, this transmission features an input shaft that passes through the whole transmission, with two input clutches, A and B, nested at the shaft end. Note that there is no band clutch in this transmission. Band clutches require actuation pistons and anchors that cannot be symmetrically mounted on the cylindrical transmission structure and are generally not as compact as multiple disk clutches. In addition, band clutches are not as responsive as multiple disk clutches in engagement or disengagement during transmission shifts. For these reasons, band clutches are no longer applied in the current generation of six‐speed or eight‐speed automatic transmissions and are now obsolete even though they have been applied in the automotive industry for almost 70 years since the first automatic transmission came into production.
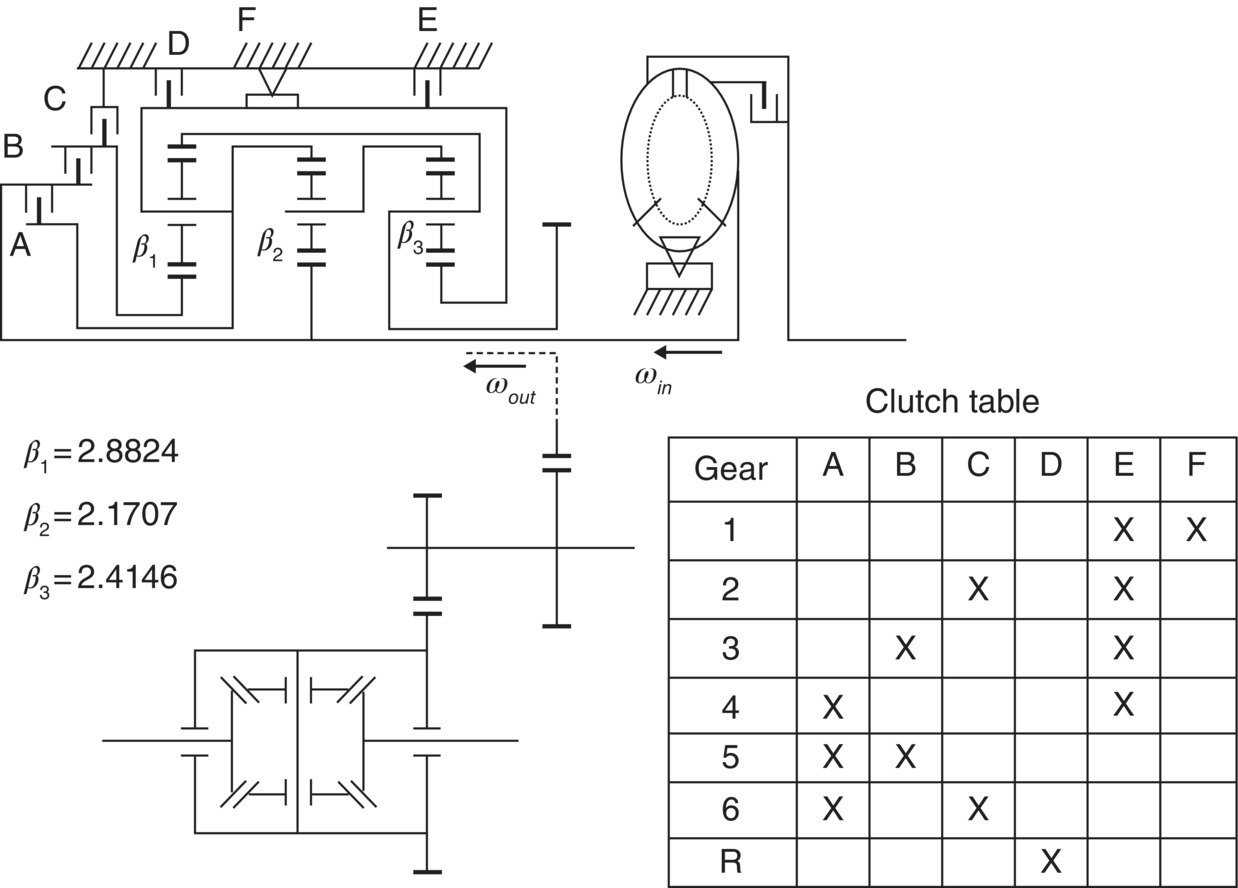
Figure 5.10 A Ford six‐speed FWD automatic transmission.
The six‐speed RWD automatic transmission developed by Ford is based on a planetary gear train setup different from the FWD version shown in Figure 5.10. This transmission is currently used in Ford RWD vehicles, including the popular F‐series pickups. The six‐speed RWD automatic is based on a setup that consists of a Ravigneaux planetary gear train and a simple planetary gear train, as shown in Figure 5.11. The transmission architecture can be considered as an extension of the four‐speed AT structure shown in Figure 5.4, with a simple PGT added in front the Ravigneaux PGT. The sun gear of the front simple PGT is fixed structurally, and the ring gear is connected to the transmission input. All shifts are clutch to clutch since no one‐way clutch is used in the transmission. This transmission uses five multiple disk clutches to realize six forward speeds and one reverse speed. In comparison, the previous generation four‐speed RWD automatics, shown in Figure 5.4, uses eight clutches to realize only four forward speed and one reverse speed. The improvements are significant in terms of not only transmission performance specifications but also component costs since the number of clutches is reduced from eight to five. These improvements are made possible thanks to the advanced technology in the transmission control hardware and software, as will be discussed in the next chapter.
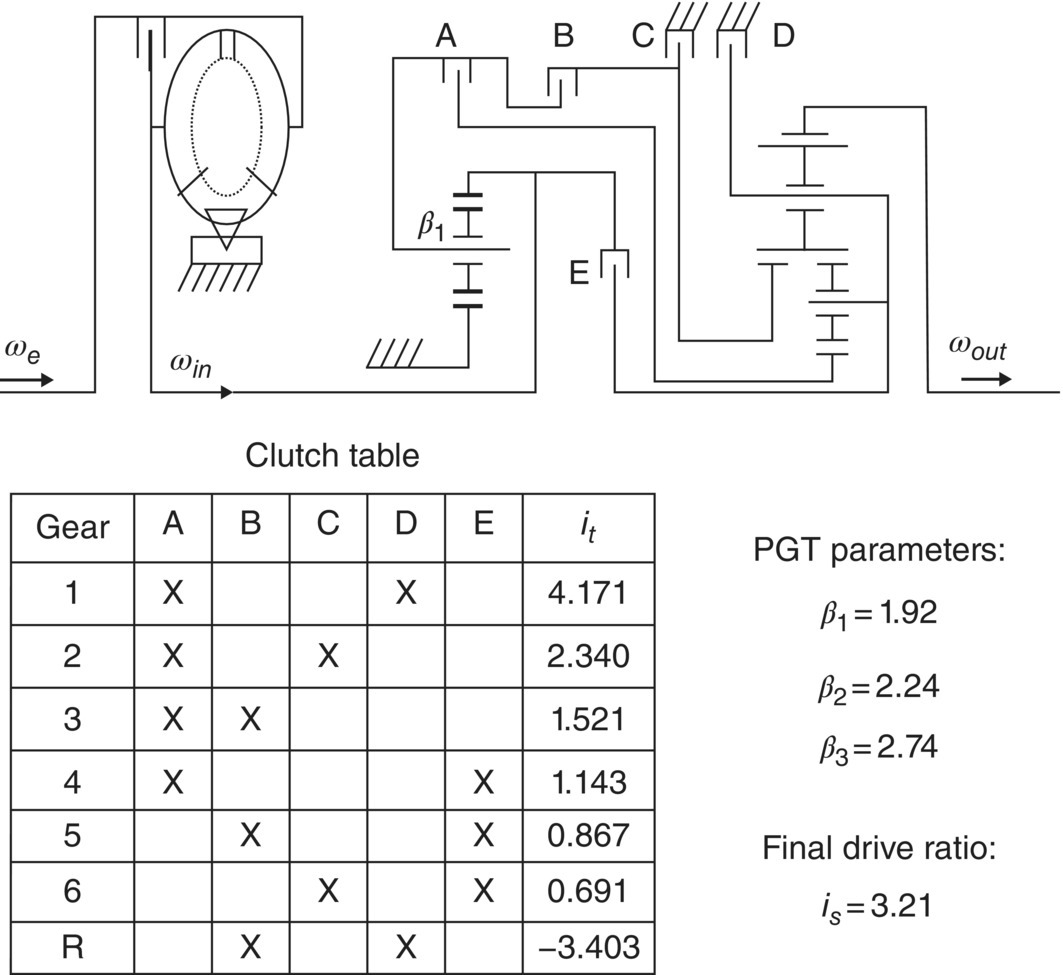
Figure 5.11 Ford six‐speed RWD Ravigneaux PGT automatic transmission.
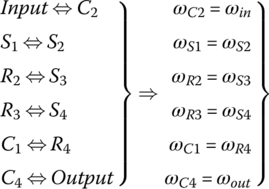
The ever more stringent demand on fuel economy led to the development of automatic transmissions with eight or more speeds. These transmissions have a wide ratio spread defined by the first gear ratio and the ratio of the highest gear, and enable engine matching close to the ideal condition due to the availability of multiple gear ratios. In addition, transmission ratios between neighboring gears are closer to each other in comparison with transmissions with six or fewer speeds, reducing intrinsically the harshness caused by shift dynamics. The design of transmissions with eight or more speeds is technically challenging because of the constraints on the overall transmission dimension and the number of clutches. In general, these transmissions need a planetary gear train setup that is difficult to achieve based on the extension from existing transmissions with fewer speeds. In the transmissions with eight or more speeds currently in production, three types of planetary gears trains – simple PGT with single planet, dual‐planet simple PGT, and Ravigneaux PGT – are used in various layouts to provide the ratio multiplicity. By using a dual‐planet PGT in a layout, more transmission ratio flexibility may appear because of the sign variations of the characteristic equation. The elements of these planetary gear trains are connected structurally and through clutches in a variety of layouts to form multiple power flows from the input to the output. In kinematics, there are six types of structural connections: sun‐sun, sun‐ring, ring‐carrier, ring‐ring, carrier‐carrier, and sun‐carrier. The planet gear only meshes with the ring gear and the sun gear, without being connected to any other element either by a clutch or structurally. Sun gear, carrier and ring gear, or an assembly containing one of them can be connected to the input by a coupling clutch, and can be grounded to the housing by a reaction clutch. Output is usually taken from a ring gear a carrier, or an assembly containing one of them. Automatic transmissions with eight or nine speeds shown below will demonstrate the basic guidelines on the mechanical structure of these transmissions described herein.
The first eight‐speed RWD automatic transmission, shown in Figure 5.12, was developed and used for Lexus vehicle models of the Toyota Motor Company. This transmission can be fitted to any RWD or 4WD vehicle. As shown in the stick diagram, the transmission is based on a setup that consists of a simple dual‐planet PGT and a Ravigneaux PGT. The ratio spread of the transmission is 6.71 and the intermediate ratios are closely populated between the first and the eight speeds. In the dual‐planet PGT, the sun is structurally fixed to the housing and the carrier is structurally connected to the input. The ring gear of the Ravigneaux PGT is the output element also structurally. It is meaningful to notice that none of the planetary gear train members are structurally interconnected. This maximizes the number of PGT elements that can be connected to the input or grounded and thus the number of power flows. There are seven clutches, including the one‐way clutch G that enables 1–2 upshift as a clutch to one‐way clutch. The one‐clutch G is redundant in kinematics and if eliminated, the transmission shifts would just be all clutch to clutch. As shown in the clutch table, two clutches are applied and five are open in each gear. The transmission realizes eight speeds in a compact design, using a planetary gear train setup that is not much more complicated than what is in a six‐speed automatics, such as the one shown in Figure 5.11, and should be credited as a significant engineering achievement. However, it uses seven clutches, even though one of them is a one‐way clutch that can be eliminated in later versions, and five clutches (or four without considering the one‐way clutch) stay open in each gear. These open clutches create drag losses that work against the fuel economy improvement gained from the availability of the eight transmission ratios.
Figure 5.12 Lexus eight‐speed RWD Ravigneaux PGT automatic transmission.
Hyundai was a latecomer to the development of automatic transmissions. However, it has made a great leap forward in transmission technologies over the past decade. The company has developed its own eight‐speed automatic transmission and successfully applied it in RWD models of its luxury Genesis brand. Figure 5.13 shows the structure of the eight‐speed automatics with the clutch table. The transmission is built on a setup that consists of three planetary gear trains, a simple PGT in the front, a dual‐planet PGT in the middle, and a Ravigneaux PGT in the rear. The PGT setup differs from the Lexus eight‐speed AT (shown in Figure 5.12) in the added front simple PGT. The transmission also has seven multiple disk clutches, including one‐way clutch G that facilitates the 1–2 upshift. Similar to the Lexus eight‐speed AT, two clutches are applied and five stay open in each gear. As shown in the clutch table, the fifth gear is a direct drive and the next three higher gears are all overdrives. By the combination of planetary gear train parameters shown with the stick diagram, the transmission achieved a first gear ratio of 3.665 and a eighth gear ratio of 0.556, with a ratio spread close to 7.0. It can be noticed from the clutch table that the transmission ratios are lower in comparison to those of the Lexus eight‐speed AT, a relatively high final drive ratio of 3.909 is therefore used for compensation of the overall powertrain ratio. The first four gear ratios are spread more widely than the higher gear ratios, as shown in the list by the ratio column. Note that different transmission ratios can be achieved by changing the values of the PGT parameters, and this is true generally for all other transmissions. Based on the ratio formulae for all gears, the four PGT parameters can be selected to optimize the combination of gear ratios that fits the requirement of a specific application. Due to the added front PGT, the Hyundai eight‐speed AT is somewhat larger in size in comparison to the Lexus eight‐speed automatics. The attributes in transmission efficiency of the two transmissions should be similar because both have six multiple disk clutches and one one‐way clutch, with two engaged and five open in each gear.
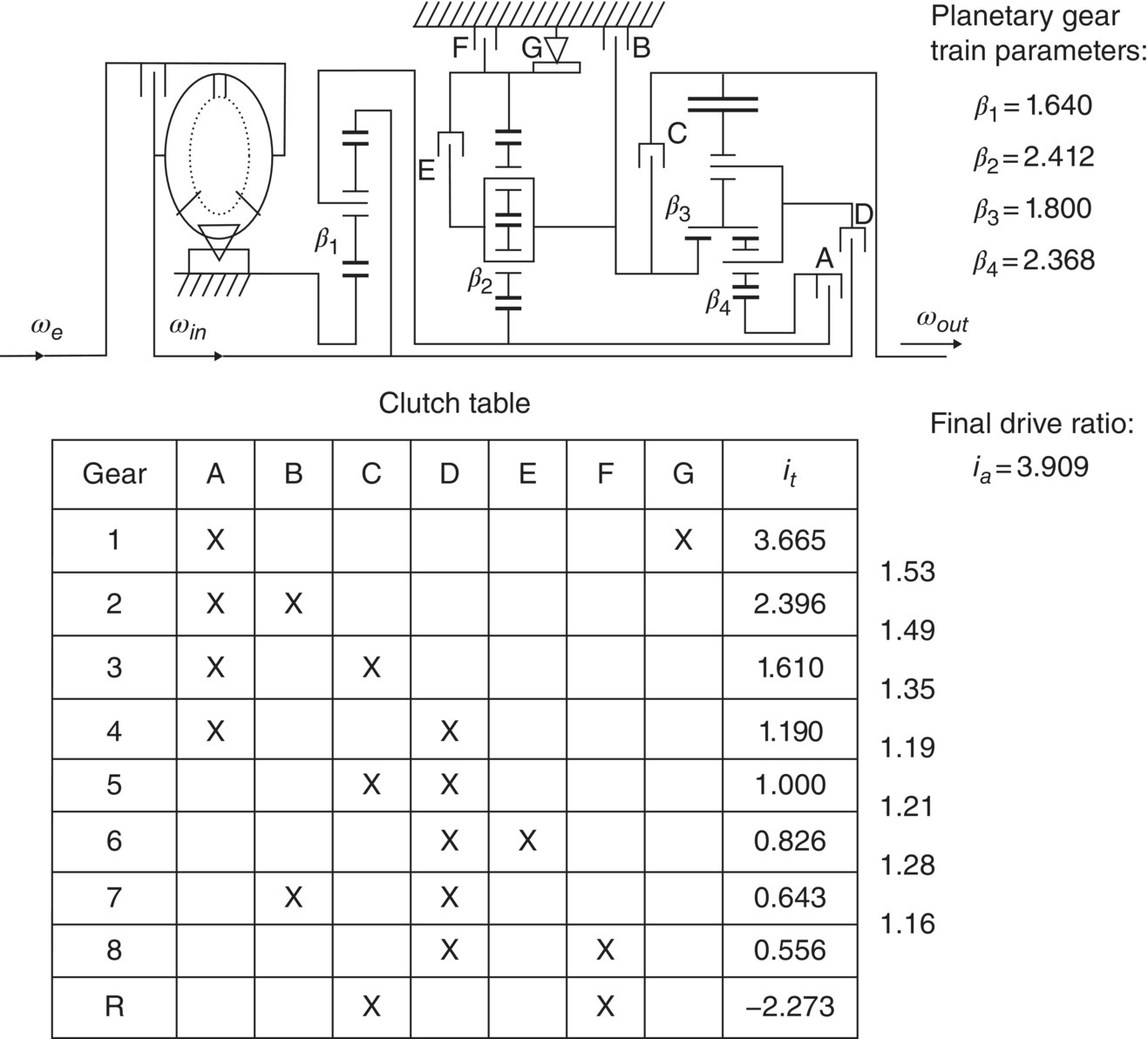
Figure 5.13 Hyundai eight‐speed RWD Ravigneaux PGT automatic transmission.
The ZF eight‐speed RWD AT, shown in Figure 5.14, features perhaps the most compact structural design for the current generation of eight‐speed automatics. This transmission is built on a planetary gear train setup that consists of four simple PGTs. Only five multiple disk clutches are used for the eight forward speeds and one reverse gear. The most remarkable aspect of this transmission is that in each gear there are only two open clutches. This minimizes the parasitic clutch drag loss and is an apparent advantage over the designs of the Lexus or Hyundai eight‐speed automatics. The sixth gear is a direct drive and the seventh and eighth gears are overdrives. The ratio spread is more than 7.0, resulting in close to optimized engine matching for acceleration and fuel economy performances. Note that the reverse gear in this transmission is achieved by a specific combination of PGT motions, instead of the common reverse gear realization where a sun gear is connected to the input, the carrier is grounded and the ring gear is connected to the output. The ZF eight‐speed RWD AT has been well received by the automotive industry and has been applied for not only luxury brands, such as BMW and Mercedes Benz, but also less expensive brands such as Chrysler and Jeep. The next section of this chapter will provide a detailed study on the structure, kinematics, and dynamics of this transmission as an example for all other transmissions.
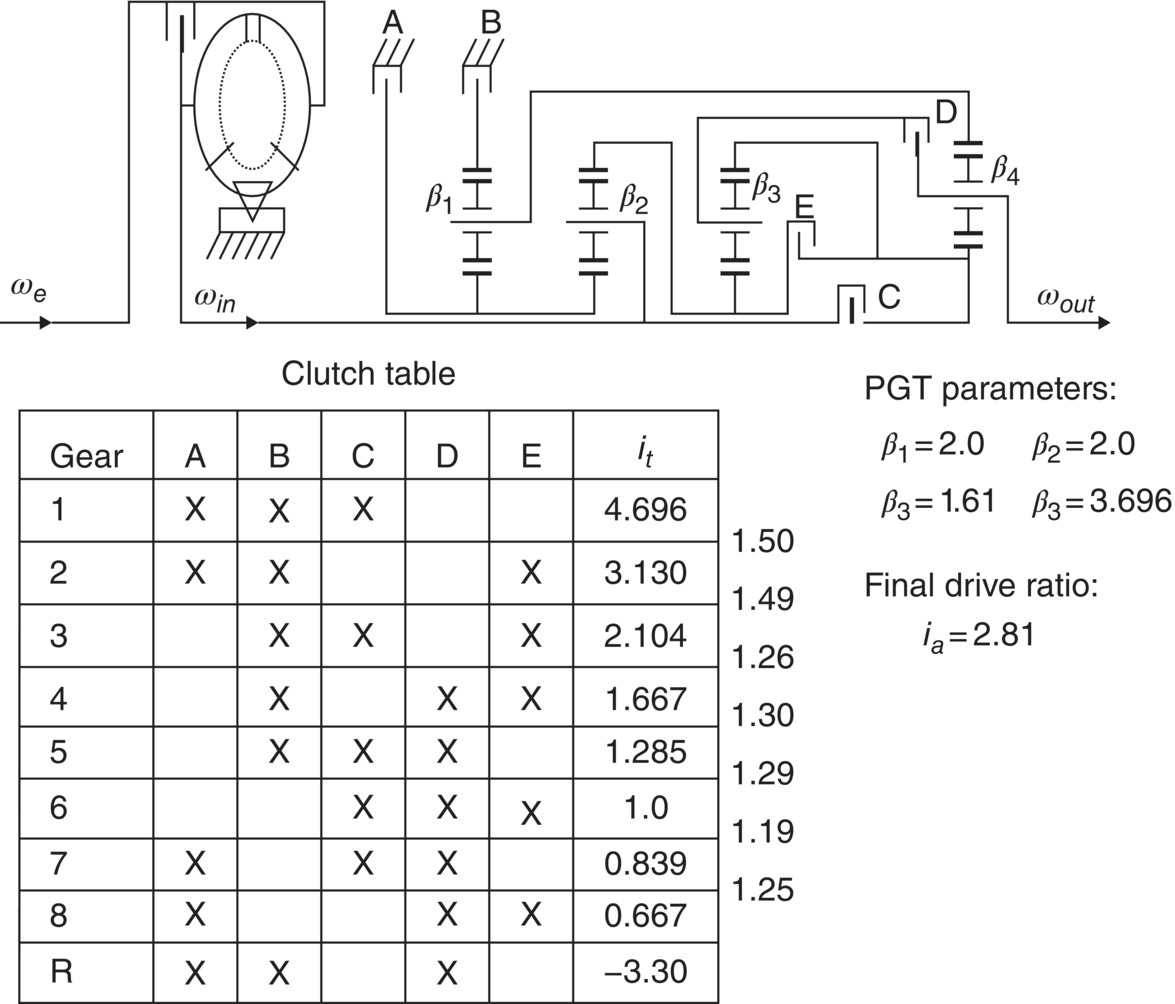
Figure 5.14 ZF eight‐speed RWD automatic transmission.
Automatic transmissions with eight speeds were first developed for luxury vehicle models which usually prefer rear wheel drive. The structural design of FWD ATs with multiple gear ratios is generally more challenging since the packaging conditions for transversely mounted engines are more stringent in comparison with longitudinal engine layouts. However, development of FWD automatic transmissions with eight or more speeds does not lag far behind and is proceeding rapidly in the automotive industry. The ZF nine‐speed FWD AT, shown in Figure 5.15, is the very first FWD automatic transmission that has nine forward speeds. This transmission is built on a planetary gear train setup that is remarkably different from all existing transmission designs. As shown in the stick diagram, there are four simple planetary gear trains, with planetary parameter β labeled with subscripts 1, 2, 3, and 4 from left to right respectively. There are two structural connections between PGT 1 and PGT 2: sun gear 1 with sun gear 2 and ring gear 1 with carrier 2. What distinguishes this transmission are the two structural connections between PGT 3 and PGT 4: carrier 3 with carrier 4 and sun 3 with ring 4. The transmission uses four multiple disk clutches, B, C, D, and E, and two shifters, A and F, to achieve nine forward speeds and one reverse, as shown in the clutch table. The two shifters, which are actually sliding sleeves with internal splines similar to those in manual transmissions discussed in Chapter 2, are hydraulically actuated to move axially to engage or disengage the dog teeth on the sun 1–sun 2 assembly and sun 3–ring 4 assembly respectively. Shifts involving the engagement or disengagement of either shifter A or shifter F must be well synchronized to avoid impact or grinding between shift sleeve and dog teeth. This can be technically challenging, especially in downshifts to the fourth or seventh gears where either shifter F or shifter A is the oncoming engagement element. The transmission has four overdrives, with the fifth gear as a direct drive. The nine forward gear ratios are spread between the first gear ratio of 4.70 and the ninth gear ratio of 0.48, resulting a high ratio spread of 9.8. The transmission output is from the carrier of PGT 1 and is transmitted to the differential carrier through two pairs of transfer gears. Because of the compact planetary gear train setup and the two space saving shifters, the transmission realizes nine forward gears and one reverse gear in a dimension comparable to that of a six‐speed FWD automatic. The Jeep Cherokee SUV is the first vehicle model that is equipped with this transmission in both FWD and RWD versions. In the RWD version, power is transferred by a spiral bevel gear pair with the pinion attached to the differential carrier to the rear axle via the drive shaft. It has been reported that the Acura MDX will also be equipped with the ZF nine‐speed automatic in the 2017 model year.
Figure 5.15 ZF nine‐speed FWD automatic transmission.
5.3 Ratio Analysis and Synthesis
Gear ratios in automatic transmissions based on planetary gear train designs are achieved by connecting and grounding different PGT elements to the input and to the housing respectively through a particular clutch combination in each speed. The kinematics of planetary gear trains, covered in Chapter 3 (Section 3.8), is the key to the analysis and synthesis of transmission gear ratios. In general, three types of planetary gear trains are used in the transmission structure: simple PGT, dual‐planer PGT, and Ravigneaux PGT. The characteristic equation for each of these three types of PGT was derived in Section 3.8 and is represented in the following for the systematic analysis and synthesis of transmission gear ratios.
Simple planetary gear train:
Dual‐planet planetary gear train:
Ravigneaux planetary gear train:
As detailed in Section 3.8, a Ravigneaux PGT is structurally a combination of a simple PGT and a dual‐planet PGT with shared carrier and ring gear. There are two mesh paths in a Ravigneaux PGT: Eq. (5.3) is the characteristic equation for the first mesh path “Sun S1 – Long Planet – Ring” and Eq. (5.4) is the characteristic equation for the other mesh path “Sun S2 – Short Planet – Long Planet – Ring”. The PGT characteristic equations listed above and the constraint equations caused by clutch engagements will be used systematically for the analysis and synthesis of transmission ratios. In this section, three production transmissions are chosen as examples for the ratio analysis and synthesis:– the Ford FWD six‐speed AT, designed with simple PGTs (Figure 5.10); the Ford six‐speed RWD AT, designed with a simple PGT and a Ravigneaux PGT (Figure 5.11); and the ZF eight‐speed RWD AT, designed with four simple PGTs (Figure 5.14). These transmissions feature structural designs typical of the current generation of multiple ratio automatics. The concepts and methods for ratio analysis and synthesis in the three examples can be readily extended to all other automatic transmissions with different structural layouts.
5.3.1 Ford FWD Six‐Speed AT
As illustrated in the stick diagram (Figure 5.10), the Ford FWD six‐speed automatics uses three simple planetary gear trains in parallel in the structure layout. The planetary gear train parameters of respectively are labeled as β1, β2, and β3, with the subscripts indicating PGT 1, PGT 2, and PGT 3. The three characteristic equations in the following are intrinsic of the three PGTs in the transmission:
In the equations above, there are nine angular velocities, three for each planetary gear train. These are two types of constraints on these nine angular velocities: structural constraints and clutch constraints. Structural constraints are from the interconnections between planetary gear train elements or members in the transmission design. As can be found from the stick diagram (Figure 5.10), there are four structural connections: Carrier 
Ring R2; Carrier 
Ring R3; Sun 
Input; Ring 
Carrier 
Output. These four structural connections yield four constraint equations upon the related angular velocities, as follows:
These four constraints are then superimposed upon Eqs (5.5–5.7), resulting in a new set of three linear equations with only six independent angular velocities, including ωin and ωout:
After the structural connections are considered, there are six independent angular velocities that are governed by the three equations above, which are characteristic of the transmission and are satisfied for all speeds. Among these six angular velocities, or six motions, one must be provided as the input, and the remaining five angular velocities, including the output, must be uniquely defined in kinematics. It is apparent that there are two equations or two constraints short for the unique determination of these five angular velocities and this shortage in constraints is filled up by the clutch engagement. As shown in the clutch table in Figure 5.10, two clutches are applied in each gear. Therefore, two additional constraints are provided by the clutch engagement in each gear and are combined with Eqs (5.8–5.10) for the unique solution of the angular velocities in terms of the input angular velocity.
5.3.1.1 Ratio Analysis
Ratio analysis concerns the determination of all gear ratios for a given transmission design and clutch table and is relatively straightforward. The first step is to write down the characteristic equations for the planetary gear trains in the transmission structure. The second step is to superimpose the structural constraints in the transmission upon the set of characteristic equations. These two steps have been completed above for the Ford FWD six‐speed AT in the example. Now, the constraints from clutch engagement in each gear are combined with Eqs (5.8–5.10) for the determination of all gear ratios for the six forward gears and one reverse gear.
First gear: In first gear, clutches E and F are applied. Sun gear S3 and carrier C1 are both grounded to the housing since both clutch E and clutch F are reaction clutches. With 
and 
, Eqs (5.8–5.10) form a linear equation system in terms of three unknown angular velocities ωS1, ωC1, and ωout with ωin given as:
This equation system can be easily solved for angular velocities ωS1, ωC2, and ωout in terms of ωin, as well as the first gear ratio i1 as follows:
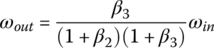
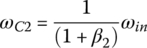
Second gear: In second gear, clutches E and C are applied. Sun gear S3 and sun gear S1 are both grounded to the housing since both clutch E and clutch C are reaction clutches. With 
and 
, Eqs (5.8–5.10) form a linear equation system in terms of three unknown angular velocities ωC1, ωC2, and ωout with ωin given as:
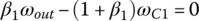
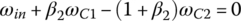
This equation system leads to the solution for the second gear ratio and angular velocities ωC1 and ωC2 in terms of ωin:
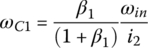
Third gear: In third gear, clutches E and B are applied. Sun gear S3 and sun gear S1 are grounded to the housing or connected to the input. With 
and 
, Eqs (5.8–5.10) form a linear equation system in terms of three unknown angular velocities ωC1, ωC2, and ωout with ωin given as:
This equation system leads to the solution for the third gear ratio and angular velocities ωC1 and ωC2 in terms of ωin:
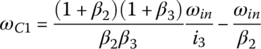
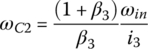
Fourth gear: In fourth gear, clutches E and A are applied. Sun gear S3 is grounded to the housing and carrier C1 is connected to the input. With 
and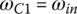 
, Eqs (5.8–5.10) form a linear equation system in terms of three unknown angular velocities ωS1, ωC2, and ωout with ωin given as:
This equation system leads to the fourth gear ratio and angular velocities ωS1 and ωC2 in terms of ωin:
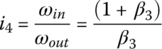
Fifth gear: In fifth gear, clutches B and A are applied, coupling sun gear S1 and carrier C1 to the input at the same time, and thus making PGT1 turn in unity. The three planetary gear trains turn as a whole body due to the structural connections, resulting in a direct drive with a gear ratio of one. This can also be demonstrated by the transmission characteristic equations. With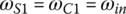 
, it is from Eqs (5.8–5.10) that all angular velocities must be the same as the input angular velocity ωin.
Sixth gear: In sixth gear, clutches C and A are applied, grounding sun gear S1 to the housing and coupling carrier C1 to the input. With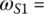 
0 and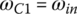 
, the transmission characteristic equations (5.8–5.10) form a system of linear equations in terms of ωC2, ωS3, and ωout with the input angular velocity ωin as given:
Since sun S1 is grounded, carrier C1 is connected to the input and ring R1 is the output, so the sixth gear of the transmission is an overdrive. The overdrive ratio and angular velocities ωC2 and ωS3 are determined by:
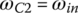
Reverse gear: In reverse gear, clutches B and D are applied, connecting sun gear S1 to the input and grounding carrier C1 to the housing. This is a typical reverse gear design used in the majority of automatic transmissions. With 
and 
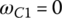, the transmission characteristic equations (5.8–5.10) form a system of linear equations in terms of ωC2, ωS3, and ωout with the input angular velocity ωin given as:
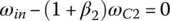
These equations lead to the solution of the reverse gear ratio and angular velocities ωC2 and ωS3 as:
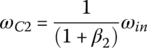
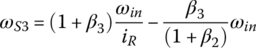
In summary, plugging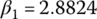 
, 
, and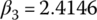 
into the ratio formulae just derived, the transmission ratios are: 
, 
, 
, 
, 
, 
, 
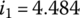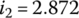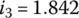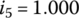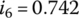. The minus sign for the reverse gear ratio means that the output angular velocity is opposite to that of forward gears.
5.3.1.2 Ratio Synthesis
The objective of ratio synthesis for automatic transmissions is to obtain the maximum number of transmission ratios with optimized ratio spread in the most compact structure with a clutch engagement sequence conducive to shift control. Ratio synthesis is implemented in three aspects: Structural synthesis, ratio formulation, and clutch sequencing. In the following, the Ford FWD six‐speed AT, as analysed, is used as an example for transmission ratio synthesis. The techniques and methods used in the example can be extended to all other transmissions with multiple ratios.
Structural synthesis: Automatic transmissions are designed in various configurations based on a series of planetary gear trains. As mentioned previously, three PGTs types, simple PGT, dual‐plane PGT, and Ravigneaux PGT, are commonly used in automatic transmission structures. The structural synthesis is the first step in ratio synthesis and focuses mainly on the number of PGTs, the structural connections between PGT elements, the number of clutches, and the element or assembly to which each clutch is attached. Although structural synthesis is a trial and error practice by nature, certain guidelines can be followed to make the practice less time consuming and more productive. In general, transmissions with six speeds can be designed with three PGTs, and the design of transmissions with eight or more speeds require three or four PGTs. The use of dual‐planet PGTs in the transmission structure may provide more flexibility in the ratio formulae that generate more useful ratios.
The key to structural synthesis is the structural interconnections between PGT elements or members. In general, there are six possible structural connections between two members in two individual PGTs:
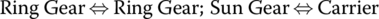
Note that planet gears are only internal PGT members that cannot be used for either input or output or reaction. In addition to the structural connections between PGT members, one PGT member or an assembly containing a PGT member must be structurally connected to the transmission output to avoid the coupling of a PGT member or assembly through a clutch to the vehicle inertia. Transmission input can also be structurally connected to a PGT member or assembly. But the connection between PGT members must not cause interference in the structural layout and must facilitate the installment of the related reaction and coupling clutches. To visualize the structural connections, the planetary gear trains to be used in the transmission can be drawn first in the stick diagram independently, i.e. without any structural connections. Possible structural connections can then be drawn in the stick diagram between PGT members or between a PGT member and the input or the output. The following tips should be useful in the process of structural synthesis:
- The total number of angular velocities or motions, Nω, is equal to 3n, with n as the number of PGTs. Since these Nω angular velocities must satisfy the n characteristic equations in kinematics, the number of independent angular velocities, NI, before any structural constraints are imposed, is equal to
. - A structural connection between a PGT member or assembly and the input is counted as a structural constraint without reducing the number of the independent angular velocities, but the structural connection between a PGT member or assembly and the output is not counted as a structural constraint.
- Each structural interconnection between two PGTs is counted as a structural constraint and reduces the number of the independent angular velocities by one.
- The total number of structural constraints, NSC, is equal to the sum of the number of structural interconnections between two PGTs, NPP, and the number of structural connections between a PGT member or assembly with the input, NPI, i.e.
. - The number of additional constraints from clutch engagement, or the number of clutches, NC, to be applied in each gear, is equal to the total number of independent angular velocities, NI, minus the total number of structural constraints, i.e.
. - The number of angular velocities available for ratio synthesis, NRS, is equal to the difference between the total number of angular velocities, Nω, and the number of structural interconnections between two PGTs, NPP, minus one. That is,
. This is because one of the angular velocities has to be the output angular velocity structurally. - The number of possible transmission ratios, NR, is then equal to the combinations of the number of clutches, NC, out of the number of angular velocities available for ratio synthesis, NRS, i.e.
. - Some of the possible power flows are useless for gear ratios and are eliminated in the rest of the ratio synthesis process.
The number of possible structural connections depends on the number of gears to be designed for the transmission. If an automatic transmission with six forward speeds and one reverse, such as the Ford FWD six‐speed AT, is to be designed with three PGTs, the structural connections can be established in the following logic. Firstly, there are nine angular velocities if the three PGTs are independent of each other, i.e. if no structural connection exists, and these nine angular velocities are only constrained by the three characteristic equations, one for each PGT. Each structural connection between two PGTs will reduce the number of angular velocities by one. For example, if three such structural connections are imposed upon the three PGTs, as is the case in the Ford FWD six‐speed AT, the number of angular velocities would then be reduced to six. The other structural connection between the input and sun gear S2 does not reduce the number of angular velocities. Secondly, these six angular velocities must still satisfy the three characteristic equations with one as the given input, so two additional constraints, from two clutches separately, must be placed in each gear upon the other five angular velocities for their unique determination. Since one of the six angular velocities must be chosen as the output structurally, the number of angular velocities available for ratio synthesis is five. Therefore the number of possible power flow paths or gear ratios is equal to the number of combinations of two out of five, i.e. 
. Since the number of possible gear ratios is larger than the required number of gear ratios, that is seven for all forward and reverse speeds, for the AT to be designed, the structural synthesis can be continued on the three PGTs with four structural connections. There may be multiple configurations based on the three PGTs with four structural connections, some of them may not be applicable for transmission designs because of the structural complexity, and others are useless gear ratio values or unacceptable clutch sequence. These useless configurations can often be eliminated by simple observation. The Ford FWD six‐speed AT shown in Figure 5.10 is based on one of the useful configurations and should be the one that offers the best ratio spread, structural compactness, and clutch sequence. It is interesting to note that three of the ten possible power flows, corresponding to clutch combinations AD, BC, and CD, are useless since they result in transmission lock‐up. All the other seven clutch combinations are used for the six forward speeds and one reverse.
Consider now that four structural interconnections between two PGTs are imposed on the three planetary gear trains. This would reduce the number of angular velocities from nine to five. The remaining five angular velocities must still satisfy the three characteristic equations, so two clutches must be applied to provide the two additional constraints. One of five angular velocities is used as the output structurally and the number of angular velocities available for ratio synthesis is equal to four. Therefore, the number of possible power flow paths or gear ratios is equal to the number of combinations of 2 out of 4, i.e. 
. This will not work since the number of possible gear ratios is less than the number of gear ratios required in the six‐speed transmission. Ratio synthesis cannot be continued on the three PGTs with four such structural connections.
These guidelines can also be applied for the structural synthesis of automatic transmissions with more than six forward speeds and should make the trial and error process more effective.
5.3.1.3 Ratio Formulation
Once a configuration is chosen from the possible combinations in the structural synthesis discussed, the ratio formulae can then be derived in terms of the PGT parameters based on the characteristic equations and the clutch constraints, as demonstrated in the ratio analysis, in which the Ford FWD six‐speed AT was used as the example. If a simple PGT in the structural configuration is replaced by a dual‐planet PGT, the corresponding PGT parameter then becomes negative in the ratio formulae. Using the ratio formulae derived for all speeds, the values of these PGT parameters can be optimized in a certain range in terms of ratio values and ratio spread. Once these PGT parameters are selected, the ratio values for all forward speeds are then calculated and arranged in a sequence from the highest to the lowest, i.e. from the first gear to the highest gear. The corresponding clutch combinations are also arranged in a sequence of the same order.
5.3.1.4 Clutch Sequencing
The principle in clutch sequencing is that all transmission shifts shall only involve two clutches, one oncoming and one off‐going. This requires the clutch combination sequence in a specific pattern, as shown in the clutch table for the Ford FWD six‐speed AT (Figure 5.10). The sequence of clutch combinations is mainly affected by the transmission structure, i.e. the result of structural syntheses, but is also affected to a lesser degree by the selection of planetary gear train parameters. It is possible that some clutch combinations fall out at the right sequence for some initial selections of planetary gear train parameters. By modifying the selected PGT parameters, it is also possible to vary the ratio values so that the clutch combinations will be in the right sequence that makes all shifts with only two clutches involved.
5.3.2 Ford six‐speed RWD Ravigneaux AT
Since a Ravigneaux PGT is structurally a combination of a simple PGT and a dual‐planet PGT with shared carrier and ring gear, automatic transmissions based on Ravigneaux PGTs are generally advantageous in terms of compactness. The procedure for the ratio analysis and synthesis of this type of automatic transmission is similar in nature to that for ATs with only simple PGTs. As shown in Figure 5.11, the Ford six‐speed RWD AT is designed structurally with a combination of a simple PGT and a Ravigneaux PGT. Three characteristic equations can be written for these two PGTs:
There are seven angular velocities, three for the simple PGT and four for the Ravigneaux PGT. The first equation, Eq. (5.11), is written for the simple PGT with β1 as the PGT parameter, and the other two, Eqs (5.12) and (5.13), are written for the two mesh paths of the Ravigneaux PGT with PGT parameters β2 and β3 respectively. As can be seen from the stick diagram (Figure 5.11), sun gear S1 is structurally fixed and ring gear R1 is structurally connected to the input, providing two structural constraints in the transmission layout. The output member of the transmission is structurally the ring gear of the Ravigneaux PGT. Therefore, Eqs (5.11–5.13), become a new set of three linear equations with six independent angular velocities, including ωin and ωout:
These three equations are characteristic of the transmission and must be satisfied in all the six forward gears and the one reverse gear. It is apparent that with the input angular velocity given, two additional conditions are needed to uniquely define the other five angular velocities. As shown in the clutch table in Figure 5.11, two clutches are applied in each gear. Therefore, the two additional constraints provided by the clutch engagement in each gear are combined with Eqs (5.14–5.16) for the unique solution of the angular velocities in terms of the input angular velocity.
5.3.2.1 Ratio Formulation
The ratio formulation for the Ford RWD six‐speed AT is similar in nature to that for the Ford FWD six‐speed AT. For example, clutch B and E are applied in the fifth gear, respectively coupling sun S2 with carrier C1 and connecting carrier C2 to the input. The three equations, Eqs (5.14–5.16), then become a system of linear equations in terms of three unknowns, ωC1, ωS3, and ωout, with ωin given as:
This equation system directly leads to the fifth gear ratio formula in terms of the PGT parameters and the solutions of angular velocities, ωC1 and ωS3:
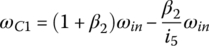
Similarly, the transmission ratio formulae for all speeds can be derived by combining the characteristic equations, Eqs (5.14–5.16), with the constraints from the respective clutch engagement shown in Figure 5.11:
The three PGT parameters,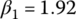 
, 
, and 
, as shown in Figure 5.11, result in the six forward ratios and the reverse ratio listed in the last column of the clutch table. These three PGT parameters also result in the clutch sequence as shown. Note that, in the Ford RWD six‐speed AT, there is no direct drive and the first PGT serve as a reduction unit for the first four speeds and the reverse speed.
For the sake of structural synthesis, it is interesting to compare the structures of the Ford RWD six‐speed AT shown in Figure 5.11 and the Lexus RWD eight‐speed AT shown in Figure 5.12. There is no significant difference in the planetary gear train layout between the two transmissions. Both use a Ravigneaux PGT, and in front of it there is a simple PGT in the Ford design and a dual‐planet PGT in the Lexus design. The Ford design uses the simple PGT as a reduction unit with the carrier as the unit output for the first four speed and reverse speed, while the Lexus design uses the dual‐planet PGT as a reduction unit with the ring gear as the unit output for the first five forward speeds. In a configuration that resembles the Ford design in PGT setup, the Lexus AT realizes eight forward speeds by adding one more multiple disk clutch in the transmission structure. The one‐way clutch in the Lexus AT is redundant in kinematics and is only used in first gear to enable clutch to one‐way clutch 1–2 upshift.
5.3.3 ZF RWD Eight‐Speed AT
The ZF RWD eight‐speed AT is designed with four simple planetary gear trains and five multiple disk clutches in the structure shown in Figure 5.14. The design has many advantages in comparison with other six‐speed or eight‐speed AT designs. Firstly, the ZF eight‐speed AT uses only five clutches, while other eight‐speed ATs, such as the Lexus eight‐speed AT and the Hyundai eight‐speed AT shown in Figures 5.12 and 5.13, use six clutches even without counting the one‐way clutch. Secondly, among the five clutches in ZF eight‐speed AT, three are applied and only two are open in all speeds, minimizing the parasitic clutch drag loss. Thirdly, due to the smaller number of clutches and other components, the ZF eight‐speed AT excels in hardware cost and compactness. There are many possible structural layouts based on a setup consisting four planetary gear trains, the ZF eight‐speed AT design should be one of the best and might be a unique layout that features the advantages mentioned.
For the four simple planetary gear trains in the ZF RWD eight‐speed AT, there are four structural interconnections, as shown in Figure 5.14. In addition, the second carrier C2 is structurally connected to the input shaft and the output of the transmission is structurally from carrier C4. There are five constraints on the angular velocities of related PGT members from structural connections, including the constraint from the input structural connection. The structural connections and the corresponding constraints are as follows:
There are 12 angular velocities and four characteristic equations for the four PGTs in the transmission. The transmission characteristic equations are formed by superimposing the constraints listed above upon the four PGT characteristic equations:
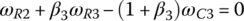
There are eight independent angular velocities, including the input angular velocity ωin, that are governed by these four transmission characteristic equations. With the input angular velocity provided to the transmission, the remaining seven angular velocities must be uniquely determinant in kinematics for each gear. Therefore, three of the five clutches must be applied to provide the three additional constraints required. The number of clutch combinations is then equal to the combination of three in five, i.e. 
. One of these ten clutch combinations, AEC, is useless since it locks up the transmission. The remaining nine clutch combinations provide eight forward speed and one reverse ratios, as listed sequentially in the clutch table in Figure 5.14. The constraints on the angular velocities in each gear are listed in the following table in accordance with the clutch engagement:
Clutch constraints
| Gear | Clutches applied | Constraints on angular velocities | Ratio |
| 1st | A, B, C | ωS1 = 0; ωR1 = 0; ωR3 = ωin | i1 |
| 2nd | A, B, E | ωS1 = 0; ωR1 = 0; ωR3 = ωR2 | i2 |
| 3rd | B, C, E | ωR1 = 0; ωR3 = ωin; ωR3 = ωR2 | i3 |
| 4th | B, D, E | ωR1 = 0; ωC3 = ωout; ωR3 = ωR2 | i4 |
| 5th | B, C, D | ωR1 = 0; ωR3 = ωin; ωC3 = ωout | i5 |
| 6th | C, D, E | ωR3 = ωin; ωC3 = ωout; ωR3 = ωR2 | i6 |
| 7th | A, C, D | ωS1 = 0; ωR3 = ωin; ωR3 = ωout | i7 |
| 8th | A, D, E | ωS1 = 0; ωC3 = ωout; ωR3 = ωR2 | i8 |
| Rev | A, B, D | ωS1 = 0; ωR1 = 0; ωC3 = ωout | iR |
All sequential upshifts or downshifts in the ZF eight‐speed AT are the so‐called direct shift, or clutch to clutch shift, with one oncoming and another off‐going. In addition to sequential shifts, the transmissions can also make direct non‐sequential shifts, should vehicle operations deem them necessary in terms of fuel economy or performance. With upshifts and downshifts counted separately, there are a total of 36 direct shifts, sequential and non‐sequential combined, as shown in Figure 5.16. Note that other non‐sequential shifts are possible in kinematics, but it would then involve three clutches during shift processes, making shift control much more technically challenging. The 36 available directs should be sufficient for the selections of gears that best fit the driver’s intention and vehicle operation conditions.
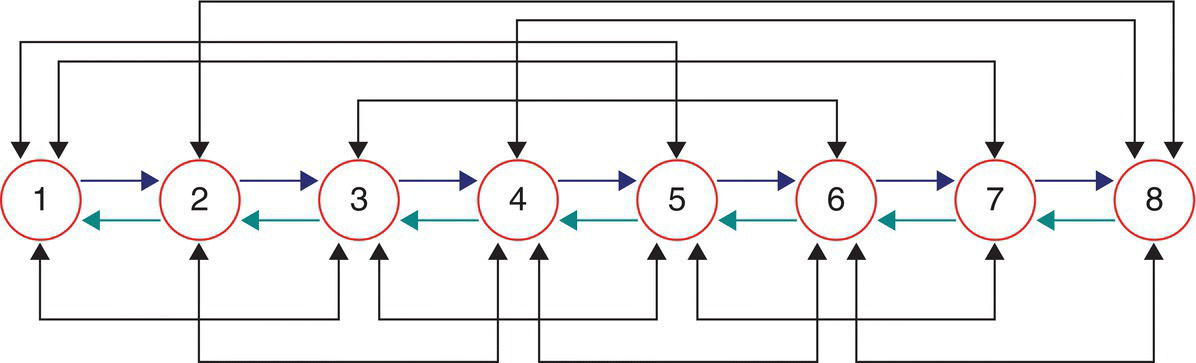
Figure 5.16 Direct shifts in ZF RWD eight‐speed automatic transmission.
5.3.3.1 Ratio Formulation
Similar to the two previous examples, the ratio formulation for the ZF Ford RWD eight‐speed AT can be derived using the combination of the characteristic equations from Eqs (5.17–5.20) and the clutch constraints on the related angular velocities in each gear. For example, the fifth gear ratio is determined in terms of the planetary parameters by plugging in the clutch constraints of the fifth gear, namely,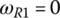 
; 
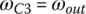; and 
, in Eqs (5.17–5.20):
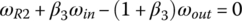
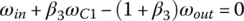
With ωin given, the other four angular velocities, ωS1, ωC1, ωR2, and ωout are solved from the linear equation system above and the fifth gear ratio is formulated in terms of the four planetary parameters β1, β2, β3, and β4 by using:
All other gear ratios can be formulated in a similar fashion in terms of the planetary parameters:
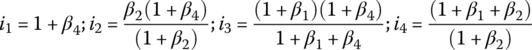
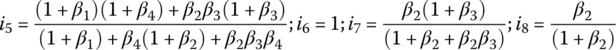
It can be observed from these formulations that the sixth gear is a direct drive, and the 7th and 8th gears are overdrives. The reverse gear ratio is negative since the term in the parenthesis is negative. With the four planetary parameters given as 
, 
, 
, and 
, the eight forward gear ratios and the one reverse ratio are calculated by the formulae above and listed in the clutch table as shown in Figure 5.14.
5.4 Transmission Dynamics
As a key component in the vehicle drive line, transmission dynamics is crucial to powertrain system responses during gear shifts. Transmission shift control is based on the understanding of transmission dynamics and quantification of transient variables during shift operations. This section presents a systematic approach to the modeling and analysis of transmission dynamics under fixed gear operations and shifting processes. The focus of the section will be on the derivation of the state variable equations of the vehicle systems and how these equations are solved for various vehicle operating statuses. Starting from the free body diagrams of powertrain components, the section shows how the equations of motion in the component level are integrated to form the vehicle state variable equation system. Under static conditions, this equation system will determine the torque of the involved clutches and the transmission output in terms of the input torque. During transmission shifts, this equation system is used to quantitatively analyse transient variables, such as speed and torque of the involved clutches, transmission output torque variations, shift time, and other variables that affect transmission shifting performance. Note that this section only concerns the rotational dynamics of the powertrain system so that the equations of motion involve only torque and angular velocity. In addition, transmission components are modeled as lumped masses with mass moments of inertia. The approach in the section is demonstrated with three case studies using the same three example transmissions as in Section 5.3.
As previously mentioned, automatic transmissions are designed with three types of planetary gear trains: simple PGT, dual‐planet PGT, and Ravigneaux PGT. As discussed in Section 3.8, the relationship between the magnitudes of the torque on the sun, carrier, and ring is characteristic of a planetary gear train, which is repeated here for the three types of PGTs.
Simple planetary gear train:
Here the torque on the sun gear and the torque on the ring gear are in the same direction. Clearly the torque on the carrier is the algebraic sum of the torque on the sun gear and the torque on the ring gear for equilibrium.
Dual‐planet planetary gear train:
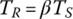
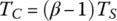
Here the torque on the ring gear is opposite in direction to the torque on the sun gear, and the torque on the carrier is opposite in direction to the torque on the ring gear since β is larger than 1.
Ravigneaux planetary gear train:
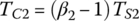
Here the Ravigneaux PGT is decomposed into two PGTs, the first two equations are for the simple PGT and the second two equations are for the dual planet PGT, as shown in Section 3.8.
5.4.1 Ford FWD Six‐Speed AT
Free body diagrams: The ratio change portion of the Ford FWD six‐speed automatic transmission illustrated Figure 5.10 contains six subassemblies: input shaft assembly, sun gear S1 assembly, output assembly, carrier C1 – ring gear R2 assembly, carrier C2 – ring gear R3 assembly, and sun gear S3 assembly, as shown in Figure 5.17. The gear ratio from the gear pairs after the output assembly is the constant final drive ratio.
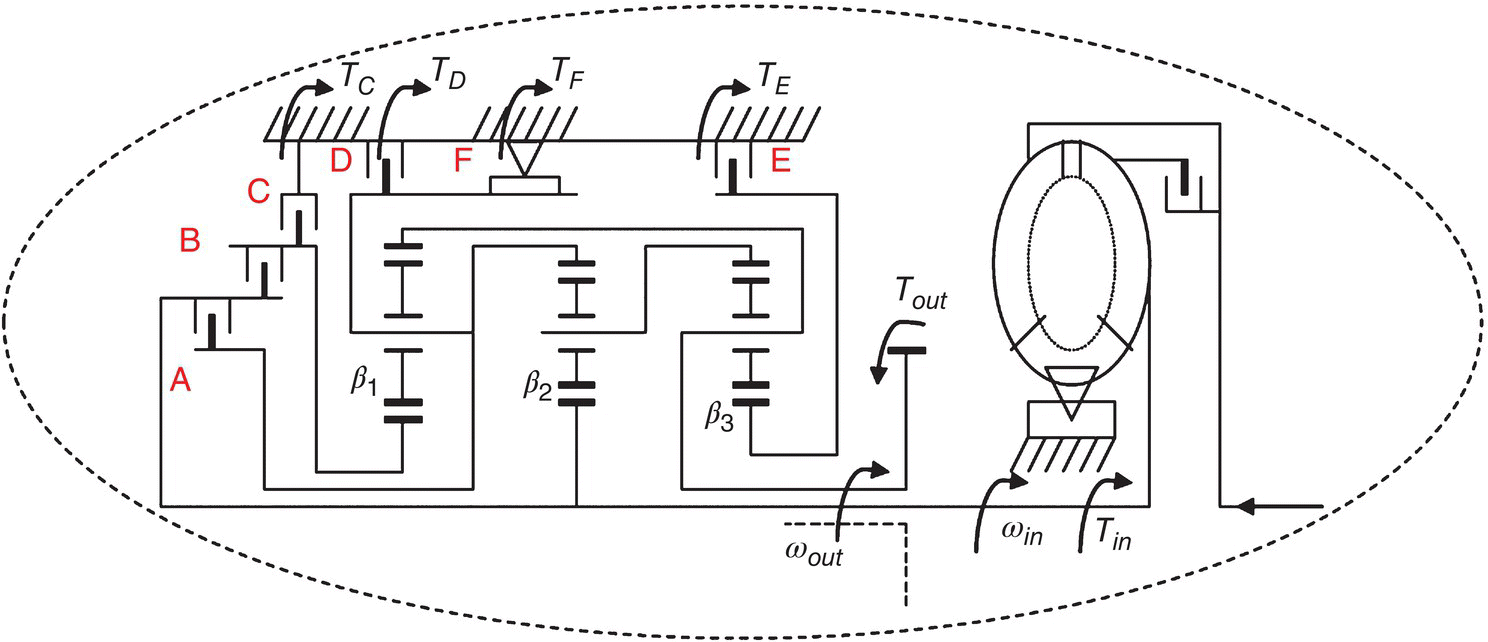
Figure 5.17 Ratio change portion of Ford FWD six‐speed AT.
The input torque Tin and the output torque Tout, as well as the reaction torques, TC, TD, TE, and TF, which are applied by the four reaction clutches to respective transmission subassemblies, are shown in the free body diagram of the transmission ratio change portion, as demonstrated in Figure 5.17. The directions of the angular velocity and the torque on the input and output are known for a given transmission. The directions of reaction torques are assumed to be the same as the input torque in the free body diagram. The free body diagram for each of the six subassemblies are shown separately in Figure 5.18.
Figure 5.18 Free body diagram of the subassemblies of Ford FWD six‐speed AT.
While drawing the free body diagrams (FBD) for the subassemblies, the directions of the internal torques, including the torques applied by the coupling clutches and gear torques, are not known and must be assumed. Once the direction of an internal torque is assumed in an FBD, it must be consistent for all other FBDs. For example, torque TA applied by clutch A to the input assembly is an internal torque and is assumed to be counter clockwise in the FBD of the input assembly. When applied, clutch A couples the C1R2 assembly with the input assembly. Therefore, the torque applied by clutch A to the C1R2 assembly is opposite in direction to the torque applied by clutch A to the input assembly. The direction of torque TA is thus clockwise in the FBD of the C1R2 assembly. The directions of gear torques with unknown directions are treated similarly. For example, TS1 is the torque applied to sun gear S1 of the S1 assembly and is assumed to be counter clockwise in the FBD. Sun gear S1 meshes with the planet gear in the C1R2 assembly. The torque applied on the planet gear in the C1R2 assembly by the sun gear in the S1 assembly has the same magnitude but is opposite in direction to the torque applied by the planet gear in the C1R2 assembly to the sun gear in the S1 assembly. The direction of TS1 is thus clockwise in the FBD of the C1R2 assembly. A planet gear is supported on a carrier and is considered as a part of the assembly that contains the carrier in the FBD. While drawing the FBD of an assembly containing a carrier, the ring gear torque and the sun gear torque are shown rather than the carrier torque directly. The torque on the carrier is of course the algebraic sum of the ring gear torque and the sun gear torque. In addition, it is worthwhile to note that a simple planet gear train, the ring gear torque, and the sun gear torque are in the same direction, as can be observed in the free body diagrams in Figure 5.18.
Equations of motion: After the FBDs for all subassemblies are correctly drawn, the equations of motion can then be written easily based on the Newton’s second law. These equations are:
where the I terms before the angular accelerations are the mass moments of inertia of the respective assemblies. In the study of transmission dynamics, the output torque and clutch torques are the key variables affecting shifting performances. These equations can be streamlined by eliminating the gear torques by various substitutions. Using Eqs (5.29), (5.30), and (5.34), the sun gear torques can be directly represented as:
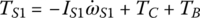
Plugging TS1, TS2, and TS3 expressed by these three equations into Eqs (5.31), (5.32) and (5.33) and noting that 
, the system equation of transmission dynamics can then be represented with only the torques of interest, namely the output torque and clutch torques remaining in the equation:
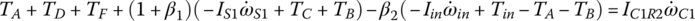
Note that Eqs (5.35–5.37) are used to calculate the dynamic loads on the gears once other variables are solved from system dynamics. These equations can be further rearranged as follows and will be integrated into the vehicle powertrain system for the modeling and analysis of the vehicle system dynamics, as will be discussed later.
Static torque magnitudes: In static terms, the angular accelerations in Eqs (5.41–5.43) are zero and all inertia terms drop out. So the input torque, the output torque, and the clutch torques are determined by the following three equations:
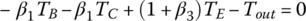
For the Ford FWD six‐speed AT with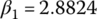 
, 
, and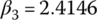 
, the three equations above are of the following form:
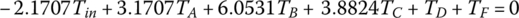
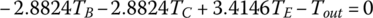
In each of the six forward gears and the one reverse gear, only two clutches are applied and the other four clutches are open. Considering the input torque as given, the two clutch torques and the output torque are uniquely determined from the linear equation system formed by the three equations above. Note that it is possible to determine the clutch torques on static conditions by just using the Eqs (5.21) and (5.22) without using Eqs (5.41–5.43). For example, in first gear,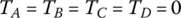 
since clutches A, B, C, D are open. It can be observed from the input assembly FBD in Figure 5.18 that 
. From the C1R2 assembly FBD, we can see that 
. It can also be seen that since 
from the S3 assembly, then from the C2R3 assembly, 
. For transmissions with more sophisticated structures, such as transmissions using Ravigneaux PGTs, it is more convenient to derive the equations of motion based on the FBDs and solve these equations after dropping the inertia terms for the clutch torques of interest. It is a common practice to express the output torque and the clutch torques as multiples of the input torque. The clutch torques and output torque for the Ford FWD six‐speed AT are tabulated here, with the input torque unitized. Note that if the clutch torque is negative, it means that the real direction of the torque is just opposite to what is assumed in the free body diagram. A box left blank in the following table indicates that the referred clutch is open.
| Gear | Applied Clutches | TA | TB | Tc | TD | TE | TF | Tout |
| 1st | E, F | 1.3131 | 2.1707 | 4.4838 | ||||
| 2nd | E, C | 0.5591 | 1.3131 | 2.8722 | ||||
| 3rd | E, B | 0.3586 | 0.8422 | 1.8422 | ||||
| 4th | E, A | 0.6846 | 0.4141 | 1.4141 | ||||
| 5th | A, B | 1.3464 | −0.3464 | 1.00 | ||||
| 6th | A, C | 1.00 | −0.2576 | 0.7424 | ||||
| Rev. | B, D | 1.00 | −3.8824 | −2.8824 |
General state variable equation system: The motions, i.e. the angular accelerations, of the transmission subsystems, are governed by the equations of motion represented by Eqs (5.41–5.43). In addition, the angular accelerations must also satisfy the transmission characteristic equations represented by Eqs (5.8–5.10). The state variable equation system for the transmission is formed by combining the equations of motion and the transmission characteristic equations with the angular accelerations differentiated with respect to time:
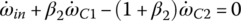
Specific state variable equation system: The general state variable equations Eqs (5.47–5.52) apply for all gears and for all vehicle operation conditions. However, note that the initial condition and clutch engagement constraints must be superimposed upon the general state variable equation system to form the specific state variable equation system for the unique solution of the state variables. For example, when the vehicle equipped with the Ford FWD six‐speed AT runs at the first gear, two clutch constraints, 
and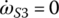 
, will be superimposed upon the general state variable equation system represented by Eqs (5.47–5.52). In addition, since clutches A, B, C, and D are open in first gear, 
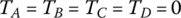. There are seven state variables remaining in the specific state variable equation system: 
, 
, 
, 
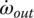, Tin, TE, TF, Tout. As will be discussed in Section 5.7, the combination of the specific state variable equation system and the vehicle equations of motion will lead to the unique solution of all state variables, with the input torque Tin as a given variable.
5.4.2 Ford RWD Six‐Speed AT
Free body diagrams: The Ford RWD six‐speed automatic transmission illustrated in Figure 5.11 contains six subassemblies: input shaft assembly, carrier C1 assembly, sun gear S2 assembly, sun gear S3 assembly, carrier C2 assembly, and ring gear R3 or output assembly. The free body diagram for the whole transmission is shown in Figure 5.19 below, with the reaction torques assumed to be in the same direction as the input torque.
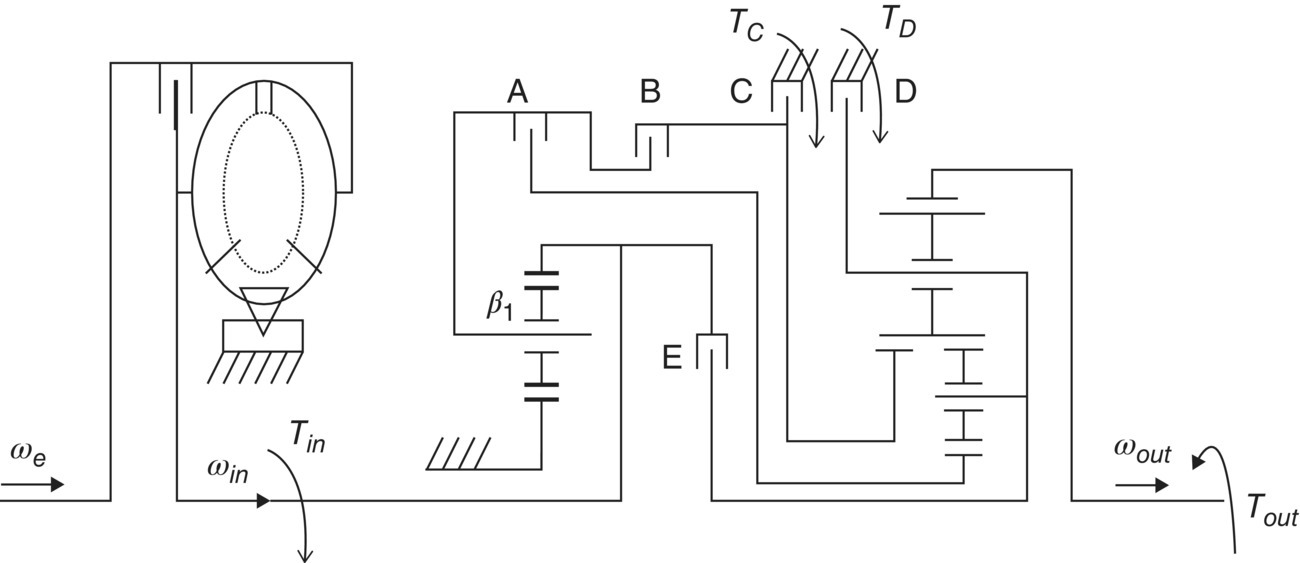
Figure 5.19 FBD of Ford RWD six‐speed AT.
The free body diagrams for the Ford RWD six‐speed AT are drawn in a similar way as in the previous example involving the Ford FWD six‐speed AT. While drawing the FBDs for the transmission subassemblies, the Ravigneaux PGT is treated as a combination of two separate PGTs, one a simple PGT and the other a dual‐planet PGT, as discussed in Section 3.8. The six subassembly FBDs are shown in Figure 5.20.
Figure 5.20 FBDs for the subassemblies of Ford RWD six‐speed AT.
As mentioned previously, the directions of the sun gear torque and the ring gear torque are the same in a simple PGT and are the opposite in a dual‐planet PGT. This is clearly demonstrated in the FBD for the C2 assembly in Figure 5.20. The carrier C2 assembly is commonly shared by the simple PGT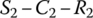 
and the dual‐planet PGT 
. The ring gear in the Ravigneaux PGT is also commonly shared by the two separate PGTs and is subject to two ring gear torques, TR2 from the simple PGT and TR3 from the dual‐planet PGT. In the FBD of the C2 assembly, it is apparent that TR2 and TS2 are in the same direction, and TR3 and TS3 are in the opposite directions. It is pointed out here again that the magnitudes of sun gear torque and ring gear torque are related as 
.
Equations of motion and static torque magnitudes: Based on the FBDs in Figure 5.20, the equations of all six subassemblies are derived as:
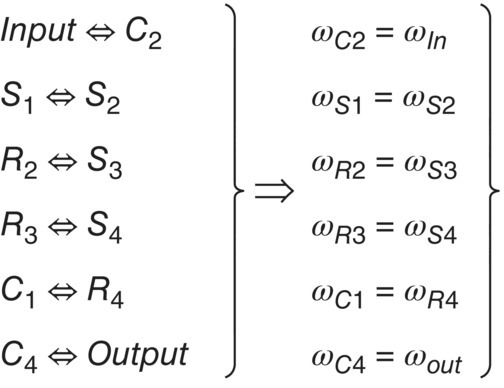
Similar to the previous example, the six equations can be simplified by eliminating the internal gear torques by variable substitution. This can be done by first solving TR1, TS2, and TS3 from Eqs (5.53), (5.55) and (5.56) respectively and then plugging them into Eqs (5.54), (5.57) and (5.58). The remaining three equations can then be combined the transmission characteristic equations represented by Eqs (5.14–5.16) to form the general state variable equation system.
The magnitudes of static clutch torque and output torque are determined following the same steps as in the previous example. Firstly, all of the inertia terms are dropped in the general state variable equation system. Then torque magnitudes of open clutches in each gear are dropped from the remaining equations respectively. The torque magnitude of the applied clutches and the output torque are then solved in terms of a unity input torque. The static clutch torque and output torque for the Ford RWD six‐speed AT are as tabulated:
| Gear | Applied clutches | TA | rB | Tc | TD | TE | Tout |
| 1st | A, D | 1.521 | 2.646 | 4.168 | |||
| 2nd | A, C | 1.521 | 0.817 | 2.338 | |||
| 3rd | A, B | 0.989 | 0.531 | 1.520 | |||
| 4th | A, E | 0.417 | 0.726 | 1.143 | |||
| 5th | B, E | −0.337 | 1.255 | 0.868 | |||
| 6th | C, E | −0.309 | 1.00 | 0.691 | |||
| Rev. | B, D | 1.521 | −4.928 | −3.928 |
5.4.3 ZF RWD Eight‐Speed AT
As shown in Figure 5.14, the ZF RWD eight‐speed AT contains eight subassemblies: input assembly, S1S2 assembly, R1 assembly, C4 or output assembly, C1R4 assembly, R2S3 assembly, C3 assembly, and R3S4 assembly. The free body diagram of the whole transmission is shown in Figure 5.21, with the reaction torque from clutches A and B assumed to be in the same direction as the input torque. The input torque Tin is the sum of turbine torque TT and the converter lock‐up clutch torque TL, i.e. 
.
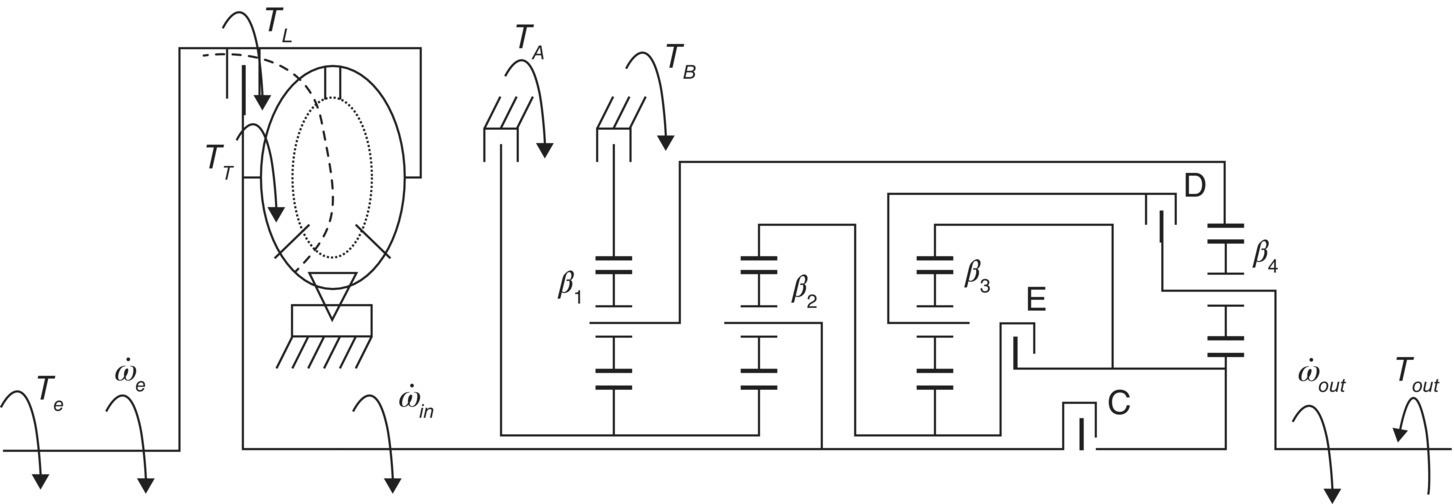
Figure 5.21 FBD for ZF RWD eight‐speed AT.
The FBDs for the eight subassemblies are drawn in Figure 5.22. Since all four planetary gear trains in the transmission are of the simple type, the sun gear torque and the ring gear torque shown on the planet gear are in the same direction Figure.
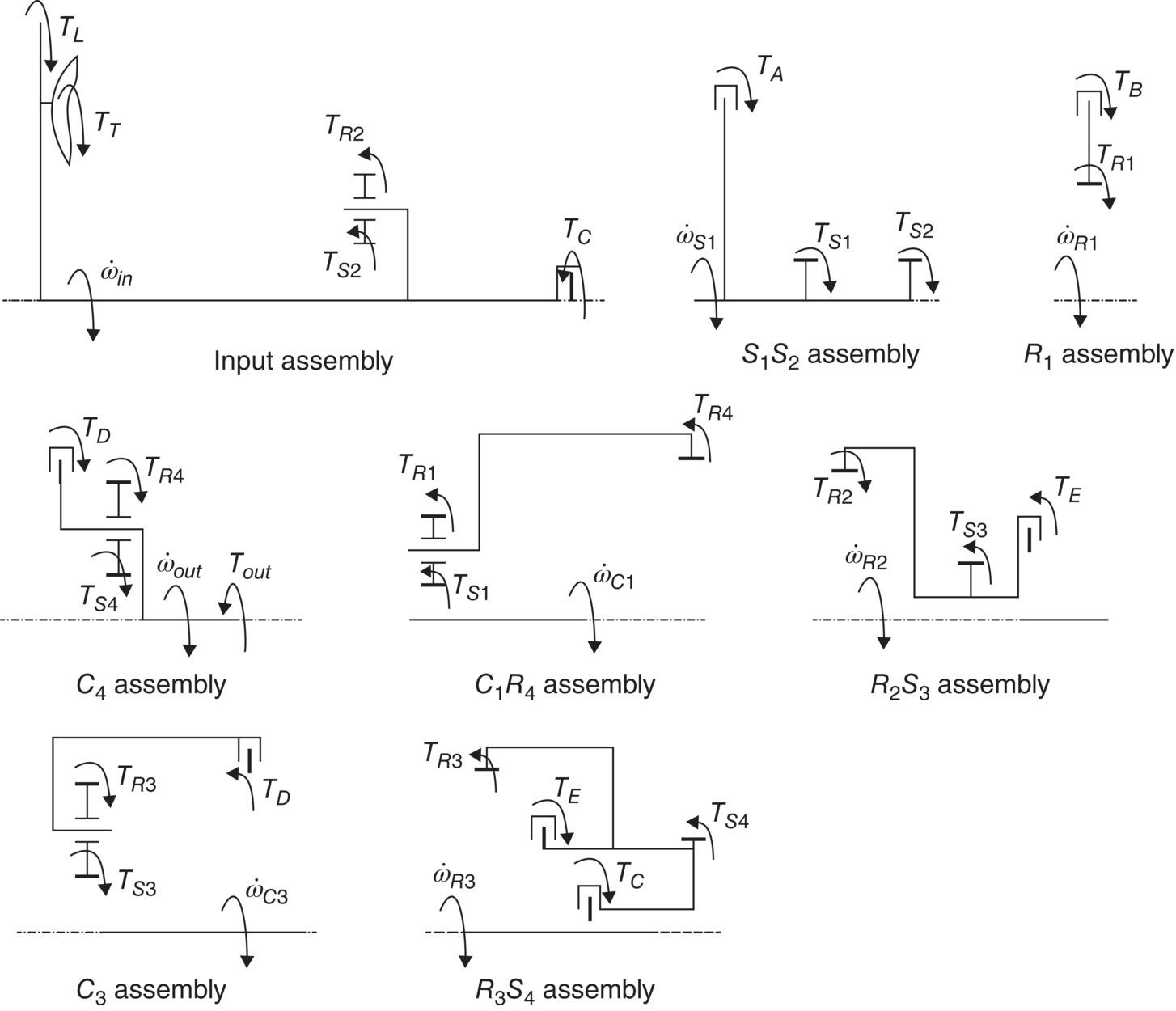
Figure 5.22 FBDs for the subassemblies of ZF RWD eight‐speed AT.
Equations of motion: The equations of motion for all of the eight subassemblies are as follows based on Newton’s second law corresponding to the respective FBD:
where the ring gear torque and the sun gear torque are related as 
with 
. The internal torques on the four sun gears can be solved from Eqs (5.59), (5.61), (5.62), and (5.65) in terms of other variables and substituted into the other four equations: Eqs (5.60), (5.63), (5.64), and (5.66). The remaining four independent equations of motion can then be represented in the following arrangement with the internal gear torques eliminated:
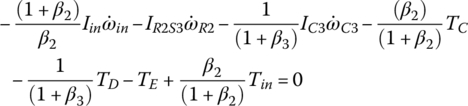
Static torque magnitudes: In static terms, the inertia terms drop out and Eqs (5.67–5.70) take the following form, as a linear equation system with the clutch torques and the output torque as unknowns:
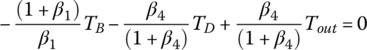
These equations apply for all eight forward speeds and reverse speed. With the input torque given, there are six torques to be determined, including five clutch torques and the output torque. In the ZF RWD eight‐speed AT, three clutches are applied in each gear. The clutch torques of the two open clutches are equal to zero. Therefore, the three clutch torques and the output torque are uniquely determined by the four equations above with the respective clutch constraints in each gear. For example, in the fifth gear, 
since clutches A and E are open. The four equations then take the following form for the ZF RWD eight‐speed AT with 
, 
, 
, and 
.
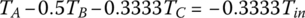
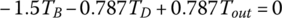
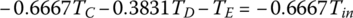
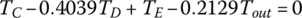
The three clutch torques and the output torque are then directly solved from these four equations in terms of the input torque: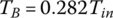 
, 
, 
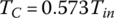, and 
. All other static clutch torques and the output torque are determined similarly and tabulated as shown in terms of unitary input torque.
| Engaged clutches | TA | TB | TC | TD | TE | Tout | |
| 1st | A, B, C | 1.232 | 2.464 | 1.0 | 4.697 | ||
| 2nd | A, B, E | 0.488 | 1.643 | 0.667 | 3.131 | ||
| 3rd | B, C, E | 1.104 | −0.656 | 1.104 | 2.104 | ||
| 4th | B, D, E | 0.667 | 0.396 | 0.515 | 1.667 | ||
| 5th | B, C, D | 0.287 | 0.573 | 0.743 | 1.282 | ||
| 6th | C, D, E | 1.0 | 1.0 | −0.383 | 1.0 | ||
| 7th | A, C, D | −0.161 | 0.518 | 0.839 | 0.839 | ||
| 8th | A, D, E | −0.333 | 0.667 | 0.411 | 0.667 | ||
| Rev | A, B, D | −1.655 | −2.644 | 1.740 | −3.30 |
General state variable equation system: The general state variable equation system is formed by combining the transmission characteristic equations systems represented by Eqs (5.17–5.20) differentiated with respect to time, and the equations of motion represented by Eqs (5.67–5.70), as shown, with the given β values.
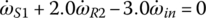
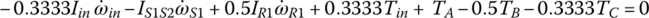
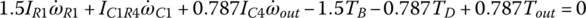
As discussed in the previous example, the general state variable equation system is characteristic of the transmission and applies for all vehicle operations, including fixed gear operations and gear shifting processes. The clutch constraints in each operation are respectively superimposed on the general state variable equation system to form the specific state variable equation system for the unique determination of transmission system dynamic status, as will be detailed in Section 5.6.
5.5 Qualitative Analysis on Transmission Shifting Dynamics
Qualitative analysis on transmission shift dynamics provides an understanding of the trends of transient behavior of dynamic variables during shifts and their effects on shift quality [5]. In this section, the Ford FWD six‐speed AT with the planetary parameters shown in Figure 5.10 will be used as the example for the qualitative analysis of shift dynamics. The general state variable equation system has been represented in Eqs (5.47–5.52). As mentioned previously, clutch constraints in each gear are superimposed upon these equations to define the transmission operation status. Without losing generality, the 1–2 shift process is used in this section as a case study for transmission shift dynamics during upshifts. For the convenience of analysis, the specific state variable equations will be derived in the following, respectively for the first gear operation, torque phase, and inertia phase in the 1–2 shift process.
First gear operation: In first gear, of the Ford FWD six‐speed AT, clutches E and F are applied, resulting in two clutch constraints: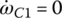 
and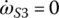 
. Superimposing these two constraints in Eqs (5.47–5.49), we can solve other angular accelerations in terms of the input angular acceleration, i.e., 
, 
, 
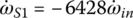. These angular accelerations are then plugged into Eqs (5.50–5.52) for the solution of the clutch torques, TE and TF, and the output torque Tout, as follows:
These equations represent the clutch torque and the output torque in terms of the input torque and the input angular acceleration. The transmission output torque is directly related to the vehicle acceleration by the equation of motion of the vehicle:
where ia is the final drive ratio, η is the final drive efficiency, r is the tire rolling radius, W is the vehicle weight, and R is the road load formulated by Eq. (1.14). It is apparent from Eq. (5.82) that the vehicle acceleration varies proportionally with the transmission output torque. If the transmission input torque Tin is given, the status of the vehicle dynamics and all of the state variables are uniquely defined by the combination of Eqs (5.79–5.82).
1–2 shift process: It must be understood that any transmission gear shift is a dynamic process during which the gear ratio is changed gradually. Let’s consider the 1–2 shift process in the Ford FWD six‐speed AT. This involves the releasing of clutch F and engaging of clutch C. As soon as the transmission enters the 1–2 shift process, the ongoing clutch C will be pressurized to apply a reaction torque to the transmission, and meanwhile, the torque in clutch F will decrease as clutch C is being pressurized. However, the off‐going clutch F will stay applied until a certain point of time during the shift process. As long as the off‐going clutch in this 1–2 upshift, or any upshift in general, stays closed, the first gear ratio, i.e. the current gear ratio, will remain unchanged, even though the oncoming clutch is being applied. This is because the clutch constraints on the transmission kinematics are still the same as in first gear, or current gear in any upshift, until the off‐going clutch starts to slip. As the torque in the oncoming cutch increases and the torque in the off‐going clutch decreases, the off‐going clutch will start to slip at some point in the process. As soon as the off‐going clutch starts to slip, the constraint placed by the off‐going clutch on transmission kinematics is released and the transmission ratio starts to change toward the target gear ratio until the completion of the upshift. Based on this analysis, the 1–2 shift process, or any shift process, consists of two phases, torque phase and inertia phase, defined in general as follows.
Torque phase: The period from the time at which the oncoming clutch is pressured to the time at which the off‐going clutch starts to slip is defined as the torque phase. During the torque phase, the transmission ratio remains to be the same as the current gear. Note that, during the torque phase, torque exists in both the off‐gong clutch and the oncoming clutch. The torque in the oncoming clutch is a control variable that depends on the clutch pressure, and the torque in the off‐going clutch is a state variable that depends on transmission dynamics.
Inertia phase: The period from the time at which the off‐going clutch starts to slip to the completion of the shift process is defined as the inertia phase. It is during the inertia phase that the current transmission ratio is gradually changed to the target transmission ratio. If the off‐going clutch in an upshift is a one‐way clutch, such as the 1–2 shift in the Ford FWD six‐speed AT, the off‐going clutch torque is zero during the inertia phase. This is because once the one‐way clutch starts to slip, it only exerts a negligible drag torque. If the off‐going clutch is a regular clutch, the torque in the off‐going clutch may exist after the inertia phase starts. Following the industry convention, a shift is termed a “clutch to clutch shift” if it involves two regular clutches, one off‐going and one oncoming. If a shift involves a regular clutch and a one‐way clutch, it is termed a “clutch to one‐way clutch shift”. For clutch to clutch shifts, both the off‐going clutch torque and the oncoming clutch torque are control variables during the inertia phase.
Torque phase of 1–2 shift process: As mentioned in the definition of torque phase, the clutch constraints in the torque phase in the 1–2 upshift are the same as in first gear. However, clutch C is now being applied and clutch torque TC in Eq. (5.50) is no longer equal to zero but rather a control variable. The relations for the angular accelerations are still the same as in first gear operation since the clutch constraints are the same. Eqs (5.50–5.52) lead to the solution of clutch torque, TE and TF, and the output torque Tout, as follows:
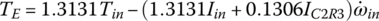
During the torque phase, the gear ratio remains the same as the first gear and 
is small in magnitude since it is coupled to the vehicle acceleration. The inertia terms in the Eqs (5.83–5.85) can be dropped without affecting the results in a qualitative analysis. As observed in Eq. (5.85), the torque applied by the oncoming clutch TC reduces the output torque by 2.8824 times its magnitude. Meanwhile, the torque in the off‐going clutch TF also decreases as the oncoming clutch torque TC increases and will become equal to zero when 
. Because the off‐going clutch in the 1–2 shift is a one‐way clutch, it will start to slip once its torque becomes equal to zero. The shift then enters the inertia phase. Furthermore, the torque in the one‐way clutch will remain at zero until the completion of the 1–2 shift.
If the off‐going clutch in the 1–2 upshift is not a one‐way clutch but rather a regular clutch, such as clutch D shown in the stick diagram of the Ford FWD six‐speed AT, then the slippage of the off‐going clutch is not self‐actuated but depends on the ATF pressure in the piston chamber of clutch D. This pressure defines the torque capacity of the off‐going clutch D as indicated by Eq. (2.8). In this case, the torque in the off‐going clutch, TD, is determined by the transmission system dynamics up to the point of slippage. The threshold of clutch slippage is at the point when the off‐going clutch torque determined by the transmission system dynamics as a state variable is equal to the clutch torque capacity. As soon as the off‐going clutch D slips, the 1–2 shift enters the inertia phase and the transmission ratio starts to change. However, the torque in clutch D is not equal to zero after the 1–2 shift enters the inertia phase but rather a control variable that depends on the clutch pressure. This residual torque must be brought to zero as quickly as possible to optimize the shift response and smoothness. If the ATF pressure in clutch D is not brought down quickly after the 1–2 shift is initiated, it can happen that even when the clutch torque TD determined by transmission system dynamics is zero already, clutch D is still not slipping. This causes the phenomenon termed “clutch tie‐up”, which is the worst‐case scenario and must definitely be avoided during any shift. To avoid clutch tie‐up, the off‐going clutch torque capacity must be controlled to drop quickly so that it will be smaller than the off‐going clutch torque determined as a state variable before it becomes equal to zero.
Summarizing the analysis above, it can be concluded in general that the torque phase in upshifts begins as soon as the oncoming clutch is pressurized and ends at the point when the off‐going starts to slip. The transmission ratio remains to as the current gear ratio and the input angular acceleration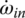 
is almost unchanged during the torque phase. The torque in the off‐going clutch is a state variable that is determined by transmission system dynamics. Generally, a clutch to one‐way clutch shift is more favorable than a clutch to clutch shift for shift quality control. The transmission output torque Tout drops in proportion to the oncoming clutch torque that is a control variable depending on the clutch pressure. The behaviors of key variables during the torque phase in the 1–2 upshift, including transmission input angular velocity ωin, off‐going clutch torque TF or TD, oncoming clutch torque TC, and output torque Tout, are demonstrated in Figure 5.22. Note here that the qualitative analysis on the 1–2 shift of the Ford FWD six‐speed AT is generally applicable to all transmission upshifts.
Inertia phase of 1–2 shift process: The constraint on angular acceleration 
is released once the 1–2 shift enters the inertia phase, i.e.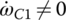 
. With clutch E applied during the inertia phase of the 1–2 shift, 
drops out in Eqs (5.47–5.49). This leads to the solution of angular accelerations, 
, 
, and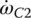 
, in terms of 
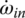and 
as:
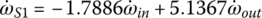
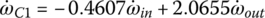
These relations on the angular accelerations and the clutch conditions with 
lead to the simplification of Eqs (5.50–5.52) in the following form:
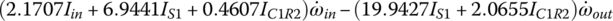
In these three equations, TC is the torque of the oncoming clutch, which is a control variable. TF is the one‐way clutch torque and is equal to zero during the inertia phase. If the off‐going clutch is not a one‐way clutch, but rather a regular clutch such as clutch D in the Ford FWD six‐speed AT, the off‐going clutch torque will not be zero when the 1–2 shift enters the inertia phase. It is pointed out here that torque TF is kept in Eq. (5.89) for generality. If clutch D is used as the reaction clutch in first gear, then as with the off‐going clutch in the 1–2 shift, its torque is not equal to zero during the inertia phase and TF in Eq. (5.89) is replaced by TD as a control variable.
The specific state variable equation system for the whole vehicle is formed by combining Eqs (5.89–5.91) with the vehicle equation of motion, i.e. Eq. (5.82). If the transmission input torque Tin and the control variables TC and TD are given, then all state variables, including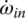 
, 
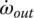, TE, and Tout, can be solved from the specific state variable equation system. By variable substitution, state variables TE, 
, and Tout can be solved in terms of Tin, TC, TF, and 
directly from Eqs (5.89–5.91) in the form:
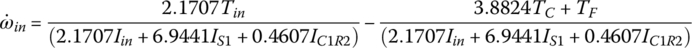
It is again emphasized here that torque TF will be replaced by torque TD if clutch D is applied in first gear instead of clutch F. Obviously, 
can be solved by combining Eq. (5.94) and Eq. (5.82) in terms of Tin, TC, and TF, and all other state variables are then solved by back substitution. This will lead to the accurate solution of the specific state variable equations for all state variables. Shift response and smoothness primarily depend on the variation patterns of three variables: output torque Tout, the input angular acceleration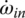 
, and the output angular acceleration 
during the shift process. These variables can be qualitatively analyzed using Eqs (5.92–5.94) and the following observations can be made on the characteristics of the inertia phase of the 1–2 upshift.
- During the 1–2 shift inertia phase, the transmission ratio it starts to change toward the lower second gear ratio. The input angular velocity must start to drop quickly, i.e.
is negative. As can be seen in Eq. (5.93), the magnitude of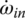 
depends on the input torque Tin and the combination of the oncoming clutch torque TC and the residual off‐going torque TD. For 
to be negative, 
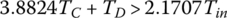. For the Ford FWD six‐speed AT which uses clutch F as the reaction clutch in first gear, 
. In order to complete the shift as quickly as possible, the oncoming clutch torque TC must be ramped up to a high value quickly to decelerate the input angular velocity ωin. To increase the magnitude of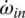 
, it is necessary to reduce the input torque Tin in the inertia phase. In the practice of transmission control, the reduction of input torque Tin is realized by “spark retarding”. The timing for spark retarding must be controlled at the end of the torque phase, otherwise the output torque will drop further in the torque phase. - Before the 1–2 upshift, or any other power on upshifts, is initiated the vehicle is being accelerated in the current gear. To avoid a sudden drop of vehicle acceleration during shift, felt as “jerk” by the driver or passenger, the output torque should be controlled above a certain level and should not oscillate at large amplitude. This also means that the output angular acceleration
determined by Eq. (5.82) is positive and varies continuously during the shift process. - During the shift process, the magnitude of the input angular acceleration is far larger than the output angular acceleration, i.e.
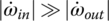. In addition, the mass moment of inertia of the input assembly is much larger than other assemblies, i.e. 
. As can be observed in Eq. (5.94), the output torque Tout is dominated by the first four terms. For a qualitative analysis, the magnitude of the output torque can be approximated by dividing both the numerator and denominator of the third and fourth terms in Eq. (5.58) by Iin and then taking the limit when Iin approaches the infinity. This will lead to the approximation of the output torque as: 
. Here TD replaces TF if clutch D is the reaction torque in first gear. - As seen above, the magnitude of the output torque during the inertia phase is proportional to the oncoming clutch torque to a large degree. To decrease ωin quickly, larger oncoming clutch torque TC is needed. But on the other hand, an overly large oncoming clutch torque can cause an overshoot in the output torque during the inertia phase. This contradiction can be solved by the input torque reduction through spark retarding, as mentioned previously. For the clutch to one‐way clutch 1–2 shift, the oncoming clutch torque is already equal to 0.5591Tin at the end of the torque phase. As soon as the shift enters the inertia phase, the input torque is reduced by engine spark retarding. The oncoming clutch torque will be immediately larger than 0.5591Tin and is controlled to increase continuously, resulting in an angular deceleration for the input assembly. As the input angular velocity decreases, the transmission ratio also decreases from the first gear ratio toward the second gear ratio. At some point toward the end of the shift, engine spark retarding is cancelled and the input torque is recovered to get close to the relation
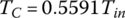. The perfect timing to end the input torque reduction would be such that when the transmission ratio reaches the target second gear ratio, the input torque is just recovered to the point at which 
. This will provide a seamless transfer from the first gear to the second gear without any torque overshoot. In engineering practice, the timing of input torque reduction through engine spark retarding and the ramping up of oncoming torque are carefully calibrated. A small amount of output torque overshoot is allowable and is mostly damped by the torque converter equipped powertrain itself. - If clutch D replaces clutch F in first gear as the reaction clutch in the Ford FWD six‐speed AT, the off‐going clutch torque TD increases the overshoot of the output torque during the inertia phase. The residual off‐going clutch torque should be brought to zero asoon as the inertia phase starts to lower the output torque overshoot. Meanwhile, the oncoming clutch torque TC must be ramped up quickly to be greater than 0.5591Tin in order to decrease the input angular velocity ωin, otherwise “engine flare” will occur at the start of the inertia phase.
- Note that the observations above are based on the qualitative analysis on the 1–2 upshift in the Ford FWD six‐speed AT. The observations can be generalized for all upshifts in other automatic transmissions. The behavior of shift quality related variables during the 1–2 shift are shown in Figure 5.22.
Criteria for shift quality: The time required to complete shifts and the variation of the vehicle acceleration during shifts are the two most important parameters for the shift quality of automatic transmissions. The shift time depends on how quickly and timely the off‐going clutch is released and the oncoming clutch is engaged. The variation of vehicle acceleration depends largely on the behavior of transmission output torque during the shift process. The size of the torque hole shown in Figure 5.22 is directly proportional to the vehicle acceleration drop and must be minimized to enhance the shift quality. The torque overshoot during the inertia phase causes sudden acceleration jerks during shifts. For the 1–2 shift of the Ford FWD six‐speed AT which uses one‐way clutch F in first gear, the oncoming clutch torque TC must be ramped up quickly to be around a magnitude of 0.5591Tin, at which the one‐way clutch starts to slip by itself and the shift enters the inertia phase. If the oncoming torque TC is controlled to be close to 0.5591Tin, that is, the reaction torque of clutch C in second gear at the end of the torque phase, then the corresponding output torque should be close to the target value in second gear and the depth of the torque hole will be minimized. As the shift enters the inertia phase, the oncoming clutch torque should be ramped up at a lower rate because excessive oncoming clutch torque in the inertia phase causes the output torque to overshoot. Meanwhile, the oncoming clutch torque TC. must be high enough to act against the input torque Tin to decelerate the input angular velocity ωin. To overcome this contradiction, it is necessary to reduce the input torque through engine spark retarding, as shown in Figure 5.22 as soon as the inertia phase starts. When the input angular velocity is reduced to be the target value corresponding to the second gear ratio, the spark retarding is cancelled to recover the input torque. Simultaneously, the oncoming clutch torque is further increased to complete the shift and secure the engagement of the oncoming clutch. Theoretically, it is possible to achieve a perfect 1–2 shift as illustrated in Figure 5.23, with a seamless output torque transfer during the shift.
Figure 5.23 Key variables in the 1–2 shift process of Ford FWD six‐speed AT.
If clutch D replaces the one‐way clutch F in first gear of the Ford FWD six‐speed AT, the characteristics of key variables during the clutch to clutch 1–2 shift are similar to those shown in Figure 5.23, but the torque profiles of the off‐going clutch and the oncoming clutch are different, as shown in Figure 5.24. In this case, the torque capacity of the off‐going clutch D must be ramped down quickly to the threshold of slippage before the actual torque in clutch D reaches zero. This means that the torque phase in the clutch to clutch 1–2 shift will end sooner than in the clutch to one‐way clutch 1–2 shift. For the same input torque, the torque in the oncoming clutch is lower at the time when the off‐going starts to slip. As the shift enters the inertia phase, there is still a torque in the off‐going clutch and this torque must be brought to zero as quickly as possible. Because the torque in the oncoming clutch is lower at the beginning of the inertia phase, it must be ramped up more quickly during the inertia phase in order to act against the input torque to decelerate the input angular velocity. Through the control of spark retarding timing and oncoming clutch torque, it is possible to achieve near perfect shifts with smooth output torque transfer similar to that shown in Figure 5.23 for the clutch to one‐way clutch shift.
Figure 5.24 Clutch torque profiles in the clutch to clutch 1–2 shift of Ford FWD six‐speed AT.
Power‐on downshifts: Power‐on downshifts are initiated during vehicle operations such as passing, slope climbing, and other deep throttle maneuvers either triggered by the driver or commanded by the transmission controller under certain road conditions. These types of downshifts occur at relatively high vehicle speed, with the transmission operating in higher gears such as fourth, fifth, and sixth. As higher vehicle acceleration is the main intention, power‐on downshifts must be implemented expeditiously and some harshness during such shifts is not a major concern. If a downshift is triggered by the driver, then the driver will anticipate it as an oncoming event and will feel the shift harshness with lessened unpleasantness. A power‐on downshift also consists of the inertia phase and torque phase. However, power‐on downshifts start with inertia phase and end with torque phase. The order of the two phases is opposite to that of power‐on upshifts discussed previously. This means that the off‐going clutch must be controlled to slip before the oncoming clutch starts to apply a clutch torque.
Shift transients during downshifts can be analyzed qualitatively similar to the previous case study which analyzes the 1–2 upshift of the Ford FWD six‐speed AT. Let’s consider the 4–3 downshift of the Ford FWD six‐speed AT in a simple qualitative analysis. In this downshift, clutch A is off‐going and clutch B is oncoming. When the transmission operates in fourth gear, the angular velocity of sun gear S1, ωS1, is higher than the input angular velocity ωin as shown the transmission ratio analysis. Clutch B, when applied, couples the input assembly with the sun S1 assembly, as shown in Figure 5.17. If clutch B is applied before clutch A starts to slip in the 4–3 downshift, it will cause backward power recirculation, or “clutch tie‐up”, because the transmission still operates in the fourth gear and thus sun gear S1 turns fast than the input assembly. To avoid this backward power recirculation, the off‐going clutch A must be brought to slip first before any clutch torque exists in the oncoming clutch B. As soon as clutch A slips, the transmission ratio will start to increase from the fourth gear ratio as the input angular velocity ωin increases due to the reduced torque in clutch A and the 4–3 downshift starts its inertia phase immediately. After the inertia phase starts, the torque in the oncoming clutch B is then ramped up from zero rapidly and the torque in the off‐going clutch A is further ramped down. The inertia phase is finished at the point when the target third gear ratio is reached. At this point, the pressure in clutch B is stepped up quickly to secure its engagement and the 4–3 downshift enters the torque phase. The residual torque in clutch A is now a drag torque on the transmission and must be rapidly brought to zero to end the torque phase. Note here that if the torque in the off‐going clutch A is brought to zero before the target third gear ratio is reached, then the 4–3 downshift will be completed without the torque phase.
A qualitative analysis based on the specific state variable equation system during a 2–1 downshift can be performed similarly to the previous case study for the 1–2 upshift of the Ford FWD six‐speed AT. The two sets of specific state variable equation systems are the same for both the upshift and downshift involving the same two gears. Equations (5.84–5.86) and (5.93–5.95) apply for both the 1–2 upshift and 2–1 downshift. Without losing generality, let’s consider that clutch D is used instead of the one‐way clutch F in first gear. Suppose a 2–1 power‐on downshift is to be implemented, then the clutch torque capacity of the off‐going clutch C must be reduced so as to start the slippage in clutch C before clutch D is pressured, otherwise clutch D would apply a drag torque on the transmission. The clutch torque capacity is reduced by the reduction of ATF pressure in the clutch piston chamber. As clutch C starts to slip, the 2–1 downshift enters the inertia phase immediately and the gear ratio starts to increase toward the first gear ratio. Meanwhile, the torque in the oncoming clutch D is ramped up gradually. As can be observed in Eq. (5.93), with Tin maintained or even increased in a power‐on downshift, 
can be increased rapidly if the off‐going clutch torque TC is decreased rapidly while the oncoming clutch torque is still low during the inertia phase. When the transmission ratio determined by 
reaches the first gear ratio, the oncoming clutch torque TD is stepped up quickly to close the clutch, and the 2–1 downshift then enters the torque phase during which the residual torque in the off‐going clutch is brought to zero rapidly. If the one‐way clutch F is used in the first as in the Ford FWD six‐speed AT, it will be actuated by itself to the holding status when the ratio 
reaches the value of the first gear ratio. Note here that the specific state variable equations for the 2–1 downshift are used here for the analysis of downshifts in general. In real world driving, power‐on 2–1 downshift is rarely implemented in transmission control.
This qualitative analysis can be generalized for all power‐on downshifts. The torque profiles of the off‐going clutch and the oncoming clutch, as well as other variables in such shifts, are illustrated in Figure 5.25. As observed in this figure, the actual downshift process does not start immediately after the shift is initiated by the transmission control system. There is a small amount of time between the shift initiation and the point at which the off‐going clutch starts to slip. During this time, the off‐going clutch torque capacity is ramped down to the threshold for slippage, which is equal to the value of the off‐going clutch torque determined by the system dynamics. In a power‐on downshift, the input torque increases after the shift is initiated and the output torque increases accordingly before the actual shift starts. As the shift enters the inertia phase, the output torque will oscillate somewhat due to the slippage of the off‐going clutch. At this time, the oncoming clutch torque starts to ramp up but is still small. The input angular velocity is therefore accelerated by the input torque which works against both the off‐going clutch torque and the oncoming clutch torque. As the input angular velocity increases, the transmission ratio is gradually changed to the target value of the lower gear. As shown in Figure 5.25, the torque phase is much shorter in time than the inertia phase in a typical power‐on downshift. If the torque profiles of the off‐going clutch and the oncoming clutch are controlled accurately and timely, power‐on downshifts can also be made with optimized responsiveness and smoothness, as indicated by the shift time and output torque behavior shown in Figure 5.25.
Figure 5.25 Clutch torque profiles and characteristics of typical downshifts.
In addition to power‐on upshifts and downshifts, power‐off upshifts and downshifts are also frequently implemented in daily driving. Typically, power‐off upshifts are used when the vehicle has been accelerated to a relatively high speed and the driver decides not to accelerate the vehicle further. A shift like this is triggered when the driver releases the gas pedal. In such shifts, it is the wheels that drive the powertrain system since the input torque is almost zero. In order to make quick and smooth power‐off upshifts, the off‐going clutch should be controlled to slip first before the oncoming clutch is pressured. In other words, the inertia phase comes before the torque phase in power‐off upshifts. Since there is almost no input torque, the control of such shifts is less challenging in comparison with power‐on upshifts.
Power‐off downshifts are used when the vehicle is being coasted to low speeds or a full stop. Such shifts occur when the vehicle speed is relatively low. Because the transmission input is the driven side in such shifts, the torque phase comes before the inertia phase. The oncoming clutch torque should be ramped up before the off‐going clutch starts to slip in power‐off downshifts for optimized shift feel. In summary, power‐off upshifts are used at high vehicle speed and power‐off downshifts are used at low vehicle speed. These two types of shifts are implemented without power input to the transmission and are less technically challenging in comparison with power‐on shifts.
5.6 General Vehicle Powertrain Dynamics
Vehicle drivetrain dynamics, especially transmission shift dynamics, have been the subject of in‐depth studies in the automotive industry [5–7]. In this section, the ZF RWD eight‐speed AT shown in Figure 5.14 will be used as an example for the study of vehicle powertrain dynamics. The example can be readily extended to all other automatic transmissions in general. For this example transmission, the general state variable equation system consists of Eqs (5.71–5.78), which were derived in Section 5.4. The vehicle general state variable equation system is formed by combining Eqs (5.71–5.78) and the vehicle equation of motion represented by Eq. (5.82). The transmission input torque Tin is considered as a given variable in the state variable equation system. Note that Tin depends on the engine output and the torque converter characteristics. The integrated vehicle system will incorporate the engine, the torque converter, and the transmission, as will be discussed later in this section.
The vehicle general state variable equation system must be combined with the clutch constraints that exist in fixed gear operations or during shifts. Any shift involves two separate statuses: torque phase and inertia phase. Not counting the reverse gear, the ZF RWD eight‐speed AT has eight forward speeds and 36 direct shifts, as mentioned previously. Therefore, there are a total of 80 operation statuses: eight fixed gear operations, and 36 torque phases and 36 inertia phases for the 36 direct shifts. Each of these 80 operation statuses requires a set of specific state variable equations to uniquely describe the system dynamics. Note that the specific state variable equations are the same for both the upshift and the downshift in any of the 36 direct shifts. That is, the state variable equations for the torque phase of the 1–2 upshift are the same as for the torque phase of the 2–1 downshift, and the state variable equations for the inertia phase of the 1–2 upshift are also the same as for the inertia phase of the 2–1 downshift.
In the vehicle general state variable equation system, formed by combining Eqs (5.71–5.78) and Eq. (5.82), there are a total of nine equations and 14 state variables, with the input torque Tin as a given variable. Of these 14 state variables, eight are angular accelerations: 
, 
, 
, 
, 
, 
, 
, and 
; five are clutch torques: TA, TB, TC, TD, and TE; and one is the output torque Tout. In fixed gear operations, three clutches are applied, providing three constraints on the angular accelerations and reducing the number of angular accelerations as state variables to five. The torques in the two open clutches are both zero, reducing the torque state variables to four. Therefore, the total number of unknown state variables, including five angular accelerations, three clutch torques, and one output torque, is nine. With the input torque Tin given, these nine state variables are uniquely determined by the vehicle state variable equation system. In the torque phase of shifts, the clutch constraints are the same as in fixed gear operations and the number of unknown state variables is also equal to nine. The oncoming clutch torque is a given control variable provided to the transmission system. In the inertia phase of shifts, only two clutches are applied and thus the number of clutch constraints is only two. But in this case, both the oncoming and off‐going clutch torques are given control variables provided to the transmission system. Therefore, the number of unknown state variables during shifts is still equal to the number of state variable equations and the dynamic status of the powertrain system is uniquely determined during all shifting operations.
5.6.1 General State Variable Equation in Matrix Form
The vehicle state variable equation system formed by Eqs (5.71–5.58) and Eq. (5.82) can also be expressed in matrix form. Firstly, the eight angular accelerations and the seven torque variable, including the five clutch torques, the input torque and the output torque, are represented by two separate column vectors:
where the column vectors [X] and [Y] contain respectively the eight angular accelerations and the seven torques. In terms of variable 
and 
, Eqs (5.71–5.78) and Eq. (5.82) can be readily rewritten in the following form:
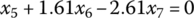
These equations can be written in matrix form:
In this matrix equation, the coefficient matrix, formed by partitioning matrices A and B, has a dimension of 
since there are nine state variable equations and 15 state variables, as shown in Eqs (5.95) and (5.96). Matrix A is 
and its elements are multipliers of the angular accelerations or variables 
in the state variable equations. Matrix B is 
and its elements are the multipliers of torques or variables 
. The column vector on the right‐hand side has 15 elements, with the ninth element equal to 
and all the other eight elements equal to zero. The general state variable equations are the characteristics of the vehicle powertrain system and apply for all vehicle operations. This means that the elements of the coefficient matrix in Eq. (5.106) are constants for a given transmission regardless of operation status. The elements of matrices A and B for the ZF RWD eight‐speed AT are represented in the following:
5.6.2 Specific State Variable Equation
The specific state variable equation system is formed by superimposing the clutch constraints upon the general state variable equation system expressed by Eq. (5.106) in each operation. For the convenience of matrix operation and linear algebra, the specific state variable equation system is formed by augmenting the general state variable equation system with the clutch constraint equations rather than by direct variable substitutions. This means that constraint equations are just treated as state variable equations and thus the number of rows in the coefficient matrix in Eq. (5.106) increases by the number of constraint equations. The clutch constraint equations are obtained from the clutch table directly, in accordance with the three operation statuses: fixed gear operation, torque phase, and inertia phase.
Fixed gear operation: Each applied clutch corresponds to a constraint equation on the angular acceleration. If a reaction clutch is applied, the constraint equation is simply formed by making the related angular acceleration equal to zero. If a coupling clutch is applied, then the constraint equation is formed by making the subtraction of the two angular accelerations of the two coupled components equal to zero. For the ZF RWD eight‐speed AT, there are three such constraint equations in each gear and the number of equations in the specific state variable equation system is 12. The two torques in the two open clutches are equal to zero and are dropped from the specific state variable equation system.
Torque phase of a shift: During the torque phase of a shift, the clutch constraint equations are the same as for the fixed gear operation. However, the oncoming clutch torque is now an input control variable that appears on the right side of the specific state variable equation system, as illustrated later.
Inertia phase of a shift: During the inertia phase of a shift, the clutch constraint equation caused by the off‐going clutch is released. For the ZF RWD eight‐speed AT, there are still two clutch constraint equations during the inertia phase of a shift. The torque in the open clutch is equal to zero and is dropped from the specific state variable equation system. The torques in both the off‐going clutch and the oncoming clutch are control variables. The number of equations in the specific state variable equation system is 11.
In what follows, the first gear operation, the torque phase and the inertia phase of the 1–2 shift in the ZF RWD eight‐speed AT are used as examples in formulating the specific state variable equation systems. These examples can be readily extended to all other operations and for all other automatic transmissions.
First gear operation: In the first gear of the ZF RWD eight‐speed AT, clutches A, B, and C are applied, resulting in three clutch constraints: 
, 
, and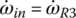 
. In terms of the variables of the column vector [X] expressed in Eq. (5.95), the three constraint equations are written in the following form:
These three constraint equations are combined with the general state variable equations from Eqs (5.97–5.105) to form the general state variable equation system, which then has 12 equations and is represented in matrix form as follows:
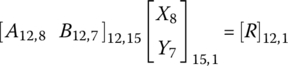
Here the coefficient matrix is 
since it has been augmented by Eqs (5.107–5.109). The right‐hand side is augmented from [R]9,1 in Eq. (5.106) by three zero elements. Matrix [A]12,8 and [B]12,7 are augmented from [A]9,8 and [B]9,7 in the general state variable equation system expressed by Eq. (5.106), in the following partitions:
In these matrix augmentations, [A]9,8 and [B]8,7 are the same as in Eq. (5.106) and are characteristic of the transmission, i.e. these two matrices are always the same regardless of transmission operations. The two augmenting matrices,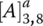 
and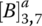 
, depend on the transmission operation status and are represented for the first gear operation of the ZF RWD eight‐speed AT as follows:
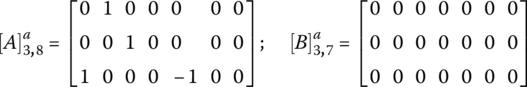
Note that, in general, the augmenting matrix 
is always a null matrix, with the number of columns equal to the number of torques and number of rows equal to the number of constraint equations. The numbers of columns and rows of matrix 
are equal to the number of angular accelerations and the number of constraint equations. In first gear, clutch torques TD and TE, or variables y5 and y6, are equal to zero and drop out of the equation system. The input torque Tin or variable y1 is considered as a given variable and is moved to the right‐hand side of the equation. The remaining 12 unknown state variables can be uniquely solved from the following linear equation system:
In this equation system, the coefficient matrix is 
since the two columns corresponding to y5 and y5 are dropped out from matrix [B]12,7 in Eq. (5.111) and the column corresponding to y1 is moved to the right‐hand side. The unknown column contains 12 variables and 
. The dynamic status of the whole vehicle powertrain system is uniquely defined by these variables.
Torque phase of 1–2 shift: As mentioned previously, the torque phase in a 1–2 shift differs from the first gear operation only in that the oncoming clutch torque TE, or variable y6, is a control variable rather than equal to zero. The corresponding specific state variable equation system is therefore represented as follows:
It is observed here that Eq. (5.113) only differs from Eq. (5.112) on the right‐hand side in an additional term reflecting the effect of the oncoming clutch torque or variable y6. The specific equation system (5.113) is used to solve the state variables until the end of the torque phase, which is determined at the time when the off‐going clutch starts to slip. The threshold of the clutch slippage is at the point when the clutch torque capacity becomes smaller than the clutch torque determined as a state variable. For the ZF RWD eight‐speed AT, the end of the 1–2 shift torque phase is judged by the following inequality:
In this inequality 
is the torque capacity of clutch C. For a given clutch, the clutch torque capacity mainly depends on the hydraulic pressure p in the clutch piston chamber and the clutch friction coefficient μ, which varies with clutch temperature. TC is the clutch torque in clutch C determined as the state variable y4. As every time step in the solution of Eq. (5.113), the clutch torque capacity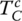 
is evaluated in terms of the clutch hydraulic pressure and compared with the clutch torque Tc solved as the state variable y4. As soon as the inequality above is satisfied, the 1–2 shift will enter the inertia phase.
Inertia phase of 1–2 shift: In the inertia phase of the 1–2 shift in the ZF RWD eight‐speed AT, clutches A and B are still applied, but clutch C is slipping. There are now only two constraint equations, represented by Eqs (5.107) and (5.108). These two constraint equations are combined with the general state variable equations from Eqs (5.97–5.105) to form the general state variable equation system for the inertia phase, which then has 11 equations and is represented in matrix form as follows:
Here the coefficient matrix is 
after being augmented by Eqs (5.107–5.108). The right‐hand side is augmented from [R]9,1 in Eq. (5.106) by two zero elements. Matrix [A]11,8 and [B]11,7 are augmented from [A]9,8 and [B]9,7 in the general state variable equation system expressed by Eq. (5.106), in the following partitions:
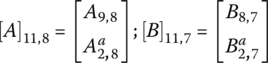
In this matrix augmentations, [A]9,8 and [B]8,7 are the same as in Eq. (5.106) and are characteristic of the transmission, as mentioned previously. The two augmenting matrices, 
and 
, depend on the transmission operation status and are represented for the 1–2 shift inertia phase of the ZF RWD eight‐speed AT as follows:
In general, the augmenting matrix 
is always a null matrix, with the number of columns equal to the number of torques and number of rows equal to the number of constraint equations in the inertia phase. The numbers of columns and rows of matrix 
are equal to the number of angular accelerations and the number of constraint equations in the inertia phase. In the inertia phase of the 1–2 shift, clutch torque TD or variable y5 is equal to zero and drops out of the equation system. The input torque Tin or variable y1, the clutch torques TC and TE, or variables y4 and y6, are considered as a given variables and are moved to the right‐hand side of the equation. The remaining 11 unknown state variables can then be uniquely solved from the following linear equation system:
In this equation system, variables y4 and y6 represent the clutch torques in the off‐going clutch C and the oncoming clutch E. Each clutch torque is controlled by the hydraulic pressure in the piston chamber, formulated in the following according Eq. (2.7) in Chapter 2.
At every time step, the right‐hand side of Eq. (5.117) is given and the 11 unknown state variables, i.e.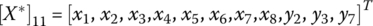 
, are uniquely solved for the determination of powertrain system dynamic status during the inertia phase of the 1–2 shift.
Note that the same procedure can be readily extended to all transmission operations for all automatic transmissions. It is just a matter of systematically augmenting the general state variable equation system by the augmenting matrices corresponding to the constraint equations in the specific operation.
5.6.3 Solution of State Variables by Variable Substitution
As shown in the qualitative analysis on the 1–2 shift of the Ford FWD six‐speed AT, the state variables in the vehicle powertrain system can be solved directly by variable substitution from the specific state variable equations in terms of the transmission input torque and the torques of the off‐going and oncoming clutches. For first gear operation, the torque phase and the inertia phase of the 1–2 shift of the Ford FWD six‐speed AT, and the solution of state variables by variable substitution are represented by Eqs (5.79–5.81), Eqs (5.83–5.85), and Eqs (5.92–5.94) respectively. The same procedure can be performed on the specific state variable equations for the ZF RWD eight‐speed AT, and all other transmissions in general. Without losing generality, the direct solution of state variables for the first gear operation, torque, and inertia phases of the 1–2 shift for the ZF RWD eight‐speed AT are illustrated in Figure 5.26.
Figure 5.26 Direct solution of state variables.
For all transmission operations, including fixed gear operations and direct shifts, the state variables can be solved from the corresponding specific state variable equations by variable substitution in terms of the transmission input torque and the torques in the off‐going clutch and oncoming clutch, as illustrated in Figure 5.26. But this can be a very lengthy process for transmissions with multiple direct shifts. For example, the ZF RWD eight‐speed AT has eight fixed gear operations and 36 direct shifts. It can be a challenging task to solve the state variable equations manually for so many operations without making any mistakes. In comparison, the matrix form representation of the state variable equation systems is more convenient for programming in the modeling of vehicle powertrain system dynamics.
5.6.4 Vehicle System Integration
The automatic transmission must be matched with the engine and the torque converter for the determination of the joint operation status of the overall vehicle powertrain system. The joint operation of the engine, the torque converter, and the transmission was illustrated in Figure 4.11 of Chapter 4, which details the characteristics of the torque converter coupling the engine and the transmission. The transmission system discussed so far in this chapter can be considered as a subsystem module to be integrated to the overall vehicle system. Model integration depends on the software platform used and the programming language. In the Matlab/Simulink environment, the vehicle system model can be structured based on the following block diagram in Figure 5.27.
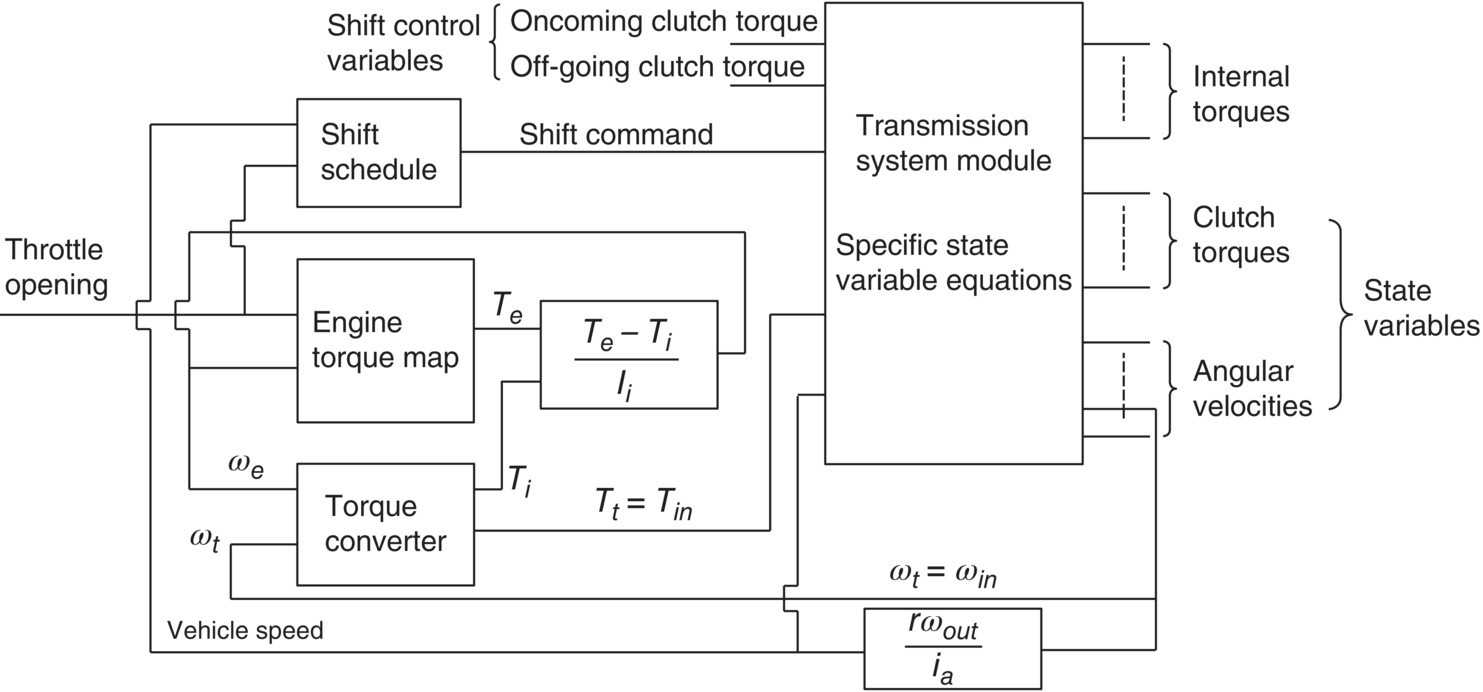
Figure 5.27 Block diagram of integrated vehicle powertrain system.
In Figure 5.27, the engine torque map describes the engine output torque in terms of the engine RPM and throttle opening, as discussed in Chapter 1. The torque converter block describes the converter input and output characteristics as discussed in Chapter 4. The shift schedule block provides shift decisions to the transmission system based on vehicle speed and engine throttle opening. The transmission system module is the core of the integrated vehicle powertrain system and is built based on the approaches presented in this chapter. Once the specific state variable equation systems of the transmission are established, either using matrix presentation or by variable substitution, the integrated vehicle powertrain system can be conveniently established on a Matlab/Simulink platform based on the structure shown in Figure 5.27. Note that the engine angular acceleration is treated as a separate state variable by a sub‐block in Figure 5.27, which implements the equation of motion for the engine flywheel and torque converter impeller assembly represented as follows:
where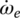 
is the engine angular acceleration, Te is the engine output torque, and Ti is the impeller torque. Ii is the mass moment of inertia of the flywheel and impeller assembly. The transmission input torque Tin, or the turbine torque Tt, is related to the impeller torque by the torque converter characteristics, which are discussed in Chapter 4 and reiterated in the following:
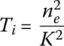
The torque ratio iq and the torque capacity factor K are functions of the speed ratio is, which is defined as the ratio between the angular velocities of the turbine and the impeller. The torque converter block in Figure 5.27 implements the four equations above with the turbine torque Tt as the transmission input torque Tin.
The vehicle powertrain system itself has certain torsional elasticity and damping characteristics that can affect system dynamics, particularly during launch and shift operations. To account for these system attributes, the transmission input and output shafts can be modeled as torsional spring dampers, as shown in Figure 5.28.
Figure 5.28 Spring–damper modeling for Input and output shafts.
In the spring–damper model shown in Figure 5.28, the angular acceleration of the turbine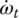 
and the angular acceleration of the transmission input 
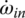are not the same because of the torsional spring damper between the turbine and the transmission input. Similarly, the angular acceleration of the transmission output 
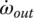and the angular acceleration of the final drive input 
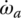are not the same because of the output spring damper. The introduction of the two torsional spring dampers will add two additional state variables: 
and 
. These two state variables are governed respectively by the equation of motion for the turbine assembly with mass moment of inertia It and the vehicle equation of motion modified from Eq. (5.82) or (5.105), as:
The input torque and output torque depend on the stiffness and the damping coefficient of the respective spring damper, as formulated by:
With the input and output shafts modeled as spring dampers, one more state variable equation will be added to the vehicle state variable equation system and the last state variable equation will be replaced by Eq. (5.126). For the ZF RWD eight‐speed AT, Eq. (5.125) can be added after Eq. (5.104) to become the new Eq. (5.105) and the old Eq. (5.105) will be replaced by Eq. (5.126) as the last equation in the new equation system. The number of equations in the general state variable system now becomes 10. The two state variables, 
and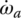 
, are included in the state variable equations, but the number of state variables increases by only one since Tout is no longer a state variable. Therefore, the specific state variable equation system in fixed gear and shift operations discussed previously will uniquely determine the state variables and the vehicle powertrain dynamics. Note that the elements of the new coefficient matrix, the state variable column, and the right‐hand side must be modified accordingly in the state variable equation system to accommodate the introduction of the spring dampers. Both the input and output torques are not state variables and will be evaluated using Eqs (5.127) and (5.128) after twice integrating the four related state variables, 
, 
, 
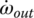, and 
.
5.7 Simulation of Vehicle Powertrain Dynamics
The formulations on the vehicle powertrain dynamics in the previous section are capable of simulating transmission performance during launch and shifting operations, or of vehicle performance in acceleration and fuel economy over a specified speed range. The former can then be termed as transmission simulation and the latter as range simulation. The powertrain model structure shown in Figure 5.27 needs be modified according to the intended objectives. The following list of data must be provided for transmission performance simulation and range simulation:
- Engine torque map and fuel map
- Torque converter characteristics
- Transmission data, including planetary gear train parameters, gear ratios and efficiency values
- Vehicle data, including weight, dimension, air drag coefficient, front projected area, tire radius
- Inertias of involved components, spring‐damper parameters
- Torque profiles of oncoming and off‐going clutches during shifts
Transmission simulation: The objectives of transmission simulation are obviously to assess the transmission performance during launch and shift operations based on shift quality criteria discussed previously. A large number of shifts under various vehicle operation conditions need to be implemented for automatic transmissions with multiple gears. The control and calibration of these shifts is a challenging and time‐consuming process that often relies on trial and error. With transmission simulation, engineers can have an upfront prediction on the transmission shift performances with selected clutch torque profiles and thus avoid the lengthy trial and error process in optimizing the clutch torque control. This will shorten greatly the transmission control and calibration time and enhance transmission shift quality.
Initial condition: If the simulation starts from standstill, then the dynamic model will start to simulate the vehicle launching in first gear. The initial condition at launch for the engine and torque converter is defined by Eq. (4.29) in Chapter 4. The values of all other state variables at launch are determined based on powertrain kinematics and static equilibrium. Generally, all angular velocities, other than the engine angular velocity are equal to zero at time zero during vehicle launching operations. The initial conditions for all shifts are set by the values of the related state variables, which are determined by the simulation model at the point of time when the shifts are initiated. Similarly, the initial condition at the start of the inertia phase is defined by the state variable values at the end of the torque phase. If the simulation of a particular shift is of interest, then the vehicle dynamic status must be determined by pre‐processing the simulation model up to the point at which the shift is initiated. The related state variable values at the point of shift initiation will define the initial condition for the particular shift.
Simulation output and applications: The simulation of transmission performance will provide output data that are directly related to shift quality:
- Transmission output torque during a shift. This shows how the output torque varies versus time during the shift process and provides the primary data for the judgment of shift quality as discussed in Section 5.5.
- Angular velocities of all rotational components, including the engine, turbine, gears, and clutches.
- Vehicle acceleration variations during the shift. This is also an indication for shift quality.
- Shift responsiveness as defined by shift time.
- Torque values for all clutches and gear members.
These output data provide a quantitative assessment of the shift quality resulting from the adopted control strategy and the related control variables which are primarily the torque profiles of the off‐going and oncoming clutches. It is possible to use the simulation model interactively to optimize the clutch torque profiles for the shift quality. In addition, the effect of engine torque reduction on shift quality can also be simulated to obtain the optimized timing and reduction amount. These model optimized control variables are then used as the initial values in the process of transmission control and calibration.
Range simulation: A drive range is the speed–time relationship specified to emulate a traffic pattern in model simulations. There are various standard Environment Protection Agency (EPA) driving cycles designed to mimic real‐world traffic conditions. For example, the speed‐time relationship of the EPA urban dynamometer driving schedule (UDDS) range is shown in Figure 5.29. The vehicle in simulation is required to follow the speed–time relationship specified in the drive range.
Figure 5.29 EPA UDDS drive range.
For range simulation, a driver model must be provided in the integrated vehicle system model to emulate the throttle and brake controls. The driver model consists of two parts: throttle controller and brake controller. Each of the two controllers is based on the difference between the simulated vehicle speed and the speed specified in the drive range. PID controllers are used for both the throttle and the brake to determine the throttle angle TA and brake force FB as shown in the following:
These two equations formulate respectively the throttle controller and the brake controller. In the two equations, Vspec and V are respectively the vehicle speed specified in the drive range and the vehicle speed obtained from model simulation, and kp, ki, and kd are the proportion, integration, and differentiation factors of the PID controller, with a second subscript indicating the throttle and the brake. The PID throttle and brake controllers can be easily integrated into the vehicle powertrain system model shown in Figure 5.27.
Output of range simulation: Range simulation provides a broad spectrum of outputs on vehicle dynamics and fuel economy performance on specified traffic patterns:
- Vehicle speed versus time traces. This demonstrates that the vehicle in simulation follows the traffic patterns closely through the throttle controller and the brake controller.
- Engine torque and speed output. This depicts the engine operation status for the whole drive range.
- Shift frequency and operation time in each gear during the simulated range. These indicate how the transmission shift schedule matches the traffic pattern.
- Transients during shifts, including shift time, output torque, and vehicle acceleration variations. These are the data that judge the transmission shift quality.
- Fuel economy and emissions for the simulated drive range obtained by engine map interpolation.
These data from range simulation listed are useful for upfront vehicle validations on acceleration and fuel economy performances, even prior to vehicle prototyping. More importantly, based on these data, engineers can modify the existing transmission shift schedule so as to optimize it for the best fuel economy for the simulated drive range. It is also possible to make the shift schedule adaptive to traffic patterns for fuel economy optimization. The data on transmission shift transients in range simulation provide model‐based validations for the transmission shift control strategy and control variables. This helps engineers to shorten the time needed to achieve the optimum transmission control and calibration.
References
- 1 https://en.wikipedia.org/wiki/Automatic_transmission
- 2 Hydra‐matic – Wikipedia https://en.wikipedia.org/wiki/Hydra‐matic
- 3 Gott, P.G.: Changing Gears: The Development of the Automotive, Society of Automotive Engineers, 1991, ISBN 1‐56091‐099‐2.
- 4 Gage, K.W. and Rhodes, P.J.: The New General Motors Hydra‐matic Transmission, SAE Transactions, Vol. 65, 1957, p. 462.
- 5 Megil, T.W., Haghgooie, M., and Colvin, D.S.: Shift characteristic of a four‐speed automatic transmission, SAE Paper # 1999‐01‐1060.
- 6 Fujii, E., Tobler, W.E., Clausing, E.M., Megli, T.W., and Haghgooie, M.: Application of Dynamic Band Model for Enhanced Drivetrain Simulation, Journal of Automobile Engineering, Vol. 216, No. 11, pp. 873–881.
- 7 Lee, S., Zhang, Y., Jung, D., and Lee, B.: 2014, A Systematic Approach for Dynamic Analysis of Vehicles with Eight or More Speed Automotive, ASME Journal of Dynamic Systems, Measurement, and Control, Vol. 136, No. 5, 051008(1‐11), 2014.
Problems
- A four‐speed AT for a FWD vehicle is shown in the stick diagram. The clutch engagement schedule is shown in the table. The second gear ratio is designed to be 1.63. The chain ratio is 1.0 and the final drive PGT parameter β3 is 1.90.
- When the transmission makes a 3–4 upshift with the torque converter locked at a vehicle speed of 45 mph, the engine speed drops by 640 RPM. Find the gear ratios for all forward and reverse gear ratios.
- Assuming that the turbine torque is T, find the reaction torque in the first, second, fourth and reverse gears respectively.
- The transmission is in the process of making a 2–3 upshift. The sensors of the control system detect a vehicle speed of 35 mph and a turbine speed of 2200 RPM. Determine the RPM of sun (S1) and the RPM of carrier (C1).
- The vehicle is being driven in first gear at a speed of 12 mph on a 5% slope and the vehicle acceleration is 5 ft/s2. Determine the combined reaction torque in clutches B2 and R3.
Vehicle data:
Front axle weight: 1800 lb Rear axle weight: 1500 lb Center of gravity height: 14 inch Wheel base: 108 in. Air drag coefficient: 0.31 Frontal projected area: 21 sq.ft Tire radius: 11.0 in. Roll resistance coefficient: 0.02 Powertrain efficiency: 0.91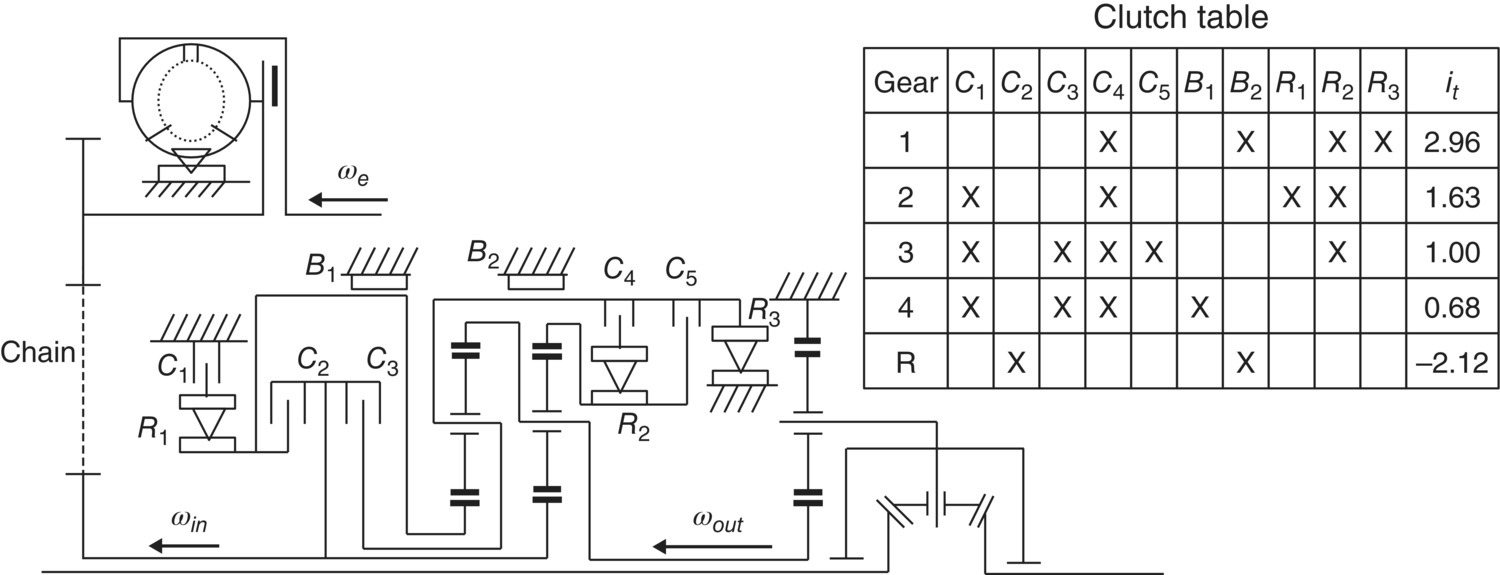 
- The stick diagram of an eight‐speed RWD automatic transmission and the clutch engagement are shown in Figure 5.12.
- Derive the characteristic equations for the planetary gear trains and superimpose the structural constraints upon these equations.
- Derive the formula for the transmission ratios for all gears in terms of the PGT parameters.
- Draw the FBD for each of the assemblies in the transmission. The input, output, and reaction torque directions are shown in the stick diagram for the whole transmission and must be followed in your FBDs. Derive the equation of motion for each of the assemblies.
- Derive the system of dynamic equations after eliminating the gear torques in the equations of motion.
- Determine the clutch torques for all gears under static condition for unity input torque.
- Derive the general state variable equation system in matrix form.
- Derive the specific state variable equation for a 1–2 shift in matrix form.
- Solve the output angular acceleration
for the 1–2 shift in (g) in terms of Tin and TE.
Symbols for vehicle data:
Vehicle weight: W Tire radius: R Air drag coefficient: Cd Frontal projected area: A Final drive efficiency: η Roll resistance coefficient: f - The stick diagram of the Ford 10‐speed RWD automatic transmission for pickup trucks and the clutch engagement are shown in Figure 5.30.
- Derive the formula for the transmission ratios for all gears in terms of the PGT parameters.
- Draw the FBD for each of the assemblies in the transmission. The input, output, and reaction torque directions are shown in the stick diagram for the whole transmission and must be followed in your FBDs. Derive the equation of motion for each of the assemblies.
- Derive the system of dynamic equations after eliminating the gear torques in the equations of motion.
- Determine the clutch torques for all gears under static condition for unity input torque.
Figure 5.30 Ford 10‐speed RWD AT.