Equilibrium Modeling of Solvent Extraction and Stripping of Copper(II), Nickel(II), and Ammonia for Ammoniacal Process Using LIX® 84-I

Abstract

Copper (II) and nickel (II) are often recovered from ammoniacal alkaline solutions by solvent extraction using hydroxyoxime extractants: both copper (II) and nickel (II) are extracted from ammoniacal alkaline solutions and, from the loaded organic phase, nickel (II) is selectively stripped with a dilute acid followed by copper (II) stripping with an acid of higher concentration. Since a small portion of ammonia is co -extracted with copper and nickel , the extracted ammonia should be scrubbed using a dilute acid before metal stripping. In the present study, a mechanistic model has been developed in order to support design and control of this process. The equilibrium distribution ratios of copper (II), nickel (II), and ammonia at 298 K using LIX^® 84-I (active component, 2-hydroxy-5-nonylacetophenone oxime) as the extractant are successfully correlated by considering the relevant equilibria . Based on these results, quantitative prediction of equilibrium distribution ratios in the process has been made possible, and suitable conditions for the efficient separation of copper (II) and nickel (II) are discussed.

Introduction

Chelating reagents such as β-hydroxyoximes and β-diketones are excellent for separating and concentrating copper (II) and nickel (II) by solvent extraction from ammoniacal alkaline solutions. Both copper (II) and nickel (II) are usually extracted at the same time, and co-extraction of ammonia is well known to occur [1–10]. The extracted ammonia is removed with a dilute acid, which is followed by the selective stripping of nickel (II) with dilute sulfuric acid and then by stripping of copper (II) with more concentrated sulfuric acid . Because the performance of this system depends on many operational parameters, quantitative modeling of this process is important in order to support its optimization ; however, the studies from this view point are scarce. Recently, using LIX^® 84-I , we have studied the equilibrium extraction of ammonia [11], copper (II)-ammonia [12], nickel (II)-ammonia , and copper (II)-nickel (II)-ammonia [13]. As a result, we have established a quantitative model of the extraction part of this ammoniacal process and thus summarize it here.

Experimental

Preparation of Reagents and Solution

The hydroxyoxime reagent LIX^® 84-I (active component: 2-hydroxy-5-nonylacetophenone oxime; lot no. 0684I001; Cognis Ireland Ltd.) and the aliphatic solvent ShellSol^® D70 (lot no. 50801 and 50713; Shell Japan Ltd.) were used as extractant and diluent without further purification , respectively.

As the feed organic phase, 10 vol.% LIX^® 84-I was used, where total hydroxyoxime (HR) concentration, C_BO, was 0.16 mol/L as determined by the maximum copper (II) loading. The feed aqueous phases were prepared by mixing the appropriate stock solutions of ammonium salt (nitrate and sulfate), copper (II) and nickel (II) nitrates, and pH adjustment reagent (various concentrations of nitric acid or sodium hydroxide) in a 50-mL centrifuge bottle.

Extraction and Analysis of Ammonia, Cu(II), and Ni(II)

The extraction equilibria were attained in a water bath thermostat at 298 K. The detailed procedure for extraction and the analysis methods for ammonia , copper , nickel , and pH were described elsewhere [11–13].

Distribution ratios of metal ions M²⁺ (M = Ni or Cu), D(M), and of NH₃, D(NH₃), were calculated as

$D({\text{M}}) = \left[ {\text{M}} \right]_{{{\text{T}},{\text{org}}}} /[{\text{M}}]_{{{\text{T}},{\text{aq}}}}$

(1)

$D\left( {{\text{NH}}_{ 3} } \right) = \left[ {{\text{NH}}_{ 3} } \right]_{{{\text{T}},{\text{org}}}} /\left( {\left[ {{\text{NH}}_{ 3} } \right]_{{{\text{init}},{\text{T}},{\text{aq}}}} - \left[ {{\text{NH}}_{ 3} } \right]_{{{\text{T}},{\text{org}}}} } \right)$

(2)

where the subscripts org, aq, T, and init denote organic phase, aqueous phase, total concentration, and initial concentration, respectively.

Results and Discussion

The equilibria and their equilibrium constants established in our model are shown in Table 1.

Table 1

Equilibria and their constants considered in our model

Equilibria	Equilibrium constant^a	No.	References
Aqueous phase
NH₄⁺_aq ↔ NH_{3 aq} + H_aq⁺	pK_a(NH₄⁺) = 0.0562I + 9.33	(3)	[14]
M_aq²⁺ + m NH_{3 aq} ↔ M(NH₃)_m²⁺_aq	log β_m = ∑₁^m (log K_m⁰ + A[NH₃]_T + B)^b	(4)	[15]
HSO₄⁻_aq ↔H_aq⁺ + SO₄²⁻_aq	ln (K_a(HSO₄⁻)/0.0104) = 5.29I^1/2/(1 + 0.56I^1/2)	(5)	[16]
M_aq²⁺ + SO₄²⁻_aq ↔ MSO_{4 aq}	log β(CuSO₄) = 2.099 − 4.05I^1/2/(1 + 1.618I^1/2) + 0.05201I log β(NiSO₄) = 2.10	(6)	[17, 18]
Organic phase
(HR)_{i org} + HR_org ↔ (HR)_{i+1 org}	K_m = 9.9	(7)	[14]
(HR)_j·NH_{3 org} + HR_org ↔ (HR)_j+1·NH_{3 org}	K₂ = 14	(8)	[12]
(HR·NH₃)_{k org} + HR·NH_{3 org} ↔ (HR·NH₃)_{k+1 org}	K₃ = 25	(9)	[12]
Extraction
NH_{3 aq} + HR_org ↔ HR·NH_{3 org}	K₁ = 0.17	(10)	[12]
M_aq²⁺ + 2 HR_org ↔ MR_{2 org} + 2 H_aq⁺	log K_e(Cu) = 0.112I + 1.07 log K_e(Ni) = 0.129I − 4.80	(11)	[12, 13]
MR_{2 aq} ↔ MR_{2 org}	log K_d(Cu) = 4.2 log K_d(Ni) = 4.3	(12)	[12, 13]
NiR_{2 org} + NH_{3 aq} ↔ NiR₂·NH_3org	K₄ = 0.1	(13)	[13]
NiR_{2 org} + 2 NH_{3 aq} ↔ NiR₂·(NH₃)_{2 org}	K₅ = 0.063	(14)	[13]

i, j and k positive integers ranging to infinity

^aThe unit of each constant is derived based on molarity

^bValues of log K_m⁰ (m = 1, 2, 3, 4) for copper (II) were 3.99, 3.34, 2.73, 1.97, respectively; values of log K_m⁰ (m = 1, 2, 3, 4, 5, 6) for nickel (II) were 2.67, 2.12, 1.61, 1.07, 0.63, −0.09, respectively. Values of A and B for copper (II) were 0.08 L/mol and 0.065, respectively; values of A and B for nickel (II) were 0.061 L/mol and 0.0375, respectively

Firstly, we measured the distribution ratios of ammonia using different concentrations of ammonium nitrate solution (1.1–5.3 mol/L) at different equilibrium pH values [11, 12]. The log D(NH₃) value at a fixed ammonium nitrate concentration monotonically increased from −3 to −1.8 with pH_eq from 8 to 10 and then tended to be constant. At a fixed pH_eq (8–10), the log D(NH₃) slightly decreased with increasing ammonium nitrate concentration. The results were analyzed assuming the ammonia extraction by HR as the adduct HR·NH₃ (Eq. 10), the successive association of the adduct with HR (Eq. 8), and the successive self-association of the adduct (Eq. 9), where acid dissociation of ammonium ion (Eq. 3) and successive association of HR (Eq. 7) both with known equilibrium constants were also considered; that is, the equilibrium constants of K₁, K₂, and K₃ were obtained by a least squares method so that the experimental data satisfied the simultaneous equations of the relevant equilibrium constants and material balances. Although K₁ contains the aqueous species (NH_{3 aq}), the K₁ value is found to be independent of ionic strength. This would be because NH₃ is a neutral species, and thus its activity coefficient is not sensitive to ionic strength in comparison with the ionic species such as Cu²⁺ and Ni²⁺ as described below. The slight decrease in D(NH₃) with increasing ammonium nitrate concentration would be due to a decrease in K_a(NH₄⁺) as expressed by Eq. (3).

Next, we measured the distribution ratios of the metal ions in the acidic region using the different concentrations of ammonium nitrate solution (1.1–5.3 mol/L) containing 0.05 mol/L Cu(NO₃)₂ or Ni(NO₃)₂ at different pH_eq values (1–3 for Cu and 2.5–6 for Ni) [12, 13]. At pH 1–3 for Cu and 2.5–5.5 for Ni, the log D(M) linearly increased with pH_eq with a slope 2 at a fixed ammonium nitrate concentration and increased slightly with ammonium nitrate concentration at a fixed pH_eq. On the basis of the extraction stoichiometry of Eq. (11), extraction equilibrium constants, K_e(Cu) and K_e(Ni), were determined from the interpolated D values at half-extraction pHs at each ammonium nitrate concentration. As shown by Fig. 1 and Eq. (11), we found a linear relationship between log K_e(M) thus determined and ionic strength, I, (equal to ammonium nitrate concentration in this case). At the pH 6–7, log D(M) is constant regardless of the ammonium nitrate concentration, because the distribution of the complex MR₂ is dominant. From the log D(M) values in this region, the distribution equilibrium constants of MR₂, K_d(M), were determined as Eq. (12).

../images/468727_1_En_167_Chapter/468727_1_En_167_Fig1_HTML.gif — Fig. 1
The effect of ionic strength on log K_e in nitrate solutions [12, 13]

The distribution ratios of M and ammonia in the alkaline region were also measured using 3.2 mol/L ammonium nitrate solution containing 0.05 mol/L M(NO₃)₂ solution, and the results were compared with the values calculated from the relevant equilibrium constants and material balances assuming the extracted metal complex was only MR₂ [12, 13]. The agreement between experiment and calculation for D(Cu) and D(NH₃) in the copper extraction was satisfactory. On the other hand, in the nickel extraction , the calculated D(NH₃) values were significantly lower than the experimental values, though the calculated D(Ni) values were in good agreement with the experimental values. Thus, the extraction equilibrium constants of ammonia with NiR₂, K₄ and K₅, were obtained by the least squares method so that the experimental data for nickel and ammonia satisfied the simultaneous equations of the relevant equilibrium constants and material balances. As a result, the K₄ and K₅ values were determined, and good fitting was obtained not only in nickel but also in ammonia .

We then measured the distribution ratios of the metal ions and ammonia using 1.5 mol/L ammonium sulfate solution containing 0.05 mol/L Cu(NO₃)₂ or Ni(NO₃)₂ at different pH_eq values (2–10 for Cu and 7–10.5 for Ni) [12, 13]. The distribution ratio of nickel at acidic region was not measured because of the formation of nickel ammonium sulfate hydrate. Figure 2a and b are the results for Cu(II) and Ni(II) extraction , respectively. At pH < 4, log D(Cu) increased with increasing pH_eq with a slope of 2. A constant D(M) value was found at pH 4–8 for Cu and 7–8 for Ni. With the increasing pH_eq from 8 to10, the D(M) decreased because of the metal-ammine complex formation, while the D(NH₃) increased because of the progress of acid dissociation of ammonium ion. The curves in Fig. 2 are calculated by solving simultaneous equations of relevant equilibrium constants and material balances at given pH_eq values, and are in good agreement with the experimental data.

../images/468727_1_En_167_Chapter/468727_1_En_167_Fig2_HTML.gif — Fig. 2
The effect of pH_eq on log D(M) for extraction from ammonium sulfate solutions [12, 13]

A similar comparison was also made at different ammonium sulfate concentrations (0.5–2.3 mol/L) with satisfactory agreement. Here, we have established the model to quantitatively calculate the distribution ratios of copper and nickel together with that of ammonia at a given pH_eq in sulfate solution.

Our final objective is to predict distribution ratios for mixed solutions of copper and nickel at a given initial pH, pH_init, or given sodium hydroxide concentration (as a pH adjustment reagent). We measured the pH values of (NH₄)₂SO₄, Ni–(NH₄)₂SO₄, Cu–(NH₄)₂SO₄, and Ni–Cu–(NH₄)₂SO₄ solutions with various sodium hydroxide concentrations [13]. We found the following empirical equation to correlate the observed pH and the added sodium hydroxide, copper , and nickel concentrations at 1.5 mol/L ammonium sulfate of pH > 8:

$\begin{aligned} {\text{pH}} & = 8.11 + 2.33\,[{\text{NaOH}}]_{\text{aq}} - 1.02\,[{\text{NaOH}}]_{\text{aq}}^{2} + 0.21\,[{\text{NaOH}}]_{\text{aq}}^{3} \\ & \quad - 3.34\,[{\text{Cu}}]_{\text{aq}} - 4.29\,[{\text{Ni}}]_{\text{aq}} \\ \end{aligned}$

(15)

When one metal ion is extracted, two hydrogen ions in HR are released into the aqueous phase to neutralize sodium hydroxide; thus, the following equation holds true:

$[{\text{NaOH}}]_{\text{aq}} = [{\text{NaOH}}]_{{{\text{init}},{\text{aq}}}} {-}2\left( {[{\text{Cu}}]_{{{\text{T}},{\text{org}}}} + [{\text{Ni}}]_{{{\text{T,}}\,{\text{org}}}} } \right)$

(16)

Therefore, by considering the equations for relevant equilibrium constants, material balances, and Eqs. (15) and (16), the distribution ratios can be calculated using initial sodium hydroxide concentration.

Finally, we measured the distribution ratios of copper , nickel , and ammonia using mixed copper −nickel solutions at 1.5 mol/L ammonium sulfate and 0.2 mol/L sodium hydroxide with the results shown in Fig. 3 [13]. Here, the effect of one metal concentration on the distribution ratios of copper , nickel , and ammonia was examined at a fixed concentration of another metal of 0.05 mol/L.

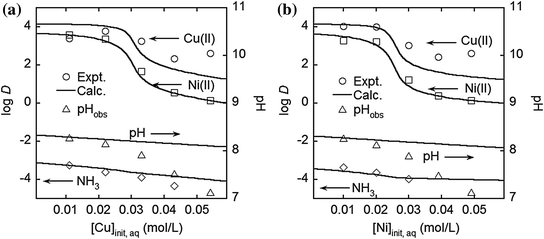
../images/468727_1_En_167_Chapter/468727_1_En_167_Fig3_HTML.gif — Fig. 3
The effect of initial total metal concentration in the aqueous phase on log D(M) for the extraction from the copper -nickel mixed solutions [13]

There is a sharp decrease in D(M) at the metal concentration of the X-axis of 0.02–0.03 mol/L, because, in this region, the total metal concentration in the organic phase is close to the loading capacity of the extractant. The distribution ratios of both metals are very high (>10³) when the metal concentration of the X-axis is less than 0.02 mol/L; thus, we can achieve complete extraction of both metals at the same time in this condition. The distribution ratio of ammonia is about 10⁻⁴, which corresponds to the ammonia concentration in the organic phase of 5 mg/L; thus, it is easy to scrub loaded ammonia before metal stripping. The curves in Fig. 3 are the predicted values which are basically in good agreement with the experimental data. When pH is less than 8, there are some deviations in the distribution ratios and pH values. This is because the empirical equation of Eq. (15) cannot be applied to this region.

Conclusions

An equilibrium model has been established for quantitative prediction of the extraction behavior of copper , nickel , and ammonia with LIX^® 84-I from ammoniacal alkaline solutions. This model will be useful for the design and control of the ammoniacal process for copper and nickel .

Acknowledgements

Mr. S. Wang sincerely thanks the China Scholarship Council for providing his scholarship (201406370020).

References

1.
Rice NM, Nedved M, Ritcey GM (1978) The extraction of nickel from ammoniacal media and its separation from copper, cobalt and zinc using hydroxyoxime extractants I. SME–529. Hydrometallurgy 3(1):35–54Crossref
2.
Flett DS, Melling J (1979) Extraction of ammonia by commercial copper chelating extractants. Hydrometallurgy 4(2):135–146Crossref
3.
Kumar V, Jana RK, Jha D, Nayak AK, Bagchi D, Akerkar DD (1987) Recovery of copper, nickel and cobalt from ammoniacal leach liquors obtained by direct ammonia leaching of sea nodules. Trans Indian Inst Met 40(1):64–70
4.
Pandey BD, Kumar V, Bagchi D, Akerkar DD (1989) Extraction of nickel and copper from the ammoniacal leach solution of sea nodules by LIX^® 64N. Ind Eng Chem Res 28(11):1664–1669Crossref
5.
Kumar V, Pandey BD, Bagchi D (1991) Application of LIX^® 84 for separation of copper, nickel and cobalt in ammoniacal leaching of ocean nodules. Mater Trans, JIM 32(2):157–163Crossref
6.
Nathsarma KC, Sarma PVRB (1993) Processing of ammoniacal solutions containing copper, nickel and cobalt for metal separation. Hydrometallurgy 33(1–2):197–210Crossref
7.
Rokukawa N (1993) Separation of cobalt, nickel and copper from ammoniacal alkaline leach liquor of cobalt crusts by solvent extraction. J MMIJ 109(5): 373–377 (in Japanese, with English abstract)
8.
Alguacil FJ (1999) Recovery of copper from ammoniacal/ammonium carbonate medium by LIX^® 973N. Hydrometallurgy 52(1):55–61Crossref
9.
Parija C, Sarma PVRB (2000) Separation of nickel and copper from ammoniacal solutions through co–extraction and selective stripping using LIX^® 84 as the extractant. Hydrometallurgy 54(2):195–204Crossref
10.
Ritcey GM (2006) Solvent extraction principles and applications to process metallurgy. Part II, Revised 2nd edn. G.M. Ritcey & Associates Inc., Ottawa
11.
Wang S, Li J, Narita H, Tanaka M (2017) Modeling of equilibria of the solvent extraction of ammonia with LIX^® 84I. Solvent Extr Res Dev Jpn 24(2):71–76Crossref
12.
Wang S, Li J, Narita H, Tanaka M (2017) Equilibrium modeling of the extraction of copper and ammonia from alkaline media with the extractant LIX^® 84I. Mater Trans 58(10):1427–1433Crossref
13.
Wang S, Li J, Narita H, Tanaka M (2018) Equilibrium modeling for solvent extraction of nickel and ammonia from alkaline media with the extractant LIX^® 84-I. Mater Trans 59(4):634–641Crossref
14.
Tanaka M, Alam S (2010) Solvent extraction equilibria of nickel from ammonium nitrate solution with LIX^® 84I. Hydrometallurgy 105(1):134–139Crossref
15.
Sillen LG, Martell AE (1964) Stability constants of metal–ion complexes. Special Publication No. 17. The Chemical Society, London
16.
Hsueh L, Newman J (1971) The role of bisulfate ions in ionic migration effects. Ind Eng Chem Fundam 10(4):615–620Crossref
17.
Näsänen R (1949) Spectrophotometric study on complex formation between cupric and sulphate ions. Acta Chem Scand 3(2):179–189Crossref
18.
Wasylkiewicz S (1990) Ion association in aqueous solutions of electrolytes. II. Mathematical model for sulphates of bivalent metals. Fluid Phase Equilib 57(3):277–296Crossref

Equilibrium Modeling of Solvent Extraction and Stripping of Copper(II), Nickel(II), and Ammonia for Ammoniacal Process Using LIX^® 84-I