Introduction
Tungsten , a strategic and rare metal, has a wide range of industrial applications, such as hard materials, high temperature technology, lighting, X-ray technology, machine and engine construction, chemical industry, laser technology, armaments and aerospace industry. The key properties are low vapor pressure and thermal expansion , high density and melting point, good thermal and electrical conductivity, and high modulus of elasticity [1, 2]. Due to the lack of viable substitutes, the European Union has included tungsten in the list of critical raw materials [3]. Similarly, the British Geological Survey ranked it as number two in a supply list containing forty one critical elements [4]. The main tungsten minerals in nature are scheelite (CaWO4) and wolframite ((Fe,Mn)WO4), with approximately two-thirds of the world tungsten reserves consisting of scheelite [1, 2]. China has more than 60% of tungsten reserves in the world, and accounts for about 80% of the world tungsten production [5]. Ammonium paratungstate (APT ), as the main intermediate in industrial tungsten production, is usually obtained from tungsten concentrates by a caustic/soda or hydrochloric acid treatment [6].
In modern industrial production technologies, caustic digestion is employed to treat wolframite producing soluble sodium tungstate and insoluble iron or manganese hydroxide at either atmospheric pressure (75–145 °C), in concentrated NaOH solutions (≥10 mol/L) [7], or under high pressures (135–255 °C), in a dilute NaOH solution (1.25–3.75 mol/L) [8]. When tungsten concentrate contains scheelite , Na2CO 3 is added in NaOH solution to extract tungsten in an autoclave operating under elevated pressures (180–310 °C) [9]. Subsequently, solvent extraction or ion exchange is used to convert Na2WO4 to (NH4)2WO4, which requires excess acid to treat the Na2WO4 solution and a large amount of water to dilute the leach solution [10]. Obviously, the caustic/soda leaching method needs a large excess of reagents, and discharges huge volumes of high-salinity wastewater [11]. Furthermore, Leal–Ayala et al. [12] pointed out that 4% of tungsten would be lost in the APT production.
Acid processing, as a classical method, can avoid the use of high temperatures and a large excess of leaching reagents, and treating or even discharging large amounts of sodium salts solutions. Hydrochloric acid , nitric acid, or sulfuric acid is used to decompose tungsten ores and produce insoluble tungstic acid. However, a solid or colloidal H2WO4 layer was observed covering the surfaces of the unreacted tungsten particles, thus hindering the reaction rate and yield. Therefore, some strategies are usually adopted to increase the feasibility, such as reducing particle size [13], using a large excess of concentrated HCl [14], utilizing heated ball mill reactors [15], and employing organic acids to dissolve solid tungstic acid [16].
Additionally, many researchers have focused on discomposing tungsten concentrates to produce soluble tungsten compounds. Martins leached synthetic scheelite in hydrochloric or nitric acid at pH 1.5–3.0 in a temperature range of about 25–100 °C to obtain soluble metatungstates [17, 18]. Potashnikov et al. [19] and Kalpakli et al. [20] treated scheelite by oxalic acid to form soluble hydrogen aqua oxalate tungstate (H2[WO3(C2O4)H2O]). Hydrochloric, nitric or sulfuric acid in the presence of phosphorus was found to decompose scheelite and form a water–soluble phosphotungstic acid chelate compound (12-tungstophosphoric heteropoly acid, H3PW12O40) [21–24]. In previous work, we systematically studied the conversion of scheelite and mixed scheelite -wolframite concentrate in sulfuric acid , and found that the tungsten concentrates can be completely converted in H2SO4 solutions by adding an oxidizing agent and controlling the H2WO4 formation in moderate acid concentrations [25, 26].
Even though tungsten extraction technology has been developed for more than a hundred years since R. Oxiland in 1874 [1], there is limited thermodynamic information on the tungsten leaching chemistry. Osseo-Asare [27] applied the Pourbaix diagram concept to tungsten hydrometallurgy , but stated a lack of sufficient thermodynamic data. Martins [28] determined the equilibrium constants for wolframite and scheelite leaching systems, and also pointed out some inherent limitations due to the estimation of selected thermodynamic data. Zhao and Li [29] used a pseudo-ternary-system phase diagram to explain scheelite digestion in high concentration NaOH and Na2CO 3 solutions.
Therefore, this paper focuses on collecting and assessing the thermodynamic data of tungsten minerals previously published. Gibbs free energy changes versus temperature were calculated with HSC software for tungsten minerals decomposing in mineral acid and alkaline solutions, using the adopted thermodynamic data. The calculations were finally compared with the experimental and industrial results previously reported in the literature. This work is beneficial to better understanding of various technologies in industrial tungsten processing.
Thermodynamics
Thermodynamic Equation
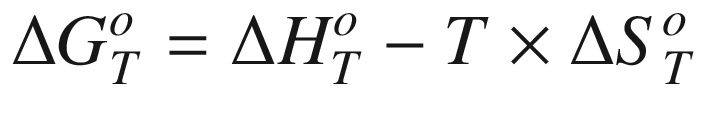
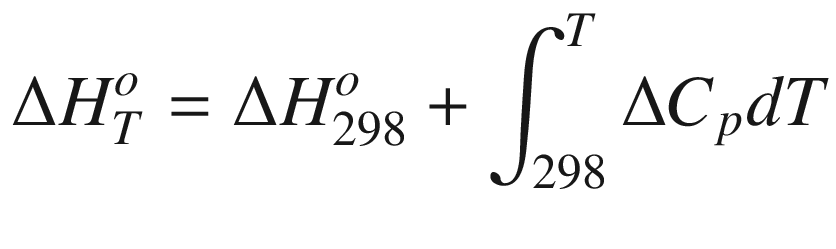
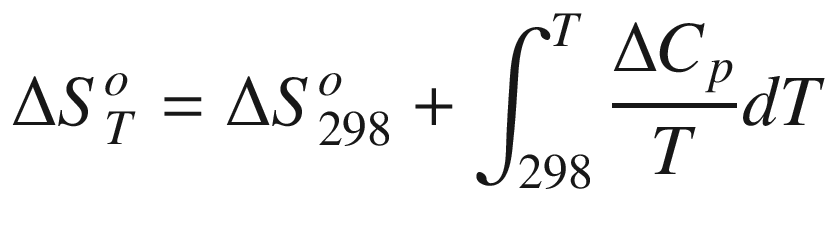
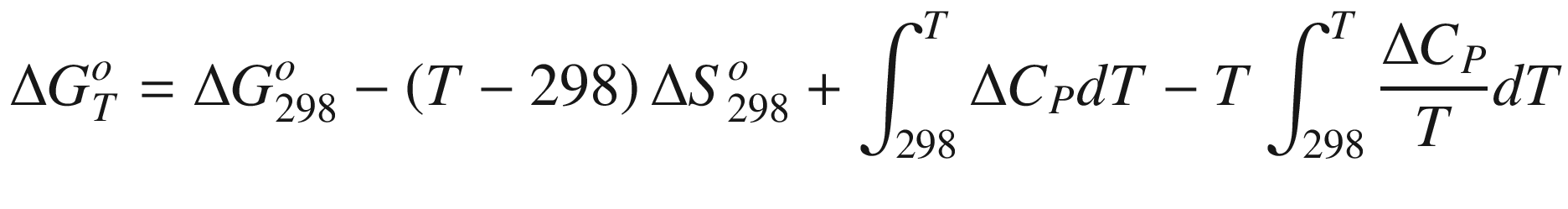
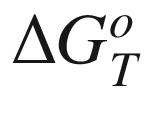 is the standard Gibbs energy
of reaction at temperature
T, (kJ mol−1);
is the standard Gibbs energy
of reaction at temperature
T, (kJ mol−1); 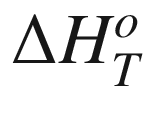 the standard enthalpy of reaction at temperature
T, (kJ mol−1);
the standard enthalpy of reaction at temperature
T, (kJ mol−1); 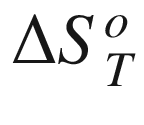 the standard entropy of reaction at temperature
T, (J mol−1);
the standard entropy of reaction at temperature
T, (J mol−1); 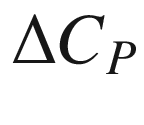 the molar heat capacity of reaction at constant pressure at temperature
T, (J mol−1 K−1); T is the temperature
(K).
the molar heat capacity of reaction at constant pressure at temperature
T, (J mol−1 K−1); T is the temperature
(K).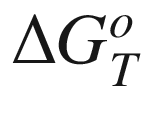 , the estimation of the heat capacity term
, the estimation of the heat capacity term 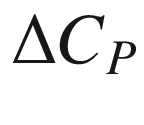 plays a critical role. Barner and Kust [30] has assessed the various approaches for estimating
plays a critical role. Barner and Kust [30] has assessed the various approaches for estimating  . The molar heat capacity
. The molar heat capacity 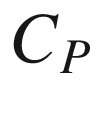 of each substance relating to temperature
T was used in the calculation, as shown in empirical Eq. (5).
of each substance relating to temperature
T was used in the calculation, as shown in empirical Eq. (5).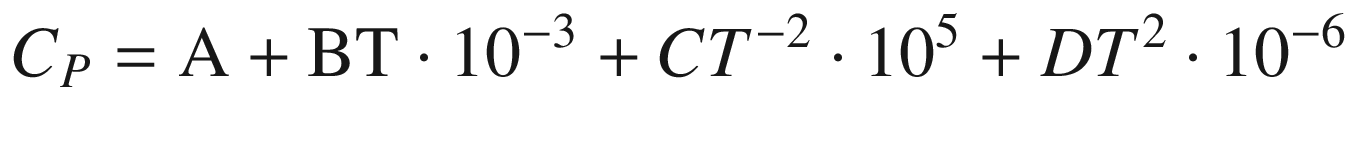
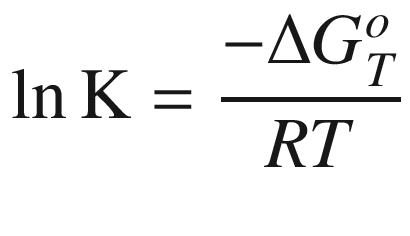
Thermodynamic Data
Standard–state thermochemical properties are prerequisites for the modeling of chemical reactions. Various thermodynamic properties of tungsten compounds have been reported. However, there is no assessment of the thermodynamic data available. So the primary target is to select the reliable data for tungsten compounds.
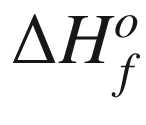 have been reported for scheelite
(CaWO4) at 298 K. The proposed value changes in the range of −1623.00 to −1683.70 kJ mol−1, as reviewed by Wood and Samon [31], and the adopted value is −1645.1 kJ mol−1. This value is widely accepted by Lange’s Handbook of Chemistry [32], HSC software [33], and last by Martins [28]. King and Weller [34] determined the heat capacity of scheelite
at low temperatures (up to 298.15 K), and from this they derived a third law entropy,
have been reported for scheelite
(CaWO4) at 298 K. The proposed value changes in the range of −1623.00 to −1683.70 kJ mol−1, as reviewed by Wood and Samon [31], and the adopted value is −1645.1 kJ mol−1. This value is widely accepted by Lange’s Handbook of Chemistry [32], HSC software [33], and last by Martins [28]. King and Weller [34] determined the heat capacity of scheelite
at low temperatures (up to 298.15 K), and from this they derived a third law entropy, 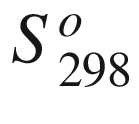 = 126.4 J K−1 mole−1, which has been adopted in all major compilations of thermodynamic data on scheelite
. Combined with the heat capacity of scheelite
(298–1000 K) from Barin and Knacke [35], the parameters for temperature
dependence of
= 126.4 J K−1 mole−1, which has been adopted in all major compilations of thermodynamic data on scheelite
. Combined with the heat capacity of scheelite
(298–1000 K) from Barin and Knacke [35], the parameters for temperature
dependence of 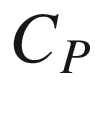 are obtained. The values of
are obtained. The values of 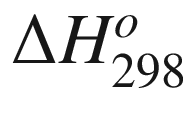 and
and 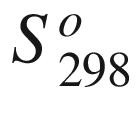 result in
result in 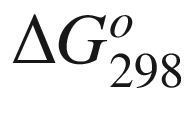 = −1538.43 kJ mole−1. The thermodynamic data adopted for scheelite
are shown in Table 1.
= −1538.43 kJ mole−1. The thermodynamic data adopted for scheelite
are shown in Table 1.Adopted thermodynamic data for tungsten compounds
Compound |
|
|
|
| |||
|---|---|---|---|---|---|---|---|
A | B | C | D | ||||
CaWO4 | −1645.10 | −1538.43 | 126.4 | 134.56 | 20.67 | −24.4 | 0 |
FeWO4 | −1154.80 | −1053.91 | 131.8 | 132.42 | 29.75 | −23.93 | 0 |
MnWO4 | −1035.83 | −1206.08 | 127.4 | 120.68 | 36.51 | −3.69 | 0 |
H2WO4 | −1131.77 | −1003.92 | 112.6 | 13.25 | 350.6 | 10.1 | −186 |
Na2WO4(aq) | −1554.02 | −1455.58 | 160.3 | 105.41 | 118 | 0 | 0 |
Similarly to scheelite
, the values of  reported for ferberite (FeWO4) at 298 K have been also reviewed by Wood and Samon [31]. As with scheelite
, the standard entropy of ferberite,
reported for ferberite (FeWO4) at 298 K have been also reviewed by Wood and Samon [31]. As with scheelite
, the standard entropy of ferberite,  = 131.8 J K−1 mole−1, was calculated from the low-temperature
calorimetric measurements of heat capacity by Weller [36]. This value was adopted in this research. Combined with the heat capacity of ferberite (5–500 K), measured by Lyon and Westrum [37] using adiabatic calorimetry, the parameters for temperature
dependence of
= 131.8 J K−1 mole−1, was calculated from the low-temperature
calorimetric measurements of heat capacity by Weller [36]. This value was adopted in this research. Combined with the heat capacity of ferberite (5–500 K), measured by Lyon and Westrum [37] using adiabatic calorimetry, the parameters for temperature
dependence of  were fitted by HSC software. However, there are big differences in the values of
were fitted by HSC software. However, there are big differences in the values of  and
and  for ferberite. The more negative values are in the range −1184 to −1192 kJ mol−1 and −1085 to −1089 kJ mol−1, while the opposed higher values range from −1154 to −1158 kJ mol−1 and −1054 to −1057 kJ mol−1 [31]. We favor the higher values because thermodynamic calculation
result show an accordant trend with the experimental
results [26], while the more negative values seem more suited to pyrometallurgical calculations. So we accept, respectively, −1154.8 and −1053.91 kJ mol−1 for
for ferberite. The more negative values are in the range −1184 to −1192 kJ mol−1 and −1085 to −1089 kJ mol−1, while the opposed higher values range from −1154 to −1158 kJ mol−1 and −1054 to −1057 kJ mol−1 [31]. We favor the higher values because thermodynamic calculation
result show an accordant trend with the experimental
results [26], while the more negative values seem more suited to pyrometallurgical calculations. So we accept, respectively, −1154.8 and −1053.91 kJ mol−1 for  and
and  of ferberite in this paper, which was also accepted in the recent research of Martins [28] and Lange’s Handbook of Chemistry [32].
of ferberite in this paper, which was also accepted in the recent research of Martins [28] and Lange’s Handbook of Chemistry [32].
There are limited thermodynamic data available for huebnerite (MnWO4). In the HSC Database, the  ,
,  , and
, and  for huebnerite are −1305.83 kJ mol−1, −1053.08 kJ mol−1, and 140.58 J K−1 mole−1, respectively. These data, together with the parameters for
for huebnerite are −1305.83 kJ mol−1, −1053.08 kJ mol−1, and 140.58 J K−1 mole−1, respectively. These data, together with the parameters for  , originate from Barin and Knacke [35], and they are very similar to the values adopted by Horner [38].
, originate from Barin and Knacke [35], and they are very similar to the values adopted by Horner [38].
The thermodynamic value for H2WO4,  , is in the range of −1003.9 to −1006.9 kJ mol−1 except for the estimate by Osseo-Asare [27], which has been compared by Martins [28]. The value in the HSC Database is −1003.92 kJ mol−1, similar to Lange’s Handbook of Chemistry [32]. This was adopted in the calculations together with the other data.
, is in the range of −1003.9 to −1006.9 kJ mol−1 except for the estimate by Osseo-Asare [27], which has been compared by Martins [28]. The value in the HSC Database is −1003.92 kJ mol−1, similar to Lange’s Handbook of Chemistry [32]. This was adopted in the calculations together with the other data.
The  of Na2WO4 in aqueous solution was reviewed by Martins [28], ending up with a value of about −1455 kJ mol−1. This value is also available in the HSC Database. As for CaWO4 and FeWO4, the entropy,
of Na2WO4 in aqueous solution was reviewed by Martins [28], ending up with a value of about −1455 kJ mol−1. This value is also available in the HSC Database. As for CaWO4 and FeWO4, the entropy,  = ~160.3 J K−1 mole−1, was calculated from low-temperature
calorimetric measurements of heat capacity by King and Weller [34]. Combined with the heat capacity in Barin and Knacke [35], the parameters for temperature
dependence of
= ~160.3 J K−1 mole−1, was calculated from low-temperature
calorimetric measurements of heat capacity by King and Weller [34]. Combined with the heat capacity in Barin and Knacke [35], the parameters for temperature
dependence of  were fitted at temperatures of 275–800 K (see Table 1).
were fitted at temperatures of 275–800 K (see Table 1).
The adopted thermodynamic data for tungsten
compounds are presented in Table 1. The other data for substances used in the calculation were taken from the HSC Database. They are close to the values adopted by Martins [28], except the  parameters.
parameters.
Thermodynamic Results
Tungsten Ores Decomposing in NaOH and Na2CO 3 Solutions
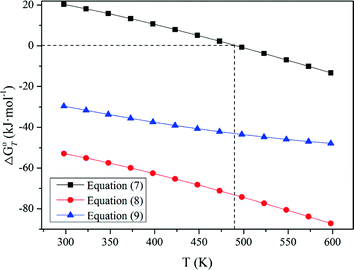
Standard Gibbs energy changes versus temperature of tungsten ores decomposing in NaOH solutions
Standard Gibbs energy changes versus temperature of tungsten ores decomposing in Na2CO 3 solutions
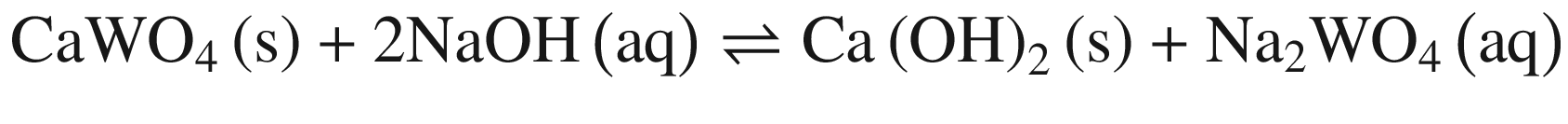
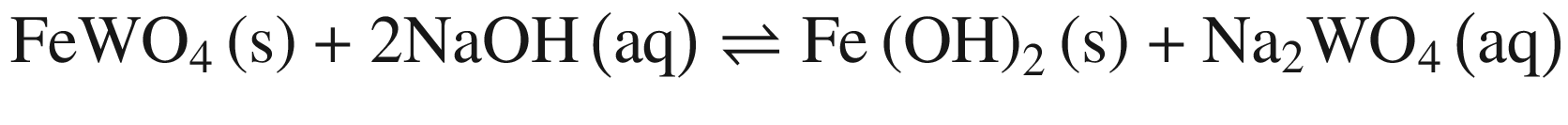
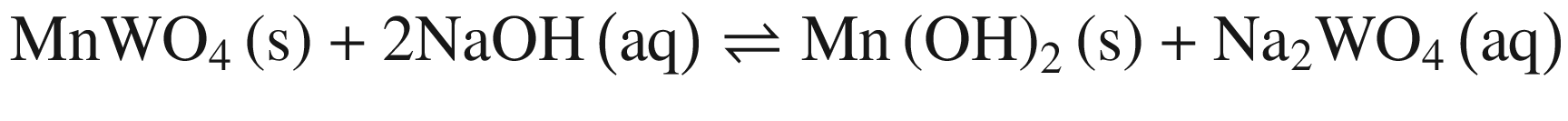
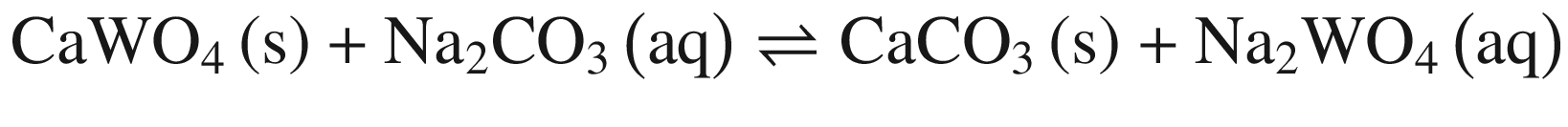
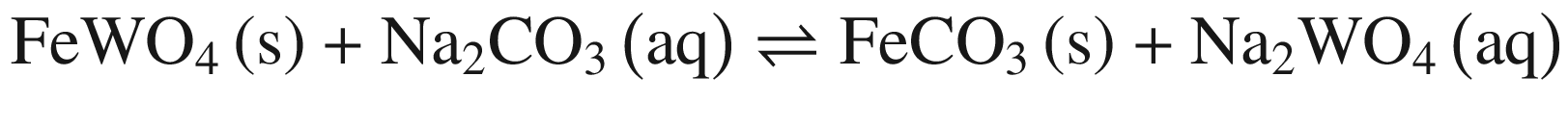
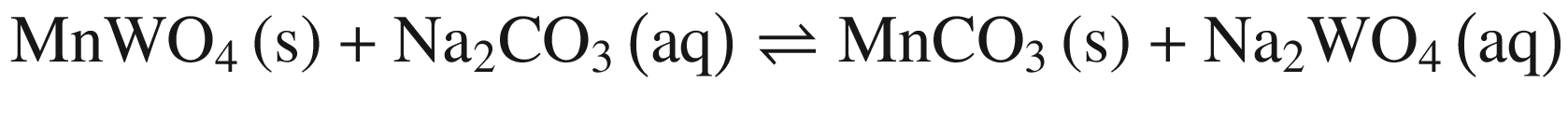
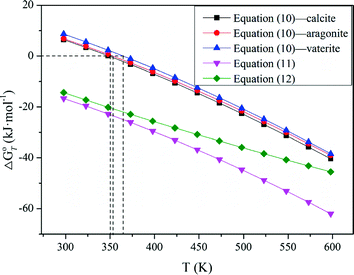
The results in Fig. 1 indicate that raising temperature favors the decomposition of tungsten ores in NaOH solution thermodynamically, especially for CaWO4. The standard Gibbs energy change of CaWO4 becomes negative at the temperature of above about 220 °C, while for FeWO4 and MnWO4 it decreases slightly with increasing temperature but is negative over the whole temperature range. The results indicate that the decomposition of CaWO4 in NaOH solutions should be done at elevated temperatures.
When these tungsten compounds are decomposed in Na2CO 3 solutions, as shown in Fig. 2, the trend is similar to that in NaOH solutions. However, the temperature , at which the standard Gibbs energy change of CaWO4 decomposition in Na2CO 3 solutions becomes negative, significantly decreases to ~75 °C, 80 °C, and 90 °C when producing calcite, aragonite, and vaterite, respectively. The standard Gibbs energy changes of FeWO4 and MnWO4 decomposition in Na2CO 3 solutions are more positive than in NaOH solutions at the same temperature .
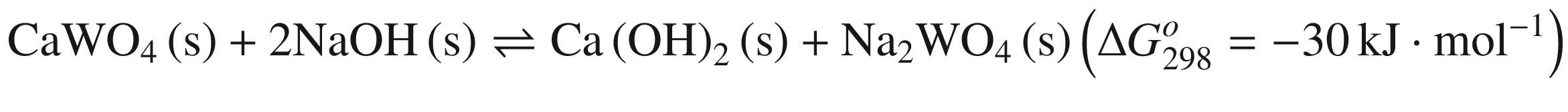
Furthermore, the stability of the products seems to influence the thermodynamic reaction sequence based on Figs. 1 and 2, especially for scheelite which has a very small equilibrium constant. The solubility product Ksp values at 298 K for Ca(OH)2, CaCO3, Fe(OH)2, FeCO3, Mn(OH)2, and MnCO3 are 10−4.38, 10−7.91 (calcite), 10−8.22 (aragonite), and 10−8.47 (vaterite), 10−16.31, 10−10.5, 10−12.72 and 10−10.63, respectively [32, 42], which is in accordance with thermodynamic calculation sequence. Chen et al. [41] used a 0.1 M Na2CO 3 solution washing the compositions of Na2WO4 and Ca(OH)2 by forming more stable CaCO3 and added Al(OH)3 to the co –grinding of CaWO4 and NaOH for producing more stable katoite [Ca3Al2(OH)12] and in order to avoid the reverse reaction. All these observations verify the above analysis.
Tungsten Ores Decomposing in Mineral Acid
The decompositions of tungsten ore (CaWO4, FeWO4, and MnWO4) in HCl, HNO3, and H2SO4 solutions occur according to reactions (14)–(23). The oxidization of Fe2+ to Fe3+ is also taken into account below, due to the strong oxidation power of HNO3 solutions.
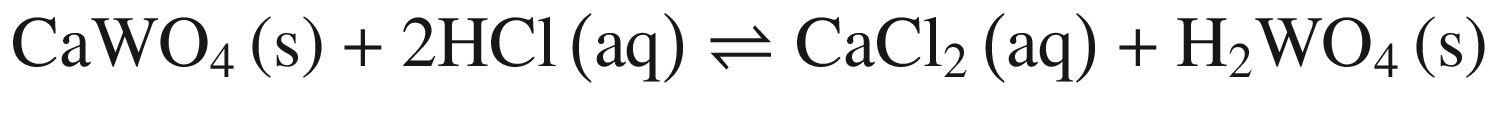
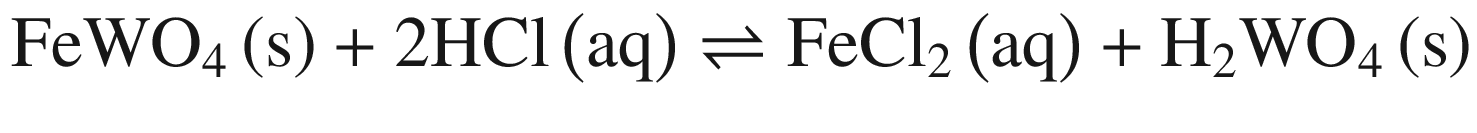
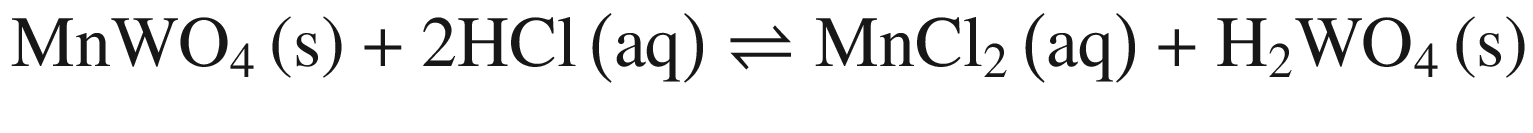
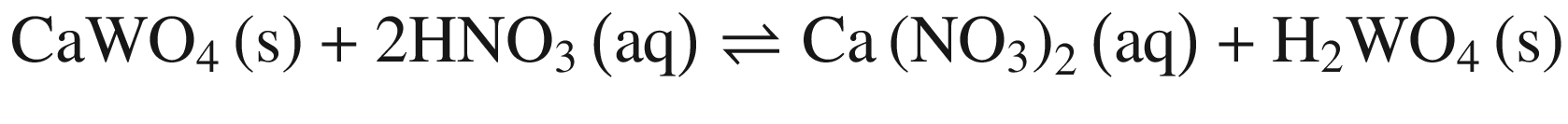
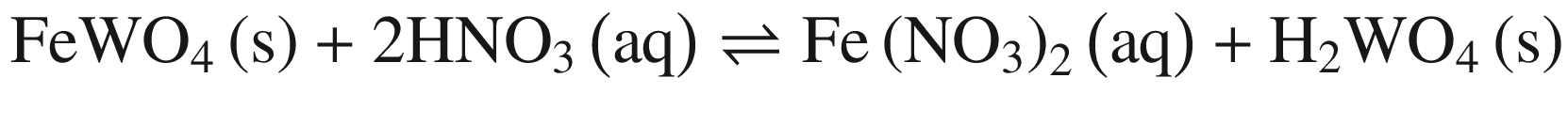
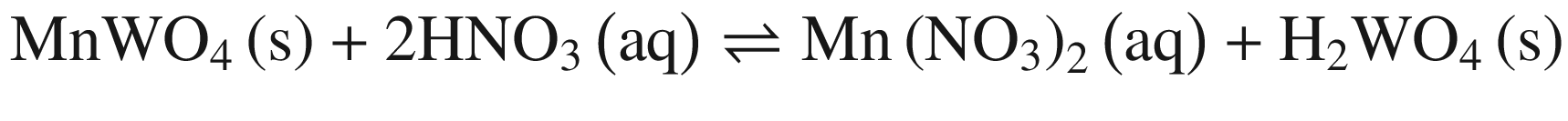
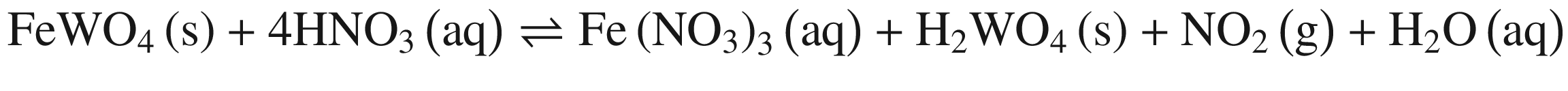
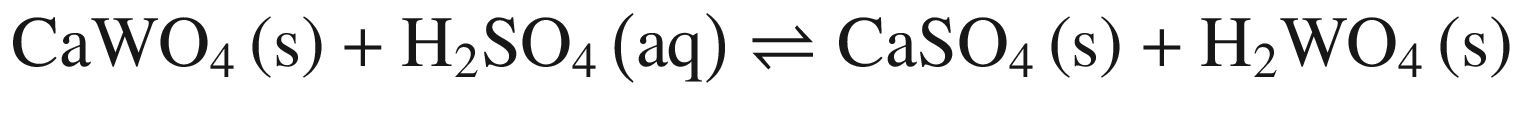
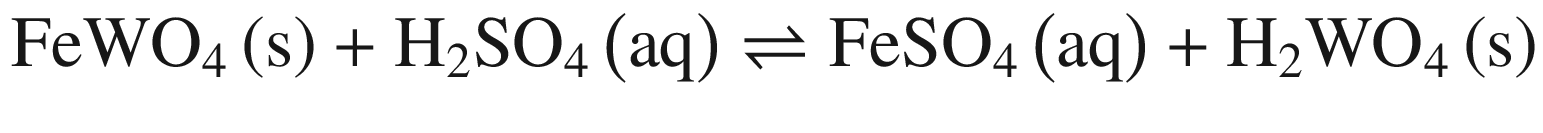
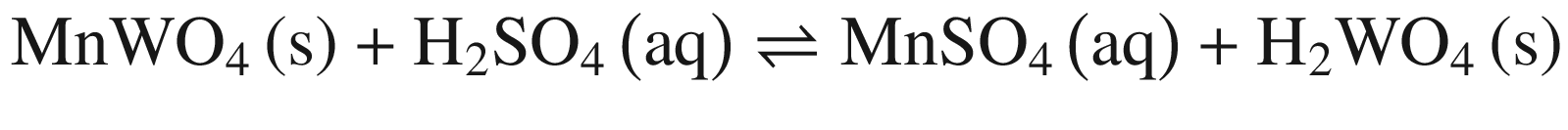
Standard Gibbs energy changes versus temperature for tungsten ore decomposition in HCl solutions

Standard Gibbs energy changes versus temperature of tungsten ore decomposition in HNO3 solutions

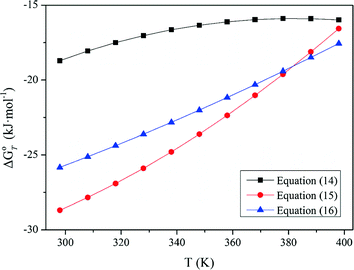
Standard Gibbs energy changes versus temperature of tungsten ore decomposition in H2SO4 solutions
Our previous research [26] showed that increasing Fe2+ in the solution hinders the FeWO4 decomposition, while oxidization of Fe2+ to Fe3+ or/and renewing the acid solution by a two–stage decomposition favors FeWO4 reaction. This explains the impact of oxidization by HNO3 in Fig. 4 and the difference between scheelite and wolframite decomposition in sulfuric acid in Fig. 5.
The current thermodynamic results give an explanation of wolframite treatment by caustic soda when scheelite is digested by soda in modern industrial APT practices. When tungsten ore is decomposed in acid solutions, a solid H2WO4 product layer will form on the surfaces of unreacted tungsten mineral particles. It can be dissolved incorporating actions, such as controlling the acid concentration and adding an oxidizing agent [25, 26, 45]. Due to the absence of thermodynamic data, unfortunately, this paper does not carry out a detailed thermodynamic analysis on tungsten ore decomposition to H2[WO3(C2O4)H2O] and H3PW12O40.
Conclusion
Thermodynamics is fundamental in metallurgical research. It plays an active role in high-temperature metallurgy, but seems to have been left out of hydrometallurgy in recent years. This paper studied the thermodynamics of tungsten ore decomposition, combining the available experimental and industrial experience. The previously published thermodynamic data of tungsten minerals were assessed to obtain a more reliable thermodynamic picture. The results explain why, in modern industrial APT practice, wolframite is usually treated with caustic soda while scheelite is treated with soda ash. Tungsten ores decompose easily in acid solutions from a thermodynamic point of view. The concentration of metal ion influences the decomposition of tungsten ores, which can be explained by kinetics, such as oxidizing to high valence ion, forming insoluble product, and multi-step decomposition. For that purpose, a dilute solution approach is inadequate in strong e.g. caustic or salt solutions, and proper solution models are needed to describe the solution properties accurately [46, 47]. This work is beneficial for further understanding the tungsten minerals decomposition process thermodynamically.








