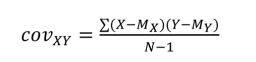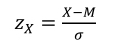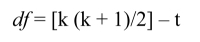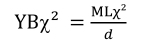1
Structural Equation Modeling
Structural Equation Modeling (SEM) is a comprehensive and flexible approach that consists of studying, in a hypothetical model, the relationships between variables, whether they are measured or latent, meaning not directly observable, like any psychological construct (for example, intelligence, satisfaction, hope, trust1). Comprehensive, because it is a multivariate analysis method that combines the inputs from factor analysis and that of methods based or derived from multiple regression analysis methods and canonical analysis [BAG 81, KNA 78]. Flexible, because it is a technique that allows not only to identify the direct and indirect effects between variables, but also to estimate the parameters of varied and complex models including latent variable means.
Mainly of a correlational nature, structural models are both linear statistical models, whose normal distribution of variables is almost necessary, and statistical models in the sense that the error terms are considered to be partly related to the endogenous variables (meaning predicted). We say almost necessary because the success of structural equation modeling is such that its application extends, certainly with risks of error, to data obtained through categorical variables (ordinal or even dichotomous) and/or by clearly violating the multivariate normal distribution. Considerable mathematical advances (like the so-called “robust” estimation methods) have helped currently minimize these risks by providing some remedies to the non-normality of the distribution of variables and the use of data collected by the means of measurement scales other than that normally required for structural equation models, namely interval scales [YUA 00]. We will discuss more on that later.
Our first goal is to introduce the reader to the use of structural equation models and understand their underlying logic; we will not delve too much into mathematical and technical details. Here, we will restrict ourselves to introducing, by way of a reminder, the concepts of correlation, multiple regression, and factor analysis, of which structural equation modeling is both a summary and a generalization. We will provide to the reader some details about the concept of normality of distribution, meaning with linearity, a basic postulate of structural equation modeling. The reader will find the mathematical details concerning the basic concepts briefly recalled here in any basic statistical manual.
1.1. Basic concepts
1.1.1. Covariance and bivariate correlation
Both covariance and correlation measure the linear relationship between two variables. For example, they make it possible to learn about the relationship between two items of a test or a measure (e.g., a questionnaire) scale. Figure 1.1 provides a graphic illustration of the same.
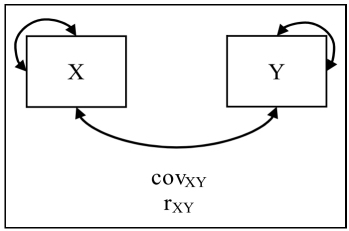
Figure 1.1. Covariance/correlation between two variables (the small curved left-right arrow indicates the variance)
Covariance, which measures the variance of a variable with respect to another (covariance), is obtained as follows:
where:
- – M = mean;
- – N = sample size.
Being the dispersion around the mean, the variance is obtained as follows:
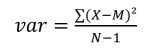
The values of a covariance have no limits. Only, it should be noted that the positive values of covariance indicate that values greater than the mean of a variable are associated with values greater than the mean of the other variable and the values lesser than the mean are associated in a similar way. Negative covariance values indicate values greater than the mean of a variable are associated with values lesser than the mean of the other variable.
Unlike covariance, correlation measures such a relationship after changing the original units of measurement of variables. This change, called “standardization” or “normalization”, involves centering-reducing (i.e. M = 0.00, standard deviation = 1.00) a variable (X) by transforming its raw score into z score:
where:
- – M = mean of X;
- – σ = standard deviation of X.
The standard deviation is simply the square root of the variance:
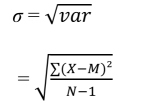
Remember that standard deviation is the index of dispersion around the mean expressing the lesser or higher heterogeneity of the data. Although standard deviation may not give details about the value of scores, it is expressed in the same unit as these. Thus, if the distribution concerns age in years, the standard deviation will also be expressed in the number of years.
The correlation between standardized variables X and Y (ZX and ZY, [1.3]) is obtained as follows:
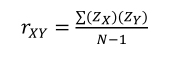
Easier to interpret than covariance, correlation, represented, among others, by the Bravais-Pearson coefficient r, makes it possible to estimate the magnitude of the linear relationship between two variables. This relationship tells us what information of the values of a variable (X) provides information on the corresponding values of the other variable (Y). For example, when X takes larger and larger values, what does Y do? We can distinguish between the two levels of responses. First, the direction of the relationship: when the variable X increases, if the associated values of the variable Y tend overall to increase, the correlation is said to be positive. On the other hand, when X increases, if the associated values of Y overall tend to reduce, the correlation is called negative. Second, the strength of the association: if information of X accurately determines information of Y, the correlation is perfect. It corresponds respectively to + 1 or – 1 in our demonstration. In this case, participants have a completely identical way of responding to two variables. If information of X does not give any indication about values assumed to be associated with Y, there is complete independence between the two variables. The correlation is then said to be null. Thus, the correlation coefficient varies in absolute value between 0.00 and 1.00. The more it is closer to + 1.00 or – 1.00, the more it indicates the presence of a linear relationship, which can be represented by a straight line in the form of a diagonal2. On the other hand, more the coefficient goes to 0, the more it indicates the lack of a linear relationship. A correlation is considered as being significant when there is a small probability (preferably less than 5%) so that the relationship between the two variables is due to chance.
As much as the covariance matrix contains information about the relationships between the two measures (scores) and their variability within a given sample, it does not allow for comparing, unlike a correlation matrix, the strength of the relationships between the pairs of variables. The difference between these two statistics is not trivial as the discussions on the consequences of the use of one or the other on the results of the analysis of structural equation models are to be taken seriously. We will discuss this further.
Furthermore, it is worth remembering that there are other types of correlation coefficients than the one that we just saw. In structural equation modeling, the use of tetrachoric and polychoric correlation coefficients is widespread, as they are suitable for measurements other than those of interval-levels. The first is used to estimate the association between two variables, called “dichotomous”; the second is used when there are two ordinal-level variables.
1.1.2. Partial correlation
The correspondence between two variables may result from various conditions that the calculation of correlation cannot always detect. Thus, assuming that only the welloff have the financial means to buy chocolate in a given country, even a very strong correlation observed between the two variables – “consumption of chocolate” and “life satisfaction” – in older people does not mean that the first is the cause of the second. First, we are right in thinking of the opposite, as a statistic expressed by a correlation can be read in two ways. In addition, we can think that these assumptions are all erroneous, and that it would perhaps come from a common cause, the “milieu” that similarly determines the two variables, which, due to this fact, prove to be correlated. In this case, life satisfaction in a category of the elderly does not come from consuming chocolate, but from the preferred milieu in which they live; it is this milieu that allows them to both consume chocolate and be happy. Here, we see a spurious (artificial) relationship that we will shed light on through the following illustration. Let us consider that the correlation matrix between these three variables measured from a sample of elderly people (Table 1.1).
Table 1.1. Correlation matrix (N = 101)
| Variable | X | Y | Z |
| X. Chocolate consumption | 1.00 | ||
| Y. Life satisfaction | .49 | 1.00 | |
| Z. Milieu | .79 | .59 | 1.00 |
The use of partial correlations is useful here, as it will allow us to estimate the relationship between X and Y controlling for Z that will be hold constant. This correlation is written in this way, rXY.Z, and is calculated as follows:
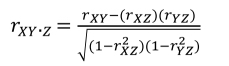
Considering the numerator of this equation, we can observe how the “milieu” variable (Z) was hold constant: we simply removed the two remaining relationships from the relationship between “chocolate consumption” (X) and “life satisfaction” (Y), namely (rXZ) and (rYZ). If we apply this formula to the data available in the matrix [1.7], the partial correlation between X and Y by controlling Z will be as follows:
We realize that by controlling for the variable “milieu”, the relationship between “chocolate consumption” and “life satisfaction” fades, as it is likely an artificial one. The milieu takes the place of confounding factor, giving the relationship between “chocolate consumption” and “life satisfaction” an artificial nature, meaning spurious.
To conclude, we put emphasis on the fact that it is often unwise to interpret the correlation or partial correlation in terms of causality. Mathematics cannot tell us about the nature of the relationship between two variables. It can only tell us to what extent the latter tend to vary simultaneously. In addition, the amplitude of a link between two variables may be affected by, among other things, the nature of this relationship (i.e. linear or non-linear), the normality of their distribution, and psychometric qualities (reliability, validity) of their measures.
As for the causality, it requires three criteria (or conditions): 1) the association rule, that is the two variables must be statistically associated; 2) the causal order between variables, the (quite often) temporal order where the cause precedes the effect must be determined without ambiguity and definitely with theoretical reasons that allow for assuming the order; 3) the non-artificiality rule, in which the association between the two variables must not disappear when we remove the effects of variables that precede them in the causal order. This requires that, in the explanation of the criterion, the intermediary variable gives an additional contribution compared to the latter.
It is clear that only experimentation is able to satisfy these three criteria, within the limits of what is possible and thinkable. It goes without saying that no statistical procedure (analysis of variance, regression, path analysis), as sophisticated and clever as it may be, allows for establishing any causal order between variables. We could at most make dynamic predictions in longitudinal research [MCA 14]. In Pearl [PEA 98], we can find an original and detailed analysis of causality in SEM, and in Bollen and Pearl [BOL 13], there is a clarification of the myths about causality in SEM.
1.1.3. Linear regression analysis
Whether single or multiple, regression has a predictive and “explanatory” function. When studying relationships, it is true that we are right in predicting one of the variables from our knowledge of the other variable(s). We can also seek to determine the relative influence of each predictor variable. It is rather this “explanatory” aspect of regression that is best suited to structural equation modeling. Regression is in fact a linear mathematical model linking a criterion variable (to be explained) to one or more explanatory variables, a model mainly built to predict the criterion variable.
Regression is called “simple” when the model, very rarely, has only one predictor variable. Figure 1.2 represents such a model where X is the predictor variable, considered as a predictor of the criterion variable, or criterion, Y. B (β) is the regression coefficient, which can be either non-standardized (B) or standardized (β), while (e) refers to the prediction error (residual), the part of variance that is unexplained and probably due to variables ignored by the model. Regression analysis aims to estimate the value of this coefficient and establish the part of the error in the variance of the criterion. In other words, Figure 1.2 shows Y as subject to the “effects” of X and as well as the error term (e).
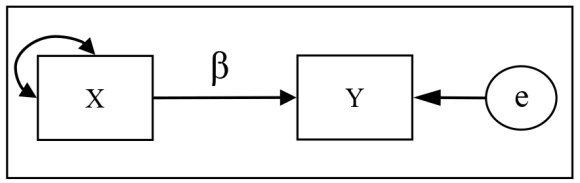
Figure 1.2. Model of a simple linear regression (the curved left-right arrow indicates the variance)
The model is then written as follows:
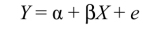
This is a regression equation describing the structural relationship between the two variables (X and Y) where α refers to Y-intercept. The estimate of the coefficient B (β) is solved using the OLS method that involves finding the values that minimize the sum of squares of the difference between the observed values and the values predicted by the linear function (we will come back to this when we discuss discrepancy functions and estimation methods).
It also allows to optimize the correlation between these two variables, considered as multiple correlation (R) and whose square (R2) shows the proportion of variance of the criterion variable attributable to the explanatory variable in the case of a simple regression, or to all the explanatory (predictor) variables in the case of a multiple regression. The R2 value is an indicator of the model fit.
In fact, the model fit is even better when the R2 value is close to 1, because it indicates that the predictor variables of the model are able to explain most of the total variance of the criterion variable (for example, an equal to 0.40 R2 means only 40% of the variance in the criterion variable are explained by the predictor variables in the model).
Here, note that the value of a non-standardized regression coefficient (B), which reflects the metric of origin of variables, has no limits, and may thus extend from +infinity to -infinity. This is why a high – very high – B value does not imply that X is a powerful predictor of Y. The values of a standardized regression coefficient (β) ranges from – 1.00 to + 1.00 (although they can sometimes slightly exceed these limits). A coefficient β indicates the expected increase of Y in standard deviation units while controlling for the other predictors in the model. And as the standard deviation of the standardized variables is equal to 1, it is possible to compare their respective β coefficients.
Regression is called “multiple” when the model has at least two predictor variables. Figures 1.3 and 1.4 show two multiple regression models. It should be noted that the only difference between them lies in the nature, whether of independence, of the predictor variables. They are supposed to be orthogonal (independent or uncorrelated) in the first figure, and oblique (correlated to each other) in the second.
In the first case, the regression coefficient is equivalent to the correlation between the explanatory variable (X) and the criterion (Y). The second case shows the interest in multiple regression, that of making it possible to distinguish different sources of variance of the criterion variable. Thus, the coefficient obtained here is a regression coefficient that expresses an effect completely independent of all the other effects in the model, giving us information about the correlation between each of the explanatory variables and the criterion as well as about the importance of intercorrelations between all of them.
As can be seen by analyzing the matrix shown in Table 1.1, to estimate figures 1.3 and 1.4 by using the maximum likelihood estimation here – we will discuss this later – the coefficients β on the graph of the first correspond exactly to the correlations between the variables of the model; while those shown in Figure 1.4 are more like partial correlations between these same variables, although they are not correlations. In fact, a coefficient of β 0.54 means that Y could increase by 0.54 deviation for a 1 standard deviation increase of Z, by controlling for X (that is by holding X constant).
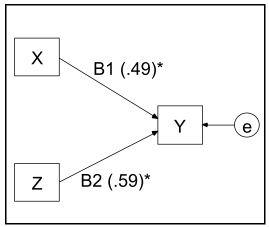
Figure 1.3. Model of a multiple linear regression (orthogonal predictor/explanatory variables) (*coefficient obtained from [1.1])
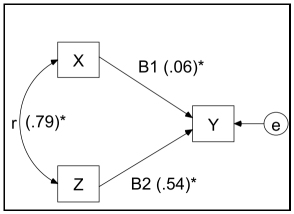
Figure 1.4. Model of a multiple linear regression (correlated predictor/explanatory variables)
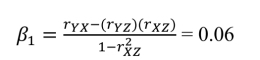
We can thus decompose the variance of Y explained by the regression, that is the square of its multiple correlation (R2):
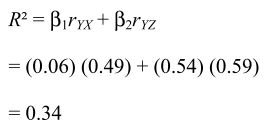
We can easily recognize the specific part attributable to each explanatory variable (X and Z) through the regression coefficient (β) as well as the common part shared by these same variables through their correlations.
However, it is well known that one of the main difficulties of multiple regression comes from relationships that may exist between the predictor variables. Researchers know nothing about these relationships since the specification of the model consists in simply referring to the criterion and the explanatory variables. If these relationships are more or less perfect, it is either the total confusion of effects or redundancy that affects the results and skews their interpretation (i.e. multicollinearity).
Furthermore, the additive nature of the regression equation seriously limits the possibilities of specifying a model in which relationships between variables can be both direct and indirect. Imagine that a researcher has an idea about the relationships between these explanatory variables. He can reformulate and arrange them by introducing, for example, intermediate explanatory variables in his model that are themselves undergoing the effect of other predictor variables that might have an effect on the criterion. Such an approach requires two conditions: first, a theoretical elaboration for the specified model, and second, an appropriate statistical tool. The approach then becomes confirmatory.
Structural equation modeling, and in this case path analysis, thus provides an answer to this second condition. The problem of multicollinearity, which arises when the correlations between variables are so high that some mathematical operations become impossible, has not been resolved so far. Theoretical conceptualization could, moreover, help researchers not introduce two redundant variables in a path model or make them indicators (for example, items, measured variables) of a latent variable if they opt for a general structural equation model. It is sometimes necessary to get rid of one of the two variables that together show a wide relationship (r > 0.80) or have a correlation coefficient higher than the square of the predictor value (R2) relating to the whole of the explanatory variables. This explains the interest in factor analysis, which helps not only to select the latter (in tracking collinearity), but also to interpret the multiple regressions. For the mathematical aspects, the reader can refer to Gendre [GEN 76]; for multicollinearity in multiple regression, you can consult, among other things, Mason and Perreault [MAS 91] or Morrow-Howell [MOR 94]; and for multicollinearity in SEM, we suggest you to refer to Grewal, Cote and Baumgartner [GRE 04].
1.1.4. Standard error of the estimate
The standard error of estimate (SE) is a measure of the prediction error. It evaluates the accuracy of the prediction. This measure will also be used to test the statistical significance of a parameter estimate (B/β). In other words, is the parameter estimate significantly different from zero? Let us take the example of the regression coefficient β equal to 0.49 for our sample (N = 101). Is the predictive effect of this coefficient obtained from this sample high enough to be able to conclude with a reasonable probability of risk that it is not zero at the population level from which the sample is taken? To find out, simply divide the regression coefficient (B/β) by its SE. This critical 
ratio is read as a statistic z whose absolute value, if greater than 1.96, means that B(β) is significantly different from zero at p < 0.05, whereas an absolute value greater than 2.58 means that B(β) is significantly different from zero at p < 0.01. In the context of a simple linear regression (Figure 1.2), the SE of the coefficient B(β) is obtained as follows:
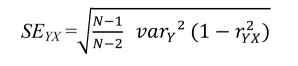
where:
- – N = sample size;
- – var = variance.
Here, we can note the importance of the sample size in calculating the SE. We will address this crucial aspect in SEM later. It should also be noted that SE can serve as an indicator of multicollinearity. In fact, more the predictor variables (IV) are strongly correlated with each other, larger the SE of regression coefficients (thus suggesting hardly accurate predictions), and less likely, therefore, their statistical significance. The reason is simple: more the IV are highly correlated, more it is difficult to determine the variation of the criterion variable for which each IV is responsible. For example, if the predictor variables X and Z, of the model shown in Figure 1.4, are highly correlated (collinear), it is difficult to determine if X is responsible for the variation of Y or if Z is. Therefore, the SE of these variables become very large, their effects on Y inaccurate, and so statistically non-significant. Finally, we can note that the multicollinearity may generate an improper solution, with inadmissible values, such as negative variances.
1.1.5. Factor analysis
We purposely keep the factor analysis in the singular – in spite of the diversity of methods that it covers – to keep our discussion general in nature. We will elaborate on some technical aspects that could enlighten us about the benefits of integrating factor analysis into structural equation models later in the book.
The key, to begin with, is in the following note. Fundamentally based on correlations or covariances between a set of variables, factor analysis is about how the latter could be explained by a small number of categories not directly observable. They are commonly called “dimensions”, “factors” or even “latent variables”, because they are not directly observable.
To set these ideas down, we will start with a simple example. A total of 137 participants were given a scale containing five items. To each item making up the measure, the participant chooses between five possible responses that correspond to a scale ranging from a score of “1” (completely disagree) to “5” (completely agree) (Table 1.2).
Table 1.2. A 5-item scale
| Item/indicator | 1 | 2 | 3 | 4 | 5 |
| In most ways my life is close to my ideal | |||||
| The conditions of my life are excellent | |||||
| I am satisfied with my life | |||||
| So far, I have gotten the important things I want in life | |||||
| If I could live my life over, I would change almost nothing |
The total scores obtained for all of the items allows, for each individual, the estimation of the construct rated. A high total score is indicative of the presence or the endorsement of the construct measured. This total aggregation offers a comprehensive representation of the model [BAG 94]. It suggests, moreover, a simple model whose nature it is to restore the essence of the measured construct, on condition however that each item is a good indicator. To test this observation, we have the factor analysis. The main application of this method is to reduce the number of intercorrelated variables in order to detect the structure underlying the relationship between these variables. This derived structure, which would be the common source of item variance, is called the “common factor”. It is a latent hypothetical variable.
Thus, the covariance (or correlation) matrix constitutes the basic information of the factor analysis. For example, what about the correlations between the five items of our scale, which are considered as measured variables (also called “manifest variables”, “indicators” or “observed variables” of our measure (Table 1.2)? Could they be explained by the existence of one or more latent common factor(s)? To know this, this correlation matrix (Table 1.3) is simply subjected to a factor analysis. But first, here is a simple illustration of the reasoning behind the extraction of common factors.
1.1.5.1. Extraction of common factors
To simplify our discussion, take the correlations between the first three items of this measure (i.e. measurement tool) scale. Figure 1.5 illustrates the covariations between these items as a diagram. The crosshatched part represents the covariance shared by the three items. The dotted parts represent the covariations between the item pairs. Empty parts represent the variance portion unique to each item.
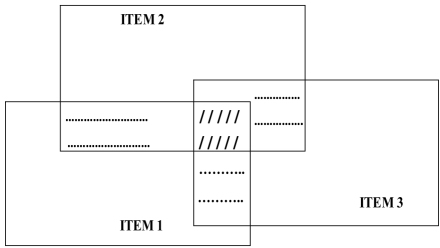
Figure 1.5. Correlations (covariances) between three items
Factor extraction procedure allows the identification of the common factor that may explain the crosshatched part, that is what these items may have in common. This factor can partially, or fully, explain the covariances between the three items. Other factors can also be extracted to explain the rest of the covariations outside the crosshatched area. The dotted parts could each be explained by a factor. However, each of these factors will take into account the covariances between two items only and exclude the third. Here, we can note that the common factors extracted do not have precise meaning hitherto. Their existence is, at this stage, purely mathematical. Then comes the interpretation of the results in order to give meaning to and name these factors. Besides, in order to facilitate the interpretation of the extracted factors, we often proceed to factorial rotations, whether they are orthogonal or oblique (the reader eager to know more can consult, among other things, the book by Comrey and Lee [COM 92], or the latest one by Fabrigar and Wegener [FAB 12]).
The passage of the analysis of correlations between variables to the underlying factors requires, in fact, linear combination of these. This combination mathematically takes the form of a regression equation, solving which requires complex estimation procedures. For each factor extracted from the factor analysis, each measured variable (or item) receives a value that varies between – 1 and + 1, called the “factor loading coefficient” (always standardized). The latter defines the importance (i.e. the weight) of the factor for this variable. This means that the correlation between each pair of variables results from their mutual association with the factor(s). Thus, the partial correlation between any pair of variables is assumed to be zero. This local independence allows the searching of factors that account for all the relationships between the variables. In Reuchlin, we find a very detailed and technical presentation on factor analysis methods.
1.1.5.2. Illustration
Let us say, for the sake of simplicity, that there is only one factor that would explain the observed correlations between the five items of our measure scale (Table 1.3). Figure 1.6a illustrates this concept because the absence of such a factor means complete independence (orthogonality) of items from each other (Figure 1.6b).
Table 1.3. Correlations between the five items of the scale shown in Table 1.2 (N = 137)
| Variable | Item1 | Item2 | Item3 | Item4 | Item5 |
| Item1 | 1.00 | ||||
| Item2 | .37 | 1.00 | |||
| Item3 | .57 | .30 | 1.00 | ||
| Item4 | .26 | .31 | .39 | 1.00 | |
| Item5 | .34 | .33 | .43 | .43 | 1.00 |
| SD | .93 | .84 | .89 | .98 | 1.27 |
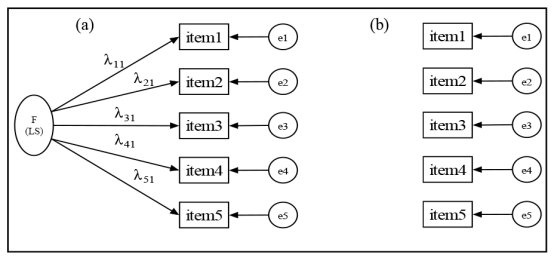
Figure 1.6. (a) Monofactorial model (one-factor model) of the scale of “life satisfaction (LS)”, and (b) null model (also called “independence model” or “baseline model”, not to be confused with the null hypothesis)
Thus, we assume that the variance of responses to each item is explained by two latent factors: one common to all items (factor F), and the other specific to the item (factor e). This specific factor is a kind of combination of item-specific variance and measurement error. We will first seek to estimate the factorial weight of each item, that is the factor loading. In case of an example as simple as ours3, the factor loading coefficient is none other than the correlation coefficient linking the factor to the measured variable. It also corresponds to the regression coefficient by keeping the factor constant. Thus, there are as many regression equations as there are items:
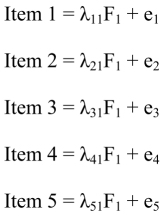
In other words, each item undergoes the effect of two latent factors: a common factor (F) and a unique factor (e or U) referring to a combination of specific factors and the measurement error. It is noteworthy that factor analysis does not provide separate estimates of specific variance and measurement error variance. Lambda “λ” designates the loading (factor weight) of the variables (λ11, λ21, …, λp1), represented by the arrow pointing from the common factor to the indicator.
In order to extract factors and solve regression equations, sophisticated parameter estimation methods, such as the principal axis method and the maximum likelihood estimation method are used. It can be noted here that, contrary to the principal axis extraction method, the maximum likelihood method requires a multivariate normal distribution of data, and needs to fix a priori the number of factors to be extracted (therefore, it is less exploratory than the principal axis method). Determining the number of factors to be extracted uses certain criteria, such as the Kaiser or Cattell criteria. It should be remembered here that the principal component analysis is not, strictly speaking, factor analysis [FAB 99].
The factor analysis will thus generate a matrix of factor loadings (i.e. model-implied matrix) that best account for the observed correlations between items. Table 1.4 summarizes the factor loadings according to the factor extraction method used. It should be noted that these coefficients shall be interpreted as standardized coefficients (β). When squared, a factor loading coefficient of an item makes it possible to give the portion of its variance attributable to the factor on which it depends (underlying factor). It is known as the communality (h2) of a variable/item. For example, a factor loading of 0.63 squared (0.632 = 0.39) means 39% of variance explained by the only common factor in our example4. The rest of the variance (1 – 0.39 = 0.61), that is 61%, is attributable to the specific factor to the item (e, sometimes designated by U2 for uniqueness). So, even if there is no golden rule, a factor loading coefficient ≥ 0.40 is considered necessary to judge the quality (validity) of an item as an indicator of one factor or another. Some may think that this criterion is quite lax since a factor loading of 0.40 means that only 16% of the explained variance depends on the factor of which one item is the indicator (see the recommendations of [COM 92], or those of [TAB 07] on this subject).
A careful reading of the five items on the scale suggests that this common factor refers to the “life satisfaction” construct. It is in fact the “life satisfaction” scale of Diener, Emmons, Larsen, Griffin [DIE 85] and [GRI 85].
Table 1.4. Factor loadings for 5 items depending on factor extraction method
| Factor loadings | ||
| Variable | Principal axis | Maximum likelihood |
| Item1 | .62 | .63 |
| Item2 | .52 | .51 |
| Item3 | .70 | .71 |
| Item4 | .56 | .56 |
| Item5 | .63 | .63 |
Remember also that these are factor loading coefficients that allow the reproducing of the correlation matrix (Σ) (model-implied matrix). In fact, in the case of a monofactorial solution5, the product of two factor loadings allows reproducing their correlation. Thus, model-based reproduced correlation between item 1 and item 2 is equal to (0.62) (0.52) = 0.32 using the principal axis method, and (0.63) (0.51) = 0.32 using the maximum likelihood estimation method. From the observed correlations, the reproduced correlations are deduced term by term. Differences, whether positive or negative, form the residual correlation matrix. Table 1.5 shows the three matrices involved: original (S), reproduced (Σ), and residual (S – Σ). The last two matrices are obtained using the maximum likelihood estimation method. The same rule applies to other methods. We will come back to this in Chapter 3 of this book, when we will deal with confirmatory factor analysis.
Table 1.5. Correlation matrices (reproduced above diagonal, observed below diagonal, as well as residual) of items of the life satisfaction scale; maximum likelihood estimation method
| Reproduced matrix ( Σ) | Residual matrix (S - Σ) | |||||||||
| Item 1 | Item 2 | Item 3 | Item 4 | Item 5 | Item 1 | Item 2 | Item 3 | Item 4 | Item 5 | |
| Item 1 | _ | 3.2 | 0.45 | 0.35 | 0.39 | _ | ||||
| Item 2 | 0.37 | _ | 0.36 | 0.28 | 0.32 | 0.05 | _ | |||
| Item 3 | 0.57 | 0.30 | _ | 0.39 | 0.44 | 0.12 | – 0.06 | _ | ||
| Item 4 | 0.26 | 0.31 | 0.39 | _ | 0.35 | – 0.09 | 0.03 | 0.00 | _ | |
| Item 5 | 0.34 | 0.33 | 0.43 | 0.43 | _ | – 0.05 | 0.01 | – 0.01 | 0.08 | _ |
| Observed matrix (S) | ||||||||||
Mostly exploratory and descriptive6, factor analysis has at least two advantages. First, direct use making it possible to: (1) identify groups of correlated variables in order to detect the underlying structures – the aim of this method is to determine the organization of variables, by identifying those that are similar and those that contrast with each other; (2) to reduce the set of variables into a smaller number of factors. In fact, it is reasonable to think that the variables that display a high degree of similarity are assumed to measure the same construct, the latter being a non-observable theoretical entity called “factor”. It is expected to account for the covariations between the measured variables by clearing the “belief”, or the “perception”, that underlies them. The “life satisfaction” construct is one such example. It is a theoretical construction that is assumed to be evaluated by indicators, or measured variables, which are the items. The perception that each participant has life satisfaction is estimated by his/her way of answering the items, for which correlations are used as an index. Associations – of high degrees – between items can be explained by the fact that they involve the same perception, or the same core belief. Second, an indirect use helps to process data – preparing them – to simplify them and avoid artifacts, such as multicollinearity (reflecting a redundancy of variables), that make a matrix ill-conditioned.
1.1.6. Data distribution normality
The normality of data distribution is at the heart of structural equation modeling because it belongs to linear models. Moreover, LISREL, still used as the generic name of this technique (specifically, we still talk of a “Lisrel model” to denote structural models), is in fact an abbreviation of LInear Structrural RELationships, the model and first SEM program, designed by Jöreskog [JÖR 73, JÖR 73].
The statistical tests used by researchers to assess these models are, in fact, based on the hypothesis of normal distribution: multivariate normal distribution of data. The entire scope of statistical inference depends on it. In order to determine the level of significance of the tests obtained, we need a theoretical model, which will tell us the probability of an error involved in the acceptance (or rejection) of the relationship between two variables depending on the size of our sample. This model is the so-called mathematical “normal distribution”. Indeed, most statistical procedures used in SEM involve the assumption of normality of distribution of observations in their derivation. A “univariate normal distribution” is when a single variable follows the normal distribution, and in the “multivariate normal distribution”, a group of variables follows the normal distribution.
Now, some simple questions are raised: what is a normal distribution? How can this normality be assessed? What to do in case of violation of this assumption?
Curved and bell shaped, the normal distribution is defined by two parameters: the mean, center of the distribution setting the symmetry of the curve, and deviation, whose value affects the appearance of the latter7. It is a unimodal and symmetric distribution. Standard normal distribution with a mean of 0.00 and standard deviation of 1.00 is its most convenient and simplest form. Such a transformation does not affect the relationship between values, and its result is the z-score (see [1.3]).
We can see from a normal curve that a distribution is said to be “normal” when 95.44% of its observations fall within an interval which corresponds to, and in absolute value, twice (or more precisely 1.96 times) the standard deviation from the same mean. These are limits within which 95.44% observations are found. As for the 4.6% of the observations (2.3% at each end of the curve), they obtain higher z-values in absolute value at 2.00 (to be more precise, at 1.96) times the standard deviation from the mean. The z-score is of crucial importance in SEM as we will use it, through the critical ratio, to test the hypothesis of statistical significance of model parameter estimates. We have already seen that an estimated parameter is considered significant when it is statistically different from zero. We will thus assess its utility and its pertinence in the model. It is important to keep in mind that some estimation methods require the hypothesis of multivariate normality. Unbiasedeness, effeciency as well as precision of the parameter estimates depend on it.
A normal empirical distribution is supposed to be superimposed on such a theoretical distribution. But there could be questions about the isomorphism of such a distribution with reality, about the reasons that make us believe that this distribution is a mathematical translation of empirical observations. In reality, there is no distribution that fully complies with the normal curve. This way of working may seem reasonable for researchers in some cases, and quite questionable in others. But, as nature does not hate irregular distributions in the famous words of Thorndike [THO 13], there are many phenomena that differ from this mathematical model. However, it is important to specify that the distribution of the normal curve constitutes a convenient model that gives a technical benchmark following which the empirical results may be assessed.
There are several indices that allow for statistically estimating the normal distribution of the curve. Among the best known, we name two that provide very useful indications in this respect: kurtosis concerning the more or less pointed appearance – or shape – of the curve, and skewness (asymmetry) that concerns the deviation from the symmetry of the normal distribution. A value significantly different from zero (with a 5% risk of error, particularly higher than 3 in absolute value) indicates that the form or the symmetry of the curve has not been respected. Regarding Kurtosis, a positive value signifies, in this case, that the distribution curve is sharper (called “leptokurtic”). In the case of a measurement tool (e.g. test), it means that there are neither very easy items nor very hard items, but too many items of average difficulty. On the other hand, a negative value suggests that the distribution has a flat shape (platykurtic) that indicates, in case of a test, that there are too many very easy items (ceiling effect) and too many very difficult items (floor effect). In the case of skewness, when the index is positive, the grouping of values is on the left side (too many difficult items). If the index is negative, the grouping is on the right side (too many easy items). Thus, a peak with an absolute value higher than 10 indicates a problematic univariate distribution, while a value higher than 20 indicates a significant violation of this distribution (the reader will find illustrated presentations of asymmetry and kurtosis in [BRO 16]).
Here, the question raised is about knowing whether the value of indices is sufficiently high to be able to conclude, with reasonable probability, that there is a risk of violating the form of the curve. To answer it, it is enough to divide the value of the index by its standard error (SE). This critical ratio reads like a z-test, of which an absolute value higher than 1.96 means that the index (asymmetry or kurtosis) is significantly different from zero to p < 0.05, while an absolute value higher than 2.58 means that it is significantly different from zero to p < 0.01. In both cases, it can be concluded that there is a violation of form of data distribution.
But the review of the univariate skewness and kurtosis indices no longer seems sufficient to prejudge multivariate distribution. The use of multivariate normality tests, like the Mardia [MAR 70] coefficient, now proves necessary and very practical. Let us note that a high value at the latter, especially higher than 5 in absolute value, indicates a deviation with respect to multivariate normality. This coefficient is available in almost all structural equation modeling software; it is often accompanied by its z-value, thus making it possible to judge its statistical significance. These SEM software have made possible extreme outlier detection, which might be the cause of deviations from normality. This makes it possible to identify observations that contribute greatly to the value of the Mardia coefficient. But, it is sometimes enough to eliminate them to return the normality to the distribution [KOR 14].
But, in the presence of data seriously violating normality, some transformations that normalize them could be a remedy. Yet, even though these transformations, in this case normalization, are processes that have been well known for long and even have some advantages, it is rare to see research in SEM using them (see [MOO 93]). Also, for ordinal and categorical scales, the aggregation of items (indicator), especially when there are multiple, may sometimes be a remedy to the non-normality of distributions mostly because they are many in number. In this case, the analysis no longer concerns all the items constituting the measure (total disaggregation), but the item parcels referring to subsets of items whose scores have been summed [LIT 02]. This is a total or partial aggregation of indicators/items of a measure. The reader will find details of use as well as examples of application of this procedure suggested by Bernstein and Teng [BER 89] in the works of Bagozzi and his collaborators [BAG 94, BAG 98, ABE 96]. However, creating item parcelling requires at least two conditions: the measure has to be one-dimensional (i.e. a congeneric model) and items constituting each parcel created have to be randomly selected. For limits concerning item parcelling, the reader can refer to [MAR 13].
However, it should be specified that when the treatment of non-normality is not conclusive (despite item parcelling), and the deviation with respect to normality remains high, it is necessary to consider using the most appropriate statistical indicators and estimation methods. We will discuss more on that later.
1.2. Basic principles of SEM
Similar to factor analysis, the reproduced matrix is a central element in structural equations modeling. To simplify, the crux is in the following clarification: the starting point of structural equation modeling also involves comparing the covariance (or correlation) matrix of the research data (S) with a covariance matrix that is reproduced (Σ) from the theoretical model that the researcher wishes to test (model-implied covariance matrix). The theoretical model specified by the represents the null hypothesis (H0) as a model assumed plausible. The purpose of this comparison is to assess the fit between the observed variables and the selected conceptual model. If the reproduced covariance matrix is equal to the observed matrix (Σ = S), it refers to the model's fit to the data, or fit between the model tested and observed data. In other words, the null hypothesis (H0 : Σ = S) is not rejected and the specified model is acceptable.
Differences between the two matrices are represented in the residual covariance (or correlation) matrix, which is obtained by subtracting the value of each element of the reproduced matrix from the corresponding element in the observed matrix (S – Σ). The degree of similarity between the two matrices indicates the overall degree of the model’s fit to the data.
The covariance matrix (Σ) is reproduced using the model parameter estimates. Estimating involves finding a value for each unknown parameter in the specified hypothetical model. But, it goes well beyond this simple objective, as it is important that the calculated values allow for reproducing a covariance matrix (∑) that resembles the observed covariance matrix (S) as much as possible. It is an iterative procedure whose general principle is to start from an initial value (specified for the set or for each individual parameter either by the user or automatically by the software) and to refine it progressively by successive iterations that stop when no new value for each parameter makes it possible any longer to reduce the difference between the observed covariance matrix and the reconstituted covariance matrix. These different operations are performed by algorithms for minimization (discrepancy functions or minimization functions, Fmin) that, despite having the same purpose of finding the best parameter estimates, nevertheless differ from the mathematical function used for it, that is for minimizing the discrepancy between the observed covariance matrix and the reproduced covariance matrix.
In order to illustrate this point, we will go back to the matrix in Table 1.1, and propose another model for it. Shown in Figure 1.7a, this model has the advantage of being simple: it has two parameters to be estimated, namely P1 and P2. These are two regression coefficients B (β). It is thus easy to test the iterative procedure by applying the ordinary least squares (OLS) method, whose purpose is to minimize a particular discrepancy function that is defined as the sum of the squares of the differences between the observed correlations and the reproduced correlations (∑d2). Table 1.6 summarizes the whole iterative method estimation.
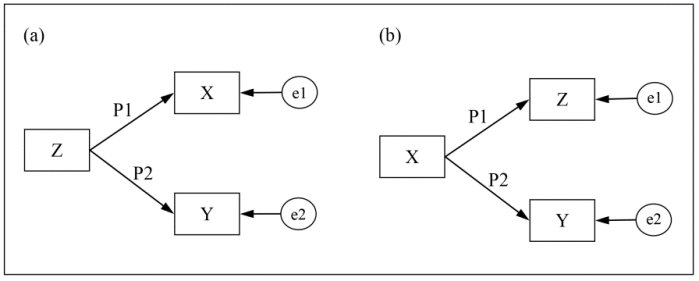
Figure 1.7. Equivalent path models (a) and (b) linking three observed variables
To begin, all estimation methods require that the starting values for all parameters to be estimated be specified. Some programs also allow for determining the maximum number of iterations allowed, and specifying a convergence condition that, once met, causes the iterative procedure to stop.
To carry out the first iteration, we have arbitrarily assigned a value of 0.50 to each of the two parameters P1 and P2 of the model. These values allow us to first reproduce a correlation matrix: rXZ = 0.50, rYZ = 0.50, and rXY = 0.25. If we now apply the OLS method, we then get the next discrepancy function, Fmin = (0.79 – 0.50)2 + (0.59 – 0.50)2 + (0.49 – 0.25)2 = 0.149 (Table 1.6).
The smaller the value of this function, the better the fit between the observed covariance matrix and the reproduced covariance matrix. Moreover, this value becomes equal to zero when parameter estimations allow for perfectly reproducing the observed matrix.
Thus, the initial values will be systematically changed from one iteration to another up to the moment when the iterative process will end, that is when no new value is able to improve the discrepancy function.
For example, changes introduced in steps 1a, 1b, and 1c of Table 1.6 aim to determine the effect that they can have on the discrepancy function (Fmin). It is shown that the simultaneous reduction of the P1 and P2 values deteriorates this function (see cycle 1a with respect to cycle 1). An alternative fall of these values confirms this tendency (see cycles 1b and 1c with respect to cycle 1). Subsequent steps aim to reverse the first trend. It remains to be determined how much the P1 and P2 can increase. It is clear that at this level, a P2 value higher than 0.61 causes an impediment to the minimization function (see cycle 3a). On the other hand, progressive increase of P1 improves this function. Finally, it can be noted that it is better to stop the process at step 4c, as the last step (i.e. step 5) begins deteriorating minimization, which goes from 0.0006 to 0.0008. And it is by obtaining 0.80 and 0.61 respectively that P1 and P2 allow for the best minimization. The iteration process can then stop with a discrepancy function with a of value Fmin = 0.0006.
The remaining differences between the observed correlations and the reproduced correlations on the basis of the estimated parameters represent elements of the residual matrix. Table 1.7 provides reproduced and residual correlation matrices of the model in Figure 1.7a, obtained by the OLS method.
Table 1.6. Solution of the iterative procedure for the model in Figure 1.7a
| Observed correlations | Discrepanc y function (Fmin) | |||||
| Parameter values | rXZ = 0.79 | rYZ = 0.59 | rXY = 0.49 | ∑d2 | ||
| Iteration cycles | P1 | P2 | Reproduced correlations | Least squares | ||
| 1 | 0.50 | 0.50 | 0.50 | 0.50 | 0.250 | 0.149 |
| 1a | 0.49 | 0.49 | 0.49 | 0.49 | 0.240 | 0.162 |
| 1b | 0.49 | 0.50 | 0.49 | 0.50 | 0.245 | 0.158 |
| 1c | 0.50 | 0.49 | 0.50 | 0.49 | 0.245 | 0.158 |
| 2 | 0.55 | 0.55 | 0.55 | 0.55 | 0.300 | 0.094 |
| 2a | 0.60 | 0.60 | 0.60 | 0.60 | 0.360 | 0.029 |
| 3 | 0.65 | 0.61 | 0.65 | 0.61 | 0.400 | 0.027 |
| 3a | 0.65 | 0.62 | 0.65 | 0.62 | 0.403 | 0.028 |
| 4 | 0.67 | 0.61 | 0.67 | 0.61 | 0.408 | 0.021 |
| 4a | 0.70 | 0.61 | 0.70 | 0.61 | 0.427 | 0.012 |
| 4b | 0.75 | 0.61 | 0.75 | 0.61 | 0.457 | 0.003 |
| 4c | 0.80 | 0.61 | 0.80 | 0.61 | 0.480 | 0.0006 |
| 5 | 0.81 | 0.61 | 0.81 | 0.61 | 0.494 | 0.0008 |
Table 1.7. Original, reproduced, and residual correlation matrices of the model in Figure 1.5a, using the OLS estimation method
| Reproduced correlations ( Σ) | Residual correlations (S – Σ) | |||||
| X | Y | Z | X | Y | Z | |
| X | _ | 0.48 | 0.80 | _ | ||
| Y | 0.49 | _ | 0.61 | 0.01 | _ | |
| Z | 0.79 | 0.59 | _ | – 0.01 | – 0.02 | _ |
| Observed correlations (S) | ||||||
It can be noted that the smallness of the discrepancy between the observed and reproduced correlations of three variables (0.01, – 0.01, and – 0.02) proves the similarity between the two matrices and consequently, the plausibility of the model. Approximation – which can be assessed based on goodness-of-fit indices – seem sufficient at first sight to even talk about the fit of the model, in other words the adequacy of the theory on which the facts are based. To be convinced of this, let us evaluate an alternative model in which the variable X (chocolate consumption) influences variables Z (milieu) and Y (life satisfaction). Figure 1.7b shows this model and Table 1.8 summarizes the iterative process generated by the OLS estimation method.
Table 1.8. Solution of the iterative procedure for the model in Figure 1.7b
| Observed correlations | Discrepancy function (Fmin) | |||||
| Parameter values | rXZ = 0.79 | rYZ = 0.59 | rXY = 0.49 | ∑d2 | ||
| Iterationcycles | P1 | P2 | Reproduced correlations | Least squares | ||
| 1 | 0.50 | 0.50 | 0.50 | 0.50 | 0.250 | 0.1998 |
| 1a | 0.49 | 0.49 | 0.49 | 0.49 | 0.240 | 0.2125 |
| 1b | 0.51 | 0.51 | 0.51 | 0.51 | 0.260 | 0.1877 |
| 2 | 0.52 | 0.52 | 0.52 | 0.52 | 0.270 | 0.1762 |
| 2a | 0.58 | 0.58 | 0.58 | 0.58 | 0.336 | 0.1167 |
| 2b | 0.60 | 0.60 | 0.60 | 0.60 | 0.360 | 0.1011 |
| 2c | 0.61 | 0.61 | 0.61 | 0.61 | 0.372 | 0.0943 |
| 2d | 0.62 | 0.62 | 0.62 | 0.62 | 0.384 | 0.0882 |
| 2e | 0.63 | 0.63 | 0.63 | 0.63 | 0.397 | 0.0824 |
| 2f | 0.64 | 0.64 | 0.64 | 0.64 | 0.409 | 0.0777 |
| 2g | 0.70 | 0.70 | 0.70 | 0.70 | 0.49 | 0.0622 |
| 2h | 0.80 | 0.80 | 0.80 | 0.80 | 0.640 | 0.0996 |
| 3 | 0.80 | 0.70 | 0.80 | 0.70 | 0.560 | 0.0451 |
| 3a | 0.85 | 0.65 | 0.85 | 0.65 | 0.552 | 0.0328 |
| 3b | 0.88 | 0.60 | 0.88 | 0.60 | 0.528 | 0.0240 |
| 4 | 0.89 | 0.59 | 0.89 | 0.59 | 0.525 | 0.0242 |
| 4a | 0.88 | 0.59 | 0.88 | 0.59 | 0.519 | 0.0231 |
| 4b | 0.88 | 0.58 | 0.88 | 0.58 | 0.510 | 0.0226 |
| 4c | 0.88 | 0.57 | 0.88 | 0.57 | 0.501 | 0.0224 |
| 4d | 0.88 | 0.56 | 0.88 | 0.56 | 0.492 | 0.0226 |
We remember that the iterative process must end when no new value is able to improve the discrepancy function any longer. It should be noted in Table 1.8 that after a cycle of improvement of the discrepancy function, the last step 4d spells a reversal of the situation. In this case, the estimation procedure should be stopped and the result from the previous step 4c should be kept. The discrepancy function thus gets a value equal to 0.0224, and parameters P1 and P2 get 0.88 and 0.57 respectively.
Table 1.9. Original, reproduced, and residual correlation matrices of the model in Figure 1.5b, using the OLS estimation method
| Reproduced correlations ( Σ) | Residual correlations (S – Σ) | |||||
| X | Y | Z | X | Y | Z | |
| X | _ | 0.57 | 0.88 | _ | ||
| Y | 0.49 | _ | 0.50 | – 0.08 | _ | |
| Z | 0.79 | 0.59 | _ | – 0.09 | – 0.09 | _ |
| Observed correlations (S) | ||||||
It is also remembered that the residual matrix provides clues as to whether the specified model is able to adequately reproduce the original correlation matrix (or variance-covariance matrix). In fact, it makes it possible to know the degree of approximation of the observed matrix, the degree of similarity between the latter and the reproduced matrix based on the model that we intend to use to describe original correlations. It can be noted in Table 1.9 that the discrepancy between the observed matrix and the reproduced matrix is such that we are right in thinking it is a model totally inconsistent with the data. We will discuss more on that later.
We have already underlined the fact that, apart from the experimental method, all other methods seem unfit to determine a causal link in a strict manner. It is true that nothing in a correlation matrix allows for changing the relational nature between the variables that it takes into account into a causal nature between them. However, while the procedure used to test the theoretical assumptions formalized by figures 1.7a and 1.7b has actually failed to demonstrate causal links, it showed that these links could now not be read equally in one way or the other (see Chapter 5 of this book). It will merely be noted that fit with the facts of a model for the benefit of another has highlighted a certain orientation in different connections. It is not absurd to think that, despite their high correlation, it is variable Z (in this case, the “milieu”) that has an effect on variable X (in this case, “chocolate consumption”), and not the other way around.
Moreover, the procedure that follows and leads to comparing matrices can be surprising. In fact, one observed correlation matrix is compared to a matrix that is derived from path coefficients that are themselves based on an estimation from this first observed matrix. Sometimes, the correlation coefficient easily reproduces the regression coefficient. It is a mathematical tautology that guarantees a perfect prediction [JAC 96]. Such a mathematical tautology that renders any comparison useless is the prerogative of saturated models (just-identified) that we will discuss later.
In Chapter 3 of this book, we will see how to reproduce a covariance matrix (Σ) from the parameters of a simple measurement model (see the topic of confirmatory factor analysis in the chapter). In what concerns general structural equation models – including latent variables – the derivation of a covariance matrix from the parameters of the estimated model is obviously more complicated because of the simultaneous presence of the measurement model and the structural model. The reader eager to know the details can consult the work of Mueller [MUE 96] among others.
1.2.1. Estimation methods (estimators)
As we just saw, the model estimation involves finding a value for each unknown (free) parameter in the specified model. But, it goes well beyond this simple objective, as it is important that the calculated values allow reproducing a covariance matrix (∑) that resembles the observed covariance matrix (S) as much as possible. It is an iterative procedure whose general principle is to start from an initial value (specified for the set or for each individual parameter either by the user or automatically by the software) and to refine it progressively by successive iterations that stop when no new value for each parameter makes it possible any longer to reduce the difference between the observed covariance matrix and the reproduced covariance matrix. These different operations are performed by minimization algorithms (i.e., discrepancy or minimization function) that, despite having the same purpose of finding the best parameter estimates, nevertheless differ from the mathematical function used for it, that is for minimizing the deviation between the observed covariance matrix and the reproduced covariance matrix. This often involves complex mathematical functions based on matrix algebra (vectors, inverse of a matrix, weighted matrix, determinant, etc.) of a level higher than that desired for this introduction, but whose details could be found in any specialized book (for example, see [BOL 89]). Thus, so much more than their purely mathematical aspects, what interests us here, in the point of view of the user wanting to get unbiased estimates of his/her model’s parameters, is to know the considerations that can guide the choice of an estimation method. In fact, since sample parameter estimates are used to infer population parameter estimates, the first must be, among other things, unbiased, accurate, and consistent. And estimator is crucial here, hence the interest that it can be the object of a deliberate and justified choice, which alone will make it possible to retain that which is most appropriate to the data present [LAD 89]. Grosso modo, this choice boils down to two options dictated by the type of data and, in particular, by the nature of their distribution. The first concerns estimation methods that require the hypothesis of multivariate normality of data, while the second concerns estimators that are most suitable to data that deviate following the normal distribution. The specificities, advantages, and disadvantages of these estimators have given rise to fairly abundant and rich work and publications [CHO 95, WES 95].
These methods all have the same main objective of rendering, iteratively, discrepancy (Fmin) as tiny as possible between two matrices. The value of the function is positive, even equal to zero when S = Σ. This means, in this case, that the model is perfectly compatible to the data, in other words, H0 : Fmin = 0.00.
The major difference between these methods lies in the manner in which the mathematical discrepancy function (F[S, Σ] = Fmin) is used to minimize deviations between the observed correlation matrix (for example, Pearson correlations, polychoric correlations, tetrachoric correlations) and the reproduced correlation matrix. Once this objective has been met, the statistical significance remains to be assessed. To this end, we use the χ2 test that is calculated in the following way in lavaan:
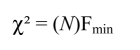
where:
- – N is the sample size;
- – Fmin denotes minimum discrepancy (F[S, Σ]) obtained by the estimation method used (for example, FML, FGLS, FWLS, which we will discuss later).
This statistical test allows for judging whether the null hypothesis (H0: S = Σ) is admissible, namely that there is no significant difference between the two matrices. The χ2 value, which tends to increase with the F value, is all the greater because the two matrices compared are dissimilar from one another. A significant (high enough) χ2 makes it possible to reject the null hypothesis, thus indicating that the specified model does not allow for adequately reproducing the observed correlation matrix. However, when χ2 is equal to zero (or insignificant), namely when the discrepancy is zero (F[S, Σ] = 0.00), it means that there is a perfect (or near perfect) fit between two matrices. Reading a statistical table of distribution of this index is based on the degrees of freedom (df). These are obtained by subtracting the number of parameters to be estimated in the model (t) from the number of variances and covariances available, that is to say k(k + 1)/2 where k denotes the number of observed variables:
The advantage of χ2, which is the only statistical test in SEM, is that it allows for proving the statistical significance of the model's fit to the data, under certain conditions concerning, in particular, the nature of data distribution and the sample size.
Limits around this test are multiple and now, well known. Apart from its sensitivity to sample size (the bigger it is and higher the risk of the model being rejected8), the multivariate normal data assumption, which is required for this test. It is true that in humanities and social sciences, data that perfectly respects normality is rarely available.
It should also be noted that the sample size directly affects the χ2 value. The sensitivity of this index to the sample size has raised some well-founded reservations that have led to the emergence of other complementary goodness-of-fit indices that will be discussed later. As for the choice of one estimation method over another, it is an important aspect and we will discuss it later.
1.2.1.1. Estimators for normally distributed data
There are two estimators for normally distributed data that are commonly used. They are the maximum likelihood method (ML, FML) and the Generalized Least Squares (GLS, FGLS).
With the maximum likelihood method (ML), the discrepancy function (Fmin) takes the following formula:
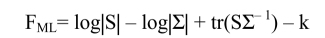
where:
- – refers to the natural logarithm function (base e);
- – || is the determinant of the matrix;
- – k is the number of variables in the correlation (or covariance) matrix;
- – is the trace matrix algebra function which sums diagonal elements;
- – S = observed matrix;
- – Σ = reproduced matrix;
- – Σ–1 = inverse of matrix Σ.
The function used by the Generalized Least Squares (GLS) estimation method is written as follows:
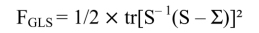
where:
- – tr = trace of the matrix (or the sum of the diagonal elements of the matrix);
- – S = observed matrix;
- – Σ= reproduced matrix;
- – S–1 = inverse of matrix S.
Finally, the third known estimation method, the Weighted Least Squares method (WLS, see [BRO 84]), based on the polychoric correlation matrix, is not recommended for samples of too small a size. However, unlike the previous ones, this method has the advantage of not depending on the form of data distribution.
1.2.1.2. Which estimators for non-normally distributed data?
Let us recall that the equivalent of the aforementioned method is also known as the Asymptotic Distribution-Free function (FADF), and as the Arbitrary Generalized Least Squares (FAGLS) function (i.e. estimator). Much later, we will discuss other estimation methods, some of which seem to be more appropriate for ordinal/categorical variables and for data whose distribution deviates from normality.
The debate on the performance of estimators based on the type of data to be analyzed (i.e. continuous variables, ordinal variables, binaries, normality of distribution) is still open [LI 16]. In fact, although it is the default estimator in all modeling software (including lavaan), the maximum likelihood estimation method (ML) which requires that variables are continuous and multivariate normal. In humanities and social sciences, there are at least two challenges that are faced in using this estimator. First, the prevalence of ordinal (for example, Likert-type scale) and dichotomous/binary (true/false) outcome measures (indicators). Second, the prevalence of non-normally distributed data. From a purist point of view, the maximum likelihood method is not at all appropriate for ordinal measurements such as Likert scale items. In fact, it is now known that such measurements often display a distribution that deviates from normality [MIC 89].
Several simulations have shown that the application of the maximum likelihood estimation method (or generalized least squares) on data that does not have a normal distribution also affects the estimation of standard errors of the parameters than the goodness-of-fit statistics: some fit indices are overestimated, and the χ2 tends to increase as the data gap increases with respect to normality [WES 95]. However, the findings of Chou and Bentler [CHO 95] make it possible to qualify these remarks. These authors showed that in the presence of a sufficiently large sample, maximum likelihood estimation method and generalized least squares method do not make the results suffer, even when the multivariate normality is slightly violated (see also [BEN 96]). The robustness of these methods is not always guaranteed. In case of a more serious violation, several options are available to SEM users [FIN 13]. They can be classified into three categories.
The first groups the family of the maximum likelihood estimation method with corrections of normality violations (Robust ML). It concerns new estimation methods considered to be more “robust”, as statistics (i.e. standard errors and χ2) that they generate are assumed to be reliable, even when distributional assumptions are violated.
The Satorra-Bentler χ2 (SBχ2) incorporates a scaling correction for the χ2 (called scaled χ2). Its equivalent in lavaan is the MLM estimator.
It is obtained as follows:
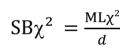
where:
- – d = the correction factor according to the degree of violation of normality;
- – ML = maximum likelihood estimator.
In fact, in the absence of any violation of the multivariate normality, SBχ2 = MLχ2. The value of this correction factor (d) is given in the results under the name scaling correction factor for the Satorra-Bentler correction.
The Yuan-Bentler χ2 (YBχ2) is a robust ML estimator similar to the aforementioned one, but more suited for a small sample size. Its equivalent in lavaan is the MLR estimator. The value of the correction factor (d) is provided in results under the name scaling correction factor for the Yuan-Bentler correction, allowing for calculating the YBχ2 as follows:
The second category groups alternative estimation methods to ML:
- a) first, the weighted least squares method (WLS). This estimator, which analyzes the polychoric or polyserial correlation matrix has at least two disadvantages. It requires a fairly large sample size [FLO 04] to hopefully get stable results (for example, at least 1,200 participants for 28 variables, according to [JÖR 89], pp. 2–8, Prelis). And, above all, it quite often runs into convergence problems and produces improper solutions where complex models are estimated. A negative variance, known as the “Heywood case”, makes the solution improper because, as we remember, a variance can hardly be negative;
- b) the Diagonally Weighted Least Squares (DWLS) method is next. Jöreskog and Sörbom [JÖR 89] encouraged using this method when the sample is small and data violates normality. This estimator, for which the polychoric or polyserial correlation matrix serves as the basis for analysis, is a compromise between the unweighted least squares method and the full weighted least squares method [JÖR 89]. Two “robust” versions of DWLS that are close to this estimator, called “WLSM” and “WLSMV” in lavaan (and Mplus), give corrected estimates improving the solution outcomes (standard errors, χ2, fit indices described as “robust”).
These methods use a particular calculation of the weighted matrix as a basis and are based on the generalized least squares method. The estimation procedure that requires the inversion of the weighted matrix generates calculations that become problematic when the number of variables exceeds 20, and require a large sample of participants in order to have stable and accurate estimates. Another limitation is the requirement to analyze raw data, and therefore have it.
The third method refers to the resampling procedure (bootstrap). This procedure requires neither a normal multivariate distribution nor a large sample (but it is not recommended for dichotomous and ordinal measures with few response categories). MacKinnon, Lockwood, and Williams [MAC 04] believe that it produces results (for example, standard errors) that are very accurate and reliable.
The principle of this procedure is simple [MAC 08]. A certain number of samples (set by the researcher, e.g. “N bootstrap = 1000”) are generated randomly with replacement from the initial sample considered, as the population. Each generated sample contains the same number of observations as the initial sample. Then there will be as many estimates of the model parameters as there are samples generated. An average of estimations of each model parameter is calculated, with a confidence interval (CI). An estimate is significant at p < 0.05 if its confidence interval at 95% (95% CI) does not include a null value (see [PRE 08a]). The resampling procedure, with lavaan, also has the possibility of getting confidence intervals of fit indices.
Table 1.10 summarizes the recommendations concerning estimators available in lavaan based on the type of data to be analyzed.
Table 1.10. Recommendations concerning the main estimators available in lavaan according to the type of data
| Data type and normality assumption | Recommended estimator |
| Continuous data | |
| 1- Approximately normal distribution | ML |
| 2- Violation of normality assumption | ML (in case of moderate violation) |
| MLM, MLR, Bootstrap | |
| Ordinal/categorical data | |
| 1- Approximately normal distribution | ML (if at least 6 response categories) |
| MLM, MLR (if at least 4 response categories) | |
| WLSMV(binary response or 3 response categories) | |
| 2- Violation of normality assumption | ML (if at least 6 response categories) |
| MLM, MLR (if at least 4 response categories) | |
| WLSMV (in case of severe violation) | |
Eventually, the choice of estimation method depends on four criteria:
- – first, the measurement level of data: it seems well established that the most appropriate estimator for binary/dichotomous variables is WLS [MUT 93] and its recent extension (WLSMV). Following the work of Muthén [MUT 83, MUT 84], it quickly became aware of the need to change the approach to the data obtained with binary or ordinal scales;
- – data distribution properties, as we saw;
- – available data: raw data or correlation/covariance matrix? Although the covariance matrix is the basis of any structural analysis, except the ML method, all other methods require using raw data. In the absence of raw data, one can instead use either a correlation matrix or a variance-covariance matrix;
- – finally, sample size. This last point deserves attention because it is linked with statistical power.
1.2.1.3. Sample size and statistical power
By opting for SEM, the researcher must immediately look at the crucial and throbbing question of the necessary number of participants to be collected to hope to obtain a proper solution, an acceptable level of accuracy and statistical power of estimates of his/her model's parameters, as well as reliable goodness-of fit indices. Today, specialists are unanimous in considering that structural equation modeling requires a lot of participants. Its application to sample sizes that are too small may bias the estimates obtained. However, it remains to be seen how many participants are needed and sufficient to obtain accurate and reliable estimates. Several general rules have been proposed. The first rule is that of a minimum sample of 100 participants as per Boomsma [BOO 82, BOO 85], 150 as per Anderson and Gerbing [AND 88] or Jaccard and Wan [JAC 96], and 200 as per Kline [KLI 16] for a standard model (a not very complex model here). Next is the rule that links the number of participants to the number of free parameters (to be estimated) in the model. Bentler [BEN 95], for example, recommends five times more participants than free parameters when applying the maximum likelihood estimation method or the generalized least squares method, and ten times more participants than free parameters when opting for the asymptotic Distribution-Free estimation method (ADF) or its equivalents. For Jackson [JAC 03], a 20:1 ratio (20 participants for 1 free parameter) will be ideal, while a 10:1 ratio would be acceptable. This rule takes into account both the complexity of the model as well as the requirements of the estimation method. Indeed, it is not uncommon to see the asymptotic distribution free estimation fail when applied to a sample with few participants. A non-positive definite covariance matrix could be the cause after having been the consequence of the small sample size.
It is clear that in both rules the characteristics of the model (complex/simple) are a decisive factor in determining the minimum required sample size. There are others that are just as important: the reliability of indicators of latent variables, the nature of the data (categorical, continuous), their distribution, and especially the type of estimator used, which we have just mentioned (e.g. ML, MLR, WLSMV).
Sample size and statistical power are intertwined such that the former determines the latter, and so the latter is used to determine the former [KIM 05]. Here, let us recall that statistical power refers to the probability of rejecting the null hypothesis (H0) when it is false. In SEM, as we have seen, the null hypothesis is represented by the model specified by the researcher (i.e. H0: Fmin = 0, i.e. the specified model fits the data perfectly). Putting this null hypothetical to test, it is important to know the probability of having a good conclusion concerning it (i.e. the probability of accepting a real H0, and the probability of rejecting a false H0). The recommended acceptability threshold is a power ≥ 0.80, that is the type II error risk should not go above 20% (or 1 – 0.80). In other words, an 80% probability to not commit a type II error. This happens when the null hypothesis (here, the fit of our model to the data) is accepted by mistake. We know that sample size and statistical power are two important levers allowing for reducing this error.
Several strategies have been proposed to solve the question of sample size and statistical power required for a given structural equation model. For example, Muthén and Muthén [MUT 02b] proposed the use of the rather complicated Monte Carlo method. MacCallum, Browne and Sugawara [MAC 96] introduced another, more practical type of analysis of statistical power and sample size for structural equations models, based on both the fit index, the Root Mean Square Error of Approximation (RMSEA) that we will discuss later, and the number of degrees of freedom of the specified theoretical model (H0). MacCallum and his collaborators [MAC 96] showed the existence of a link between the number of degrees of freedom and the minimum sample size to reach the acceptable statistical power (0.80). For example, a model showing only 8 df (a not very parsimonious model), needs at least 954 participants (Nmin = 954) are needed, while only 435 participants are needed for a model showing 20 df (so, a more parsimonious model).
The R “semTools” package has a function (findRMSEAsamplesize) using the procedure suggested by MacCallum, Browne, and Cai [MAC 06] making it possible to determine the minimum sample size for a statistical specified a priori, based on a hypothetical RMSEA value (for example, 0.05). To determine the minimum sample size for a model, the reader can also use the calculator offered by Daniel Soper at the following address: https://www.danielsoper.com/statcalc/references. aspx?id=89. Based on the approach suggested by Westland [WES 10], this calculator allows you to determine the sample size by taking into account the number of observed and latent variables in the model, and, a priori, the effect size, the level of probability (typically α ≤ 0.05), and the desired statistical power (usually ≥ 0.80). The calculator gives both the required minimum sample size to detect the specified effect and the minimum sample size, taking the complexity of the model into account, in the results.
Let us conclude here that sample size in SEM is a subject that specialists have not finished debating [WES 10, WOL 13], therefore making it impossible to reach a consensus on this subject.
1.3. Model evaluation of the solution of the estimated model
This step corresponds to examine and read the results of the specified model estimation. The confirmatory nature of the approach obviously requires the use of goodness-of-fit indices to judge the compatibility between the specified theoretical model and the data. The only statistical test is χ2 the use of which is, as we have seen, limited by its sensitivity to sample size. Moreover, structural equation modeling is covered throughout by a paradox: as much as it needs a large sample size, its only statistical test is just that sensitive to it; hence adequacy fit indices that are not statistical tests are used. We can distinguish two types: overall goodness-of-fit indices, which can reject or accept the model applied to the data, and local tests, which make it possible to analytically review the solution obtained (i.e. individual parameter estimates), ensure that it is a proper solution, and determine the significance of the parameter estimates. Let us see them one by one.
1.3.1. Overall goodness-of-fit indices
Currently, two dozen are available in all SEM software, including lavaan. But this wealth of indices constitutes the difficulty in selecting the most reliable and appropriate ones, especially as the growing number of books dedicated to them are unanimous neither in their acceptability threshold nor in their meaning and how to interpret them [BAR 07, WIL 11]. Several classifications have been proposed to sort this out, the most commonly known ones being that of Marsh and his colleagues [MAR 88], of Tanaka [TAN 93], and especially that of Hu and Bentler [HU 99], which is still authoritative. Thus, and for the sake of simplification, we chose to group them into three different categories: absolute fit indices, incremental fit indices, and parsimonious fit indices. For each category, we will present the most commonly used indices from the recommendations of Hu and Bentler [HU 99], indicating their level of acceptability and the interpretation given to them.
1.3.1.1. Absolute fit indices
These indices are based on a comparison between the observed variance-covariance matrix (S) and the variance-covariance matrix reproduced based on the theoretical model (∑). The deviations between homologous elements of these two matrices give rise to, as we saw earlier in this chapter, a residual matrix (S – ∑) used to calculate the Root Mean Square Residual (RMR) or the Standardized Root Mean Square Residual (SRMR). Easier to interpret, standardization makes it possible to eliminate the effects of the scale of the variable on the residuals of the model. The more the deviations between the elements of S and ∑ are reduced, the lesser the value of the RMR or SRMR. This value is obtained by dividing the sum of each element of the residual correlation matrix squared by the number of variances and covariances of the matrix. The value ranges from 0.00 to 1.00. The fit is better when this value is close to 0.00; but a value equal or less than 0.08 indicates that the model fits the data well. Finally, we will add the Weighted Root Mean Square Residual (WRMR), which is an index suitable for categorical data estimated using the WLS or DWLS method. A value less than 1 indicates that the model fits the data well.
1.3.1.2. Parsimonious fit indices
These indices show the originality in taking the parsimony of the theoretical model into account. Parsimony is a central concept in structural equation modeling [PRE 06]. It refers to the small number of parameters to be estimated required to achieve a given goodness of fit. Moreover, it is important to consider that a good model fit as indicated by the fit indices is usually due to either the plausibility of the theoretical representation specified by the researcher or the over parameterization of the model, that is its lack of parsimony. In fact, although it perfectly fits the data, a saturated model has no use because its adequacy is due to its lack of parsimony. It is a complex model with a number of parameters to be estimated equal to the number of variances and covariances observed, and, thus, zero degrees of freedom. In contrast, seen in Figure 1.8, the null model (not to be confused with the null hypothesis), as it is highly parsimonious, is severely disadvantaged. This is a simple model that has little, if any, parameters to be estimated, and therefore a very high number of degrees of freedom, but which fits the data very poorly. The reason is that the scarcity of parameters to be estimated leaves more opportunities for data to freely differ from reproduced data. It is therefore clear that the less parsimonious models tend to approximate data more easily, hence the need to penalize them, otherwise, as pointed out by Browne and Cudeck [BRO 93], there would be great temptation to include meaningless parameters for the sole purpose of making it seem as though the model is a good fit. A goodness-of fit indice that neglects information concerning parsimony can be misleading.
And since the number of degrees of freedom is linked to parsimony, and as it somewhat represents the number of independent and objective conditions according to which a model can be rejected due to the lack of fit, it constitutes an important detail for estimating the plausibility of the model. The parsimony ratio (PRATIO) captures this information. It is the relationship between the model and the number of degrees of freedom of the theoretical model (dft) and that of the null model (dfn) which is equal to k(k – 1)/2 where k is the number of measured variables:
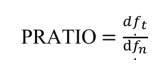
But we can get a different ratio by dividing the number of degrees of freedom of the theoretical model by the maximum possible number of degrees of freedom (dfmax), which is here equal to k(k + 1)/2. The values of these ratios vary between 0 and 1. A model is even more parsimonious when this value is close to 1. In fact, a saturated model (i.e. the less parsimonious one) gets a zero PRATIO. Some authors, such as Mulaik, James, Van Alstine, Bennett et al. [MUL 89), advocate multiplying this ratio with the fit indices to get the adjusted indices taking parsimony into account.
However, the most recommended index in this category is the Root Mean Square Error of Approximation (RMSEA)9 with its confidence interval of 90%:
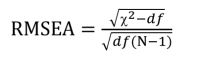
where:
- – χ2 = the chi2 value of the specified and estimated theoretical model;
- – df = degrees of freedom of the specified and estimated theoretical model;
- – N = sample size.
The value of this index ranges from 0.00 to 1.00, with a ≤ 0.06 value indicating that the model fits the data well. Ideally, this value should have a confidence interval of 90%, with a minimum close to 0.00 and a maximum not exceeding 0.100.
In the presence of alternative non-nested models (in competition), some parsimonious fit indices help us discern which of them is the best fitting model. The Akaike Information Criterion (AIC) as well as the Bayesian Information Criterion (BIC) also perform this function.
The first is obtained in lavaan in the following way10:
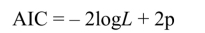
where:
- – logL = log-likelihood of the model estimated (H0);
- – p = number of parameters to be estimated in the model.
lavaan provides the value of log-likelihood (“logl”) as well as the number of free parameters to be estimated (“npar”).
The second is obtained in lavaan as follows:
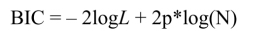
where:
- – logL = log-likelihood of the model estimated (H0);
- – p = number of free parameters to be estimated in the model;
- – log(N) = logarithm of the sample size.
When one has to choose between several alternative non-nested models (competitive models), it should be one for which the AIC and BIC values are the lowest, or even negative. But as there are no standard indices, it is impossible to indicate the smallest desirable value as well as the broader unacceptable value [HAY 96].
We clearly see through their calculations whether, for these two indices, the lack of parsimony is to be penalized. Thus, models with a large number of free parameters to be estimated, that is the least parsimonious models (those tending towards model saturation, because over-parameterized), are penalized by an inflation of their AIC and BIC value. The BIC is, from this point of view, more uncompromising than the AIC, and more severely penalizing of the lack of parsimony.
1.3.1.3. Incremental fit indices
These indices evaluate the goodness of fit of the specified model against a more restrictive model considered to be nested in the specified model. The concept of nested models (nestedness) is important and needs to be explained. Two models are considered as being nested when one is a special case of the other. And several models can form a nested sequence when, hierarchically, each model includes the previous models as special cases. In fact, they are alternative models that, while they have the same specifications, differ only in the restrictions that each of them can be subjected to. Such a sequence can be represented on a continuum whose extremes are, on the one hand, the simplest model, that is the null model (Mn) that, undergoing the maximum restrictions, contains no free parameters to be estimated; and, on the other hand, the most complex model, that is the saturated model (Ms) in which the number of free parameters is equal to the number of variances and covariances of the observed variables. The first provides the worst approximation of the data, while the second provides the perfect fit. Figure 1.8 illustrates the same. It will be noted that Mn is nested in Ma; Mn and Ma in Mt; Mn, Ma, and Mt in Mb ; and finally Mn, Ma, Mt, and Mb in Ms.
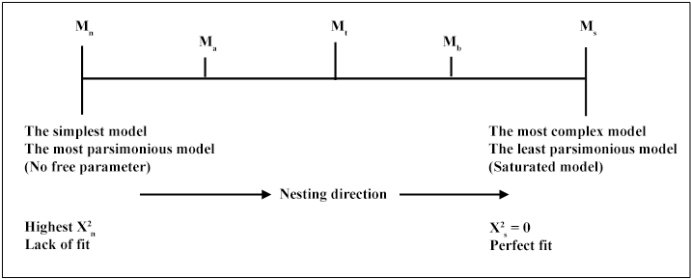
Figure 1.8. Nested SEM models (inspired by [MUE 96])
Incremental fit indices are based on the comparison between the specified theoretical model (Mt) and a nested model called the “baseline model”, in which the null model (Mn) – also called the “independence model”, as it postulates that all covariances are zero, which implies a complete (but unlikely) independence between variables of the model – is the simplest and most widely used version for this type of comparison.
In fact, these indices measure the relative decline of the discrepancy function (Fmin) (or the relative increase of the fit, which amounts to the same) when we replace a null model (Mn) with a more complex model (for example, Ma, Mt or Mb). Their values range from 0, indicating a lack of fit, and 1 a perfect fit (although they may exceed these limits for some indices). But according to Hu and Bentler [HU 99], a ≥ 0.95 value suggests a good fitting model. However, a value greater than 0.90 is still used for judging whether a model is acceptable or not. A 0.95 value indicates the increase in the goodness of fit of the specified model with respect to the null model: it can indeed be inferred that, applied to the same data, the first model is 95% better than the second. The Comparative Fit Index (CFI) and the Tucker-Lewis Index (TLI) are the best representatives:
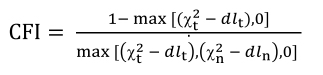
where:
- – χ2t = the chi2 value of the specified and estimated theoretical model;
- – dft = the degrees of freedom of the specified and estimated theoretical model;
- – χ2n = the chi2 value of the baseline model (“null” model);
- – dfn = degrees of freedom of the baseline model (“null” model);
- – max = indicates the use of the highest value, or even zero if this is the highest value.
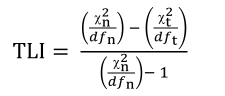
where:
- – χ2t = the chi2 value of the specified and estimated theoretical model;
- – dft = the degrees of freedom of the specified and estimated theoretical model;
- – χ2n = the chi2 value of the baseline model (“null” model);
- – dfn = degrees of freedom of the baseline model (“null” model).
The advantage of TLI with respect to CFI is that it penalizes the model's lack of parsimony. It always results in fewer degrees of freedom (Figure 1.8). We can recall that the less a model is parsimonious (tending towards saturation) the more likely it is to fit the data. Thus, the model fit is attributable more to the lack of parsimony than the theoretical construction that it represents.
It should be emphasized that, unlike the AIC and BIC indices that are used to compare non-nested models, the CFI and the TLI can be used to compare nested models. We will discuss more on that later.
Which one to choose? The answer is far from simple, as both opinions are still divided about fit indices. Hoyle and Panter [HOY 95] recommend using χ2 (or scale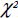 
), Goodness-of-Fit Index (GFI)11, at least two incremental fit indices, in this case the TLI and CFI, as well as parsimonious fit indices when necessary. As for Jaccard and Wan [JAC 96], they propose retaining χ2, GFI, and SRMR in the category of absolute fit indices, RMSEA in the parsimonious fit indices and finally, CFI in the incremental fit indices.
These opinions are sufficient to show that it is not possible to recommend a standard list of fit indices that could be unanimously accepted, especially since the choice of a fit indice could be guided by theoretical and methodological considerations (e.g. sample size, estimation method, model complexity, data type). In Hu and Bentler [HU 98, HU 99], readers will find details about the sensitivity of these fit indices to all these methodological aspects. The only advice we can afford to give, however, is to closely follow developments concerning fit indices. In the meantime, you can carefully follow the recommendations of Hu and Bentler [HU 99] or Schreiber and his co-authors [SCH 06] who suggest the following guidelines for judging a model goodness-of-fit (based on the hypothesis where the maximum likelihood method is the estimation method): 1) RMSEA value ≤ 0.06, with confidence interval at 90% values should be between 0 and 1.00; 2) SRMR value ≤ 0.08; and 3) CFI and TLI values ≥ 0.95.
However, we will subscribe to the idea of Chen et al. [CHE 08] that not only is there no “golden rule” on these fit indices, but there can be no universal, interchangeably ready-to-use threshold for them in all models. In fact, [CHE 08] showed how the universal threshold of 0.05 for RMSEA penalizes (rejects) good models estimated with a small sample size (N < 100). And these authors conclude quite rightly about the use of fit indices that in fine, a researcher must combine these statistical tests with human judgment when he takes a decision about the goodness-of-fit of the model (p. 491). Table 1.11 summarizes all the goodness-of-fit indices presented in this chapter.
Table 1.11. Some goodness-of-fit indices available in lavaan
| Fit type | Index | Interpretation for guidance |
| Absolute | RMR/SRMR | ≤ 0.08 = good fit |
| WRMR | ≤ 1.00 = good fit | |
| Parsimonious | PRATIO | Between 0.00 (saturated model) and 1.00 (parsimonious model) |
| RMSEA | ≤ 0.05 = very good fit ≤ 0.06 and ≤ 0.08 = good fit | |
| AIC | Comparative index: the lower value of this index, the better the fit | |
| Incremental | BIC | Comparative index: the lower value of this index, the better the fit |
| CFI | ≥ 0.90 and ≤ 0.94 = good fit ≥ 0.95 = very good fit | |
| TLI | ≥ 0.90 and ≤ 0.94 = good fit ≥ 0.95 = very good fit |
1.3.2. Local fit indices (parameter estimates)
These indices concern all the individual parameter estimates of the model and allow for a more analytical examination of the solution. They make it possible to ensure that it is a proper solution, that is to ensure that it contains no inadmissible values devoid of all statistical sense like standardized estimates higher than 1 or negative variances. These offending values are known as Heywood cases, which have multiple causes. In Dillon, Kumar and Mulani [DIL 87], there are clear details on the sources as well as the solutions for these Heywood cases. Furthermore, the reader may refer to Hayduk [HAY 96] with regard to negative R2, which are often the ones to suffer in non-recursive models (see Chapter 3 of this book). The author proposes a very interesting solution.
Convergence to a proper solution is compulsory for it to be accepted. Another factor is the coherence of the parameter estimate values from preliminary theoretical considerations. Indeed, to obtain values devoid of any theoretical meaning (as opposed to those predicted, for example) makes a solution nonsensical, even if the overall goodness-of-fit indices point in its favor.
Thus, individually reviewing each parameter is necessary to interpret results, and is useful for improving a model when it fails to fit the data. In fact, it is important to know whether the value of a parameter is statistically significant, to know the error variance (i.e. the unexplained variance portion of a variable) as well as the total proportion of variance of an endogenous variable explained by other variables in the model (R2). In addition, standard errors, which refer to the precision with which parameters were estimated, must be neither too small (close to zero) nor excessively large (even though there are no precise criteria on this subject).
The significance of a parameter estimate is worth consideration. It refers to using a statistical test to determine if the value of a parameter significantly differs from zero. To do this, we simply divide the non-standard value of the parameter by its standard error (“std.err” in the lavaan results). The ratio obtained is interpreted, when the distribution is normal and the sample large enough, as a z-test (“z-value” in lavaan), meaning an absolute value greater than 1.96 helps conclude that the parameter estimate is different from zero at a threshold of statistical significance of 0.05. The threshold of significance of 0.01 requires an absolute value greater than 2.58. However, when the sample size is small with normal distribution, the ratio is read as a t-test requiring the use of a table to assess its statistical significance at a fixed threshold. It is useful to know that in the case of a large sample, some very low estimates are often significant.
As we already know, the path coefficient measures the direct effect of a variable that is a predictor of a criterion variable. We also know that there is an effect only when the value of the coefficient is significantly different from zero. What remains to be seen now is the relative importance of an effect.
It is clear that, although statistically significant, standardized path coefficients may differ in the magnitude of their respective effects. Some authors, especially Kline [KLI 16], suggested taking into account significant standardized values close to 0.10 with a weak effect, values that are approximately 0.30 with a medium effect, and those greater than 0.50 with a large effect.
1.3.3. Modification indices
Modification indices help identify areas of potential weakness in the model. Their usefulness lies in their ability to suggest some changes to improve the goodness-of-fit of the model. In fact, modification indices (provided by all software) can detect the parameters, which contribute significantly to the model’s fit when added to it. They even indicate how the discrepancy function (and therefore χ2) would decrease if a specific additional parameter, or even a set of parameters (in this case, we use multivariate Lagrange multiplier test; see Bentler [BEN 95] is included. These indices are generally accompanied by a statistic called the Parameter change, indicating the value and its tendency (positive versus negative) that a parameter would get if it were freed. According to Jöreskog and Sörbom [JÖR 93], such information is useful to be able to reject models, in which the tendency of the values of freed parameters turns out to be incompatible with theoretical orientations. The Wald test, which is to our knowledge available only in the EQS [BEN 85, BEN 95] and SAS [SAS 11] software, reveals parameters that do not contribute to the model fit of the model and removing which will improve this fit. More detailed and illustrated information on using the Wald and Lagrange multiplier tests can be found in the book by Byrne [BYR 06].
Let us remember that such operations are used with the risk of severely betraying the initial theoretical representation and compromising the confirmatory approach. Whatever it may be, any revision is part of a re-specification approach of the model. We thus move from the actual model evaluation to model specification, and rather model respecification. And a re-specification is all the more sufficient when it is supported by and coherent with the initial theoretical specification. This return to the starting point closes a loop, the outcome of which – after a new model evaluation – is the final rejection of either the model or its acceptance and, consequently, its interpretation.
To conclude, it should be stressed that any solution must be examined in the light of three important aspects: (1) the quality of the solution and the location of areas of potential weakness and misfit (i.e. absence of offending estimates values such as negative variances) and potential areas of weakness of the model (to be identified using modification indices); (2) the overall model fit of the model; (3) local fit indices of the solution (individual parameter estimates and their significance).
Thus, reducing the assessment of a model to its overall fit is a mistake that should not be committed. We will discuss more on that later.
1.4. Confirmatory approach in SEM
In most cases, using multiple regression involves integrating a set of predictor variables in the hope that some will turn out to be significant. And we would have as much chance as the variables introduced in the model. Although guided by some knowledge of the phenomenon in under study, this approach is considered as exploratory. Everyone knows that we often proceed by trial and error, trying various successive combinations, and sometimes getting a little fortunate through this. Moreover, it is this exploratory side that makes this a pretty exciting technique. It is fully covered by the motivation to discover. It is to researchers what excavations are to archaeologists. It is the same with most factor analysis methods whose exploratory nature represents the main purpose.
Structural analyses are part of a confirmatory approach: a model is first specified and then put to the test. A rather simplified representation of reality, a model designates a hypothetical system in which several phenomena maintain various relations with each other. The hypothesis, for which the model is a simple formalization, concerns the exact organization of these phenomena within an explanatory system. It should also be mentioned that apart from the strictly confirmatory approach that seeks to accept or reject a model that is put to the test, we can recognize, with Jöreskog and Sörbom [JÖR 93], two other strategies: the competing models and the model generating, as befits structural equation modeling.
In the case of competing models, researchers specify several alternative models for the same data that they would have specified earlier, in order to retain the best fitting model. For this purpose, they have comparative statistical fit indices that will be discussed later in the book.
Model generating occurs when the initial model fails to fit the data or when a researcher proposes a test model whose limits he knows in advance despite the theoretical contribution that led to its development. The researcher proceeds by way of modification-retest as many times as is necessary to obtain a model that fits its data. This is rather a model generating procedure and not a mdel testing in itself. Each model respecification may theory-driven or data-driven. But, as pointed out by [JÖR 93], the aim of this approach is both the statistical fit of the re-specified model as well as its plausibility and its theoretical likelihood. For, while perfect and statistically adequate, a model has value only if it has an acceptable theoretical plausibility.
It turns out that the model generating strategy is increasingly successful with SEM users. There are at least two reasons for this. The first is the flexibility of this approach with respect to the “all or nothing” advocated by the strictly confirmatory approach. The second is the existence of tests that will help the user examine the model to improve its fit. These tests, the best known of which are the modification indices, the Lagrange multiplier and the Wald tests [BEN 95], are important because they are available in almost all SEM software, and because they are easy to use and interpret even if their effectiveness remains to be proven. The modification index, for example, helps detect parameters that would improve the model fit when included into the model.
The use of post-hoc modifications in model generating approach gives rise to a fundamental problem, that of the confirmatory nature of SEM. Moreover, although these modifications are technically easy to use, their usefulness and effectiveness in generating the right model are still to be proved. The various studies and simulations carried out by MacCallum [MAC 86, MAC 88, MAC 92, SUY 88,], whose fierce hostility towards the model generating strategy is known [MAC 96], show the difficulty in finding the good model, some parameters of which have been deliberately altered for research purposes, despite all the indices and procedures available.
Not that this strategy, which is now popular with the research community, should be banned, but it is important to specify the precautions as regards its use. First, any modification must be supported by theory-based rationale, failing which there is a risk of compromising the original confirmatory approach. Then, it is preferable to opt for competing models that have been previously specified on a clear, theoretical basis. Finally, it is imperative to validate the model generated with a new sample. It is a cross-validation procedure [CUD 89, CUD 83], which also applies to the case where we have a single sample. In fact, it is possible to randomly partition a sample, whose size is large enough, into two parallel subsamples, a calibration sample and a validation sample, or even carry out a multigroup analysis with these two subsamples. There is also an index proposed by Browne and Cudeck [BRO 89], called the Cross-Validation Index (CVI), that helps assess the similarity between models from each of these two subsamples. This index is the discrepancy function (F) between the reproduced covariance matrix of the calibration sample Σc and the covariance matrix of the validation sample Sv [BRO 93]. Cross-validation is much better when the value of this index is close to zero, indicating that the model is identical in the two sub-samples:
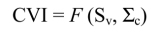
Ultimately, the researcher should not lose sight of the confirmatory nature of the approach for which he uses structural equation modeling. It is fully an approach for confirmation of an a priori specified model within a hypothetico-deductive reasoning. In this case, the hypotheses are based on a well-defined nomologic network.
Although it is sometimes necessary to ease the strictly confirmatory approach, it is perilous to completely deviate from it. Here, we share the appeal by MacCallum [MAC 95] to the editors of scientific journals, inviting them to reject any article using SEM that does not conform to the confirmatory approach or does not take account of precautions and demands that SEM requires. But we also see that, in reality, the inductive and deductive approaches intermingle constantly, and that the borders between the two are less thick than it seems. In fact, it is rare for even an inductive approach to be atheoretical and completely extrinsic to any hypothesis a priori, and for its empirical results to rely on pure laws of chance.
1.5. Basic conventions of SEM
The best way to formalize a theoretical model is to diagramm it. It involves making a graph to represent relationships in a system of variables on the basis of prior theoretical information. It is clear that the causal nature of these relationships can not be demonstrated; however, we refer to causal models (Jöreskog & Sörbom, 1996) and causal diagrams when we deal with path analysis. We will also use “effect” or “effect” to describe the relationships that variables have within a causal model.
There is twofold interest in a diagram. As clear and comprehensive as possible, it should be a faithful translation of the theoretical model; it also establishes an isomorphic representation of all structural equations that can replace the command syntax, thus becoming an input diagram for structural equation modeling software (input) for software through a diagrammer.
Although each software has some specificity, all of them share some conventions concerning diagramming models. Thus, with the beginner user in mind, we opted to present these conventions. This presentation seems fundamental to us, as the diagram is now the emblem of structural equation modeling. It is also essential for fully mastering modeling.
Figure 1.9 shows a standard diagram of structural equation modeling. Here, the modifier “standard” is used to designate basic and simple models with respect to more complex ones that have, for example, correlations between measurement error or feedback loops (i.e. non-recursive models that we will discuss in Chapter 3 of this book).
Figure 1.9. Standard SEM diagram
It is easily seen that this diagram contains five objects with different facets summarized in Figure 1.10.
Figure 1.10. Conventions for drawing diagrams
1.6. Place and status of variables in a hypothetical model
Whether manifest (observable) or latent, variables can either be exogenous or endogenous. They are considered to be exogenous when they never seem to be criterion variables in any structural equation of a model. They are easily identifiable in a diagram because they have no single arrow pointed at them. Correlated factors F1 and F2 in Figure 1.9 are two exogenous latent variables. Generally, they are the starting point of the model. However, endogenous variables are those that seem like criterion variables in at least one of the structural equations of the model. They are easily identifiable in a diagram, owing to the fact that at least one arrow points to them. Factors F3, F4, and F5 in Figure 1.9 represent endogenous latent variables. An endogenous variable is said to be “ultimate” when it is the last variable in the system. It is in fact the case with F5 in Figure 1.9.
1.7. Conclusion
After having defined structural equation modeling, we tried to show how its foundations are based on regression analysis and factor analysis. By combining them in one approach, structural equation modeling makes them richer and more flexible. And Reuchlin [REU 95] had every reason to write, “the recent structural models are […] a progress rather than an innovation”.
The regression coefficient seemed like a key element in the calculations of structural models. In fact, we have seen its usefulness in the derivation of the matrix that would serve to test the model fit. Model fitting is primarily statistical. It involves knowing whether the dissimilarity between the reproduced correlation matrix and the observed correlation matrix is statistically significant. If such were the case, and with the χ2 test making it possible for us to confirm it, the model from which the matrix was reproduced is deemed to be unsatisfactory. Otherwise, when χ2 is not so significant, the question of no statistically significant, the proposed (specified) model provides a good fit to the data. But let us remember that χ2 is far from being a reliable and robust model fit indice.
Structural equation modeling, which is the generalization of regression analysis and factor analysis, naturally has some points in common with the two. First, all three come under linear statistical models, which are based on the assumption of multivariate normal distribution. The statistical tests used by all these approaches are also based on this assumption. Then, none of them is able to establish a causal link between variables, like any other statistical method. As for the differences between these approaches, three are memorable. The first relates to the approach. It is confirmatory with structural equation modeling and not exploratory, as this is the case with factor analysis or regression analysis. The second lies in the fact that equation models are the only ones able to estimate the relationship between latent variables. The last point concerns the possibility of equation models to insert and invoke mediating variables within a theoretical model. Such an opportunity is not negligible, especially if one accepts like Tolman [TOL 38] that “theory is a set of intervening variables” (p. 344). We will explore these features in more detail in the following chapters.
1.8. Further reading
Readers who wish to deepen their understanding of the main basic concepts in this chapter may refer to the following books:
BOLLEN K.A., Structural Equations with Latent Variables, John Wiley & Sons, Oxford, 1989.
FABRIGAR L.R., WEGENER D.T., Exploratory Factor Analysis, Oxford University Press, New York, 2012.
GRIMM L.G., YARNOLD R., Reading and Understanding Multivariate Statistics, APA, Washington, 1995.
HOWELL D.C., Fundamental Statistics for the Behavioral Sciences, CENGAGE, Wadsworth, 2017.
LOEHLIN J.C., Latent Variable Models. An Introduction to Factor, Path and Structural Analysis, 3rd edition, Lawrence Erlbaum Associates, New York, 1998.