1772

Lagrange Points

Isaac Newton (1643–1727), Joseph-Louis Lagrange (1736–1813), Pierre-Simon Laplace (1749–1827)

With his 1687 publication of the Principia, Isaac Newton had expanded Kepler’s Laws of Planetary Motion into laws of gravitation and motion in general, thus establishing a reliable framework within which astronomers, physicists, and mathematicians could begin to understand the detailed intricacies of not only how planets, moons, and comets moved in the sky but why they did so. Among the most challenging applications of Newton’s laws was the so-called three-body problem. Newton’s equations could be easily applied to understand the gravitational effects that governed the motions of two masses, like the Earth and the Moon, or the Sun and the Earth, but the calculations got pretty thorny when theorists introduced the gravitational effects of a third body.

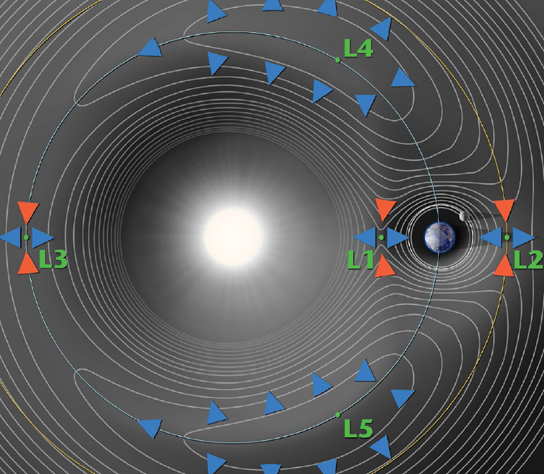
The first to successfully solve one particular case of the three-body problem was the French mathematician Joseph-Louis Lagrange, who predicted in 1772 that there should be five special places in any three-body system that has two large masses and one small mass where the gravitational forces among the bodies would be balanced. These places are now called Lagrange points. Lagrange’s prediction was verified with the twentieth-century discovery of the Trojan asteroids, which are “trapped” in the L4 and L5 Lagrange points of the Sun–Jupiter system.

The French mathematician Pierre-Simon Laplace coined the phrase “celestial mechanics” in 1799 to describe the physics and math of studying complex solar system motions. Lagrange’s solution of the three-body problem turned out to be relatively “easy” because it assumed one small object was interacting with two large, massive objects, one of which was in an essentially circular orbit around the other. Celestial mechanicians expanded on Lagrange’s discovery to eventually tackle more general three-body problems; indeed, twenty-first-century researchers often use high-speed computers to solve even more complicated N-body problems—those in which the Newtonian motions of huge numbers of individual bodies (be they planets, moon, and asteroids; ring particles; or even grains of cosmic dust) are tracked by computer in order to understand, explain, and predict very complex motions in our solar system.

A contour map of the gravitational forces (white lines) in the Sun-Earth-Moon system and the five special Lagrange points (L1 through L5) where those forces are balanced. The image is not to scale (L2 is only about 932,000 miles [1.5 million kilometers] from Earth; the Sun is 100 times that in the other direction).