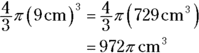Chapter 8
Test-Taking Strategies for Core Math
IN THIS CHAPTER
 Saving time with shortcuts
Saving time with shortcuts
 Whittling down the answer choices
Whittling down the answer choices
 Coming up with the correct answer on your own
Coming up with the correct answer on your own
Mathematical knowledge and practice are very important for taking the Praxis Core exam’s math section, but the arsenal you take into battle doesn’t have to stop there. Test-taking strategies can make your weapons even more effective. What you know is extremely important, but so is what you do with what you know. This chapter is about making the best of the knowledge you have.
Using Helpful Shortcuts
Getting answers that are correct on the Praxis Core exam is really important. However, coming up with the right answers isn’t your only concern. You must consider something else of major relevance: The exam is timed. You have 90 minutes to answer 56 problems. Any methods you can use to reduce the time you take to answer questions without sacrificing accuracy will help you. The methods we outline in the following sections are real, and they work. We encourage you to give them a trial run as you take the practice tests in Part 5 and online.
Solving equations versus determining what must be solved
You will almost definitely have word problems that require setting up and solving algebraic equations when you take the Praxis Core exam. Solving these problems requires more than the ability to solve equations. You also need to determine what information the problem is asking you for, that is, what needs to be solved. You can use a variable to represent the unknown quantity that must be determined.
The next step is to put the algebraic expressions into an equation and solve the equation. The solution to the equation will be the value of the first unknown. Once you know it, you can find the values of any other unknowns by putting the value of the variable for which you just solved into the expressions used to represent the values you have not yet determined.
 John is four years older than Adam. John was twice Adam’s age 33 years ago. What is John’s age now?
John is four years older than Adam. John was twice Adam’s age 33 years ago. What is John’s age now?
(A) 42
(B) 8
(C) 25
(D) 41
(E) 37
The correct answer is Choice (D). The question asks for John’s age, so you can make John’s age the first unknown and represent it with a variable, such as x. Because John is four years older than Adam, you can represent Adam’s age with the expression x – 4. The next step is to write an equation with the two expressions. Just translate the information in the word problem into mathematical language. John was twice Adam’s age 33 years ago. Their ages 33 years ago can be represented by subtracting 33 from their current ages:
- John:
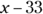
- Adam:
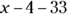
“Twice Adam’s age 33 years ago” can be represented by 2 multiplied by 33 less than Adam’s current age.
Adam:
Then set up an equation that shows their ages 33 years ago with John’s being twice as much as Adam’s:
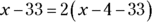
Notice the direct translation of worded information in that equation. It says exactly the same thing in a different way. The solution to the equation is 41. (For a review of how to solve algebraic equations, turn to Chapter 5.) John’s age is therefore 41.
Using estimation and approximation
Estimation is the act of using known information to get a number that is close to the answer to a question although it may not be the actual answer. This can be helpful on the Praxis Core exam because most of the test is multiple choice. When you estimate, you have a good chance of getting the answer right by choosing the one that’s closest to your estimate. Because the test is timed, estimation may be handy for a few last answers before time’s up.
Estimation can also help you to eliminate choices that are definitely wrong, and it can help you make sure the answer you get is not something beyond the fringe of reason or the result of a miscalculation. However, don’t spend too much time estimating for just that purpose. You’ll be performing a juggling act with time and caution.
Approximation is using numbers that are very close to numbers given in a problem for the purpose of making calculating easier. This, too, can save you time when time is running short, and it can also help you eliminate wrong answers. If you have to make a wild guess, your chances of guessing the correct choice increase when you can eliminate some of the choices.
When you multiply with irrational numbers in decimal form, you often have to approximate. An irrational number is a number that can’t be represented as a ratio of two integers. An irrational number in decimal form doesn’t terminate or repeat. In other words, the digits after the decimal don’t have a pattern and continue infinitely. Because you don’t have time to calculate with an infinite number of digits, approximation can often help.
For example, the number 7.32960584965105… is an irrational number. You may come across a number like that when you use your calculator. Rounding such a number to four decimal places should be sufficient to get a correct result in almost all cases. Rounding also saves time, and time is precious on the Praxis Core exam. In some cases, you can just leave a number in your calculator and do the necessary operation with it.
Using the calculator
An on-screen calculator is provided for you on the math section of the Praxis Core exam. That makes computation easier and saves time over doing calculations on paper. The calculator’s keypad includes keys for all the digits, the four basic operations (adding, subtracting, multiplying, and dividing), square roots, making numbers negative, a decimal, parentheses, memory, clearing, transfer display (which can transfer your answers to the answer box on constructed response questions), and, of course, the highly important equal sign. The calculator is also programmed to follow the order of operations. However, you still need to know the order of operations for solving variable equations.
Identifying calculations you can make in your head
We highly encourage caution when making calculations for the Praxis Core exam. That involves writing out work on scratch paper and using the calculator, but only when you actually have time to do those things. You should write and use the calculator even for the calculations you’re sure you can do in your head when you’re keeping a good pace, though we don’t recommend using the calculator for calculations that can come from pure memory.
However, when time becomes a major issue, you need to know what more complex calculations you can do in your head relatively safely. The first category to consider is problems for which writing and using the calculator don’t actually help you figure out the answer. For these calculations, the paper and calculator will only help you avoid careless errors. Suppose you have to calculate 2 + 2. We recommend using paper even for that when you’re good on time. Using paper allows you to write out every step of the calculations, better ensuring that you avoid careless errors. When you’re way behind on time, you should speed up by making such a calculation only in your head. Timing is important, but so is caution.
While we believe in writing every step involved in answering a math question, we don’t think the calculator should be used for every single calculation. The more you have in your brain’s memory, the faster your pace will be.
The art of guessing as a last resort
If time really wears thin on the exam and you only have time to make wild guesses, go ahead and make nothing but wild guesses. A point may come where you don’t even have time to estimate, approximate, or do quick calculations in your head. That’s when you need to just start hitting answers as fast as you can.
If you make all of your choices randomly, you have some probability of getting all of them right. However, the flip side to that coin is that you have equal probability of getting all of them wrong. Still, you’ll most likely get some right if you answer enough of them that way.
A small number of questions tell you that more than one answer choice may apply. If you notice one of those during a pure guessing phase, you should mark at least two answers of the choices presented.
A few of the questions don’t have choices presented with them. You should answer those last if you’re in a guessing phase. When you get around to guessing on them, see how much time you have left. Quickly look at the problem and give the best guess you can give. If you still have a few more seconds to actually think about the answer, do all of the thinking you have time to do and then give the best answer you can.
Working backward
When you’re in doubt about how to answer a math problem by using the conventional calculation methods, you can increase the probability of getting the correct answer by working backward. This approach can be used in various situations and in different ways. For example, if an end result is given and you’re asked about what was involved in getting the result, you can start at the end and work toward the beginning. This technique can be used for age problems, problems concerning final amounts of money, final locations, and other types of problems. The technique is sometimes the only one that will work.
 Robert went for a walk on a trail that runs north and south after getting a ride on a four-wheeler. At the end of his walk, he was 14 miles north of his campsite. He had previously walked 10 miles south, and before that he walked 20 miles north. How far north of his campsite was Robert when he began his walk?
Robert went for a walk on a trail that runs north and south after getting a ride on a four-wheeler. At the end of his walk, he was 14 miles north of his campsite. He had previously walked 10 miles south, and before that he walked 20 miles north. How far north of his campsite was Robert when he began his walk?
(A) 24 miles
(B) 0 miles
(C) 4 miles
(D) 44 miles
(E) 6 miles
The correct answer is Choice (C). You can answer this problem by using positive and negative numbers and adding them, with north distances being positive and south distances being negative. However, you can also work backward from the final distance and trace Robert’s travel back to the beginning of the hike. If Robert was 14 miles north and had previously walked 10 miles south, he was 24 miles from his campsite before the final part of the walk. If he got to that point by walking 20 miles north, he was 20 miles back, which is 4 miles from the campsite. Choice (A) is the distance Robert was from his campsite before changing directions, but not the initial distance. Choice (D) results from adding 20 to 24 instead of subtracting it.
 If you decide to use only one bit of advice on test-taking strategies, let it be this: Never stay on a question that looks like it will take an extreme amount of time to answer when you first get to it. You can save it for after you have answered the questions that do not take long to answer. This advice applies to any type of question. You can write down the number of the question in the hope of going back to it later. Some people get so caught up in a challenge to answer a time-consuming question that they use up time they could have used to answer four or five other questions.
If you decide to use only one bit of advice on test-taking strategies, let it be this: Never stay on a question that looks like it will take an extreme amount of time to answer when you first get to it. You can save it for after you have answered the questions that do not take long to answer. This advice applies to any type of question. You can write down the number of the question in the hope of going back to it later. Some people get so caught up in a challenge to answer a time-consuming question that they use up time they could have used to answer four or five other questions. All the Praxis Core exam math questions are worth the same number of points, so make sure you don’t treat any one of them as if it’s more important than the others. Whether you’re asked to solve a simple equation or find the volume of a remaining region of a cone, the question is worth as much as the other 55. Timing is part of the challenge, so use it well.
All the Praxis Core exam math questions are worth the same number of points, so make sure you don’t treat any one of them as if it’s more important than the others. Whether you’re asked to solve a simple equation or find the volume of a remaining region of a cone, the question is worth as much as the other 55. Timing is part of the challenge, so use it well. If the problem has more than one unknown, see whether you can represent the others in terms of the first. For example, if Bob’s score in bowling is in question and the problem says that Frank scored 10 points higher than Bob, you can use x to represent Bob’s score and
If the problem has more than one unknown, see whether you can represent the others in terms of the first. For example, if Bob’s score in bowling is in question and the problem says that Frank scored 10 points higher than Bob, you can use x to represent Bob’s score and 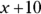 to represent Frank’s score.
to represent Frank’s score.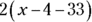
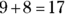 , you can quickly conclude that
, you can quickly conclude that 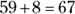 . Also, make very sure that you know all the multiplication tables for 2 through 12.
. Also, make very sure that you know all the multiplication tables for 2 through 12.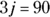 , what is the value of j?
, what is the value of j?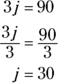

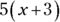 is equal to
is equal to 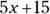 , not
, not 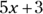 .
.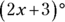 , in which case you would have to figure out the value of a variable to determine the answer. For such a question, make sure your answer is the measure of the angle and not the value of the variable. That is one example of when paying close attention to the question is necessary.
, in which case you would have to figure out the value of a variable to determine the answer. For such a question, make sure your answer is the measure of the angle and not the value of the variable. That is one example of when paying close attention to the question is necessary.

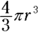 .
.