Chapter 2
Six Sigma and Visual Six Sigma
This chapter introduces the key ideas behind Six Sigma and Visual Six Sigma; our focus is on the latter. Six Sigma is a potentially huge topic, so we only have space to mention some of its essential ideas. There are already numerous well-written books and articles dealing with the many and diverse aspects of Six Sigma as commonly practiced.1 We also note that today, digital tools (software, databases, visual media, etc.) are leveraged extensively in Six Sigma initiatives.2
Our goal in this chapter is to provide an overview of Six Sigma so that you start to see how Visual Six Sigma fits into this picture. However, it is worth pointing out in advance that you can only gain a proper appreciation of the power of visualization techniques by working with data that relate to real problems in the real world.
BACKGROUND: MODELS, DATA, AND VARIATION
There is no doubt that science and technology have transformed the lives of many and will continue to do so. Like many fields of human endeavor, science proceeds by building pictures, or models, of what we think is happening. These models can provide a framework in which we attempt to influence or control inputs so as to provide better outputs. Unlike the models used in some other areas, the models used in science are usually constructed using data that arise from measurements made in the real world.
At the heart of the scientific approach is the explicit recognition that we may be wrong in our current world view. Saying this differently, we recognize that our models will always be imperfect, but by confronting them with data, we can strive to make them better and more useful. Echoing the words of George Box, one of the pioneers of industrial statistics, we can say, “Essentially, all models are wrong, but some are useful.”3
MODELS
The models of interest in this book can be conceptualized as shown in Exhibit 2.1. This picture demands a few words of explanation:
- In this book, and generally in Six Sigma, the outcomes of interest to us are denoted with a Y. For example, Y1 in Exhibit 2.1 could represent the event that someone will apply for a new credit card after receiving an offer from a credit card company.
- Causes that may influence a Y will be shown as an X. To continue the example, X1 may denote the age of the person receiving the credit card offer.
- Rather than using a lengthy expression such as “we expect the age of the recipient to influence the chance that he or she will apply for a credit card after receiving an offer,” we can just write Y = f(X). Here, f is called a function, and Y = f(X) describes how Y changes as X changes. If we think that Y depends on more than one X, we simply write an expression like Y = f(X1, X2). Since the function f describes how the inputs X1 and X2 affect Y, the function f is called a signal function.
- Note that we have two different kinds of causes: (X1, X2, X3), shown in the diagram with solid arrows, and (X4, X5, X6), shown with dotted arrows. The causes with dotted arrows are the causes that we do not know about or care about, or causes that it is impossible or uneconomic to control. Often, these are called nuisance or noise variables. For example, X4 could be the number of credit cards that the recipient of the offer already has, or the time since the recipient received a similar offer. The function that represents the combined effect of the noise variables on Y is called a noise function, and the result is sometimes referred to simply as error.
- Just because we do not know about the noise variables does not mean that they do not influence Y. If X4, X5, or X6 change, as they typically will, then they will necessarily lead to some apparently inexplicable variation in the outcome Y, even when we do our best to keep X1, X2, and X3 fixed. For example, whether an offer recipient applies for a new credit card may well be influenced by the number of credit cards that the recipient already has.
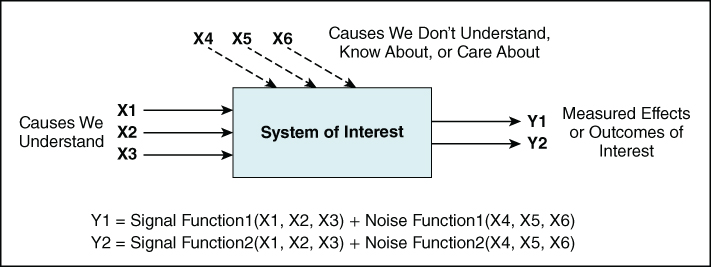
Exhibit 2.1 Modeling of Causes before Improvement
As you can see in the exhibit, a key aspect of such a model is that it focuses on some specific aspects (i.e., X1, X2, and X3) in order to better understand them. By intention or simply lack of current knowledge, the model necessarily omits some aspects that may actually be important (X4, X5, and X6).
Depending on whether you are being optimistic or pessimistic, Six Sigma can be associated with improvement or problem solving. Very often, an explicit model relating the Ys to Xs may not exist; to effect an improvement or to solve a problem, you need to develop such a model. The process of developing this model first requires arriving at a starting model and then confronting that model with data to try to refine it. Later in this chapter, in the section “Visual Six Sigma: Strategies, Process, Roadmap, and Guidelines,” we discuss a process for refining the model.
If you succeed in refining it, then the new model might be represented as shown in Exhibit 2.2. Now X4 has a solid arrow rather than a dotted arrow and is within the scope of the signal function rather than the noise function. When we gain a new understanding of a noise variable, we gain leverage in explaining the outcome (Y) and so can often make the outcome more favorable to us. In other words, we are able to make an improvement.
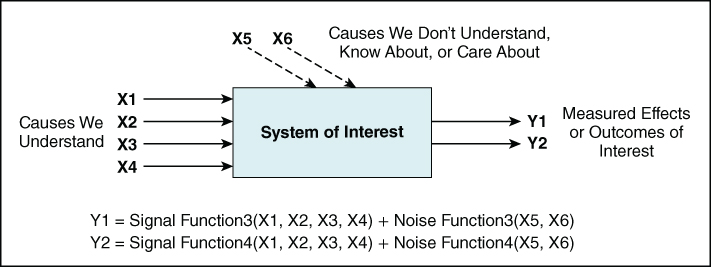
Exhibit 2.2 Modeling of Causes after Improvement
The use of the term error to refer to a noise function has technical origins, and its use is pervasive, though noise might be a better term. Useful models that encompass variation rely on making a correct separation of the noise and the signal implied by the data. Indeed, the inclusion of noise in the model is essentially the definition of a statistical model (see the section “Variation and Statistics”), and in such models the relevance or statistical significance of a signal variable is assessed in relation to the noise.
MEASUREMENTS
The use of data-driven models to encapsulate and predict how important aspects of a business operate is still a new frontier. Moreover, there is a sense in which a scientific approach to business is more challenging than the pursuit of science itself. In science, the prevailing notion is that knowledge is valuable for its own sake. But for any business striving to deliver value to its customers and stakeholders—usually in competition with other businesses doing the same thing—knowledge does not necessarily have an intrinsic value. This is particularly so since the means to generate, store, and use data and knowledge are in themselves value-consuming, including database and infrastructure costs, training costs, cycle time lost to making measurements, and so on.
Therefore, for a business, the only legitimate driving force behind a scientific, data-driven approach that includes modeling is a failure to produce or deliver what is required. This presupposes that the business can assess and monitor what is needed, which is a nontrivial problem for at least two reasons:
- A business is often a cacophony of voices, expressing different views as to the purpose of the business and needs of the customer.
- A measurement process implies that a value is placed on what is being measured, and it can be very difficult to determine what should be valued.
It follows that developing a useful measurement scheme can be a difficult, but vital, exercise. Moreover, the analysis of the data that arise when measurements are actually made gives us new insights that often suggest the need for making new measurements. We will see some of this thinking in the case studies that follow.
OBSERVATIONAL VERSUS EXPERIMENTAL DATA
Before continuing, it is important to note that the data we will use come in two types, depending on how the measurements of Xs and Ys are made: observational data and experimental data. Exhibit 2.1 allows us to explain the crucial difference between these two types of data.
- Observational data arise when, as we record values of the Ys, the values of the Xs are allowed to change at will. This occurs when a process runs naturally and without interference.
- Experimental data arise when we deliberately manipulate the Xs and then record the corresponding Ys.
Observational data are collected with no control over associated Xs. Often we simply assume that the Xs are essentially constant over the observational period, but sometimes the values of a set of Xs are recorded along with the corresponding Y values.
In contrast, the collection of experimental data requires us to force variation in the Xs. This involves designing a plan that tells us exactly how to change the Xs in the best way, leading to the topic of experimental design, or design of experiments (DOE). DOE is a powerful and far-reaching approach that has been used extensively in manufacturing and design environments.4 Today, DOE is finding increasing application in nonmanufacturing environments as well.5 The book Optimal Design of Experiments: A Case Study Approach guides readers in designing and analyzing experiments using JMP.6
In both manufacturing and nonmanufacturing settings, DOE is starting to find application in the Six Sigma world through discrete choice experiments.7 In such experiments, users or potential users of a product or service are given the chance to compare attributes and express their preferences or choices. This allows market researchers and developers to take a more informed approach to tailoring and trading off the attributes of the product or service in advance. Because one attribute can be price, such methods allow you to address an important question: What will users pay money for? We note that JMP has extensive, easy-to-use facilities for both the design and analysis of choice models.
Even in situations where DOE is relevant, preliminary analysis of observational data is advised to set the stage for designing the most appropriate and powerful experiment. The case studies in this book deal predominantly with the treatment of observational data, but Chapters 7 and 9 feature aspects of DOE as well.
SIX SIGMA
Some common perceptions and definitions of Six Sigma include:
- A management philosophy
- Marketing hype
- A way to transform a company
- A way to create processes with no more than 3.4 defects per million opportunities
- Solving problems using data
- A way to use training credits
- Something a company has to do before Lean
- Making improvements using data
- A way to make money from consulting, training, and certification
- A pseudo-religion
- A way to get your next job
- Something a company does after Lean
In spite of this diversity of perspectives, there seems to be broad agreement that a Six Sigma initiative involves a variety of stakeholders and is a project-based method utilizing cross-functional teams. A performance gap is the only legitimate reason for spending the time and resources needed to execute a Six Sigma project. From this point of view, questions such as the following are vital to a Six Sigma deployment:
- How big should the performance gap be to make a project worth doing?
- How can you verify that a project did indeed have the expected impact?
However, for reasons of space, our brief discussion will only address the steps that are followed in a typical Six Sigma project once it has been kicked off.
Using the background presented in the beginning of this chapter, we offer our own succinct definition of Six Sigma:
- Six Sigma is the management of sources of variation in relation to performance requirements.
Here, management refers to some appropriate modeling activity fed by data. Depending on both the business objectives and the current level of understanding, management of sources of variation can mean:
- Identifying and quantifying sources of variation
- Controlling sources of variation
- Reducing sources of variation
- Anticipating sources of variation
A Six Sigma deployment effort typically starts with the following infrastructure:
- A senior executive, often a president or chief executive officer, provides the necessary impetus and alignment by assuming a leadership role.
- An executive committee, working operationally at a level similar to that of the senior executive, oversees the Six Sigma deployment.
- A champion sponsors and orchestrates an individual project. This individual is usually a member of the executive committee and has enough influence to remove obstacles or allocate resources without having to appeal to a more senior individual.
- A process owner has the authority and responsibility to make improvements to operations.
- A black belt supports project teams, taking a leadership role in this effort. This individual is a full-time change agent who is allocated to several projects. A black belt is usually a quality professional, but is often not an expert on the operational processes within the scope of the project.
- A green belt works part-time on a project or perhaps leads a smaller-scope project.
- A master black belt mentors the Six Sigma community (black belts and green belts), often provides training, and advises the executive committee. A master black belt must have a proven track record of effecting change and be a known and trusted figure. This track record is established by having successfully completed and led numerous Six Sigma projects, ideally within the same organization.
To guide Six Sigma projects that seek to deliver bottom-line results in the short or medium term, black belts typically use the Define, Measure, Analyze, Improve, and Control (DMAIC) structure, where DMAIC is an acronym for the five phases involved:
- Define. Define the problem or opportunity that the project seeks to address, along with the costs, benefits, and the customer impact. Define the team, the specific project goals, the project timeline, and the process to be improved.
- Measure. Construct or verify the operational definitions of the Ys, also called the critical to quality (CTQ) metrics or measures. Plot a baseline showing the level and current variation of the Ys. Quantify how much variation there is in the measurement process itself, in order to adjust the observed variation in the Ys and to improve the measurement process, if needed. Brainstorm or otherwise identify as many Xs as possible, in order to include the Xs that represent root causes.
- Analyze. Use process knowledge and data to determine which Xs represent root causes of variation in the Ys.
- Improve. Find the settings for Xs that deliver the best possible values for the Ys, develop a plan to implement process changes, pilot the process changes to verify improvement in the Ys, and institutionalize the changes.
- Control. Lock in the performance gains from the Improve phase.
Depending on the state of the process, product, or service addressed by the project, a different set of steps is sometimes used. For instance, for products or processes that are being designed or redesigned, the Define, Measure, Analyze, Design, Verify (DMADV) or the Identify, Design, Optimize, Validate (IDOV) framework is often used. These structures form the basis of Design for Six Sigma (DFSS).8 Briefly, the phases of the DMADV approach consist of the following:
- Define. Similar to the Define phase of DMAIC.
- Measure. Determine internal and external customer requirements, measure baseline performance against these requirements, and benchmark against competitors and industry standards.
- Analyze. Explore product and process design options for satisfying customer requirements, evaluate these options, and select the best design(s).
- Design. Create detailed designs of the product and process, pilot these, and evaluate the ability to meet customer requirements.
- Verify. Verify that the performance of the product and process meets customer requirements.
This brings us back full circle to our own definition of Six Sigma: management of sources of variation in relation to performance requirements. With a little thought, perhaps you can see how large parts of DMAIC, DMADV, or IDOV involve different ways to manage variation. For example, a DFSS project would involve techniques and tools to “anticipate sources of variation” in the product, process, or service.
VARIATION AND STATISTICS
In the previous section, we mentioned the following aspects of managing variation:
- Identify and quantify sources of variation.
- Control sources of variation.
- Reduce sources of variation.
- Anticipate sources of variation.
The first point, “Identify and quantify sources of variation,” is a vital step and typically precedes the others. In fact, Six Sigma efforts aside, many businesses can derive useful new insights and better knowledge of their processes and products simply by understanding what their data represent and by interacting with their data to literally see what has not been seen before. Identification of sources of variation is a necessary step before starting any modeling associated with the other Six Sigma steps. Even in those rare situations where there is already a high level of understanding about the data and the model, it would be very unwise to begin modeling without first investigating the data. Every set of data is unique, and in the real world, change is ubiquitous, including changes in the patterns of variation.
Given that the study of variation plays a central role in Six Sigma, it would be useful if there were already a body of knowledge that we could apply to help us make progress. Luckily, there is: statistics! One of the more enlightened definitions of statistics is learning in the face of uncertainty; since variation is a result of uncertainty, then the relevance of statistics becomes immediately clear.
However, statistics tends to be underutilized in understanding uncertainty. We believe that one of the reasons is that the fundamental difference between an exploratory study and a confirmatory study is not sufficiently emphasized or understood. This difference can be loosely expressed as the difference between statistics as detective and statistics as lawyer. Part of the difficulty with fully appreciating the relevance of statistics as detective is that the process of discovery it addresses cannot fully be captured within an algorithmic or theoretical framework. Rather, producing new and valuable insights from data relies on heuristics, rules of thumb, serendipity, and contextual knowledge. In contrast, statistics as lawyer relies on deductions that follow from a structured body of knowledge, formulas, statistical tests, and p-values.
The lack of appreciation of statistics as detective is part of our motivation in writing this book. A lot of traditional Six Sigma training overly emphasizes statistics as lawyer. This generally gives an unbalanced view of what Six Sigma should be, as well as making unrealistic and overly time-consuming demands on practitioners and organizations.
Six Sigma is one of many applications where learning in the face of uncertainty is required. In any situation where statistics is applied, the analyst will follow a process, more or less formal, to reach findings, recommendations, and actions based on the data.9 There are two phases in this process:
- Exploratory Data Analysis
- Confirmatory Data Analysis
Exploratory Data Analysis (EDA) is nothing more than a fancy name for statistics as detective, whereas Confirmatory Data Analysis (CDA) is simply statistics as lawyer. In technical jargon, the emphasis in EDA is on hypothesis generation. In EDA efforts, the analyst searches for clues in the data that help identify theories about underlying behavior. In contrast, the focus of CDA is hypothesis testing and inference. CDA consists of confirming these theories and behaviors. CDA follows EDA, and together they make up statistical modeling. A paper by Jeroen de Mast and Albert Trip provides a detailed discussion of the crucial role of EDA in Six Sigma.10
MAKING DETECTIVE WORK EASIER THROUGH DYNAMIC VISUALIZATION
To solve a mystery, a detective has to spot clues and patterns of behavior and then generate working hypotheses that are consistent with the evidence. This is usually done in an iterative way, by gathering more evidence and by enlarging or shifting the scope of the investigation as knowledge is developed. So it is with generating hypotheses through EDA.
We have seen that the first and sometimes only step in managing uncertainty is to identify and quantify sources of variation. Building on the old adage that “a picture is worth a thousand words,” it is clear that graphical displays should play a key role here. This is especially desirable when the software allows you to interact freely with these graphical views. Thanks to the advance of technology, most Six Sigma practitioners now have capabilities on their desktops that were only the province of researchers 10 years ago, and were not even foreseen 30 years ago. Although it is not entirely coincidental, we are fortunate that the wide availability of this capability comes at a time when data volumes continue to escalate.
Incidentally, many of the statistical methods that fall under CDA, which are in routine use by the Six Sigma community, were originally developed for squeezing the most out of a small volume of data, often with the use of nothing more than a calculator or a pen and paper. Increasingly, the Six Sigma practitioner is faced with a quite different challenge: The sheer volume of data (rows and columns) can make the naïve application of statistical testing, should it be needed, difficult and questionable.
At this point, let us consider the appropriate role of visualization and, tangentially, data mining within Six Sigma. Visualization, which has a long and interesting history of its own, is conventionally considered valuable in three ways:11
- Checking raw data for anomalies (EDA)
- Exploring data to discover plausible models (EDA)
- Checking model assumptions (CDA)
Given the crucial role of communication in Six Sigma, we can add two additional ways in which visualization has value:
- Investigating model outcomes (EDA and CDA)
- Communicating results to others (EDA and CDA)
There are a wide variety of ways to display data visually. Many of these, such as histograms, scatterplots, Pareto plots, and box plots, are already in widespread use. However, the simple idea of providing multiple linked views of data with which you can interact via software takes current Six Sigma analysis to another level of efficiency and effectiveness. For example, imagine clicking on a bar in a Pareto chart and seeing the corresponding points in a scatterplot become highlighted. Imagine what can be learned! Unfortunately, however, a lot of software is still relatively static, offering little more than a computerized version of what is possible on the printed page. In contrast, we see the dynamic aspect of good visualization software as critical to the detective work of EDA, which relies on an unfolding, rather than preplanned, set of steps.
Visualization remains an active area of research, particularly when data volumes are high,12 but there are already many new, useful graphical displays. For example, the parallel coordinates plots used for visualizing data with many columns are well known within the visualization community, but have not yet spread widely into the Six Sigma world.13
Additionally, although there are established principles about the correct ways to represent data graphically, the fact that two individuals will perceive patterns differently means that good software should present a wide repertoire of representations, ideally all dynamically linked with one another.14 We hope to demonstrate through the case studies that this comprehensive dynamic linking is a powerful capability for hypothesis generation. To emphasize this desirable aspect, from now on, we will refer to dynamic visualization, rather than simply visualization.
Not only does dynamic visualization support EDA when data volumes are large, but it is also our experience that dynamic visualization is very powerful when data volumes are modest. For instance, if the distributions of two or more variables are linked together, you can quickly and easily see the balance of the data, that is, which values or levels of one variable occur with those of another. If the data are perfectly balanced, then tabulation may also provide the same insight, but if the data are only nearly balanced or if they are unbalanced, as is more often the case, the linked distributions will usually be much more easily interpreted. With dynamic visualization, we can assess many views of the data quickly and efficiently.
The mention of large data volumes inevitably raises the topic of data mining. This is a rapidly moving field, so a precise definition is difficult. Essentially, data mining (also known as predictive analytics) is the process of sorting through large amounts of data and picking out relevant information using techniques from machine learning and statistics.15 In many cases, the data are split into at least two sets, and a model is built using one set, then validated or tested on the second set. Once the model is built, it is used to score new data as they arrive, thereby making (hopefully) useful predictions.
As with traditional statistical analysis, there are several processes that you can use in data mining.16 In most data-mining applications, the software used automates each step in the process, usually involving some prescribed stopping rule to determine when there is no further structure in the data to model. As such, many data-mining efforts have a strong flavor of CDA. However, EDA can bring high value to data-mining applications, especially in Six Sigma settings. In our case studies, we will see two such applications.
VISUAL SIX SIGMA: STRATEGIES, PROCESS, ROADMAP, AND GUIDELINES
In this section, we will explore the three strategies that underlie Visual Six Sigma. We then present the Visual Six Sigma Data Analysis Process that supports these strategies through six steps and define the Visual Six Sigma Roadmap that expands on three of the key steps. This section closes with guidelines that help you assess your performance as a Visual Six Sigma practitioner.
Visual Six Sigma Strategies
As mentioned earlier, Visual Six Sigma exploits the following three key strategies to support the goal of managing variation in relation to performance requirements:
- Using dynamic visualization to literally see the sources of variation in your data
- Using exploratory data analysis techniques to identify key drivers and models, especially for situations with many variables
- Using confirmatory statistical methods only when the conclusions are not obvious
Note that with reference to the section “Variation and Statistics,” Strategy 1 falls within what was called EDA, or statistics as detective. Strategy 3 falls within what we defined as CDA, or statistics as lawyer. Strategy 2 has aspects of both EDA and CDA.
Earlier, we stressed that by working in the EDA mode of statistics as detective we have to give up the possibility of a neat conceptual and analytical framework. Rather, the proper analysis of our data has to be driven by a set of informal rules or heuristics that allow us to make new, useful discoveries. However, there are still some useful principles that can guide us. Jeroen de Mast and Albert Trip offer an excellent articulation and positioning of these principles in the Six Sigma context.17 Unsurprisingly, these principles are applicable within Visual Six Sigma and appear in a modified form in the Visual Six Sigma Roadmap presented later (Exhibit 2.4).
If you recall from Chapter 1, one of the goals of Visual Six Sigma is to equip users who know their business with some simple ideas and tools to get from data to decisions easily and quickly. Indeed, we would argue that the only prerequisite for a useful analysis, other than having high-quality data, is knowledge of what the different variables that are being analyzed actually represent. We cannot emphasize strongly enough this need for contextual knowledge to guide interpretation; it is not surprising that this is one of the key principles listed by de Mast and Trip.
As mentioned earlier, a motivating factor for this book is our conviction that the balance in emphasis between EDA and CDA in Six Sigma is not always correct. Yet another motivation for this book is to address the perception that a team must strictly adhere to the phases of DMAIC, even when the data or problem context does not warrant doing so. The use of the three key Visual Six Sigma strategies provides the opportunity to reengineer the process of going from data to decisions. In part, this is accomplished by freeing you, the practitioner, from the need to conduct unnecessary analyses.
Visual Six Sigma Data Analysis Process
We have found the simple process shown in Exhibit 2.3 to be effective in many real-world situations. We refer to this in the remainder of the book as the Visual Six Sigma (VSS) Data Analysis Process.
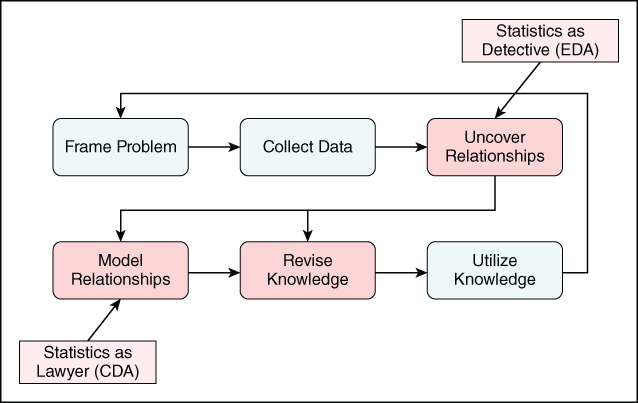
Exhibit 2.3 Visual Six Sigma Data Analysis Process
This process gives rise to the subtitle of this book, Making Data Analysis Lean. As the exhibit shows, it may not always be necessary to engage in the “Model Relationships” activity. This is reflective of the third Visual Six Sigma strategy. An acid test for a Six Sigma practitioner is to ask, “If I did have a model of Ys against Xs from CDA, how would it change my recommended actions for the business?”
The steps in the VSS Data Analysis Process may be briefly described as follows:
- Frame Problem. Identify the specific failure to produce what is required (see prior section titled “Measurements”). Identify your general strategy for improvement, estimate the time and resources needed, and calculate the likely benefit if you succeed. Identify the Y or Ys of interest.
- Collect Data. Identify potential Xs using techniques such as brainstorming, process maps, data mining, failure modes and effects analysis (FMEA), and subject matter knowledge. Passively or actively collect data that relate these to the Ys of interest.
- Uncover Relationships. Assess your data's strengths, weaknesses, and relevance to your problem. Using exploratory tools and your understanding of the data context, generate hypotheses and explore whether and how the Xs relate to the Ys.
- Model Relationships. Build statistical models relating the Xs to the Ys. Determine statistically which Xs explain variation in the Ys and may represent causal factors.
- Revise Knowledge. Optimize settings of the Xs to give the best values for the Ys. Explore the distribution of Ys as the Xs are allowed to shift a little from their optimal settings. Collect new data to verify that the improvement is real.
- Utilize Knowledge. Implement the improvement and monitor or review the Ys with an appropriate frequency to see that the improvement is maintained.
Visual Six Sigma Roadmap: Uncover Relationships, Model Relationships, and Revise Knowledge
In this section, we expand on the three steps in the VSS Data Analysis Process that benefit the most from the power of visual methods: Uncover Relationships, Model Relationships, and Revise Knowledge. These activities are reflective of where we see the biggest opportunities for removing waste from the process of going from data to decisions.
The Visual Six Sigma Roadmap in Exhibit 2.4 guides you through these three important steps. Given that the displays used for visualization and discovery depend upon your own perceptive and cognitive style, the Visual Six Sigma Roadmap focuses on the goal, or the what, of each step. However, in Chapter 3, we will make specific suggestions about how each step can be accomplished using JMP.
Exhibit 2.4 The Visual Six Sigma Roadmap: What We Do
| Visual Six Sigma Roadmap—What We Do |
| Uncover Relationships |
| Dynamically visualize the variables one at a time |
| Dynamically visualize the variables two at a time |
| Dynamically visualize the variables more than two at a time |
| Visually determine the Hot Xs that affect variation in the Ys |
| Model Relationships |
| For each Y, identify the Hot Xs to include in the signal function |
| Model Y as a function of the Hot Xs; check the noise function |
| If needed, revise the model |
| If required, return to the Collect Data step and use DOE |
| Revise Knowledge |
| Identify the best Hot X settings |
| Visualize the effect on the Ys should these Hot X settings vary |
| Verify improvement using a pilot study or confirmation trials |
This Roadmap uses the Six Sigma convention that a variable is usually assigned to a Y role (an outcome or effect of interest) or to an X role (a possible cause that may influence a Y). The phrase Hot X in Exhibit 2.4 relates to the fact that according to the available data this variable really does appear to have an impact on the Y of interest. Of course, in order to make such a determination, this X variable must have been included in your initial picture of how the process operates. Those X variables that are not Hot Xs, in spite of prior expectations, can be thought of as being moved into the noise function for that Y. Other terms for Hot X are Red X and Vital X. Whatever terminology is used, it is important to understand that for any given Y, there may be more than one X that has an impact, and, in such cases, it is important to understand the joint impact of these Xs.
Note that, although the designations of Y or X for a particular variable are useful, whether a variable is a Y or an X depends both on how the problem is framed and on the stage of the analysis. Processes are often modeled as both serial (a set of connected steps) and hierarchical (an ordered grouping of levels of steps, where one step at a higher level comprises a series of steps at a lower level). Indeed, one of the tough choices to be made in the Frame Problem step (Exhibit 2.3) is to decide on an appropriate level of detail and granularity for usefully modeling the process. Even when a manufacturing process is only moderately complex, it is often necessary to use a divide-and-conquer approach in process and product improvement and design projects, which are often subdivided into pieces that reflect how the final product is made and operates. In transactional situations, modeling the process is usually more straightforward.
Uncover Relationships and Model Relationships
Earlier, we used the phrase “data of high quality.” Although data cleansing is often presented as an initial step prior to any data analysis, we feel that it is better to include this vital activity as part of the Uncover and Model Relationships steps (Exhibit 2.3), particularly when there are large numbers of variables. For example, it is perfectly possible to have a multivariate outlier that is not outlying in any single variable. Therefore the assessment of data quality and any required remedial action is understood to be woven into the Visual Six Sigma Roadmap. Chapter 4, “Managing Data and Data Quality,” shows some examples.
The Uncover and Model Relationships steps also require a sound understanding and validation of the measurement process for each variable in your data. You can address measurement process variation using a Gauge Repeatability and Reproducibility (Gauge R&R) study or a Measurement System Analysis (MSA) study. Whatever your approach, addressing measurement variability is critically important. It is only when you understand the pattern of variation resulting from repeatedly measuring the same item that you can correctly interpret the pattern of variation when you measure different items of that type.18
In many ways, an MSA is best seen as an application of DOE to a measurement process, and properly the subject of a Visual Six Sigma effort of its own. To generalize, we would say that:
- In a transactional environment, the conventional MSA is often too sophisticated.
- In a manufacturing environment, the conventional MSA is often not sophisticated enough.
As an example of the second point: If the process to measure a small feature is automated, involving robot handling and vision systems, then the two Rs in Gauge R&R (corresponding to repeatability and reproducibility variation) may not be of interest. Instead we may be concerned with the variation when the robot loads and orients the part, when the camera tracks to supposedly fixed locations, and when the laser scans in a given pattern to examine the feature.
Revise Knowledge
The Revise Knowledge activity is where we integrate what we have learned in the Uncover Relationships and possibly the Model Relationships steps with what we already know. There are many aspects to this, and most of them are particular to the specific context.
Regardless, one of the vital tasks associated with the Revise Knowledge step is to consider how, or if, our new findings will generalize. Note that Step 4 in Model Relationships already alerts us to this kind of problem, but this represents an extreme case.
Perhaps unsurprisingly, the best way to tackle this issue is to collect additional, new data via confirmatory runs to check how these fit with what we now expect. This is particularly important when we have changed the settings of the Hot Xs to achieve what appear to be better outcomes. As we acquire and investigate more and more data under the new settings, we have more and more assurance that we did indeed make a real improvement. Many businesses develop elaborate protocols to manage the risk of making such changes. Although there are some statistical aspects, there are at least as many contextual ones, so it is difficult to give general guidance.
In any case, confirmatory runs, no matter how they are chosen, are an expression of the fact that learning should be cumulative. Assuming that the performance gap continues to justify it, the continued application of the VSS Data Analysis Process (Exhibit 2.3) gives us the possibility of a virtuous circle.
Guidelines
Finally, the following are some guidelines that may help you as a practitioner of Visual Six Sigma:
- Customer requirements of your process or product should establish the context and objectives for all the analyses you conduct.
- These objectives can always be rephrased in terms of the identification, control, reduction, and/or anticipation of sources of variation.
- If you do not measure it, then you are guessing.
- If you do not know the operational definition of your measurement or the capability of your measurement process, then you are still guessing.
- If you spend more time accessing and integrating data than with Visual Six Sigma, then your information system needs to be carefully examined.
- The choice of which variables and observational units to include in constructing a set of data should be driven by your current process or product understanding and the objectives that have been set.
- Given that you have made such a choice, you need to be concerned about how your findings are likely to generalize to other similar situations.
- Any analysis that ignores business and contextual information and tries to just manipulate numbers will always fail.
- Any data set has information that can be revealed by dynamic visualization.
- Models can be used to make predictions, but a useful prediction need not involve a formal model.
- All models are wrong, but some are useful.
- The more sophisticated the model you build, the more opportunity for error in constructing it.
- If you cannot communicate your findings readily to business stakeholders, then you have failed.
- If the course of action is not influenced by your findings, then the analysis was pointless.
CONCLUSION
In this chapter, we have given an overview of Six Sigma and Visual Six Sigma. The “Six Sigma” section presented our definition of Six Sigma as the management of variation in relation to performance requirements, and briefly described some wider aspects of Six Sigma. The section “Variation and Statistics” emphasized the key role of statistics as detective, namely, EDA. The next section dealt briefly with dynamic visualization as a prerequisite for successful detective work while the section “Visual Six Sigma: Strategies, Process, Roadmap, and Guidelines” aimed to summarize the three key strategies and the process that will allow you to solve data mysteries more quickly and with less effort. Through the Visual Six Sigma Data Analysis Process and the Visual Six Sigma Roadmap, the application of these strategies will be illustrated in the case studies.
Chapter 3 aims to familiarize you a little with JMP, the enabling technology we use for Visual Six Sigma. Its purpose is to equip you to follow the JMP usage in the Visual Six Sigma case studies that form the heart of this book. With the background in Chapter 3 and the step-by-step details given in the case studies, you will be able to work through the case study chapters, reproducing the appropriate graphs and reports. Maybe you will even venture beyond these analyses to discover new knowledge on your own! In any case, you will learn to use a large repertoire of techniques that you can then apply to your own data and projects.