Appendix to Chapter 9

GENERATING NORM MAPS IN
THE DEMOGRAPHIC COORDINATION GAME

 

 

ONE NATURAL research question is this: What happens if, keeping everything else (movement, space, cloning) as is, we simply change the payoff structure from PD to the symmetric two-person coordination game? Does the demographic variant produce an outcome different from both one-shot rational play and the replicator dynamics? The answer is, again, yes.

For expository purposes, assume the payoff matrix below:

	Left	Right
Left	1	–3
Right	–3	1

We imagine two drivers approaching one another on a road. If each drives on his left, they pass without incident, whereas a failure to coordinate in this sense eventuates in a collision, and negative payoff. The pure strategy pairs—(L, L) and (R, R)—are both Nash equilibria. Traditional game theory does not offer a compelling account of how either is attained in populations of interacting agents.¹ Hence, as before, we turn to evolutionary game theory.

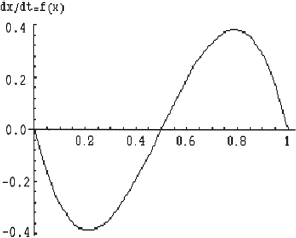
Figure 9.A.1. Replicator dynamics phase portrait for coordination game.

Run 9.A.1. Evolution of norm maps in the demographic coordination game.

The phase diagram for the replicator dynamics, assuming the payoff matrix above, is shown in figure 9.A.1.

There are three equilibria: 0, 1/2, and 1. Since df/dx > 0 at the interior equilibrium and is strictly negative at 0 and 1, we see that the interior equilibrium is unstable, and the coordination equilibria are attractors. Hence, the replicator dynamics predicts convergence to either zero (everyone driving on the left) or one (everyone driving on the right).

In the demographic variant, however, we find quite a different result: spatial maps divided into connected regions within each of which a specific norm prevails, with “accidents” on the region boundaries. A full animation is provided on the CD. The frames shown in run 1, however, are typical.

Agents are, of course, colored by their norm. Events progress from an initial random distribution (frame 1) to a spatial map of the sort described above (frame 3).

To generate norm maps of this sort using the CD, open the Prisoners Dilemma Ascape applet.² When the Ascape Control Bar appears, click on the Globe icon (for global variables) and a dialog box will pop up. In it, change Death Age to 1000, Mutation Rate to 0.0, and the Payoffs to [1, – 3, – 3, 1]. Leave all other settings at their default values. Then click Done, and restart the model. You are unlikely to get the exact run captured here, because Ascape uses a new random seed for every run. But they should agree qualitatively, generating spatial norm maps with accidents on the boundaries.

REFERENCE

Young, H. P. The Economics of Convention. 1996. Journal of Economic Perspectives 10(2): 105–322.

---

¹ Young (1996) offers an elegant account using Best Reply to Recent Sample Evidence. However, as noted (somewhat self-critically) in the prelude to chapter 10, this learning scheme does assume that agents continue sampling long after a norm is firmly entrenched.

² See the Read Me file on the CD for further details