Chapter 3
NON-EXPLANATORY EQUILIBRIA: AN EXTREMELY
SIMPLE GAME WITH (MOSTLY) UNATTAINABLE
FIXED POINTS
JOSHUA M. EPSTEIN AND ROSS A. HAMMOND*
EQUILIBRIUM ANALYSIS PERVADES mathematical social science. This paper calls into question the explanatory significance of equilibrium by offering an extremely simple game, most of whose equilibria are unattainable in principle from any of its initial conditions. Moreover, the number of computation steps required to reach those (few) equilibria that are attainable is shown to grow exponentially with the number of players—making long-run equilibrium a poor predictor of the game's observed state. The paper also poses a number of combinatorially challenging problems raised by the game.
Much of game theory and mathematical economics is concerned with equilibria (see Kreps 1990, 405). Nash equilibrium is an important example. Indeed, in many quarters, “explaining an observed social pattern” is understood to mean “demonstrating that it is the Nash equilibrium of some game.” But, there is no explanatory significance to an equilibrium that is unattainable in principle. And there is debatable significance to equilibria that are attainable only on astronomical time scales. Yet, in a great many instances, the social pattern to be explained is simply shown to be an equilibrium. The questions, “Is the equilibrium attainable?” and “On what time scale is it attainable?” are not raised.
There is a literature on unattainability—or uncomputability—of equilibria, undecidability in games, and related topics. But it is quite technical.1 This article contributes an extremely simple game—easily played by school children—that drives home the core distinction between attainable and unattainable equilibria. Indeed, the overwhelming preponderance of this game's equilibria are unattainable from any initial configuration of the game.
We hope this arresting example stimulates skepticism about the explanatory significance of equilibrium.2 As we will show, the game—despite its surface simplicity—also raises a number of combinatorially very challenging questions.
DESCRIPTION OF THE GAME
The game's ingredients are few and simple:
1. Events transpire on a linear array of sites, extending from an origin (the leftmost site) to the right.
2. Agents are numbered consecutively from 1 to n. These numbers do not change in the course of the game.
3. Initially, we require that agents be arrayed in a contiguous row, beginning at the origin, in some arbitrary order. Figure 3.1 gives one such admissible initial configuration for three agents. Each agent is represented as a number, and each empty site is represented as an asterisk.
Figure 3.1. An initial three-agent configuration.
4. The agents’ only rule of behavior is as follows:
AGENT RULE: If there is a lower-numbered agent anywhere to your right, go to the head of the line (the site immediately to the right of the rightmost agent). Otherwise, remain in place.
The rule is reminiscent of the Schelling segregation model (1971, 1978) and the variant of Young (1998).3 In each case, agents have some preference for immediate neighbors. In our case, agents hate living anywhere with a lower numbered agent to their right. And (with bounded rationality) they move to the one site that is certain to remove the problem, at least in the immediate term—the front site.
5. In any given round, agents are queried in descending order from the highest number.4 As we shall see below, not all agents may wish to move. The first agent who does wish to move does so, resulting in a new configuration. That ends the round. Play continues until equilibrium is reached, where:
6. An equilibrium is a configuration from which no agent would move further under the rule. It is a fixed point. An equilibrium is termed attainable if there is some initial configuration (see under item 3) from which it can be attained. An unattainable equilibrium is an equilibrium for which no such initial configuration exists.
That is the complete model specification.
CHILD'S PLAY
One can imagine the model as a children's game, played on a linear sequence of hopscotch squares. Assume the kids differ by height. They form a line extending out from the school wall into the playground, one in front of the next, in some random order by height. Then they move, as specified under item 5 above, each according to the simple rule: If there's a shorter kid anywhere in front of you, jump to the very head of the line (the square immediately in front of the front kid). Otherwise, remain in place.
The game ends when equilibrium is attained—when no kid would move further under the rule.5 (This equilibrium notion is Nash-like: no agent has any incentive to unilaterally depart under the rule.)
A NUMERICAL EXAMPLE
As a simple illustration of how the configurations progress, let us walk the game forward from the figure 3.1 configuration (see table 3.1).
TABLE 3.1
A Complete Game
| Configuration Number | Configuration |
| 1 | 3 2 1 * * * |
| 2 | * 2 1 3 * * |
| 3 | * * 1 3 2 * |
| 4 | * * 1 * 2 3 |
Starting in Configuration 1, agent “3” (the highest numbered) is queried first. Since there is a lower numbered agent to her right, she jumps to the head of the line, leaving a space in her former position—yielding Configuration 2. That ends the round. So, we begin a new round. As before, we query agent “3” (the highest numbered) first. This time, she declines to change position. So, we query the next highest numbered agent: “2”. Since there is a lower numbered agent to her right, she now jumps to the head of the line, leaving a space in her former spot—yielding Configuration 3. This, of course, “upsets” agent 3, who moves when queried at the beginning of the next round, generating Configuration 4. In Configuration 4, agent 3 does not wish to move, so agent 2 is queried. She declines, so agent 1 is (at last) queried, but declines as well (as the lowest numbered agent always does). Configuration 4 is therefore an equilibrium. It is obviously attainable. Notice that it requires 6 spaces in total.
SPACE AND TIME REQUIREMENTS FOR ATTAINABLE EQUILIBRIA
For n agents, how many spaces are required to ensure enough space for all attainable equilibria? Perhaps surprisingly, the answer is
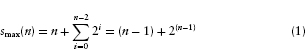
This space requirement grows exponentially in n. Values of smax(n), for various n values are given in table 3.2.
Regarding time (i.e., number of computation steps), the equilibrium of table 3.1 required 3 rounds to compute, from the initial configuration 321***. In general, equilibria occupying smax (n) (as in Equation 1) spaces will be obtainable in smax(n) – n rounds, which, quite notably, is also exponential in n. Daunting numerical examples are left to the reader.
TABLE 3.2
Maximum Space Requirements for All Attainable Equilibria, Various n
| n | Sites |
| 3 | 6 |
| 4 | 11 |
| 5 | 20 |
| 20 | 524,307 |
| 25 | 16,777,240 |
| 30 | 5.37 × 108 |
| 50 | 5.63 × 1014 |
| 100 | 6.34 × 1029 |
As prosaic examples with kids, assume each hopscotch square is 2 feet deep and that the games begin on a playground in Cambridge, Massachusetts. Then, for 20 kids (an average kindergarten class), there are initial line-ups such that, when (after 524,287 moves) equilibrium is attained, the tallest kid is standing in Central Park. For 25 kids, there are initial line-ups such that, when (after about 17 million moves) equilibrium is attained the tallest kid is standing in Tokyo. For 30 kids, there are initial line-ups such that, when (after more than 500 million moves) equilibrium is attained, the tallest kid has circumnavigated the earth 10 times. For 50 players, there are attainable equilibria extending over roughly 563 trillion sites. And for games involving 100 agents—a standard population size in the literature of n-person games and agent-based models—even the set of attainable equilibria is uncomputable on all practical time scales. And, in fact, most equilibria are unattainable in principle.
ATTAINABLE EQUILIBRIA
A full treatment of the n = 3 case will be instructive. There are 3! acceptable initial configurations, and 5 distinct attainable equilibria, as shown in table 3.3. Notice that the equilibrium **1*23 is attainable from the initial configurations: 231*** and 321***. In general, a given attainable equilibrium may be attainable from multiple initial configurations.6
TABLE 3.3
The 5 Attainable Equilibria for n = 3
| Initial Configuration | Resulting Equilibrium |
| 1 2 3 * * * | 1 2 3 * * * |
| 1 3 2 * * * | 1 * 2 3 * * |
| 2 3 1 * * * | * * 1 * 2 3 |
| 2 1 3 * * * | * 1 * 2 3 * |
| 3 1 2 * * * | * 1 2 3 * * |
| 3 2 1 * * * | * * 1 * 2 3 |
UNATTAINABLE EQUILIBRIA
While (as shown in table 3.3) there are 5 distinct attainable equilibria for the n = 3 case, there are 20 equilibria in total (see eq. 2). Ipso facto, there are 15 unattainable equilibria! They are listed in table 3.4. In each of these configurations, every agent is happy with her immediate neighborhood, but none of these configurations are attainable from any initial configuration.
For n = 3, then, unattainability is the norm among equilibria. This pattern only gets more dramatic as n increases. Indeed, the ratio of attainable to unattainable equilibria approaches zero very quickly. For n = 4, there are 330 equilibria, of which 12 are attainable, a mere 4%.
TABLE 3.4
The 15 Unattainable Equilibria for n = 3
| 1. | 1 * 2 * * 3 |
| 2. | * 1 2 * * 3 |
| 3. | 1 * * 2 * 3 |
| 4. | * 1 * 2 * 3 |
| 5. | * * 1 2 * 3 |
| 6. | 1 * * * 2 3 |
| 7. | * 1 * * 2 3 |
| 8. | * * * 1 2 3 |
| 9. | 1 2 * 3 * * |
| 10. | 1 2 * * 3 * |
| 11. | 1 * 2 * 3 * |
| 12. | * 1 2 * 3 * |
| 13. | 1 * * 2 3 * |
| 14. | 1 2 * * * 3 |
| 15. | * * 1 2 3 * |
For n = 5, there are 15,504 equilibria, of which 41 are attainable, or 0.2%. For n > 5, the attainable percentage is effectively zero.
The formula for the total number of equilibria, T(n), even for the n = 4 case, turns out to be quite complex:
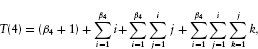
where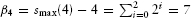 
.7 For n agents, the appropriate generalization is as follows. First, the index variables will run from v1 to vn–1. Then,
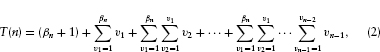
where ßn = smax(n) – n =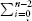 
2i, as before.
Now, for n agents, the number of distinct initial configurations is n!, but the number of attainable equilibria is less than n! (as illustrated in table 3.4). Hence, the fraction of attainable to total is bounded above by n!/[T(n)]. Since n!/[T(n)] → 0 extremely fast, so does the fraction of attainables. Hence the generic equilibrium is, in fact, unattainable from any initial conditions.8
Clearly, restricting the space of permissible initial configurations is important to this result. While at first glance, such restrictions may seem artificial, they are the norm in games and contests generally. Chess, checkers, and many other board games possess required initial set-ups. Straight pool, 9-Ball, and 8-Ball (stripes and solids) each begin with the billiard balls “racked” in a specified way. In racquet sports, such as tennis, squash, and ping-pong, players are not permitted to serve (i.e., begin a point) from “just anywhere.” Football prohibits certain lineups and allows others. Jousts and pistol duels had highly stylized initial positions, as do fencing matches. Further examples will come readily to mind. Indeed, on reflection, some restriction on initial configurations would seem to be the rule across formalized contests, rather than the exception. In this light, our restriction seems natural enough.
EQUILIBRIUM AND EXPLANATION
Here, then, is an extremely simple playground game that admits a huge number of equilibria, virtually all of which are not attainable from any initial configuration, once there are 5 or more players. So, returning to the central issue of explanatory significance, imagine being a theoretical playgroundologist. Your colleagues, the empirical playgroundologists, have documented a powerful regularity: They observe kids all over the world lined up from shortest to tallest on playgrounds; they are spaced in all sorts of bizarre ways, but they're lined up in order by height. What is the explanation? This is the central empirical puzzle of playgroundology.
Now, given an analogous empirical regularity, the standard and ostensibly explanatory practice in the formal social sciences is as follows: Provide a game for which the observed regularity is an equilibrium.
But, this is easily done for playgroundology—the game we've just been exploring fits the bill. Any line-up from shortest to tallest observed by our empiricists in the field will, indeed, be an equilibrium of this game. As we have shown, however, it will almost certainly not be attainable: kids could not have arrived there from any initial line-up. Clearly, then, the rules of this particular game are supremely unlikely to be those followed on real playgrounds.
Nonetheless, under the standard practice above, these rules would be regarded as explanatory! This seems unsatisfactory for playgroundology because the generic equilibrium of the game is not attainable even in principle, much less on time scales of any plausibility. So why, absent demonstrations of attainability, should the same practice be accepted as explanatory in social science? We believe it should not be.
An acceptable notion of “explanation” should include attainability. A candidate is the generative notion advanced in Epstein 1999, in which a set of individual rules, a microspecification, is regarded as explanatory only if it suffices to generate the observed regularity—incorporating the requirement of attainability.
Beyond its explanatory shortcomings, equilibrium may be a bad predictor of observed configurations.9 Obviously, unattainable equilibria (because they will never be observed) are not predictive of the game's state on any time scale. However, even attainable equilibria (given the exponential time complexity of the process) are, in almost all cases, poor predictors on time scales of any interest to humans.
CONCLUSION
For the social sciences more broadly, there would appear to be two lessons of this simple exercise. First, implicit claims that equilibrium analysis is explanatory or predictive should be challenged and require the most careful defense. Second, a successful defense of any such claims must include a demonstration of attainability, on time scales of interest, by agents employing plausible rules.10
APPENDIX: FURTHER COMBINATORIAL QUESTIONS
Although the playground game was contrived as a stark illustration of these points, it happens to raise a number of interesting combinatorial questions.
Garden of Eden Configurations
First, by way of definition, if there exists no previous configuration from which a given configuration can be attained, then the latter is termed a Garden of Eden (GE) configuration.11 For example, the following configuration is GE:
*1*2*3
If 3 had been located anywhere to the left of 2 (or 1), it would have jumped to the site immediately to 2's right, not to the position shown. This is both an equilibrium and a GE state.
We know that there are unattainable equilibria (i.e., unattainable from any admissible initial configurations). Now, for many of these, there are prior configurations. So, beginning with such an unattainable equilibrium, if we back calculate, we must stop short of the origin (i.e., the set of permissible initial configurations) since otherwise the equilibrium would have been attainable. Where we stop must therefore be a Garden of Eden configuration! Hence, we have the following proposition:
Proposition: For every non-GE unattainable equilibrium, there exists (at least one) GE non-equilibrium preceding configuration.
For example, consider the string: 1**23*. It is an equilibrium, but it is not attainable from any permitted initial condition. The non-equilibrium configurations from which it is derivable, however, are the following: 1*32** and 13*2**, both of which are GE, since neither one has a predecessor that could occur initially.
The set of GE configurations from which a given configuration is attainable shall be referred to as its basin of attraction. Naturally, this suggests the following (evidently hard) question: For any equilibrium configuration not attainable from an initial configuration, determine its basin of attraction, or since all initial conditions are themselves GE, the general problem is simply:
Problem 1. For any equilibrium (attainable or not), determine its basin of attraction.
In pondering the computational complexity of this general problem, bear in mind that even for n = 50 players there are many unattainable equilibria consuming 563 trillion sites—in general, smax(n) sites.
For the sake of completeness, it would be of further interest to solve the following:
Problem 2. From each “point” of a given equilibrium's basin, how many computation steps are required to attain the equilibrium?
REFERENCES
Epstein, Joshua M. 1999. Agent-Based Computational Models and Generative Social Science. Complexity 4(5): 41-60.
Foster, Dean P., and H. Peyton Young. 2001. On the Impossibility of Predicting the Behavior of Rational Agents. Proceedings of the National Academy of Sciences 98(22): 12848-53.
Jordan, J. S. 1993. Three Problems in Learning Mixed-Strategy Equilibria. Games and Economic Behavior 5:368-86.
Kreps, David M. 1990. A Course in Microeconomic Theory. Princeton: Princeton University Press.
Moore, E. F. 1962. Machine Models of Self-Reproduction. In Mathematical Problems in the Biological Sciences. Proceedings of Symposia in Applied Mathematics, 14. Providence, RI: American Mathematical Society.
Nachbar, J. H. 1997. Prediction, Optimization, and Learning in Games. Econometrica 65:275-309.
Prasad, Kislaya. 1997. On the Computability of Nash Equilibria. Journal of Economic Dynamics and Control 21:943-53.
Saari, Donald G., and Carl P. Simon. 1978. Effective Price Mechanisms. Econometrica 50:1097-1125.
Schelling, Thomas C. 1971. Dynamic Models of Segregation. Journal of Mathematical Sociology 1:143-86.
——. 1978. Micromotives and Macrobehavior. New York: Norton.
Simon, Herbert A. 1982. Models of Bounded Rationality. Vol. 1. Cambridge: MIT Press.
Skyrms, Brian. 1997. Chaos and the Explanatory Significance of Equilibrium: Strange Attractors in Evolutionary Game Dynamics. In The Dynamics of Norms, ed. Cristina Bicchieri, Richard Jeffrey, and Brian Skyrms. New York: Cambridge University Press.
Toffoli, Tommaso, and Norman Margolus. 1987. Cellular Automata Machines: A New Environment for Modeling. Cambridge: MIT Press.
Wolfram, Stephen, ed. 1986. Theory and Applications of Cellular Automata. Singapore: World Scientific.
Young, H. Peyton. 1998. Individual Strategy and Social Structure: An Evolutionary Theory of Institutions. Princeton: Princeton University Press.
* Joshua M. Epstein: Economic Studies Program, The Brookings Institution, Washington, DC and External Faculty, Santa Fe Institute, Santa Fe, New Mexico; Ross A. Hammond: Department of Political Science, University of Michigan, Ann Arbor, Michigan.
For insightful comments, the authors thank Robert Axelrod, Robert Axtell, Jim Crutchfield, William Dickens, Samuel David Epstein, John Miller, Scott Page, Duncan Watts, and Peyton Young. This research was conducted at the Brookings Institution—Johns Hopkins University Center on Social and Economic Dynamics.
This essay was previously published in Complexity 7(4): 18-22.
1 See, for example, Foster and Young 2001; Saari and Simon 1978; Prasad 1997; Jordan 1993; and Nachbar 1997.
2 For an insightful discussion of this issue in the context of chaos and evolutionary games, see Skyrms 1997.
3 Note, however, that the model is not a cellular automaton, because it involves a nonlocal operation (agents go to the head of the line and are queried in sequence order). We thank Jim Crutchfield for this observation. On cellular automata, see Wolfram 1986; and Toffoli and Margolus 1987.
4 This sentence is revised from the original 2002 version, which may have suggested, wrongly, that all agents are queried in each round. See also the appendix to this chapter.
5 In effect, the kids have invented a type of decentralized (albeit highly inefficient) sorting algorithm.
6 In this connection, the reader might find it interesting to consider the following general problem: Give a formula, f(n), for the number of distinct equilibria attainable from the n! distinct initial configurations of the n-agent game.
7 A closed form representation of the result would obscure the iterative nature of the solution. Hence, the iterated summations shown.
8 Whether or not an equilibrium can be easily diagnosed as unattainable is beside the point we are making here. But, to discuss this briefly, some cases are clear on inspection. For example, the equilibrium ***123 is unattainable, because the digit “1” never moves (as noted earlier) and appears too far to the right to be permissible initially. Similarly, the equilibrium *1*2*3 can be easily identified as a Garden of Eden configuration (see below) and is therefore not attainable. However, some cases are not so obvious: **123* is unattainable. Now, in principle, one can classify equilibria as unattainable by brute force. For each of the n! initial conditions, one simply grinds out the attainable equilibria. Then, for any candidate equilibrium, one “simply” checks—by bitwise comparison—whether it is in the list of attainables or not. However, the number of required comparisons grows exponentially in n. Mechanical “space counting” tests for unattainability, although more direct, nonetheless require inspection of ßn sites, and will be computationally prohibitive in practice for agent populations of any significance.
9 Explanation and prediction are different matters: plate tectonics explains earthquakes but does not predict when they will occur. Similarly, electrostatics explains lightning, but does not predict where it will strike.
10 By plausible rules, we have in mind those involving bounded information and bounded individual computing capacity. See Simon 1982.
11 According to E. F. Moore (1962), this term was first suggested by John Tukey.