Economic Theory and Causal Inference
1 Reductionist and Structuralist Accounts of Causality
Economists have intermittently concerned themselves with causality at least since David Hume in the 18th century. Hume is the touchstone for all subsequent philosophical analyses of causality. He is frequently regarded as a causal skeptic; yet, as an economist, he put a high priority on causal knowledge.1 In “On Interest” [Hume, 1754, p. 304], one of his justly famous economic essays, he writes:
it is of consequence to know the principle whence any phenomenon arises, and to distinguish between a cause and a concomitant effect …nothing can be of more use than to improve, by practice, the method of reasoning on these subjects
The utility of causal knowledge in economics is captured in Hume’s conception of what it is to be a cause: “we may define a cause to be an object, followed by another, …where, if the first had not been, the second never had existed” [Hume, 1777, p. 62]. Causal knowledge lays the groundwork for counterfactual analyses that underwrite economic and political policy judgments.
At least two questions remain open: first, what exactly are causes “in the objects” [Hume, 1739. p. 165]? second, how can we infer them from experience? Hume answers the first question by observing that the idea of cause comprises spatial contiguity of cause to effect, temporal precedence of cause over effect, and necessary connection between cause and effect. Necessary connection “is of much greater importance” then the other two elements [Hume, 1739, p. 77]. Necessary connection is the basis for practical counterfactual analysis.
Hume answers the second question by pointing out that contiguity and temporal precedence are given in experience, but that no experience corresponds to the notion of necessary connection. Since Hume famously believed that all knowledge is either logical and mathematical or empirical, the failure to find an a priori or an empirical provenance for the idea of necessary connection provides the basis for the view that Hume is a causal skeptic.
According to Hume, the closest that we can come to an empirical provenance for the idea of necessary connection is the habit of mind that develops when two objects or events are constantly conjoined. Unfortunately, constant conjunction is too weak a reed to support a satisfactory account of the connection between causal knowledge and counterfactual analysis — however practically important Hume deemed the latter.
After Hume, the dominant strategy in the analysis of causality has been reductive. Its objects are, first, to define causes in terms of something less mysterious with the object of eliminating causality as a basic ontological category and, second, to provide a purely empirically grounded mode of causal inference. An important modern example is found in Patrick Suppes [1970] probabilistic theory of causality. For Suppes, A prima facie causes B, if the probability of B conditional on A is higher than the unconditional probability of B (P(B|A) > P(B)). The type of empirical evidence that warrants calling one thing the cause of another becomes, in this approach, the meaning of cause: the ontological collapses to the inferential.
Such approaches are not successful. As Suppes and others realized, the concept of cause must be elaborated in order to capture ordinary understandings of its meaning. For example, cause is asymmetrical: if A causes B, B does not (in general) cause A. It is easy to prove that if A is a prima facie cause of B, then B is a prima facie cause of A.2 Asymmetry can be restored by the Humean device of requiring causes to occur before their effects: P(Bt+1|At) > P(Bt+1) does not imply P(At+1|Bt) > P(At+1).
Another standard counterexample to prima facie cause as an adequate rendering of cause simpliciter is found in the correlation between a falling barometer and the onset of a storm. Although these fulfill the conditions for prima facie cause, we are loath to say that the barometer causes the storm. The standard device for avoiding this conclusion is to say the barometer will not be regarded as a cause of the storm if some other variable — say, falling air pressure — screens off the correlation between the putative cause and effect. The probability of a storm conditional on a falling barometer and falling air pressure is the same as the probability of a storm conditional on falling air pressure alone. The falling barometer does not raise the probability of the storm once we know the air pressure. Such a screening variable is known either as a common cause (as in this example in which the falling air pressure causes both the falling barometer and the storm) or as an intermediate cause (when the variable is a more direct cause that stands between the effect and a less direct cause in a chain).
These are only two examples of the various additional conditions that have to be added to bring the simple notion of prima facie cause into line with our ordinary notions of causation. Such strategies suggest, however, that the reductive notion is haunted by the ghost of a more fundamental concept of causality and that we will not be satisfied until the reductive notion recapitulates this more fundamental notion.
Recognition of the specter of necessary connection suggests another possibility: simply give the reductive strategy up as a bad job and to embrace causality as a primitive category, admitting that no satisfactory reduction is possible. Such an approach once again distinguishes the ontology of causality from the conditions of causal inference that had been conflated in reductivist accounts. Such a non-reductive strategy implies that we can never step outside of the causal circle: to learn about particular causes requires some prior knowledge of other causes. Nancy Cartwright [1989, ch. 2] expresses this dependence in a slogan: “no causes in; no causes out.” It is also the basis for James Woodward’s [2003] “manipulability” account of causality (cf. [Holland, 1986]). Roughly, a relationship is causal if an intervention on A can be used to alter B. The notion of a manipulation or an intervention may appear to be, but is not in fact, an anthropomorphic one, since it can be defined in terms of independent variations that may arise with or without human agency. Nor is the circularity implicit in this approach vicious. What is needed is that some causal relationship (say, C causes A) permits manipulation of A, while what is demonstrated is the existence of a causal relationship between A and B — what is proved is not what is assumed.
Causal knowledge in a manipulability account is the knowledge of the structure of counterfactual dependence among variables — for example, how a clock works or how it will react to various interventions. Whereas in reductive accounts of causality, the connection between the structure of causes and counterfactual analysis was too weak to be satisfactory, here it is basic. Woodward’s account is closely allied with the analyses of Pearl [2000] and Hoover [2001]. I prefer the term structural account to manipulability account, since manipulations are used to infer structures and structures are manipulated. Still, that preference is merely a matter of terminology — the underlying causal ontology is the same in all three accounts.
A structural account seems particularly suited to economics. Economics is distinguished from other social sciences in its dedication to a core theory that is shared, to one degree or another, by most economists. The core theory can be seen as articulating economic mechanisms or structures not unlike physical mechanisms that provide the classic illustrations of causal structure. While the very notion of an economic structure seems to favor the manipulability or structural account of causality, with its fundamentally causal ontology, the same tensions already evident in Hume’s account of causality are recapitulated through the history of economics. These tensions are reflected in two problems: the inferential problem (how do we isolate causes or identify structure?) and counterfactual problem (how do we use a knowledge of causal structure to reason to unobserved outcomes?).
John Stuart Mill, one of a distinguished line of philosopher/economists, contributed answers to both questions. In his System of Logic (1851), he describes various canons for inferring causes from empirical data. But in his Principles of Political Economy(1848) he denies that economic structures can be inferred from these or other inductive rules. For Mill, economics involves many considerations and many confounding causes, as well as human agency. While there may be some coarse regularities, it is implausible that any economic laws or any strict causal relationships could be inferred from data. But economics is not, therefore, hopeless as a counterfactual science. Rather it is “an inexact and separate science” [Hausman, 1992]. Economics is the science of wealth in which the choices of human actors, known to us by direct acquaintance, interact with the production possibilities given by nature and social organization. From our a priori understanding, we can deduce axiomatically the effects of causes in cases in which there are no interfering factors. When we compare our deductions to the data, however, we do not expect a perfect fit, because there are in fact interfering factors and our deductions must be thought of as, at best, tendencies. There is no simple mapping between the deductions of theory and any sort of empirical test or measurement. Implicitly at least, Mill’s view has been highly influential in economics. Yet it gives rise to a perennial conundrum: if we know the true theory, we can dispense with empirical study; but how do we know that the theory is true?
I shall use the tension between the epistemological, inferential problem and the ontological, counterfactual problem as a background against which to situate four approaches to causality in economics. These four approaches are different, yet overlapping and sometimes complementary. The goal will not be to ask, which is right? Rather, what is right about each? They are 1) the notion of causal order implicit in the Cowles Commission [Koopmanns, 1950; Hood and Koopmanns, 1953] analysis of structural estimation, revived in, for example, Heckman [2000]; 2) Granger-causality [Granger, 1969; 1980; Sims, 1972]; 3) the structural account of causality that appeals to invariance under intervention as an inferential tool [Hoover, 2001]; and 4) the graph-theoretic approaches associated with Judea Pearl [2000] and Glymour, Spirtes, and Scheines [2000].
Both economic theory and econometrics have become sciences expressed in models. My approach will be to discuss causality in relationship to the mapping between theoretical and econometric models. This mapping is related in a complex way to the distinction between the inferential and the counterfactual problems. To keep things concrete, I will use macroeconomic models to illustrate the key points.
2 Structual Estimation and Causality
Trygve Haavelmo’s monograph “The Probability Approach in Econometrics” (1944) marks a watershed in the history of empirical economics. Appropriately defined, econometrics is an old discipline, going back perhaps to William Petty and the tradition of “political arithmetic.” Some of the characteristic tools of econometrics are traceable to William Stanley Jevons if not to earlier economists (see [Morgan, 1990]). Yet, until Haavelmo there was considerable doubt whether classical statistics had any relevance for econometrics at all. Haavelmo’s great innovation was to suggest how economic tendencies could be extracted from nonexperimental economic data — that is, to suggest how to do what Mill thought could not be done. The true interpretation of Haavelmo’s monograph is highly disputed (see [Spanos, 1995]). On one interpretation, economic theory permits us to place enough structure on an empirical problem that the errors can be thought to conform to a probability model analyzable by standard statistical tools. On another interpretation (associated with the “LSE (London School of Economics) approach” in econometrics), analysis is possible only if the econometric model can deliver errors that in fact conform to standard probability models and the key issue is finding a structure that ensures such conformity [Mizon, 1995].
The Cowles Commission took the first approach. The problem, as they saw it, was how to identify and measure the strength of the true causal linkages between variables. To do this, one started with theory. Suppose, to take a textbook example, that theory told us that money (m) depended on GDP (y) and GDP on money as
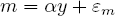 (1)
(1)
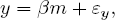 (2)
(2)
where the variables should be thought of as the logarithms of the natural variables and  m and
m and  y are error terms that indicate those factors that are irregular and cannot be explained. Following Haavelmo, the Cowles Commission program argues that if a model is structural then these error terms will follow a definite probability distribution and can be analyzed using standard statistical tools. Furthermore, if the structural model is complete, then the error terms will be independent of (and uncorrelated with) each other.
y are error terms that indicate those factors that are irregular and cannot be explained. Following Haavelmo, the Cowles Commission program argues that if a model is structural then these error terms will follow a definite probability distribution and can be analyzed using standard statistical tools. Furthermore, if the structural model is complete, then the error terms will be independent of (and uncorrelated with) each other.
If we have a model like equations (1) and (2), including knowledge of α and β and of the statistical properties of  m and
m and  y, then answering counterfactual questions (probabilistically) would be easy. The problem in the Cowles Commission view is that we do not know the values of the parameters or the properties of the errors. The real problem is the inferential one: given data on y and m, can we infer the unknown values? As the problem is set out, the answer is clearly, “no.”
y, then answering counterfactual questions (probabilistically) would be easy. The problem in the Cowles Commission view is that we do not know the values of the parameters or the properties of the errors. The real problem is the inferential one: given data on y and m, can we infer the unknown values? As the problem is set out, the answer is clearly, “no.”
The technique of multivariate regression, which chooses the coefficients of an equation in such a manner as to minimize the variance of the residual errors, implicitly places a directional arrow running from the right-hand to the left-hand side of an equation. The error terms are themselves estimated, not observed, and are chosen to be orthogonal to the left-hand side regressors — the implicit causes. Although if we knew the direction of causation, a regression run in that direction would quantify the relationship, we cannot use the regression itself to determine that direction. Any regression run in one direction can be reversed, and the coefficient estimates are just different normalizations of the correlations among the variables — here of the single correlation between m and y.3 We have no reason to prefer one normalization over another.
Of course, if we knew the values of  m and
m and  y, it would be easy to distinguish equation (1) from equation (2). But this is just what we do not know. Our best guesses of the values of
y, it would be easy to distinguish equation (1) from equation (2). But this is just what we do not know. Our best guesses of the values of  m and
m and  y are determined by our estimates of α and β, and not the other way round.
y are determined by our estimates of α and β, and not the other way round.
The problem is made easier if equations (1) and (2) are influenced by other, and different, observable factors. Suppose the theoretical model is
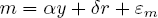 (3)
(3)
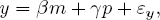 (4)
(4)
where r is the interest rate and p is the price level. Relative to the two-equation structure y and m are endogenous and r and p are exogenous variables. The values of the parameters can be inferred from regressions of the endogenous variables on the exogenous variables. First, eliminate the endogenous variables by substituting each equation into the other and simplifying to yield:
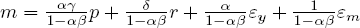 (3′)
(3′)
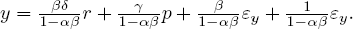 (4′)
(4′)
Next estimate regressions of the form
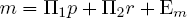 (5)
(5)
 (6)
(6)
where Π1,Π2, Γ1 and Γ2 are estimated coefficients and Em and Ey are regression residuals. Such a regression is known as a reduced form because it expresses the endogenous variables as functions of the exogenous variables and errors only.
The estimated coefficients of (5) and (6) can be matched with the coefficients on the corresponding variables in (3′) and (4′): 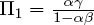 ,
, 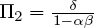 ,
, 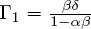 , and
, and 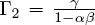 . Given this identification of the estimated coefficients with the theoretical coefficients, the parameters are easily recovered. A little calculation shows that
. Given this identification of the estimated coefficients with the theoretical coefficients, the parameters are easily recovered. A little calculation shows that 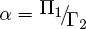 ,
, 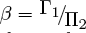 ,
, 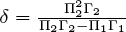 and
and 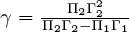 . It is only the assumption that we know the theoretical structure of (3′) and (4′) that allows us to recover these parameter estimates. In the argot of econometrics, we have achieved identification through “exclusion restrictions”: theory tells us that p is excluded as a cause of m and that r is excluded as a cause of y.
. It is only the assumption that we know the theoretical structure of (3′) and (4′) that allows us to recover these parameter estimates. In the argot of econometrics, we have achieved identification through “exclusion restrictions”: theory tells us that p is excluded as a cause of m and that r is excluded as a cause of y.
It is easy to see why we need factors that are included in one equation and excluded from another simply by looking at the formulae that define the mapping between the theoretical and estimated coefficients. For example, if r did not appear in (3′), we could interpret δ as equal to zero, so that (3′) would collapse to (3). Then Π2 and Γ1 would both equal zero, and β (the causal strength of m on y in (4′), the other equation) would not be defined.
The Cowles Commission approach privileges economic theory in manner that is strikingly anti-empirical. We can use the strategy to measure a causal strength, such as β, only on the assumption that we have the form of the structure correct as in (3′) and (4′). Not only is that assumption untested, it is untestable. Only if the theory implies more restrictions than the minimum needed to recover the structural parameters — that is, only if it implies “over-identifying restrictions” — is a statistical test possible. What is more, the Neyman-Pearson statistical testing strategy adopted by Haavelmo and the Cowles Commission has been interpreted as implying one-shot tests, in which the theoretical implication to be tested must be designated in advance (see [Spanos, 1995]). Mutual adaptation between the empirical tests and the theory that generated the testable implications invalidates the statistical model.4 While there is some possibility of adapting the Neyman-Pearson procedures to account for specification search, only the simplest cases can be analyzed. Mutual adaptation is certainly practiced, but it lacks a sound foundation given the statistical approach generally adopted in economics.
Herbert Simon [1953] clarified how identified structural models could be interpreted causally. If we know that the parameters α,β,δ, and γ are mutually independent — that is, the values taken by one places no restrictions on the range of values open to the others — we can place the arrows of causation in a system like (3) and (4), say, as
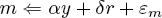 (3″)
(3″)
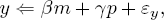 (4″)
(4″)
where the symbol “⇐” is interpreted as a directional equality. In this case, m and y are mutual causes. If α were zero under all circumstances - that is, if y were omitted from equation (4″), then m would cause y, but y would not cause m. Such systems with a one-way causal order are called recursive.
Simon pointed out an inferential problem closely related to the identification problem. To keep things simple, consider a recursive system without error terms:
 (7)
(7)
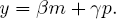 (8)
(8)
In this system, if β,δ, and γ are mutually independent parameters, mcauses y. But can we infer the causal structure from data alone? Unfortunately not. Adding (7) and (8) yields
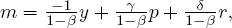 (7′)
(7′)
While substituting (7) into (8) yields
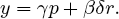 (8′)
(8′)
Every solution to (7) and (8) is also a solution to (7′) and (8′), yet in the first system m appears to cause y, and in the second system y appears to cause m. One might say, “yes, but the second system is clearly derived from the first.” But this is not so clear. If we replace the second system with
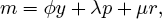 (7″)
(7″)
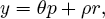 (8″)
(8″)
then what appear to be coefficients that are functions of more basic parameters in (7′) and (8′) can be treated as themselves basic parameters. Taking an appropriate linear transformation of (7″) and (8″) will convert it to a system with a causal order like that of (7) and (8) in which the coefficients are functions of its parameters. The same set of values for m, y, r, and p are consistent with this new system as with the three previous systems. The data alone do not seem to prefer one causal order over another. This is the problem of observational equivalence.
If we had some assurance that we knew which coefficients were true parameters and which were functions of more basic parameters, or even if we knew for certain which exogenous variables could be excluded from which equations, then we could recover the causal order.
At this point, the theoretical causal analyst is apt to turn to the economist and say, “we rely on you to supply the requisite subject matter knowledge.” Surprisingly, economists have often been willing to oblige on the basis of a priori theory or detailed knowledge of the economy. But we are entitled to ask: “Where did such detailed knowledge come from? How was the theory validated? Was the validation done in a way that did not merely assume that the problem of observational equivalence had been solved at some earlier stage? And, if it were soluble, at the earlier stage, why is it a problem now?”
3 The Assault on Macroeconometric Models
The epistemic problem of inferring causal strengths threatens to undermine the counterfactual uses of causal structure. Macroeconometric models are wanted in large part to conduct policy analysis. Without knowledge of the parameter values true policy analysis — that is, working out the effects of previously unobserved policy — is not possible (see [Marschak, 1953]). Despite the fact that the Cowles Commission program had clearly articulated the central difficulties in inferring causal structure, macromodeling in the 1950s and 1960s was undaunted. I believe that the main reason for ignoring the vast epistemic problems of structural modeling can be traced to the confidence in our direct, nonempirical acquaintance with true economic theory that many economists shared with (or inherited from) Mill. The Cowles Commission program pointed to the need for a priori theory.
Yet, this was not a problem, because what most distinguished economics from all other social sciences was, as Cartwright [1989, p. 14] later put it, “economics is a discipline with a theory.”
But was it well enough articulated? The structural econometric models of Jan Tinbergen, starting in the 1930s, through Lawrence Klein in the 1950s were models of macroeconomic aggregate data reflecting commonsensical assumptions about their interrelationships. Deep economic theory typically referred to the decision problems of individual agents — it was microeconomic. Even Keynes’s General Theory (1936), the bible of macroeconomics, had referred to individual behavior as a basis for aggregate relationships, such as the consumption function or the money-demand function. In his early review of the General Theory, Leontief [1936] called for grounding these relationships in a general-equilibrium framework in which the interactions of all agents had to be mutually consistent. Klein [1947] himself called for deriving each macroeconomic relationship from the optimization problems of individual economic actors. Together these quests formed the program of microfoundations for macroeconomics.
Klein’s leg of the microfoundational program developed more rapidly than Leontief’s. It was soon discovered that because decision-making is oriented toward the future, expectations are important. This was particularly clear in the investment literature of the late 1950s and early 1960s and led to a flowering of theoretical studies of expectation formation associated with the Carnegie Institute (now Carnegie-Mellon University). Because expectations must be grounded in past information and because the economic effects are slow to unfold, the current values of variables depend on past values. In other words, the quest for microfoundations underscored the dynamical character of economic relationships, reviving lines of inquiry that had begun in the interwar period.
The Leontief leg of the microfoundational program finally took off around 1970. Robert Lucas, in a series of papers that launched the new classical macroeconomics, insisted that models should respect the constraints of general equilibrium.5 Lucas made two key assumptions. Up to this point, most economists had thought that macroeconomic phenomena arose in part because one market or other failed to clear. Modeling non-clearing markets is theoretically difficult. Lucas’s first assumption is that markets in fact (at least to a first approximation) clear. His second assumption is that expectations are formed according to Muth’s [1961] rational expectations hypothesis. The rational expectations hypothesis assumed that what economic actors expect is, up to a random error, what the economic model predicts. Rational expectations are appealing to economists because they do not imply an informational advantage on the part of the modeler. If models could actually outpredict economic actors, then there would be easy profit opportunities for the modeler. But the modelers are themselves economic actors (and inform other economic actors) who would themselves take advantage of the profit opportunities with the effect of changing prices in such a way that the opportunity disappeared (the process referred to as arbitrage). In effect, acting on non-rational expectations would help to make the economy conform to rational expectations.
Lucas’s assumptions had strong implications for monetary policy as well. In a world in which markets clear, under conditions that many economists regard as reasonable, increases in the stock of money raise prices but do not change real quantities: there is pure inflation. In such a world, only an expectational error would allow a monetary-policy action to have a real (as opposed to a purely inflationary) effect. If people have rational expectations, then monetary policy actions can induce such errors at best randomly. Systematic monetary policy cannot, therefore, have real effects on the economy. This is the policy-ineffectiveness proposition, which was the most startling result of the early new classical macroeconomics [Sargent and Wallace, 1976].
We can see how Lucas’s analysis relates to causality and the Cowles Commission program through a simple structural model (again the variables should be interpreted as the logarithms of natural variables):
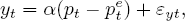 (9)
(9)
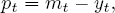 (10)
(10)
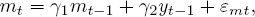 (11)
(11)
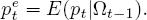 (12)
(12)
The variables are the same as those defined earlier, except that now the dynamic relationships are indicated by time subscripts. Equation (9) says that prices affect real GDP only if they differ from expectations formed a period earlier. Equation (10) shows that the level of prices is determined by the size of the money stock relative to real GDP. Equation (11) is the monetary-policy rule: the central bank sets the money supply in response to last period’s levels of money and real GDP. Finally, (12) says that expected prices are formed according to the rational expectations hypothesis — i.e., they are the mathematical expectation of actual prices based on all the information available up to time t−1. The information set (Ωt−1) includes the structure of the model and the values of all variables and parameters known at t − 1, but does not include the values of the current error terms.
The model is easily solved for an expression governing GDP,
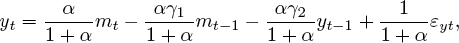 (13)
(13)
as well as one governing money that merely recapitulates the earlier equation
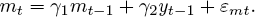 (11)
(11)
The system (11) and (13) is identified. In some sense, it shows mutual causality: m causes y, and y causes m. Yet, if we restrict ourselves to current (time t) values, then contemporaneously mt causes yt.
The coefficients in (13) are functions of the parameters of the model (9)-(12) because of the way expectations are formed: economic actors are seen as accounting for the structure of the model itself in forming expectations. Lucas [1976] criticized macromodelers for failing to incorporate expectations formation of this sort into their models. In his view, despite the claim that they were “structural,” previous macromodelers had estimated forms such as
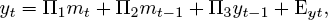 (14)
(14)
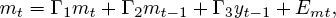 (15)
(15)
with enough exclusion restrictions to claim identification. He argued that these estimates were not grounded in theory — at least not in a theory that took dynamics, general equilibrium, and rational expectations seriously. In effect, Lucas argued that the coefficients in (14) and (15) were not casual, structural parameters but coefficients that were functions of deeper parameters. Mapping these coefficients onto those in (11) and (13) yields: 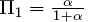 ,
, 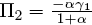 ,
,  , Γ1= 0, Γ2 = γ1, and Γ3 = γ2.
, Γ1= 0, Γ2 = γ1, and Γ3 = γ2.
Notice that Γ2 and Γ3just recapitulate the parameters of the policy function (11). In contrast Π1, Π2, and Π3 are coefficients that shift with any change in one of the policy parameters. Equation (14) may have appeared to the macromodeler to be a structural relationship, but if Lucas’s theory is correct it would not be invariant to policy manipulation, as Haavelmo and the Cowles Commission had insisted that a causal relationship should be. This is the policy noninvariance proposition or Lucas critique.
While the Lucas critique is a celebrated contribution to macroeconomic analysis, in this context it is secondary. It might be interpreted as little threat to the Cowles Commission program. Instead of identifying structure through exclusion restrictions, Lucas seems to show us that a more complicated, nonlinear identification is needed. The demands on a priori theoretical knowledge are higher, but they are of the same kind. Once the parameters are identified and estimated, counterfactual analysis can proceed using (11) and (13). In fact, the combination of the idea that only unexpected prices can have real effects (encapsulated in the “surprise-only” aggregate-supply function (9)) and rational expectations renders counterfactual analysis impossible. To see this, substitute (11) into (13) to yield
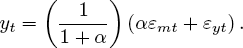 (16)
(16)
Equation (16) says that real GDP depends only on random shocks and on the shape of the aggregate-supply function (the parameter α), but not in any way on the policy parameters γ1 and γ2. This is the formal derivation of the policy ineffectiveness proposition.
One might be inclined to dismiss policy-ineffectiveness as a very special and very likely non-robust result. In particular, economists typically place less confidence in dynamic theory than in equilibrium theory. But, as it turns out, policy ineffectiveness is a generic property of models with a surprise-only supply structure and rational expectations. Although there are alternatives, it characterizes a broad and attractive class of models.
The new classical approach can be seen as placing extreme faith in economic theory and, nevertheless, completely undermining the counterfactual analysis that causal analysis in the Cowles Commission framework was meant to support. Toward the end of the 1970s, macromodels were assaulted from the opposite extreme. Rejecting the typical identifying restrictions used in macromodels as literally “incredible” — not grounded in theory or other sure knowledge — Christopher Sims [1980] advocated the abandonment of the Cowles Commission program in favor of a nonstructural characterization of macroeconomic data, the so-called vector autoregression (VAR). A VAR might take a form such as
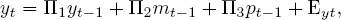 (17)
(17)
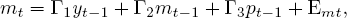 (18)
(18)
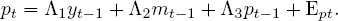 (19)
(19)
These equations should be understood as reduced forms. The coefficients are not structural and the error terms are not in general independent. While only a single lagged value of each variable is shown, in general these lags should be taken as standing for a set of longer (possibly infinite) lagged values.
Having eschewed structure, the Cowles Commission analysis of causal order is not available to the VAR modeler. VAR analysis, however, grew out of an older tradition in time-series statistics. Sims [1972] had introduced Granger’s [1969] approach to causality into macroeconometric analysis. Granger’s notion is temporal (causes must precede effects) and informational (A causes B if A carries incremental information useful in predicting B). In (17), for instance, m does not Granger-cause y if the estimate of Π2 is statistically insignificant.
Granger-causality does not suffer from the inferential problem: systems like (17)-(19) are easily estimated and the statistical tests are straightforward. But it is no help with the counterfactual problem, despite the ease with which many practicing economists have jumped from a finding of Granger-causality to an assumption of controllability. Just recalling that the reduced-form parameters of the VAR must be complicated functions of the underlying structure should convince us of the unsuitability of Granger-causal ordering to counterfactual analysis.
More specifically, Granger-causality is easily shown not to be necessary for counterfactual control. Imagine that structurally m causes y, and that m is chosen in such a way to offset any systematic (and, therefore, predictable) fluctuations in y, then m will not be conditionally correlated with y (i.e., Π2 = 0). For example, suppose that the wheel of ship causes it to turn port or starboard, but that the helmsman tries to hold a perfectly steady course. The ship is buffeted by the waves and swells. Yet, if the helmsman is successful, the ship travels in straight line, while the wheel moves from side to side in an inverted counterpoint to the movements of the sea. There should be no observable correlation between the direction of the ship and that of the wheel along a single heading.
Granger-causality may not be sufficient in practice for counterfactual control. Suppose that ceteris paribus the higher the stock of money or the lower the demand for money, the higher the price level. Further suppose that the demand for money will be lower when people anticipate inflation (i.e., prices higher in future than today). If people know that the money stock will rise in future, then prices will rise in future, so that inflation is higher and the demand for money is lower today. In that case, prices will rise somewhat today as a fixed supply of money would otherwise exceed the lower demand. Now if people are better able to predict the future course of money than are econometricians, then the econometricians will find that prices today help to predict the future stock of money. In this case, prices Granger-cause money, even though money structurally causes prices ex hypothesi[Hoover, 1993, 2001, ch. 2].
One might counter this argument by saying that it simply shows that the econometrician has relied on incomplete information. It raises an important ontological issue for macroeconomics. Given the way that macroeconomic aggregates are formed, it is likely that there is always more information reflected in the behavior of people than is reflected in even an ideal aggregate. If that is so, then conflicts between structural and Granger-causality are inevitable.
A similar point applies to the assumption of time order implicit in Grangercausality: causes strictly precede effects. Practically, this is clearly not true. Contemporaneous Granger-causality easily shows up with data sampled at coarse intervals: months, quarters, years. But would it go away if we could take finer and finer cuts of the data? The existence of an aggregate such as real GDP as a stable, causally significant variable is threatened by taking too fine a cut. Real GDP measures the flow of goods and services — the amount of final products produced over a unit of time. While one could in principle add up such a quantity over intervals of an hour or a second, such an aggregate would fluctuate wildly with the time of day (think what happens to GDP at night or meal times) in a way that has no causal significance in macroeconomics. At any interval over which it is causally significant, the relationships may be contemporaneous rather than strictly time-ordered.
As already observed, the most developed theory is about static equilibrium or steady states. The relationships in such steady states are essentially timeless, yet this does not rule out a structural causal order (notice that there are no time subscripts in (3″) and (4″) above).
Economists have found it hard to get by with just Granger-causality and VARs. This is because they are not ready to abandon counterfactual analysis. The VAR program started at the nonstructural extreme. It has gradually added just enough structure to permit a minimal counterfactual analysis. A key feature of the VAR is that all variables are modeled as endogenous. Ultimately, it is only the errors (or “shocks”) that cause movements in the variables. But the shocks in (17)-(19) are intercorrelated. What does it mean to evaluate, say, a money shock when any randomly selected value of Emt changes the probability distribution of Eyt and Ept as well? In the wake of criticism from Cooley and LeRoy [1985], Leamer [1985] and others, Sims [1982; 1986] and other VAR analysts quickly admitted that contemporaneous structure was needed.
The preferred structures involved a linear transformations of the VAR that eliminated the correlation between the error terms. A typical structural VAR (or SVAR) takes the form:
 (20)
(20)
 (21)
(21)
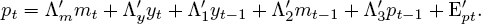 (22)
(22)
This system is recursively ordered with yt causing mt, and yt and mt causing pt. (The transformation of the VAR into an SVAR in which each variable is a direct cause of every variable below it in the recursive order is called triangular and is achieved through a Choleski decomposition.) At all other lags the system remains causally unstructured. But this minimal structure is enough to eliminate the correlations among the error terms. So now, a unique shock to the money equation or the price equation makes sense. The typical way of evaluating SVARs is to calculate the effects of a shock to a single equation, setting all other shocks to zero. These are called impulse-response functions and are usually displayed as a separate graph of the path of each variable in response to each shock.
Unfortunately, the Choleski transformation that generated the triangular ordering of the contemporaneous variables is not unique. There are six possible Choleski orderings. These are observationally equivalent in the sense that they are all transformations of the same reduced form. And with n variables, as long as at least n(n − 1)/2 restrictions are imposed to secure identification, there can be non-Choleski (i.e., not strictly recursive) orderings as well.
Not only does formal economic theory not often express a preference for a particular contemporaneous ordering, the founding sentiment of the VAR program was that theory was not to be trusted to provide structure. In practice macroeconomists have offered casual, often temporal, arguments to support particular orderings. For example, commodity prices are observed daily but the Federal Reserve’s policy action must act slowly, so the commodity-price index must be ordered ahead of the Federal Reserve’s targeted interest rate. These are mostly “Just So” stories and easily fall foul of some of the problems with temporal arguments that applied in the case of Granger-causality.
Structural VARs have become the dominant tool of empirical macroeconomics, often adopted by researchers who subscribe to the fundamental tenets of the new classical macroeconomics, even while distrusting the details of any theoretical model that could generate identifying restrictions. But the SVAR stands in an uneasy relationship with the new classical analysis.6 If the Lucas critique is correct, then are not the coefficients of the SVAR likely to shift with changes in economic policy, rendering the impulse-response functions inaccurate?
One response has been to admit the Lucas critique on principle but to argue that true changes in policy are rare [Sims, 1986]. Most monetary-policy actions are seen as realizations of particular processes. Impulse-response functions may prove to be accurate on this view; yet, once again, how is one to conduct counter-factual analysis? LeRoy [1995] has argued — unpersuasively in my view — that a policymaker can be seen as delivering a set of nonrandom shocks without violating rational expectations. Leeper and Zha [2003] do not go quite so far. They argue that there is a threshold of perceptibility for violations of randomness. Below that threshold (defined by the duration of the string and the size of the shocks), a policymaker can deliver a string of nonrandom shocks that do not trigger the Lucas critique and, yet, are economically significant.
The example of the new classical model in (9)-(13) demonstrates a generalizable point that in those cases in which the Lucas critique is relevant, policy is innocuous. Counterfactual analysis needs some structure, the SVAR does not provide enough. I return to this point in Section 5 below.
4 Inferring Causes from Interventions
The Cowles Commission approach put theory to the forefront in order to support counterfactual policy analysis. The skeptical SVAR program tried to do with as little theory as possible. The SVAR program sees the Lucas critique as a threat, since true changes in policy regime would vitiate the VAR estimates. My own approach in earlier work (summarized in Hoover 2001, chs. 8–10) is, in sense, to embrace the Lucas critique as a source of information about the underlying causal structure. The idea is an essential one for the structural or manipulability account: the causal relationship is defined as one that possesses a certain type of invariance. The previous equations used to illustrate Simon’s account of causal order can be used to show this point.
Suppose that the system (7) and (8), in which m causes y, reflect the true — but unknown — causal order. A policy intervention might be a change in the parameter δ. The parameter may not be identified, and, so, the change will not be directly observed. Yet, we may know from, for example, institutional (or other nonstatistical) information that a policy change has occurred. Such a change would, however, not alter the parameters of (8). Now suppose that the system (7′) and (8′), which could be interpreted (incorrectly, of course) as reflecting y causing m, is considered as an alternative. Again, if we know that a policy change has occurred, we see that both the coefficients of the mequation (7′) and the yequation (8′) have shifted. The stability of (7) and (8) against the instability of (7′) and (8′) argues in favor of the causal direction running from m to y. There is no free lunch here. Where identification in structural models is achieved through a priori theoretical knowledge, identification of causal direction is achieved here through knowledge of independent interventions.
This invariance approach is closely related to the econometric notion of superexogeneity [Engle, Hendry, and Richard, 1983; Hendry 1995]. Superexogeneity is defined with reference to the stability of the statistical distribution in the face of interventions. My own approach emphasizes the importance of referring to the causal structure itself and is, in that sense, more fundamentally indebted to the Cowles Commission analysis of structure. The importance of this distinction can be seen in the new classical model whose solution is given in (11) and (13). On a superexogeneity standard, the instability of the coefficients of (13) in the face of a change in policy that (observable or not) changes γ1 or γ2, might be taken to count against mt contemporaneously causing yt. Yet, on the Cowles Commission standard, the causal order clearly runs from mt to yt. The important point is that the effects of interventions do not run against the arrow of causation. This is still true in this case, an intervention in the aggregate-supply process (a change in α) does not result in any shift of the coefficients of (11).
Favero and Hendry [1992] and Ericsson and Hendry [1999] have used superexogeneity tests to check whether the Lucas critique matters in practice (see also [Ericsson and Irons, 1995]). This is exactly right. And if it does not — probably because expectations are not formed according to the rational-expectations hypothesis — then the inference of causal direction from invariance is easier. But if the Lucas critique in fact matters, then more subtlety is needed to tease causal direction out of information about invariance.
The key point is that it is not invariance but structure that defines causality; invariance only provides information that is often helpful in causal inference. There is always invariance at some level, but not always at the level of ordinary correlations or regression relationships.
5 Graph-Theoretic Accounts of Causal Structure
Causal inference using invariance testing is easily overwhelmed by too much happening at once. It works best when one or, at most, a few causal arrows are in question, and it requires (in economic applications, at least) the good fortune to have a few — but not too many — interventions in the right parts of the structure. Over the past twenty years, a new analysis of causal structure based in graph theory has provided important theoretical and practical advances in causal analysis [Spirtes, Glymour, Scheines, 2000; Pearl, 2000]. These advances have, however, barely touched economics, yet they may help to overcome some of the limitations of the invariance approach.
In the Cowles Commission account an adequate econometric model has two distinct but related parts: the probability distribution of the variables and their causal structure. Spirtes et al., [2000] and Pearl [2000] subscribe completely to this view of structure, but offer a more perspicacious way of keeping track of causal relations. Graphs have been used for more than a century to indicate causal structure, but only recently have the mathematical tools of graph theory given researchers a highly efficient way to express causal connections and to analyze and manipulate them in relations to the associated probability distributions.
The key idea of the graph-theoretic approach is related to Reichenbach’s [1956] principle of the common cause. If A and B are probabilistically dependent, then either A causes B or B causes A or both have a common cause. The common cause might be a parent as in Figure 1 or a set of ancestors as in Figure 2. The causal Markov condition is closely related to Reichenbach’s principle. Roughly, it says that if C is a set of ancestors to A and B and if A and B are not directly causally connected and are not probabilistically independent, then A and B are independent conditional on C.
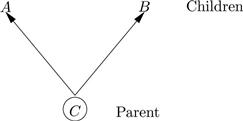
Figure 1 A Common Cause
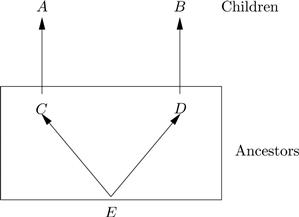
Figure 2 Common Ancestors
In practice, independence is usually judged by estimating (conditional) correlations among variables. This raises three issues. First, independence implies an absence of correlation, but an absence of correlation does not imply independence. (For an example, see Lindgren [1976, p. 136].)
Second, the independence relationships of interest are those of the population, and not the sample. Inference about sample correlations is statistical and thus reliable only subject to the usual caveats of statistical inference.
But, third, even measured correlations are meaningful only in the context of a maintained model of the probability distribution of the variables. This distinction becomes important when statistics that apply to stationary or homogeneous data interpreted as applying equally well to nonstationary or inhomogeneous data. For example, the well-known counterexample to Reichenbach’s principle of the common causes due to Elliott Sober [1994; 2001] states that bread prices in England and sea levels in Venice, which ex hypothesi, are not causally connected are nonetheless correlated, violating Reichenbach’s principle. Hoover [2003] shows that Sober implicitly assumes a stationary probability model when the best model would involve variables that either trend or follow a random walk. Time-series statisticians have known for a long time than ordinary measures of correlation fail to indicate probabilistic dependence in such models. Keeping these caveats in mind, we shall, for purposes of exposition, assume that correlations measure independence.
The idea of vanishing conditional correlation is also found in the notion of screening, familiar from the literature on probabilistic causation. If cor(A, B) ≠ 0 and C is causally between A and B (A → C → B or A ← C ← B), then cor(A, B|C) = 0.
Conditioning can also induce correlation. The classic example if shown in Figure 3. Here cor(A,B) = 0, but cor(A,B|C) ≠ 0. C is called an unshielded collider on the path ACB. It is a “collider” because two causal arrows point into it, and it is “unshielded” because A and B are not directly causally connected. Figure 4 shows two shielded colliders. In each case cor(A,B) ≠ 0.
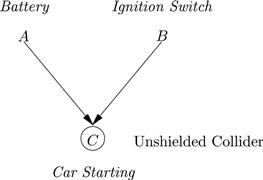
Figure 3 An Unshielded Collider
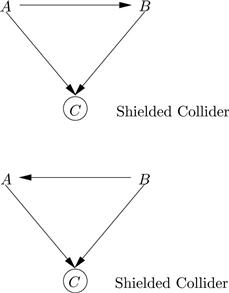
Figure 4 Shielded Colliders
There is a number of algorithms that start with all the first-order correlations of a set of variables and search for patterns of unshielded colliders, common causes, and screens consistent with the observed correlations. The best known software for implementing these algorithms is the Tetrad program of Sprites et al. [1996].
The Observational Equivalence Theorem [Pearl, 2000, p. 19, Theorem 1.2.8; Sprites et al., 2000, ch. 4] states that any probability distribution that can be faithfully represented in a causally sufficient, acyclical (or what econometricians would call a recursive) graph can equally well be represented by any other acyclical graph that has the same skeleton (i.e., the same causal connections ignoring direction) and the same unshielded colliders. Such graphs form an observationally equivalent class. Figure 4 shows two observationally equivalent graphs. They have identical skeletons and no unshielded colliders. The following two graphs are also observationally equivalent:
 (i)
(i)
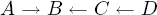 (ii)
(ii)
In each case, they have the same causal connections and an unshielded collider at A on the path ABC but differ in the direction of causation between C and D. A program such as Tetrad can direct the arrows between A and B and between B and C, it cannot direct the arrow between C and D.
How can graph-theoretic ideas be applied to macroeconomics? One limitation is worth noting at the outset. Search algorithms based on the causal Markov condition can easily miss causal linkages in situations of optimal control (for example, the helmsman in section 3 who tries to steer on a constant heading) for exactly the same reason that Granger-causality tests failed: in the ideal case, the values of the control variable are chosen to minimize the variability of the controlled variable, and the correlation between them vanishes [Hoover, 2001, pp. 168–170]. Spirtes et al. [2000, p. 66] and Pearl [2000, p. 63] dismiss this as a “Lebesgue measure-zero” result. While this may do in some cases, it will not do in economics, because such cases arise naturally in economics when policies are chosen optimally to minimize the variability of a target. (Stabilizing GDP around its trend is much like stabilizing the movements of a ship around the preferred heading.) This, by no means, renders the approach or the algorithms useless, but it does serve remind us that it is the causal structure that is primary and not the tools that are used to uncover it. When tools do not work in some circumstances, other tools are needed.
Another problem in applying these tools to macroeconomic applications is that, in most cases, they have been developed with stationary, non-time-dependent data in mind. But macroeconomics works primarily with time-series and often with nonstationary time series. Swanson and Granger (1997) made a first pass at applying these methods to VARs. Their method can be explained with reference to the VAR in (17)–(19). Although the variables the variables themselves are time-dependent and possibly nonstationary, the error terms are not. If the VAR is correctly specified, then the residual errors are serially uncorrelated with a zero mean and constant variance. Instead of looking at the correlations among the primary variables, Swanson and Granger look at the correlations among their corresponding error terms, reinterpreted as the variables with their time-series dynamics filtered out.
Swanson and Granger limit themselves to causation in a line without considering common causes (e.g., 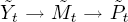 , where the tildes over the variables indicate that they are filtered). They do not use the common algorithms available in Tetrad. Instead, they check for screening directly. This allows them to put the variables in order, but not to orient the arrows of causation. Like other VAR analysts, once they have selected an order, they rely on an argument of temporal priority to orient the chain of causation. Once they have determined the order among the filtered variables, they impose them on the original VAR and transform it into an SVAR.
, where the tildes over the variables indicate that they are filtered). They do not use the common algorithms available in Tetrad. Instead, they check for screening directly. This allows them to put the variables in order, but not to orient the arrows of causation. Like other VAR analysts, once they have selected an order, they rely on an argument of temporal priority to orient the chain of causation. Once they have determined the order among the filtered variables, they impose them on the original VAR and transform it into an SVAR.
6 A Synthetic Program for Uncovering The Causal Structure of Vars
I have been highlighting the tensions between causal inference and the counter-factual uses of causation and the parallel tensions between structural and non-structural econometric models. But despite these tensions, my aim is essentially the irenic one of looking for the best in the various approaches. The best available account of causal order in economics is found in the Cowles Commission structural analysis. But as a strategy of causal inference it is infeasible. It provides no mechanism for effective feedback from empirical facts about the world to the theory that is used to structure the empirical measurement of causes. The VAR program has that much right. The identification assumptions of the Cowles Commission program are incredible. Unfortunately, the VAR program also needs structure to proceed. The questions are: how little structure can we get away with and still have something useful to say? and how are we to learn about structure? I want to conclude by briefly describing my research program on the causal orderings of VARs (joint work with Selva Demiralp and Stephen J. Perez). Our approach emphasizes the complementarity of various approaches to causation in macroeconomics.
We start where Swanson and Granger left off. Their useful idea is that the contemporaneous causal order of the SVARs can be determined by applying graphtheoretic methods to the filtered variables. Along with a small group of other researchers, we have extended their methods to consider recursive or acylical orderings more generally and not just simple causal chains (see [Demiralp and Hoover, 2003] and the references therein). For this we used the PC algorithm in Tetrad. What makes this a nontrivial exercise is that the algorithms in Tetrad are data search procedures in which the search path involves multiple sequential testing. Economists are famously wedded to a Neyman-Pearson statistical testing philosophy in which such “data mining” is viewed with the greatest skepticism. Previously, Hoover and Perez [1999; 2004] have investigated LSE search methodologies in Monte Carlo studies and have demonstrated that properly disciplined search algorithms can, despite economists fears, have extremely well-behaved statistical properties. Demiralp and Hoover [2003] demonstrate in a Monte Carlo study that the PC algorithm is very effective when applied to the SVAR at recovering the skeleton of underlying causal graphs and, provided that signal strengths are high enough, at oriented the edges as well.
The problem of whether or not (or to what degree) an algorithm identifies a causal order is not as straightforward as determining the distribution of a statistical test — the typical application of Monte Carlo studies. In particular, the effectiveness is likely to be highly dependent on the true underlying causal structure — something that cannot be known in advance in actual empirical applications. Demiralp, Hoover, and Perez [2008] have therefore developed a bootstrap method in which simulations can be adapted to actual data without knowing the true underlying structure. The bootstrap method starts by estimating a VAR, in the same way as one normally obtains the filtered variables, but then treats the error terms as a pool of random variates from which to construct a large number of simulated data sets. A causal search algorithm is then applied to each simulated data set and the chosen causal order is recorded. Statistics summarizing the frequency of occurrence of different causal structures are then used in the manner of Monte Carlo simulations in the earlier study to construct measures of the reliability of the causal identification for the specific case under study.
Graph-theoretic methods are attractive in the VAR context partly because they are well suited to handle relatively large numbers of variables. Nevertheless, as we have already seen, there may remain some observational equivalence, so that some causal links cannot be oriented. Macroeconomics quite commonly involves policy regime changes and structural breaks that can be exploited as in my own earlier approach to causal inference.
The impulse-response functions of VARs are known to be inaccurately estimated. In part, this arises because they include large numbers of lagged and often highly correlated regressors. Conditional on the contemporaneous causal order being held fixed, it should be possible to conduct systematic exclusion restrictions of variables and their lags from the different equations of the structure. These are effectively Granger-causality tests. The elimination of variables which are not Granger-causal should help to sharpen the estimates.
This program of discovering the structure of the VAR from data helps to preserve the insight that a priori theory alone cannot get us too far. But let me end on a cautionary note. The discovery of the contemporaneous causal VAR through graph-theoretic methods supplemented by invariance-based methods and refined by Granger-causality tests may still not deliver enough structure to support counterfactual analysis.
To illustrate the problem, the structure in (11) and (13) is compatible with an SVAR in which contemporaneous money causes contemporaneous real GDP. And, as we have seen, it delivers policy ineffectiveness. It is a simple model, but policy ineffectiveness generalizes to complex models.
Since the 1970s, however, many — if not most — macroeconomists have come to believe that, in the short run, systematic monetary policy does have real effects. This might be because expectations are not formed rationally (or because economic actors follow rules of thumb that make no reference to expectations at all) or because slowly adjusting wages and prices undermine the surprise-only aggregate supply relationship. To make the point in a simple way, we can imagine that for either of these reasons (11) is replaced by
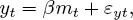 (23)
(23)
which shows that money directly affects real GDP.
Notice that (11) and (23) form a system which is, again, consistent with an SVAR in which money is contemporaneously causally ordered ahead of real GDP. But the system (11) and (23) does not display policy ineffectiveness. Indeed, systematic monetary policy can be quite powerful in this system. Both the system (11) and (13) and the system (11) and (23) are compatible with the same SVAR. But the counterfactual experiment of what happens to real GDP when systematic monetary policy is changed (that is, what happens when γ1 or γ2) is changed are radically different: in the first case, nothing; in the second case, a great deal [Cochrane, 1998].
In a sense, we have come full circle. The initial problem was that we needed to assume that we already knew the causal structure in order to make measurements of causal strengths and to conduct counterfactual analysis. We argued that a variety of methods of causal inference may allow us to discover large parts of causal structure. And now we see that even if we are very successful, it still may not be enough for counterfactual analysis. None of our methods definitively resolves the initial tension.
It is, perhaps, not ultimately resolvable. Yet, I do not view the process as hopeless. Rather it is one of iterating between whichever pole is most immediately obstructing our progress. For example, in a more complicated version of the problem just set out Òscar Jordá and I [Hoover and Jordá, 2001] assume that the economy consists partly of agents who follow an analogue to (11) and (13) and partly agents who follow an analogue of (11) and (23). On the assumption that the shares of each type of agent is stable, we use changes in monetary policy regimes to recover the shares and to identify the underlying structure. This approach parallels closely the invariance-based methods of causal inference. But notice that it still relies on strong assumptions not only of the constancy of the shares, but also of the particular forms of the two aggregate-supply functions. We try to make these as generic and general as possible, but they cannot be perfectly general. So, we are again brought round to the conclusion that counterfactual analysis requires strong untestable, a priori assumptions, and to the open question: how do we know that they are true?
BIBLIOGRAPHY
1. Cartwright N. Nature’s Capacities and Their Measurement Oxford: Clarendon Press; 1989.
2. Cochrane JH. What Do the VARs Mean? Measuring the Output Effects of Monetary Policy. Journal of Monetary Economics. 1998;41(7):277–300.
3. Cooley TF, LeRoy SF. Atheoretical Macroeconometrics: A Critique. Journal of Monetary Economics. 1985;16(3):283–308.
4. Demiralp S, Hoover KD. Searching for the Causal Structure of a Vector Autoregression. Oxford Bulletin of Economics and Statistics 2003;(65):745–767 [supplement], 2003.
5. Demiralp S, Hoover KD, Perez SJ. A Bootstrap Method for Identifying and Evaluating a Structural Vector Autoregression. Oxford Bulletin of Ecoomics and Statistics. 2008;70(4):509–533.
6. Engle RF, Hendry DF, Richard J-F. Exogeneity. Econometrica. 1983;51(2):277–304.
7. Ericsson NR, Hendry DF. Encompassing and Rational Expectations: How Sequential Corroboration Can Imply Refutation. Empirical Economics. 1999;24(1):1–21.
8. Ericsson NR, Irons J. The Lucas Critique in Practice: Theory Without Measurement. In: Hoover Kevin D, ed. Macroeconometrics: Developments, Tensions and Prospects. Boston: Kluwer; 1995;263–312.
9. Favero C, Hendry DF. Testing the Lucas Critique: A Review. Econometric Reviews. 1992;11(3):265–306.
10. Granger CWJ. Investigating Causal Relations by Econometric Models and Cross-Spectral Methods. Econometrica. 1969;37(3):424–438.
11. Granger CWJ. Testing for Causality: A Personal Viewpoint. Journal of Economic Dynamics and Control. 1980;2(4):329–352 November.
12. Haavelmo T. The Probability Approach in Econometrics. Econometrica 1944; 12 (supplement], July.
13. Hausman DM. The Inexact and Separate Science of Economics Cambridge: Cambridge University Press; 1992.
14. Heckman JJ. Causal Parameters and Policy Analysis in Economics: A Twentieth Century Retrospective. Quarterly Journal of Economics. 2000;115(1):45–97.
15. Hendry DF. Dynamic Econometrics Oxford: Oxford University Press; 1995.
16. Holland PW. Statistics and Causal Inference [with discussion]. Journal of the American Statistical Association. 1986;81(396):945–960.
17. Hood WC, Koopmans TC, eds. Studies in Econometric Method. New York: Wiley; 1953; Cowles Commission Monograph 14.
18. Hoover KD. The New Classical Macroeconomics: A Sceptical Inquiry Oxford: Basil Blackwell; 1988.
19. Hoover KD. The Rational Expectations Revolution: An Assessment. The Cato Journal. 1992a;12(1):81–96.
20. Hoover KD, ed. The New Classical Macroeconomics in 3 volumes. Edward Elgar: Aldershot; 1992b.
21. Hoover KD. Causality and Temporal Order in Macroeconomics or Why Even Economists Don’t Know How to Get Causes from Probabilities. British Journal for the Philosophy of Science. 1993;44(4):693–710.
22. Hoover KD. Causality in Macroeconomics Cambridge: Cambridge University Press; 2001.
23. Hoover KD. Nonstationary time series, cointegration, and the principle of the common cause. British Journal for the Philosophy of Science. 2003;54(4):527–551.
24. Hoover KD, Jordá Ò. Measuring Systematic Monetary Policy. Federal Reserve Bank of St Louis Review. 2001;83:113–138.
25. Hoover KD, Perez SJ. Data Mining Reconsidered: Encompassing and the General-to-Specific Approach to Specification Search. Econometrics Journal. 1999;2(2):167–191.
26. Hoover KD, Perez SJ. Truth and Robustness in Cross Country Growth Regressions. Oxford Bulletin of Economics and Statistics. 2004;66(5):765–798.
27. Hume D. A Treatise of Human Nature. Page numbers refer to the edition edited by L.A Selby-Bigge. Oxford: Clarendon Press; 1739; 1888.
28. Hume D. Of Money,’ in Essays: Moral, Political, and Literary. Page references to the edition edited by Eugene F Miller Indianapolis: LibertyClassics; 1754; 1885.
29. Hume D. An Enquiry Concerning Human Understanding. In: Selby-Bigge LA, ed. Enquiries Concerning Human Understanding and Concerning the Principles of Morals. Oxford: Clarendon Press; 1777; Page numbers refer to, 1902.
30. Keynes JM. The General Theory of Money, Interest and Prices London: Macmillan; 1936.
31. Klein LR. The Keynesian Revolution New York: Macmillan; 1947.
32. Koopmans TC. Statistical Inference in Dynamic Economic Models. Cowles Commission Monograph 10 New York: Wiley; 1950.
33. Leamer E. Vector Autoregressions for Causal Inference?. In: Brunner Karl, Meltzer Alan H, eds. 1985;225–304. Understanding Monetary Regimes, Carnegie-Rochester Conference Series on Public Policy. 22 North Holland, Amsterdam.
34. Leeper EM, Tao Zha. Modest Policy Interventions. Journal of Monetary Economics. 2003;50(8):1673–1700.
35. Leontief W. The Fundamental Assumption of Mr Keynes’s Monetary Theory of Unemployment. Quarterly Journal of Economics. 1936;51(1):192–197.
36. LeRoy SF. On Policy Regimes. In: Hoover Kevin D, ed. Macroeconometrics: Developments, Tensions and Prospects. Boston: Kluwer; 1995;235–252.
37. Lindgren B. Statistical Theory 3rd ed. New York: Macmillan; 1976.
38. Lucas Jr RE. Econometric Policy Evaluation: A Critique. In: Brunner Karl, Meltzer Allan H, eds. Amsterdam: North-Holland: Spring; 1976;161–168. The Phillips Curve and Labor Markets Carnegie-Rochester Conference Series on Public Policy. 11.
39. Marschak J. Economic Measurements for Policy and Predictions. In: Hood WC, Koopmans TC, eds. Studies in Econometric Method. New York: Wiley; 1953; Cowles Foundations Monograph no. 14.
40. Mill JS. In: Ashley WJ, ed. Principles of Political Economy with Some of Their Applications to Social Philosophy. London: Longman, Green; 1848; 1909.
41. Mill J S. A System of Logic, Ratiocinative and Deductive: Being a Connected View of the Principles of Evidence and the Methods of Scientific Investigation 3rd. ed. London: John W. Parker; 1851; vol. I.
42. Mizon GE. Progressive Modelling of Economic Time Series: The LSE Methodology. In: Hoover Kevin D, ed. Macroeconometrics: Developments, Tensions and Prospects. Boston: Kluwer; 1995;107–170.
43. Morgan MS. The History of Econometric Ideas Cambridge: Cambridge University Press; 1990.
44. Muth JF. Rational Expectations and the Theory of Price Movements. Econometrica. 1961;29(3):315–335.
45. Pearl J. Causality: Models, Reasoning, and Inference Cambridge: Cambridge University Press; 2000.
46. Reichenbach H. The Direction of Time Berkeley and Los Angeles: University of California Press; 1956.
47. Sargent TJ, Wallace N. Rational Expectations and the Theory of Economic Policy. Journal of Monetary Economics. 1976;2(2):169–183.
48. Simon HA. Causal Ordering and Identifiability. In: Simon Herbert A, ed. Models of Man. New York: Wiley; 1953; 1957, ch. 1.
49. Sims C. Money, Income and Causality. In: Lucas Jr Robert E, Sargent Thomas J, eds. Rational Expectations and Econometric Practice. 1972;387–403. George Allen and Unwin, 1981.
50. Sims CA. Macroeconomics and reality. Econometrica. 1980;48:1–48.
51. Sims CA. Policy Analysis with Econometric Models. Brookings Papers on Economic Activity. 1982;1:107–152.
52. Sims CA. Are Forecasting Models Usable for Policy Analysis?. Federal Reserve Bank of Minneapolis Quarterly Review. 1986;10(1):2–15 Winter.
53. Sober E. The Principle of the Common Cause. In: From a Biological Point of View. Cambridge: Cambridge University Press; 1994;158–174.
54. Sober E. Venetian Sea Levels, British Bread Prices, and the Principle of the Common Cause. British Journal for the Philosophy of Science. 2001;52(2):331–346.
55. Spanos A. On Theory Testing in Econometrics: Modeling with Nonexperimental Data. Journal of Econometrics. 1995;67(1):189–226.
56. Spirtes P, Glymour C, Scheines R. Causation, Prediction, and Search 2nd edition Cambridge, MA: MIT Press; 2000.
57. P. Spirtes, R. Scheines, C. Meek, T. Richardson, C. Glymour, H. Hoijtink and A. Boomsma. TETRAD 3: Tools for Causal Modeling, program (beta version, October 1996) and user’s manual on the worldwide web at http://www.phil.cmu.edu/tetrad/tet3/master.htm.
58. Suppes P. A Probabilistic Theory of Causality. Acta Philosophica Fennica 1970; Fasc. XXIV.
59. Swanson NR, Granger CWJ. Impulse Response Functions Based on a Causal Approach to Residual Orthogonalization in Vector Autoregressions. Journal of the American Statistical Association. 1997;92(437):357–367.
60. Woodward J. Making Things Happen Oxford: Oxford University Press; 2003.
1 See Hoover [2001, ch. 1] for a fuller discussion of Hume’s views on causality as a philosophical and economic problem.
2 See Hoover [2001, p. 15]. The joint probability of A and B can be factored two ways into a conditional and a marginal distribution: P(B, A) = P(B|A)P(A) = P(A|B)P(B). If A is a prima facie cause of B, then P(B|A) > P(B). Substituting for P(B) in the joint probability distribution gives us P(B|A)P(A) < P(A|B)P(B|A) or P(A|B) > P(A) — that is, B is a prima facie cause of A.
3 If ρ is the correlation between y and m, then the regression estimate of α is 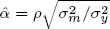 and the estimate of β is
and the estimate of β is 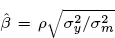 , where ρ is the correlation coefficient between y and m,
, where ρ is the correlation coefficient between y and m, 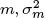 is the estimated variance of m, and
is the estimated variance of m, and 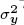 is the estimated variance of y.
is the estimated variance of y.
4 In the simplest cases, this is obvious. If one adopts a rule of trying different regressors until one finds one that passes a t−test at a 5 percent critical value, then the probability of finding a “significant” relationship when the null hypothesis of no relationship is in fact true is much greater than one in twenty. For more complicated search procedures, the effect of search on the true size of statistical tests is hard to work out analytically. In can be shown, however, that some search procedures impose a large cost to search, while others impose quite small costs [Hoover and Perez, 1999; 2004].
5 See Hoover [1988; 1992a; 1992b].
6 On the tension within the new classical macroeconomics between the SVAR and structural approaches, see Hoover [2005].