Experimentation in Economics
1 Introduction
Experimental economics has been the protagonist of one of the most stunning methodological revolutions in the history of economics. In less than three decades economics has been transformed from a discipline where laboratory experimentation was considered impossible, useless, or at any rate largely irrelevant, into a science where some of the most exciting discoveries and developments are driven by experimental data. From a historical point of view, we still lack a detailed and comprehensive account of how this revolution took place.1 The methodological literature, in contrast, is relatively rich — partly because the founders of experimental economics were driven by serious philosophical concerns about the state of their discipline, and partly because philosophers of science are becoming increasingly interested in this new approach.
Like many other scientific disciplines, experimental economics raises a number of interesting philosophical issues. Given the limits of space, it will be impossible to cover them all. I will rather focus on the topics and problems that have attracted most attention in the literature so far, reserving some space at the end for a survey of other relevant issues. The central philosophical problem of experimental economics concerns the validity of experiments. Following an established tradition in psychology, the issue of validity can be analysed in at least two sub-problems, internal and external validity. Internal validity is the problem of understanding the working of a causal relation or causal mechanism within a given experimental setting. External validity is the problem of generalising from a given experimental setting to some other situation of interest.
The two validity problems however are more or less tightly related to a number of other issues in the philosophy of science and the methodology of economics in particular. Before we come to the core of this chapter, then, we will have to cover briefly important topics such as the relation between theory and empirical evidence, the role of experimentation, the notion of causation, confirmation and theory testing, and so forth. In doing that, I shall try to bridge the gap between the fairly abstract way in which such problems are addressed in the philosophy of science literature, and the way they arise concretely from the practice of experimental economics.
1.1 The concept of experiment
What is an experiment? Despite its prominent role in scientific practice, until recently the notion of experiment was rather peripheral in the philosophy of science literature. Traditional epistemology tended to endorse a theory-centred view of scientific knowledge, according to which what we know is encapsulated in our (best) theories, and the latter are supported by the available empirical evidence. Under the influence of logical positivism philosophers of science in the 20th century have come to represent empirical evidence as sets of linguistic reports of perceptual experience. Indeed, in the 1960s and 1970s, prompted by the work of Popper, Quine, Kuhn, and Feyerabend, philosophers of science even came to doubt that a sharp distinction between theoretical and observational statements could be drawn in principle. As Karl Popper puts it in an often-quoted passage, “theory dominates the experimental work from its initial planning up to its finishing touches in the laboratory” [1934, p. 107].
During the 1980s a series of studies of experimental practice challenged the theory-dominated approach.2 However, the new studies of experiment came up with a rather patchy view of experimentation; a new consensus seemed to coalesce around the view that what constitutes an experiment — and especially a good experiment — may well be a context-dependent matter that cannot be settled by a priori philosophical analysis. Different disciplines and different epochs have endorsed different standards of experimental practice, thus making it very difficult to come up with a unified normative philosophical account. If this is right, a philosophical analysis of the notion of economic experiment must emerge from the study of experimental practices in economics. This approach - as a useful heuristics, rather than as a philosophical thesis — will be adopted in this chapter. At this stage, then, it will only be possible to sketch a preliminary, and admittedly vague notion of experiment.
So what is, intuitively, an experiment? The key idea is control: experimenting involves observing an event or set of events in controlled circumstances. It is useful to distinguish at least two important dimensions of control: (1) control over a variable that is changed or manipulated by the experimenter, and (2) control over other (background) conditions or variables that are set by the experimenter. Both dimensions involve the idea of design or manipulation of the experimental conditions: the experimental laboratory is in some intuitive way an “artificial” situation compared to what is likely to happen in the “natural” or “real” world.3
An experiment is usually designed with the aim of getting a clear-cut answer to a fairly specific scientific question. As we shall see, many different kinds of questions can be answered in the laboratory. But typically, such questions regard the 0mutual dependence of some variables or quantities, and in particular the causal relations holding between them. Consider for example a classic medical experiment: here the main question is the effect of a certain drug (X) on a given population of patients suffering from the symptoms of a disease (Y). The experimenter divides a sample of patients in two groups and gives the drug to the patients in one group (the “treatment group”). The variable X (drug) is thus directly controlled or manipulated by the experimenter, who then measures the difference in recovery rates between the patients in the two groups. In order for the comparison to be useful, however, the researcher must make sure that a number of other “background conditions” (for example the other drugs taken by these patients, their age, general health, psychological conditions, etc.) are kept under control — for if the two groups are too different in other respects, we will never know whether the changes are to be attributed to the manipulated variable (the drug) or not.
The experimental method is widely accepted in the medical sciences as well as in physics, chemistry, biology, and other advanced sciences. There are, to be sure, debates concerning the importance of specific experimental procedures, and also regarding the status of experimental vis a vis other kinds of data (is non-experimental evidence necessarily of an inferior quality than experimental evidence, for example?).4 But very few respectable medical researchers, say, would dare questioning the usefulness of the experimental method in general. In contrast, many economists and philosophers find the idea of experimenting with social phenomena dubious, if not plainly ridiculous. This was once the received view in economics, and it took many years for experimental economists to convince their peers that their project was worth pursuing.
1.2 Traditional objections
Economists have generally worried about the practical hurdles that make experimentation difficult or ineffective: experimentation in economics may well be possible in principle, in other words, but is usually unfeasible for unfortunate contingent reasons. John Stuart Mill presents this idea in full-fledged form already in the nineteenth century:
There is a property common to all the moral sciences, and by which they are distinguished from many of the physical; that is, that it is seldom in our power to make experiments in them. In chemistry and natural philosophy [i.e. physics], we can not only observe what happens under all combinations of circumstances which nature brings together, but we may also try an indefinite number of new combinations. This we can seldom do in ethical, and scarcely ever in political science. We cannot try forms of government and systems of national policy on a diminutive scale in our laboratories, shaping our experiments as we think they may most conduce to the advancement of knowledge. [Mill 1836, p. 124]
This view has been dominant until at least the 1980s: there is nothing intrinsic to economics that prevents us from applying the scientific methods of the natural sciences. The limitations are only of a practical kind, for the phenomena we are interested in are typically “macro”, and unfortunately economists cannot experiment with firms, markets, or entire countries in the same way as a biologist can experiment with a cell or a population of fruit flies.
The obstacles to experimentation thus have mostly to do with size and lack of access (and as a consequence, lack of control). These two obstacles of course are not unrelated, lack of access being often derivative from the big size of the object of study. One key move against practical objections consisted therefore in showing that, contrary to the received opinion, economic phenomena can be studied on a small scale, and that it is possible to achieve control of the most important variables of a small-scale economic system.
The study of small-scale laboratory economies became a legitimate method of inquiry only after World War II. Post-war economics was characterised by a number of important transformations. Following Morgan [2003a], we can summarise by saying that in the middle of the twentieth century economics was in the process of becoming a “tool-based science”: from the old, discursive “moral science” of political economy, to a scientific discipline where models, statistics, and mathematics fulfilled the role both of instruments and, crucially, of objects of investigation. In this sense, the rise of modelling is probably the most relevant phenomenon for the birth of experimental economics. Whereas from Mill to Marshall it was more or less taken for granted that economics was mainly concerned with the study of “real-world” markets, it was now possible to argue that economics was concerned with the study of whatever could be modelled by economic theory.
Walrasian economic theory however posed a serious obstacle to laboratory experimentation, for among the various conditions introduced to prove the existence of a unique efficient market equilibrium, the theory postulates a high (indeed, infinite) number of traders with perfect information and no transaction costs. One of the early important results of experimental economics was precisely the demonstration that in practice neither a high number of traders nor perfect information are necessary for the convergence of laboratory markets to competitive equilibria [Smith, 1962]. This result, together with the new systematization of microeconomics around expected utility and game theory, laid down the preconditions for the laboratory revolution to take place. As soon as economic theory turned to the study of small-scale systems, experimental economics became a real possibility.
Charles Plott, one of the pioneers of experimental economics, expresses this thought with great clarity: experimental economists had to remove two “constraints” that stood in the way of laboratory research:
The first was a belief that the only relevant economies to study are those in the wild. The belief suggested that the only effective way to create an experiment would be to mirror in every detail, to simulate, so to speak, some ongoing natural process. […] As a result the experiments tended to be dismissed either because as simulations the experiments were incomplete or because as experiments they were so complicated that tests of models were unconvincing. […] Once models, as opposed to economies, became the focus of research the simplicity of an experiment and perhaps even the absence of features of more complicated economies became an asset. The experiment should be judged by the lessons it teaches about the theory and not by its similarity with what nature might have happened to have created. [Plott 1991, p. 906]
According to such an approach, experimental economics is theory-driven, just like economics as a whole. Useful experiments are always theory-testing experiments, in other words.
2 Theory and Experiment
It is generally agreed now that experiments have many more functions in economics than just theory-testing [Roth, 1995; Smith, 1982; 1994; Friedman and Sunder, 1994]. Plott’s position however has been highly influential for many years and is worth discussing in some detail. One major advantage is that it promises to solve internal and external validity problems with a single stroke. By focusing on theory-testing one can perform the remarkable trick of generating knowledge that is automatically generalisable to non-laboratory conditions:
The logic is as follows. General theories must apply to simple special cases. The laboratory technology can be used to create simple (but real) economies. These simple economies can then be used to test and evaluate the predictive capability of the general theories when they are applied to the special cases. In this way, a joining of the general theories with data is accomplished. [Plott, 1991, p. 902]
General models, such as those applied to the very complicated economies found in the wild, must apply to simple special cases. Models that do not apply to the simple special cases are not general and thus cannot be viewed as such [ibid., p. 905].5
This view is strikingly similar to philosophers’ Hypothetico-Deductive (HD) model of testing:
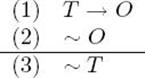
T is a scientific theory or model, and must include some universal statements (laws) of the form: “For all objects x, if x has property P then it must also have property Q”. The argument represented in (1-3) is a case of refutation of falsification, where the predicted observational statement O turns out to be false, and this prompts the conclusion that the theory T must also be false. Falsification of course only accounts for half of the story. Plott says nothing about the other important case, when the evidence seems to confirm the hypothesis under test.6 It is also important to notice that we are assuming here a particularly tight relationship between the theory and the experimental claim that is being tested. In the above examples, the relation is maximally tight, i.e. deductive (T implies O). But is this a correct representation of what goes on in real experimental practice? In order to answer this question, we must have a look at a concrete example.
2.1 An economic experiment
As a matter of historical record, it is undeniable that experimental economics was initially motivated by the desire to test propositions derived from economic theory. “Gaming” — playing game-theoretic problems for real — was common practice in the small community of game theorists in the 1940s and 50s (cf. e.g. [Shubik, 1960]). Some paradigmatic experiments of this period, like the famous “Allais paradox” [Allais, 1953], were explicitly devised to test the implications of von Neumann and Morgenstern’s expected utility theory. And Vernon Smith’s experiments with market institutions were originally presented as testing some propositions of the neoclassical theory of competitive markets [Smith, 1962]. In this section however we shall examine a more recent experiment, as an example of productive interaction between theory and experimentation. In 1988 Jim Andreoni reported in the American Economic Review the results of an experiment that has become a little classic and has since been replicated several times. The experiment — known as the “Partners and Strangers” design — belongs to the family of so-called “public goods” experiments.
Public goods experiments investigate an important but disputable proposition of economic theory, namely that the absence of property rights over certain goods leads inevitably to their under-production. A so-called public good has two essential characteristics: it is (a) nonrivalled and (b) nonexcludable. This means that once it has been produced, (a) many people can consume it at the same time and (b) you cannot make individuals pay for what they consume.
We can start by representing the situation in terms of the familiar prisoner’s dilemma game, as in Table 1. As customary, the first number in each cell represents the payoffs of the row player, the second one of the column player. Notice that given the other player’s move, “defect” always generates a higher payoff than “cooperate.” In game-theoretic jargon, “defect” is a dominant strategy. But then if all players play the dominant strategy, they end up with a Pareto-inferior outcome.
Table 1. A prisoner’s dilemma game

A public goods game is basically a prisoner’s dilemma game with a higher number of players and strategies. Each player has an endowment of x tokens, to be divided in two separate accounts. The first account is “private”, and guarantees a unit of profit for each invested unit; the second is “public” and gives a fraction of the profits of the total number of tokens invested by all the players. For example, suppose there are five players with 50 tokens each. Suppose also that the “production function” of the public good is .5 (each player gets half of the total number of tokens invested in the public account). If everybody invests 25 tokens in the public account, their revenue will be equal to
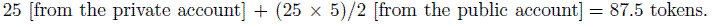
In the standard public goods game all players play simultaneously and anonymously — at the moment of taking her decision, each subject ignores the identity of the other subjects in her group, and how much they are contributing. According to standard economic theory, the public good should not be produced, that is, there should be no contribution to the public project. This conclusion is reached by assuming that each player is indifferent to the others’ payoffs, tries to maximise her own monetary gains, and is perfectly rational in the sense of Nash rationality.7 Under these assumptions the best move — regardless of what the others do — is to contribute nothing. If the others do not contribute anything, why should one give her own tokens, given that she would get back only half of each token contributed to the project? If the others do contribute one token, it is still best not to contribute anything, and to enjoy the fruits of the others’ contribution plus one’s own full endowment. And so on: this reasoning can be iterated for all levels of contribution, and the moral will always be the same.
The Nash solution however is “Pareto-inferior” or sub-optimal with respect to the outcome that would be achieved if everybody were willing to cooperate by contributing to the public account. Using the previous example, in fact, it is easy to calculate that the Nash solution (contribute nothing) gives each player an individual payoff of

The Pareto-optimal solution, instead, would have everybody contributing their full endowment to the public project, thus achieving

Despite the “irrationality” of cooperation, many experimental subjects are willing to give it a go. In a standard one-shot public goods experiment it is common to observe an average level of contribution of about fifty percent of the endowment. If you let the subjects play the game more than once, however, giving them constant feedback about the payoffs and the average contribution levels in previous rounds, their behaviour seems to change. The relatively high initial levels of contribution tend to diminish over time, converging toward the Nash equilibrium. These two phenomena are sometimes referred to in the literature as “overcontribution” and “decay” (cf. [Ledyard, 1995]).
Notice that in a finitely repeated game, according to standard economic theory, a rational homo oeconomicus who tries to maximise his monetary payoffs should still contribute nothing to the public account right from the start. It is a counter-intuitive result, obtained by means of “backward induction”: in the last round it makes no sense to cooperate, because the game will not continue and thus there is no point in maintaining a reputation of cooperator. Whatever the others do, one is better off by free riding, just like in the one-shot game. But everybody knows this, and so at the penultimate round they will not cooperate because they know that at the last round the others will not cooperate. And so on until one reaches the first round of the game: in theory, it is never rational to cooperate.
But in reality, as we have seen, we observe overcontribution and decay. The fact that cooperation is not robust to repetition has suggested the following explanation: initially perhaps some players do not understand the logic of the game. As the game proceeds, they understand that there is a unique equilibrium and that one must always defect. This explanation has stimulated the creation of models with “error and learning”, in which individuals contribute initially above the Nash equilibrium, but slowly converge towards it. Not all the observed initial cooperation however may be due to errors. If some individuals are prone to make mistakes, in fact, some free riders could try to exploit the situation by offering cooperation at the beginning of the game and defecting towards the end. This hypothesis of “strategic play” has been modelled formally by a group of game theorists (Kreps, Milgrom, Roberts and Wilson [1981] — the “Gang of Four” as it is sometimes called) and has provided material for further experimental tests.
In his experiment, Andreoni [1988] has tried to test both the “learning” and the “strategic play” hypotheses. His two main conditions are variants of the baseline public goods game, where subjects play with an endowment of fifty tokens, for ten rounds, in groups of five players. The first important variant is that there are two types of groups: “Partners” who play always with the same players (under anonymity), and “Strangers” who change group at every round. In a group of Partners it could make sense to play strategically in order to build a reputation of cooperative player. In a group of Strangers instead, to build such a reputation is pointless, and a rational player should always defect.
The first interesting result reported by Andreoni is that Strangers do not contribute less than Partners, contrary to the hypothesis of strategic play. As shown in Figure 1, surprisingly, Strangers actually contribute more. The other interesting result concerns the learning hypothesis. Andreoni introduces a simple interruption in the middle of the game, and observes that a break of just a few minutes is sufficient to raise the average contribution to the level observed at the beginning of the game (Figure 2). The idea that decay is due to learning is therefore discredited — or, at any rate, if learning takes place it must be of a very fragile kind.

Figure 1 Partners vs. Strangers
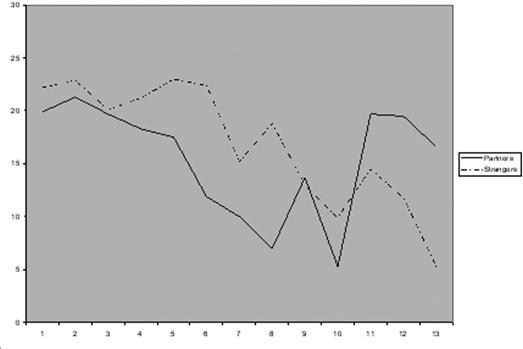
Figure 2 Effect of restart at round 10
2.2 The Duhem-Quine problem
In some obvious sense, Andreoni’s experiment is aimed at theory-testing. The Partners/Strangers design is clearly motivated by the model of the “Gang of Four”, for example. It is important to notice nevertheless that the relationship between model and experimental design is quite slack. Kreps and his colleagues for example do not model a public goods game situation explicitly. Their theoretical analysis focuses on related games like the prisoner’s dilemma, and Andreoni simply assumes that it can be extended unproblematically to public goods situations. In the case of learning, similarly, Andreoni does not test specifically any of the various models that have been proposed in the literature. He focuses instead on a broad proposition (that learning is somehow robust to short interruptions) that seems to be implicitly assumed by all such theories.
Notice also that the very concept of “economic theory” under test is not so clear-cut after all. Standard microeconomics does not impose strong restrictions on the contents of individual preferences. An agent can in principle maximise all sorts of things (her income, her fun, her sleep) and still behave “economically”. In order to make the theory testable, therefore, it is necessary to add several auxiliary assumptions regarding the contents of people’s preferences (or, equivalently, regarding the argument of their utility functions), their constraints, their knowledge, and so forth. In our example, Andreoni is really testing only a very specific prediction obtained by adding to the basic theory some strong assumptions about people’s preferences, e.g. that they are trying to maximise their monetary gains and do not care about others’ payoffs.
We are of course dealing with a typical Duhem-Quine issue here. Experimental results usually do not indicate deductively the truth/falsity of a theoretical hypothesis in isolation, but rather of a whole body of knowledge or “cluster” of theoretical and auxiliary hypotheses at once.8 Formally, the Duhem-Quine thesis can be presented as follows:
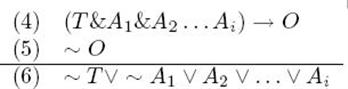
The argument states that from (4) and (5) we can only conclude that at least one element, among all the assumptions used to derive the prediction O, is false. But we cannot identify exactly which one, from a purely logical point of view. The last point is worth stressing because the moral of the Duhem-Quine problem has been often exaggerated in the methodological literature. The correct reading is that deductive logic is an insufficient tool for scientific inference, and hence we need to complement it by means of a theory of induction. The Duhem-Quine problem does not imply, as sometimes suggested, the impossibility of justifiably drawing any inference from an experimental result. Scientists in fact do draw such inferences all the time, and it takes a good dose of philosophical arrogance to question the possibility of doing that in principle. What we need is an explication of why some such inferences are considered more warranted than others. If, as pointed out by Duhem and Quine, deductive logic is insufficient, this must be a task for a theory of induction.9
2.3 Testing theoretical models
As pointed out earlier the theory-testing position, as formulated by Plott and others, tries to solve both problems of validity at once. The Duhem-Quine problem is an obstacle for this project, to the extent that experimental results do not seem to imply deductively the truth or falsity of a particular scientific hypothesis. It is not, however, an insurmountable obstacle, provided we can define an adequate set of inductive rules to tackle Duhemian problems in a non-trivial range of situations. If this were possible, the theory-testing view would be vindicated.
Still, there are other implicit assumptions behind the Plott position that ought to be challenged. The theory-testing view assumes that theories come fully interpreted and presented in a form that makes them amenable to direct empirical testing. Remember the key passage in Plott’s argument: the laboratory is a legitimate testing domain because economic models are unrestricted or universal in scope of application. So whatever situation falls in the domain of the theory (within or without the laboratory) is a legitimate testing site. But what is the domain of economic theory?
Robin Cubitt [2005] distinguishes between three different relevant domains of an economic model: the base domain, the intended domain, and the testing domain. The base domain is a set of situations or phenomena to which the theoretical model seems to be unambiguously applicable — for example the domain of random draws from an urn, for a model of individual choice under risk. The intended domain, which does not necessarily coincide with the base domain, is instead the set of situations to which the model is expected to apply — the set of phenomena we want the model to explain, which is usually broader than the base domain. (We expect a theory of choice under risk to throw light on, e.g., insurance purchasing, to use Cubitt’s example.) The testing domain, finally, is the set of situations where the theory can be legitimately tested, and in principle it should not necessarily be identical with any of the previous two.
Using this framework, one can read Plott as saying that the testing domain of a model must include its base-domain. Cubitt instead takes a more cautious stance. He argues that the base belongs in the testing domain only prima facie, i.e. unless there is some clearly specified reason to believe that the base and the intended domains differ in important respects. Economic models, in other words, are usually put forward with a certain target in mind — a set of phenomena or mechanisms they are intended to explain. The intended domain of a theory is often only vaguely specified, which explains why it is tempting to do away with it and simply interpret the theory literally. Interpreted literally, however, the theory applies only to a rather narrow set of phenomena (the base domain). We still need an argument showing that results obtained in the base carry over to the intended domain. Cubitt suggests that we should take this as the default case, absent a proof to the contrary.
I shall return to this argument later on. For the time being, it is important to realise that even the base domain of a model cannot always be sharply identified. In translating an abstract model into a concrete design, a series of decisions have to be made at various steps during the translation, many of which are highly arbitrary. For example, there is no particular theoretical reason why there should be four, five, or fifty subjects in each group of a public goods experiment; there could be more or less. Similarly, the theory does not say much about the production function; in theory, it should not matter, although in practice we suspect that it might. At no point the theory identifies the “right” design for experimental purposes, in other words. As Marc Isaac [1983] points out, one great virtue of laboratory work is that it forces to operationalise theoretical models, and in doing so the scientist is led to reflect on several aspects of the model and the experiment that wouldn’t otherwise have been considered problematic.
Perhaps we should simply recognise that in empirical work we are never really testing a theoretical model, but rather one of its (many) possible interpretations or applications [Guala, 2005a, Ch.10; Hausman, 2005]. In this sense, then, an experiment in the base domain does not speak unambiguously about the truth/falsity of a theoretical model. It rather tells us something about the way it can be operationalised. But there are many ways of operationalising the model, some within and others outside the base domain. An inferential move from an experiment in the base domain to one in the intended domain requires independent justification. If this is the case, then, why has the base domain of theories become a privileged site for experimentation? In order to answer this question it will be necessary to investigate some important similarities between theoretical models and controlled experiments.
2.4 Models and experiments
To operationalise, or to transform a theoretical model into an applied one, may be conceived of as a process of adding more detail to the description of a given situation. During such process, one moves progressively from abstract towards a concrete account [Cartwright, 1989, Ch. 5]. This conception is consistent with a linguistic view of scientific models — i.e. of models as set of propositions. Plott and Cubitt seem to have a linguistic view in mind, when they speak of theoretical models being able to specify (or not) their own domain of application. An alternative view, which has gained the status of quasi-orthodoxy in contemporary philosophy of science, in contrast sees models as structures — sets of entities with certain relations and properties. Under this approach — known as the “semantic view of theories” — a more concrete model is an object endowed with more realistic properties than its abstract counterpart. Speaking of models as objects or structures leads naturally to emphasise the analogies between models and experiments. In this section we discuss their relation along three important axes, namely the manipulative, the representative, and the isolative analogy.
Morrison and Morgan [1998] claim that many scientific models work as “mediators” between the abstract principles of a scientific theory and empirical reality. In a mediating model theoretical principles are combined with substantive information from the real world, to create a tool that can be used to investigate both realms: the theoretical realm by deriving interesting implications that were not obvious from an examination of the theory itself, and the real world by deriving testable predictions about observable phenomena. Morrison and Morgan’s account of mediating models draws explicitly from the philosophy of experiment of the 1980s, in particular from the work of those scholars, like Ian Hacking [1983], who have emphasized the importance of intervention and manipulation in experimental science. Morrison and Morgan highlight the analogies between reasoning with models and experimental reasoning by stressing the importance of intervention and manipulation in either realm. This is the “manipulative analogy” between experiments and models, as I shall call it from now on.
Recent philosophical work on experimental economics has traveled the same path backwards, so to speak, from models to experiments. Economic models and experiments are both “mediating” entities, surrogate systems that can be used to study other entities that are too big or small in size, too complex, or too distant to be directly investigated [Guala, 1998; 2005a]. The “mediators” idea originally was meant to highlight that a laboratory experiment is rarely the final step in a research project, for experimental results must eventually be transferable to the real world systems that constituted the original target of research. Using Cubitt’s terminology, the mediating metaphor highlights the gap between the testing domain and the intended domain, which ought to be bridged by a special inferential move (an external validity inference). Besides the manipulative analogy, thus, there is also a “representative analogy” between experiments and models: both stand for some other system, or set of systems, that is the ultimate target of investigation.
Finally, the “isolative analogy” highlights that both experiments and models derive their inferential power from their being designed so as to (1) eliminate some real-world complications, and (2) keep some potentially disturbing factors “fixed” in the background (see [Boumans and Morgan, 2001; Mäki, 2005; Morgan, 2005]). Theoretical models — especially the most abstract ones — ignore or assume away several properties of real economic systems that are potentially relevant for their behavior. This sort of abstraction or isolation10 results in a simpler model that is more amenable to analysis, and is therefore typically justified on heuristic or pragmatic grounds. The experimental counterpart of a simple (relatively abstract) model is a relatively simple experiment in the base domain of that model. Such experiment will also be more amenable to manipulation, and interpretation. For this reason economists tend to privilege experiments in the base domain of a theory, at least at the beginning of a research program. Experimenters replicate the base domain because they try to instantiate the isolative assumptions of the model.
Uskali Mäki [2005] has formulated probably the boldest proposition regarding models and experiments. Pushing the analogy to the extreme, he has proposed to turn it into an identity: “models are experiments and experiments are models”. There are reasons to resist such a move, however. One is that scientists themselves seem to find it useful to have a separate terminology to denote these scientific tools. Philosophers of course can be revisionary with respect to scientific language to a certain extent, but must also be aware that differences in language often reflect substantial differences at the level of methodology and scientific practice. What could this difference be in the case of experiments and models? Experimental economists often put it in terms of the materials they experiment with: “laboratory microeconomies are real live economic systems, which are certainly richer, behaviorally, than the systems parametrized in our theories” [Smith, 1982, pp. 923–5].
In order to articulate this idea, Guala [2002a] has adapted Herbert Simon’s [1969] distinction between simulating and experimental devices. In a simulation one reproduces the behavior of a certain entity or system by means of a mechanism and/or material that is radically different in kind from that of the simulated entity. Paradigmatic examples may be the simulation of a historical battle by means of miniature toys, or the simulation of the propagation of light waves using a ripple tank. Although water and light waves display the same patterns and thus can be described by the same models at a relatively superficial theoretical level, the underlying mechanisms are not the same nor obey the same fundamental laws of nature.
In this sense, models simulate whereas experimental systems do not. Theoretical models are conceptual entities, whereas experiments are made of the same “stuff” as the target entity they are exploring and aiming at understanding. The difference between models and experiments is thus relational rather than intrinsic — whether a mediating tool counts as a model or an experimental system depends on how it is used, and what it is used for (what its target is). Experiments are not models, in this sense, and models are not experiments — although both are mediating epistemic tools (different species of the same genus, in other words).11
As a consequence, modeling and experimenting have different virtues and defects. According to Morgan [2005], the advantage of experimentation over modeling is that in manipulating a model we can only be “surprised” but not “confounded”. We might derive a surprising result that we had no idea was implicit in the premises/components of the model, but we rarely misinterpret the inner workings of a model, because we have built it ourselves. In contrast, an experimental system is always opaque to a certain extent, because the builder/experimenter has left some degree of freedom of expression in the system that will teach us something previously unknown. This opaqueness may be the principal source of misinterpretation of the experimental result, but is a resource for at least two reasons: (1) because it can teach us something new, as we have seen; but also (2) because it allows one to use some systems as “black boxes” that we do not understand perfectly, provided we are confident that the same basic principles (whatever they may be) are at work in the target. For example: one can use real individual agents in market experiments even though we have no general understanding of individual decision making, if we are confident that such agents are good representatives of those in the target [Guala, 2002a].
In general, it is worth keeping in mind that these conceptual distinctions probably do not reflect a sharp divide at the level of scientific tools and practices. In reality we rather find a continuum, with many “hybrid epistemic tools” that do not fall in either category neatly. In a series of papers Morgan [2002; 2003b] uses the expression “virtually experiments” to denote systems that embed a real-world material component within a predominantly simulated (model) environment.12
3 Experimental Inferences
Economists often test models in their base domain in order to replicate the isolation assumptions of the models. But highlighting the isolative analogy exacerbates the problem of making inferences from base to intended domain. Since most experiments test theories in the base domain, and even the identification of the base domain requires some arbitrary interpretative choices, an inference from the testing or base domain to the intended domain requires independent justification.
This point underlies the crucial distinction between internal and external validity. To recall: problems of internal validity have to do with the drawing of inferences from experimental data to the causal mechanisms of a given laboratory situation. Typical internal validity questions are: Do we understand what goes on in this particular experimental situation? Are we drawing correct inferences within the experiment? External validity problems instead have to do with the drawing of inferences from experimental data to what goes on in other (laboratory or, more typically, non-laboratory) situations of interest. They involve asking questions like: Can we use experimental knowledge to understand what goes on in the “real world”? Are we drawing correct inferences from the experiment?13
So far I have said almost nothing about the inferential strategies employed to tackle the two validity problems. For various reasons it is wise to start by looking at internal validity first. The analysis of internal validity ideally should provide some basic conceptual tools to tackle the admittedly more difficult problem of external validity later on. The reasoning is as follows: both inferences within and from the experiment belong to the general category of inductive inferences. We should therefore be able to use the techniques that economists use (rather successfully) to solve internal validity problems to construct a more general theory of inductive inference. Once that has been done, the theory can be used to shed some light on external validity too.
The approach endorsed in this chapter and elsewhere (e.g. [Guala, 2005a]) is distinctively normative in character. This means that we shall not just look at the inferences that experimental economists as a matter of fact do draw when they interpret their results. We shall also be concerned with the justification of such inferences, and aim at capturing the normative core underlying experimenters’ intuitive distinction between “good” and “bad”, “strong and “weak”, warranted and unwarranted inferences. This does not mean that descriptive approaches to inductive inference are useless or uninteresting. On the contrary, we can learn a lot by investigating the way in which psychological propensities or social conditions affect inferential performance. But just as a purely normative approach carries the risk of leading to an unrealistic theory of induction, a purely descriptive approach is unable answer the important question of the efficacy or adequacy of an inferential method, given certain goals. The answer surely must be a combination of normative and descriptive investigation that is able to overcome the limitations of both.
That an intuitive distinction between good and bad inductive practices exists and is not merely a philosophical construct is of course a hypothesis, but a hypothesis that is supported by several observable facts. The birth of experimental economics for example was motivated by the desire to improve the methodological practice of economic science. I will articulate this idea by saying that the experimental method enables one to test economic hypotheses more severely than traditional testing with econometric data would allow. The notion of severity thus will be at the centre of the discussion. While illustrating the method of severe testing, however, it will also turn out to be useful to discuss some alternative proposals that depart in various ways from the severity approach.
3.1 Experiments and causal analysis
It is interesting that Andreoni, when he illustrates the logic of his experiment, does not refer directly to theory-testing:
The experiment reported in this paper is intended to separate learning from strategic play. The design is subtractive: subjects participate in a repeated-play environment, but are denied the opportunity to play strategically. Without strategic play, we can isolate the learning hypothesis. Furthermore, by comparing this group to one that can play strategically, we can attribute the difference, if any, to strategic play [1988, p. 294].
Andreoni says that he is trying to “isolate” some factors, by “subtracting” their influences, and studying their effects in isolation. When strategic play has been eliminated (by means of the Partner and Strangers device) all the remaining contributions to the pubic good can be attributed to learning. But should it be so attributed? This leads to the second design: “to isolate the learning hypothesis, the experiment included a ‘restart”’ [Andreoni, 1988, p. 295]. The answer, as we have seen, is eventually negative — there is more going on in public goods experiments than just error, learning, and strategic play.
Notice the remarkably causal flavour of Andreoni’s language: there are several causal factors at work, whose effects can be separated, added, and subtracted by experimental means. Andreoni’s reasoning suggests that experimental economists are not interested in testing theoretical models per se. Models are attempts to represent formally the working of some basic causal mechanisms in isolation. It is these mechanisms that economists are interested in understanding, and therefore their experiments sometimes depart from the letter of the theory, to “isolate” or “separate” the effects of different causal factors. In what follows we shall take this language seriously, and reconstruct the distinctive character of the experimental method as an attempt to investigate the causal influence of separate factors working in isolation.
Economists are traditionally wary of causal language (Hoover 2004), so this claim requires a bit of elaboration. Despite centuries of philosophical attempts to reduce causation to more “respectable” concepts (such as constant conjunction or statistical association), it is now generally agreed that causal relations have intrinsic properties — like asymmetry, counterfactual dependence, invariance to intervention — that cannot be fully eliminated by means of a reductive analysis. There are now several non-reductive theories of causation in the philosophical and the economic literature, which for reasons of space cannot be reviewed here (but see e.g. [Hausman, 1998; Woodward, 2003]).
Despite continuing disagreement on the central metaphysical issue of causation (its very meaning and essence), there is broad agreement that the method of the controlled experiment is a powerful tool for the discovery of causal relations. The reason, in a nutshell, is that controlled experimentation allows underlying causal relations to become manifest at the level of empirical regularities. In a competently performed experiment, single causal connections can be “read off” directly from statistical associations.
It is better to start with a homely example. Imagine you want to discover whether flipping the switch is an effective means for turning the light on (or whether “flipping the switch causes the light to turn on”). The flipping of course will have such effect only if other enabling background conditions are in place, for example if the electricity supply is in good working order. Thus first we will have to design an experimental situation where the “right” circumstances are instantiated. Then, we will have to make sure that no other extraneous variation is disturbing the experiment. Finally, we will check whether by flipping the switch on and off we are producing a regular association between the position of the switch (say, up/down) and the light (on/off). If such an association is observed, and if we are confident that every plausible source of mistake has been controlled for, we will conclude that flipping the switch is causally connected with turning the light on.
The moral, in a nutshell, is that causal discovery requires variation, but not too much variation, and of the right kind. In general, you want variation in one factor while keeping all the other putative causes fixed “in the background”. This logic is neatly exemplified in the model of the perfectly controlled experiment:
Table 2. The perfectly controlled experimental design

The Ki are the background factors, or the other causes that are kept fixed across the experimental conditions. The conditions must differ with respect to just one factor (X, the treatment) so that any significant difference in the observed values of Y (Y1 − Y2) can be attributed to the presence (or absence) of X. A good experimenter thus is able to discover why one kind of event is associated regularly with another kind of event, and not just that it does. In the model of the perfectly controlled experiment one does not simply observe that “if X then Y”, nor even that “X if and only if Y”. Both such conditionals are material implications, and their truth conditions depend on what happens to be the case, regardless of the reasons why it is so. In science in contrast — and especially in the sciences that are used regularly for policy-making, like economics — one is also interested in “what would be the case if” such and such a variable was manipulated. Scientific intervention and policy-making must rely on counterfactual conditionals. A great advantage of experimentation is that it allows to check what would happen if X was not the case, while keeping all the other relevant conditions fixed.
We can now draw a first important contrast between the experimental method and traditional econometric inferences from field data. Econometricians apply statistical techniques to establish the strength of various correlations between economic variables. But except in some special happy conditions, the spontaneous variations found in the data do not warrant the drawing of specific causal inferences. Typically, field data display either too little or too much concomitant variation (sometimes both). Some variations of course can be artificially reconstructed post-hoc by looking at partial correlations, but the ideal conditions instantiated in a laboratory are rarely be found in the wild — except in so-called “natural experiments”.14
This does not mean that total experimental control is always achieved in the laboratory. We must keep in mind that the perfectly controlled experiment is an idealisation, and in reality there are always going to be uncontrolled background factors, errors of measurement, and so forth. In order neutralise these imperfections, experimenters use various techniques, like for example randomization.15 In a randomized experiment subjects are assigned by a chance device to the various experimental conditions, so that in the long run the potential errors and deviations are evenly distributed across them. This introduces an important element in the inference from data, i.e. probabilities. A well-designed randomized experiment makes it highly likely that the effect of the treatment be reflected in the data, but does not guarantee that this is going to be the case. Assuming for simplicity that we are dealing with bivariate variables (X and ∼ X; Y and ∼ Y), in a randomized experiment if (1) the “right” background conditions are in place, and (2) X causes Y, then P(Y | X) > P(Y |∼ X). In words: if (1) and (2) are satisfied, X and Y are very likely to be statistically correlated.
Some authors (notably [Cartwright, 1983]) have used this relation or some close variant thereof to define the very notion of causation. Such a definition is essentially a probabilistic equivalent of J.L. Mackie’s [1974] famous INUS account, with the important addition of a “screening off” condition.16 The latter is encapsulated in the requirement that all other causal factors in the background are kept fixed, so as to avoid problems of spurious correlation. Several interesting philosophical implications follow from choosing such a definition of causation, which however would take us too far away from our present concerns. In the following sections I shall build on the model of the perfectly controlled experimental design to articulate a more general theory of inductive inference. The perfectly controlled experiment is a “model” in a sense that should be familiar to economists: it is an idealisation that captures the essential features of a broader set of inferential strategies. Moreover, like economic models, it has also the ambition of capturing some normative truth about how we ought to do science, as opposed to just describing what experimenters do as a matter of fact.
3.2 The severity approach
The above analysis suggests an obvious way to tackle the Duhem-Quine problem, by simply asserting the truth of the background and auxiliary assumptions that are used in designing an experiment. In a competently performed controlled experiment, in other words, we are entitled to draw an inference from a set of empirical data (or evidence, E) and some background assumptions (Ki) to a causal hypothesis (H = “X causes Y”). The inference consists of the following three steps:

This is an instance of the Hypothetico-Deductive model of testing. In this case the evidence indicates or supports the hypothesis. The symmetric case is the following:
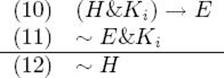
In the latter case, the inference is deductive. If (and sometimes this is a big “if”) we are ready to assert the truth of the background assumptions Ki, then it logically follows that the evidence E refutes or falsifies H. Since we are not often in the position to guarantee that the Ki are instantiated in reality a refutation is usually followed by a series of experiments aimed at testing new hypotheses H′, H′′, etc., each concerned with the correctness of the design and the functioning of the experimental procedures. If these hypotheses are all indicated by the evidence, then the experimenter usually feels compelled to accept the original result.
Notice that in the first case (7–9) the conclusion of the argument is not logically implied by the premises, or in other words the inference is inductive. Of course many scientific inferences have this form, so the point of using the experimental method is to make sure that the inductive step is highly warranted, or that the inference is as strong as possible. The conditions for a strong inductive inference are outlined in normative theories of scientific testing. Although there is presently no generally agreed theory of inductive inference in the literature, the model of the perfectly controlled experiment suggests a few basic principles that any adequate theory should satisfy. When an experiment has been competently performed — i.e. when the experimenter has achieved a good degree of control over the background circumstances Ki — the experimental data have the following, highly desirable characteristics:
(a) if X causes Y, the observed values of the experimental variables X and Y turn out to be statistically correlated;
Another way to put it is this. In the “ideal” experiment the evidence E (correlation between X and Y) indicates the truth of H (X causes Y) unequivocally. Or, in the “ideal” experiment you are likely to get one kind of evidence (E) if the hypothesis under test is true, and another kind of evidence (∼ E) if it is false [Woodward, 2000]. Following Deborah Mayo [1996; 2005], we shall say that in such an experiment the hypothesis H is tested severely by the evidence E.17
More precisely, severe testing implies that (i) the evidence fits the hypothesis, and (ii) that such a good fit would have been unlikely, had the hypothesis been false. One (but not the only) measure of fit is the ratio between the likelihoods P(E | H) and P(∼ E | H). When P(E | H)/P(E |∼ H) is high, we will say that the evidence fits the hypothesis very well. A good fit however is not the end of the story: according to the second severity requirement it is necessary that such a good fit would have been highly unlikely, had H been false. This second, crucial condition is established by considering not just E and H (and its alternatives) but the entire distribution of data-sets that would have been obtained if the experiment had been repeated in various circumstances.18
It is important to notice that we are here dealing with objective conditions or states of affair. The model of the perfectly controlled experiment does not describe an epistemic state. It tries to describe an ideal testing device: in the model of the perfectly controlled experiment there is an objectively high probability of obtaining E if H is true. The probabilities of severe testing, in other words, are properties of the experimental set-up, and not to be read as epistemic (logical or subjective) probabilities.
The logic of severe testing accords with the widely adopted practice of using formal statistical tests in experimental science. Suppose we are testing the hypothesis H1 = “X causes Y”, by designing an experiment along the lines of the perfectly controlled model. Because of the impossibility of eliminating the influence of all disturbing factors and errors of observation, we will almost certainly observe some (perhaps quite small) difference between the values of Y in the treatment (let us call them Y1) and in the control condition (Y2), even if H1 is false. The observed frequency of Xs and Ys, in other words, will be such that some (positive or negative) correlation will almost certainly exist between the two variables, come what may. But is such a correlation big enough to count in favour of H1? The job of statistical testing is to help us determine what counts as “small” or “big” in such a context by specifying a range of values for Y1 −Y2 that we consider too unlikely to be compatible with the truth of H1. Using certain statistical assumptions and the statistical properties of the data-set, experimenters can calculate the significance levels of the test (customarily, the 5% or 1% levels are used) and thus effectively identify what sort of evidence counts as E (as indicating H1) and what as ∼ E (as refuting H1) in this particular experiment.
Suppose for example that we observe a relatively large discrepancy between Y1 and Y2, so large in fact that such a difference would be observed only less than 1% of the time, if H1 were false (if X did not cause Y, that is). Such a large discrepancy is our positive evidence E. Statistically, E can be used to reject the null hypothesis H0 = ∼ H (= “X does not cause Y”) at the 1% level. According to the severity approach, E counts as a strong piece of evidence in favour of H1, because in such circumstances P(E; ∼ H) is very low, and P(E; H) is high.
3.3 Objectivist vs. subjectivist approaches
The first distinctive characteristic of the logic of severe testing is that it is an “objectivist” approach to inductive inference, in the sense that probabilities are used to measure the objective properties of testing devices. To appreciate the importance of such a feature, in this section I shall compare the severity approach with an alternative theory of induction (belonging to the “subjectivist” approach) that uses probabilities to measure the strength of belief or the degree of confirmation of a hypothesis in light of the evidence. This alternative theory is so-called “Personalist Bayesianism”. Bayesians see the logic of science as the business of updating one’s beliefs in light of the evidence, using Bayes’ theorem as an engine to derive posterior subjective probabilities from prior probabilities concerning hypotheses and evidence.19
As we have seen in discussing the HD model, a piece of evidence E can typically be derived from a hypothesis H only with the help of a series of auxiliary assumptions concerning background and boundary conditions Ki : (H&Ki) → E. It follows that from the point of view of deductive logic the observation of E or ∼E cannot be used to derive unambiguous conclusions regarding the truth or falsity of H (Duhem-Quine thesis). The severity approach tackles the Duhem-Quine problem by identifying the conditions in which the two severity requirements (i) and (ii) are satisfied. The way of satisfying the requirements is to design a severe experimental test, i.e. to set the experimental conditions Ki in such a way as to obtain the desired severity. It is important to stress that this does not imply the attribution of a certain (presumably high) degree of belief in a hypothesis Ki = “the background assumptions are true”. The severity approach is not looking for a quantitative measure of our degrees of belief as an outcome of the testing procedure, and therefore does not need a quantitative input either.
Personalist Bayesians in contrast do need such an input. Bayes’ theorem is a calculative engine that transforms prior probabilities into posterior ones. The relevant inputs are the prior probability of the evidence, the prior probability of the hypothesis, and the prior probability of the background assumptions. Bayesians do not impose any restriction on the subjective degrees of belief that may be accorded to any of these (beyond some basic consistency requirements). They just impose some dynamic constraints to make sure that we can learn from the evidence, for example by stipulating that P(Ht+1) = P(Ht | E).20 This machinery ensures that the Duhem-Quine problem can be tackled dynamically, i.e. by updating the probability of a hypothesis in a series of replications.
Following Redhead [1980], Morten Søberg [2005] shows that by testing a hypothesis repeatedly in conjunction with different sets of auxiliary assumptions,
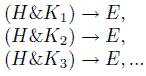
one can reach a (subjectively) highly probable conclusion about the truth of H. If the series of experiments or “replications” produces consistent results (say, E), in fact, it is possible to show that whatever prior probability was originally assigned to H, it will be “washed out” by the accumulating evidence.
There are several important differences between the Bayesian and the severity approach, but one of the most striking is the diachronic character of Bayesian rationality. In the severity approach one competently performed experiment suffices to provide strong evidence in favor of H. According to Bayesianism, in contrast, it may take some time to raise (or lower) the probability of a hypothesis, because of the heavy reliance on subjective priors.
Bayesians at this point appeal to the distinction between confirmation and support: H may not be highly confirmed (i.e. P(H | E) may be low for all sorts of reasons, including a low subjective prior) and yet highly supported by E. The impact of E on the probability of H, in fact, depends crucially on the likelihoods P(E | H) and P(E |∼ H), which are independent of a scientist’s subjective beliefs.
Although a high P(E | H) and a low P(E |∼ H) imply a strong degree of support for H, it is important to stress again that the likelihoods differ markedly from the two severity conditions outlined above. Whereas severity measures the objective chance of a testing procedure to give rise to evidence E, under the assumption that H is correct, P(E |∼ H) is a measure of the logical relation between E and whatever alternatives to H one is able to conceive of. Suppose for example that H: “the coin is biased”. It is always possible to create an alternative hypothesis that makes E maximally likely from a logical point of view (“the coin is fair but a Cartesian devil makes the coin land tail every time I flip it”). In contrast, it is not always possible to raise severity in a similar fashion, because a given experimental procedure (e.g. flipping the coin) is not necessarily appropriate to test such alternatives. (In order to test the devil hypothesis, you need an exorcist, not a coin-flipper.)
Another way to put it is that Bayesian theories of inductive inference are happy to process whatever piece of evidence one is able to come up with. The impact of the evidence as well as the final posterior probability depend on various factors that do not necessarily have to do with how the evidence was generated. Severity testing is more selective: the goal is not belief updating, but rather producing a piece of evidence that is really able to speak for or against H. And whether this is the case depends crucially on the experimental set-up. In this sense, the severity approach seems to make better sense of the logic and practice of experimental science, where an enormous care is taken to make sure that the “right” conditions are created to generate a truly informative piece of evidence.21
3.4 “Low” vs. “high-level” hypothesis testing
A second important characteristic of the severity approach then is that it turns hypothesis-testing into a fairly “local” business, in the sense that a given experimental design is usually appropriate for testing only a fairly precise hypothesis, but has no direct implications about the truth of broader theories. Consider the coin-flipping example in the previous section. By flipping a coin and observing that we invariably obtain “head”, we can only test a hypothesis concerning the fairness of the experimental procedure, but we are not necessarily able to check the source of the bias. In order to do so, we would have to design other experiments, for example by inspecting the weight and balance of the coin itself, or the presence of a magnetic field in its vicinity. Another way to put it is that by repeatedly tossing a coin we can test a low-level hypothesis about the existence of a phenomenon (the coin’s propensity to systematically land “head”), but we are not able to say much about its explanation (why it has got such a propensity).
To provide explanations for scientific phenomena is usually the job of scientific theories and models. The testing of complex theories however requires many years of experimentation with several different designs, each one concerned with the testing of a fairly specific or “local” aspects of the theory itself. Fortunately, experimental activity can proceed for a long time quite autonomously from high-level explanatory theory. This point has been established over many years of study of experimental practice by philosophers, historians and sociologists of science.22 Students of experiments have long recognised that in many scientific disciplines there exists a body of experimental knowledge that is largely independent from high theory. Much of this experimental knowledge takes the form of an ability to create and replicate at will robust phenomena, which then take a “life of their own” independently of the explanations that are devised to explain their occurrence.
The severity approach can account for both types of experimentation — experiments devoted to theory-testing, but also of experiments devoted to the discovery and investigation of laboratory phenomena. In a recent article, Robert Sugden [2005] distinguishes between experiments as tests of theories and experiments as exhibits. An “exhibit” is an experimental design coupled with an empirical phenomenon it reliably brings about. According to Sugden, in the case of theory-testing experiments “we gain confidence in a theory by seeing it withstand those tests that, when viewed in any perspective other than that of the theory itself, seem most likely to defeat it” [2005, p. 299]. A good theory-testing experiment, in other words, maximizes the probability of obtaining a negative result, if the theory is false.
Sugden’s analysis is entirely compatible with the severity approach. Remember that for a hypothesis to pass a severe test, E must have a good fit with H, but must also be observed in an experimental set-up such that such a good fit would not be expected, had H been false. In the case of theory-testing experiments Sugden clearly focuses on the second requirement (a good experiment must produce negative evidence with high probability, when viewed from the perspective of the falsity of H). But implicitly, he is also assuming that the initial conditions of the experiment have been designed in such a way so as to obtain a high probability of observing evidence that fits H. When testing a theory, in fact, one usually derives a prediction about the occurrence of a certain phenomenon, given certain assumptions about the initial and boundary conditions (T → E). T only issues conditional predictions and does not say what will happen when the appropriate conditions are not in place, so the conditions that make E probable (if the theory is true) must be instantiated if this is to count as a genuine test of T.
Turning to the case of exhibits, Sugden argues that experimenters often focus on those conditions where the phenomenon is most likely to be displayed. “Is it legitimate to focus my attention on decision problems in which my intuition suggests that the kind of effect I want to display is particularly likely to be found? […] My inclination is to answer ‘Yes’ […]” [Sugden 2005, p. 300]. The search for a phenomenon is usually guided by some (possibly quite vague and informal) “hunch” about the mechanisms that may produce a certain regularity of behaviour. Because such a hunch is not precisely formulated, it is usually impossible to devise a testing situation that is able to establish the existence of a phenomenon and to test an explanation of why it came about. In such cases, experimenters end up designing experiments where the phenomenon is highly likely to be observed, assuming the truth of the hunch, but that do not minimise the probability of observing the phenomenon if that hunch was mistaken.23
Does this mean that the second severity requirement (that it is unlikely to observe a good fit with H if H were false) is violated in exhibit experiments? No. We want to distinguish between theory-testing and exhibit experiments precisely to keep in mind that a different kind of hypothesis is under test in each type of experiment. Although an exhibit experiment usually does not test severely an explanation of the phenomenon, it can (and should) test severely a low-level hypothesis concerning the existence of some regularity in the data (i.e. the phenomenon). The hypothesis under test is usually the null H0: “the regularity is a chance effect”. When this hypothesis has been rejected with a high level of significance, the second severity requirement has been satisfied.
The moral is that it is important always to ask what, if anything, has been severely tested in a given experimental set-up. Quite often, it will turn out that only low-level, fairly local claims are warranted by the evidence, whereas high-level theoretical hypotheses or explanations remain untested. The fact that one can construct a theory to explain some data does not mean that the theory has been tested by those data at all.
3.5 Novelty and construct independence
A third distinguishing characteristic of the severity requirement is its being formulated in purely logical or synchronic terms. Whether a hypothesis has been proposed before, during or after the collection of the evidence is irrelevant in itself. It matters only if it affects the severity of the test. Severity theorists, to put it differently, deny that the temporal relation between evidence collection and theory-formation can be used to define some necessary condition for evidential support. There may well be cases of hypotheses proposed after the collection of the evidence that are nevertheless supported by that very evidence.
This indifference to temporal matters is in stark contrast with the standard methodological rule in economics — popularised by Milton Friedman [1953] — that the only relevant test of a theory is the success of its predictions. Despite paying lip-service to the Friedmanian rule, as a matter of fact economists tend to interpret the term “prediction” loosely and to allow all sorts of exceptions. This is wise, because it is easy to find episodes in the history of science where scientists felt no embarrassment in using some “old” evidence to argue in favour of a new theory. The fact that Einstein’s relativity theory was able to account for the shifting perihelion of Mercury (a phenomenon that had been known for centuries), for example, was widely considered an important element in support of the new theory. But consider also the econometric practice of splitting a sample of data in two parts, one for estimating the parameters of a model, and one for testing the predictions (but we should say “retro-dictions”) derived from the estimated model. Again, the fact that the data had been collected before the estimated model was formulated seems to be irrelevant for the issue of evidential support.
Some philosophers have tried to weaken the temporal requirement by endorsing a so-called “construct-independence” criterion that captures some intuitions behind such examples. The idea is that a piece of old evidence can legitimately speak in favour of a new theory, provided it has not been used to construct the theory itself — or, in other words, only if the theory had not been designed with the explicit aim of accounting for such body of evidence (cf. [Giere, 1983; Worrall, 1985]). This would rule out, for example, the malpractice of “data-snooping”, or the blatant use of the same set of data to both estimate and test an econometric model.
Severity theorists argue that construct independence matters only if (or in virtue of the fact that) it helps satisfying the severity requirements. Construct independence is not a necessary condition for empirical support, and there may well be cases where the evidence can be legitimately used both to construct and to indicate the correctness of a theory (see [Mayo, 1996, Ch. 8]). Consider a simple case of picking balls of different colour (black or white) from an urn. Suppose the urn contains n balls and we can pick up only m < n balls. Having counted how many white balls are in our sample, we can easily construct a hypothesis regarding the proportion of white/black balls in the urn, with a certain margin of error. Such hypothesis would not only be constructed after the evidence has been collected, but indeed would be constructed on the basis of that very evidence. And yet, it would be silly to deny that the evidence supports the hypothesis so constructed.
In the context of experimental economics, Larry Samuelson [2005] has recently proposed an intriguing argument in favour of the construct independence criterion. Samuelson’s article is devoted to discussing the relation between economic theory and experiments. At one point he asks “How can we use experiments to evaluate economic theories?” [2005, p. 79], and answers by outlining an evaluation procedure that resembles in many respects the one advocated by supporters of the severity criterion.
The basic elements of Samuelson’s framework are an experimental outcome (in the form of a statistical distribution), E; a predicted outcome ET by theory T; and a true distribution E* representing the probability distribution (propensity) over the set of possible outcomes that would be obtained if we were to perform an infinitely long series of replications of the same experiment.24 An evaluationrule R combines the information provided by E and ET to produce a verdict of acceptance or rejection of theory T in light of E.
For example: imagine you are tossing a coin and you are interested in knowing whether it is biased, and if so, how. For some unfortunate circumstance, you can toss the coin only once (this is a one-shot experiment, in other words). An evaluation rule R(E, ET) could take for example the following form [Samuelson 2005, p. 81]:
• Accept if T predicts head with P <1/3, and the result is tail; or if T predicts head with P ≥1/3, and the result is head.
This evaluation rule has the property of accepting a true hypothesis with probability 1/3, and conversely rejects (does not recognise) a true hypothesis with probability 2/3. Samuelson notices that this “does not sound very impressive. By altering the evaluation rule, we could manage to boost this probability to 1/2, but could not go further in this case” [2005, p. 81] because a one-shot experiment has some obvious limitations.
But do we want to raise the probability of accepting a true theory? In principle it seems a desirable thing to do, but we must also guard ourselves from another kind of error, i.e. the mistake of accepting a false theory. Samuelson suggests (Proposition 1, p. 80) that raising the probability of accepting a true theory automatically raises the probability of making this second kind of mistake.
To understand this claim, we must define another technical term: an evaluation rule blindly passes a given theory if it gives a verdict of acceptance no matter what the experimental outcome is going to be. Samuelson proves that
PROPOSITION 1. Any evaluation rule that accepts the truth with probability 1-ϵ can be blindly passed with probability 1-ϵ.
On top of a formal proof [p. 101], Samuelson provides a little game-theoretic argument to back up this result. Suppose you are playing a zero-sum game against a malevolent opponent called “Nature”. Nature can choose the true distribution E*, and you can choose ET . You win if T is accepted by whatever evaluation rule R is in place, otherwise Nature wins. Assume R accepts the truth with probability at least 1 − η. If you could choose Tafter you have observed Nature’s choice, you could simply choose it so that ET = E*, and guarantee a probability of success of at least 1-η. Similarly, if Nature could make her move after it has observed your choice of T, she would try to minimize your success rate by choosing an appropriate E* ≠ ET . At this point, we know from the minimax theorem of zero-sum games that your chances of succeeding in the second circumstance can be no worse than in the first one, hence that you can always win with probability at least 1-η. Since in practice at the moment of choosing T you don’t know the truth, and fortunately Nature cannot change the truth after it has seen your move, you must be somewhere in between the best and worse scenario, which means that the theory you will choose can pass at least with probability 1 − η [Samuelson 2005, p. 81].
What does this mean? Samuelson is adamant that he is providing a strong argument in favour of the criterion of construct-independence:
Interpreting experimental evidence as supporting a theory, or offering a theory as an interpretation of experimental evidence, thus acquires bite only if the theory is clear and complete enough that it can be extended to answer new questions and confront new tests that did not play a role in the construction of the theory. Is the theory clear enough that others could design new tests, and is one willing to risk the theory in such tests? If not, then it is not clear that progress has been made. [2005, p. 82]25
But in fact Samuelson does not prove that construct independence is a necessary condition for empirical support. His argument merely proves that it is always possible to construct a theory that blindly passes a test with high probability. But why should you like to construct such a theory? Such a theory would obviously fail to be tested severely by the evidence, as the definition of “blindly passing” makes clear. Remember that according to the severity criterion in a good test the probability of observing fitting evidence must be low; in contrast a test that blindly passes a theory has a maximally high probability of having a good fit with H. Thus Samuelson only proves that there is always going to be some theory (constructed so as to blindly pass the test) that (a) has been constructed to fit E, and (b) is not tested severely by E. Or, in other words, that being constructed to fit E is not sufficient to pass a severe test with E.
But of course this is hardly disputable. What we want is not only a good fit but also a high severity of the test, which is denied by the definition of “blindly passing”. Samuelson fails to prove that not being constructed to fit E is necessary in order to pass a severe test with E. This is what construct-independence theories of scientific testing should achieve, what Samuelson falsely claims to have proven, and what is disputed by the severity approach.
4 External Validity
There is a lot more to be said about the severity approach and alternative theories of inductive inference. For reasons of space we limit the discussion to the three features discussed in the previous sections: objectivity, locality, and a-temporality.26 The next part of this chapter is devoted to the second issue of validity, i.e. the problem of drawing inferences from a specific experiment to other (non-experimental) circumstances of interest. Both validity issues are specific examples of what we might call the “practical” problem of induction, as opposed to Hume’s well-known “logical” problem. Hume was concerned with the logical or rational justification of inductive inferences in general; validity, instead, has to do with the reliability of particular inductive moves, or in other words with the problem of distinguishing between “good” and “bad” inductive inferences. To put it differently, we are more in the realm of “Russell’s chicken” than of “Hume’s riddle”.27 It is worth making this distinction because it is generally recognised today that there may well not be a solution to the logical problem of induction, not at least in the form required by Hume. So it is important to stress that in asking economists to think about validity, one is not posing an unreasonable or idle philosophical challenge.
The two problems of validity have attracted very different levels of attention. Experimenters have devoted a lot of time and energy to internal validity, especially by proposing methodological rules or principles that would improve the reliability of experimental inferences within the laboratory.28 External validity issues in contrast are often raised by the critics of experimental economics. Experimenters have sometimes dismissed such critiques as unhelpful, because they distract from other important issues of research. The general feeling was that external validity critiques must be either unanswerable because inappropriately formulated, or, if appropriately formulated, in principle answerable by means of more experimental work. In this sense, the critic is supposed to carry the burden of proving the lack of validity of economic experiments.
Philosophers also seem to have strangely neglected the external validity problem. This is due to a number of reasons, including the fact that most philosophy of science tends to be physics-based, and experimental physicists do not recognise external validity as a separate problem of inference. Be that as it may, it is a fact that, of the two validity issues, external validity is the least studied. It is also the one that raises more controversy, and where philosophers may have both something to contribute and something to learn from experimental economics.
4.1 External validity and representativeness
We have seen that the logic of the perfectly controlled experiment leads quite naturally to endorse a severity approach to inductive inference. The method of the perfectly controlled experiment however is maximally useful to solve internal validity problem — when the issue is to find out what is going on within a given experimental set-up or laboratory system. Since the method relies importantly on the control of background conditions (Ki) in order to obtain truly informative evidence, there is usually a trade-off between internal and external validity. A simple experiment that reproduces many of the idealisations of a theoretical model is usually easier to control in the laboratory; but it also constitutes a weaker starting point for extending the experimental knowledge thus obtained to other situations of interests (where such idealisations do not hold).
So how can we tackle the external validity problem constructively? And can we indicate a solution that is consistent with the logic of the severity approach? Ideally, we would like to have a unique inductive methodology that is able to capture both types of inferential moves.
Following an old tradition in experimental psychology, Robin Hogarth [2005] argues that the problem of external validity should be framed in terms of representativeness. There are, more precisely, at least two dimensions of representativeness in an economic experiment: subjects sample and design. Whereas statistical techniques and random sampling can be used to tackle subject representativeness, the choice of the design is rarely seen as a problem of the same kind. The designs of economic and psychology experiments are often highly idiosyncratic if compared to real-world situations, and are certainly not randomly picked from the target population (e.g. the set of real-life choice-situations or real market decisions). For this reason, the “representativeness” framework might be helpful to highlight the nature of the problem, but does not do much in terms of pointing to a solution, as far as problems of design are concerned.
Why is the method of random sampling from a set of real-life situations not followed by experimental economists? Random sampling makes sense only if you are trying to capture a central tendency in a population of individuals with varying traits. But there may be no such central tendency in a set of, say, market exchanges. Consider bargaining: economic theory suggests that different details of the bargaining situation can influence the outcome drastically. If this is true, then an average description of different bargaining outcomes is likely to be rather uninformative and to obscure all the interesting variations in the data. What we want is instead to be able to understand how different factors or causal mechanisms interact to generate different outcomes. This is why experimenters sometimes privilege simple designs or game-situations that capture the working of just one mechanism in isolation, where somewhat “extreme” results are vividly instantiated.
4.2 Shifting the burden of proof
For these reasons, external validity inferences usually do not take the form of an inference from sample to population. They rather look like inferences from a specific experimental environment to another specific real-world environment. Consider the phenomenon known as the “winner’s curse”, for example. In so-called “common-value sealed-bid auctions” bidders are trying to purchase an item that has approximately the same value for all the competitors, but the exact value of which is unknown to all. Each bidder makes an estimate of the value of the item, which is likely to diverge from its true value. The standard theory assumes perfect rationality; in this case, bidders are supposed to be able to anticipate that the winner of the auction will probably be the one who most overestimates the value of the item. To correct for this bias, the theory assumes that the bidders should revise their offers downwards.
Experimental data have shown that this revision does not take place or takes place imperfectly, and thus the winners turn out to be systematically “cursed” [Kagel and Levin, 1986]. But is this result valid outside the narrow experimental conditions where it was generated? By raising the problem of external validity, we are not necessarily asking whether the experimental design has been sampled from some relevant population of designs. We are rather asking whether the results can be transferred from the laboratory to some specific real-world situation of interest.
Experimental research on the winner’s curse started precisely with the aim of replicating a target phenomenon, allegedly observed in the auctions of the Outer Continental Shelf, selling leases to drill oil in the Gulf of Mexico.29 The experiments had a fairly precise intended domain of application, which makes the external validity problem tractable. If you observe a certain phenomenon in the laboratory, but you are not sure about its generalizability to real-world circumstances in general, it is difficult to tackle the problem constructively. You can do much better in contrast if you know exactly the sort of circumstances you want to export your results to: in this case you can look for specific reasons why the result may not be exportable. These reasons will usually take the form of some relevant (causal) dissimilarity between the experimental and the target system. Thus, the obvious way to proceed is by modifying the experiment to include the features of the target that could be responsible for the alleged external validity failure, and see whether they in fact make a difference or not.
Chris Starmer [1999, p. 9] defends a view of external validity inferences that is very close to the one just sketched. He points out that the putative lack of external validity of a specific experiment can usually be attributed to one or more “unrealistic” features of the experimental design (the lack of a potentially important factor, or the presence of an artificial condition) — where “unrealistic” here is clearly defined with reference to a target of investigation. If this is the case, whenever a potential flaw has been highlighted, it should be possible at least in principle to design a new experiment that controls for the effective causal relevance of those factors or conditions.30
Starmer’s position improves upon traditional defences of experimentation such as Plott’s. By focusing on theory-testing, Plott is concerned with defending experimental economics as a whole from the charge of irrelevance, and tries to shift the burden of proof by identifying experimental economics narrowly with theory-testing. “I’m only testing theoretical models”, the experimenter says. “If the model is incomplete or too simple to be applicable to a real-world system, that’s a problem for the theorist, not for the experimenter”. But this is disingenuous, of course. Demonstrating that experimental economics is not just a laboratory game offers little comfort, if it turns out to be just a game between theory and experiment. The critic is ultimately concerned with the real-world applicability of both experimental and theoretical knowledge. But even more worrying is the fact that many theoretical models are nowadays constructed with an eye to capturing robust experimental regularities. When experimental results guide theory-formation, the risk of engaging in a self-referential process of theorising and experimentation that is totally insulated from the real world becomes very high indeed [Schram, 2005, pp. 234-5].
In a recent textbook Friedman and Cassar also argue that “an honest skeptic of external validity bears the burden of guessing what makes the lab environment substantially different than the real world” [Friedman and Cassar, 2004, p. 29]. This implies that in absence of a specific critique of a given experimental design (i.e. unless one identifies a potential flaw) the external validity of an experiment should be accepted by default. As Deborah Mayo [2008] points out, however, this conclusion is based on a fallacy known as “argument from ignorance”. The fact that I have no reason to believe that ∼ X is the case, is not in itself a good reason to believe that X is the case. In terms of the severity approach, suppose we are dealing with two hypotheses, H (= experiment X has external validity) and ∼ H (= experiment X has no external validity). To prove that ∼ H passes a sever test is not equivalent to prove that H has passed such a test. The only legitimate way to argue for the external validity of an experimental result is by showing that there is good evidence (“good” according to the severity criteria) in favour of H.
The correct position, to sum up, is to recognise that external validity critiques have a bite only when they refer to specific experimental designs (to worry about external validity in general is pretty useless). But at the same time we cannot let the experimenter shift the burden onto the critic — the burden always lies with whoever is drawing the inference from laboratory to real-world circumstances, who is expected to prove the relevance of the experimental design for the investigation of a given target.31 Whenever an inference is made, it must be warranted by the data — the absence of evidence indicating the contrary does not provide positive support for the inference itself.
4.3 Experimental localism and economic ontology
Dyer and Kagel [1996] have studied the winner’s curse phenomenon in the context of the North-American construction industry. They identify a number of mechanisms that effectively defend bidders in that industry from the “curse” of overbidding. One of them is a rule allowing the withdrawal of winning bids in case of “arithmetical errors” in the submission of the offer. In practice the notion of arithmetical error is interpreted so broadly that almost any offer can be withdrawn without penalty if the bidder so wishes. This rule provides cover for both the contractors and their clients, because a grossly mistaken estimate can put the construction firm and the project itself at risk. Nobody wants to work with an unhappy firm that are aware of the fact that they will lose money from the contract.
Dyer and Kagel point out that traditional experiments on the winner’s curse do not reproduce such rules for the withdrawal of bids. Hence, their results cannot be generalized straightforwardly to the construction industry. This is a typical case where only the detailed study of the institutional rules and practices of a specific market allows the evaluation of an external validity claim. The experimental result of course is still of some value in trying to understand what is going on in that specific market, but only as a contrast case. In principle, a new experiment could be designed which incorporates the institutional mechanisms that supposedly neutralise the effects of the winner’s curse. Prior to this sort of investigation, no moral can be drawn about the applicability of the winner’s curse experiments to the construction industry.
This point is of great philosophical significance. In this section we shall elaborate and investigate its implications in two directions: first, I shall look more specifically at the use of evidence in external validity arguments. Secondly, I shall examine what experimental economics can teach us about the ontology of economics and the social sciences in general.
As shown by the Dyer and Kagel article, external validity inferences require a combination of field and experimental evidence. This has been occasionally recognised by the founders of the discipline (e.g. [Smith, 1989, p. 152]), but until recently very little has been said about the specific ways in which the two sources of evidence should be combined so as to be most effective. This issue, incidentally, is by no means an exclusive concern of experimental economics. It has been discussed also in the context of experimental medicine [La Follette and Shanks, 1994; Thagard, 1999], biochemistry [Strand et al., 1996], and molecular biology [Weber, 2004; Steel, 2007]. The structure of external validity inferences can be articulated as a case of causal-analogical reasoning. The analogical aspect of the inference can be reconstructed as follows:
(a) The target system displays phenomenon Y.
(b) The experimental system displays phenomenon Y.
(c) In the laboratory, the phenomenon is caused by factor X.
An obvious objection can be raised at this point: the number of analogies that can be drawn between any two objects or systems is potentially infinite. So which analogies in this infinite set are “strong” or of greater epistemic significance? Analogies such as those in (a)–(d) are instructive only if we are confident that the other (background) conditions are “right”. Consider the case of internal validity: a correlation between two variables is too weak a basis to infer that a causal relation exists between the two. We also need to be sure that no background variation (in the Ki) is confounding the inference. Similarly, the fact that X causes Y in A does not guarantee that X causes Y in B. We must make sure that no other causal factor is confounding the inference. The second important point then is that disanalogies are also crucial. As in the case of the winner’s curse, one must always check that no relevant causal differences exist that are able to disrupt the inferences from laboratory to target. In a nutshell, the laboratory and the target system must be made similar in all causally relevant respects. If we suspect there may be a causally important difference, we must check it experimentally [Guala, 2005a, Ch. 9].
Daniel Steel [2007, Ch. 8] has criticized the analogical approach for being too conservative: external validity inferences can be drawn even when we do not have the resources or the possibility to check all causally relevant disanalogies between the laboratory system and its target. Causes leave marks that are transmitted through causal mechanisms. According to the method of “comparative process tracing”, it is sufficient to compare the working of an experimental and a target system by checking the presence of marks at some crucial stages of the mechanisms. Perfect identity among the systems, moreover, is no required either according to Steel. Our background knowledge of causal mechanisms sometimes allows the inference of the direction of a causal relation even when we know that some differences exist between the lab and the real world.
The analogical and the process tracing methods are both distinctively empirical approaches to the problem of external validity, and constitute sharp improvements with respect to previous discussions. External validity has too often been addressed by means of metaphysical arguments about the nature of economic and social reality, which unfortunately are of little utility. It has been argued, for example, that experimentation is impossible because there are no universal laws in economics [Economics Focus, 1999]. But there may well be no universal laws in biology, as far as we know, and yet experiments have been profitably used for decades in that discipline. Similarly, some have posited the necessity of tendency laws for experimentation [Siakantaris, 2000]. Following John Stuart Mill [1836], a tendency law is usually understood as a “super-causal” law of the following kind: “A → B” is a tendency law if not only A has the capacity of making B happen in the “right” set of circumstances, but also if it tends to make it happen when the conditions are not right. Or, to put it slightly differently, if A contributes to the instantiation of B even when other “disturbing” or “counteracting” factors are at work [Hausman, 1992].
Of course laws of this kind can be tested in the laboratory. The worry is that if the (numerous) factors that are kept fixed in the background during an experiment (factors that often are not even modelled theoretically, but rather relegated in a ceteris paribus clause) do not combine additively but interact with the main experimental variables, then the experimental result will not be valid outside the narrow domain of its instantiation. We can still discover causal laws valid in a narrow domain, but unless they are tendency laws that are robust to changes in the boundary conditions, this knowledge will be of rather limited use.
The ontology of tendencies, then, seems to be a desideratum for the generalizability of experimental results, rather than a necessary requirement for the success of the experimental method itself. As a matter of fact, according to Anna Alexandrova [2006], the most successful applications of experimental economics to date do not presuppose the existence of tendencies at all. Applied economists start from the pessimistic assumption that the causal properties modelled in economic theory may be rather fragile, and then test repeatedly their robustness to changes in the boundary and background conditions (see also [Guala, 2005a, Ch. 8], for some examples).
In general, the existence of tendency laws is a post-scientific issue to be resolved by empirical evidence, rather than a pre-scientific issue to be addressed by metaphysical speculation. By combining experimental economics with field data we have got the unique chance of testing empirically whether the phenomena and causal relations discovered in the laboratory are “robust” and can be exported into the field. Of course we should expect different degrees of success — there may well be areas in which experimental results turn out to be more easily transferable and robust, other areas where they are less so. More tendencies are obviously preferable, but a limited degree of robustness and modularity is still preferable to nothing at all [Guala, 2002b].
5 The Philosophical Relevance of Experimental Economics’ Results
Methodology has been at the centre of this chapter right from the start. This reflects partly my own interests, and partly the concentration of the existing literature on methodological matters. The philosophical relevance of experimental economics however is not exhausted by the problems of validity, and the related issues of causal inference, experimental design, and data-analysis. Experiments are beginning to change rather drastically the landscape of economic science, and thus carry deep implications on a number of other ontological, normative, and political issues. This is perhaps where the interaction between philosophers and economists will be most productive in the future.
Experimental economics is often perceived to have come up with two important sets of results: that neoclassical economic theory can predict remarkably well the aggregate outcome of market processes, and that the neoclassical theory of individual choice is repeatedly falsified by laboratory evidence. Although on a superficial reading these two results may appear mutually incompatible, this is in fact not the case. Both sets of results, to begin with, must be qualified by an important proviso: the neoclassical theory of markets predicts well in the right circumstances, and similarly the individual theory of choice suffers from robust anomalies in specific circumstances. In both cases, the circumstances matter.
Among the circumstances that matter, institutions have emerged as particularly important. Social institutions can be usefully divided in two categories, that we shall call “rules” and “norms”. On the one hand we have very specific, explicitly formulated and often legally enforced rules, such as those regulating exchange in the stock market. On the other, we have fairly broad, informal norms such as those that govern market interactions in everyday life — norms such as “honour done deals”, “do not cheat”, and so forth.
Informal norms are behind some of the most robust anomalies of strategic and individual choice. There is a general agreement, for example, that norms of cooperation and especially reciprocation (cooperate only if the others do the same) cause the phenomena of overcontribution and decay in repeated public goods experiments. Other examples are the anomalous offers observed in ultimatum game experiments, dictator’s games, investment games, and other similar experimental situations.32
Market experiments have proven that the convergence of competitive markets on efficient prices depends crucially on the institutions that govern the exchange — for example the type of auction, or the coordinating mechanism that matches buyers and sellers in a multilateral exchange [Plott and Smith, 1978]. These results fill an enormous gap in the economic literature, which until recently was occupied by an idealized fiction, the Walrasian auctioneer.
The importance of rules and norms teaches important lessons regarding the scope and character of economic theory, as well as its use in policy-making. First, it reminds us of the incompleteness of theory and of the constant need to supplement it by means of empirical investigation and insights from neighbor disciplines like psychology and sociology. Secondly, it highlights the importance of collecting local information about the context of application of a theoretical model, before policy intervention takes place. The most blatant examples of the context-sensitivity of economic knowledge are the huge failures in reforming the economies of Eastern European countries after the fall of the Soviet regimes. A common reading of these failures is that the institutional conditions that are necessary for a healthy functioning of markets simply were not in place when the transition took place.
However, experimental economists have also shown that when policy intervention has been carefully planned and, crucially, tested empirically, market institutions can do an egregious job at achieving certain policy goals. Examples of successful reforms of this kind are the various market design enterprises informed by game theory and experimental economics over the last couple of decades (cf. [Miller, 2002; Roth, 2002] for overviews and general discussions).33
All these developments have important political implications. Economics has been for much of the last two centuries dominated by the invisible hand metaphor, in its various guises. The results of experimental economics carry two messages that will probably disappoint both the enthusiasts and the radical critics of market liberalism. Experiments have shown on the one hand that markets can work, and not just in the abstract realm of economic theory. On the other, experiments have shown that markets are relatively delicate machines, whose smooth functioning may require a lot of careful planning, artificial design, and supervision. The interesting challenge is to learn from the institutions that have spontaneously evolved in history, while at the same time identifying their shortcomings and fixing them using the most advanced theoretical and experimental knowledge that is available.34 The “economist as engineer” [Roth, 2002] is a character that will probably gain increasing prominence and influence in the future. Whether this is good or bad news is for all of us to decide.
6 Other Issues and Readings
The most comprehensive philosophical discussion of experimental economics to date is to be found in my book The Methodology of Experimental Economics [Guala, 2005a]. Bardsley et al. [2009] will be the second monograph on the same topic to be published in a short period. An especially valuable source of ideas and debate is a symposium recently published in the Journal of Economic Methodology [Sugden, 2005]. To get a sense of what experimental economics is all about, however, the novice is warmly encouraged to try a few simple experiments in his/her own class, like those illustrated in [Bergstrom and Miller, 1997] for example. Davis and Holt [1993], Friedman and Sunder [1994], and Friedman and Cassar [2004] are widely used textbooks. Excellent surveys of experimental results can be found in [Kagel and Roth, 1995; Plott and Smith, 2008]. Holt’s [2000] bibliography is an extremely useful resource, and Roth’s [2005] webpage is a good point of entry into the world of game theory and experimentation.
Among the issues that have not been covered in this chapter I should mention the sensitive issue of the divide between economics and psychology [Rabin, 1998; 2001; Smith, 1991], and the related issue of the importance of monetary incentives in experimental design [Hertwig and Ortmann, 2001; Read, 2005; Guala, 2005a, Ch. 11]. In relation to the issue of external validity, there is now a growing body of research carried out by means of “field experiments” — a mix of laboratory control in real-world circumstances — that is calling for methodological systematisation [Harrison and List, 2004]. Philosophers interested in normative issues will be interested in the way in which experimental results have been used to support or criticise models of normative reasoning such as Bayesian belief-updating or expected utility theory. This tradition goes back to Allais’ [1953] seminal work, but has come to prominence with the so-called “human rationality debate” of the 1970s (see e.g. [Cohen, 1981; Stein, 1996]). Guala [2000] and Starmer [2005] discuss the symmetric issue of how the impact of experimental results on economic theory has been heavily influenced by normative considerations.
Finally, it seems likely that in the future the methods of experimental economics will be employed more and more frequently by naturalistically-minded philosophers interested in tackling epistemological and ontological issues using the resources of the human and social sciences (see e.g. the new “Experimental Philosophy” movement as presented by Knobe [2007]). A most fertile area or research lies at the intersection between experimental economics and social ontology: Bicchieri [2006] for example relies extensively on experimental results in economics and social psychology to develop a new formal model of social norms. Guala [2006], Mirowski and Nik-Kah [2006], and Callon and Muniesa [2006] discuss whether and in what sense the experimental practice can have a “performative” effect on economic reality — i.e. whether by experimenting one not only observes but also creates socio-economic entities that did not previously exist.
Acknowledgements
Many ideas appearing in this paper were proposed and discussed at a workshop on the methodology of experimental economics held at Virginia Tech in June 2005. I must thank Deborah Mayo, Aris Spanos, Chris Starmer, Jim Woodward, Vernon Smith, Catherine Eckel, Sheryl Ball, Cristina Bicchieri and Robin Cubitt for many exchanges before, during and after the workshop. Bob Sugden also provided some useful clarifications. The remaining mistakes are of course entirely mine.
BIBLIOGRAPHY
1. Achinstein P, ed. Scientific Evidence: Philosophical Theories and Applications. Baltimore: John Hopkins University Press; 2005.
2. Alexandrova A. Connecting Economic Models to the Real World: Game Theory and the FCC Spectrum Auctions. Philosophy of the Social Sciences. 2006;36:173–192.
3. Allais M. The Foundations of a Positive Theory of Choice Involving Risk and a Criticism of the Postulate and Axioms of the American School. In: Allais M, Hagen O, eds. Expected Utility Hypothesis and the Allais Paradox. Dordrecht: Reidel; 1953;257–332.
4. Andreoni J. Why Free Ride? Strategies and Learning in Public Goods Experiments. Journal of Public Economics. 1988;37:291–304.
5. Bardsley N. Experimental Economics and the Artificiality of Alteration. Journal of Economic Methodology. 2005;12:239–251.
6. Bardsley N, Cubitt R, Loomes G, Moffatt P, Starmer C, Sugden R. Economics and the Laboratory Princeton: Princeton University Press; 2009.
7. Bergstrom TC, Miller JH. Experiments with Economic Principles: Microeconomics New York: McGraw-Hill; 1997.
8. Bicchieri C. The Grammar of Society Cambridge: Cambridge University Press; 2006.
9. Boumans M, Morgan MS. Ceteris Paribus Conditions: Materiality and the Application of Economic Theory. Journal of Economic Methodology. 2001;8:11–26.
10. Callon M, Muniesa F. Economic Experiments and the Construction of Markets. In: MacKenzie D, Muniesa F, Siu L, eds. Do Economists Make Markets? On the Performativity of Economics. Princeton: Princeton University Press; 2006.
11. Cartwright N. How the Laws of Physics Lie Oxford: Clarendon Press; 1983.
12. Cartwright N. Nature’s Capacities and Their Measurement Oxford: Oxford University Press; 1989.
13. Christensen LB. Experimental Methodology 8 Needham Heights, Mass: Allyn & Bacon; 2001.
14. Cohen LJ. Can Human Irrationality Be Experimentally Demonstrated?. Behavioral and Brain Sciences. 1981;4:417–470.
15. Collins HM. Changing Order: Replication and Induction in Scientific Practice London: Sage; 1985.
16. Cubitt R. Experiments and the Domain of Economic Theory. Journal of Economic Methodology. 2005;12:297–1210.
17. Davis DD, Holt CH. Experimental Economics Princeton: Princeton University Press; 1993.
18. Duhem P. La théorie physique Son objet et sa structure Paris: Chevalier et Rivière; 1906; Engl. transl. The Aim and Structure of Physical Theory. Princeton: PrincetonUniversity Press.
19. Dyer D, Kagel JH. Bidding in Common Value Auctions: How the Commercial Construction Industry Corrects for the Winner’s Curse. Management Science. 1996;42:1463–1475.
20. Economics Focus. News from the Lab. In: The Economist. 1999;96. May 8.
21. Franklin A. Experiment in Physics. In: Zalta EN, ed. The Stanford Encyclopaedia of Philosophy. 1998;In: http://plato.stanford.edu/entries/physics-experiment; 1998.
22. Friedman D, Cassar A. Economics Lab: An Intensive Course in Experimental Economics London: Routledge; 2004.
23. Friedman D, Sunder S. Experimental Methods: A Primer for Economists Cambridge: Cambridge University Press; 1994.
24. Friedman M. The Methodology of Positive Economics. In: Essays in Positive Economics. Chicago: University of Chicago Press; 1953;3–43.
25. Galison P. How Experiments End Chicago: University of Chicago Press; 1987.
26. Giere RN. Testing Theoretical Hypotheses. In: Earman J, ed. Testing Scientific Theories. Minneapolis: University of Minnesota Press; 1983;269–298.
27. Giere RN. Explaining Science Chicago: University of Chicago Press; 1988.
28. Gooding D, Pinch T, Shapin S, eds. The Uses of Experiment. Cambridge: Cambridge University Press; 1989.
29. Guala F. Experiments as Mediators in the Non-Laboratory Sciences. Philosophica. 1998;62:901–918.
30. Guala F. The Logic of Normative Falsification: Rationality and Experiments in Decision Theory. Journal of Economic Methodology. 2000;7:59–93.
31. Guala F. Models, Simulations, and Experiments. In: Magnani L, Nersessian N, eds. Model-Based Reasoning: Science, Technology, Values. New York: Kluwer; 2002a;:59–74.
32. Guala F. On the Scope of Experiments in Economics: Comments on Siakantaris. Cambridge Journal of Economics. 2002b;26:261–267.
33. Guala F. The Methodology of Experimental Economics New York: Cambridge University Press; 2005.
34. Guala F. How to Do Things with Experimental Economics. In: MacKenzie D, Muniesa F, Siu L, eds. Do Economists Make Markets? On the Performativity of Economics. Princeton: Princeton University Press; 2006.
35. Guala F. Experimental Economics, History of In The New Palgrave Dictionary of Economics London: Palgrave-MacMillan; 2008a.
36. Guala F. The Experimental Philosophy of Experimental Economics: Replies to Alexandrova, Hargreaves-Heaps, Hausman, and Hindriks. Journal of Economic Methodology. 2008b;15:224–231.
37. Hacking I. Representing and Intervening Cambridge: Cambridge University Press; 1983.
38. Harrison GW, List JA. Field Experiments. Journal of Economic Literature. 2004;42:1009–1045.
39. Hausman DM. The Inexact and Separate Science of Economics Cambridge: Cambridge University Press; 1992.
40. Hausman DM. Causal Asymmetries Cambridge: Cambridge University Press; 1998.
41. Hausman DM. Testing’ Game Theory. Journal of Economic Methodology. 2005;12:211–223.
42. Hausman DM. Experimenting on Models and in the World. Journal of Economic Methodology. 2008;15:209–216.
43. Hertwig R, Ortmann A. Experimental Practices in Economics: A Methodological Challenge for Psychologists?. Behavioral and Brain Sciences. 2001;24:383–451.
44. Hogarth RM. The Challenge of Representative Design in Psychology and Economics. Journal of Economic Methodology. 2005;12:253–263.
45. Holt CH. The Y2K Bibliography of Experimental Economics and Social Science 2000;http://www.people.virginia.edu/~cah2k/y2k.htm; 2000; [29/12/1999 version].
46. Hoover KD. Causality in Macroeconomics Cambridge: Cambridge University Press; 2001.
47. Hoover KD. Lost Causes. Journal of the History of Economic Thought. 2004;26:149–164.
48. Howson C, Urbach P. Scientific Reasoning: The Bayesian Approach Chicago: Open Court; 1989.
49. Kagel JH, Levin D. The Winner’s Curse Phenomenon and Public Information in Common Value Auctions. American Economic Review. 1986;76:894–920.
50. Kagel JH, Roth AE, eds. The Handbook of Experimental Economics. Princeton: Princeton University Press; 1995.
51. Knobe J. Experimental Philosophy. Philosophy Compass. 2007;2:81–92.
52. Kreps DM, Milgrom P, Roberts J, Wilson R. Rational Cooperation in the Finitely Repeated Prisoners Dilemma. Journal of Economic Theory. 1981;27:245–252.
53. Isaac M. Laboratory Experimental Economics as a Tool in Public Policy Analysis. Social Science Journal July 1983;45–58.
54. LaFollette H, Shanks N. Two Models of Models in Biomedical Research. Philosophical Quarterly. 1995;45:141–160.
55. Ledyard JO. Public Goods: A Survey of Experimental Research. In: Kagel JH, Roth AE, eds. The Handbook of Experimental Economics. Princeton: Princeton University Press; 1995;111–194.
56. Lee KS, Mirowski P. The Energy Behind Vernon Smith’s Experimental Economics. Cambridge Journal of Economics. 2008;32:257–271.
57. Leonard R. Laboratory Strife: Higgling as Experimental Science in Economics and Social Psychology. In: De Marchi NB, Morgan MS, eds. Durham: Duke University Press; 1994; Higgling History of Political Economy Supplement. 26.
58. Loomes G. Experimental Economics. In: Hey JD, ed. Current Issues in Microeconomics. New York: St. Martin’s Press; 1989;152–178.
59. Mackie JL. The Cement of the Universe Oxford: Clarendon Press; 1974.
60. Mäki U. On the Method of Isolation in Economics. Poznan Studies in the Philosophy of the Sciences and Humanities. 1992;26:317–351.
61. Mäki U. Models Are Experiments, Experiments Are Models. Journal of Economic Methodology. 2005;12:303–315.
62. Mayo D. Error and the Growth of Experimental Knowledge Chicago: University of Chicago Press; 1996.
63. Mayo D. Evidence as Passing Severe Tests: Highly Probable versus Highly Probed Hypotheses. In: Achinstein Peter, ed. Scientific Evidence: Philosophical Theories and Applications. Baltimore: John Hopkins University Press; 2005;95–127.
64. Mayo D. Some Methodological Issues in Experimental Economics. Philosophy of Science. 2008;75:633–645.
65. Mill JS. On the Definition of Political Economy and the Method of Investigation Proper to It. In: Toronto: University of Toronto Press; 1836;120–164. Collected Works of John Stuart Mill. 4 1967.
66. Miller RM. Paving Wall Street: Experimental Economics and the Quest for the Perfect Market. New York: John Wiley & Sons; 2002.
67. Mirowski P, Nik-Kah E. Markets Made Flesh: Callon, Performativity, and a Crisis in Science Studies, Augmented with Consideration of the FCC Auctions. In: MacKenzie D, Muniesa F, Siu L, eds. Do Economists Make Markets? On the Performativity of Economics. Princeton: Princeton University Press; 2006.
68. Morgan MS. Model Experiments and Models in Experiments. In: Magnani L, Nersessian N, eds. Model-Based reasoning: Science, Technology, Values. New York: Kluwer; 2002.
69. Morgan MS. Economics. In: Porter T, Ross D, eds. The Cambridge History of Science, Vol 7: The Modern Social Sciences. Cambridge: Cambridge University Press; 2003a;:275–305. edited by.
70. Morgan MS. Experiments without Material Intervention: Model Experiments, Virtual Experiments and Virtually Experiments. In: Radder H, ed. The Philosophy of Scientific Experimentation. Pittsburgh: Pittsburgh University Press; 2003b.
71. Morgan MS. Experiments versus Models: New Phenomena, Inference and Surprise. Journal of Economic Methodology. 2005;12:317–329.
72. Morrison MC. Experiment. In: Craig E, ed. The Routledge Encyclopaedia of Philosophy. London: Routledge; 1998;514–518.
73. Morrison MC, Morgan MS. Models as Mediating Instruments. In: Morgan MS, Morrison MC, eds. Models as Mediators. Cambridge: Cambridge University Press; 1999;10–37.
74. Moscati I. Early Experiments in Consumer Demand Theory: 1930-1970. History of Political Economy. 2007;39:359–401.
75. Parker W. Does Matter Really Matter? Computer Simulations, Experiments and Materiality. Synthese. 2009;169:483–496.
76. Plott CR. Will Economics Become an Experimental Science?. Southern Economic Journal. 1991;57:901–919.
77. Plott CR, Smith VL. An Experimental Examination of Two Exchange Institutions. Review of Economic Studies. 1978;45:133–153.
78. Plott CR, Smith VL, eds. The Handbook of Results in Experimental Economics. London: Elsevier; 2006.
79. Popper KR. Logik der Forschung Vienna: Springer, 1934 Vienna: Springer; 1934; Engl. transl. Logic of Scientific Discovery. London: Hutchinson, 1959.
80. Quine WO. Two Dogmas of Empiricism. In: From A Logical Point of View. Cambridge, Mass: Harvard University Press; 1953;20–46.
81. Rabin M. Psychology and Economics. Journal of Economic Literature. 1998;35:11–46.
82. Rabin M. A Perspective on Psychology and Economics. European Economic Review. 2002;46:657–685.
83. Read D. Monetary Incentives, What Are They Good for?. Journal of Economic Methodology. 2005;12:265–276.
84. Redhead MLG. A Bayesian Reconstruction of the Methodology of Scientific Research Programmes. Studies in History and Philosophy of Science. 1980;11:341–347.
85. Roth AE. Introduction to Experimental Economics. In: Kagel JH, Roth AE, eds. The Handbook of Experimental Economics. Princeton: Princeton University Press; 1995;3–109.
86. Roth AE. The Economist as Engineer: Game Theory, Experimentation, and Computation as Tools for Design Economics. Econometrica. 2002;70:1341–1378.
87. A. E. Roth. Al Roth’s Game Theory and Experimental Economics Page. http://kuznets.fas.harvard.edu/~aroth/alroth.html (10/10/2005 version).
88. Russell B. On Induction, 1912. In: The Problems of Philosophy. Oxford: Oxford University Press; 1912.
89. Samuelson L. Economic Theory and Experimental Economics. Journal of Economic Literature. 2005;43:65–107.
90. Santos AC. The ‘Materials’ of Experimental Economics: Technological versus Behavioral Experiments. Journal of Economic Methodology. 2007;14:311–337.
91. Schram A. Artificiality: The Tension between Internal and External Validity in Economic Experiments. Journal of Economic Methodology. 2005;12:225–237.
92. Shubik M. Bibliography on Simulation, Gaming, Artificial Intelligence and Allied Topics. Journal of the American Statistical Association. 1960;55:736–751.
93. Simon HA. The Sciences of the Artificial Boston: MIT Press; 1969.
94. Smith VL. An Experimental Study of Competitive Market Behavior. Journal of Political Economy. 1962;70:111–137.
95. Smith VL. Experimental Economics: Induced Value Theory. American Economic Review. 1976;66:274–277.
96. Smith VL. Microeconomic Systems as an Experimental Science. American Economic Review. 1982;72:923–955.
97. Smith VL. Theory, Experiment and Economics. Journal of Economic Perspectives. 1989;3:151–169.
98. Smith VL. Rational Choice: The Contrast Between Economics and Psychology. Journal of Political Economy. 1991;99:877–897.
99. Smith VL. Game Theory and Experimental Economics: Beginnings and Early Influences. In: Weintraub ER, ed. Towards A History of Game Theory. Durham: Duke University Press; 1992;241–282.
100. Smith VL. Rationality in Economics: Constructivist and Ecological Forms New York: Cambridge University Press; 2008.
101. Søberg M. The Duhem-Quine Thesis and Experimental Economics: A Reinterpretation. Journal of Economic Methodology. 2005;12:581–597.
102. Starmer C. Experiments in Economics: Should We Trust the Dismal Scientists in White Coats?. Journal of Economic Methodology. 1999;6:1–30.
103. Steel D. Across the Boundaries: Extrapolation in Biology and in the Social Sciences New York: Oxford University Press; 2007.
104. Stein E. Without Good Reason The Rationality Debate in Philosophy and Cognitive Science Oxford: Clarendon Press; 1996.
105. Sugden R. Experiments as Exhibits and Experiments as Tests. Journal of Economic Methodology. 2005;12:291–302.
106. Sugden R. Experiment, Theory, World: A Symposium on the Role of Experiments in Economics. Journal of Economic Methodology. 2005;12.
107. Siakantaris N. Experimental Economics under the Microscope. Cambridge Journal of Economics. 2000;24:267–281.
108. Strand R, Fjelland R, Flatmark T. In Vivo Interpretation of In Vitro Effect Studies. Acta Biotheoretica. 1996;44:1–21.
109. Taper M, Lee S, eds. The Nature of Scientific Evidence. Chicago: University of Chicago Press; 2004.
110. Thagard P. How Scientists Explain Disease Princeton: Princeton University Press; 1999.
111. Weber M. Philosophy of Experimental Biology Cambridge: Cambridge University Press; 2004.
112. Wilde LL. On the Use of Laboratory Experiments in Economics. In: Pitt JC, ed. Philosophy in Economics. Dordrecht: Reidel; 1981;137–148.
113. Woodward J. Data, Phenomena, and Reliability. Philosophy of Science. 2000;67:S163–S179.
114. Woodward J. Making Things Happen: A Theory of Causal Explanation Oxford: Oxford University Press; 2003.
115. Worrall J. Scientific Discovery and Theory-Confirmation. In: Pitt J, ed. Change and Progress in Modern Science. Dordrecht: Reidel; 1985;301–331.
116. Worrall J. What Evidence in Evidence-Based Medicine?. Philosophy of Science. 2002;69:S316–S330.
1 But there are some scattered pieces: Smith [1992], Roth [1995], Leonard [1994], Moscati [2007], Guala [2008a], Lee and Mirowski [2008].
2 Hacking [1983] is widely recognized as the precursor of this “new experimentalism”. Useful surveys of the literature can be found in Franklin [1998] and Morrison [1998].
3 These terms are misleading if taken literally — of course a laboratory situation is as real or natural as anything that happens spontaneously, because scientists are part of the natural real world. Keeping this in mind, however, I’ll keep using these expressions for simplicity throughout the chapter.
4 Cf. Worrall [2002] for a discussion of so-called “evidence-based medicine”.
5 Similar claims can be found in Wilde [1981, p. 143], Smith [1982, p. 268], Loomes [1989, p. 173].
6 The neglect of confirmation is probably due to the vague Popperianism that informs much economic rhetoric and practice. But it may also be a tactical neglect, for the case of confirmation is much more problematic for Plott’s position. The observation of O, in fact, does not elicit any deductive inference to the truth of the theory T; we need induction. An inductive inference from O, however, does not necessarily warrant the conclusion that Tis the case. Whether it does or not, depends on the theory of inductive inference one decides to adopt. We shall come back to such issues in section 3 below.
7 A Nash equilibrium is such that the strategy implemented by each player is the best move given the strategies of the other players: in equilibrium, no player has an incentive to change her own strategy, in other words.
8 Cf. Duhem [1905] and Quine [1953].
9 I’m using the term “theory of induction” broadly, because such a theory does not necessarily have to be modeled on deductive logic as we know it. We could have a sociological theory of induction, for example, along the lines of Collins [1985], a cognitive psychological theory such as Giere’s [1988], and so forth. There are many ways of “naturalising” the study of inductive inference, and the approach endorsed in this chapter is by no means exclusive.
10 I’m using these two terms interchangeably here, although there are philosophically important differences between these procedures; see for instance Cartwright [1989, Ch. 5] and Mäki [1992].
11 Different experiments of course may deal with different “materials”; Santos [2007] provides a wider comparative discussion of the materiality of economic experiments.
12 “Virtual experiments” in contrast are according to Morgan entirely simulating systems, which are constructed so as to generate interesting data patterns reproducing real-world features. See also Guala [2002a] for a different discussion of hybrid experiments/simulations that follows closely Simon’s framework, and Parker [2009] for a critique of the materiality-based distinction between simulations and experiments.
13 Experimental economists sometimes use the term “parallelism” instead of external validity (which is more common in psychology) to label the problem of generalising from laboratory to real world (see e.g. [Smith, 1982]).
14 The art of causal analysis from econometric data has received increasing attention in recent economic methodology, see for example Hoover [2001].
15 There are other techniques that are used when the model of the perfectly controlled experiment cannot be applied for some reason, but I shall not examine them in detail here (they are illustrated in most textbooks and handbooks of experimental methodology, cf. e.g. [Christensen, 2001]).
16 INUS stands for an Insufficient Non-redundant condition within a set of jointly Unnecessary but Sufficient conditions for an effect to take place. There are several problems with such an approach, some of which are discussed by Mackie himself. The “screening-off” condition fixes some of the most obvious flaws of the INUS account.
17 The terminology (and, partly, the concept) of severity is Popperian. Mayo’s error-probabilistic approach however departs substantially from Popper’s theory of scientific testing — see Mayo [2005] for a discussion. The account of severity given below departs in some important respects from the one I defend in Guala [2005]; see Hausman [2008] for a critique of the former, and Guala [2008] for an amendment.
18 This gives us an error probability, which is obtained by a very different route than likelihood reasoning. In reasoning about likelihoods, we keep E fixed and consider various Hi; in errorprobabilistic reasoning we consider various Ei and reason about their distribution under different assumptions about the data-generating process.
19 In its simplest version, Bayes’ theorem states that P(H | E) = P(E | H)P(H)/P(E). P(H) is the “prior probability” of H; P(E) is the “prior probability” of E(= P(E | H)P(H) + P(E |∼ H)P(∼ H)), and P(E | H) is the “likelihood” of E given H. For a comprehensive defence of Bayesian inductivism see Howson and Urbach [1989].
20 The new (prior) probability of H at time t + 1 (after the observation of E at t) must be equal to the conditional probability of H at t (before E was observed) given E.
21 For a more thorough comparison of the Bayesian and the severity approach, see Mayo [1996], from which many of the points of this section are taken.
22 See e.g. Galison [1987], Gooding, Pinch and Schaffer, eds. [1989].
23 I should thank Sugden for clarifying his thought on this particular point (personal correspondence).
24 I have modified Samuelson’s original notation, to make it consistent with the one I have used so far. Notice that, crucially for Samuelson’s proof,ET is itself a distribution that has been randomly drawn from a set of possible distributions — or, in other words, the prediction of an indeterministic theory that is made conditional on the instantiation of some indeterministic background condition or event. (Think of the prediction that tomorrow it will rain with probability P, a prediction made conditional on the expectation that the temperature will (probably) be quite low.) [Samuelson, 2005, p. 72]. Since this assumption is not important for my argument, I won’t comment on it here.
25 Samuelson also stresses that his argument is not a restatement of the view that one should commit to a theory before testing it with data; and that he is not simply repeating the common prescription to test a theory “out of sample”, i.e. using new data that did not motivate the search for the theory in question [2005, p. 82].
26 Achinstein [2005] and Taper and Lee [2004] provide useful overviews of the current debates on inductive inference and scientific testing.
27 Russell [1912] mentions the predicament of a chicken that sees the farmer bringing food every morning at the same time, and thus runs towards him until, of course, one day the farmer comes to cut the chicken’s neck. The chicken had made an unreliable generalization.
28 See for example Smith [1976; 1982], Wilde [1981].
29 Cf. Kagel and Levin [1986].
30 An interesting question is whether every property of a real-world economy can be transferred and reproduced in the laboratory. Bardsley [2005] argues that this may not be the case, and discusses two concrete cases of experimentation to back up his claim. If Bardsley is right, there may well be some economic phenomena that cannot be studied in the laboratory. How common such phenomena are is entirely an empirical matter of course.
31 It should be stressed that experimenters are often concerned with proving the existence of certain mechanisms or phenomena in the lab only, and leave it to policy-makers or applied economists to apply such knowledge in the field. There is an important division of labor in (applied and pure) science that should not be overlooked by unreasonably imposing on experimenters the task of establishing the external validity of all the experiments they make. See Guala [2005a, Ch. 10].
32 See [Bicchieri, 2006] for a survey and philosophical discussion.
33 For a skeptical view of the “successes” of market design, see [Mirowski and Nik-Kah, 2006].
34 Vernon Smith, co-recipient of the 2002 Nobel Prize, speaks of a constant interaction between “constructive” and “ecological” rationality [Smith, 2008]. Smith follows Hayek in arguing that we should trust the beneficial effects of evolutionary adaptation in the social as well as the biological realm. The postulation of an evolutionary “invisible hand” of course opens another huge and exciting area of research at the intersection between economics and philosophy.