Judgment Aggregation: A Short Introduction
1 Introduction
The aim of this article is to introduce the theory of judgment aggregation, a growing research area in economics, philosophy, political science, law and computer science. The theory addresses the following question: How can a group of individuals make consistent collective judgments on a given set of propositions on the basis of the group members’ individual judgments on them? This problem is one of the fundamental problems of democratic decision-making and arises in many different settings, ranging from legislative committees to referenda, from expert panels to juries and multi-member courts, from boards of companies to the WTO and the UN Security Council, from families to large social organizations. While each real-world case deserves social-scientific attention in its own right, the theory of judgment aggregation seeks to provide a general theoretical framework for investigating some of the properties that different judgment aggregation problems have in common, abstracting from the specifics of concrete cases.
The recent interest in judgment aggregation was sparked by the observation that majority voting, perhaps the most common democratic procedure, fails to guarantee consistent collective judments whenever the decision problem in question exceeds a certain level of complexity, as explained in detail below. This observation, which has become known as the ‘discursive dilemma’, but which can be seen as a generalization of a classic paradox discovered by the Marquis de Condorcet in the 18th century, was subsequently shown to illustrate a deeper impossibility result, of which there are now several variants in the literature. Roughly speaking, there does not exist any method of aggregation – an ‘aggregation rule’ — which (i) guarantees consistent collective judgments and (ii) satisfies some other salient properties exemplified by majority voting, such as determining the collective judgment on each proposition as a function of individual judgments on that proposition and giving all individuals equal weight in the aggregation. This impossibility result, in turn, enables us to see how far we need to deviate from majority voting, and thereby from conventional democratic principles, in order to come up with workable solutions to judgment aggregation problems. In particular, the impossibility result allows us to construct a map of the ‘logical space’ in which different possible solutions to judgment aggregation problems can be positioned.
Just as the theory of judgment aggregation is thematically broad, so its intellectual origins are manifold. Although this article is not intended to be a comprehensive survey, a few historical remarks are useful.1 The initial observation that sparked the recent development of the field goes back to some work in jurisprudence, on decision-making in collegial courts [Kornhauser and Sager, 1986; 1993; Kornhauser, 1992], but was later reinterpreted more generally — as a problem of majority inconsistency — by Pettit [2001], Brennan [2001] and List and Pettit [2002]. List and Pettit [2002; 2004] introduced a first formal model of judgment aggregation, combining social choice theory and propositional logic, and proved a simple impossibility theorem, which was strengthened and extended by several authors, beginning with Pauly and van Hees [2006] and Dietrich [2006]. Independently, Nehring and Puppe [2002] proved some powerful results on the theory of strategy-proof social choice which turned out to have significant corollaries for the theory of judgment aggregation [Nehring and Puppe, 2007a]. In particular, they first characterized the class of decision problems for which certain impossibility results hold, inspiring subsequent related results by Dokow and Holzman [forthcoming], Dietrich and List [2007a] and others. A very general extension of the model of judgment aggregation, from propositional logic to any logic within a large class, was developed by Dietrich [2007a]. The theory of judgment aggregation is also related to the theories of ‘abstract’ aggregation [Wilson, 1975; Rubinstein and Fishburn, 1986], belief merging in computer science [Konieczny and Pino Pérez, 2002; see also Pigozzi, 2006] and probability aggregation (e.g., [McConway, 1981; Genest and Zidek, 1986; Mongin, 1995], and has an informal precursor in the work of Guilbaud [1966] on what he called the ‘logical problem of aggregation’ and perhaps even in Condorcet’s work itself. Modern axiomatic social choice theory, of course, was founded by Arrow [1951/1963]. (For a detailed discussion of the relationship between Arrovian preference aggregation and judgment aggregation, see [List and Pettit, 2004; Dietrich and List, 2007a].)
This article is structured as follows. In section 2, I explain the observation that initially sparked the theory of judgment aggregation. In section 3, I introduce the basic formal model of judgment aggregation, which then, in section 4, allows me to present some illustrative variants of the generic impossibility result. In section 5, I turn to the question of how this impossibility result can be avoided, going through several possible escape routes. In section 6, I relate the theory of judgment aggregation to other branches of aggregation theory. And in section 7, I make some concluding remarks. Rather than offering a comprehensive survey of the theory of judgment aggregation, I hope to introduce the theory in a succinct and pedagogical way, providing an illustrative rather than exhaustive coverage of some of its key ideas and results.
2 A Problem of Majority Inconsistency
Let me begin with Kornhauser and Sager’s [1986] original example from the area of jurisprudence: the so-called ‘doctrinal paradox’ (the name was introduced in [Kornhauser, 1992]). Suppose a collegial court consisting of three judges has to reach a verdict in a breach-of-contract case. The court is required to make judgments on three propositions:
| p: | The defendant was contractually obliged not to do a particular action. |
| q: | The defendant did that action. |
| r: | The defendant is liable for breach of contract. |
According to legal doctrine, propositions p and q are jointly necessary and sufficient for proposition r. Suppose now that the three judges are divided in their judgments, as shown in Table 1. The first thinks that p and q are both true, and hence that r is true as well. The second thinks that p is true, but q is false, and consequently r is also false. The third thinks that, while q is true, p is false, and so r must be false too. So far so good. But what does the court as a whole think?
Table 1. A doctrinal paradox

If the judges take a majority vote on proposition r — the ‘conclusion’ - the outcome is the rejection of this proposition: a ‘not liable’ verdict. But if they take majority votes on each of p and q instead — the ‘premises’ — then both of these propositions are accepted and hence the relevant legal doctrine dictates that r should be accepted as well: a ‘liable’ verdict. The court’s decision thus appears to depend on which aggregation rule it uses. If it uses the first of the two approaches outlined, the so-called ‘conclusion-based procedure’, it will reach a ‘not liable’ verdict; if it uses the second, the ‘premise-based procedure’, it will reach a ‘liable’ verdict. Kornhauser and Sager’s ‘doctrinal paradox’ consists in the fact that the premise-based and conclusion-based procedures may yield opposite outcomes for the same combination of individual judgments.2
But we can also make a more general observation from this example. Relative to the given legal doctrine — which states that r is true if and only if both p and q are true — the majority judgments across the three propositions are inconsistent. In precise terms, the set of propositions accepted by a majority, namely {p, q, not r}, is logically inconsistent relative to the constraint that r if and only if p and q. This problem — that majority voting may lead to the acceptance of an inconsistent set of propositions — generalizes well beyond this example and does not depend on the presence of any legal doctrine or other exogenous constraint; nor does it depend on the partition of the relevant propositions into premises and conclusions.
To illustrate this more general problem, consider any set of propositions with some non-trivial logical connections; below I say more about the precise notion of ‘non-triviality’ required. Take, for instance, the following three propositions on which a multi-member government may seek to make collective judgments:
| p: | We can afford a budget deficit. |
| if p then q: | If we can afford a budget deficit, then we should increase spending on education. |
| q: | We should increase spending on education. |
Suppose now that one third of the government accepts all three propositions, a second third accepts p but rejects if p then q as well as q, and the last third accepts if p then q but rejects p as well as q, as shown in Table 2.
Table 2. A problem of majority inconsistency
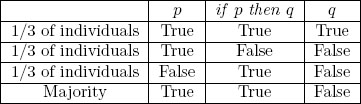
Then each government member holds individually consistent judgments on the three propositions, and yet there are majorities for p, for if p then q and for not q, a logically inconsistent set of propositions. The fact that majority voting may generate inconsistent collective judgments is sometimes called the ‘discursive dilemma’ [Pettit, 2001; List and Pettit, 2002; see also Brennan, 2001], but it is perhaps best described as the problem of ‘majority inconsistency’.
How general is this problem? It is easy to see that it can arise as soon as the set of propositions (and their negations) on which judgments are to be made exhibits a simple combinatorial property: it has a ‘minimally inconsistent’ subset of three or more propositions [Dietrich and List, 2007b; Nehring and Puppe, 2007b]. A set of propositions is called ‘minimally inconsistent’ if it is inconsistent and every proper subset of it is consistent. In the court example, a minimally inconsistent set with these properties is {p, q, not r}, where the inconsistency is relative to the constraint r if and only if p and q. In the government example, it is {p, if p then q, not q}. As soon as there exists at least one minimally inconsistent subset of three or more propositions among the proposition-negation pairs on the agenda, combinations of judgments such as the one in Table 2 become possible, for which the majority judgments are inconsistent. Indeed, as explained in section 6 below, Condorcet’s classic paradox of cyclical majority preferences is an instance of this general phenomenon, which Guilbaud [1952] described as the ‘Condorcet effect’.
3 The Basic Model of Judgment Aggregation
In order to go beyond the observation that majority voting may produce inconsistent collective judgments and to ask whether other aggregation rules may be immune to this problem, it is necessary to introduce a more general model, which abstracts from the specific decision problem and aggregation rule in question. My exposition of this model follows the formalism introduced in List and Pettit [2002] and extended beyond standard propositional logic by Dietrich [2007a].
There is a finite set of (two or more) individuals, who have to make judgments on some propositions.3 Propositions are represented by sentences from propositional logic or a more expressive logical language, and they are generally denoted p, q, r and so on. Propositional logic can express ‘atomic propositions’, which do not contain any logical connectives, such as the proposition that we can afford a budget deficit or the proposition that spending on education should be increased, as well as ‘compound propositions’, with the logical connectives not, and, or, if-then, if and only if, such as the proposition that if we can afford a budget deficit, then spending on education should be increased. Instead of propositional logic, any logic with some minimal properties can be used, including expressively richer logics such as predicate, modal, deontic and conditional logics [Dietrich, 2007a]. Crucially, the logic allows us to distinguish between ‘consistent’ and ‘inconsistent’ sets of propositions. For example, the set {p, q, p and q} is consistent while the sets {p, if p then q, not q} or {p, not p} are not.4
The set of propositions on which judgments are to be made in a particular decision problem is called the ‘agenda’. Formally, the ‘agenda’ is defined as a non-empty subset of the logical language, which is closed under negation, i.e., if p is on the agenda, then so is not p.5 In the government example, the agenda contains the propositions p, if p then q, q and their negations. In the court example, it contains p, q, r and their negations, but here there is an additional stipulation built into the logic according to which r if and only if p and q.6
Now each individual’s ‘judgment set’ is the set of propositions that this individual accepts; formally, it is a subset of the agenda. On the standard interpretation, to accept a proposition means to believe it to be true; on an alternative interpretation, it could mean to desire it to be true. For the present purposes, it is easiest to adopt the standard interpretation, i.e., to interpret judgments as binary cognitive attitudes rather than as binary emotive ones. A judgment set is called ‘consistent’ if it is a consistent set of propositions in the standard sense of the logic, and ‘complete’ if it contains a member of each proposition-negation pair on the agenda. A combination of judgment sets across the given individuals is called a ‘profile’. Thus the first three rows of Tables 1 and 2 are examples of profiles on the agendas in question.
To complete the exposition of the basic model, it remains to define the notion of an ‘aggregation rule’. As illustrated in Figure 1, an ‘aggregation rule’ is a function that maps each profile of individual judgment sets in some domain to a collective judgment set, interpreted as the set of propositions accepted by the collective as a whole.
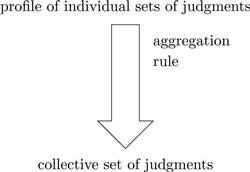
Figure 1 An aggregation rule
Examples of aggregation rules are ‘majority voting’, as already introduced, where each proposition is collectively accepted if and only if it is accepted by a majority of individuals; ‘supermajority’ or ‘unanimity rules’, where each proposition is collectively accepted if and only if it is accepted by a certain qualified majority of individuals, such as two thirds, three quarters, or all of them; ‘dictatorships’, where the collective judgment set is always the individual judgment set of the same antecedently fixed individual; and ‘premise’- and ‘conclusion-based procedures’, as briefly introduced in the court example above.
Although at first sight there seems to be an abundance of logically possible aggregation rules, it is surprisingly difficult to find one that guarantees consistent collective judgments. As we have already seen, majority voting notoriously fails to do so as soon as the propositions on the agenda are non-trivially logically connected. Let me therefore turn to a more general, axiomatic investigation of possible aggregation rules.
4 A General Impossibility Result
Are there any democratically compelling aggregation rules that guarantee consistent collective judgments? The answer to this question depends on two parameters: first, the types of decision problems — as captured by the given agenda — for which we seek to employ the aggregation rule; and second, the conditions that we expect it to meet. Before presenting some illustrative results, let me briefly explain why both parameters matter.
Suppose, for example, that we are only interested in decision problems that involve making a single binary judgment, say on whether to accept p or not p. In other words, the agenda contains only a single proposition-negation pair (or, more generally, multiple logically unconnected such pairs). Obviously, we can then use majority voting without any risk of collective inconsistency. As we have already seen, the problem of majority inconsistency arises only if the agenda exceeds a certain level of complexity (i.e., it has at least one minimally inconsistent subset of three or more propositions). So the complexity of the decision problem in question is clearly relevant to the question of which aggregation rules, if any, produce consistent collective judgments.
Secondly, suppose that, instead of using an aggregation rule that satisfies strong democratic principles, we content ourselves with installing a dictatorship, i.e., we appoint one individual whose judgments are deemed always to determine the collective ones. If this individual’s judgments are consistent, then, trivially, so are the resulting collective ones. The problem of aggregation will have been resolved under such a dictatorial arrangement, albeit in a degenerate way. This shows that the answer to the question of whether there exist any aggregation rules that ensure consistent collective judgments depends very much on what conditions we expect those rules to meet.
With these preliminary remarks in place, let me address the question of the existence of compelling aggregation rules in more detail. The original impossibility theorem by List and Pettit [2002] gives a simple answer to this question for a specific class of decision problems and a specific set of conditions on the aggregation rule:
THEOREM 1 List and Pettit, 2002. Let the agenda contain at least two distinct atomic propositions (say, p, q) and either their conjunction (p and q), or their disjunction (p or q), or their material implication (if p then q). Then there exists no aggregation rule satisfying the conditions of ‘universal domain’, ‘collective rationality’, ‘systematicity’ and ‘anonymity’.
What are these conditions? The first, universal domain, specifies the admissible inputs of the aggregation rule, requiring the aggregation rule to admit as input any possible profile of consistent and complete individual judgment sets on the propositions on the agenda. The second, collective rationality, constrains the outputs of the aggregation rule, requiring the output always to be a consistent and complete collective judgment set on the propositions on the agenda. The third and fourth, systematicity and anonymity, constrain the way the outputs are generated from the inputs and can thus be seen as responsiveness conditions. Systematicity is the two-part requirement that (i) the collective judgment on each proposition on the agenda depend only on individual judgments on that proposition, not on individual judgments on other propositions (the ‘independence’ requirement), and (ii) the criterion for determining the collective judgment on each proposition be the same across propositions (the ‘neutrality’ requirement). ‘Anonymity’ requires that the collective judgment set be invariant under permutations of the judgment sets of different individuals in a given profile; in other words, all individuals have equal weight in the aggregation.
Much can be said about these conditions — I discuss them further in the section on how to avoid the impossibility — but for the moment it is enough to note that they are inspired by key properties of majority voting. In fact, majority voting satisfies them all, with the crucial exception of the consistency part of collective rationality (for non-trivial agendas), as shown by the discursive dilemma. The fact that majority voting exhibits this violation illustrates the theorem just stated: no aggregation rule satisfies all four conditions simultaneously.
As mentioned in the introduction, this impossibility result has been significantly generalized and extended in a growing literature. Different impossibility theorems apply to different classes of agendas, and they impose different conditions on the aggregation rule. However, they share a generic form, stating that, for a particular class of agendas, the aggregation rules satisfying a particular combination of input, output and responsiveness conditions are either non-existent or otherwise degenerate. The precise class of agendas and input, output and responsiveness conditions vary from result to result. For example, Pauly and van Hees’s [2006] first theorem states that if we take the same class of agendas as in List and Pettit’s theorem and the same input and output conditions (universal domain and collective rationality), keep the responsiveness condition of systematicity but drop anonymity, then we are left only with dictatorial aggregation rules, as defined above. Other theorems by Pauly and van Hees [2006] and Dietrich [2006] show that, for more restrictive classes of agendas, again with the original input and output conditions and without anonymity, but this time with systematicity weakened to its first part (‘independence’), we are still left only with dictatorial or constant aggregation rules. The latter are another kind of degenerate rules, which assign to every profile the same fixed collective judgment set, paying no attention to any of the individual judgment sets. Another theorem, by Mongin [forthcoming], also keeps the original input and output conditions, adds a responsiveness condition requiring the preservation of unanimous individual judgments7 but weakens systematicity further, namely to an independence condition restricted to atomic propositions alone. The theorem then shows that, for a certain class of agendas, only dictatorial aggregation rules satisfy these conditions together.
The most general theorems in the literature are so-called ‘agenda characterization theorems’. They do not merely show that for a certain class of agendas, a certain combination of input, output and responsiveness conditions lead to an empty or degenerate class of aggregation rules, but they fully characterize those agendas for which this is the case and, by implication, those for which it is not. The idea underlying agenda characterizations was introduced by Nehring and Puppe [2002] in a different context, namely the theory of strategy-proof social choice. However, several of their results carry over to judgment aggregation (as discussed in [Nehring and Puppe, 2007a]) and have inspired other agenda characterization results (e.g., [Dokow and Holzman, forthcoming; Dietrich and List, 2007]).
To give a flavour of these results, recall that only agendas which have at least one minimally inconsistent subset of three or more propositions are of interest from the perspective of impossibility theorems; call such agendas ‘non-simple’. For agendas below this level of complexity, majority voting works perfectly well.8 Non-simple agendas may or may not have some additional properties. For example, they may or may not have a minimally inconsistent subset with the special property that, by negating some even number of propositions in it, it becomes consistent; call an agenda of this kind ‘even-number-negatable’.9
It now turns out that, for all and only those agendas which are both non-simple and even-number-negatable, every aggregation rule satisfying universal domain, collective rationality and systematicity — i.e., the original input, output and responsiveness conditions — is either dictatorial or inversely dictatorial (the latter means that the collective judgment set is always the propositionwise negation of the judgment set of some antecedently fixed individual) [Dietrich and List, 2007a]. Further, for all and only those agendas which are just non-simple (whether or not they are even-number-negatable), every aggregation rule satisfying the same conditions and an additional ‘monotonicity’ condition10 is dictatorial [Nehring and Puppe, 2002; 2007a]. If we restrict these two classes of agendas by adding a further property (called ‘total blockedness’ or ‘path-connectedness’11), then similar results hold with systematicity weakened to independence and an additional responsiveness condition of ‘unanimity preservation’ ([Dokow and Holzman, forthcoming; Nehring and Puppe, 2002; 2007a] respectively).12 Table 3 surveys those results.
Table 3. Agenda characterization results
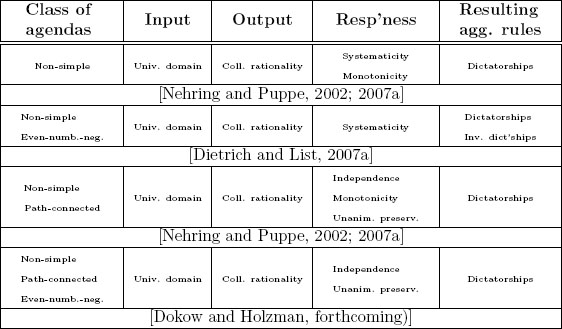
For each of the four rows of the table, the following two things are true: first, if the agenda has the property described in the left-most column, every aggregation rule satisfying the specified input, output and responsiveness conditions is of the kind described in the right-most column; and second, if the agenda violates the property in the left-most column, there exist aggregation rules other than those described in the right-most column which still satisfy the specified conditions.
The theorems reviewed in this section show that if (i) we deal with decision problems involving agendas with some of the identified properties and (ii) we consider the specified input, output and responsiveness conditions to be indispensable requirements of democratic aggregation, then judgment aggregation problems have no non-degenerate solutions. To avoid this implication, we must therefore deny either (i) or (ii). Unless we can somehow avoid non-trivial decision problems altogether, denying (i) does not seem to be a viable option. Therefore we must obviously deny (ii). So what options do we have? Which of the conditions might we relax?
5 Avoiding the Impossibility
As noted, the conditions leading to an impossibility result — i.e., the non-existence of any non-degenerate aggregation rules — fall into three types: input, output and responsiveness conditions. For each type of condition, we can ask whether a suitable relaxation would enable us to avoid the impossibility.
5.1 Relaxing the input conditions
All the impossibility theorems reviewed so far impose the condition of universal domain on the aggregation rule, by which any possible profile of consistent and complete individual judgment sets on the propositions on the agenda is deemed admissible as input to the aggregation. At first sight this condition seems eminently reasonable. After all, we want the aggregation rule to work not only for some special inputs, but for all possible inputs that may be submitted to it. However, different groups may exhibit different levels of pluralism, and in some groups there may be significantly more agreement between the members’ judgments than in others. Expert panels or ideologically well structured societies may be more homogeneous than some large and internally diverse electorates. Thus the profiles of individual judgment sets leading to collective inconsistencies under plausible aggregation rules such as majority voting may be more likely to occur in some heterogeneous groups than in other more homogeneous ones. Can we say something systematic about the type of ‘homogeneity’ that is required for the avoidance of majority inconsistencies — and by implication for the avoidance of the more general impossibility of judgment aggregation?
It turns out that there exist several combinatorial conditions with the property that, on the restricted domain of profiles of individual judgment sets satisfying those conditions, majority voting generates consistent and (absent ties) complete individual judgment sets and — of course - satisfies the various responsiveness conditions introduced in the last section. For brevity, let me here discuss just two illustrative such conditions: a very simple one and a very general one.
The first is called ‘unidimensional alignment’ [List, 2003]. It is similar in spirit, but not equivalent, to a much earlier condition in the theory of preference aggregation, called ‘single-peakedness’, which was introduced in a classic paper by Black [1948]. (Single-peakedness is a constraint on profiles of preference orderings rather than judgment sets.) A profile of individual judgment sets is ‘unidimensionally aligned’ if it is possible to align the individuals from left to right such that, for every proposition on the agenda, the individuals accepting the proposition are either all to the left, or all to the right, of those rejecting it, as illustrated in Table 4.
Table 4. A unidimensionally aligned profile of individual judgment sets

The relevant left-right alignment of the individuals may be interpreted as capturing their position on some cognitive or ideological dimension (e.g., from socio-economic left to right, or from urban to rural, or from secular to religious, or from environmentally risk-averse to environmentally risk-taking etc.), but what matters from the perspective of achieving majority consistency is not the semantic interpretation of the alignment but rather the combinatorial constraint it imposes on individual judgments.
Why is unidimensional alignment sufficient for consistent majority judgments? Since the individuals accepting each proposition are opposite those rejecting it on the given left-right alignment, a proposition cannot be accepted by a majority unless it is accepted by the middle individual on that alignment13 - individual 3 in the example of Table 4. In particular, the majority judgments must coincide with the middle individual’s judgments.14 Hence, so long as the middle individual holds consistent judgments, the resulting majority judgments will be consistent too.15 When restricted to the domain of unidimensionally aligned profiles of individual judgment sets,16 majority voting therefore satisfies all the conditions introduced in the last section, except of course universal domain.
However, while unidimensional alignment is sufficient for majority consistency, it is by no means necessary. A necessary and sufficient condition is the following [Dietrich and List, 2007c]. A profile is called ‘majority consistent’ if every minimally inconsistent subset of the agenda contains at least one proposition that is not accepted by a majority. Is it easy to see that this is indeed enough to ensure consistent majority judgments. If the set of propositions accepted by a majority is inconsistent, it must have at least one minimally inconsistent subset, but not all propositions in this set can be majority-accepted if the underlying profile satisfies the combinatorial condition just defined. An important special case is given by the condition of ‘value-restriction’ [Dietrich and List, 2007c], which generalizes an equally named classic condition in the context of preference aggregation [Sen, 1966]. A profile of individual judgment sets is called ‘value-restricted’ if every minimally inconsistent subset of the agenda contains a pair of propositions p, q not jointly accepted by any individual. Again, this is enough to rule out that any minimally inconsistent set of propositions can be majority-accepted: if it were, then, in particular, each of the propositions p and q from the definition of value-restriction would be majority-accepted and thus at least one individual would accept both, contradicting value-restriction. (Several other domain restriction conditions are discussed in [Dietrich and List, 2007c].)
How plausible is the strategy of avoiding the impossibility of non-degenerate judgment aggregation via restricting the domain of admissible inputs to the aggregation rule? The answer to this question depends on the group, context and decision problem at stake. As already noted, different groups exhibit different levels of pluralism, and it is clearly an empirical question whether or not any of the identified combinatorial conditions are met by the empirically occurring profiles of individual judgment sets in any given case. Some groups may be naturally homogeneous or characterized by an entrenched one-dimensional ideological or cognitive spectrum in terms of which group members tend to conceptualize issues under consideration. Think, for example, of societies with a strong tradition of a conventional ideological left-right polarization. Other societies or groups may not have such an entrenched structure, and yet through group deliberation or other forms of communication they may be able to achieve sufficiently ‘cohesive’ individual judgments, which meet conditions such as unidimensional alignment or value-restriction. In debates on the relationship between social choice theory and the theory of deliberative democracy, the existence of mechanisms along these lines has been hypothesized [Miller, 1992; Knight and Johnson, 1994; Dryzek and List, 2003]. However, the present escape route from the impossibility is certainly no ‘one size fits all’ solution.
5.2 Relaxing the output conditions
Like the input condition of universal domain, the output condition of collective rationality occurs in all the impossibility theorems reviewed above. Again the condition seems prima facie reasonable. First of all, the requirement of consistent collective judgments is important not only from a pragmatic perspective — after all, inconsistent judgments would fail to be action-guiding when it comes to making concrete decisions — but also from a more fundamental philosophical one. As argued by Pettit [2001], collective consistency is essential for the contestability and justifiability of collective decisions (for critical discussions of this point, see also [Kornhauser and Sager, 2004; List, 2006]). And secondly, the requirement of complete collective judgments is also pragmatically important. One would imagine that only those propositions will be included on the agenda that require actual adjudication; and if they do, the formation of complete collective judgments on them will be essential.
Nonetheless, the case for collective consistency is arguably stronger than that for collective completeness. There is now an entire sequence of papers in the literature that discuss relaxations of completeness (e.g., [List and Pettit, 2002; Gärdenfors, 2006; Dietrich and List, 2007b; 2007d; 2008a; Dokow and Holzman, 2006]). Gärdenfors [2006], for instance, criticizes completeness as a ‘strong and unnatural assumption’. However, it turns out that not every relaxation of completeness is enough to avoid the impossibility of non-degenerate judgment aggregation. As shown by Gärdenfors [2006] for a particular class of agendas (so-called ‘atomless’ agendas) and subsequently generalized by Dietrich and List [2008a] and Dokow and Holzman [2006], if the collective completeness requirement is weakened to a ‘deductive closure’ requirement according to which propositions on the agenda that are logically entailed by other accepted propositions must also be accepted, then the other conditions reviewed above restrict the possible aggregation rules to so-called ‘oligarchic’ ones. An aggregation rule is ‘oligarchic’ if there exists an antecedently fixed non-empty subset of the individuals — the ‘oligarchs’ — such that the collective judgment set is always the intersection of the individual judgment sets of the oligarchs. (A dictatorial aggregation rule is the limiting case in which the set of oligarchs is singleton.) In fact, a table very similar to Table 3 above can be derived in which the output condition is relaxed to the conjunction of consistency and deductive closure and the right-most column is extended to the class of oligarchic aggregation rules (for technical details, see [Dietrich and List, 2008a]).
However, if collective rationality is weakened further, namely to consistency alone, more promising possibilities open up. In particular, groups may then use supermajority rules according to which any proposition on the agenda is collectively accepted if and only if it is accepted by a certain supermajority of individuals, such as more than two thirds, three quarters, or four fifths of them. If the supermajority threshold is chosen to be sufficiently large, such rules produce consistent (but not generally deductively closed) collective judgments [List and Pettit, 2002]. In particular, any threshold above  is sufficient to ensure collective consistency, where k is the size of the largest minimally inconsistent subset of the agenda [Dietrich and List, 2007b]. In the court and government examples above, this numer is three, and thus a supermajority threshold above two thirds would be sufficient for collective consistency. Supermajority rules, of course, satisfy all the other (input and responsiveness) conditions that I have reviewed.
is sufficient to ensure collective consistency, where k is the size of the largest minimally inconsistent subset of the agenda [Dietrich and List, 2007b]. In the court and government examples above, this numer is three, and thus a supermajority threshold above two thirds would be sufficient for collective consistency. Supermajority rules, of course, satisfy all the other (input and responsiveness) conditions that I have reviewed.
Groups with a strongly consensual culture, such as the UN Security Council or the EU Council of Minister, may very well take this supermajoritarian approach to solving judgment aggregation problems. The price they have to pay for avoiding the impossibility of non-degenerate judgment aggregation in this manner is the risk of stalemate. Small minorities will be able to veto judgments on any propositions.17 As in the case of the earlier escape route — via relaxing universal domain — the present one is no ‘one size fits all’ solution to the problem of judgment aggregation.
5.3 Relaxing the responsiveness conditions
Arguably, the most compelling escape-route from the impossibility of non-degenerate judgment aggregation opens up when we relax some of the responsiveness conditions used in the impossibility theorems. The key condition here is independence, i.e., the first part of the systematicity condition, which requires that the collective judgment on each proposition on the agenda depend only on individual judgments on that proposition, not on individual judgments on other propositions. The second part of systematicity, requiring that the criterion for determining the collective judgment on each proposition be the same across propositions, is already absent from several of the impossibility theorems (namely whenever the agenda is sufficiently complex), and relaxing it alone is thus insufficient for avoiding the basic impossibility result in general.
If we give up independence, however, several promising aggregation rules become possible. The simplest example of such a rule is the premise-based procedure, which I have already briefly mentioned in the context of Kornhauser and Sager’s doctrinal paradox. This rule was discussed, originally under the name ‘issue-by-issue voting’, by Kornhauser and Sager [1986] and Kornhauser [1992], and later by Pettit [2001], List and Pettit [2002], Chapman [2002], Bovens and Rabinowicz [2006], Dietrich [2006] and many others. Abstracting from the court example, the ‘premise-based procedure’ involves designating some propositions on the agenda as ‘premises’ and others as ‘conclusions’ and generating the collective judgments by taking majority votes on all premises and then deriving the judgments on all conclusions from these majority judgments on the premises; by construction, the consistency of the resulting collective judgments is guaranteed, provided the premises are logically independent from each other. If these premises further constitute a ‘logical basis’ for the entire agenda – i.e., they are not only logically independent but any assignment of truth-values to them also settles the truth-values of all other propositions – then the premise-based procedure also ensures collective completeness.18 (The conclusion-based procedure, by contrast, violates completeness, in so far as it only ever generates collective judgments on the conclusion(s), by taking majority votes on them alone.)
The premise-based procedure, in turn, is a special case of a ‘sequential priority procedure’ [List, 2004]. To define such an aggregation rule, we must specify a particular order of priority among the propositions on the agenda such that earlier propositions in that order are interpreted as epistemically (or otherwise) prior to later ones. For each profile of individual judgments sets, the propositions are then considered one-by-one in the specified order and the collective judgment on each proposition is formed as follows. If the majority judgment on the proposition is consistent with the collective judgments on propositions considered earlier, then that majority judgment becomes the collective judgment; but if the majority judgment is inconsistent with those earlier judgments, then the collective judgment is determined by the implications of those earlier judgments. In the example of Table 2 above, the multi-member government might consider the propositions in the order p, if p then q, q (with negations interspersed) and then accept p and if p then q by majority voting while accepting q by logical inference. The collective judgment set under such an aggregation rule is dependent on the specified order of priority among the propositions. This property of ‘path-dependence’ can be seen as a virtue or as a vice, depending on the perspective one takes. On the one hand, it appears to do justice to the fact that propositions can differ in their status (consider, for example, constitutional propositions versus propositions of ordinary law), as emphasized by Pettit [2001] and Chapman [2002]. But on the other hand, it makes collective judgments manipulable by an agenda setter who can influence the order in which propositions are considered [List, 2004], which in turn echoes a much-discussed worry in social choice theory (e.g., [Riker, 1982]).
Another class of aggregation rules that give up independence — the class of ‘distance-based rules’ — was introduced by Pigozzi [2006], drawing on related work on the theory of belief merging in computer science [Konieczny and Pino Pérez, 2002]. Unlike premise-based or sequential priority procedures, these rules are not based on the idea of prioritizing some propositions over others. Instead, they are based on a ‘distance metric’ between judgment sets. We can define the ‘distance’ between any two judgment sets for instance by counting the number of propositions on the agenda on which they ‘disagree’ (i.e., the number of propositions for which it is not the case that the proposition is contained in the one judgment set if and only if it is contained in the other). A ‘distance-based aggregation rule’ now assigns to each profile of individual judgment sets the collective judgment set that minimizes the sum-total distance from the individual judgment sets (with some additional stipulation for dealing with ties). Distance-based aggregation rules have a number of interesting properties. They can be seen to capture the idea of reaching a compromise between different individuals’ judgment sets. Most importantly, they give up independence while still preserving the spirit of neutrality across propositions (so long as we adopt a definition of distance that treats all propositions on the agenda equally).
What is the cost of violating independence? Arguably, the greatest cost is manipulability of the aggregation rule by the submission of insincere individual judgments [Dietrich and List, 2007e]. Call an aggregation rule ‘manipulable’ if there exists at least one admissible profile of individual judgment sets such that the following is true for at least one individual and at least one proposition on the agenda: (i) if the individual submits the judgment set that he/she genuinely holds, then the collective judgment on the proposition in question differs from the individual’s genuine judgment on it; (ii) if he/she submits a strategically adjusted judgment set, then the collective judgment on that proposition coincides with the individual’s genuine judgment on it. If an aggregation rule is manipulable in this sense, then individuals may have incentives to misrepresent their judgments.19 To illustrate, if the court in the example of Table 1 were to use the premise-based procedure, sincere voting among the judges would lead to a ‘liable’ verdict, as we have seen. However, if judge 3 were sufficiently strongly opposed to this outcome, he or she could strategically manipulate it by pretending to believe that q is false, contrary to his or her sincere judgment; the result would be the majority rejection of proposition q, and hence a ‘not liable’ verdict. It can be shown that an aggregation rule is non-manipulable if and only if it satisfies the conditions of independence and monotonicity introduced above ([Dietrich and List, 2007e]; for closely related results in a more classic social-choice-theoretic framework, see [Nehring and Puppe, 2007b]). Assuming that, other things being equal, the relaxation of independence is the most promising way to make non-degenerate judgment aggregation possible, the impossibility theorems reviewed above can therefore be seen as pointing to a trade-off between degeneracy of judgment aggregation on the one hand (most notably, in the form of dictatorship) and its potential manipulability on the other. As in other branches of social choice theory, a perfect aggregation rule does not exist.
6 The Relationship to Other Aggregation Problems
Before concluding, it is useful to consider the relationship between the theory of judgment aggregation and other branches of aggregation theory. Let me focus on three related aggregation problems: preference aggregation, abstract aggregation and probability aggregation.
6.1 Preference aggregation
The theory of preference aggregation in the long and established tradition of Condorcet and Arrow addresses the following question: How can a group of individuals arrive at a collective preference ordering on some set of alternatives on the basis of the group members’ individual preference orderings on them? Condorcet’s classic paradox illustrates some of the challenges raised by this problem. Consider a group of individuals seeking to form collective preferences over three alternatives, x, y and z, where the first individual prefers x to y to z, the second y to z to x, and the third z to x to y. It is then easy to see that majority voting over pairs of alternatives fails to yield a rational collective preference ordering: there are majorities for x over y, for y over z, and yet for z over x — a ‘preference cycle’. Arrow’s theorem [1951/1963] generalizes this observation by showing that, when there are three or more alternatives, the only aggregation rules that generally avoid such cycles and satisfy some other minimal conditions are dictatorial ones. Condorcet’s paradox and Arrow’s theorem have inspired a massive literature on axiomatic social choice theory, a review of which is entirely beyond the scope of this paper.
How is the theory of preference aggregation related to the theory of judgment aggregation? It turns out that preference aggregation problems can be formally represented within the model of judgment aggregation. The idea is that preference orderings can be represented as sets of accepted preference ranking propositions of the form ‘x is preferable to y’, ‘y is preferable to z’, and so on.
To construct this representation formally (following [Dietrich and List, 2007], extending [List and Pettit, 2004]), it is necessary to employ a specially devised predicate logic with two or more constants representing alternatives, denoted x, y, z and so on, and a two-place predicate ‘_is preferable to_’. To capture the standard rationality conditions on preferences (such as asymmetry, transitivity and connectedness), we define a set of propositions in our predicate logic to be ‘consistent’ just in case this set is consistent relative to those rationality conditions. For example, the set {x is preferable to y, y is preferable to z} is consistent, while the set {x is preferable to y, y is preferable to z, z is preferable to x} — representing a preference cycle — is not. The agenda is then defined as the set of all propositions of the form ‘v is preferable to w’ and their negations, where v and w are alternatives among x, y, z and so on. Now each consistent and complete judgment set on this agenda uniquely represents a rational (i.e., asymmetric, transitive and connected) preference ordering. For instance, the judgment set {x is preferable to y, y is preferable to z, x is preferable to z} uniquely represents the preference ordering according to which x is most preferred, y second-most preferred, and z least preferred. Furthermore, a judgment aggregation rule on the given agenda uniquely represents an Arrovian preference aggregation rule (i.e., a function from profiles of individual preference orderings to collective preference orderings).
Under this construction, Condorcet’s paradox of cyclical majority preferences becomes a special case of the problem of majority inconsistency discussed in section 2 above. To see this, notice that the judgment sets of the three individuals in the example of Condorcet’s paradox are as shown in Table 5. Given these individual judgments, the majority judgments are indeed inconsistent, as the set of propositions accepted by a majority is inconsistent relative to the rationality condition of transitivity.
Table 5. Condorcet’s paradox translated into jugdment aggregation
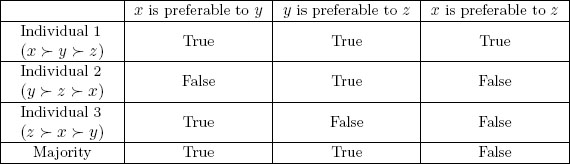
More generally, it can be shown that, when there are three or more alternatives, the agenda just defined has all the complexity properties introduced in the discussion of the impossibility theorems above (i.e., non-simplicity, even-number-negatability, and total blockedness / path-connectedness), and thus those theorems apply to the case of preference aggregation. In particular, the only aggregation rules satisfying universal domain, collective rationality, independence and unanimity preservation are dictatorships [Dietrich and List, 2007; Dokow and Holzman, forthcoming]; for a similar result with an additional monotonicity condition, see [Nehring, 2003]. This is precisely Arrow’s classic impossibility theorem for strict preferences: the conditions of universal domain and collective rationality correspond to Arrow’s equally named conditions, independence corresponds to Arrow’s so-called ‘independence of irrelevant alternatives’, and unanimity preservation, finally, corresponds to Arrow’s ‘weak Pareto principle’.
6.2 Abstract aggregation
The problem of judgment aggregation is closely related to the problem of abstract aggregation first formulated by Wilson [1975] (in the binary version discussed here) and later generalized by Rubinstein and Fishburn [1986] (in a non-binary version). In recent work, the problem has been discussed by Dokow and Holzman [forthcoming] and in a slightly different formulation (the ‘property space’ formulation) by Nehring and Puppe [2002; 2007a]. Again let me begin by stating the key question: How can a group of individuals arrive at a collective vector of yes/no evaluations over a set of binary issues on the basis of the group members’ individual evaluations over them, subject to some feasibility constraints? Suppose there are multiple binary issues on which a positive (1) or negative (0) view is to be taken. An ‘evaluation vector’ over these issues is an assignment of 0s and 1s to them. Let Z ⊆ {0,1}k be the set of evaluation vectors deemed ‘feasible’, where k is the total number of issues. Now an ‘abstract aggregation rule’ is a function that maps each profile of individual evaluation vectors in a given domain of feasible ones to a collective evaluation vector. To represent Kornhauser and Sager’s court example in this model, we introduce three issues, corresponding to propositions p, q and r, and define the set of feasible evaluation vectors to be Z = {(0,0,0),(0,1,0),(1,0,0),(1,1,1)}, i.e., the set of 0/1 assignments that respect the doctrinal constraint whereby positive evaluations on the first two issues (corresponding to p and q) are necessary and sufficient for a positive evaluation on the third one (corresponding to r). More generally, a judgment aggregation problem can be represented in the abstract aggregation model by defining the set of feasible evaluation vectors to be the set of admissible truth-value assignments to the unnegated propositions on the agenda. The problem of majoritarian inconsistency then reemerges as a failure of issue-wise majority voting to preserve feasibility from the individual to the collective level.
As discussed in List and Puppe [forthcoming], the model of abstract aggregation is informationally sparser than the logic-based model of judgment aggregation. To see that by translating judgment aggregation problems into abstract ones we lose some information, notice that the same set of feasible evaluation vectors may result from very different agendas and thus from very different decision problems. For example, the set of feasible evaluation vectors resulting from the agenda containing p, p if and only if q, p and q (and negations), without any doctrinal constraint, coincides with that resulting from the agenda in the court example — namely Z as just defined — although syntactically and interpretationally those agendas are clearly very different from each other.
The abstract aggregation model is arguably at its strongest when our primary interest lies in how the existence of non-degenerate aggregation rules depends on the nature of the feasibility constraints, as opposed to the particular syntactic structure or interpretation of the underlying propositions. Indeed, the agenda characterization theorems reviewed above have their intellectual origins in the literature on abstract aggregation (and here particularly in Nehring and Puppe’s [2002]work as well as in Dokow and Holzman’s [forthcoming] subsequent paper). When the logical formulation of a decision problem is to be made explicit, or when the rationality constraints on judgments (and their possible relaxations) are to be analyzed using logical concepts, on the other hand, the logic-based model of judgment aggregation seems more natural.
6.3 Probability aggregation
In the theory of probability aggregation, finally, the focus is not on making consistent acceptance/rejection judgments on the propositions of interest, but rather on arriving at a coherent probability assignment to them (e.g., [McConway, 1981; Genest and Zidek, 1986; Mongin, 1995]). Thus the central question is: How can a group of individuals arrive at a collective probability assignment to a given set of propositions on the basis of the group members’ individual probability assignments, while preserving probabilistic coherence (i.e., the satisfaction of the standard axioms of probability theory)? The problem is quite a general one. In a number of decision-making settings, the aim is not so much to come up with acceptance/rejection judgments on certain propositions but rather to arrive at probabilistic information about the degree of belief we are entitled to assign to them or the likelihood of the events they refer to.
Interestingly, the move from a binary to a probabilistic setting opens up some non-degenerate possibilities of aggregation not existent in the standard case of judgment aggregation. A key insight is that probabilistic coherence is preserved under linear averaging of probability assignments. In other words, if each individual coherently assigns probabilities to a given set of propositions, then any weighted linear average of these probability assignments across individuals still constitutes an overall coherent probability assignment. Moreover, it is easy to see that this method of aggregation satisfies the analogues of all the input, output and responsiveness conditions introduced above: i.e., it accepts all possible profiles of coherent individual probability assignments as input, produces a coherent collective probability assignment as output and satisfies the analogues of systematicy and unanimity preservation; it also satisfies anonymity if all individuals are given equal weight in the averaging. A classic theorem by McConway [1981] shows that, if the agenda is isomorphic to a Boolean algebra with more than four elements, linear averaging is uniquely characterized by an independence condition, a unanimity preservation condition as well as the analogues of universal domain and collective rationality. Recently, Dietrich and List [2008b] have obtained a generalization of (a variant of) this theorem for a much larger class of agendas (essentially, the analogue of non-simple agendas). A challenge for the future is to obtain even more general theorems that yield both standard results on judgment aggregation and interesting characterizations of salient probability aggregation methods as special cases.
7 Concluding Remarks
The aim of this article has been to give a brief introduction to the theory of judgment aggregation. My focus has been on some of the central ideas and questions of the theory as well as a few illustrative results. Inevitably, a large number of other important results and promising research directions within the literature have been omitted (for surveys of other important results and directions, see, for example, [List and Puppe, forthcoming; List, 2006; Dietrich, 2007a; Nehring and Puppe, 2007a] as well as the online bibliography on judgment aggregation at http://personal.lse.ac.uk/list/JA.htm). In particular, the bulk of this article has focused on judgment aggregation in accordance with a systematicity or independence condition that forces the aggregation to take place in a proposition-by-proposition manner. Arguably, some of the most interesting open questions in the theory of judgment aggregation concern the relaxation of this propositionwise restriction and the move towards other, potentially more ‘holistic’ notions of responsiveness. Without the restriction to propositionwise aggregation, the space of possibilities suddenly grows dramatically, and I have here reviewed only a few simple examples of aggregation rules that become possible, namely premise-based, sequential priority and distance-based ones.
To provide a more systematic perspective on those possibilities, Dietrich [2007b] has recently introduced a general condition of ‘independence of irrelevant information’, defined in terms of a relation of informational relevance between propositions. An aggregation rule satisfies this condition just in case the collective judgment on each proposition depends only on individual judgments on propositions that are deemed relevant to it. In the classical case of propositionwise aggregation, each proposition is deemed relevant only to itself. In the case of a premise-based procedure, by contrast, premises are deemed relevant to conclusions, and in the case of a sequential priority procedure the relevance relation is given by a linear order of priority among the propositions. Important future research questions concern the precise interplay between the logical structure of the agenda, the relevance relation and the conditions on aggregation rules in determining the space of possibilities.
Another research direction considers the idea of decisiveness rights in the context of judgment aggregation, following Sen’s classic work [1970] on the liberal paradox. In judgment aggregation, it is particularly interesting to investigate the role of experts and the question of whether we can arrive at consistent collective judgments when giving different individuals different weights depending on their expertise on the propositions in question. Some existing impossibility results [Dietrich and List, 2008c] highlight the difficulties that can result from such deference to experts, but many open questions remain.
Finally, as in other areas of social choice theory, there is much research to be done on the relationship between aggregative and deliberative modes of decision-making. In many realistic settings, decision-makers do not merely mechanically aggregate their votes or judgments, but they exchange and share information, communicate with each other and update their beliefs. Some authors have begun to consider possible connections between the theory of judgment aggregation and the theory of belief revision [Pettit, 2006; List, 2008; Dietrich, 2008c; Pivato, 2008]. But much of this terrain is still unexplored. My hope is that this article will contribute to stimulating further research.
Acknowledgements
I am very grateful to Franz Dietrich and Laura Valentini for comments and suggestions on this paper.
BIBLIOGRAPHY
1. Arrow K. Social Choice and Individual Values New York: Wiley; 1951/1963.
2. Black D. On the Rationale of Group Decision-making. Journal of Political Economy. 1948;56(1):23–34.
3. Bovens L, Rabinowicz W. Democratic Answers to Complex Questions — An Epistemic Perspective. Synthese. 2006;150(1):131–153.
4. Brennan G. Collective coherence?. International Review of Law and Economics. 2001;21(2):197–211.
5. Dietrich F. Judgment Aggregation: (Im)Possibility Theorems. Journal of Economic Theory. 2006;126(1):286–298.
6. Dietrich F. A generalised model of judgment aggregation. Social Choice and Welfare. 2007a;28(4):529–565.
7. Dietrich F. Aggregation theory and the relevance of some issues to others University of Maastricht 2007b; Working paper.
8. Dietrich F. Bayesian group belief University of Maastricht 2008; Working paper.
9. Dietrich F, List C. Arrow’s theorem in judgment aggregation. Social Choice and Welfare. 2007a;29(1):19–33.
10. Dietrich F, List C. Judgment aggregation by quota rules: majority voting generalized. Journal of Theoretical Politics. 2007b;19(4):391–424.
11. Dietrich F, List C. Majority voting on restricted domains London School of Economics 2007c; Working paper.
12. Dietrich F, List C. Judgment aggregation with consistency alone London School of Economics 2007d; Working paper.
13. Dietrich F, List C. Strategy-proof judgment aggregation. Economics and Philosophy. 2007e;23:269–300.
14. Dietrich F, List C. Judgment aggregation without full rationality. Social Choice and Welfare. 2008a;31:15–39.
15. Dietrich F, List C. Opinion pooling on general agendas London School of Economics 2008b; Working paper.
16. Dietrich F, List C. A liberal paradox for judgment aggregation. Social Choice and Welfare. 2008c;31:59–78.
17. F. Dietrich and C. List. Judgment aggregation under constraints. In T. Boylan and R. Gekker (eds.), Economics, Rational Choice and Normative Philosophy. London (Routledge), forthcoming.
18. Dietrich F, Mongin P. The premise-based approach to judgment aggregation University of Maastricht 2007; Working paper.
19. E. Dokow and R. Holzman. Aggregation of binary evaluations. Journal of Economic Theory, forthcoming.
20. Dokow E, Holzman R. Aggregation of binary evaluations with abstentions Technion — Israel Institute of Technology 2006; Working paper.
21. Dryzek J, List C. Social Choice Theory and Deliberative Democracy: A Reconciliation. British Journal of Political Science. 2003;33(1):1–28.
22. Gärdenfors P. An Arrow-like theorem for voting with logical consequences. Economics and Philosophy. 2006;22(2):181–190.
23. Genest C, Zidek JV. Combining Probability Distributions: A Critique and Annotated Bibliography. Statistical Science. 1986;1(1):113–135.
24. Th. Guilbaud G. Theories of the General Interest, and the Logical Problem of Aggregation. In: Lazarsfeld PF, Henry NW, eds. Readings in Mathematical Social Science. Cambridge/MA: MIT Press; 1966;262–307.
25. Knight J, Johnson J. Aggregation and Deliberation: On the Possibility of Democratic Legitimacy. Political Theory. 1994;22(2):277–296.
26. Konieczny S, Pino Pérez R. Merging Information Under Constraints: A Logical Framework. Journal of Logic and Computation. 2002;12(5):773–808.
27. Kornhauser LA, Sager LG. Unpacking the Court. Yale Law Journal. 1986;96(1):82–117.
28. Kornhauser LA, Sager LG. The One and the Many: Adjudication in Collegial Courts. California Law Review. 1993;81:1–59.
29. Kornhauser LA. Modeling Collegial Courts II Legal Doctrine. Journal of Law, Economics and Organization. 1992;8:441–470.
30. Kornhauser LA, Sager LG. The Many as One: Integrity and Group Choice in Paradoxical Cases. Philosophy and Public Affairs. 2004;32:249–276.
31. List C. A Possibility Theorem on Aggregation over Multiple Interconnected Propositions. Mathematical Social Sciences. 2003;45(1):1–13 with Corrigendum in Mathematical Social Sciences 52: 109-110.
32. List C. A Model of Path-Dependence in Decisions over Multiple Propositions. American Political Science Review. 2004;98(3):495–513.
33. List C. The Discursive Dilemma and Public Reason. Ethics. 2006;116(2):362–402.
34. List C. Group deliberation and the revision of judgments: an impossibility result London School of Economics 2008; Working paper.
35. List C, Pettit P. Aggregating Sets of Judgments: An Impossibility Result. Economics and Philosophy. 2002;18(1):89–110.
36. List C, Pettit P. Aggregating Sets of Judgments: Two Impossibility Results Compared. Synthese. 2004;140(1-2):207–235.
37. List C, Pettit P. On the Many as One. Philosophy and Public Affairs. 2005;33(4):377–390.
38. C. List and C. Puppe. Judgment aggregation: a survey. In P. Anand, C. Puppe and P. Pattaniak (eds.), Oxford Handbook of Rational and Social Choice. Oxford (Oxford University Press), forthcoming.
39. McConway K. Marginalization and Linear Opinion Pools. Journal of the American Statistical Association. 1981;76:410–414.
40. Miller D. Deliberative Democracy and Social Choice. Political Studies. 1992;40:54–67 Special Issue.
41. Mongin P. Consistent Bayesian aggregation. Journal of Economic Theory. 1995;66:313–351.
42. P. Mongin. Factoring Out the Impossibility of Logical Aggregation. Journal of Economic Theory, forthcoming.
43. Nehring K. Arrow’s theorem as a corollary. Economics Letters. 2003;80(3):379–382.
44. Nehring K, Puppe C. Strategyproof Social Choice on Single-Peaked Domains: Possibility, Impossibility and the Space Between University of California at Davis 2002; Working paper.
45. Nehring K, Puppe C. Abstract Arrovian Aggregation University of Karlsruhe 2007a; Working paper.
46. Nehring K, Puppe C. The structure of strategy-proof social choice — Part I: General characterization and possibility results on median spaces. Journal of Economic Theory. 2007b;135(1):269–305.
47. Pauly M, van Hees M. Logical Constraints on Judgment Aggregation. Journal of Philosophical Logic. 2006;35(6):569–585.
48. Pettit P. Deliberative Democracy and the Discursive Dilemma. Philosophical Issues. 2001;11:268–299.
49. Pettit P. When to defer to majority testimony — and when not. Analysis. 2006;66:179–187.
50. Pigozzi G. Belief merging and the discursive dilemma: an argument-based account to paradoxes of judgment aggregation. Synthese. 2006;152(2):285–298.
51. Pivato M. The Discursive Dilemma and Probabilistic Judgement Aggregation Munich Personal RePEc Archive 2008.
52. Riker W. Liberalism Against Populism San Franscisco: W. H. Freeman; 1982.
53. Rubinstein A, Fishburn PC. Algebraic Aggregation Theory. Journal of Economic Theory. 1986;38(1):63–77.
54. Sen AK. A Possibility Theorem on Majority Decisions. Econometrica. 1966;34(2):491–499.
55. Sen AK. The Impossibility of a Paretian Liberal. Journal of Political Economy. 1970;78:152–157.
56. Wilson R. On the Theory of Aggregation. Journal of Economic Theory. 1975;10(1):89–99.
1 For short technical and philosophical surveys of salient aspects of the theory of judgment aggregation, see, respectively, [List and Puppe, forthcoming; List, 2006].
2 For recent discussions of the ‘doctrinal paradox’, see [Kornhauser and Sager, (2004; List and Pettit, 2005]).
3 The agenda characterization results discussed further below require three or more individuals.
4 In propositional logic, a set of propositions is ‘consistent’ if all its members can be simultaneously true, and ‘inconsistent’ otherwise. More generally, consistency is definable in terms of a more basic notion of ‘logical entailment’ [Dietrich, 2007a].
5 For some formal results, it is necessary to exclude tautological or contradictory propositions from the agenda. Further, some results simplify when the agenda is assumed to be a finite set of propositions. In order to avoid such technicalities, I make these simplifying assumptions (i.e., no tautologies or contradictions, and a finite agenda) throughout this paper. To render finiteness compatible with negation-closure, I assume that double negations cancel each other out; more elaborate constructions can be given.
6 The full details of this construction are given in [Dietrich and List, forthcoming].
7 More formally, ‘unanimity preservation’ is the requirement that if all individuals unanimously accept any proposition on the agenda, then that proposition be collectively accepted.
8 For such agendas, the majority judgments are always consistent and in the absence of ties also complete.
9 This property was introduced by Dietrich [2007a] and Dietrich and List [2007a]. A logically equivalent property is the algebraic property of ‘non-affineness’ introduced by Dokow and Holzman [forthcoming].
10 Roughly speaking, monotonicity is the requirement that if any proposition is collectively accepted for a given profile of individual judgment sets and we consider another profile in which an additional individual accepts that proposition (other things being equal), then this proposition remains accepted.
11 This property, first introduced by Nehring and Puppe [2002], requires that any proposition on the agenda can be deduced from any other via a sequence of pairwise logical entailments conditional on other propositions on the agenda.
12 A weaker variant of the result without monotonicity (specifically, an ‘if’ rather than ‘if and only if’ result) was also proved by Dietrich and List [2007a]
13 Or the middle two individuals, if the total number of individuals is odd.
14 Or the intersection of the judgments of the two middle individuals, if the total number of individuals is even.
15 Similarly, if the total number of individuals is even, the intersection of the individually consistent judgment sets of the two middle individuals is still a consistent set of propositions.
16 Assuming consistency and completeness of the individual judgment sets.
17 Furthermore, when both individual and collective judgment sets are only required to be consistent, a recent impossibility theorem suggests that an asymmetry in the criteria for accepting and for rejecting propositions is a necessary condition for avoiding degenerate aggregation rules [Dietrich and List, 2007d].
18 A first general formulation of the premise-based procedure in terms of a subset Y of the agenda interpreted as the set of premises was given in List and Pettit [2002]. Furthermore, as shown by Dietrich [2006], the premise-based procedure can be axiomatically characterized in terms of the key condition of ‘independence restricted to Y’, where Y is the premise-set. In some cases, an impossibility result reoccurs when the condition of unanimity preservation is imposed, as shown for certain agendas by Mongin’s [forthcoming] theorem mentioned in the previous section. For recent extensions, see [Dietrich and Mongin, 2007].
19 The precise relationship between opportunities and incentives for manipulation is discussed in [Dietrich and List, 2007e].