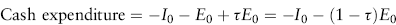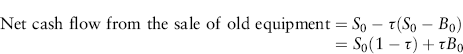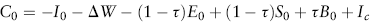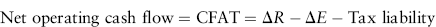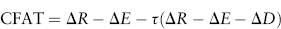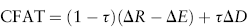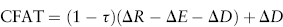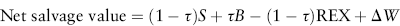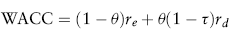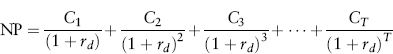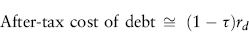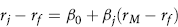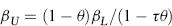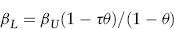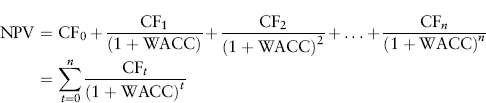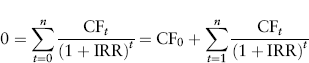Chapter 10
Discounted Cash Flow Analysis
Projects typically involve the purchase of capital assets—long-lived tangible assets such as land, plant, and machinery. When considering a proposed project that would involve investing in capital assets, the sponsors should evaluate the expected future cash flows in relation to the amount of the initial investment.
Discounted cash flow techniques are available to facilitate the evaluation process. The objective is to find projects that are worth more to the sponsors than they cost—projects that have a positive net present value (NPV).
A sponsor's evaluation of a proposed project is not unlike an individual's investment decision. The steps are the same:
In this chapter, we develop a discounted cash flow framework for assessing the profitability of a proposed project. The chapter explains and illustrates sound methods of evaluating capital investments, which can be applied to any capital investment, whether or not it is a discrete project.
Incremental After-Tax Cash Flows
The initial step in measuring the value of a capital investment project is estimating the expected incremental after-tax cash flows. Three important concepts are involved.
First, as with any investment, the costs and benefits associated with a project should be measured in terms of cash flow rather than earnings. This distinction is critical. Earnings calculations also reflect certain noncash items. But ultimately, cash, not earnings, is required to meet the firm's financial obligations. Failure to raise enough cash can cause a firm to pay penalty fees or can even bring bankruptcy to an otherwise healthy firm. And, only cash flow can be paid to the sponsors, either immediately or through reinvestment and later disbursement. The timing of a cash flow affects its value, because of the time value of money. Finally, including indirect noncash benefits leads to ambiguity and subjective (nonfinancial) choices that can greatly confuse the analysis.1
The second important concept is that the cash flows must be measured on an incremental basis. They are the difference between the sponsor's cash flows with and without the project. So, if a cash flow will occur regardless of whether the project is undertaken, it is not relevant. Funds that have already been expended—for example, for preliminary work—are sunk costs. They are irrelevant to the analysis. Only future expenditures and revenues are relevant to the decision of whether to proceed with the project.
Third, the expected future cash flows should be measured on an after-tax basis. A project sponsor is concerned with after-tax cash flows in the same way that an individual is interested in take-home pay: Ultimately, that's the amount available to spend for other purposes. Because taxes represent one of the costs of doing business, they must be subtracted from the pretax operating cash flows.
Finally, by convention, cash flows are assumed to occur at the end of each time period unless their occurrence is explicitly stated otherwise. This is done for convenience in making computations.
Tax Considerations
Although some sections of the Internal Revenue Code are complex and are changed periodically, we can make some generalized statements about tax effects. Three things affect a firm's taxes: (1) revenues, (2) expenses and credits, and (3) how and when those revenues and expenses are declared for tax purposes. Just as the timing of any cash flow affects its value, when a cash flow is recognized for tax purposes affects the present value of the taxes paid.
One very important tax effect occurs whenever there is a discrepancy between cash flow timing and recognition of the cash flow for tax purposes. The present value of taxes paid is less on a revenue item, the further into the future that tax payment actually occurs. For example, suppose a firm takes in a cash advance of $1,000 on goods that are yet to be manufactured but are promised for delivery one year from today. If the tax will be $100, the firm will earn $900. But if the tax need not be paid until the goods are delivered, the present value of the tax is only $92.59 at an 8 percent discount rate (= $100/1.08). With that result, the firm actually earns $907.41 ($1,000 − $92.59) rather than $900.
Similarly, the present value of taxes saved is greater on an expense item, the sooner the reduction in taxes paid actually occurs. The most frequent discrepancy between cash flow timing and tax recognition occurs with respect to depreciation.
Depreciation plays an important role in the determination of cash flow. Over time, machines wear out. The accounting treatment of depreciation expense, whereby it is deducted in each reporting period, reflects this wear.
For capital budgeting decisions, depreciation has an important impact on the timing of the firm's tax payments. Depreciation is a non-cash expense. Cash was expended to acquire the asset. Depreciation is simply the recognition of the expense as the asset is used over time. Because depreciation is deducted from revenue when calculating taxable income, it affects the timing of the firm's tax payments. Similarly, depletion expense is recognized as natural resource reserves (e.g., a coal deposit or a natural gas reserve) are used up, and amortization expense is recorded as the remaining value of intangible assets (e.g., a patent) dissipates.
Depreciation (as well as depletion and amortization) arises when assets are capitalized—when the cost of the asset is allocated to two or more time periods. The entire cost is not an immediately recognized expense. Instead, the expenditure is recognized as a prespecified series of expenses at various times in the future. By contrast, cash expenditures for items that are not required to be capitalized can be expensed immediately. Cash expenditures that are expensed (including those that qualify for limited expensing under Section 179 of the Internal Revenue Code) are recognized for tax purposes entirely at the time of expenditure. Therefore, expensed items do not have any subsequent tax consequences, because they do not involve the process of depreciation. To contrast these two different tax treatments, consider the following example.
Example
Suppose General Mining Corporation is going to purchase an asset that costs $1 million. Suppose further that General's marginal tax rate is 40 percent. How does the pattern of expenses recognized for tax purposes differ between (1) capitalizing the asset and depreciating it on a straight-line basis over four years and (2) expensing the $1 million now?
The pattern of expenses recognized over time for expensing versus capitalizing the expenditure for the asset is (in $ millions):
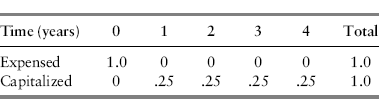
Note that the total amount of expenses claimed in both cases is $1 million. The only difference is the time at which the expense is claimed. Because of the time value of money, General is clearly better off if it can expense the asset rather than having to capitalize it.
The Internal Revenue Code requires that certain assets be capitalized. The preceding example suggests that a project sponsor is generally best off when it uses, for each asset, the most accelerated depreciation method available under the Code.
Incremental Cash Flows
The cash flows associated with a capital investment project fall into four basic categories:
Note that financing charges are not included in the incremental cash flow computation because the cost of capital implies a financing cost. Therefore, only extraordinary financing costs, such as special transaction costs explicitly tied to the project, are included in the incremental cash flow computations. Such costs will most often be included in the net initial investment outlay.
1. Net initial investment outlay. The net initial investment outlay can be broken down into cash expenditures, changes in net working capital, net cash flow from the sale of old equipment, and investment tax credits.
As already noted, capitalized expenditures do not affect taxes at the start of the project, whereas expensed items have an immediate tax effect. If we denote the net expenditure to be capitalized as I0, the net expenditure to be expensed immediately as E0, and the company's marginal income tax rate as τ, then the first component of the initial outlay is:
The negative signs indicate cash outflows. As of year-end 2012, the federal statutory corporate income tax rate was 35 percent. To allow also for state income taxes, many financial analysts use τ = 0.40.
Changes in net working capital at the start of an investment project are also part of the initial outlay for the project. For example, additional cash may be needed to open up an expansion outlet. Additional inventory and accounts receivable may be required to process a greater level of production and sales. The additional net working capital requires funding. Similarly, if the project reduces the firm's net working capital, those funds are freed up to be invested elsewhere.
The third component of the initial outlay is the net cash flow from the sale of old equipment. When an asset is sold, there is revenue and maybe an expense, but there may also be a tax effect. A tax effect will occur if the asset is sold for a net sale price that is different from the tax basis of the asset at the time of its sale (i.e., its net, or depreciated, book value). For example, suppose an asset was purchased five years ago for $2,000, and $300 of depreciation expense has been claimed for tax purposes for each of the past five years. The net book value of that asset is currently $500 ($2,000 − 5($300)). If the asset is sold today for more than $500, then “too much” depreciation was claimed and the government will “recapture” the excess depreciation by taxing the amount above the net book value. Likewise, if the asset is sold today for less than $500, “too little” depreciation was claimed and the firm can now claim the rest of the depreciation. The firm gets a tax credit by claiming the amount below the net book value as an expense. If we denote the net sale price (revenues minus expenses) S0 and the net book value B0, then the after-tax cash flow for selling the old equipment is:2
Finally, the purchase of certain capitalized assets may give rise to an investment tax credit. This aspect of the tax law has changed fairly often, so we include it only as a reminder to check the Code at the time the project is to be undertaken. Denoting the investment tax credit Ic and the change in net working capital ΔW, then the net initial outlay, C0, can be expressed as:
2. Net operating cash flow. Let ΔR and ΔE denote, respectively, the changes in revenue and expense connected with undertaking the project in each period. Therefore, the net operating cash flow, CFAT (cash flow after tax), can be expressed as the pretax cash flow ΔR – ΔE, less the tax liability on this amount:
The tax liability depends in part on the incremental change in depreciation. For simplicity, we assume that all depreciation is recognized on a straight-line basis. Therefore, the change in depreciation expense is identical each period. Denoting the depreciation change ΔD, the tax liability will be τ(ΔR − ΔE − ΔD), and
Rearranging gives
In this form, CFAT is represented as the after-tax revenue minus expenses plus the “tax shield” from the depreciation expense. Equivalently, we can rearrange the expression:
In this alternative form, CFAT can be thought of as net income plus depreciation. This is because (1 − τ)(ΔR − ΔE − ΔD) would be the net income from the project if the firm were entirely equity-financed.
3. Nonoperating cash flows. The treatment of nonoperating cash flows parallels that of cash expenditures for the initial investment outlay. Nonoperating cash flows are either required to be capitalized or allowed to be expensed immediately. Therefore, their effect on net cash flow is like initial cash expenditures. The expensed nonoperating cash flows are multiplied by (1 − τ) to adjust for taxes. Capitalized nonoperating cash flows involve an initial cash outflow when they occur, and they give rise to a series of depreciation expenses that follow.
4. Net salvage value. The net salvage value is the after-tax net cash flow for terminating the project. It can be broken into: sale of assets, cleanup and removal expenses, and release of net working capital.
The adjustment for the sale of assets was described earlier, in our discussion of the net initial investment outlay. Dropping the zero subscripts from equation (10.2), the adjustment is [(1 − τ)S + τ B]. Cleanup and removal expenses are generally expensed immediately. Therefore, they are multiplied by (1 − τ) to adjust for taxes. The release of net working capital is unaffected by tax considerations. Tax law treats it as an internal transfer of funds, such as exchanging inventory and accounts receivable for cash. Therefore, the release of net working capital is simply an added cash flow. With cleanup and removal expenses denoted REX, net salvage value is:
The term salvage value typically refers to the before-tax difference between the sale price (S) and the cleanup and removal expense (REX). That is, salvage value = S − REX.
An Example of Incremental Cash Flow Analysis
Rocky Mountain Mining Corporation is thinking of investing in a mining project that would involve purchasing equipment costing $55 million. The new equipment would be depreciated over a 10-year period on a straight-line basis to a net book value of $5 million. The mining project would produce pretax cash flow of $15 million per year for 10 years.
Rocky Mountain estimates that the project would involve additional start-up costs amounting to $6 million. Of this amount, $5 million would be capitalized in the same way as the equipment, and the remaining $1 million would be expensed immediately. The project would also require an investment in net working capital of $3 million. Finally, it is expected that, at the end of 10 years, the project will require $500,000 of removal and cleanup costs. Rocky Mountain estimates a marginal tax rate of 40 percent for the project.
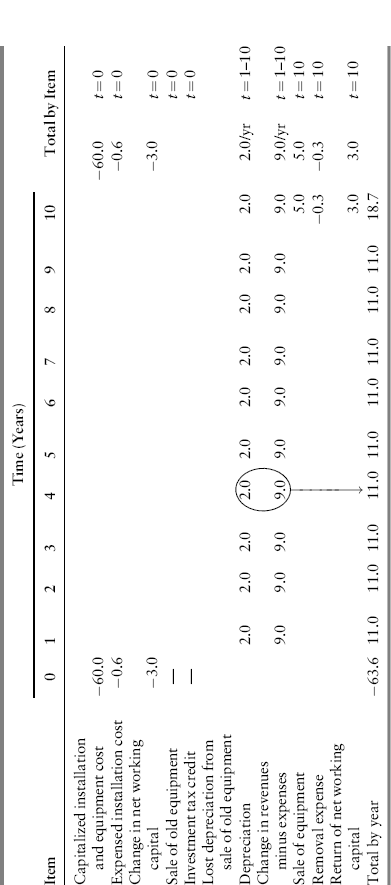
The cash expenditures for the initial outlay in this case are: the $55 million purchase price, the $5 million capitalized installation cost, and the $1 million expensed installation cost; therefore, I0 = $60 million, and E0 = $1 million. The increase in net working capital is ΔW = $3 million. No investment tax credit has been specified. The net initial investment outlay can now be computed, using equation (10.3):
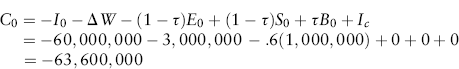
Note that care must be taken to treat correctly sunk costs that have been incurred more recently. Dollars that have already been spent—for example, on feasibility studies, prior research and development, and site preparation—are irrelevant for purposes of capital investment analysis. They are sunk costs; whether or not Rocky Mountain proceeds with the project, the timing and levels of prior capital expenditures cannot change because these expenditures have already been incurred.
The net operating cash flows resulting from investing in the project can be calculated using either equation (10.6) or equation (10.7). The change in revenue minus expenses, ΔR − ΔE, is $15 million. Depreciation will amount to $5 million per year (($55 million − $5 million)/10) for the next 10 years. Therefore, ΔD is $5 million for years 1 through 10. Using equation (10.6):
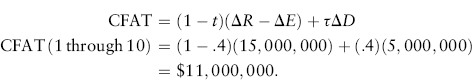
Because no nonoperating cash flows are anticipated over the life of this project, no additional adjustments are necessary.
The equipment is expected to have a market value of $5 million at the end of the project's life. A removal and cleanup expenditure of $500,000 is expected. From equation (10.8), the net salvage value is:
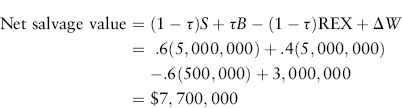
The incremental cash flows for this project are then (in $ millions):

The Hurdle Rate
How high a rate of return do investors require, to compensate for a particular degree of risk? A required rate of return can be thought of as an opportunity cost. Investors will require a rate of return at least as great as the percentage return they could earn in the most nearly comparable investment opportunity. But suppose there's no comparable opportunity from which to estimate a required rate of return? What factors determine a required rate of return? In other words, how does the market determine a required rate of return?
The Weighted Average Cost of Capital
The weighted average cost of capital (WACC) serves as the hurdle rate for a project. It can be described in terms of financing rates. More importantly, it can always be represented as the weighted average cost of the components of any financing package that will allow the project to be undertaken. For example, such a financing package could be 20 percent debt plus 80 percent equity; 55 percent debt plus 45 percent equity; and so on. Or, it could be 30 percent 30-year debt, 10 percent 180-day debt, 10 percent preferred stock, 15 percent 20-year convertible debt, and 35 percent common stock. The cost of capital is the rate of return required by a group of investors to take on the risk of the project.
Before proceeding, we need to specify exactly what is meant by the components of a financing package. For simplicity, we will restrict the analysis to the proportions of financing provided by debt and equity. Let θ denote the ratio of debt financing to total investment value. For example, suppose a capital investment project has a total present value of $10,000, and $4,000 of debt will be used to finance the project. Then θ = .4. It is important to note that θ does not depend on the initial cost of the investment project; θ depends on the total value of the project.
Suppose our example project has an initial cost of $8,000 and an NPV of $2,000, making its present value $10,000. Then the sponsors of this project will be putting up $4,000 and getting $6,000, because they get the NPV. The sponsors then own 60 percent of the value, even though they will be putting up only 50 percent of the initial cost ($4,000 of the $8,000). The project is referred to as 40 percent debt-financed and 60 percent equity-financed because those proportions reflect the distribution of the market value of the project among the claimants. The proportions of the initial cost are not relevant because they would disregard the project's NPV.
The required rate of return to the sponsors depends on the degree of leverage in the project's financial structure. The debtholders' required rate of return also depends on the degree of leverage. When default is possible, the required rate of return to the debt holders must increase to reflect the risk that debt holders might not receive full payment.
A Cost of Capital Formula
The weighted average cost of capital (WACC) can be expressed as the weighted average of the required rate of return for equity, re, and the required rate of return for debt, rd:
where τ represents the marginal income tax rate on the project's income. Equation (10.9) reduces the task of estimating the WACC to a calculation of the cost of debt and the cost of equity and an appropriate weighting of these component costs.
Note that the WACC is expressed as an after-tax rate of return. Because the returns to equity investors are paid after corporate taxes, re is also an after-corporate-tax rate of return (to equity). The return to debt, rd, is a pretax rate of return; it must be multiplied by (1 − τ) to convert it to an after-tax basis.
Estimating the Cost of Debt
The pretax cost of debt can be calculated by solving the following equation for rd:
where NP represents the net proceeds from the debt issue (i.e., gross proceeds minus flotation expenses, such as underwriting fees, legal fees, and so on), and Ci represents the pretax cash debt service requirement payable in period i (i.e., interest plus principal). Typically, project debt must be repaid in installments. When this is so, Ci includes the portion of principal that must be repaid in period i.
The after-tax cost of debt can be calculated in either of two ways. The after-tax payment obligations, rather than the pretax amounts, can be used in equation (10.10). This procedure requires adjusting interest payments for taxes—because interest is a tax-deductible expense—as well as allowing for the amortization of new issue expenses. The amortization of new issue expenses is treated in the same manner as the depreciation of capital assets, which was discussed earlier in this chapter.
Alternatively, the after-tax cost of debt can be approximated as:
which appears in equation (10.9). Equation (10.11) will usually produce a very close approximation to the true after-tax cost of debt. Differences occur when a project entity cannot utilize the interest tax deductions on a current basis—for example, when a project entity is organized as a corporation and construction extends over several periods during which there is no income to offset the interest deductions for income tax purposes.
Estimating the Cost of Equity: The Capital-Asset-Pricing Model
Debt involves contractual payment obligations; equity does not. Thus, the procedure for estimating the cost of equity differs from the procedure for estimating the cost of debt. The capital-asset-pricing model is useful for estimating the cost of equity for a project.
An investor will purchase a risky asset only if he or she expects to get a rate of return that makes it worthwhile to take on the risk. The greater the risk, the higher the required rate of return. The capital-asset-pricing model (CAPM) expresses the required rate of return as the risk-free rate plus a risk premium. It has the following form:
The risk premium is a function of two variables. Beta measures the asset's incremental contribution to the riskiness of a diversified portfolio. As a measure of the asset's riskiness, beta reflects the correlation between an asset's returns and those of the market portfolio. The difference (the expected return on the market portfolio minus the risk-free rate), called the market risk premium, can be thought of as the additional return investors require to compensate for bearing each additional unit of risk. This very simple structure for the risk premium is what distinguishes the CAPM from other models.
How individual stock returns vary with respect to the market portfolio's return can be estimated by applying a statistical method called linear regression. We can express the actual historical excess rate of return on a stock rj – rf as a linear function of the actual historical excess rate of return on the market portfolio (rM − rf), so that:
We can then apply the technique of linear regression to estimate βj from historical data. That procedure involves collecting a sample of simultaneous observations of rj, rM, and rf, and fitting equation (10.13) to the historical data to estimate the value of the regression coefficient βj.3
Because of equation (10.13), the correlation coefficient between a common stock's excess rate of return and the excess rate of return on the market portfolio has come to be called the common stock's beta. Beta plays a particularly important role in asset pricing. It is a linear measure of how much an individual asset contributes to the standard deviation of the market portfolio. So the beta of an asset is a simple, well-behaved measure of the risk of the individual asset.
Beta indicates the sensitivity of a security's returns to changes in the returns on the market portfolio. If a security's beta is 1.0, its returns tend to track the market portfolio. If the market portfolio increases or decreases by 10 percent, the stock also tends to move up or down by 10 percent. If a stock has a beta less than 1.0, it will rise or fall less than the market. For example, suppose a stock has a beta of 0.5. If the market portfolio increases or decreases by 10 percent, the stock will tend to move up or down only 5 percent. A stock with a beta greater than 1.0 will rise or fall more than the market. For example, a stock with a beta of 1.5 will tend to rise or fall by 15 percent when the market portfolio increases or decreases 10 percent. Values of beta for most common stocks fall within the range from 0.75 to 1.50.
Sample Cost of Capital Calculation
Rocky Mountain Mining Corporation's mining project will utilize only long-term debt and common equity financing. Rocky Mountain has identified similar securities that are traded regularly in active markets. What is the WACC for Rocky Mountain's proposed project?
To begin, Rocky Mountain gathered the following information:
| Risk-free interest rate | 6 percent |
| Common equity beta | 1.25 |
| Expected excess return on the market portfolio | 8.4 percent |
| Expected cost of debt (pretax) | 10 percent |
| Proportion of debt financing | 60 percent |
| Project's marginal income tax rate | 40 percent |
Based on this information, we can use the capital-asset-pricing model to estimate re:
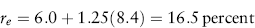
The proportion of debt financing, θ, is .60. From equation (10.9), the WACC for Rocky Mountain's project is:
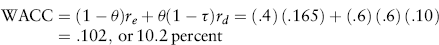
Adjusting for Financial Risk
If a project is all-equity-financed (no money owed at any time, no matter what), then the project involves no financial risk. Note that such a project would not have even one creditor. All of the risk of this hypothetical project would be its operating risk because the project never owes anyone anything. Note also that, in such a case, default is not a possibility or an option. In effect, the shareholders' limited liability has no effect on value. Such a project could fail. But, although the sponsors could lose everything they invested in the project, no wealth can be transferred because no loss can ever be inflicted on anyone other than the project sponsors. So, although the sponsors still cannot lose more than they have invested in the project, they also cannot benefit from limited liability and the default option.
Because financial risk depends on (financial) leverage, adjustment for the impact of financial risk must be done on the basis of whatever unit has responsibility for that financial obligation. In a project financing—and in contrast to a conventional debt financing—the financial obligation is specific to the project. In evaluating a prospective project financing, the financing considerations should be accounted for on a project-by-project basis. By way of contrast, in connection with projects financed on a conventional basis, the financial obligations are at the level of the firm. The impact of leverage on required rates of return is determined in such situations by the capital structure of the whole firm.
Impact of Project Financing
When a firm employs project financing and thereby limits its liability with respect to project debt, the capital structure of the project becomes the relevant consideration for calculating the required returns and the cost of capital. Therefore, if a firm is considering financing something on a project basis, which would achieve limited liability for the firm, the cost of capital for the project should reflect the capital structure of the project.
Estimating the Cost of Capital for a Project
This section explains how to estimate the cost of capital for a project. Two alternatives are considered. In the first, the project has the same operating risk profile and the same capital structure as the sponsor. In the second, either the operating risk profile is different or the capital structure is different (or both are different).
Lone Star Mining Corporation, which has worldwide mining operations, is planning to finance a copper mine on a project basis. The mine would cost $100 million, which would be 60 percent debt-financed and 40 percent equity-financed.
When the Sponsor's WACC Can Be Used
Suppose Lone Star believes the mining project will be of “average risk” when compared to all of the projects Lone Star is operating. Suppose also that Lone Star is 60 percent debt-financed and that Lone Star's common stock is publicly traded. Thus, the proposed project has the same operating risk profile and the same capital structure (and hence, the same financial risk profile) as Lone Star. Therefore, Lone Star's WACC can be used to evaluate the project. Lone Star's common stock beta is 1.25. Lone Star can issue additional long-term debt at a pretax yield of 10 percent. Lone Star's marginal income tax rate is 40 percent. Finally, rf and rM are 6 percent and 14 percent, respectively. Therefore, based on equations (10.9) and ((10.13)), Lone Star should use a cost of capital for the proposed project of about 10 percent:
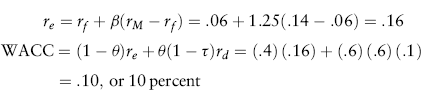
When the Sponsor's WACC Should Not Be Used
Suppose now that Lone Star is a diversified mining company that is one-third debt-financed. Lone Star's WACC is not a good estimate of the project's cost of capital because (1) the copper mining project may have an operating risk profile different from Lone Star's other assets, and (2) the project will be more highly leveraged and therefore involve greater financial risk.
The steps for estimating the beta for this project are:
where βU denotes the average unleveraged beta for the pure plays, θ denotes the debt ratio for the project, and τ denotes Lone Star's income tax rate.
Table 10.1 Estimating Beta for Lone Star's Copper Mining Project.
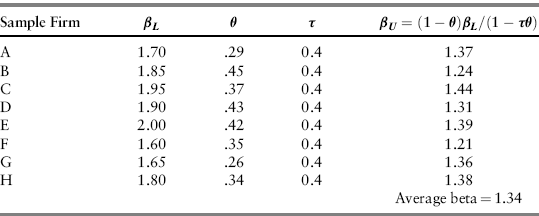
For the proposed copper mining project, βU = 1.34 and θ = 0.6, so:
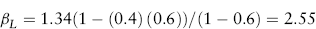
The riskless rate is 6 percent, and rM is 14 percent. The cost of capital for the project is:
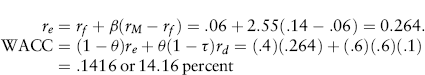
Choice of Operating Method
Operating risk affects the beta of an investment project. The cost of capital calculation method outlined above requires one additional consideration when there is a choice of operating method. If there are significant differences in operating risk among potential production methods, the sample of representative firms must be restricted to firms that are using a set of assets and production methods that are approximately equivalent to those in the proposed investment project.
Net Present Value Analysis
The net present value (NPV) of a project is the difference between what the project costs and what it is worth. The best we can do in advance is estimate a project's NPV. We will not know its true market value, or what it is really worth, until the project is completed and the returns are collected.
The Procedure
The NPV of a capital investment project is the present value of all of the after-tax cash flows (CF) connected with the project—all its costs and revenues, now and in the future:
The decision rule to follow when applying NPV is: Undertake the capital investment project if the NPV is positive.
We estimate the value of a project by using discounted cash flow (DCF) analysis and computing the present value of all the cash flows connected with ownership. This procedure is similar to discounting the interest payments on a bond or dividends on a stock, and it is the essence of the net present value method.
An Example
To illustrate, let's continue our earlier example of Rocky Mountain Mining Corporation's mining project. Previously, we found that the project's cost of capital is 10.2 percent. What is the project's NPV?
Applying equation (10.16) to the project's annual incremental cash flows, we have:
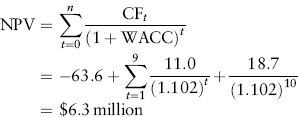
The project should be accepted because its NPV is positive.
Table 10.2 illustrates a format that can be used to present the periodic cash flows for an NPV analysis.
Table 10.2 NPV Analysis of Rocky Mountain Mining's Proposed Project (Dollar Amounts in Millions).
Internal Rate of Return Analysis
Another method of evaluating a proposed project is called the internal rate of return method. The internal rate of return (IRR) is the capital investment project's expected rate of return. If the cost of capital (required rate of return) equals the IRR (expected rate of return), the NPV would equal zero. But because of the uncertainty connected with risky cash flows, the realized rate of return will almost surely be different from the IRR. Earlier in this chapter, we showed how to find the expected rate of return for a bond—the pretax cost of debt. Here, we apply those same time-value-of-money techniques to compute IRRs, the expected internal rates of return for capital investment projects.
The IRR for a project is the discount rate that makes the NPV zero:
Most financial calculators will calculate the IRR of a cash flow stream.
The decision rule to apply when using the internal rate of return method is: Undertake the capital investment project if the IRR exceeds the WACC, the project's cost of capital.
In its simplest form, the IRR rule is intuitively appealing. In essence, it says: Does the expected rate of return on the investment exceed the required rate of return? In other words, will it create value? At first glance, this seems to be saying the same thing the NPV rule says. As we shall see, this is generally but not always true. The intuitive appeal, however, probably does account for the widespread use (and in some cases, even the preference) for the IRR method in practice.
Example
The mining project Rocky Mountain Mining Corporation has under consideration has a cost of capital of 10.2 percent. What is the IRR of the project, and should Rocky Mountain undertake it?
The IRR solves the equation:
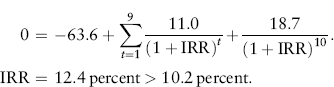
Because the IRR exceeds the project's WACC, Rocky Mountain should undertake the project.
Comparing IRR and NPV Analyses
In the Rocky Mountain example, the IRR and NPV methods agree. This will happen whenever the projects are both independent and conventional. An independent project is one that can be chosen independently of other projects; that is, undertaking it neither requires nor precludes any other investment. A project that requires other investments is simply part of a larger project and must be evaluated together with all of its parts. When undertaking one project prevents investing in another project, and vice versa, the projects are said to be mutually exclusive.
A conventional project is a project with an initial cash outflow that is followed by one or more expected future cash inflows; that is, after making the investment, the total cash flow in each future year is expected to be positive. A purchase of a stock or bond is a simple example of a conventional project. An investor buys the security (a negative cash flow), and the terminal sale price and any dividends or interest payments received while the investor owns it will be positive (recall that liability is limited).
NPV Profile
Another way to look at NPV is to graph it as a function of the discount rate. This graph, called an NPV profile, includes both NPV and IRR. It also shows the value of the project at different possible costs of capital. Therefore, if sponsors are unsure about a project's cost of capital, the NPV profile would identify costs of capital at which the project would and would not add value.
Figure 10.1 shows an NPV profile for the Rocky Mountain Mining Project. To construct this profile, vary the discount rate in equation (10.16). When WACC = 0, the NPV is just the sum of the cash flows:
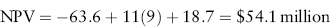
Figure 10.1 NPV Profile for the Rocky Mountain Mining Project
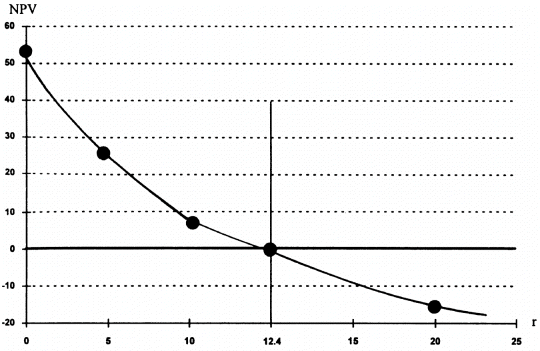
When r = 12.4 percent, NPV = 0 because IRR = 12.4 percent. We also calculated what the NPV would be at discount rates of 5 percent, 10 percent, and 20 percent, and then drew the curve through these points.
The NPV profile in Figure 10.1 shows the general relationship between IRR and NPV for independent, conventional projects. If the IRR exceeds the cost of capital, the NPV is positive. If the IRR is less than the cost of capital, the NPV is negative. The vertical distance from the x-axis to the NPV line is the NPV of the project at each cost of capital, WACC.
When IRR and NPV Can Differ: Mutually Exclusive Projects
So far, we've only looked at the question of whether to undertake an independent project. Often, in practice, we have to choose from a set of mutually exclusive projects. If we undertake one, we can't undertake any of the others.
For example, a firm that plans to build a new processing plant might have three possible locations and four possible plant configurations. But the firm only needs one plant. Therefore, it has to choose one configuration in one location, and the alternatives are mutually exclusive. In such situations, we can get conflicting recommendations from the IRR and NPV methods because of a difference in (1) the size of the projects, or (2) the cash flow timing. An example of the latter is when cash flows from one project come in mainly in the beginning, and cash flows from another project come in later. We'll look at each of these differences in turn.
Size Differences
When one project is larger than another, the smaller project often has a larger IRR but a smaller NPV. For example, let's say project A has an IRR of 30 percent and an NPV of $100, and project B has an IRR of 20 percent and an NPV of $200. The choice between these two projects—and therefore the resolution of such conflicts—is fairly straightforward. Take the project that will add the most wealth, the one with the greater NPV. In general, the NPV decision rule is the better rule to follow when there is a size difference between mutually exclusive projects.
Cash Flow Timing Differences
The problem of cash flow timing can arise because of reinvestment rate assumptions. The question is: What will the cash inflows from the project earn when they are subsequently reinvested in other projects? The IRR method assumes that the future cash inflows will earn the IRR. The NPV method assumes they will earn the cost of capital.
The following example illustrates the reinvestment rate assumption conflict that results from a difference in cash flow timing.
Suppose a company can invest in only one of two projects, A and B. The cost of capital is 10 percent, and the projects have the expected future cash flows shown in Table 10.3. Which is the better project?
Table 10.3 Cash Flow Streams for Two Projects.
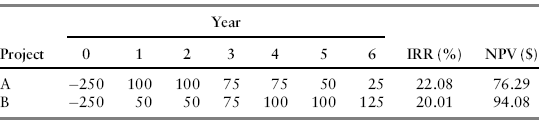
Project A has an IRR of 22.08 percent, and project B has an IRR of 20.01 percent. But project A has an NPV of $76.29, and project B has an NPV of $94.08. The IRR method tells us to choose A, but the NPV method says to choose B.
A look at Figure 10.2 indicates that project A will have a higher NPV than project B whenever the cost of capital is higher than 15.40 percent, the crossover point.4 Both projects would have an NPV of $37.86 if the cost of capital were 15.40 percent. Project B has a steeper NPV profile than project A because the present values of cash flows further in the future are more sensitive to the discount rate. A similar profile occurs for bond market values; the market value of a long-term bond changes more than that of a short-term bond in response to a given interest rate change.
Figure 10.2 IRR versus NPV
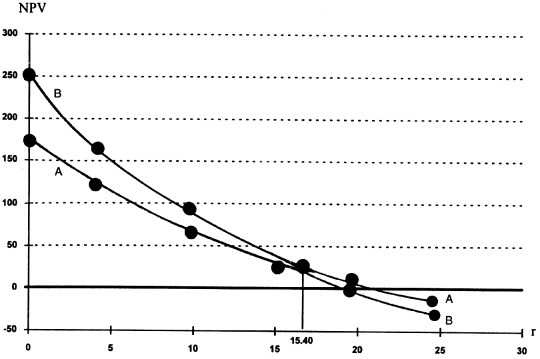
Which method makes the more reasonable assumption about the rate of return the reinvested cash flows will earn? If the cost of capital is computed correctly, it's the required rate of return for the capital investment project. Over time, competitive forces will ensure that the required rate of return equals the expected rate of return. In the long run, then, reinvested cash flows can earn the cost of capital, but not the extra—positive—NPV. The NPV method's assumption that the reinvestment rate will equal the cost of capital is the better assumption. Again, the NPV decision rule is superior to the IRR decision rule.
Conclusion
This chapter has described the basics of discounted cash flow analysis. Projects typically require substantial investments in long-lived assets. Consequently, it is very important to analyze the profitability of a proposed project before committing funds to it.
Discounted cash flow analysis involves estimating the amount of the initial investment, projecting the incremental after-tax cash flows, estimating the cost of capital, and then using the NPV method or the IRR method to determine whether the project is worth more than it will cost. The cost of capital depends on the risk of the capital investment project, not on the firm that undertakes the project. The value of the project is based on its ability to generate future cash flows, just as the value of a share of stock is based on its expected future cash dividends. If, compared to other firms, a particular firm can generate higher expected future cash flows using the project's assets, the project will add more value to that firm than to the other firms. However, the risk of the asset is the same, regardless of which firm owns it. Therefore, the project's cost of capital must be the same for all firms; differences in the value of a project among firms are reflected in the expected cash flows, not in the cost of capital.
In practice, we might be tempted to “add a few points” to a cost of capital “just for insurance.” Ad hoc adjustments for “judgmental” factors should be avoided. This is not to belittle the valuable role that specialized judgment can play in a firm's choice of assets. But there are better methods of incorporating those important “other” factors into the decision-making process.