Strategies for Solving Math Problems
Several methods are extremely useful when you don’t know—or don’t have time to use—the textbook approach to solving the question. In addition, performing all the calculations called for in the question can often be more time-consuming than using a strategic approach and can increase the potential for mistakes.
Two problem-solving strategies that may be new to you are Backsolving and Picking Numbers. These strategies are a great way to make confusing problems more concrete. If you know how to apply these strategies, you’ll nail the correct answer every time you use them.
Strategic Guessing Using Logic and using a combination of approaches are other useful shortcuts to getting more correct answers more quickly. Remember, you get points for correct answers, not for how you got those answers, so efficiency is key to maximizing your score. This section will discuss each of these strategies in turn.
Backsolving
Sometimes it’s easiest to work backward from the answer choices. Since many Arithmetic Reasoning questions are word problems with numbers in the answer choices, you can often use this to your advantage by using Backsolving. After all, the test gives you the correct answer—it’s just mixed in with the wrong answer choices. If you try an answer choice in the question and it fits with the information given, then you’ve got the right answer.
Here’s how it works. When the answer choices are numbers, you can expect them to be arranged from small to large (or occasionally from large to small). Start by trying either choice (B) or (C). If that number works when you plug it into the problem, you’ve found the correct answer. If it doesn’t work, you can usually figure out whether to try a larger or smaller answer choice next. Even better, if you deduce that you need a smaller (or larger) number, and only one such smaller (or larger) number appears among the answer choices, that choice must be correct. You do not have to try that answer choice: simply select it and move on to the next question.
By backsolving strategically this way, you won’t have to try out more than two answer choices before you zero in on the correct answer. To see an example of Backsolving, check out the following problem and explanation.
| Question | Analysis |
|---|---|
| An appliance store reduced the price of a refrigerator by 20% and then raised the price by 10% from the lower price. What was the original price of the refrigerator, if the final price was $70.40? Answer choices: | Step 1: The price of a refrigerator is reduced 20% and then that reduced price is raised 10%. The final price is $70.40. |
| Step 2: The correct answer represents the original price, before the changes. | |
| (A) $50 (B) $70 (C) $80 (D) $100 |
Step 3: To answer this question using algebra would be complex and time-consuming and would afford many opportunities for errors. Instead, since all the answer choices are numbers, backsolve. Start by trying out (B) $70. Now try either (C) or (D). (D) is easier for a percent problem. That final price is far too high, so (C) must be the correct answer. |
| Step 4: The answer of $80 is the only one that is neither too large nor too small to yield the final price of $70.40 specified in the question. Done. |
In Backsolving, when you start with (B) or (C) and that answer doesn’t work, you’ll usually know which direction to go. For example, if the answer choices are listed smallest to largest and (B) is too large when you plug it in, you will know that (A) is the correct answer. If, on the other hand, (B) had been too small, you would know that the answer was (C) or (D).
Now, try this one on your own. Use Backsolving.
(Hint: The hypotenuse (or longest side) of a right triangle is equal to the square root of the sum of the squares of the other two sides. In other words, if the other two sides are a and b and the hypotenuse is c, then a2 + b2 = c2.)
-
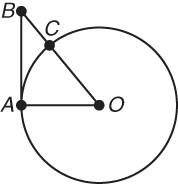
In the figure above, the circle with center O has a radius of 6 (in other words, AO = 6). If AB = 10 and ∠OAB is a right angle, what is the length of BC? -

- 4
-
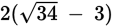
- 6
-
Explanation
Step 1: You are told that the length of the circle’s radius is 6, and you are given the length of one leg of a right triangle that is partly embedded in the circle. Because the other leg of the triangle, OA, is a radius of the circle, you know it has a length of 6. Also, a portion of the hypotenuse of the triangle, OC, is another a radius of the circle and, likewise, has a length of 6.
Step 2: Your task is to determine the part of the hypotenuse outside the circle, or the entire hypotenuse minus 6.
Step 3: You could use the Pythagorean theorem here: a2 + b2 = c2, where a and b are the lengths of the legs of a right triangle and c is the length of the hypotenuse. However, a look at the answer choices reveals that you might have to do some really burdensome calculations.
Instead, backsolve. Choosing between answer choices (B) or (C), start with (B) because 4 is much easier to work with than
 . If BC = 4, the hypotenuse would equal 4 + 6 = 10. Since one of the legs has that same length, and the hypotenuse is always the longest side of a right triangle, this is too short. Eliminate (A) and (B).
. If BC = 4, the hypotenuse would equal 4 + 6 = 10. Since one of the legs has that same length, and the hypotenuse is always the longest side of a right triangle, this is too short. Eliminate (A) and (B).
Next, try (D) 6. If BC = 6, the hypotenuse would equal 6 + 6 = 12. Using the Pythagorean theorem, test to see if 62 + 102 equals 122. In fact, 36 + 100 does not equal 144, so the correct answer must be (C).
Step 4: Because the other answer choices cannot be correct, choice (C) must represent the length of BC.
Picking Numbers
Another strategy that comes in handy on many Mathematics Knowledge questions and also on some Arithmetic Reasoning questions is Picking Numbers. Just because the question contains numbers in the answer choices, that doesn’t mean that you can always backsolve. There may be numbers in the answer choices, but sometimes you won’t have enough information in the question to easily match up an answer choice to a specific value in the question stem. For example, a problem might present an equation with many variables, or it might give you information about percentages of some unknown quantity and ask you for another percent. If the test maker hasn’t provided you with a quantity that would be really helpful to have in order to solve the problem, you may be able to simply pick a value to assign to that unknown. The other case in which you can pick numbers is when there are variables in the answer choices.
When you are picking numbers, be sure that the numbers you select are permissible (follow the rules of the problem) and manageable (easy to work with). In general, it’s a good idea to avoid picking −1, 0, or 1 because they have unique number properties that can skew your results.
Here’s a great example showing how Picking Numbers can make an abstract problem concrete.
| Question | Analysis |
| When n is divided by 14, the remainder is 9. What is the remainder when n is divided by 7? | Step 1: An unknown number, n, is 9 larger than a multiple of 14. |
| Step 2: The correct answer represents the remainder when n is divided by 7. | |
| (A) 1 (B) 2 (C) 3 (D) 4 |
Step 3: To make this abstract question concrete, pick a number for n that leaves a remainder of 9 when divided by 14. The most manageable number to pick that is also permissible in the problem is n = 23 (because 14 + 9 = 23). Now try out your number: 23 ÷ 7 = 3 with a remainder of 2. (B) is the correct answer. |
| Step 4: Briefly look back over the math to check that you are solving for the correct value. Done. |
Now, try this one on your own using the Picking Numbers strategy.
-
If a bicyclist in motion increases his speed by 30 percent and then increases this speed by 10 percent, what percent of the original speed is the total increase in speed? - 10%
- 40%
- 43%
- 140%
Explanation
Step 1: The question gives information about two increases to the speed of a bicyclist.
Step 2: The question asks for the total percent increase.
Step 3: You are not told how fast the bicyclist is going when he starts his trip, so this is a great opportunity for Picking Numbers. The easiest number to use in percent problems is 100, so start the bicyclist at a speed of 100 miles per hour. Remember, the numbers you pick should be permissible and manageable, but they do not have to be realistic.
The first increase in speed is 30%. Because 30% of 100 is 30, the new speed is 100 + 30 = 130. The second increase in speed is 10%, but not 10% of the original speed—10% of the new speed. Because 10% of 130 is 13, the final speed is 130 + 13 = 143. Subtract the original speed from the final speed, and the increase in speed is 143 − 100 = 43. Since 100 was the initial number, 43 is simply 43% of the original, answer choice (C).
Step 4: When confirming the answer for questions that ask about multiple percent changes, make sure that you calculated the percent changes appropriately and didn’t simply add the percentages given in the question, as (B) does. Also, check to make sure that you solved for the correct value, here the increase in speed as a percentage of the original speed. Answer choice (D) makes the same mistake as (B) but may look tempting to some test takers, because it is close to the final speed of 143.
When there are variables in the problem and in the answer choices, you can pick numbers for those variables. Evaluate the expression in the question stem using your chosen numbers and then evaluate each answer choice using the same numbers. Your goal is to find the answer that yields the same numerical result as the one you calculated using your chosen numbers. When you use this method, you must evaluate all of the answer choices. If more than one yields the same numerical result, choose a different set of numbers to evaluate only the remaining choices that gave matching solutions with the first set of numbers that you chose.
To solve problems containing variables in the question stem and answer choices using Picking Numbers, start by picking permissible and manageable numbers for the variables. Answer the question using the numbers you’ve picked. This answer is your target number. Then, substitute the numbers you picked for the variables into the answer choices. You are looking for the answer choice that gives you the target number.
Take a look at this example.
| Question | Analysis |
|---|---|
| Camilla spent d dollars on groceries each week for w weeks, and p percent of the amount she spent on groceries was spent on fresh vegetables. How much money did she spend over the whole time period on groceries other than fresh vegetables? | Step 1: The question contains no numbers; only variables: d = the amount Camilla spent on groceries each week |
| Step 2: The correct answer represents the amount of grocery money not spent on fresh vegetables. | |
|
(A)
(B)
(C)
(D)
|
Step 3: Make this problem concrete by replacing all the variables with numbers. Pick manageable numbers: d = 20 With those numbers, Camilla spent $20 a week on groceries for 5 weeks, for a total of $100. 10% of that, or $10, was on fresh veggies. This means that $100 − $10 = $90 was on other groceries. $90 is the target number. See what number results from plugging the same values into choice (A): 
That matches! However, because you chose numbers for the variables, more than one answer might match the target number. Keep testing the other answer choices. (B)
(C)
(D)
Only one answer choice, (A), matches the target number, so it is correct. |
| Step 4: Briefly look back over the math you did when checking choice (A). If you plugged in the numbers correctly, you’re done. |
Try this one on your own. Use the Picking Numbers strategy.
-
For all r, s, t, and u, what does r(t + u) − s(t + u) equal? - (r + s)(t + u)
- (r − s)(t − u)
- (r + s)(t − u)
- (r − s)(t + u)
Explanation
Step 1: You are given an algebraic expression and asked to find an equivalent expression.
Step 2: The correct answer simplifies the expression r(t + u) − s(t + u).
Step 3: Since you are given no values for any of the four variables, you can pick numbers for each of them. Some good numbers to pick here are r = 5, s = 4, t = 3, and u = 2. You can, however, use any permissible and manageable numbers you wish.
Replacing the variables in the expressions with the numbers picked, you get:
5(3 + 2) − 4(3 + 2) = 25 − 20 = 5.
Then replace the variables in each answer choice to see which choice gives the target number of 5:
| (A) (r + s) (t + u) | (5 + 4)(3 + 2) = (9)(5) = 45 | Incorrect |
| (B) (r − s) (t − u) | (5 − 4)(3 − 2) = (1)(1) = 1 | Incorrect |
| (C) (r + s) (t − u) | (5 + 4)(3 − 2) = (9)(1) = 9 | Incorrect |
| (D) (r − s) (t + u) | (5 − 4)(3 + 2) = (1)(5) = 5 | Correct! |
Step 4: In this example, only choice (D) works. If more than one choice had worked, you would need to pick another set of numbers and try only those answer choices again.
Not only does Picking Numbers make some problems easier to understand, but also you can be sure you got the right answer because you’ve already proven the answer works with real numbers.
Strategic Guessing Using Logic
Sometimes, you can determine the characteristics of a correct answer without doing a lot of calculations. Study the example below.
| Question | Analysis |
|---|---|
| After eating 25 percent of the pretzels, Sonya had 42 left. How many pretzels did Sonya have originally? | Step 1: Original # of pretzels ? 25% of pretzels = 42. |
| Step 2: The correct answer represents the original number of pretzels, before Sonya ate any. | |
| (A) 50 (B) 54 (C) 56 (D) 58 |
Step 3: Because 25% is the same as one-quarter, the correct answer must be divisible by 4 with no remainder. If the number of pretzels Sonia started with was not divisible by 4, and she then ate
Of the answer choices, only (C) 56 is evenly divisible by 4, so it has to be the correct answer. |
| Step 4: One-quarter of 56 is 14, and 56 ? 14 = 42, the number of pretzels Sonya had left. |
Now, try this one on your own. Try to avoid doing extensive calculations; rather, see if you can eliminate some answer choices based on logic.
-
Mark can paint a room in 3 hours, and Kevin can paint an identical room in 4 hours. How many hours would it take Mark and Kevin to paint the room if they work together at their respective rates? -

-

-

- 4
-
Explanation
Step 1: You are told the rates at which two people can paint a room separately.
Step 2: The correct answer represents how long it would take the two people to paint the room together, each working at the same rate at which he works alone.
Step 3: If Mark, the faster painter, works completely on his own, he will complete the task in 3 hours. With help, he will take even less time to complete the job, so you can eliminate answer choices (C) and (D), which are greater than 3. Since Kevin is slower than Mark, working together will take longer than half of 3 hours. Since (A) is half of 3, you can eliminate it. That leaves only answer choice (B), which must be correct.
Step 4: Check to make sure that the question asked for how long it took to paint just one room. It did, so (B) is correct.
Combination of Approaches
There is no rule that says you have to use just one approach to get the correct answer. Study the example below.
| Question | Analysis |
|---|---|
| Youssef can either walk from his home to his workplace or ride his bicycle. He walks at a pace of 1 block per minute, but he can travel 1 block in 20 seconds on his bicycle. If it takes Youssef 10 minutes longer to walk to work than to ride his bike, how many blocks away from work does he live? | Step 1: The question involves two different units of time. In order to be able to compare the rates, first convert Youssef’s biking rate into minutes. Since a minute is 60 seconds, he bikes to work at a rate of
 , or
, or
 , minute per block.
, minute per block.He walks to work at 1 minute per block. Time to walk − time to bike = 10 minutes. |
| Step 2: The correct answer represents the number of blocks Youssef lives from his workplace. | |
| (A) 5 (B) 10 (C) 15 (D) 20 |
Step 3: This problem could be solved with algebra, but using some logic mixed with Backsolving can get the correct answer more quickly. If Youssef walks 1 block per minute and it takes him 10 minutes longer to walk than to ride his bike, the correct answer must be greater than 10 blocks. Otherwise his bike time would be zero or less. That leaves only two choices, 15 or 20, so pick one and see if it works. If Youssef lived 15 blocks from work, walking to work would take him 15 minutes. Riding his bike at the rate of 20 seconds per block, he can travel 3 blocks every minute, so he could ride to work in 15 ÷ 3 = 5 minutes. Then 15 minutes − 5 minutes = 10 minutes longer to walk, so 15 is the correct answer. (Had you chosen to start with 20 instead, you could quickly have determined that 20 is incorrect, leaving 15 as the only possible correct answer.) |
| Step 4: You tested the correct answer based on the information given in the question, and it worked. (C) is correct. |
Now, try this one on your own. A combination of strategies may be helpful on this problem.
-
Shoshanna bought a new cell phone, cell phone case, and wall charger. The cell phone cost $149.99, the case cost $19.99, and the wall charger cost $29.99. If tax on each of these items was 9.5%, which of the following is closest to the total amount Shoshanna spent? - $180
- $200
- $205
- $220
Explanation
Step 1: You are told the prices of three items that Shoshanna purchased, plus a sales tax rate.
Step 2: You are asked to find the answer that is closest to the total amount Shoshanna paid for her purchases.
Step 3: Because you are asked for the closest amount, you do not have to use an exact calculation to find the correct answer. Estimation will work well. Round the prices for each item before tax to the nearest dollar: Shoshanna spent $150 + $20 + $30 = $200 before tax. You can eliminate answer choices (A) and (B) because they are too small. Now round the tax rate to 10%. Because 10% of $200 is $20, Shoshanna spent about $200 + $20 = $220 in total. Answer choice (D) is correct.
Step 4: Check that you did the arithmetic correctly and that the answer makes sense. All the other answer choices are too low to be close to what she spent.
Sometimes, you’ll find that you have to make a guess, but don’t guess at random. Narrow down the answer choices to increase your odds of guessing the correct one. First, eliminate answer choices you know are wrong. Next, avoid answer choices that don’t make logical sense. Finally, choose one of the remaining answer choices.
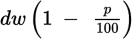



 Incorrect.
Incorrect. This will be negative, which is incorrect.
This will be negative, which is incorrect.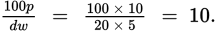 Incorrect.
Incorrect. of the pretzels, she’d be left with fractions of pretzels left over.
of the pretzels, she’d be left with fractions of pretzels left over.