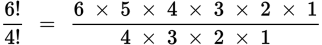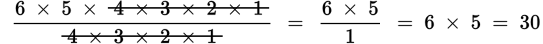Arithmetic Review
Arithmetic Definitions
It is important that you use certain critical arithmetic terms in exactly the same manner as the ASVAB. Familiarize yourself with these key terms and concepts.
| Concept | Definition | Examples |
| Integers | All whole numbers, including zero, and their negative counterparts. | −900, −3, 0, 1, 54 |
| Fractions |
A fraction is a number that is written in the form
An improper fraction has a numerator with a greater absolute value than that of the denominator. A mixed number consists of a whole number and a fraction. An improper fraction can be converted to a mixed number and vice versa. |
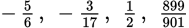
|

|
||

|
||

|
||
| Positive/Negative | Numbers greater than 0 are positive numbers; numbers less than 0 are negative numbers. 0 is neither positive nor negative. | Positive:
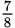 , 1, 5.6, 900
, 1, 5.6, 900Negative: −64, −40, −1.11, 
|
| Even/Odd | An even number is an integer that is a multiple of 2. An odd number is an integer that is not a multiple of 2. Fractions and mixed numbers are neither even nor odd. | Even numbers: −8, −2, 0, 12, 188 Odd numbers: −17, −1, 3, 9, 457 |
| Factor | A factor is a positive integer that divides evenly into a given number. | The complete list of factors of 12: 1, 2, 3, 4, 6, 12 |
| Prime number | An integer greater than 1 that has no factors other than 1 and itself. 2 is the only even prime number. |
2, 3, 5, 7, 11, 59, 83 |
| Consecutive numbers | Numbers that follow one after another, in order, without skipping any. In a series of consecutive numbers, the differences between any consecutive numbers are equal. | Consecutive integers: 3, 4, 5, 6 Consecutive even integers: 2, 4, 6, 8, 10 Consecutive multiples of −9: −9, −18, −27, −36 |
| Multiple | A multiple of a number is the product of that number and an integer. | Some multiples of 12: 0, 12, 24, 60 |
Number Properties
Certain number properties follow rules that will never vary. Often, you can use these rules as an effective way to help you solve problems on the ASVAB.
There are only a few things to remember about positive and negative numbers.
Adding a negative number is the same as subtracting a positive number with the same absolute value.
6 + (−4) is equal to 6 − 4 which equals 2.
4 + (−6) is equal to 4 − 6 which equals −2.
Subtracting a negative number is the same as adding a positive number with the same absolute value.
6 − (−4) is equal to 6 + 4 which equals 10.
−6 − (−4) is equal to −6 + 4 which equals −2.
Multiplying and dividing positive and negative numbers is the same as all other multiplication and division, with one catch: you need to figure out whether the solution is positive or negative. To do this, count the number of negative numbers. If you had an odd number of negatives, the answer will be negative. If you started with an even number of negative numbers, the answer will be positive.
| (−6) × (−4)= 24 | (2 negatives → positive product) |
| (−1) × (−6) × (−4) = −24 | (3 negatives → negative product) |
Similarly,
| −24 ÷ 6 = −4 | (1 negative → negative quotient) |
| −24 ÷ (−4) = 6 | (2 negatives → positive quotient) |
The rules for working with integers are very brief. If you add, subtract, or multiply two integers, the result will always be an integer. However, if you divide two integers, the result may or may not be an integer.
8 ÷ 4 = 2 which is an integer, but
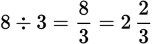 which is not an integer.
which is not an integer.
Working with odd and even numbers can be described with a few rules as well. When you add or subtract two odd numbers or two even numbers, the result will always be an even number.
6 + 4 = 10 (even + even = even)
7 − 3 = 4 (odd − odd = even)
When you add or subtract an even with an odd, the result will be odd.
2 + 7 = 9 (even + odd = odd)
5 − 4 = 1 (odd − even = odd)
When multiplying two numbers, the rule for determining whether the result is even or odd is that any integer times an even integer will result in an even number. The only way the product of two integers will be an odd number is if you multiply two odd numbers.
6 × 4 = 24 (even × even = even)
3 × 4 = 12 (odd × even = even)
3 × 5 = 15 (odd × odd = odd)
There are no rules predicting whether the outcome of division will be even or odd, because division does not always result in an integer. Sometimes dividing produces a fraction, and fractions are neither odd nor even.
Study how a well-prepared test taker would apply these rules to an AR question.
| Question | Analysis |
| If n is an integer, what is 2(n) + 1? | Step 1: The question tells you that n is an integer. |
| Step 2: The question asks for the value of a formula with a variable, n. | |
| (A) an even integer (B) an odd integer (C) an even non-integer (D) possibly either even or odd |
Step 3: Even though you don’t know whether n is odd or even, it is an integer. When any integer is multiplied by an even number the result is also an even number, so the term 2(n) must be even. If the odd number 1 is added to an even number, then the result is an odd number. Answer choice (B) is correct. |
| Step 4: Check that you used number properties correctly throughout the problem. Note that (C) is impossible no matter what the result of the equation because only integers can be odd or even. |
Absolute Value
When you see a number or expression bracketed by two vertical lines like this |−3|, you are seeing the symbol for absolute value. The absolute value of what is between the vertical lines is the positive magnitude of the number, regardless of whether it is positive or negative.
If |x| = 5, then x = ?
Clearly x can equal 5, but x could also equal −5 since absolute value is the positive magnitude of what is between the vertical lines. Therefore x = +5 or −5.
If |x − 5| = 5, then x = ?
The definition of absolute value says that the expression between the lines can be either 5 or −5. Therefore, in order to find the possible values of x you must write two equations:
x − 5 = 5 and x − 5 = −5
If x − 5 = 5, then x = 10, but if x − 5 = −5, then x = 0. This makes the two possible values of x: 10 and 0.
When you encounter an absolute value problem on the ASVAB you must solve for both the positive and negative values of whatever is between the vertical lines. Test your understanding of the absolute value concept on the following problem:
| Question | Analysis |
| If |x − 2| + 3 = 7 which of the following is a possible value of x? | Step 1: The question gives you a formula with variable x. |
| Step 2: The question asks for one possible value of x. | |
| (A) 6 (B) -6 (C) 2 (D) 4 |
Step 3: First, subtract 3 from both sides. |x − 2| + 3 = 7 becomes |x − 2| = 4. Thus, x − 2 must equal either +4 or −4. If x − 2 = 4, then x = 6 If x − 2 = −4, then x = −2. Since −2 is not among the answer choices, (A), 6, is the only correct choice. |
| Step 4: Check your math and check to make sure you solved for the proper variable. In this case, the only variable was x, but other problems might contain more than one variable and require you to choose correctly. |
Factors, Multiples, and Prime Numbers
In order to determine the factors of a number, find the pairs of positive integers which can be multiplied together to produce the number that is being factored. Start with 1 and the number itself, which are always factors of any integer. Then examine 2, 3, 4 and so on, as shown in this example of finding the factors of 36:
1 × 36
2 × 18
3 × 12
4 × 9
6 × 6
Examining the two columns shows that the factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, and 36. When creating the list of factors, as soon as you reach a factor on the left which is equal to or greater than a factor already listed on the right, you can stop, since you’re about to start repeating factor pairs. In this table, you need go no higher than 6 because any number greater than 6 that is a factor of 36 is already in the right column.
Multiples are, in a way, the opposite of factors. For instance, in the example above, 1, 2, 3, 4, 6, 9, 12, and 18 are factors of 36. Conversely, 36 is a multiple of 1, 2, 3, 4, 6, 9, 12, and 18.
If you become confused between the terms factor and multiple, you can remember that multiples are larger because you can produce them by multiplying. There are a finite number of factors of any number, but there are an infinite number of multiples.
Prime numbers, by their very definition, cannot be multiples of any integers other than 1 and the prime number itself. However, prime numbers can be factors of other numbers.
3 × 13 = 39 (3 and 13 are prime numbers, but 39 is not because it is a multiple of 3 and a multiple of 13.)
A number’s prime factors are factors that are prime. The prime factorization of a number is the number expressed using multiplication containing only primes, even if some of those primes repeat.
To determine the prime factorization of a number, keep dividing by prime numbers until you can no longer divide because you are left with only prime numbers.
For example, to find the prime factorization of 168:
Since 168 is an even number, the prime number 2 is a factor of 168.
168 = 84 × 2, so 2 is a prime factor of 168.
84 is still an even number equal to 42 × 2, so 2 is a prime factor for a second time.
42 is still an even number equal to 21 × 2, so 2 is a prime factor for the third time.
21 is the product of 3 and 7.
Since these are both prime numbers, the process of finding the prime factors is complete.
An efficient way to determine the prime factors of any number is to use a “tree” as shown below.
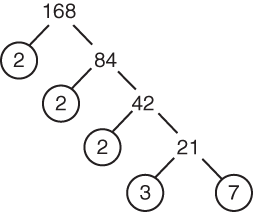
Based on the above operations and tree, the prime factorization of 168 is 2 × 2 × 2 × 3 × 7. All the prime factors, including repeated numbers, must be listed because the original number is the product of all of these numbers.
Prime factorization can be a very useful tool to help answer some questions on the ASVAB. For instance, if you need to find the greatest common factor (GCF) of two integers, break down both integers into their prime factorizations and multiply all prime factors they have in common, as shown in the example below:
| Question | Analysis |
| Find the greatest common factor of 40 and 140. | Step 1: You are given two numbers, 40 and 140. |
| Step 2: The question asks for the greatest common factor of the two numbers. | |
|
Step 3: The prime factors of 40 are 2, 2, 2, and 5. The prime factors of 140 are 2, 2, 5, and 7. Both numbers share two 2s and a 5 as prime factors, so the GCF is 2 × 2 × 5 = 20. |
|
| Step 4: Double-checking the result, 40 = 20 × 2 and 140 = 20 × 7. |
This can be helpful when you need to reduce a fraction, because you can find the GCF and then divide the top and bottom of the fraction by that number.
If you need to find a common multiple of two integers, you can just multiply them. However, in other cases you may need to find the least common multiple (LCM). You can use prime factors to efficiently identify LCMs. Take a look at this example to see how that works.
| Question | Analysis |
| Find the least common multiple of 20 and 16. | Step 1: You are given two numbers, 20 and 16. |
| Step 2: The question asks for the least common multiple of the two numbers. | |
|
Step 3: First, identify the prime factors of each number: 16 = 2 × 2 × 2 × 2 20 = 2 × 2 × 5 Any integer that is a multiple of 16 must have four prime factors of 2. Any integer that is a multiple of 20 must have two prime factors of 2 and one prime factor of 5. Therefore, any number that is a multiple of both 16 and 20 must have four prime factors of 2 and one prime factor of 5. The least common multiple equals 2 × 2 × 2 × 2 × 5 = 80. |
|
| Step 4: Double-check that all of the prime factors for each number were included in the least common multiple. |
Practice the technique on this question:
-
Marcus needs to order some parts for his machine shop. His supplier sometimes fills orders with boxes that contain 15 of these parts and sometimes with boxes of 18, depending upon what he happens to have in stock. The supplier will only ship complete boxes, and will ship only one size of box in a given order. What is the minimum quantity of parts that Marcus can order and be assured that he will receive exactly that many parts regardless of which boxes his supplier uses? - 15
- 18
- 90
- 270
Explanation
Step 1: The question gives you a situation in which Marcus is ordering parts. He wants to receive the exact number of parts he needs. You are told that the company ships parts in boxes of 15 and 18.
Step 2: You are asked to find the smallest number of parts that can be filled with full boxes of 15 parts or full boxes of 18 parts. Thus, you need to find the least common multiple of 15 and 18.
Step 3: The prime factors of 18 are 2 × 3 × 3 and the prime factors of 15 are 5 × 3. Therefore, the least common multiple must have two factors of 3, one factor of 2, and one factor of 5. This is 2 × 3 × 3 × 5 = 90. Answer choice (C) is correct.
Notice that (D), 270, is a common multiple of 15 and 18, but it is not the least common multiple.
Step 4: Confirm that 15 and 18 both divide evenly into 90.
Divisibility
Whether evaluating integers to determine if they are prime numbers, finding factors, or finding prime factors, you can check whether a number is a factor of another number more quickly and effectively if you use the following tips to check for divisibility.
Divisibility Rules
| Number | Divisibility Rule |
| 2 | All even numbers are divisible by 2. |
| 3 | Add up the individual digits of the number. If the total is divisible by 3, then the number itself is divisible by 3; for example, 243 is divisible by 3 because the sum of its digits is 2 + 4 + 3 = 9, but 367 is not because the sum of its digits is 3 + 6 + 7 = 16 and 16 is not a multiple of 3. |
| 4 | Take the last two digits and divide them by 2. If the result is even, the number is divisible by 4. If the result is odd, then the number is not divisible by 4. |
| 5 | All numbers ending in 5 or 0 are divisible by 5. |
| 6 | All even numbers that meet the test for divisibility by 3 are divisible by 6. |
| 8 | Divide the number by 2 twice; if the result is even, then the number is divisible by 8. |
| 9 | Add up the digits of the number; if the total is divisible by 9, then the number is divisible by 9. |
Practice divisibility rules on this question:
| Question | Analysis |
| What are all the prime numbers between 60 and 70 inclusive? | Step 1: You are given a range of numbers. |
| Step 2: The question asks for the number of primes within a given range. | |
|
(A) 61, 67 (B) 61, 63, 67 (C) 61, 63, 65, 67 (D) 62, 64, 66, 68 |
Step 3: Use divisibility tests to eliminate numbers that are not prime. Eliminate 60, 62, 64, 66, 68, and 70 because they are all divisible by 2. Eliminate 65 because it is divisible by 5. Checking for divisibility by 3 eliminates 63 (sum of the digits is 9) and 69 (sum of the digits is 15). The only remaining numbers are 61 and 67. Answer choice (A) is correct. |
| Step 4: All of the other answer choices contain numbers that were eliminated by using divisibility rules. |
Fractions and Decimals
Generally, it’s a good idea to reduce fractions when solving math questions. To do this, use your knowledge of factors to cancel all factors that the numerator and denominator have in common.
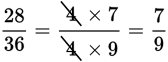
When you perform operations on fractions, always remember to perform the same operation on both the numerator and the denominator. For instance, in the example above, both the numerator and denominator were divided by 4.
To add or subtract fractions, you must convert all the fractions so that they have a common denominator. Think of the process of converting to a common denominator as finding the least common multiple of all the denominators. Don’t forget to multiply the individual numerators by the same number that was used to convert to a common denominator. Once you have converted the individual fractions so that they have common denominators, you merely add or subtract the numerators to obtain your result.
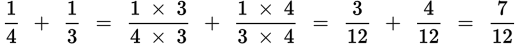
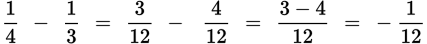
To multiply fractions, multiply the numerators together and then multiply the denominators together.

To divide one fraction by another you invert (flip) the second fraction and multiply. In other words, multiply the first fraction by the reciprocal of the second fraction.
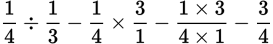
Occasionally a question may require that you compare fractions to determine which has the greater value. The most straightforward way to do this is to convert the fractions being compared to a common denominator and compare their numerators.
| Question | Analysis |
Compare
 and
and
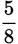 .
. |
The lowest common denominator is 3 × 8 = 24. |
Multiple the first fraction by
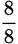 and the second fraction by
and the second fraction by
 .
. |
|
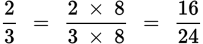
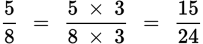
|
|
16 is greater than 15, so
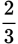 is greater than
is greater than
 .
. |
Practice the operations for fractions to answer the following question:
-
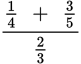 = ?
= ?
-
Explanation
Step 1: You are given an equation.
Step 2: You need to solve the equation using fraction rules.
Step 3: Dividing by a fraction is the same as multiplying by its reciprocal, so you can get rid of the cumbersome double-stack fraction by rewriting:

You need to add the two fractions in the left parentheses before multiplying. In order to add the two fractions, convert them to have a common denominator of 20.

Now add the first two fractions.
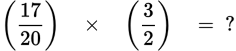
Multiplying the numerators and denominators results in an answer of
 . But this answer is not in the answer choices as written. For this problem, you must convert an improper fraction to a mixed number.
. But this answer is not in the answer choices as written. For this problem, you must convert an improper fraction to a mixed number.
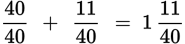 . Select answer choice (C).
. Select answer choice (C).
Step 4: Check to be sure you used the proper order of operations and check your math.
To convert a fraction to a decimal, divide the denominator into the numerator.
To convert
 to a decimal, divide 25 into 8.
to a decimal, divide 25 into 8.
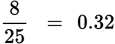
To convert a decimal to a fraction, first set the decimal as the numerator of a fraction with a denominator of 1. Then, move the decimal over as many places as it takes until it is immediately to the right of the units digit. Count the number of places that you moved the decimal. Then add that many 0s to the 1 in the denominator.
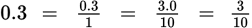
Try this one on your own:
-
0.0025 = ? -
Explanation
Step 1: The question gives you a number in decimal format.
Step 2: The answer choices show you that you will need to convert to a fraction.
Step 3: First, convert to a fraction with a denominator of 1,
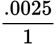 . In order to get rid of the decimal in the numerator, you will need to move it four places to the right and simultaneously add four 0s to the denominator. This results in the fraction
. In order to get rid of the decimal in the numerator, you will need to move it four places to the right and simultaneously add four 0s to the denominator. This results in the fraction
 .
.
To reduce this fraction to its simplest terms, divide both the numerator and denominator by 5 to get
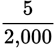 . Since both the numerator and denominator are still divisible by 5, repeat the process to get
. Since both the numerator and denominator are still divisible by 5, repeat the process to get
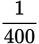 . Select answer choice (B).
. Select answer choice (B).
Step 4: Since many of the answer choices vary by the number of zeros in the denominator, double-check that you added the appropriate number of zeros to the denominator before you started simplifying.
Decimal Division
One common type of arithmetic problem on the ASVAB involves dividing numbers that contain decimals. Keeping track of the decimal places can complicate a division problem, so get rid of the decimal places before you divide. You can accomplish this by multiplying both numbers by 10 as many times as necessary. When you multiply a number with decimals by 10, simply move the decimal point one place to the right. When multiplying numbers without decimals by ten, add a zero at the end.
As an example,
1.22 × 10 = 12 2
12.2 × 10 = 122
122 × 10 = 1,220
When presented with a decimal division question you should write the division problem as a fraction:
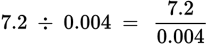
Then you will move the decimal points in the denominator and the numerator the same number of places to the right, adding zeros as necessary, until you have completely gotten rid of any decimal points.

The example below shows how to tackle an ASVAB question about decimal operations.
| Question | Analysis |
| David is drawing a blueprint for a model home. Due to the scale he used, the width of the bathroom floor is 0.18 inches on his paper. He needs to draw 30 tiles across that width. What is the width of each individual tile in his sketch in inches? | Step 1:You are told that there are 0.18 inches to draw 30 tiles. |
| Step 2: The question asks for the measurement of width in inches of each tile as drawn on the paper. | |
| (A) 0.006 (B) 0.06 (C) 0.6 (D) 6 |
Step 3: You need to divide 30 into 0.18. Write the problem as a fraction:
A quick glance at the answer choices reveals that they are in decimal format rather than fractions, so you need to convert to a decimal. Divide both the numerator and denominator by the common factor of 3 so that the numbers are easier to work with:
You have to get rid of the 3 zeros in the denominator so that the denominator becomes 1. Move the decimal point in the numerator 3 places to the left, inserting zeros after the decimal as needed, resulting in
|
| Step 4:Check your math carefully. Double-check that you inserted the correct number of zeros. |
Scientific notation is a method of writing very large and very small numbers that also involves moving decimal points. The first part of a number in scientific notation will be equal to or greater than 1 and less than 10. The second part of the number will be a power of 10. For powers of 10, the exponent is the number of zeroes the number has when written out. For example, 104 = 10,000. For numbers written in scientific notation, where the first number always has exactly one digit to the left of the decimal point, the long version of the number can be written out by moving the decimal to the right by the same number of places as the value in the exponent of the power of 10.
1.23 × 104 = 12,300
Scientific notation also uses negative exponents to indicate the proper placement of the decimal point in a very small number. A negative exponent in scientific notation means that you move the decimal point to the left. Once the decimal point has been moved as far left as possible, start adding zeros to the right of the decimal.
4.321 × 10−2 = 0.04321
Use this problem to practice your understanding of scientific notation:
| Question | Analysis |
| Sam writes for a scientific journal. In her research, she finds a number written as 6,483,000. How can she express that in scientific notation? | Step 1: You are given a number. |
| Step 2: You are asked to rewrite the number in scientific notation. | |
|
(A) 6.483 × 103 (B) 6.483 × 105 (C) 6.483 × 106 (D) 6.483 × 107 |
Step 3: Move the decimal point 6 places to the left so 6,483,000 becomes 6.483000. If you move the decimal 6 places to the left, you must write 106. Thus, written in scientific notation the number becomes (C) 6.483 × 106. |
| Step 4: Check to be sure you moved the decimal over the correct number of places. |
Exponents and Radicals
Exponents are the small raised numbers written above and to the right of a variable or number (the base). They indicate the number of times that the variable or number is multiplied by itself. The rules for performing different operations on terms involving a base and an exponent will require you to pay close attention to the details. There are two important things to remember about exponents. First, any number or variable with an exponent of 1 is equal to the base itself. Second, any number or variable with an exponent of 0 equals 1.
x1 = x 51 = 5 x0 = 1 50 = 1
To add or subtract terms involving variables and exponents, both the variables and the exponents must be the same.
2x2 + x2 = 3x2
3x4 − 2x4 = x4
x2 + x3 cannot be combined.
a2 + b2 cannot be combined.
To multiply terms with the same base, merely add the exponents. This can be done because exponents represent how many times the base is multiplied by itself.
23 × 22 = (2 × 2 × 2) × (2 × 2) = 23+2 = 25
Similarly, to divide terms with the same base, subtract the exponent that is in the denominator from the exponent in the numerator.
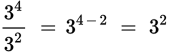
To raise a term involving an exponent to another exponent, multiply the exponents.
(x2)4 = x2×4 = x8
A coefficient is a number multiplied by a variable in a term. For instance, in the term 2x², the coefficient is 2. To multiply terms consisting of coefficients and exponents that have the same variable in the base, multiply the coefficients and add the exponents.
6x7 × 2x5 = (6 × 2) (x7+5) = 12x12
To divide terms consisting of coefficients and exponents that have the same variable in the base, divide the coefficients and subtract the exponents.
6x7 ÷ 2x5 = (6 ÷ 2) (x7−5) = 3x2
You might see a negative exponent in a problem on the ASVAB. Don’t panic! Negative exponents are just the reciprocal of their positive counterparts.
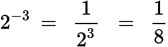
Practice working with exponents on this problem:
| Question | Analysis |
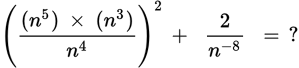
|
Step 1: You are given an equation. |
| Step 2: You need to simplify the equation. | |
|
(A) n8 (B) 2n8 (C) 3n8 (D) n20 |
Step 3: Since there are variables in the question stem and the answer, you can use Picking Numbers here. Pick a number for n and solve for the equation in the question stem. The result is your target number. Then plug your initial number for n into all of the answer choices and the one that yields the target number would be correct. To solve with straightforward math, apply the exponent rules one at a time. Using the rule for multiplying two terms with the same base (in this case, n) the numerator of the first expression can be simplified to read:
Use the rule for raising an exponent to an exponent and you have
A number to a negative exponent is the same as the reciprocal of that number to a positive exponent. Thus, the expression on the right can be rewritten as: n8 + 2n8. Since both terms have the same base and the same exponent, you can add them together to get the correct answer, 3n8, choice (C). |
| Step 4: Briefly confirm that you performed the steps correctly. |
Try this problem both by Picking Numbers and by using straightforward math so that you get a sense of which method you will be more comfortable with for this type of problem on Test Day.
Perfect squares are integers that are the result of squaring (multiplying by itself) another integer. For instance, 25 is a perfect square because it is 5 × 5. You can save time and trouble on the ASVAB if you memorize the perfect squares up through 12 × 12 = 144 .
Hone your skills with the following practice problem:
| Question | Analysis |
| Which of the following numbers is NOT a perfect square? | Step 1: The question stem doesn’t give much information, but you can infer that three of the answer choices ARE perfect squares. |
| Step 2: You are looking for a number that is not equal to an integer times itself. | |
|
(A) 1 (B) 16 (C) 27 (D) 36 |
Step 3: 1 = 1 × 1, so it is a perfect square. 16 = 4 × 4, which is also a perfect square. 27 = 3 × 3 × 3, which is not a perfect square because it is a number multiplied by itself three times rather than twice. Answer choice (C) is correct. |
|
Step 4: Check to see if the remaining answer choice is a perfect square. 36 = 6 × 6, so it is a perfect square. |
A square root is a number that, when multiplied by itself, produces the given quantity. The radical sign is used to represent the positive square root of a number, so
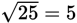 , since 5 × 5 = 25. (Even though (−5) × (− 5) is also 25, when you are asked for the square root, the answer will be a positive number.) To add or subtract radicals, make sure the numbers under the radical sign are the same. If they are, you can add or subtract the coefficients outside the radical signs.
, since 5 × 5 = 25. (Even though (−5) × (− 5) is also 25, when you are asked for the square root, the answer will be a positive number.) To add or subtract radicals, make sure the numbers under the radical sign are the same. If they are, you can add or subtract the coefficients outside the radical signs.
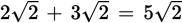
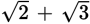 cannot be combined.
cannot be combined.
To simplify radicals, factor out the perfect squares under the radical, calculate the square roots of the perfect squares, and put the results in front of the radical sign.

Note that when you have simplified to the point where the number under the radical does not contain any perfect squares, your result will be sufficient for the ASVAB.
To multiply or divide radicals, multiply or divide the coefficients outside and inside the radical separately.
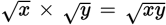
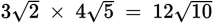

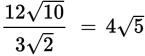
To take the square root of a fraction, you can break the fraction into two separate roots and take the square root of the numerator and the denominator separately.

Practice computations with radicals on this problem:
| Question | Analysis |
Simplify

|
Step 1:The question gives an expression in the form of a fraction. |
| Step 2: You are asked to simplify the fraction as much as possible. | |
|
(A)
(B)
(C)
(D)
|
Step 3: First, check to see if there is anything you can divide out of the top and bottom to make the fraction easier to work with. In this case, there is not. Since the example contains a radical sign, check to see if any of the numbers (as written) are perfect squares. None of the numbers are perfect squares, so complete the multiplication on the top and on the bottom.
Before performing the division, check to see if any of the numbers are perfect squares. 81 = 9 × 9 64 = 8 × 8 Since both numbers are perfect squares, take the square root of the top and bottom independently.
Scanning the answer choices,
Answer choice (C) is correct. |
| Step 4: Check your math and check to be sure you solved for the correct question. |
Factorials
On the ASVAB math sections, you may see an occasional factorial question. You’ll know you’re dealing with a factorial when you see an integer followed by an exclamation point (!). A factorial is the product of the integer before the factorial sign and all the positive integers below it. For instance, when you see the following:
7! = ?
The question is actually asking you what “7 factorial” is, and the answer to that question is:
7! = 7 × 6 × 5 × 4 × 3 × 2 × 1 = 5,040
If you’re ever given a fraction with factorials, there’s often a lot of canceling that you can do before you try to multiply out the factorials.
Look at the following example.
| Question | Analysis |
Solve for
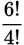
|
Step 1: You are given a fraction containing factorials. |
| Step 2: You need to perform the calculations. | |
|
Step 3: Write out the factorials
Cancel out the numbers that appear on the top and bottom.
The correct answer is 30. |
|
| Step 4: Double-check your calculations and your elimination. |
If you see a problem with factorials in a fraction on Test Day, simplify before attempting to solve.
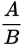 , where A is the numerator and B is the denominator.
, where A is the numerator and B is the denominator.
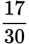
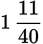
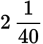
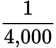



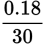 . Eliminate the decimal point by moving it two places to the right and adding 2 zeros to the denominator:
. Eliminate the decimal point by moving it two places to the right and adding 2 zeros to the denominator:
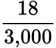 .
.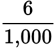 .
.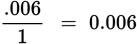 . Answer choice (A) is correct.
. Answer choice (A) is correct.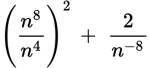 . Next, apply the rule for division of terms with the same base so that the expression on the left becomes:
. Next, apply the rule for division of terms with the same base so that the expression on the left becomes:
 .
. .
.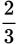
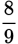

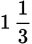

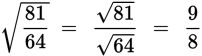
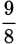 is not present as written. However, since the numerator is greater than the denominator, this is an improper fraction that can be converted to a mixed number.
is not present as written. However, since the numerator is greater than the denominator, this is an improper fraction that can be converted to a mixed number.