Arithmetic Reasoning Practice Set 1

Answers and Explanations

1. C

   To simplify an absolute value problem by eliminating the absolute value function, write two equations, one of which sets whatever is inside the vertical lines to its positive value, and the other of which sets that equal to its negative value. So, either y − 3 = 3 or y − 3 = −3. Clearly, y has a greater value in the first equation. By adding 3 to both sides of the equation, y = 6.

2. D

   This problem tells you that the number of pieces of candy in the box can be divided evenly by 5 and 3. So the correct answer is the choice that has a 0 or 5 as its last digit, and the sum of whose digits is divisible by 3. Eliminate (B) because it doesn’t end in either 0 or 5. Of the remaining choices, only 555, (D), is also divisible by 3, since 5 + 5 + 5 = 15.

3. B

   To find the least common multiple, you should identify the prime factors of each number. The prime factor of 7 is 7, since it is a prime number. The prime factors of 9 are 3 and 3. The prime factors of 21 are 7 and 3. Therefore the LCM must have two factors of 3 and one factor of 7; 3 × 3 × 7 = 63. To check your work, you can confirm that 7, 9 and 21 all divide evenly into 63.

4. C

   When given a complex expression such as the one in this problem, simplify it one step at a time. Dividing by a fraction is the same as multiplying by its reciprocal, so

   =

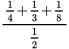   In order to add these fractions, you’ll have to use a common denominator. Since 4, 3, and 8 are all factors of 24:

   

   Because this is an improper fraction and the answer choices are written as mixed numbers, convert it to

5. B

   While this problem may look formidable at first glance, it can be solved by reducing the fraction to simpler terms before attempting to identify the square root. When you see a complex calculation that makes you wonder how you are going to do the math without a calculator, that is often a hint to use prime factorization. If you restate the problem as you can see that many terms in the numerator and denominator of the radical cancel out: so that you are left with

6. C

   Set up a proportion:

   Now cross-multiply and solve: 150x = 4,500. So

   

7. A

   so here the average is Thus ; multiply both sides by 5 to get 170 = 141 + n. Subtract 141 from both sides and n = 29.

8. D

   This is a percent change problem, so you will need to identify the original and new values that are being compared and use the formula for calculating percent change: In order to subtract powers, they must have the same base and exponent, so you’ll have to convert one of the terms

   This can be simplified to

9. B
   Follow PEMDAS to get the answer. Since there is a set of Parentheses, start there and change the expression to 30 − 5 × 4 + 4² ÷ 8. There is an Exponent, so calculate the value of the exponent term next: 30 − 5 × 4 + 16 ÷ 8. Now you can calculate the Multiplication and Division parts of the expression from left to right to get 30 − 20 + 2. Finish up with the Addition and Subtraction from left to right to get the answer, 12.
10. C
    This is a probability question with multiple events. In order for the last person to get stuck with the red ball, the first person must draw a green ball and so must the 2nd, 3rd, and 4th persons. The number of green balls will decrease with each successive pick, so the probability is
11. C

    Each of the tests counts once and the final exam counts twice, which means there are 3 + 2 = 5 total parts. The final exam is 2 parts, so it counts as 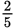  of the final grade.

12. A

    First, solve   for  . Divide by 5: 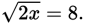 Square both sides, so  , then divide both sides by 2 so  . Lastly, multiply by 5:  .

13. A

    Since half of the 10 liters of diluted juice are consumed, there must be only 5 liters remaining. 20% is water and 80% is pure juice, so there is now 1 liter of water and 4 liters of pure juice. Another liter of pure juice is added, so there are 5 liters of pure juice. The ratio is 1:5. 

14. A

    Since x is an integer, multiplying any integer by 4 will result in an even integer. So 4x must be even. Adding 4 to an even value must result in an even number. Therefore, 4x + 4 must be even.

15. C

    The formula to use to find time when given the speed and the distance is 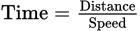. Since the distance given here is 420, and the speed is 60, 

16. B

    The question provides a part to whole ratio and asks for a part to part ratio. If 2 of the 5 floors are above ground, then 5 – 2 = 3 floors must be below ground. So the ratio of floors below ground to floors above ground is 3:2.
    

Arithmetic Reasoning Practice Set 2

Answers and Explanations

1. D

   , so multiply that by 25. However, there is a faster way to solve this. To find the value, you would calculate 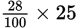 , but since multiplication can be done in any order, this is the same as  .   can be simplified to  , and multiplying that by 28 equals 7.

2. C

   The average of a set of numbers is found by adding the numbers, and then dividing by how many terms there are. So, add the three fractions, and then divide by 3, which is the number of terms. To add the three fractions, start by finding the common denominator, which is 20. Then convert each fraction to have a denominator of 20.  ,  , and  . So the sum is 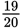 . Then divide by 3 or multiply by the reciprocal,  . The result will be  .

3. C

   To find the number of possible combinations consisting of two different elements, multiply how much of each element you have. Since each outfit consists of one shirt and one pair of pants, take the number of shirts (3) and the number of pairs of pants (4), and multiply them together.  .

4. A

   In order to solve this in the most efficient manner, avoid the temptation to just multiply and divide the terms. Instead, look for common factors in the numerator and denominator among the terms that are being multiplied. The factor of 25 in the numerator and 75 in the denominator can be simplified to 1 on the top and 3 on the bottom, leaving  . The 3s in the numerator and denominator can be divided out as well, leaving  . The 8 and 2 can be canceled out to a 4 and a 1 (so you can remove the denominator), which leaves  . Simplifying the expression gives  .

5. C

   Follow the order of operations (PEMDAS) to simplify this expression correctly. First, simplify what is in the parentheses: in this case, 2 + 1, which equals 3. Then apply the exponent to what's in the parentheses.  . So now the expression is  . Next, perform the operations of multiplication and division, from left to right. 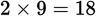  and  . The expression is now 50 – 3, which equals 47.

6. B

   For an equation with an expression inside the absolute value signs, create two equations: one with a positive value (in this case, 10) and one with a negative value (in this case, –10). Since the question asks for the smallest possible value of x, start with the equation with the negative value. Since  , add 5 to both sides, and the resulting equation is  .

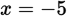7. C

   To find the average of the three terms, first find the sum of the terms and then divide by 3. There's no way to know the exact values of x and y, but since the average of the two terms is 30, the sum must be 2(30) = 60. Since z equals 15, then the sum of the three terms is 60 + 15 = 75. Lastly, divide 75 by 3, which equals 25.

8. B

   First, combine the fractions in the denominator. The common denominator of these is 10, so   and  . Once all the denominators are the same, add or subtract the numerators: 5 + 8 – 1 = 12. So the fraction in the denominator is  . Then, when dividing by a fraction (in this case,  ), take the reciprocal and multiply that by the numerator.  . Both the numerator and denominator have a common factor of 6, so divide both the numerator and denominator by 6, and the fraction simplifies to  .

9. B

   To find common factors of a number, first break down each number into its prime factors. Then see which factors they have in common, and find the product of those common factors. The prime factors of 50 are 2, 5, and 5. The prime factors of 60 are 2, 2, 3, and 5. The prime factors of 75 are 3, 5, and 5. Since one factor of 5 is in each of those sets of prime factors, but the prime factors 2 and 3 are not found in all of the numbers, the greatest common factor is 5.

10. B

    Since the price of the watch has gone down, the percent change must represent a decrease. Using the formula for percent change, divide the actual change by the original amount. Since the watch was originally $200 and during the sale it is $160, the watch decreased in price by $40. Divide $40 by the original amount of $200 to get 0.2, or 20%.

11. B

    Since the problem states how long it takes each person to wash the car, the units of which are hours/car, take the reciprocal of the times to get the rates in terms of cars/hour and add them together to get the combined rate: 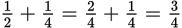  cars/hour working together. Invert that combined rate to determine that they can wash 1 car in 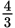  hour. However, the question asks how long it will take to wash two cars, so that would be 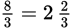  hours.

12. D

    Don't calculate or even estimate the value of  . The prime factorization of 26 is  . So, since there are three factors of 26, there are three factors of 2 and three factors of 13.  , or  .

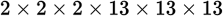13. A

    Avoid the temptation to use the formula for finding the arithmetic mean, or average. Instead, notice that each number in the set has the same difference from the previous number so that they form an arithmetic sequence. Whenever that is true of a set of numbers, the arithmetic mean is equal to the median. Since there are 9 numbers in this set, the 5th number (when all the numbers are in order) is the median. In this case, the 5th number is 13.

14. B

    For an equation with an absolute value sign, consider both the positive and the negative values for what is inside the signs. 4x – 6 can equal either 18 or –18. If 4x – 6 = 18, first add 6 to both sides: 4x = 24. Then divide both sides by 4, and x = 6. However, 6 is not one of the answer choices. So try the other equation: 4x – 6 = –18. Add –6 to both sides, so 4x = –12. Divide both sides by 4, and x = –3.

    Alternatively, the answer could be determined by backsolving. For (A), . For (B),  .

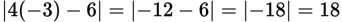15. D

    Any number divisible by both 3 and 5 must be divisible by  , since 3 and 5 are both prime numbers. That’s 15, which is the smallest number. Add another 15 to 15 to find the next number, 30. Then add another 15, which equals 45. The next number would be 60, but that’s above the range of values indicated in the question. So there are 3 possible values: 15, 30, and 45.

16. C

    Since the number of dollars in the cash prize must be equally divided among all members of each team and there is no remainder, the number of dollars must be a multiple of each. First, find the prime factors of each number:  ,  , and  . The correct answer will be a common multiple of the different cash prize amounts. The least common multiple is found by taking each distinct prime factor (in this case, 2, 3, and 5), and raising each to the highest power of each factor. Because 2 shows up once, 3 shows up once, and 5 shows up twice, the lowest common multiple is . The correct answer must have at least one 2, one 3, and two 5s to be a multiple. The factorization of 120 is  , so it's missing one factor of 5 to be a multiple. The factorization of 375 is  , so it's missing a 2. The factorization of 750 is  , so this is a multiple. The factorization of 1,250 is  , so it's missing a factor of 3.

    Note that because  , another way to find the correct answer would be to look for a choice that is a multiple of 150.  , so 750 is correct.

Review and Reflect

After completing this chapter, think about the areas that you fully understand. Are there any areas still giving you trouble? Pay close attention to the themes that help you on multiple types of questions, such as finding the least common multiple and determining factors. Also, be sure that you practice simplifying fractions and performing basic calculations without a calculator.