Answers and Explanations

Part 5: Mathematics Knowledge (MK)

  1. D

    Use FOIL to solve:

    (3x + 4)(4x− 3)

    = (3x)(4x) + (3x)(−3) + (4)(4x) + (4)(−3)

    = 12x2− 9x + 16x − 12

    = 12x2 + 7x − 12

  2. A

    Pick numbers to solve this one. If n = 2, the tree grew 5 feet, or 60 inches, in 2 years, which means it grew at a rate of 30 inches per year. Plug in 2 for n into the answer choices, and only (A) gives the target number, 30.

  3. D

    If the perimeter of ABCD is 56, then half that, or 28, is the sum of the length and the width, since the perimeter of a rectangle = 2(length + width). If AD = 16, then AB = 28 − 16 = 12, and the area of ABCD must be 16 × 12 = 192.

  4. A

    A square is a rectangle with four equal sides. Choice (B) may be tempting, but in fact, any two opposing sides of a square are parallel. It would be inaccurate to say that a square has four sides, all of which are parallel. Choice (D), curvilinear, means “curved” and is not correct.

  5. D

    The question gives two inequalities here: a < b and b < c, which can combine into one, a < b < c. Go through the answer choices to see which must be true. If you add the corresponding sides of these inequalities: a + b < c + c, or a + b < 2c. This statement is always true, so it must be the correct answer.

    This question could also be approached by picking numbers. That might look like this:

    Choose a = 2, b = 3, and c = 4, to conform to the information in the question stem. Now try each choice to see whether it is a true statement about those numbers:

    (A) 3 + 4 < 4 No way! Incorrect.

    (b) 2 + 3 < 4 Also not true. Incorrect.

    (c) 2 − 3 < 3 − 4 Nope. Incorrect.

    (d) 2 + 3 < 8 Definitely true. This choice is correct.

    If more than one answer choice had produced a true statement, you would have tried again using different numerical values until you had only one true statement.

  6. C

    Since the angle marked x° and the angle marked y° together form a straight angle, their measures must sum to 180°. Substitute in 2z for x and 3z for y, and solve for z:

  7. B

    There are 360 degrees in a circle and 60 minutes in an hour, so you could solve this question by setting up a proportion in which n is the number of minutes Then cross-multiply and reduce the fraction:

  8. C

    The area of a triangle is

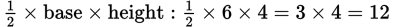
  9. B

    Since lines p and q are parallel, use the rule about alternate interior angles. The angle marked y° is supplementary to a 65° angle, so y = 180 − 65 = 115.

  10. A

    You could either turn the percentages into decimals and multiply: 0.15 × 0.15 × 200 = 0.15 × 30 = 4.5 and get the answer (A), or you could take it one step at a time. 15% of 200 is 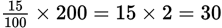. 15% of 30 is

    .

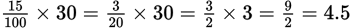  11. B

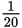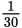    Don’t fall for the answer choice trap and assume that the average of and is 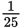. Instead, use the average formula: 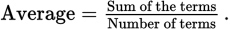In this case:

    .

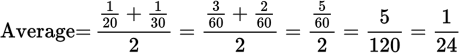  12. C

    This question is testing your knowledge of definitions. The supplement of an angle is the angle that when added to the original angle equals 180°. So if an angle measures y°, its supplement is 180 − y.

  13. B

    If Diane has of her room still to paint, she’ll need 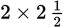or 5 more cans to do the job.

  14. D

    You can’t find the value of either variable alone, but you don’t need to. Rearranging the equation, you get:

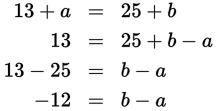
  15. C

    When you multiply terms that have exponents over the same base, you add the exponents and multiply the coefficients:

    3x2 × 5x3 = (3 × 5)x2 + 3 = 15x5

  16. D

    You can pick numbers to make sense of this geometry problem. You are asked to increase the sides of a square by 10%, so you want to pick a number for the original sides of the square of which it’s easy to take 10%. For instance, you could say that the original square is 10 by 10. 10% of 10 is 1, so the dimensions of the increased square are 11 by 11. In this case, the area of the original square is 100, and the area of the new square is 121, which represents a 21% increase.

  17. B

    If 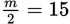, then m = 15 × 2 = 30

    Plug 30 in for m to solve the expression asked for in the question:

  18. C

    To factor 6x2 − 13x + 6, you need a pair of binomials whose “first” terms will give you a product of 6x 2 and whose “last” terms will give you a product of 6. Since the middle term of the result is negative and the last term is positive, the two last terms of the factors must both be negative. One of the factors is among the answer choices, so you can use the answer choices in your trial-and-error effort to factor. You’re looking for a factor with a minus sign in it, so the answer’s either (C) or (D). Try (C) first: Its first term is 3x, so the other factor’s first term would have to be 2x (to get that 6x 2 in the product). (C)’s last term is −2, so the other factor’s last term would have to be −3.

    Check to see if (3x − 2)(2x − 3) works:

    (3x − 2)(2x − 3)

    = (3x)(2x) + 3x (−3) + (−2)(2x) + (−2)(−3)

    = 6x2− 9x− 4x + 6

    = 6x2−13x + 6

    It works. There’s no need to check (D).

  19. D

    Just be careful and translate the English into math: “the product of 3 and x is equal to 2 less than y ” becomes 3x = y − 2. But all of the equations in the answer choices set the right side of the equation to zero, so do that to your equation:

    3x = y − 2

    3x − y = −2

    3x − y + 2 = 0

  20. A

    Since 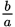is the reciprocal of , 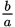must be the reciprocal of 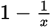as well. Combine the terms in and then find the reciprocal: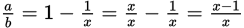

    Therefore,

  21. C

    This figure is an unfamiliar solid, so don’t try to calculate the volume directly. The question says that the solid in question is half of a cube. Imagine the other half lying on top of the solid, forming a complete cube.

    Notice that the diagonal with length 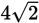and two of the cube’s edges form an isosceles right triangle. In an isosceles right triangle, the hypotenuse is 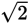times the length of a leg. Here the hypotenuse has length 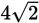, so the legs have length 4. Thus, the edges of the cube have a length of 4. The volume of a cube is the length of an edge cubed. So the volume of the whole cube is 4 × 4 × 4, or 64. The volume of the solid in question is of this, or 32.

  22. B

    Begin by writing the division problem as a fraction: . Now move the decimal points on the top and the bottom of the fraction the same number of places to the right until you are dealing with whole numbers: . Now divide: .

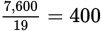  23. B

    The circumference of a circle = 2π(radius), so . The circumference is 8: The area of a circle = π(radius)2, so the area of a circle with a radius of 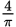is:

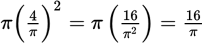
  24. B

    You could translate the English into math to get:

    .36 × 18 = .18 × n

    However, you don’t have to go through all that work if you realize that x percent of y = y percent of x.

  25. C

    Here you’re looking for an extremely rough approximation (the answer choices all have a range of 100), so square the upper bounds of the ranges in the answer choices, until you find the range that encompasses 104,906. Start with the upper bound of (A): (200)2 = 40,000, which is less than 104,906. Now try (B): (300)2 = 90,000, which is still too low. Now check (C): (400)2 = 160,000. 104,906 is between 90,000 and 160,000, so (C) is the correct answer.