In my second lecture, I’m going to talk about the quantum theory of black holes. It seems to lead to a new level of unpredictability in physics over and above the usual uncertainty associated with quantum mechanics. This is because black holes appear to have intrinsic entropy and to lose information from our region of the universe. I should say that these claims are controversial: many people working on quantum gravity, including almost all those who entered it from particle physics, would instinctively reject the idea that information about the quantum state of a system could be lost. However, they have had very little success in showing how information can get out of a black hole. Eventually I believe they will be forced to accept my suggestion that it is lost, just as they were forced to agree that black holes radiate, which went against all their preconceptions.
I should start by reminding you about the classical theory of black holes. We saw in the last lecture that gravity is always attractive, at least in normal situations. If gravity had been sometimes attractive and sometimes repulsive, like electrodynamics, we would never notice it at all because it is about 1040 times weaker. It is only because gravity always has the same sign that the gravitational force between the particles of two macroscopic bodies like ourselves and the Earth add up to give a force we can feel.
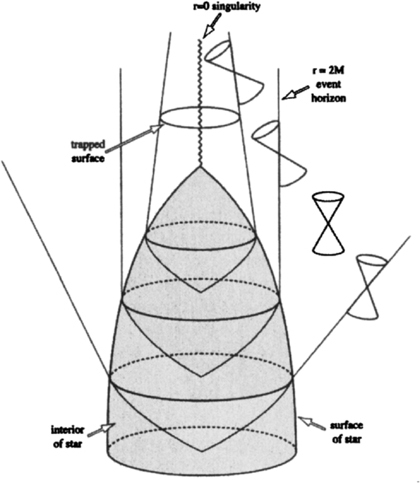
The fact that gravity is attractive means that it will tend to draw the matter in the universe together to form objects like stars and galaxies. These can support themselves for a time against further contraction by thermal pressure, in the case of stars, or by rotation and internal motions, in the case of galaxies. However, eventually the heat or the angular momentum will be carried away and the object will begin to shrink. If the mass is less than about one and a half times that of the Sun, the contraction can be stopped by the degeneracy pressure of electrons or neutrons. The object will settle down to be a white dwarf or a neutron star, respectively. However, if the mass is greater than this limit there is nothing that can hold it up and stop it continuing to contract. Once it has shrunk to a certain critical size the gravitational field at its surface will be so strong that the light cones will be bent inward, as in figure 3.1. I would have liked to draw you a four-dimensional picture. However, government cuts have meant that Cambridge University can afford only two-dimensional screens. I have therefore shown time in the vertical direction and used perspective to show two of the three space directions. You can see that even the outgoing light rays are bent toward each other and so are converging rather than diverging. This means that there is a closed trapped surface, which is one of the alternative third conditions of the Hawking-Penrose theorem.
Figure 3.1 A spacetime picture of die collapse of a star to form a black hole, showing the event horizon and a closed trapped surface.
If the cosmic censorship conjecture is correct, the trapped surface and the singularity it predicts cannot be visible from far away. Thus there must be a region of spacetime from which it is not possible to escape to infinity. This region is said to be a black hole. Its boundary is called the event horizon and is a null surface formed by the light rays that just fail to get away to infinity. As we saw in the last lecture, the area of a cross section of the event horizon can never decrease, at least in the classical theory. This, and perturbation calculations of spherical collapse, suggest that black holes will settle down to a stationary state. The no-hair theorem, proved by the combined work of Israel, Carter, Robinson, and myself, shows that the only stationary black holes in the absence of matter fields are the Kerr solutions. These are characterized by two parameters, the mass M and the angular momentum J. The no-hair theorem was extended by Robinson to the case where there was an electromagnetic field. This added a third parameter Q, the electric charge (see box 3.A). The no-hair theorem has not been proved for the Yang-Mills field, but the only difference seems to be the addition of one or more integers that label a discrete family of unstable solutions. It can be shown that there are no more continuous degrees of freedom of time-independent Einstein-Yang-Mills black holes.
What the no-hair theorems show is that a large amount of information is lost when a body collapses to form a black hole. The collapsing body is described by a very large number of parameters. There are the types of matter and the multipole moments of the mass distribution. Yet the black hole that forms is completely independent of the type of matter and rapidly loses all the multipole moments except the first two: the monopole moment, which is the mass, and the dipole moment, which is the angular momentum.
This loss of information didn’t really matter in the classical theory. One could say that all the information about the collapsing body was still inside the black hole. It would be very difficult for an observer outside the black hole to determine what the collapsing body was like. However, in the classical theory it was still possible in principle. The observer would never actually lose sight of the collapsing body. Instead, it would appear to slow down and get very dim as it approached the event horizon. But the observer could still see what it was made of and how the mass was distributed. However, quantum theory changed all this. First, the collapsing body would send out only a limited number of photons before it crossed the event horizon. They would be quite insufficient to carry all the information about the collapsing body. This means that in quantum theory there’s no way an outside observer can measure the state of the collapsed body. One might not think this mattered too much, because the information would still be inside the black hole even if one couldn’t measure it from the outside. But this is where the second effect of quantum theory on black holes comes in. As I will show, quantum theory will cause black holes to radiate and lose mass. It seems that they will eventually disappear completely, taking with them the information inside them. I will give arguments that this information really is lost and doesn’t come back in some form. As I will show, this loss of information would introduce a new level of uncertainty into physics over and above the usual uncertainty associated with quantum theory. Unfortunately, unlike Heisenberg’s uncertainty principle, this extra level will be rather difficult to confirm experimentally in the case of black holes. But as I will argue in my third lecture (chapter 5), there’s a sense in which we may have already observed it in the measurements of fluctuations in the microwave background.
The fact that quantum theory causes black holes to radiate was first discovered by doing quantum field theory on the background of a black hole formed by collapse. To see how this comes about it is helpful to use what are normally called Penrose diagrams. However, I think Penrose himself would agree they really should be called Carter diagrams because Carter was the first to use them systematically. In a spherical collapse the spacetime won’t depend on the angles θ and ø All the geometry will take place in the r-t plane. Because any two-dimensional plane is conformal to flat space one can represent the causal structure by a diagram in which null lines in the r-t plane are at ±45° to the vertical.
Let’s start with flat Minkowski space, which has a Carter-Penrose diagram that is a triangle standing on one corner (fig. 3.2). The two diagonal sides on the right correspond to the past and future null infinities I referred to in my first lecture. These are really at infinity but all distances are shrunk by a conformal factor as one approaches past or future null infinity. Each point of this triangle corresponds to a two-sphere of radius r. r = 0 on the vertical line on the left, which represents the center of symmetry, and r → ∞ on the right of the diagram.
One can easily see from the diagram that every point in Minkowski space is in the past of future null infinity I+. This means there is no black hole and no event horizon. However, if one has a spherical body collapsing the diagram is rather different (fig. 3.3). It looks the same in the past but now the top of the triangle has been cut off and replaced by a horizontal boundary. This is the singularity that the Hawking-Penrose theorem predicts. One can now see that there are points under this horizontal line that are not in the past of future null infinity I+. In other words, there is a black hole. The event horizon, the boundary of the black hole, is a diagonal line that comes down from the top right corner and meets the vertical line corresponding to the center of symmetry.
Figure 3.2 The Carter-Penrose diagram for Minkowski space.
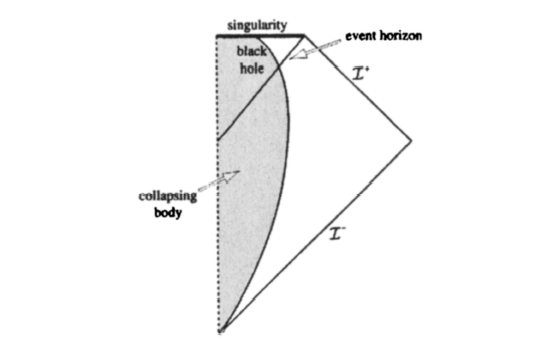
Figure 3.3 The Carter-Penrose diagram for a star that collapses to form a black hole.
One can consider a scalar field ø on this background. If the space-time were time independent, a solution of the wave equation that contained only positive frequencies on I- would also be of positive frequency on I+. This would mean that there would be no particle creation, and there would be no outgoing particles on I+ if there were no scalar particles initially.
However, the metric is time dependent during the collapse. This will cause a solution that is positive frequency on I- to be partly negative frequency when it gets to I+. One can calculate this mixing by taking a wave with time dependence e-iωu on I+ and propagating it back to I-. When one does that, one finds that the part of the wave that passes near the horizon is very blue shifted. Remarkably, it turns out that the mixing is independent of the details of the collapse in the limit of late times. It depends only on the surface gravity K that measures the strength of the gravitational field on the horizon of the black hole. The mixing of positive and negative frequencies leads to particle creation.
When I first studied this effect in 1973 I expected I would find a burst of emission during the collapse but that then the particle creation would die out and one would be left with a black hole that was truly black. To my great surprise, I found that after a burst during the collapse there remained a steady rate of particle creation and emission. Moreover, the emission was exactly thermal with a temperature of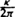 
. This was just what was required to make the idea that a black hole had an entropy proportional to the area of its event horizon consistent. Moreover, it fixed the constant of proportionality to be a quarter in Planck units, in which G = c = h = 1. This makes the unit of area 10-66 cm2, so a black hole of the mass of the Sun would have an entropy of the order of 1078. This would reflect the enormous number of different ways in which it could be made.
When I made my original discovery of radiation from black holes it seemed a miracle that a rather messy calculation should lead to emission that was exactly thermal. However, joint work with Jim Hartle and Gary Gibbons uncovered the deep reason. To explain it I shall start with the example of the Schwarzschild metric.
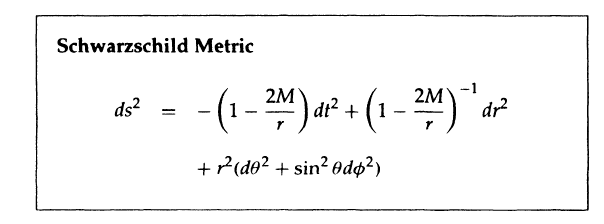
This represents the gravitational field that a black hole would settle down to if it were nonrotating. In the usual r and t coordinates there is an apparent singularity at the Schwarzschild radius r = 2M. However, this is just caused by a bad choice of coordinates. One can choose other coordinates in which the metric is regular there.
The Carter-Penrose diagram has the form of a diamond with flattened top and bottom (fig. 3.4). It is divided into four regions by the two null surfaces on which r = 2 M. The region on the right, marked 
on the diagram, is the asymptotically flat space in which we are supposed to live. It has past and future null infinities I- and I+ like flat spacetime. There is another asymptotically flat region 
on the left that seems to correspond to another universe that is connected to ours only through a wormhole. However, as we shall see, it is connected to our region through imaginary time. The null surface from bottom left to top right is the boundary of the region from which one can escape to the infinity on the right. Thus, it is the future event horizon, the epithet future being added to distinguish it from the past event horizon which goes from bottom right to top left.
Figure 3.4 The Carter-Penrose diagram of an eternal Schwarzschild black hole.
Let us now return to the Schwarzschild metric in the original r and t coordinates. If one puts t = i τ one gets a positive definite metric. I shall refer to such positive definite metrics as Euclidean, even though they may be curved. In the Euclidean-Schwarzschild metric there is again an apparent singularity at r = 2M. However, one can define a new radial coordinate x to be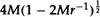 
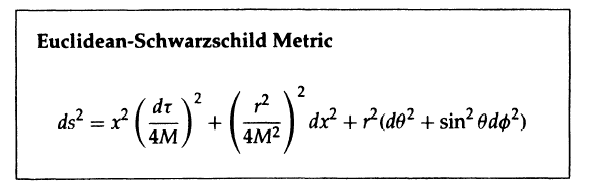
Figure 3.5 The Euclidean-Schwarzschild solution, in which r is identified periodically.
The metric in the x - τ plane then becomes like the origin of polar coordinates if one identifies the coordinate r with period 8πM. Similarly, other Euclidean black hole metrics will have apparent singularities on their horizons that can be removed by identifying the imaginary time coordinate with period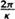 
(fig. 3.5).
So what is the significance of having imaginary time identified with some period β? To see this, consider the amplitude to go from some field configuration ø1 the surface t1 to a configuration ø2 on the surface t2. This will be given by the matrix element of e-iH(t2-t1). However, one can also represent this amplitude as a path integral over all fields ø between t1 and t2 that agree with the given fields ø1 and ø2 on the two surfaces (fig. 3.6).
One now chooses the time separation (t2 - t1) to be pure imaginary and equal to β (fig. 3.7). One also puts the initial field ø1 equal to the final field ø2 and sums over a complete basis of states øn. On the left one has the expectation value of e-βH summed over all states. This is just the thermodynamic partition function Z at the temperature T = β-1
On the right hand of the equation one has a path integral. One puts ø1 = ø2 and sums over all field configurations øn. This means that effectively one is doing the path integral over all fields ø on a spacetime that is identified periodically in the imaginary time direction with period β. Thus the partition function for the field ø at temperature T is given by a path integral over all fields on a Euclidean spacetime. This spacetime is periodic in the imaginary time direction with period β= T-1.
Figure 3.6 The amplitude to go from the state ø1 at t1 to ø2 at t2.
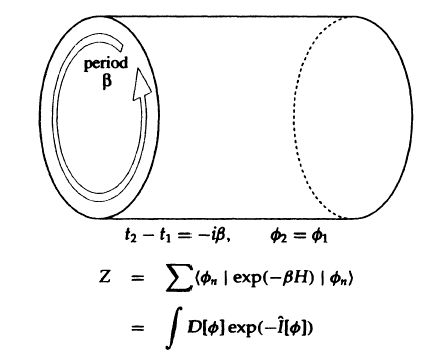
Figure 3.7 The partition function at temperature T is given by the path integral over all fields on a Euclidean spacetime with period β = T-1 in the imaginary time direction.
If one does the path integral in flat spacetime identified with period β in the imaginary time direction, one gets the usual result for the partition function of black body radiation. However, as we have just seen, the Euclidean-Schwarzschild solution is also periodic in imaginary time with period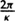 
. This means that fields on the Schwarzschild background will behave as if they were in a thermal state with temperature .
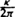The periodicity in imaginary time explained why the messy calculation of frequency mixing led to radiation that was exactly thermal. However, this derivation avoided the problem of the very high frequencies that take part in the frequency mixing approach. It can also be applied when there are interactions between the quantum fields on the background. The fact that the path integral is on a periodic background implies that all physical quantities such as expectation values will be thermal. This would have been very difficult to establish in the frequency mixing approach.
One can extend these interactions to include interactions with the gravitational field itself. One starts with a background metric g0 such as the Euclidean-Schwarzschild metric that is a solution of the classical field equations. One can then expand the action I in a power series in the perturbations δg about g0:
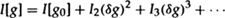
The linear term vanishes because the background is a solution of the field equations. The quadratic term can be regarded as describing gravitons on the background, while the cubic and higher terms describe interactions between the gravitons. The path integral over the quadratic terms is finite. There are nonrenormalizable divergences at two loops in pure gravity, but these cancel with the fermions in supergravity theories. It is not known whether supergravity theories have divergences at three loops or higher because no one has been brave or foolhardy enough to try the calculation. Some recent work indicates that they may be finite to all orders. But even if there are higher loop divergences they will make very little difference except when the background is curved on the scale of the Planck length, 10-33 cm.
More interesting than the higher-order terms is the zeroth order term, the action of the background metric g0:
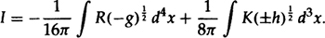
The usual Einstein-Hilbert action for general relativity is the volume integral of the scalar curvature R. This is zero for vacuum solutions, so one might think that the action of the Euclidean-Schwarzschild solution was zero. However, there is also a surface term in the action proportional to the integral of K, the trace of the second fundamental form of the boundary surface. When one includes this and subtracts off the surface term for flat space, one finds that the action of the Euclidean-Schwarzschild metric is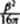 
, where β is the period in imaginary time at infinity. Thus the dominant contribution to the path integral for the partition function Z is 
:
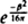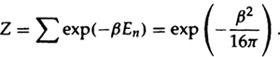
If one differentiates log Z with respect to the period β, one gets the expectation value of the energy or, in other words, the mass:
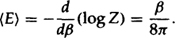
So this gives the mass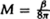 
. This confirms the relation between the mass and the period, or inverse temperature, that we already knew. However, one can go further. By standard thermodynamic arguments, the log of the partition function is equal to minus the free energy F divided by the temperature T:
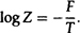
Figure 3.8 The boundary at infinity in the Euclidean-Schwarzschild solution.
And the free energy is the mass or energy plus the temperature times the entropy S:
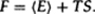
Putting all this together one sees that the action of the black hole gives an entropy of 4πM2:
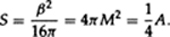
This is exactly what is required to make the laws of black holes the same as the laws of thermodynamics.
Why does one get this intrinsic gravitational entropy which has no parallel in other quantum field theories? The reason is gravity allows different topologies for the spacetime manifold. In the case we are considering, the Euclidean-Schwarzschild solution has a boundary at infinity that has topology S2 × S1. The S2 is a large spacelike two-sphere at infinity and the S1 corresponds to the imaginary time direction which is identified periodically (fig. 3.8). One can fill in this boundary with metrics of at least two different topologies. One of course is the Euclidean-Schwarzschild metric. This has topology R2 × S2, that is, the Euclidean two-plane times a two-sphere. The other is R3 × Sl, the topology of Euclidean flat space periodically identified in the imaginary time direction. These two topologies have different Euler numbers. The Euler number of periodically identified flat space is zero, while that of the Euclidean-Schwarzschild solution is two. The significance of this is as follows: on the topology of periodically identified flat space, one can find a periodic time function τ whose gradient is nowhere zero and which agrees with the imaginary time coordinate on the boundary at infinity. One can then work out the action of the region between two surfaces τ1 and τ2. There will be two contributions to the action, a volume integral over the matter Lagrangian plus the Einstein-Hilbert Lagrangian and a surface term. If the solution is time independent, the surface term over τ =τ1 will cancel with the surface term over τ = τ2. Thus the only net contribution to the surface term comes from the boundary at infinity. This gives half the mass times the imaginary time interval (τ2 - τ1). If the mass is nonzero there must be nonzero matter fields to create the mass. One can show that the volume integral over the matter Lagrangian plus the Einstein-Hilbert Lagrangian also gives ½M(τ2 — τ1). Thus the total action is M(τ2 — τ1) (fig. 3.9). If one puts this contribution to the log of the partition function into the thermodynamic formulae, one finds the expectation value of the energy to be the mass, as one would expect. However, the entropy contributed by the background field will be zero.
Figure 3.9 The action of periodically identified Euclidean flat space = M(τ2-τ1).
Total action including corner contribution = M(τ2 — τ1)
Total action without corner contribution = -½M(τ2 — τ1)
Figure 3.10 The total action for the Euclidean-Schwarzschild solution = ½M(τ2- τ1), as we don’t include the corner contribution from r= 2M.
The situation is different, however, with the Euclidean-Schwarzschild solution. Because the Euler number is two rather than zero, one can’t find a time function τ whose gradient is everywhere nonzero. The best one can do is choose the imaginary time coordinate of the Schwarzschild solution. This has a fixed two-sphere at the horizon, where τ behaves like an angular coordinate. If one now works out the action between two surfaces of constant τ, the volume integral vanishes because there are no matter fields and the scalar curvature is zero. The trace K surface term at infinity again gives ½M(τ2 - τ1). However, there is now another surface term at the horizon where the τ1 and τ2 surfaces meet in a corner. One can evaluate this surface term and find that it also is equal to ½M(τ2 — τ1)(fig. 3.10). Thus the total action for the region between τ1 and τ2 is M(τ2 — τ1). If one used this action with τ2 — τ1 = β one would find that the entropy was zero. However, when one looks at the action of the Euclidean-Schwarzschild solution from a four-dimensional point of view rather than a 3 + 1, there is no reason to include a surface term on the horizon, because the metric is regular there. Leaving out the surface term on the horizon reduces the action by one quarter the area of the horizon, which is just the intrinsic gravitational entropy of the black hole.
The fact that the entropy of black holes is connected with a topological invariant, the Euler number, is a strong argument that it will remain even if we have to go to a more fundamental theory. This idea is anathema to most particle physicists, who are a very conservative lot and want to make everything like the Yang-Mills theory. They agree that the radiation from black holes seems to be thermal and independent of how the hole was formed if the hole is large compared to the Planck length. But they would claim that when the black hole loses mass and gets down to the Planck size, quantum general relativity will break down and all bets will be off. However, I shall describe a thought experiment with black holes in which information seems to be lost, yet the curvature outside the horizons always remains small.
It has been known for some time that one can create pairs of positively and negatively charged particles in a strong electric field. One way of looking at this is to note that in flat Euclidean space a particle of charge q such as an electron would move in a circle in a uniform electric field E. One can analytically continue this motion from the imaginary time τ to real time t. One gets a pair of positively and negatively charged particles accelerating away from each other pulled apart by the electric field (fig. 3.11).
The process of pair creation is described by chopping the two diagrams in half along the t = 0 or τ = 0 lines. One then joins the upper half of the Minkowski space diagram to the lower half of the Euclidean space diagram (fig. 3.12). This gives a picture in which the positively and negatively charged particles are really the same particle. It tunnels through Euclidean space to get from one Minkowski space world line to the other. To a first approximation the probability for pair creation is e-l, where
Figure 3.11 In Euclidean space, an electron moves on a circle in an electric field. In Minkowski space, we get a pair of oppositely charged particles accelerating away from each other.
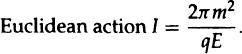
Pair creation by strong electric fields has been observed experimentally and the rate agrees with these estimates.
Black holes can also carry electric charges so one might expect that they could also be pair created. However, the rate would be tiny compared to that for electron-positron pairs because the mass-to-charge ratio is 1020 times bigger. This means that any electric field would be neutralized by electron-positron pair creation long before there was a significant probability of pair creating black holes. However, there are also black hole solutions with magnetic charges. Such black holes couldn’t be produced by gravitational collapse because there are no magnetically charged elementary particles. But one might expect that they could be pair created in a strong magnetic field. In this case there would be no competition from ordinary particle creation because ordinary particles do not carry magnetic charges. So the magnetic field could become strong enough that there was a significant chance of creating a pair of magnetically charged black holes.
Figure 3.12 Pair creation is described by joining half the Euclidean diagram to half the Minkowski diagram.
In 1976 Ernst found a solution that represented two magnetically charged black holes accelerating away from each other in a magnetic field (fig. 3.13). If one analytically continues it to imaginary time, one has a picture very like that of the electron pair creation (fig. 3.14). The black hole moves on a circle in a curved Euclidean space just like the electron moves in a circle in flat Euclidean space. There is a complication in the black hole case, because the imaginary time coordinate is periodic about the horizon of the black hole as well as about the center of the circle on which the black hole moves. One has to adjust the mass-to-charge ratio of the black hole to make these periods equal. Physically this means that one chooses the parameters of the black hole so that the temperature of the black hole is equal to the temperature it sees because it is accelerating. The temperature of a magnetically charged black hole tends to zero as the charge tends to the mass in Planck units. Thus for weak magnetic fields, and hence low acceleration, one can always match the periods.
Figure 3.13 A pair of oppositely charged black holes accelerating away from each other in a magnetic field.
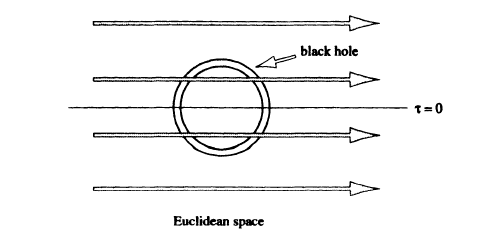
Figure 3.14 A charged black hole moving on a circle in Euclidean space.
As in the case of pair creation of electrons, one can describe pair creation of black holes by joining the lower half of the imaginary time Euclidean solution to the upper half of the real time Lorentzian solution (fig. 3.15). One can think of the black hole as tunneling through the Euclidean region and emerging as a pair of oppositely charged black holes that accelerate away from each other pulled apart by the magnetic field. The accelerating black hole solution is not asymptotically flat because it tends to a uniform magnetic field at infinity. But one can nevertheless use it to estimate the rate of pair creation of black holes in a local region of magnetic field. One could imagine that after being created, the black holes move far apart into regions without magnetic field. One could then treat each black hole separately as a black hole in asymptotically flat space. One could throw an arbitrarily large amount of matter and information into each hole. The holes would then radiate and lose mass. However, they couldn’t lose magnetic charge because there are no magnetically charged particles. Thus they would eventually get back to their original state with the mass slightly bigger than the charge. One could then bring the two holes back together again and let them annihilate each other. The annihilation process can be regarded as the time reverse of the pair creation. Thus it is represented by the top half of the Euclidean solution joined to the bottom half of the Lorentzian solution. In between the pair creation and the annihilation, one can have a long Lorentzian period in which the black holes move far apart, accrete matter, radiate, and then come back together again. But the topology of the gravitational field will be the topology of the Euclidean-Ernst solution. This is S2 × S2 minus a point (fig. 3.16).
Figure 3.15 Tunneling to produce a pair of black holes is also described by joining half the Euclidean diagram to half the Lorentzian diagram.
Figure 3.16 A pair of black holes are produced by tunneling and eventually annihilated again by tunneling.
One might worry that the generalized second law of thermodynamics would be violated when the black holes annihilated because the black hole horizon area would have disappeared. However, it turns out that the area of the acceleration horizon in the Ernst solution is reduced from the area it would have if there were no pair creation. This is a rather delicate calculation because the area of the acceleration horizon is infinite in both cases. Nevertheless, there is a well-defined sense in which their difference is finite and equal to the black hole horizon area plus the difference in the action of the solutions with and without pair creation. This can be understood as saying that pair creation is a zero energy process; the Hamiltonian with pair creation is the same as the Hamiltonian without. I’m very grateful to Simon Ross and Gary Horowitz for calculating this reduction just in time for this lecture. It is miracles like this—and I mean the result, not that they got it—that convince me that black hole thermodynamics can’t just be a low energy approximation. I believe that gravitational entropy won’t disappear even if we have to go to a more fundamental theory of quantum gravity.
One can see from this thought experiment that one gets intrinsic gravitational entropy and loss of information when the topology of spacetime is different from that of flat Minkowski space. If the black holes that are pair created are large compared to the Planck size, the curvature outside the horizons will be everywhere small compared to the Planck scale. This means that the approximation I have made of ignoring cubic and higher terms in the perturbations should be good. Thus the conclusion that information can be lost in black holes should be reliable.
If information is lost in macroscopic black holes it should also be lost in processes in which microscopic, virtual black holes appear because of quantum fluctuations of the metric. One could imagine that particles and information could fall into these holes and get lost. Maybe that is where all those odd socks went. Quantities like energy and electric charge that are coupled to gauge fields would be conserved, but other information and global charge would be lost. This would have far-reaching implications for quantum theory.
It is normally assumed that a system in a pure quantum state evolves in a unitary way through a succession of pure quantum states. But if there is loss of information through the appearance and disappearance of black holes, there can’t be a unitary evolution. Instead, the loss of information will mean that the final state after the black holes have disappeared will be what is called a mixed quantum state. This can be regarded as an ensemble of different pure quantum states, each with its own probability. But because it is not with certainty in any one state, one cannot reduce the probability of the final state to zero by interfering with any quantum state. This means that gravity introduces a new level of unpredictability into physics over and above the uncertainty usually associated with quantum theory. I shall show in the next lecture (chapter 5) that we may have already observed this extra uncertainty. It means an end to the hope of scientific determinism, that we could predict the future with certainty. It seems God still has a few tricks up his sleeve (fig. 3.17).
Figure 3.17
