© Springer Nature Switzerland AG 2019
J. L. BellThe Continuous, the Discrete and the Infinitesimal in Philosophy and MathematicsThe Western Ontario Series in Philosophy of ScienceA Series of Books in Philosophy of Science, Methodology, Epistemology, Logic, History of Science, and Related Fields82https://doi.org/10.1007/978-3-030-18707-1_8

8. Nonstandard Analysis

John L. Bell1 
(1)
Department of Philosophy, University of Western Ontario, London, ON, Canada
 
Once the continuum had been provided with a set-theoretic foundation, the use of the infinitesimal in mathematical analysis was largely abandoned.1 And so the situation remained for a number of years. The first signs of a revival of the infinitesimal approach to analysis surfaced in 1958 with a paper by A. H. Laugwitz and C. Schmieden.2 But the major breakthrough came in 1960 when it occurred to the mathematical logician Abraham Robinson (1918–1974) that “the concepts and methods of contemporary Mathematical Logic are capable of providing a suitable framework for the development of the Differential and Integral Calculus by means of infinitely small and infinitely large numbers.”3 This insight led to the creation of nonstandard analysis (NSA),4 which Robinson regarded as realizing Leibniz’s conception of infinitesimals and infinities as ideal numbers possessing the same properties as ordinary real numbers . In the introduction to his book on the subject he writes:

It is shown in this book that Leibniz’s ideas can be fully vindicated and that they lead to a novel and fruitful approach to classical Analysis and to many other branches of mathematics. The key to our method is provided by the detailed analysis of the relation between mathematical languages and mathematical structures which lies at the bottom of contemporary model theory. 5

After Robinson’s initial insight, a number of ways of presenting nonstandard analysis were developed. Here is a sketch of one of them.6

Starting with the classical real line ℝ, a set-theoretic universe—the standard universe —is first constructed over it: here by such a universe is meant a set U containing ℝ which is closed under the usual set-theoretic operations of union, power set, Cartesian products and subsets. Now write U for the structure (U, ∈), where ∈ is the usual membership relation on U: associated with this is the extension L (U) of the first-order language of set theory to include a name u for each element u of U. Now, using the well-known compactness theorem for first-order logic, U is extended to a new structure ∗ U = (∗ U, ∗∈), called a nonstandard universe, satisfying the following key principle:

Saturation Principle . Let Φ be a collection of L(U)-formulas with exactly one free variable. If Φ is finitely satisfiable in u, that is, if for any finite subset Φ’ of Φ there is an element of U which satisfies all the formulas of Φ’ in U, then there is an element of ∗U which satisfies all the formulas of Φ in ∗ U.

The saturation property expresses the intuitive idea that the nonstandard universe is very rich in comparison to the standard one. Indeed, while there may exist, for each finite subcollection F of a given collection of properties P , an element of U satisfying the members of F in u, there may not necessarily be an element of U satisfying all the members of P . The saturation of ∗ U guarantees the existence of an element of ∗U which satisfies, in ∗ U, all the members of P . For example, suppose the set ℕ of natural numbers is a member of U; for each n ∈ ℕ let P n(x) be the property x ∈ ℕ & n < x. Then clearly, while each finite subcollection of the collection P = {P n: n ∈ ℕ} is satisfiable in u, the whole collection is not. An element of ∗U satisfying all the members of P in ∗u will then be an “natural number” greater than every member of ℕ, that is, an infinite number.

From the saturation property it follows that ∗ U satisfies the important

Transfer Principle . If σ is any sentence of L(U), then σ holds in U if and only if it holds in ∗ U.

The transfer principle may be seen as a version of Leibniz’s continuity principle : it asserts that all first-order properties are preserved in the passage to or “transfer” from the standard to the nonstandard universe .

The members of U are called standard sets, or standard objects; those in ∗U – U nonstandard sets or nonstandard objects: ∗U thus consists of both standard and nonstandard objects. The members of ∗U will also be referred to as ∗-sets or ∗-objects Since U ⊆ ∗U, under this convention every set (object) is also a ∗-set (object). The ∗-members of a ∗-set A are the ∗-objects x for which x ∗∈ A

If A is a standard set, we may consider the collection A ★ —the inflate of A—consisting of all the ∗-members of A: this is not necessarily a standard set nor even a ∗-set. The inflate of a standard set may be regarded as the same set viewed from a nonstandard vantage point. While clearly A ⊆ A ★, A ★ may contain “nonstandard” elements not in A. It can in fact be shown that infinite standard sets always get “inflated” in this way. Using the transfer principle , any function f between standard sets automatically extends to a function—also written f—between their inflates.

Each mathematical structure A= (A, R) has an inflate A ★ = (A ★, R ★). From the transfer principle it follows that A and A ★ have precisely the same first-order properties.

Now suppose that the set ℕ of natural numbers is a member of U. Then so is the set ℝ of real numbers , since each real number may be identified with a set of natural numbers. ℝ may be regarded as an ordered field, and the same is therefore true of its inflate ℝ★.This, the hyperreal line , has precisely the same first-order properties as ℝ. The members of ℝ★ are called hyperreals. A standard hyperreal is then just a real, to which we shall refer for emphasis as a standard real. Since ℝ is infinite, nonstandard hyperreals must exist. The saturation principle implies that there must be an infinite (nonstandard) hyperreal,7 that is, a hyperreal a such that a > n for every n ∈ ℕ. In that case its reciprocal $$ \frac{1}{a} $$ is infinitesimal in the sense of exceeding 0 and yet being smaller than $$ \frac{1}{n+1} $$ for every n ∈ ℕ. In general. we call a hyperreal a infinitesimal if its absolute value |a| is $$ &lt;\frac{1}{n+1} $$ for every n ∈ ℕ. In that case the set I of infinitesimals contains not just 0 but a substantial number (in fact, infinitely many) of other elements. Clearly I is an additive subgroup of ℝ, that is, if a, b ∈ I, then a – b ∈ I.

The members of the inflate ℕ★ of ℕ are called hypernatural numbers . As for the hyperreals, it can be shown that ℕ★ also contains nonstandard elements which must exceed every member of ℕ: these are called infinite hypernatural numbers .

For hyperreals a, b we define a ≈ b and say that a and b are infinitesimally close if a – b ∈ I. This is an equivalence relation on the hyperreal line : for each hyperrreal a we write μ(a) for the equivalence class of a under this relation and call it the monad of a. The monad of a hyperreal a thus consists of all the hyperreals that are infinitesimally close to a: it may thought of as a small cloud centred at a. Note also that μ(0) = I.

A hyperreal a is finite if it is not infinite; this means that |a| < n for some n ∈ ℕ. It is not difficult to show that finiteness is equivalent to the condition of near-standardness: here a hyperreal a is near-standard if a ≈ r for some standard real r.

Much of the usefulness of nonstandard analysis stems from the fact that statements of classical analysis involving limits or the (ε, δ) criterion admit succinct, intuitive translations into statements involving infinitesimals or infinite numbers, in turn enabling comparatively straightforward proofs to be given of classical theorems. Here are some examples of such translations8:

  • Let < s n > be a standard infinite sequence of real numbers and let s be a standard real number . Then s is the limit of < s n > within ℝ, $$ \underset{n\to \infty }{\lim }{s}_n=s $$ in the classical sense, if and only if s n ≈ s for all infinite subscripts n.

  • A standard sequence < s n > converges if and only if s n ≈ s m for all infinite n and m. (Cauchy ’s criterion for convergence .)

Now suppose that f is a real-valued function defined on some open interval (a, b). We have remarked above that f automatically extends to a function—also written f—on (a, b)∗.

  • In order that the standard real number c be the limit of f(x) as x approaches x 0 , $$ \underset{x\to {x}_0}{\lim }f(x)=c $$ , with x 0 a standard real number in (a, b), it is necessary and sufficient that f(x) ≈ f(x 0 ) for all x ≈ x 0.

  • The function f is continuous at a standard real number x 0 in (a, b) if and only if f(x) ≈ f(x 0 ) for all x ≈ x 0. (This is equivalent to saying that f maps the monad of x 0 into the monad of f(x 0 ).

  • In order that the standard number c be the derivative of f ay x 0 it is necessary and sufficient that
    $$ \frac{f(x)-f\left({x}_0\right)}{x-{x}_0}\approx c $$

    for all x ≠ x 0 in the monad of x 0 .

Many other branches of mathematics admit neat and fruitful nonstandard formulations. We end this chapter with a sketch of how topology looks from a nonstandard point of view.

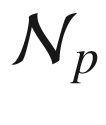We fix a nonempty X ∈ U, and a topology T on X: necessarily T ∈ U. For each point p ∈ X let $$ {\mathcal{N}}_p $$ be the collection of neighbourhoods of p with respect to the topology T. We define the monad of p to be the collection
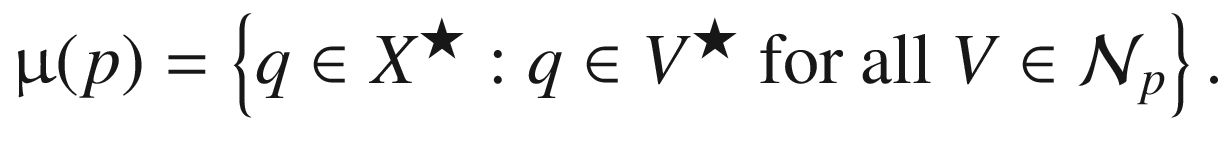
$$ \upmu (p)=\left\{q\in {X}^{\bigstar }:q\in {V}^{\bigstar }\ \mathrm{for}\ \mathrm{all}\ V\in {\mathcal{N}}_p\right\}. $$
The mapping μ thus defined, which maps X into the collection of all subcollections of X ★, is called the monadology of the space X (that is, of the space (X, T)). If q ∈ μ(p) we write q ≈ p and say that q is near p. If q ≈ p for some p ∈ X, we say that q is near-standard . Clearly every point of X is near-standard, but there may be near-standard points of X ★ which are not standard.
One can now proceed to formulate nonstandard characterizations of various standard topological notions. For example:

  • A subset A of X is open if and only if p ∈ A ⇒ μ(p) ⊆ A ★; A is closed if and only if μ(p) ∩ A ★ ≠ ∅ ⇒ p ∈ A. (It follows from this that the topology of a space can be recovered from its monadology .)

  • X is a Hausdorff space if and only if the monads of distinct points are disjoint.

  • X is compact if and only if every point of X ★ is near-standard .

  • Let f: X → Y be a map of X into a topological space Y. Then f is continuous if, for all p ∈ X, q ∈ X ★, q ≈ p ⇒ f(q) ≈ f(p).

Thus f:X → Y is continuous if, for any point p ∈ X, points of X ★ near p are mapped by f to points of Y ★ near f(p). Indeed, “this is what mathematicians always wanted to say about continuity, but didn’t quite know how. In nonstandard analysis, this highly intuitive characterization is at the same time completely rigorous.”9

Finally, it should be pointed out that while the usual models of nonstandard analysis are obtained using highly nonconstructive tools, other methods have been developed for producing such models which are constructively acceptable.10