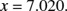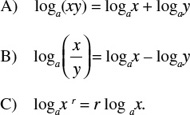
Logarithms were invented to make calculations with large numbers easier by expressing them in terms of their exponents. Given the exponential expression x = by, b ∈ N, b ≠ 1, and b is a positive real number, we can rewrite it in its logarithmic form so that x is in terms of its exponent y, y = logbx. This expression is read as “y is equal to the logarithm to the base b of x.”
If x, y, and a are positive real numbers, a ≠ 1, and r is any real number, then
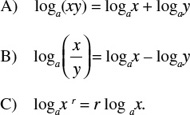
Common logarithms are logarithms with a base of 10. We omit writing the base when working with base 10. That is
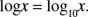
The following formula will enable us to calculate non-common logarithms by using common logarithms.
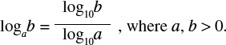
For example, to find the value of log73, we use the above rule to obtain:
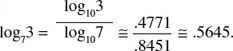
These values can be found by referring to log tables.
The antilogarithm is the number corresponding to a given logarithm. The cologarithm of a positive number is the logarithm of its reciprocal.
The common logarithm of any number is expressible as a combination of two parts:
A) the characteristic, which is the integral part; and
B) the mantissa, which is the decimal part of the number. To find the common logarithm of a positive number:
A) Express the number in scientific notation.
B) Determine the index of the number, which is the characteristic.
C) To find the mantissa, see a table of common logarithms of numbers.
Example: Find the logarithm of 30,700.
Solution: First express 30,700 in scientific notation. 30,700 = 3.07 × 104. Four is the characteristic. To find the mantissa, see a table of common logarithms of numbers. The mantissa is .4871. Thus, log 30,700 = 4 + .4871 = 4.4871.
To find the antilogarithm:
A) Use the logarithm table to find the number that corresponds to that specific mantissa.
B) Rewrite that number in standard form.
C) Use the characteristic as the index for the number in standard form.
Example: Find Antilog 0.8762 − 2.
Solution: Let N = Antilog10 0.8762 − 2. The following relationship between log and antilog exists; logx = a is the equivalent of x = antilog10a. Therefore,
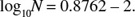
The characteristic is −2. The mantissa is 0.8762. The number that corresponds to this mantissa is 7.52. This number is found from a table of common logarithms, base 10. Therefore,
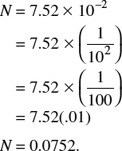
Therefore, N = Antilog100.8762 − 2 = 0.0752.
Problem Solving Examples:
Write 53 = 125 in logarithmic form.
The statement by = x is equivalent to the statement logbx = y, where b is the base and y is the exponent. The latter form is the logarithmic form. Thus, 53 = 125 in logarithmic form is log5125 = 3, where the base is 5 and the logarithm of 125 is 3.
Find log10 100.
The following solution presents two methods for solving the given problem.
Method I. The statement log10 x = y is equivalent to 10y = x; hence, log10 100 = x is equivalent to 10x = 100.
Since 102 = 100, log10 100 = 2.
Method II. Note that 100 = 10 × 10; thus log10 100 = log (10 × 10). Recall: logx (a × b) = logx a + logx b, therefore
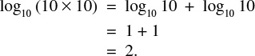
The function f(x) = xn is called a power function in x. An exponential function in x is of the form f(x) = ax. A logarithmic function in x is of the form f(x) = log x.
An equation involving one or more unknowns in an exponent is called an exponential equation. 2x + 6x + 8y+7 = y is an exponential equation in two unknowns.
Figure 12.1 through 12.5 are examples of the graphs of power, exponential, and logarithmic functions.
Figure 12.1 Exponential function
Figure 12.2 Exponential function
Figure 12.3 Power function
Figure 12.4 Exponential and logarithmic functions
Figure 12.5 Logarithmic function
Problem Solving Examples:
If f is the logarithmic function with base 4, find f (4),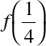 
, and f(8).
Since f is the logarithmic function with base 4, then y = f(x) = log4 x. The values f(4),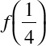 
, and f(8) can be found by replacing x by 4, 
, and 8 in the logarithmic function y = f(x) = log4 x. Hence, f(4) = log44. Let N1 = f(4) = log4 4. By definition, logx a = N is equivalent to xN = a. Therefore, N1 = log4 4 is equivalent to 4N = 4. Since 41 = 4, N1 = 1. Then, N1 = 1 = f(4).
For the second value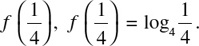 
Let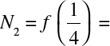 
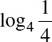. Hence, 
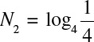is equivalent to 
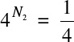. Since 
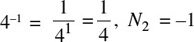. Then, 
.
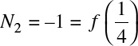For the third value f(8), f(8) = log4 8. Let N 3 = f (8) = log4 8. Hence, N = log4 8 is equivalent to 4N, = 8. Since 4 = 22, N3 = log4 8 is equivalent to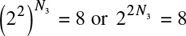 
. Since 23 = 8, 2 N3 = 3. Dividing both sides of the equation 2N3 = 3 by 2:
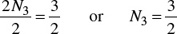
Then,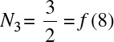 
.
Solve the “exponential” equation: 20.4x = 7.
Taking the log of both sides of the given equation,
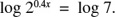
Since logb ya = a logb y, log 20.4x = 0.4x log 2.
Thus, 0.4x log 2 = log 7
or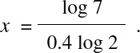 
In a log table we find log 7 = .8451 and log 2 = .3010. Thus,
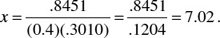
Or, if we wish, we may complete the solution by using logarithms again:
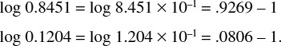
Since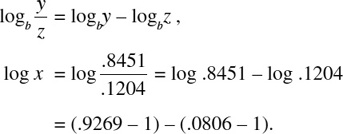 
We look up the mantissa, 0.8463, in a table of common logarithms and find its corresponding number to be 7020. We adjust the decimal point by noting the characteristic 0 of 0.8463 is one less than the number of digits to the left of the decimal point of the number we seek. In this case, therefore, there should be one digit to the left of the decimal point. Hence,
