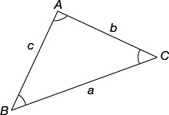
The following results hold for any oblique triangle ABC with sides of length a, b, c opposite to vertices A, B, C, respectively.
Figure 20.1
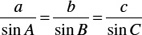
a2 = b2 + c2 − 2bc cos A
b2 = a2 + c2 − 2ac cos B
c2 = a2 + b2 − 2ab cos C
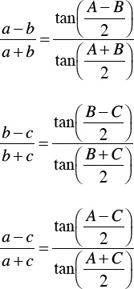
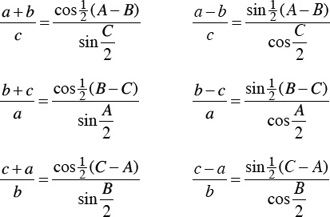
BC = b cos C + c cos B
AC = a cos C + c cos A
AB = a cos B + b cos A
In a 30°– 60° right triangle (Figure 20.2), the hypotenuse is twice the length of the side opposite the 30° angle. The side opposite the 60° angle is equal to the length of the side opposite the 30° angle multiplied by 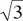 .
.
In an isosceles 45° right triangle (Figure 20.3), the hypotenuse is equal to the length of one of its arms multiplied by 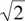 .
.
Figure 20.2
Figure 20.3
The altitude h on the hypotenuse of a right triangle is the mean proportional between the segments of the hypotenuse, also called the geometric mean (Figure 20.4).
Figure 20.4
In a right triangle Δ ABC, the altitude to the hypotenuse, 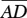 , separates the triangle into two triangles that are similar to each other and to the original triangle (Figure 20.5).
, separates the triangle into two triangles that are similar to each other and to the original triangle (Figure 20.5).
Figure 20.5
The length of the median to the hypotenuse of a right triangle is equal to one-half the length of the hypotenuse (Figure 20.6).
Figure 20.6
In solving triangles, terms such as line of sight, angle of elevation, and angle of depression are often used. These terms are illustrated in Figure 20.7 and 20.8.
Figure 20.7
Figure 20.8
Example: At a point on the ground 40 feet from the foot of a tree, the angle of elevation to the top of the tree is 42°. Find the height of the tree to the nearest foot.
Figure 20.9
Solution: The geometric figure formed is a right triangle (see Figure 20.9). Since the unknown height of the tree is opposite the given angle of elevation, and we are given the side adjacent to this angle, we can solve the problem using the tangent ratio. The tangent is the ratio of the length of the leg opposite the acute angle to the length of the leg adjacent to the acute angle in any right triangle. In this example,

Let x = AT, and consult a standard table of tangents or use your calculator to find that tan 42° = 0.9004. Since BA = 40, we obtain
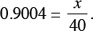
Therefore, 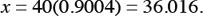 .
.
Therefore, the height of the tree, to the nearest foot, is 36 feet.
The following theorems are often used for finding the area of a triangle.
Theorem: The area of a triangle is given by 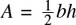 , where b is the length of the base and h is the perpendicular height of the triangle (Figure 20.10).
, where b is the length of the base and h is the perpendicular height of the triangle (Figure 20.10).
Figure 20.10
Theorem: The area of a triangle equals one-half the product of any two adjacent sides and the sine of the included angle (Figure 20.11).
Figure 20.11
Theorem: Triangles that share the same base and have their third vertex on a line parallel to the base have equal areas (Figure 20.12).
Figure 20.12
The areas of two triangles having equal bases have the same ratio as that of their altitudes and vice versa.
The area of a triangle, the length of whose three sides are a, b, and c, is given by the formula

where 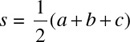 ; the semiperimeter of the triangle. The above formula is commonly referred to as Heron’s formula.
; the semiperimeter of the triangle. The above formula is commonly referred to as Heron’s formula.
The area of an equilateral triangle is given by the formula,
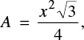
where x is the length of a side of the triangle (Figure 20.13).
Figure 20.13
Theorem: The area of an equilateral triangle equals 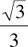 times the square of the altitude of the triangle (Figure 20.14).
times the square of the altitude of the triangle (Figure 20.14).
Figure 20.14
Theorem: A median drawn to a side of a triangle divides the triangle into two triangles of equal area (Figure 20.15).
Figure 20.15
Theorem: The area of an isosceles triangle whose congruent sides have length l, with included angle α is:
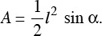
Area is also given by the formula
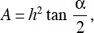
where h is the length of the altitude to the side opposite angle α.
Problem Solving Examples:
 Solve the oblique triangle ABC for side c and the two unknown angles, where a = 20, b = 40, α = 30; and α is the angle between sides b and c.
Solve the oblique triangle ABC for side c and the two unknown angles, where a = 20, b = 40, α = 30; and α is the angle between sides b and c.
Figure 20.16
 If we draw an altitude h from b to c, as in the accompanying diagram, we can find the length of this altitude by trigonometry.
If we draw an altitude h from b to c, as in the accompanying diagram, we can find the length of this altitude by trigonometry.
Figure 20.17

Thus, the triangle must have the altitude as one of its sides; therefore, we have a right triangle with angles 30°, 60°, and 90°. Sides of such right triangles are in proportion 1 : 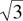 : 2, and the lengths are therefore 20 :
: 2, and the lengths are therefore 20 : 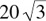 : 40. Hence,
: 40. Hence, 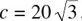 , and the two unknown angles are 60° and 90°.
, and the two unknown angles are 60° and 90°.
 Solve triangle ABC, given a = 30, b = 50, ∠C = 25°.
Solve triangle ABC, given a = 30, b = 50, ∠C = 25°.
Figure 20.18
 Two of the sides of ΔABC and their included angle are given. We wish to find the third side, c. Therefore, use the law of cosines to find c.
Two of the sides of ΔABC and their included angle are given. We wish to find the third side, c. Therefore, use the law of cosines to find c.

Use the law of sines to find one of the remaining angles.
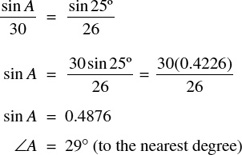
∠B can be found from ∠A and ∠C.

 In triangle ABC, if a = 675, α = 48°36′, find b, c, and β.
In triangle ABC, if a = 675, α = 48°36′, find b, c, and β.
Figure 20.19
 If we wish to work with α, the functions of α involving a and one other side are
If we wish to work with α, the functions of α involving a and one other side are
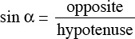
sin α = a/c
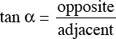
tan α = a/b, and

cot α = b/a. Either of these ratios can be chosen. If the first is chosen, sin α = a/c or c sin α = a and c = a/sin α. Thus,
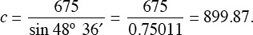
Using tan α = a/b or b = a/tan α, we obtain
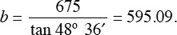
To find β,
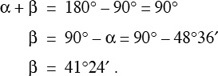
1. In the right triangle below, determine the measure of ∠A and ∠B.
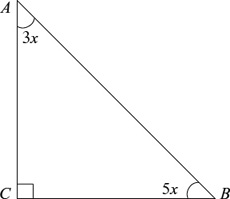
(A) 22.50°, 67.50°
(B) 30.00°, 60.00°
(C) 33.75°, 56.25°
(D) 11.25°, 78.75°
(E) None of the above.
2. In the triangle shown below, cosω is equal to

(A)  .
.
(B) 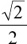 .
.
(C) 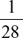 .
.
(D) 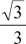 .
.
(E) 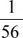 .
.
3. Given the triangle below, what is the value of θ?
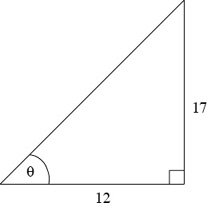
(A) 54.8°
(B) 35.2°
(C) 45.0°
(D) 42.8°
(E) 59.2°
4. In the figure, what is the length of x?
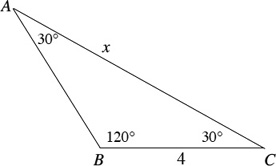
(A) 6.93
(B) 6.52
(C) 6.15
(D) 5.84
(E) 5.66
5. In the right-angled triangle, c is equal to which of the following?
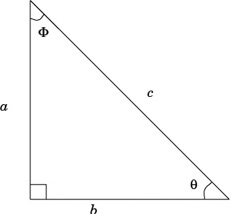
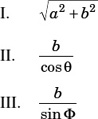
(A) I only.
(B) II only.
(C) III only.
(D) I and III only.
(E) I, II, and III.
6. If α = 63.7°, what is the length of a?
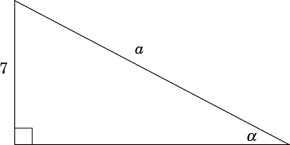
(B) 7.81
(C) 8.70
(D) 0.13
(E) 5.21
7. Evaluate:  .
.
(A) 0.5
(B) −0.5
(C) 0.866
(D) −0.866
(E) Undefined
8. Evaluate 2cos(θ) sin(θ) when θ = 15.
(A) 1.9318
(B) 0.2588
(C) 0.5
(D) −0.2588
(E) −0.5
9. If 0 < θ < 90 and 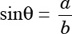 , then tanθ =
, then tanθ =
(A) 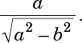
(B) 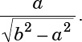
(C) 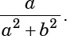
(D) 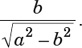
(E) 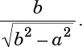
10. if 0° ≤ θ ≤ 45 and 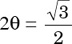 , then (cosθ + sinθ)2 =
, then (cosθ + sinθ)2 =
(A) 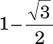 .
.
(B) 1.
(C) 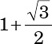 .
.
(D) 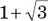 .
.
(E) 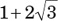 .
.
1. (C)
2. (E)
3. (A)
4. (A)
5. (E)
6. (B)
7. (C)
8. (C)
9. (B)
10. (C)