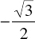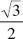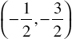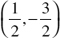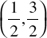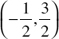Analytic geometry refers to the study of geometric figures using algebraic principles. This approach, commonly referred to as coordinate geometry, has been accredited to a seventeenth-century French mathematician, René Descartes.
Postulate: The points on a straight line can be placed in a one-to-one correspondence with real numbers such that for every point of the line there corresponds a unique real number, and for every real number there corresponds a unique point of the line.
A number scale is a straight line on which distances from a point are numbered in equal units; positively in one direction and negatively in the opposite direction. The origin is the zero point from which all distances are measured.
The Cartesian product of a set X and a set Y is the set of all ordered pairs (x, y) where x belongs to X and y belongs to Y.
The graph of  ×
×  is called the Cartesian coordinate plane (Figure 22.1). Graphically, it consists of a pair of perpendicular lines called coordinate axes, and the plane they lie in. The vertical axis is the y-axis and the horizontal axis is the x-axis. The point of intersection of these two axes is called the origin. It is the zero point of both axes. Furthermore, points to the right of the origin on the x-axis and above the origin on the y-axis represent positive real numbers. The negative numbers are represented similarly below and to the left of the origin. Each element of the set
is called the Cartesian coordinate plane (Figure 22.1). Graphically, it consists of a pair of perpendicular lines called coordinate axes, and the plane they lie in. The vertical axis is the y-axis and the horizontal axis is the x-axis. The point of intersection of these two axes is called the origin. It is the zero point of both axes. Furthermore, points to the right of the origin on the x-axis and above the origin on the y-axis represent positive real numbers. The negative numbers are represented similarly below and to the left of the origin. Each element of the set 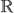 ×
×  is represented by a point on the Cartesian coordinate plane.
is represented by a point on the Cartesian coordinate plane.

Figure 22.1
The abscissa is the x-coordinate of a given point, and the ordinate is the y-coordinate of the given point.
The plane is divided into four regions by the coordinate axes. These regions are numbered from one to four starting from the region where both x and y values are positive and proceeding counterclockwise.
The distance between any two points on a number scale is the absolute value of the difference between the corresponding numbers.
Theorem 1: For any two points A and B with coordinates (xA, yA) and (xB, yB) respectively, the distance between A and B is
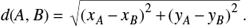
This is commonly known as the distance formula (graphed in Figure 22.2).
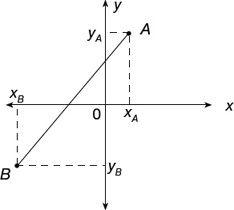
Figure 22.2
Theorem 2: Given a line segment with endpoints (xA, yA) and (xB, yB), the coordinates of the midpoint of the line segment are (xm, ym) where

This is commonly known as the midpoint formula (graphed in Figure 22.3).
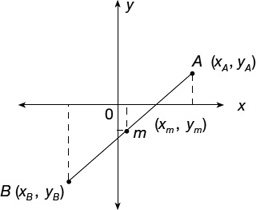
Figure 22.3
The distance d between a given point A with coordinates (xA, yA) and a line l defined as ax + by + c = 0 is given by the following formula:
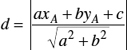
A parabola is the locus of points whose distance from a fixed line, called the directrix, and a fixed point, called the focus, is equal (Figure 22.4).
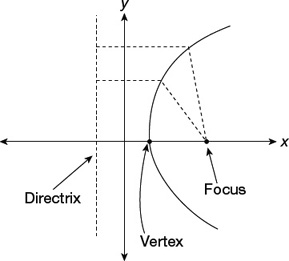
Figure 22.4
An ellipse is the locus of points, the sum of whose distances from two fixed points (foci) is a constant (Figure 22.5).
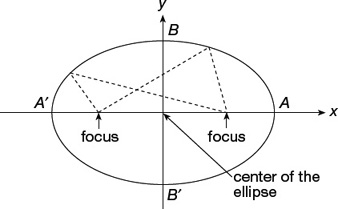
Figure 22.5
The line segment BB′ is called the minor axis and the line segment AA′ is called the major axis.
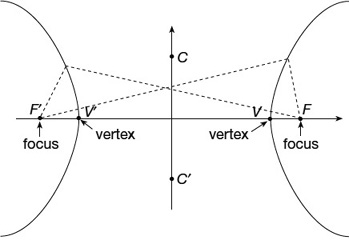
Figure 22.6
A hyperbola is the locus of all points the difference of whose distance from two fixed points (foci) is a constant (Figure 22.6).
The line segment VV′ joining the two vertices is the hyperbola’s transverse axis and the segment CC′ is the conjugate axis.
The equation of a circle centered at (x0, y0) with radius r is given by: (x − x0)2 + (y − y0)2 = r2, where x0 and y0 are the coordinates of the center of the circle and r is the length of the radius (Figure 22.7).
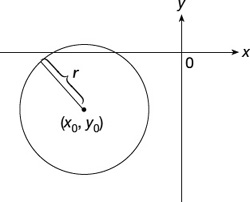
Figure 22.7
The equation of a parabola with vertex V at (x0, y0) and directrix d at x = x0 − P is
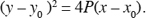
Note that the focus is then at (x0 + P, y0) (Figures 22.8 and 22.9).
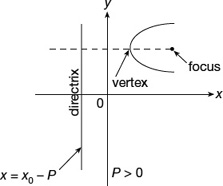
Figure 22.8
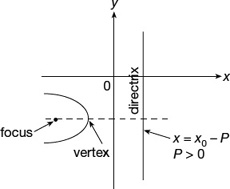
Figure 22.9
The equation of a parabola with vertex, V(x0, y0) (Figure 22.10), and directrix, d, y = y0 − p (Figure 22.11) is
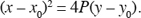
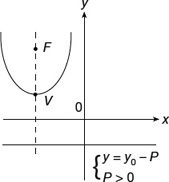
Figure 22.10
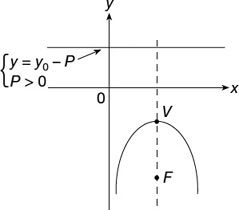
Figure 22.11
Theorem: The equation of an ellipse with center C(x0, y0) and the major and minor axes parallel respectively to the x-axis and y-axis are given below (Figures 22.12, 22.13, and 22.14):
A) 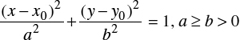
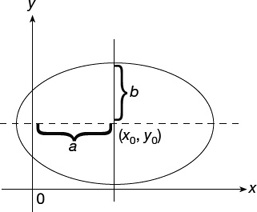
Figure 22.12
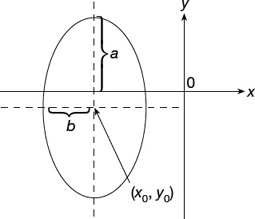
Figure 22.13
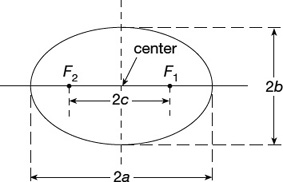
Figure 22.14
B) 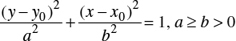
where the length of the major axis is 2a and the length of the minor axis is 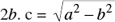 is half the distance between the two foci.
is half the distance between the two foci.
Theorem: The equation of a hyperbola with center C(x0, y0), with transverse axis parallel to the x-axis is:
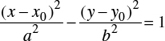
where the length of the transverse axis is 2a and the length of the conjugate axis is 2b (Figure 22.15).
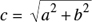 is half the distance between the two foci F1 and F2 (Figure 22.16).
is half the distance between the two foci F1 and F2 (Figure 22.16).
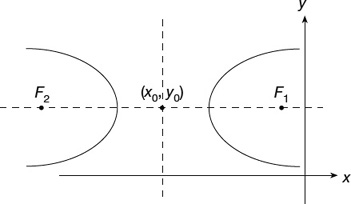
Figure 22.15
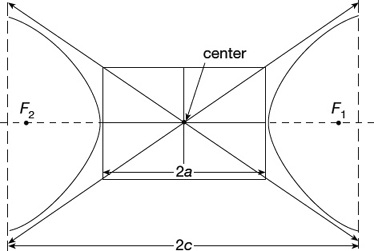
Figure 22.16
A point is expressed in polar form, (r, θ), as a distance and an angle instead of an x-coordinate and a y-coordinate. Draw a line from the point to the origin. r is the length of that line θ is the angle the line makes positively (counterclockwise) with the positive x-axis (Figure 22.17).
For example (5, 60°) represents the point five units from the origin and 60° around from the positive x-axis.
To change rectangular to polar coordinates:
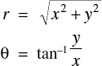
To change polar to rectangular coordinates:
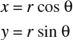
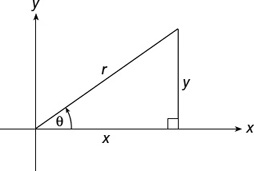
Figure 22.17
Problem Solving Examples:
 A line segment AB is
A line segment AB is 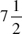 in. long. Locate the point C between A and B so that AC is
in. long. Locate the point C between A and B so that AC is  in. shorter than twice CB.
in. shorter than twice CB.
 See Figure 22.18.
See Figure 22.18.
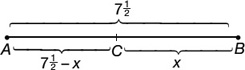
Figure 22.18
Let x = the length of CB in inches. Then 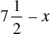 is the length of AC.
is the length of AC.
We are told AC is  in. shorter than twice CB. Thus, AC =
in. shorter than twice CB. Thus, AC = 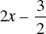 . Therefore:
. Therefore:
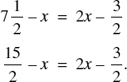
Multiplying both members by 2,
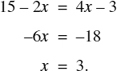
Therefore, CB = 3 and 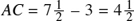 . Hence, C is located
. Hence, C is located 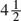 inches from A and 3 in. from B.
inches from A and 3 in. from B.
 What is the distance between the points P(−4, 5) and Q(1, −7)?
What is the distance between the points P(−4, 5) and Q(1, −7)?
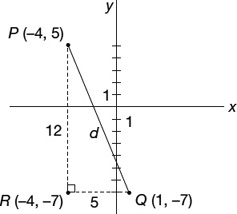
Figure 22.19
 Observe Figure 22.19. P being four units to the left of the Y-axis and Q being one unit to the right, the horizontal distance between P and Q is five units. Similarly, the vertical distance between P and Q is 12 units. The Pythagorean Theorem states that the sum of the squares of the legs of a right triangle equals the square of the hypotenuse. Thus, in right triangle PQR,
Observe Figure 22.19. P being four units to the left of the Y-axis and Q being one unit to the right, the horizontal distance between P and Q is five units. Similarly, the vertical distance between P and Q is 12 units. The Pythagorean Theorem states that the sum of the squares of the legs of a right triangle equals the square of the hypotenuse. Thus, in right triangle PQR,
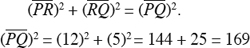
Taking the square root of both sides, 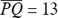 . Thus, the distance between (−4, 5) and (1, −7),
. Thus, the distance between (−4, 5) and (1, −7), 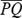 , is 13.
, is 13.
1. What is the distance between the point (5,4) and the line whose equation is 2x + y − 3 = 0?
(A) 7.14
(B) 6.35
(C) 5.48
(D) 4.92
(E) 3.77
2. What is the distance between the foci of an ellipse whose equation
is 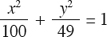 ?
?
(A) 14.28
(B) 13.64
(C) 12.13
(D) 11.72
(E) 10.35
3. Evaluate 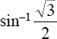 .
.
(A) 0.866
(B) 60°
(C) 1.155
(D) 0.6
(E) −60°
4. Find sin−1 0.4075.
(A) 24° 3′
(B) −66° 57′
(C) 66− 57′
(D) −24′ 3′
(E) Not given here.
5. What is the value of 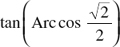 ?
?
(A) 45°
(B) .45
(C) .707
(D) 1
(E) −0.707
6. Evaluate 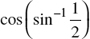 .
.
(A) .500
(B) −0.866
(C) 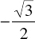
(D) 60°
(E) 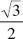
7. Find the midpoint of the segment from R(−3, 5) to S(2, −8).
(A) 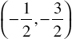
(B) 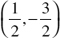
(C) 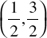
(D) 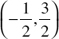
(E) Not given here.
8. Find the distance between P(5, 3) and Q(8, 7).
(A) 25
(B) 5
(C) 4
(D) 3
(E) 16
9. Which of the following is an equation of a circle with radius r and with center at point C (j, −k)?
(A) (x − j)2 + (y − k)2 = r
(B) (x − j)2 + (y + k)2 = r2
(C) (x − j)2 + (y + k)2 = r2
(D) (x + j)2 + (y + k)2 = r2
(E) (x + j)2 + (y − k)2 = r2
10. Write the equation of a circle with center at (−1, 3) and radius 9.
(A) (x + 1)2 + (y − 3)2 = 81
(B) (x − 1)2 + (y + 3)2 = 9
(C) (x − 1)2 + (y − 3)2 = 81
(D) (x + 1)2 + (y + 3)2 = 81
(E) (x + 1)2 + (y − 3)2 = 9
1. (D)
2. (A)
3. (B)
4. (A)
5. (D)
6. (E)
7. (A)
8. (B)
9. (C)
10. (A)
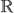 ×
× 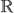 is called the Cartesian coordinate plane (Figure 22.1). Graphically, it consists of a pair of perpendicular lines called coordinate axes, and the plane they lie in. The vertical axis is the y-axis and the horizontal axis is the x-axis. The point of intersection of these two axes is called the origin. It is the zero point of both axes. Furthermore, points to the right of the origin on the x-axis and above the origin on the y-axis represent positive real numbers. The negative numbers are represented similarly below and to the left of the origin. Each element of the set
is called the Cartesian coordinate plane (Figure 22.1). Graphically, it consists of a pair of perpendicular lines called coordinate axes, and the plane they lie in. The vertical axis is the y-axis and the horizontal axis is the x-axis. The point of intersection of these two axes is called the origin. It is the zero point of both axes. Furthermore, points to the right of the origin on the x-axis and above the origin on the y-axis represent positive real numbers. The negative numbers are represented similarly below and to the left of the origin. Each element of the set 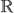 ×
× 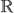 is represented by a point on the Cartesian coordinate plane.
is represented by a point on the Cartesian coordinate plane.
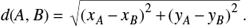



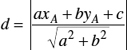




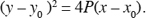


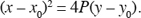


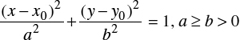



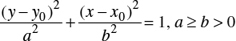
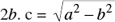 is half the distance between the two foci.
is half the distance between the two foci.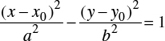
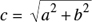 is half the distance between the two foci
is half the distance between the two foci 

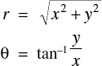
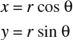

 A line segment
A line segment 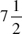 in. long. Locate the point
in. long. Locate the point  in. shorter than twice
in. shorter than twice  See
See 
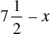 is the length of
is the length of  in. shorter than twice
in. shorter than twice 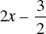 . Therefore:
. Therefore: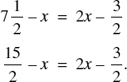
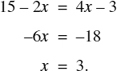
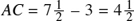 . Hence,
. Hence, 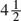 inches from
inches from 
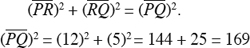
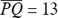 . Thus, the distance between (−4, 5) and (1, −7),
. Thus, the distance between (−4, 5) and (1, −7), 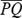 , is 13.
, is 13.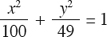 ?
?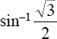 .
.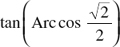 ?
?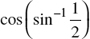 .
.