
Albert Einstein, who had a way with words as well as with equations, was the one who stuck quantum mechanics with the label it has been unable to shake ever since: spukhaft, usually translated from German to English as “spooky.” If nothing else, that’s the impression we get from most public discussions of quantum mechanics. We’re told that it’s a part of physics that is unavoidably mystifying, weird, bizarre, unknowable, strange, baffling. Spooky.
Inscrutability can be alluring. Like a mysterious, sexy stranger, quantum mechanics tempts us into projecting all sorts of qualities and capacities onto it, whether they are there or not. A brief search for books with “quantum” in the title reveals the following list of purported applications:
Quantum Success
Quantum Leadership
Quantum Consciousness
Quantum Touch
Quantum Eating
Quantum Psychology
Quantum Mind
Quantum Glory
Quantum Forgiveness
Quantum Theology
Quantum Happiness
Quantum Poetry
Quantum Teaching
Quantum Faith
Quantum Love
For a branch of physics that is often described as only being relevant to microscopic processes involving subatomic particles, that’s a pretty impressive résumé.
To be fair, quantum mechanics—or “quantum physics,” or “quantum theory,” the labels are all interchangeable—is not only relevant to microscopic processes. It describes the whole world, from you and me to stars and galaxies, from the centers of black holes to the beginning of the universe. But it is only when we look at the world in extreme close-up that the apparent weirdness of quantum phenomena becomes unavoidable.
One of the themes in this book is that quantum mechanics doesn’t deserve the connotation of spookiness, in the sense of some ineffable mystery that it is beyond the human mind to comprehend. Quantum mechanics is amazing; it is novel, profound, mind-stretching, and a very different view of reality from what we’re used to. Science is like that sometimes. But if the subject seems difficult or puzzling, the scientific response is to solve the puzzle, not to pretend it’s not there. There’s every reason to think we can do that for quantum mechanics just like any other physical theory.
Many presentations of quantum mechanics follow a typical pattern. First, they point to some counterintuitive quantum phenomenon. Next, they express bafflement that the world can possibly be that way, and despair of it making sense. Finally (if you’re lucky), they attempt some sort of explanation.
Our theme is prizing clarity over mystery, so I don’t want to adopt that strategy. I want to present quantum mechanics in a way that will make it maximally understandable right from the start. It will still seem strange, but that’s the nature of the beast. What it won’t seem, hopefully, is inexplicable or unintelligible.
We will make no effort to follow historical order. In this chapter we’ll look at the basic experimental facts that force quantum mechanics upon us, and in the next we’ll quickly sketch the Many-Worlds approach to making sense of those observations. Only in the chapter after that will we offer a semi-historical account of the discoveries that led people to contemplate such a dramatically new kind of physics in the first place. Then we’ll hammer home exactly how dramatic some of the implications of quantum mechanics really are.
With all that in place, over the rest of the book we can set about the fun task of seeing where all this leads, demystifying the most striking features of quantum reality.

Physics is one of the most basic sciences, indeed one of the most basic human endeavors. We look around the world, we see it is full of stuff. What is that stuff, and how does it behave?
These are questions that have been asked ever since people started asking questions. In ancient Greece, physics was thought of as the general study of change and motion, of both living and nonliving matter. Aristotle spoke a vocabulary of tendencies, purposes, and causes. How an entity moves and changes can be explained by reference to its inner nature and to external powers acting upon it. Typical objects, for example, might by nature be at rest; in order for them to move, it is necessary that something be causing that motion.
All of this changed thanks to a clever chap named Isaac Newton. In 1687 he published Principia Mathematica, the most important work in the history of physics. It was there that he laid the groundwork for what we now call “classical” or simply “Newtonian” mechanics. Newton blew away any dusty talk of natures and purposes, revealing what lay underneath: a crisp, rigorous mathematical formalism with which teachers continue to torment students to this very day.
Whatever memory you may have of high-school or college homework assignments dealing with pendulums and inclined planes, the basic ideas of classical mechanics are pretty simple. Consider an object such as a rock. Ignore everything about the rock that a geologist might consider interesting, such as its color and composition. Put aside the possibility that the basic structure of the rock might change, for example, if you smashed it to pieces with a hammer. Reduce your mental image of the rock down to its most abstract form: the rock is an object, and that object has a location in space, and that location changes with time.
Classical mechanics tells us precisely how the position of the rock changes with time. We’re very used to that by now, so it’s worth reflecting on how impressive this is. Newton doesn’t hand us some vague platitudes about the general tendency of rocks to move more or less in this or that fashion. He gives us exact, unbreakable rules for how everything in the universe moves in response to everything else—rules that can be used to catch baseballs or land rovers on Mars.
Here’s how it works. At any one moment, the rock will have a position and also a velocity, a rate at which it’s moving. According to Newton, if no forces act on the rock, it will continue to move in a straight line at constant velocity, for all time. (Already this is a major departure from Aristotle, who would have told you that objects need to be constantly pushed if they are to be kept in motion.) If a force does act on the rock, it will cause acceleration—some change in the velocity of the rock, which might make it go faster, or slower, or merely alter its direction—in direct proportion to how much force is applied.
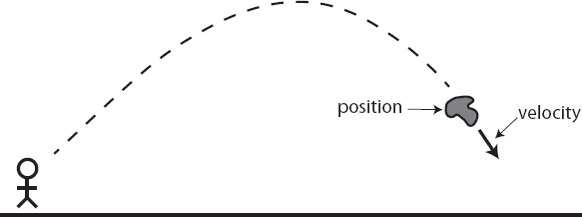
That’s basically it. To figure out the entire trajectory of the rock, you need to tell me its position, its velocity, and what forces are acting on it. Newton’s equations tell you the rest. Forces might include the force of gravity, or the force of your hand if you pick up the rock and throw it, or the force from the ground when the rock comes to land. The idea works just as well for billiard balls or rocket ships or planets. The project of physics, within this classical paradigm, consists essentially of figuring out what makes up the stuff of the universe (rocks and so forth) and what forces act on them.
Classical physics provides a straightforward picture of the world, but a number of crucial moves were made along the way to setting it up. Notice that we had to be very specific about what information we required to figure out what would happen to the rock: its position, its velocity, and the forces acting on it. We can think of those forces as being part of the outside world, and the important information about the rock itself as consisting of just its position and velocity. The acceleration of the rock at any moment in time, by contrast, is not something we need to specify; that’s exactly what Newton’s laws allow us to calculate from the position and the velocity.
Together, the position and velocity make up the state of any object in classical mechanics. If we have a system with multiple moving parts, the classical state of that entire system is just a list of the states of each of the individual parts. The air in a normal-sized room will have perhaps 1027 molecules of different types, and the state of that air would be a list of the position and velocity of every one of them. (Strictly speaking, physicists like to use the momentum of each particle, rather than its velocity, but as far as Newtonian mechanics is concerned the momentum is simply the particle’s mass times its velocity.) The set of all possible states that a system could have is known as the phase space of the system.
The French mathematician Pierre-Simon Laplace pointed out a profound implication of the classical mechanics way of thinking. In principle, a vast intellect could know the state of literally every object in the universe, from which it could deduce everything that would happen in the future, as well as everything that had happened in the past. Laplace’s demon is a thought experiment, not a realistic project for an ambitious computer scientist, but the implications of the thought experiment are profound. Newtonian mechanics describes a deterministic, clockwork universe.
The machinery of classical physics is so beautiful and compelling that it seems almost inescapable once you grasp it. Many great minds who came after Newton were convinced that the basic superstructure of physics had been solved, and future progress lay in figuring out exactly what realization of classical physics (which particles, which forces) was the right one to describe the universe as a whole. Even relativity, which was world-transforming in its own way, is a variety of classical mechanics rather than a replacement for it.
Then along came quantum mechanics, and everything changed.

Alongside Newton’s formulation of classical mechanics, the invention of quantum mechanics represents the other great revolution in the history of physics. Unlike anything that had come before, quantum theory didn’t propose a particular physical model within the basic classical framework; it discarded that framework entirely, replacing it with something profoundly different.
The fundamental new element of quantum mechanics, the thing that makes it unequivocally distinct from its classical predecessor, centers on the question of what it means to measure something about a quantum system. What exactly a measurement is, and what happens when we measure something, and what this all tells us about what’s really happening behind the scenes: together, these questions constitute what’s called the measurement problem of quantum mechanics. There is absolutely no consensus within physics or philosophy on how to solve the measurement problem, although there are a number of promising ideas.
Attempts to address the measurement problem have led to the emergence of a field known as the interpretation of quantum mechanics, although the label isn’t very accurate. “Interpretations” are things that we might apply to a work of literature or art, where people might have different ways of thinking about the same basic object. What’s going on in quantum mechanics is something else: a competition between truly distinct scientific theories, incompatible ways of making sense of the physical world. For this reason, modern workers in this field prefer to call it “foundations of quantum mechanics.” The subject of quantum foundations is part of science, not literary criticism.
Nobody ever felt the need to talk about “interpretations of classical mechanics”—classical mechanics is perfectly transparent. There is a mathematical formalism that speaks of positions and velocities and trajectories, and oh, look: there is a rock whose actual motion in the world obeys the predictions of that formalism. There is, in particular, no such thing as a measurement problem in classical mechanics. The state of the system is given by its position and its velocity, and if we want to measure those quantities, we simply do so. Of course, we can measure the system sloppily or crudely, thereby obtaining imprecise results or altering the system itself. But we don’t have to; just by being careful, we can precisely measure everything there is to know about the system without altering it in any noticeable way. Classical mechanics offers a clear and unambiguous relationship between what we see and what the theory describes.
Quantum mechanics, for all its successes, offers no such thing. The enigma at the heart of quantum reality can be summed up in a simple motto: what we see when we look at the world seems to be fundamentally different from what actually is.

Think about electrons, the elementary particles orbiting atomic nuclei, whose interactions are responsible for all of chemistry and hence almost everything interesting around you right now. As we did with the rock, we can ignore some of the electron’s specific properties, like its spin and the fact that it has an electric field. (Really we could just stick with the rock as our example—rocks are quantum systems just as much as electrons are—but switching to a subatomic particle helps us remember that the features distinguishing quantum mechanics only become evident when we consider very tiny objects indeed.)
Unlike in classical mechanics, where the state of a system is described by its position and velocity, the nature of a quantum system is something a bit less concrete. Consider an electron in its natural habitat, orbiting the nucleus of an atom. You might think, from the word “orbit” as well as from the numerous cartoon depictions of atoms you have doubtless been exposed to over the years, that the orbit of an electron is more or less like the orbit of a planet in the solar system. The electron (so you might think) has a location, and a velocity, and as time passes it zips around the central nucleus in a circle or maybe an ellipse.
Quantum mechanics suggests something different. We can measure values of the location or velocity (though not at the same time), and if we are sufficiently careful and talented experimenters we will obtain some answer. But what we’re seeing through such a measurement is not the actual, complete, unvarnished state of the electron. Indeed, the particular measurement outcome we will obtain cannot be predicted with perfect confidence, in a profound departure from the ideas of classical mechanics. The best we can do is to predict the probability of seeing the electron in any particular location or with any particular velocity.
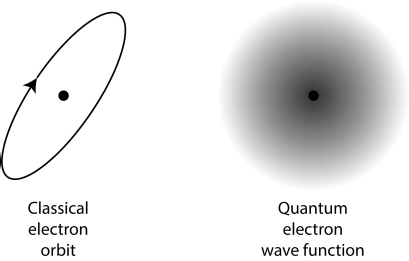
The classical notion of the state of a particle, “its location and its velocity,” is therefore replaced in quantum mechanics by something utterly alien to our everyday experience: a cloud of probability. For an electron in an atom, this cloud is more dense toward the center and thins out as we get farther away. Where the cloud is thickest, the probability of seeing the electron is highest; where it is diluted almost to imperceptibility, the probability of seeing the electron is vanishingly small.
This cloud is often called a wave function, because it can oscillate like a wave, as the most probable measurement outcome changes over time. We usually denote a wave function by Ψ, the Greek letter Psi. For every possible measurement outcome, such as the position of the particle, the wave function assigns a specific number, called the amplitude associated with that outcome. The amplitude that a particle is at some position x0, for example, would be written Ψ(x0).
The probability of getting that outcome when we perform a measurement is given by the amplitude squared.
Probability of a particular outcome = |Amplitude for that outcome|2
This simple relation is called the Born rule, after physicist Max Born.* Part of our task will be to figure out where in the world such a rule came from.
We’re most definitely not saying that there is an electron with some position and velocity, and we just don’t know what those are, so the wave function encapsulates our ignorance about those quantities. In this chapter we’re not saying anything at all about what “is,” only what we observe. In chapters to come, I will pound the table and insist that the wave function is the sum total of reality, and ideas such as the position or the velocity of the electron are merely things we can measure. But not everyone sees things that way, and for the moment we are choosing to don a mask of impartiality.

Let’s place the rules of classical and quantum mechanics side by side to compare them. The state of a classical system is given by the position and velocity of each of its moving parts. To follow its evolution, we imagine something like the following procedure:
Rules of Classical Mechanics
1. Set up the system by fixing a specific position and velocity for each part.
2. Evolve the system using Newton’s laws of motion.
That’s it. The devil is in the details, of course. Some classical systems can have a lot of moving pieces.
In contrast, the rules of standard textbook quantum mechanics come in two parts. In the first part, we have a structure that exactly parallels that of the classical case. Quantum systems are described by wave functions rather than by positions and velocities. Just as Newton’s laws of motion govern the evolution of the state of a system in classical mechanics, there is an equation that governs how wave functions evolve, called Schrödinger’s equation. We can express Schrödinger’s equation in words as: “The rate of change of a wave function is proportional to the energy of the quantum system.” Slightly more specifically, a wave function can represent a number of different possible energies, and the Schrödinger equation says that high-energy parts of the wave function evolve rapidly, while low-energy parts evolve very slowly. Which makes sense, when we think about it.
What matters for our purposes is simply that there is such an equation, one that predicts how wave functions evolve smoothly through time. That evolution is as predictable and inevitable as the way objects move according to Newton’s laws in classical mechanics. Nothing weird is happening yet.
The beginning of the quantum recipe reads something like this:
Rules of Quantum Mechanics (Part One)
1. Set up the system by fixing a specific wave function Ψ.
2. Evolve the system using Schrödinger’s equation.
So far, so good—these parts of quantum mechanics exactly parallel their classical predecessors. But whereas the rules of classical mechanics stop there, the rules of quantum mechanics keep going.
All the extra rules deal with measurement. When you perform a measurement, such as the position or spin of a particle, quantum mechanics says there are only certain possible results you will ever get. You can’t predict which of the results it will be, but you can calculate the probability for each allowed outcome. And after your measurement is done, the wave function collapses to a completely different function, with all of the new probability concentrated on whatever result you just got. So if you measure a quantum system, in general the best you can do is predict probabilities for various outcomes, but if you were to immediately measure the same quantity again, you will always get the same answer—the wave function has collapsed onto that outcome.
Let’s write this out in gory detail.
Rules of Quantum Mechanics (Part Two)
3. There are certain observable quantities we can choose to measure, such as position, and when we do measure them, we obtain definite results.
4. The probability of getting any one particular result can be calculated from the wave function. The wave function associates an amplitude with every possible measurement outcome; the probability for any outcome is the square of that amplitude.
5. Upon measurement, the wave function collapses. However spread out it may have been pre-measurement, afterward it is concentrated on the result we obtained.
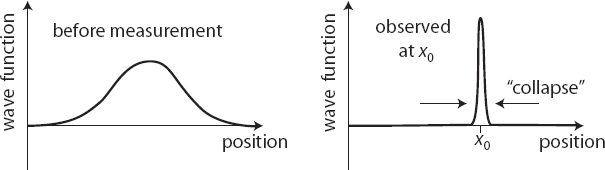
In a modern university curriculum, when physics students are first exposed to quantum mechanics, they are taught some version of these five rules. The ideology associated with this presentation—treat measurements as fundamental, wave functions collapse when they are observed, don’t ask questions about what’s going on behind the scenes—is sometimes called the Copenhagen interpretation of quantum mechanics. But people, including the physicists from Copenhagen who purportedly invented this interpretation, disagree on precisely what that label should be taken to describe. We can just refer to it as “standard textbook quantum mechanics.”
The idea that these rules represent how reality actually works is, needless to say, outrageous.
What precisely do you mean by a “measurement”? How quickly does it happen? What exactly constitutes a measuring apparatus? Does it need to be human, or have some amount of consciousness, or perhaps the ability to encode information? Or maybe it just has to be macroscopic, and if so how macroscopic does it have to be? When exactly does the measurement occur, and how quickly? How in the world does the wave function collapse so dramatically? If the wave function were very spread out, does the collapse happen faster than the speed of light? And what happens to all the possibilities that were seemingly allowed by the wave function but which we didn’t observe? Were they never really there? Do they just vanish into nothingness?
To put things most pointedly: Why do quantum systems evolve smoothly and deterministically according to the Schrödinger equation as long as we aren’t looking at them, but then dramatically collapse when we do look? How do they know, and why do they care? (Don’t worry, we’re going to answer all these questions.)

Science, most people think, seeks to understand the natural world. We observe things happening, and science hopes to provide an explanation for what is going on.
In its current textbook formulation, quantum mechanics has failed in this ambition. We don’t know what’s really going on, or at least the community of professional physicists cannot agree on what it is. What we have instead is a recipe that we enshrine in textbooks and teach to our students. Isaac Newton could tell you, starting with the position and velocity of a rock that you have thrown into the air in the Earth’s gravitational field, just what the subsequent trajectory of that rock was going to be. Analogously, starting with a quantum system prepared in some particular way, the rules of quantum mechanics can tell you how the wave function will change over time, and what the probability of various possible measurement outcomes will be should you choose to observe it.
The fact that the quantum recipe provides us with probabilities rather that certainties might be annoying, but we could learn to live with it. What bugs us, or should, is our lack of understanding about what is actually happening.
Imagine that some devious genius figured out all the laws of physics, but rather than revealing them to the rest of the world, they programmed a computer to answer questions concerning specific physics problems, and put an interface to the program on a web page. Anyone who was interested could just surf over to that site, type in a well-posed physics question, and get the correct answer.
Such a program would obviously be of great use to scientists and engineers. But having access to the site wouldn’t qualify as understanding the laws of physics. We would have an oracle that was in the business of providing answers to specific questions, but we ourselves would be completely lacking in any intuitive idea of the underlying rules of the game. The rest of the world’s scientists, presented with such an oracle, wouldn’t be moved to declare victory; they would continue with their work of figuring out what the laws of nature actually were.
Quantum mechanics, in the form in which it is currently presented in physics textbooks, represents an oracle, not a true understanding. We can set up specific problems and answer them, but we can’t honestly explain what’s happening behind the scenes. What we do have are a number of good ideas about what that could be, and it’s past time that the physics community started taking these ideas seriously.
* There’s a slight technicality, which we’ll mention here and then pretty much forget about: the amplitude for any given outcome is actually a complex number, not a real number. Real numbers are the ones that appear on the number line, any number between minus infinity and plus infinity. Anytime you take the square of a real number, you get another real number that is greater than or equal to zero, so as far as real numbers are concerned there’s no such thing as the square root of a negative number. Mathematicians long ago realized that square roots of negative numbers would be really useful things to have, so they defined the “imaginary unit” i as the square root of -1. An imaginary number is just a real number, called “the imaginary part,” times i. Then a complex number is just a combination of a real number and an imaginary one. The little bars in the notation |Amplitude|2 in the Born rule mean that we actually add the squares of the real and the imaginary parts. All that is just for the sticklers out there; henceforth we’ll be happy to say “the probability is the amplitude squared” and be done with it.