
“Sometimes I’ve believed as many as six impossible things before breakfast,” notes the White Queen to Alice in Through the Looking Glass. That can seem like a useful skill as one comes to grips with quantum mechanics in general, and Many-Worlds in particular. Fortunately, the impossible-seeming things we’re asked to believe aren’t whimsical inventions or logic-busting Zen koans; they are features of the world that we are nudged toward accepting because actual experiments have dragged us, kicking and screaming, in that direction. We don’t choose quantum mechanics; we only choose to face up to it.
Physics aspires to figure out what kinds of stuff the world is made of, how that stuff naturally changes over time, and how various bits of stuff interact with one another. In my own environment, I can immediately see many different kinds of stuff: papers and books and a desk and a computer and a cup of coffee and a wastebasket and two cats (one of whom is extremely interested in what’s inside the wastebasket), not to mention less solid things like air and light and sound.
By the end of the nineteenth century, scientists had managed to distill every single one of these things down to two fundamental kinds of substances: particles and fields. Particles are point-like objects at a definite location in space, while fields (like the gravitational field) are spread throughout space, taking on a particular value at every point. When a field is oscillating across space and time, we call that a “wave.” So people will often contrast particles with waves, but what they really mean is particles and fields.
Quantum mechanics ultimately unified particles and fields into a single entity, the wave function. The impetus to do so came from two directions: first, physicists discovered that things they thought were waves, like the electric and magnetic fields, had particle-like properties. Then they realized that things they thought were particles, like electrons, manifested field-like properties. The reconciliation of these puzzles is that the world is fundamentally field-like (it’s a quantum wave function), but when we look at it by performing a careful measurement, it looks particle-like. It took a while to get there.

Particles seem to be pretty straightforward things: objects located at particular points in space. The idea goes back to ancient Greece, where a small group of philosophers proposed that matter was made up of point-like “atoms,” for the Greek word for “indivisible.” In the words of Democritus, the original atomist, “Sweet is by convention, bitter by convention, hot by convention, cold by convention, color by convention; in truth there are only atoms and the void.”
At the time there wasn’t that much actual evidence in favor of the proposal, so it was largely abandoned until the beginning of the 1800s, when experimenters had begun to study chemical reactions in a quantitative way. A crucial role was played by tin oxide, a compound made of tin and oxygen, which was discovered to come in two different forms. The English scientist John Dalton noted that for a fixed amount of tin, the amount of oxygen in one form of tin oxide was exactly twice the amount in the other. We could explain this, Dalton argued in 1803, if both elements came in the form of discrete particles, for which he borrowed the word “atom” from the Greeks. All we have to do is to imagine that one form of tin oxide was made of single tin atoms combined with single oxygen atoms, while the other form consisted of single tin atoms combined with two oxygen atoms. Every kind of chemical element, Dalton suggested, was associated with a unique kind of atom, and the tendency of the atoms to combine in different ways was responsible for all of chemistry. A simple summary, but one with world-altering implications.
Dalton jumped the gun a little bit with his nomenclature. For the Greeks, the whole point of atoms was that they were indivisible, the fundamental building blocks out of which everything else is made. But Dalton’s atoms are not at all indivisible—they consist of a compact nucleus surrounded by orbiting electrons. It took over a hundred years to realize that, however. First the English physicist J. J. Thomson discovered electrons in 1897. These seemed to be an utterly new kind of particle, electrically charged and only 1/1800th the mass of hydrogen, the lightest atom. In 1909 Thomson’s former student Ernest Rutherford, a New Zealand physicist who had moved to the UK for his advanced studies, showed most of the mass of the atom was concentrated in a central nucleus, while the atom’s overall size was set by the orbits of much lighter electrons traveling around that nucleus. The standard cartoon picture of an atom, with electrons circling the nucleus much like planets orbit the sun in our solar system, represents this Rutherford model of atomic structure. (Rutherford didn’t know about quantum mechanics, so this cartoon deviates from reality in significant ways, as we shall see.)
Further work, initiated by Rutherford and followed up by others, revealed that nuclei themselves aren’t elementary, but consist of positively charged protons and uncharged neutrons. The electric charges of electrons and protons are equal in magnitude but opposite in sign, so an atom with an equal number of each (and however many neutrons you like) will be electrically neutral. It wasn’t until the 1960s and ’70s that physicists established that protons and neutrons are also made of smaller particles, called quarks, held together by new force-carrying particles called gluons.

Chemically speaking, electrons are where it’s at. Nuclei give atoms their heft, but outside of rare radioactive decays or fission/fusion reactions, they basically go along for the ride. The orbiting electrons, on the other hand, are light and jumpy, and their tendency to move around is what makes our lives interesting. Two or more atoms can share electrons, leading to chemical bonds. Under the right conditions, electrons can change their minds about which atoms they want to be associated with, which gives us chemical reactions. Electrons can even escape their atomic captivity altogether in order to move freely through a substance, a phenomenon we call “electricity.” And when you shake an electron, it sets up a vibration in the electric and magnetic fields around it, leading to light and other forms of electromagnetic radiation.
To emphasize the idea of being truly point-like, rather than a small object but with some definite nonzero size, we sometimes distinguish between “elementary” particles, which define literal points in space, and “composite” particles that are really made of even smaller constituents. As far as anyone can tell, electrons are truly elementary particles. You can see why discussions of quantum mechanics are constantly referring to electrons when they reach for examples—they’re the easiest fundamental particle to make and manipulate, and play a central role in the behavior of the matter of which we and our surroundings are made.

In bad news for Democritus and his friends, nineteenth-century physics didn’t explain the world in terms of particles alone. It suggested, instead, that two fundamental kinds of stuff were required: both particles and fields.
Fields can be thought of as the opposite of particles, at least in the context of classical mechanics. The defining feature of a particle is that it’s located at one point in space, and nowhere else. The defining feature of a field is that it is located everywhere. A field is something that has a value at literally every point in space. Particles need to interact with each other somehow, and they do so through the influence of fields.
Think of the magnetic field. It’s a vector field—at every point in space it looks like a little arrow, with a magnitude (the field can be strong, or weak, or even exactly zero) and also a direction (it points along some particular axis). We can measure the direction in which the magnetic field points just by pulling out a magnetic compass and observing what direction the needle points in. (It will point roughly north, if you are located at most places on Earth and not standing too close to another magnet.) The important thing is that the magnetic field exists invisibly everywhere throughout space, even when we’re not observing it. That’s what fields do.
There is also the electric field, which is also a vector with a magnitude and a direction at every point in space. Just as we can detect a magnetic field with a compass, we can detect the electric field by placing an electron at rest and seeing if it accelerates. The faster the acceleration, the stronger the electric field.* One of the triumphs of nineteenth-century physics was when James Clerk Maxwell unified electricity and magnetism, showing that both of these fields could be thought of as different manifestations of a single underlying “electromagnetic” field.
The other field that was well known in the nineteenth century is the gravitational field. Gravity, Isaac Newton taught us, stretches over astronomical distances. Planets in the solar system feel a gravitational pull toward the sun, proportional to the sun’s mass and inversely proportional to the square of the distance between them. In 1783 Pierre-Simon Laplace showed that we can think of Newtonian gravity as arising from a “gravitational potential field” that has a value at every point in space, just as the electric and magnetic fields do.

By the end of the 1800s, physicists could see the outlines of a complete theory of the world coming into focus. Matter was made of atoms, which were made of smaller particles, interacting via various forces carried by fields, all operating under the umbrella of classical mechanics.
What the World Is Made Of (Nineteenth-Century Edition)
• Particles (point-like, making up matter).
• Fields (pervading space, giving rise to forces).
New particles and forces would be discovered over the course of the twentieth century, but in the year 1899 it wouldn’t have been crazy to think that the basic picture was under control. The quantum revolution lurked just around the corner, largely unsuspected.
If you’ve read anything about quantum mechanics before, you’ve probably heard the question “Is an electron a particle, or a wave?” The answer is: “It’s a wave, but when we look at (that is, measure) that wave, it looks like a particle.” That’s the fundamental novelty of quantum mechanics. There is only one kind of thing, the quantum wave function, but when observed under the right circumstances it appears particle-like to us.
What the World Is Made Of (Twentieth Century and Beyond)
• A quantum wave function.
It took a number of conceptual breakthroughs to go from the nineteenth-century picture of the world (classical particles and classical fields) to the twentieth-century synthesis (a single quantum wave function). The story of how particles and fields are different aspects of the same underlying thing is one of the underappreciated successes of the quest for unification in physics.
To get there, early twentieth-century physicists needed to appreciate two things: fields (like electromagnetism) can behave in particle-like ways, and particles (like electrons) can behave in wave-like ways.
The particle-like behavior of fields was appreciated first. Any particle with an electrical charge, such as an electron, creates an electric field everywhere around it, fading in magnitude as you get farther away from the charge. If we shake an electron, oscillating it up and down, the field oscillates along with it, in ripples that gradually spread out from its location. This is electromagnetic radiation, or “light” for short. Every time we heat up a material to sufficient temperature, electrons in its atoms start to shake, and the material begins to glow. This is known as black-body radiation, and every object with a uniform temperature gives off a form of blackbody radiation.
Red light corresponds to slowly oscillating, low-frequency waves, while blue light is rapidly oscillating, high-frequency waves. Given what physicists knew about atoms and electrons at the turn of the century, they could calculate how much radiation a blackbody should emit at every different frequency, the so-called blackbody spectrum. Their calculations worked well for low frequencies, but became less and less accurate as they went to higher frequencies, ultimately predicting an infinite amount of radiation coming from every material body. This was later dubbed the “ultraviolet catastrophe,” referring to the invisible frequencies even higher than blue or violet light.
Finally in 1900, German physicist Max Planck was able to derive a formula that fit the data exactly. The important trick was to propose a radical idea: that every time light was emitted, it came in the form of a particular amount—a “quantum”—of energy, which was related to the frequency of the light. The faster the electromagnetic field oscillates, the more energy each emission will have.
In the process, Planck was forced to posit the existence of a new fundamental parameter of nature, now known as Planck’s constant and denoted by the letter h. The amount of energy contained in a quantum of light is proportional to its frequency, and Planck’s constant is the constant of proportionality: the energy is the frequency times h. Very often it’s more convenient to use a modified version ħ, pronounced “h-bar,” which is just Planck’s original constant h divided by 2π. The appearance of Planck’s constant in an expression is a signal that quantum mechanics is at work.
Planck’s discovery of his constant suggested a new way of thinking about physical units, such as energy, mass, length, or time. Energy is measured in units such as ergs or joules or kilowatt-hours, while frequency is measured in units of 1/time, since frequency tells us how many times something happens in a given amount of time. To make energy proportional to frequency, Planck’s constant therefore has units of energy times time. Planck himself realized that his new quantity could be combined with the other fundamental constants—G, Newton’s constant of gravity, and c, the speed of light—to form universally defined measures of length, time, and so forth. The Planck length is about 10-33 centimeters, while the Planck time is about 10-43 seconds. The Planck length is a very short distance indeed, but presumably it has physical relevance, as a scale at which quantum mechanics (h), gravity (G), and relativity (c) all simultaneously matter.
Amusingly, Planck’s mind immediately went to the possibility of communicating with alien civilizations. If we someday start chatting with extraterrestrial beings using interstellar radio signals, they won’t know what we mean if we were to say human beings are “about two meters tall.” But since they will presumably know at least as much about physics as we do, they should be aware of Planck units. This suggestion hasn’t yet been put to practical use, but Planck’s constant has had an immense impact elsewhere.
The idea that light is emitted in discrete quanta of energy related to its frequency is puzzling, when you think about it. From what we intuitively know about light, it might make sense if someone suggested that the amount of energy it carried depended on how bright it was, but not on what color it was. But the assumption led Planck to derive the right formula, so something about the idea seemed to be working.
It was left to Albert Einstein, in his singular way, to brush away conventional wisdom and take a dramatic leap into a new way of thinking. In 1905, Einstein suggested that light was emitted only at certain energies because it literally consisted of discrete packets, not a smooth wave. Light was particles, in other words—“photons,” as they are known today. This idea, that light comes in discrete, particle-like quanta of energy, was the true birth of quantum mechanics, and was the discovery for which Einstein was awarded the Nobel Prize in 1921. (He deserved to win at least one more Nobel for the theory of relativity, but never did.) Einstein was no dummy, and he knew that this was a big deal; as he told his friend Conrad Habicht, his light quantum proposal was “very revolutionary.”
Note the subtle difference between Planck’s suggestion and Einstein’s. Planck says that light of a fixed frequency is emitted in certain energy amounts, while Einstein says that’s because light literally is discrete particles. It’s the difference between saying that a certain coffee machine makes exactly one cup at a time, and saying that coffee only exists in the form of one-cup-size amounts. That might make sense when we’re talking about matter particles like electrons and protons, but just a few decades earlier Maxwell had triumphantly explained that light was a wave, not a particle. Einstein’s proposal was threatening to undo that triumph. Planck himself was reluctant to accept this wild new idea, but it did explain the data. In a wild new idea’s search for acceptance, that’s a powerful advantage to have.

Meanwhile another problem was lurking over on the particle side of the ledger, where Rutherford’s model explained atoms in terms of electrons orbiting nuclei.
Remember that if you shake an electron, it emits light. By “shake” we just mean accelerate in some way. An electron that does anything other than move in a straight line at a constant velocity should emit light.
From the picture of the Rutherford atom, with electrons orbiting around the nucleus, it certainly looks like those electrons are not moving in straight lines. They’re moving in circles or ellipses. In a classical world, that unambiguously means that the electrons are being accelerated, and equally unambiguously that they should be giving off light. Every single atom in your body, and in the environment around you, should be glowing, if classical mechanics was right. That means the electrons should be losing energy as they emit radiation, which in turn implies that they should spiral downward into the central nucleus. Classically, electron orbits should not be stable.
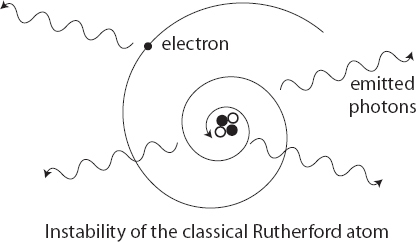
Perhaps all of your atoms are giving off light, but it’s just too faint to see. After all, identical logic applies to the planets in the solar system. They should be giving off gravitational waves—an accelerating mass should cause ripples in the gravitational field, just like an accelerating charge causes ripples in the electromagnetic field. And indeed they are. If there was any doubt that this happens, it was swept away in 2016, when researchers at the LIGO and Virgo gravitational-wave observatories announced the first direct detection of gravitational waves, created when black holes over a billion light years away spiraled into each other.
But the planets in the solar system are much smaller, and move more slowly, than those black holes, which were each over thirty times the mass of the sun. As a result, the emitted gravitational waves from our planetary neighbors are very weak indeed. The power emitted in gravitational waves by the orbiting Earth amounts to about 200 watts—equivalent to the output of a few lightbulbs, and completely insignificant compared to other influences such as solar radiation and tidal forces. If we pretend that the emission of gravitational waves were the only thing affecting the Earth’s orbit, it would take over 1023 years for it to crash into the sun. So perhaps the same thing is true for atoms: maybe electron orbits aren’t really stable, but they’re stable enough.
This is a quantitative question, and it’s not hard to plug in the numbers and see what falls out. The answer is catastrophic, because electrons should move much faster than planets and electromagnetism is a much stronger force than gravity. The amount of time it would take an electron to crash into the nucleus of its atom works out to about ten picoseconds. That’s one-hundred-billionth of a second. If ordinary matter made of atoms only lasted for that long, someone would have noticed by now.
This bothered a lot of people, most notably Niels Bohr, who had briefly worked under Rutherford in 1912. In 1913, Bohr published a series of three papers, later known simply as “the trilogy,” in which he put forth another of those audacious, out-of-the-blue ideas that characterized the early years of quantum theory. What if, he asked, electrons can’t spiral down into atomic nuclei because electrons simply aren’t allowed to be in any orbit they want, but instead have to stick to certain very specific orbits? There would be a minimum-energy orbit, another one with somewhat higher energy, and so on. But electrons weren’t allowed to go any closer to the nucleus than the lowest orbit, and they weren’t allowed to be in between the orbits. The allowed orbits were quantized.
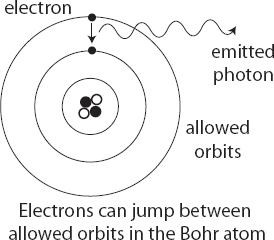
Bohr’s proposal wasn’t quite as outlandish as it might seem at first. Physicists had studied how light interacted with different elements in their gaseous form—hydrogen, nitrogen, oxygen, and so forth. They found that if you shined light through a cold gas, some of it would be absorbed; likewise, if you passed electrical current through a tube of gas, the gas would start glowing (the principle behind fluorescent lights still used today). But they only emitted and absorbed certain very specific frequencies of light, letting other colors pass right through. Hydrogen, the simplest element with just a single proton and a single electron, in particular had a very regular pattern of emission and absorption frequencies.
For a classical Rutherford atom, that would make no sense at all. But in Bohr’s model, where only certain electron orbits were allowed, there was an immediate explanation. Even though electrons couldn’t linger in between the allowed orbits, they could jump from one to another. An electron could fall from a higher-energy orbit to a lower-energy one by emitting light with just the right energy to compensate, or it could leap upward in energy by absorbing an appropriate amount of energy from ambient light. Because the orbits themselves were quantized, we should only see specific energies of light interacting with the electrons. Together with Planck’s idea that the frequency of light is related to its energy, this explained why physicists saw only certain frequencies being emitted or absorbed.
By comparing his predictions to the observed emission of light by hydrogen, Bohr was able to not simply posit that only some electron orbits were allowed, but calculate which ones they were. Any orbiting particle has a quantity called the angular momentum, which is easy to calculate—it’s just the mass of the particle, times its velocity, times its distance from the center of the orbit. Bohr proposed that an allowed electron orbit was one whose angular momentum was a multiple of a particular fundamental constant. And when he compared the energy that electrons should emit when jumping between orbits to what was actually seen in light emitted from hydrogen gas, he could figure out what that constant needed to be in order to fit the data. The answer was Planck’s constant, h. Or more specifically, the modified h-bar version, ħ = h/2π.
That’s the kind of thing that makes you think you’re on the right track. Bohr was trying to account for the behavior of electrons in atoms, and he posited an ad hoc rule according to which they could only move along certain quantized orbits, and in order to fit the data his rule ended up requiring a new constant of nature, and that new constant was the same as the new constant that Planck was forced to invent when he was trying to account for the behavior of photons. All of this might seem ramshackle and a bit sketchy, but taken together it appeared as if something profound was happening in the realm of atoms and particles, something that didn’t fit comfortably with the sacred rules of classical mechanics. The ideas of this period are now sometimes described under the rubric of “the old quantum theory,” as opposed to “the new quantum theory” of Heisenberg and Schrödinger that came along in the late 1920s.

As provocative and provisionally successful as the old quantum theory was, nobody was really happy with it. Planck and Einstein’s idea of light quanta helped make sense of a number of experimental results, but was hard to reconcile with the enormous success of Maxwell’s theory of light as electromagnetic waves. Bohr’s idea of quantized electron orbits helped make sense of the light emitted and absorbed by hydrogen, but seemed to be pulled out of a hat, and didn’t really work for elements other than hydrogen. Even before the “old quantum theory” was given that name, it seemed clear that these were just hints at something much deeper going on.
One of the least satisfying features of Bohr’s model was the suggestion that electrons could “jump” from one orbit to another. If a low-energy electron absorbed light with a certain amount of energy, it makes sense that it would have to jump up to another orbit with just the right amount of additional energy. But when an electron in a high-energy orbit emitted light to jump down, it seemed to have a choice about exactly how far down to go, which lower orbit to end up in. What made that choice? Rutherford himself worried about this in a letter to Bohr:
There appears to me one grave difficulty in your hypothesis, which I have no doubt you fully realize, namely, how does an electron decide what frequency it is going to vibrate at when it passes from one stationary state to the other? It seems to me that you would have to assume that the electron knows beforehand where it is going to stop.
This business about electrons “deciding” where to go foreshadowed a much more drastic break with the paradigm of classical physics than physicists in 1913 were prepared to contemplate. In Newtonian mechanics one could imagine a Laplace demon that could predict, at least in principle, the entire future history of the world from its present state. At this point in the development of quantum mechanics, nobody was really confronting the prospect that this picture would have to be completely discarded.
It took more than ten years for a more complete framework, the “new quantum theory,” to finally come on the scene. In fact, two competing ideas were proposed at the time, matrix mechanics and wave mechanics, before they were ultimately shown to be mathematically equivalent versions of the same thing, which can now simply be called quantum mechanics.
Matrix mechanics was formulated initially by Werner Heisenberg, who had worked with Niels Bohr in Copenhagen. These two men, along with their collaborator Wolfgang Pauli, are responsible for the Copenhagen interpretation of quantum mechanics, though who exactly believed what is a topic of ongoing historical and philosophical debate.
Heisenberg’s approach in 1926, reflecting the boldness of a younger generation coming on the scene, was to put aside questions of what was really happening in a quantum system, and to focus exclusively on explaining what was observed by experimenters. Bohr had posited quantized electron orbits without explaining why some orbits were allowed and others were not. Heisenberg dispensed with orbits entirely. Forget about what the electron is doing; ask only what you can observe about it. In classical mechanics, an electron would be characterized by position and momentum. Heisenberg kept those words, but instead of thinking of them as quantities that exist whether we are looking at them or not, he thought of them as possible outcomes of measurements. For Heisenberg, the unpredictable jumps that had bothered Rutherford and others became a central part of the best way of talking about the quantum world.
Heisenberg was only twenty-four years old when he first formulated matrix mechanics. He was clearly a prodigy, but far from an established figure in the field, and wouldn’t obtain a permanent academic position until a year later. In a letter to Max Born, another of his mentors, Heisenberg fretted that he “had written a crazy paper and did not dare to send it in for publication.” But in a collaboration with Born and the even younger physicist Pascual Jordan, they were able to put matrix mechanics on a clear and mathematically sound footing.
It would have been natural for Heisenberg, Born, and Jordan to share the Nobel Prize for the development of matrix mechanics, and indeed Einstein nominated them for the award. But it was Heisenberg alone who was honored by the Nobel committee in 1932. It has been speculated that Jordan’s inclusion would have been problematic, as he became known for aggressive right-wing political rhetoric, ultimately becoming a member of the Nazi Party and joining a Sturmabteilung (Storm trooper) unit. At the same time, however, he was considered unreliable by his fellow Nazis, due to his support for Einstein and other Jewish scientists. In the end, Jordan never won the prize. Born was also left off the prize for matrix mechanics, but that omission was made up for when he was awarded a separate Nobel in 1954 for his formulation of the probability rule. That was the last time a Nobel Prize has been awarded for work in the foundations of quantum mechanics.
After the onset of World War II, Heisenberg led a German government program to develop nuclear weapons. What Heisenberg actually thought about the Nazis, and whether he truly tried as hard as possible to push the weapons program forward, are matters of some historical dispute. It seems that, like a number of other Germans, Heisenberg was not fond of the Nazi Party, but preferred a German victory in the conflict to the prospect of being run over by the Soviets. There is no evidence that he actively worked to sabotage the nuclear bomb program, but it is clear that his team made very little progress. In part that must be attributed to the fact that so many brilliant Jewish physicists had fled Germany as the Nazis took power.

As impressive as matrix mechanics was, it suffered from a severe marketing flaw: the mathematical formalism was highly abstract and difficult to understand. Einstein’s reaction to the theory was typical: “A veritable sorcerer’s calculation. This is sufficiently ingenious and protected by its great complexity, to be immune to any proof of its falsity.” (This from the guy who had proposed describing spacetime in terms of non-Euclidean geometry.) Wave mechanics, developed immediately thereafter by Erwin Schrödinger, was a version of quantum theory that used concepts with which physicists were already very familiar, which greatly helped accelerate acceptance of the new paradigm.
Physicists had studied waves for a long time, and with Maxwell’s formulation of electromagnetism as a theory of fields, they had become adept at thinking about them. The earliest intimations of quantum mechanics, from Planck and Einstein, had been away from waves and toward particles. But Bohr’s atom suggested that even particles weren’t what they seemed to be.
In 1924, the young French physicist Louis de Broglie was thinking about Einstein’s light quanta. At this point the relationship between photons and classical electromagnetic waves was still murky. An obvious thing to contemplate was that light consisted of both a particle and a wave: particle-like photons could be carried along by the well-known electromagnetic waves. And if that’s true, there’s no reason we couldn’t imagine the same thing going on with electrons—maybe there is something wave-like that carries along the electron particles. That’s exactly what de Broglie suggested in his 1924 doctoral thesis, proposing a relationship between the momentum and wavelength of these “matter waves” that was analogous to Planck’s formula for light, with larger momenta corresponding to shorter wavelengths.

Like many suggestions at the time, de Broglie’s hypothesis may have seemed a little ad hoc, but its implications were far-reaching. In particular, it was natural to ask what the implications of matter waves might be for electrons orbiting around a nucleus. A remarkable answer suggested itself: for the wave to settle down into a stationary configuration, its wavelength had to be an exact multiple of the circumference of a corresponding orbit. Bohr’s quantized orbits could be derived rather than simply postulated, simply by associating waves with the electron particles surrounding the nucleus.
Consider a string with its ends held fixed, such as on a guitar or violin. Even though any one point can move up or down as it likes, the overall behavior of the string is constrained by being tied down at either end. As a result, the string only vibrates at certain special wavelengths, or combinations thereof; that’s why the strings on musical instruments emit clear notes rather than an indistinct noise. These special vibrations are called the modes of the string. The essentially “quantum” nature of the subatomic world, in this picture, comes about not because reality is actually subdivided into distinct chunks but because there are natural vibrational modes for the waves out of which physical systems are made.
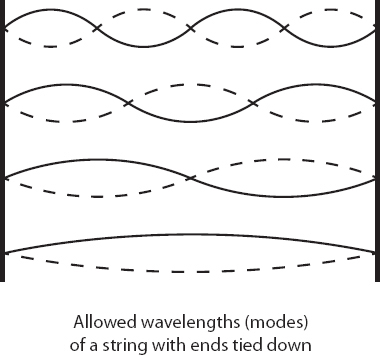
The word “quantum,” referring to some definite amount of stuff, can give the impression that quantum mechanics describes a world that is fundamentally discrete and pixelated, like when you zoom in closely on a computer monitor or TV screen. It’s actually the opposite; quantum mechanics describes the world as a smooth wave function. But in the right circumstances, where individual parts of the wave function are tied down in a certain way, the wave takes the form of a combination of distinct vibrational modes. When we observe such a system, we see those discrete possibilities. That’s true for orbits of electrons, and it will also explain why quantum fields look like sets of individual particles. In quantum mechanics, the world is fundamentally wavy; its apparent quantum discreteness comes from the particular way those waves are able to vibrate.
De Broglie’s ideas were intriguing, but they fell short of providing a comprehensive theory. That was left to Erwin Schrödinger, who in 1926 put forth a dynamical understanding of wave functions, including the equation they obey, later named after him. Revolutions in physics are generally a young person’s game, and quantum mechanics was no different, but Schrödinger bucked the trend. Among the leaders of the discussions at Solvay in 1927, Einstein at forty-eight years old, Bohr at forty-two, and Born at forty-four were the grand old men. Heisenberg was twenty-five, Pauli twenty-seven, and Dirac twenty-five. Schrödinger, at the ripe old age of thirty-eight, was looked upon as someone suspiciously long in the tooth to appear on the scene with radical new ideas like this.
Note the shift here from de Broglie’s “matter waves” to Schrödinger’s “wave function.” Though Schrödinger was heavily influenced by de Broglie’s work, his concept went quite a bit further, and deserves a distinct name. Most obviously, the value of a matter wave at any one point was some real number, while the amplitudes described by wave functions are complex numbers—the sum of a real number and an imaginary one.
More important, the original idea was that each kind of particle would be associated with a matter wave. That’s not how Schrödinger’s wave function works; you have just one function that depends on all the particles in the universe. It’s that simple shift that leads to the world-altering phenomenon of quantum entanglement.

What made Schrödinger’s ideas an instant hit was the equation he proposed, which governs how wave functions change with time. To a physicist, a good equation makes all the difference. It elevates a pretty-sounding idea (“particles have wave-like properties”) to a rigorous, unforgiving framework. Unforgiving might sound like a bad quality in a person, but it’s just what you want in a scientific theory. It’s the feature that lets you make precise predictions. When we say that quantum textbooks spend a lot of time having students solve equations, it’s mostly the Schrödinger equation we have in mind.
Schrödinger’s equation is what a quantum version of Laplace’s demon would be solving as it predicted the future of the universe. And while the original form in which Schrödinger wrote down his equation was meant for systems of individual particles, it’s actually a very general idea that applies equally well to spins, fields, superstrings, or any other system you might want to describe using quantum mechanics.
Unlike matrix mechanics, which was expressed in terms of mathematical concepts most physicists at the time had never been exposed to, Schrödinger’s wave equation was not all that different in form from Maxwell’s electromagnetic equations that adorn T-shirts worn by physics students to this day. You could visualize a wave function, or at least you might convince yourself that you could. The community wasn’t sure what to make of Heisenberg, but they were ready for Schrödinger. The Copenhagen crew—especially the youngsters, Heisenberg and Pauli—didn’t react graciously to the competing ideas from an undistinguished old man in Zürich. But before too long they were thinking in terms of wave functions, just like everyone else.
Schrödinger’s equation involves unfamiliar symbols, but its basic message is not hard to understand. De Broglie had suggested that the momentum of a wave goes up as its wavelength goes down. Schrödinger proposed a similar thing, but for energy and time: the rate at which the wave function is changing is proportional to how much energy it has. Here is the celebrated equation in its most general form:
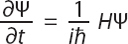
We don’t need the details here, but it’s nice to see the real way that physicists think of an equation like this. There’s some maths involved, but ultimately it’s just a translation into symbols of the idea we wrote down in words.
Ψ (the Greek letter Psi) is the wave function. The left-hand side is the rate at which the wave function is changing over time. On the right-hand side we have a proportionality constant involving Planck’s constant ħ, the fundamental unit of quantum mechanics, and i, the square root of minus one. The wave function Ψ is acted on by something called the Hamiltonian, or H. Think of the Hamiltonian as an inquisitor who asks the following question: “How much energy do you have?” The concept was invented in 1833 by Irish mathematician William Rowan Hamilton, as a way to reformulate the laws of motion of a classical system, long before it gained a central role in quantum mechanics.
When physicists start modeling different physical systems, the first thing they try to do is work out a mathematical expression for the Hamiltonian of that system. The standard way of figuring out the Hamiltonian of something like a collection of particles is to start with the energies of the particles themselves, and then add in additional contributions describing how the particles interact with each other. Maybe they bump off each other like billiard balls, or perhaps they exert a mutual gravitational interaction. Each such possibility suggests a particular kind of Hamiltonian. And if you know the Hamiltonian, you know everything; it’s a compact way of capturing all the dynamics of a physical system.
If a quantum wave function describes a system with some definite value of the energy, the Hamiltonian simply equals that value, and the Schrödinger equation implies that the system just keeps doing the same thing, maintaining a fixed energy. More often, since wave functions are superpositions of different possibilities, the system will be a combination of multiple energies. In that case the Hamiltonian captures a bit of all of them. The bottom line is that the right-hand side of Schrödinger’s equation is a way of characterizing how much energy is carried by each of the contributions to a wave function in a quantum superposition; high-energy components evolve quickly, low-energy ones evolve more slowly.
What really matters is that there is some specific deterministic equation. Once you have that, the world is your playground.
Wave mechanics made a huge splash, and before too long Schrödinger, English physicist Paul Dirac, and others demonstrated that it was essentially equivalent to matrix mechanics, leaving us with a unified theory of the quantum world. Still, all was not peaches and cream. Physicists were left with the question that we are still struggling with today: What is the wave function, really? What physical thing does it represent, if any?
In de Broglie’s view, his matter waves served to guide particles around, not to replace them entirely. (He later developed this idea into pilot-wave theory, which remains a viable approach to quantum foundations today, although it is not popular among working physicists.) Schrödinger, by contrast, wanted to do away with fundamental particles entirely. His original hope was that his equation would describe localized packets of vibrations, confined to a relatively small region of space, so that each packet would appear particle-like to a macroscopic observer. The wave function could be thought of as representing the density of mass in space.
Alas, Schrödinger’s aspirations were undone by his own equation. If we start with a wave function describing a single particle approximately localized in some empty region of space, the Schrödinger equation is clear about what happens next: it quickly spreads out all over the place. Left to their own devices, Schrödinger’s wave functions don’t look particle-like at all.*
It was left to Max Born, one of Heisenberg’s collaborators on matrix mechanics, to provide the final missing piece: we should think about the wave function as a way of calculating the probability of seeing a particle in any given position when we look for it. In particular, we should take both the real and imaginary parts of the complex-valued amplitude, square them both individually, and add the two numbers together. The result is the probability of observing the corresponding outcome. (The suggestion that it’s the amplitude squared, rather than the amplitude itself, appears in a footnote added at the last minute to Born’s 1926 paper.) And after we observe it, the wave function collapses to be localized at the place where we saw the particle.
You know who didn’t like the probability interpretation of the Schrödinger equation? Schrödinger himself. His goal, like Einstein’s, was to provide a definite mechanistic underpinning for quantum phenomena, not just to create a tool that could be used to calculate probabilities. “I don’t like it, and I’m sorry I ever had anything to do with it,” he later groused. The point of the famous Schrödinger’s Cat thought experiment, in which the wave function of a cat evolves (via the Schrödinger equation) into a superposition of “alive” and “dead,” was not to make people say, “Wow, quantum mechanics is really mysterious.” It was to make people say, “Wow, this can’t possibly be correct.” But to the best of our current knowledge, it is.

A lot of intellectual action was packed into the first three decades of the twentieth century. Over the course of the 1800s, physicists had put together a promising picture of the nature of matter and forces. Matter was made of particles, and forces were carried by fields, all under the umbrella of classical mechanics. But confrontation with experimental data forced them to think beyond this paradigm. In order to explain radiation from hot objects, Planck suggested that light was emitted in discrete amounts of energy, and Einstein pushed this further by suggesting that light actually came in the form of particle-like quanta. Meanwhile, the fact that atoms are stable and the observation of how light was emitted from gases inspired Bohr to suggest that electrons could only move along certain allowed orbits, with occasional jumps between them. Heisenberg, Born, and Jordan elaborated this story of probabilistic jumps into a full theory, matrix mechanics. From another angle, de Broglie pointed out that if we think of matter particles such as electrons as actually being waves, we can derive Bohr’s quantized orbits rather than postulating them. Schrödinger developed this suggestion into a full-blown quantum theory of its own, and it was ultimately demonstrated that wave mechanics and matrix mechanics were equivalent ways of saying the same thing. Despite initial hopes that wave mechanics could explain away the apparent need for probabilities as a fundamental part of the theory, Born showed that the right way to think about Schrödinger’s wave function was as something that you square to get the probability of a measurement outcome.
Whew. That’s quite a journey, taken in a remarkably short period of time, from Planck’s observation in 1900 to the Solvay Conference in 1927, when the new quantum mechanics was fleshed out once and for all. It’s to the enormous credit of the physicists of the early twentieth century that they were willing to face up to the demands of the experimental data, and in doing so to completely upend the fantastically successful Newtonian view of the classical world.
They were less successful, however, at coming to grips with the implications of what they had wrought.
* Annoyingly, the electron accelerates in precisely the opposite direction that the electric field points, because by human convention we’ve decided to call the charge on the electron “negative” and that on a proton “positive.” For that we can blame Benjamin Franklin in the eighteenth century. He didn’t know about electrons and protons, but he did figure out there was a unified concept called “electric charge.” When he went to arbitrarily label which substances were positively charged and which were negatively charged, he had to choose something, and the label he picked for positive charge corresponds to what we would now call “having fewer electrons than it should.” So be it.
* I’ve emphasized that there is only one wave function, the wave function of the universe, but the alert reader will notice that I often talk about “the wave function of a particle.” This latter construction is perfectly okay if—and only if—the particle is unentangled from the rest of the universe. Happily, that is often the case, but in general we have to keep our wits about us.