
A police officer pulls over Werner Heisenberg for speeding. “Do you know how fast you were going?” asks the cop. “No,” Heisenberg replies, “but I know exactly where I am!”
I think we can all agree that physics jokes are the funniest jokes there are. They are less good at accurately conveying physics. This particular chestnut rests on familiarity with the famous Heisenberg uncertainty principle, often explained as saying that we cannot simultaneously know both the position and the velocity of any object. But the reality is deeper than that.
It’s not that we can’t know position and momentum, it’s that they don’t even exist at the same time. Only under extremely special circumstances can an object be said to have a location—when its wave function is entirely concentrated on one point in space, and zero everywhere else—and similarly for velocity. And when one of the two is precisely defined, the other could be literally anything, were we to measure it. More often, the wave function includes a spread of possibilities for both quantities, so neither has a definite value.
Back in the 1920s, all this was less clear. It was still natural to think that the probabilistic nature of quantum mechanics simply indicated that it was an incomplete theory, and that there was a more deterministic, classical-sounding picture waiting to be developed. Wave functions, in other words, might be a way of characterizing our ignorance of what was really going on, rather than being the total truth about what is going on, as we’re advocating here. One of the first things people did when learning about the uncertainty principle was to try to find loopholes in it. They failed, but in doing so we learned a lot about how quantum reality is fundamentally different from the classical world we had been used to.
The absence of definite quantities at the heart of reality that map more or less straightforwardly onto what we can eventually observe is one of the deep features of quantum mechanics that can be hard to accept upon first encounter. There are quantities that are not merely unknown but do not even exist, even though we can seemingly measure them.
Quantum mechanics forces us to confront this yawning chasm between what we see and what really is. In this chapter we’ll see how that gap manifests itself in the uncertainty principle, and in the next chapter we’ll see it again more forcefully in the phenomenon of entanglement.

The uncertainty principle owes its existence to the fact that the relationship between position and momentum (mass times velocity) is fundamentally different in quantum mechanics from what it was in classical mechanics. Classically, we can imagine measuring the momentum of a particle by tracking its position over time, and seeing how fast it moves. But if all we have access to is a single moment, position and momentum are completely independent from each other. If I tell you that a particle has a certain position at one instant, and I tell you nothing else, you have no idea what its speed is, and vice versa.
Physicists refer to the different numbers we use to specify something as that system’s “degrees of freedom.” In Newtonian mechanics, to tell me the complete state of a bunch of particles, you have to tell me the position and momentum of every one of them, so the degrees of freedom are the positions and the momenta. Acceleration is not a degree of freedom, since it can be calculated once we know the forces acting on the system. The essence of a degree of freedom is that it doesn’t depend on anything else.
When we switch to quantum mechanics and start thinking about Schrödinger’s wave functions, things become a little different. To make a wave function for a single particle, think of every location where the particle could possibly be found, were we to observe it. Then to each location assign an amplitude, a complex number with the property that the square of each number is the probability of finding the particle there. There is a constraint that the squares of all these numbers add up to precisely one, since the total probability that the particle is found somewhere must equal one. (Sometimes we speak of probabilities in terms of percentages, which are numerically 100 times the actual probability; a 20 percent chance is the same as a 0.2 probability.)
Notice we didn’t mention “velocity” or “momentum” there. That’s because we don’t have to separately specify the momentum in quantum mechanics, as we did in classical mechanics. The probability of measuring any particular velocity is completely determined by the wave function for all the possible positions. Velocity is not a separate degree of freedom, independent of position. The basic reason why is that the wave function is, you know, a wave. Unlike for a classical particle, we don’t have a single position and a single momentum, we have a function of all possible positions, and that function typically oscillates up and down. The rate of those oscillations determines what we’re likely to see if we were to measure the velocity or momentum.
Consider a simple sine wave, oscillating up and down in a regular pattern throughout space. Plug such a wave function into the Schrödinger equation and ask how it will evolve. We find that a sine wave has a definite momentum, with shorter wavelengths corresponding to faster velocity. But a sine wave has no definite position; on the contrary, it’s spread out everywhere. And a more typical shape, which is neither localized at one point nor spread out in a perfect sine wave of fixed wavelength, won’t correspond to either a definite position or a definite momentum, but some mixture of each.

We see the basic dilemma. If we try to localize a wave function in space, its momentum becomes more and more spread out, and if we try to limit it to one fixed wavelength (and therefore momentum) it becomes more spread out in position. That’s the uncertainty principle. It’s not that we can’t know both quantities at the same time; it’s just a fact about how wave functions work that if position is concentrated near some location, momentum is completely undetermined, and vice versa. The old-fashioned classical properties called position and momentum aren’t quantities with actual values, they’re possible measurement outcomes.
People sometimes refer to the uncertainty principle in everyday contexts, outside of the equation-filled language of physics texts. So it’s important to emphasize what the principle does not say. It’s not an assertion that “everything is uncertain.” Either position or momentum could be certain in an appropriate quantum state; they just can’t be certain at the same time.
And the uncertainty principle doesn’t say we necessarily disturb a system when we measure it. If a particle has a definite momentum, we can go ahead and measure that without changing it at all. The point is that there are no states for which both position and momentum are simultaneously definite. The uncertainty principle is a statement about the nature of quantum states and their relationship to observable quantities, not a statement about the physical act of measurement.
Finally, the principle is not a statement about limitations on our knowledge of the system. We can know the quantum state exactly, and that’s all there is to know about it; we still can’t predict the results of all possible future observations with perfect certainty. The idea that “there’s something we don’t know,” given a certain wave function, is an outdated relic of our intuitive insistence that what we observe is what really exists. Quantum mechanics teaches us otherwise.

You’ll sometimes hear the idea, provoked by the uncertainty principle, that quantum mechanics violates logic itself. That’s silly. Logic deduces theorems from axioms, and the resulting theorems are simply true. The axioms may or may not apply to any given physical situation. Pythagoras’s theorem—the square of the hypotenuse of a right triangle equals the sum of the squares of the other two sides—is correct as a formal deduction from the axioms of Euclidean geometry, even though those axioms do not hold if we’re talking about curved surfaces rather than a flat tabletop.
The idea that quantum mechanics violates logic lives in the same neighborhood of the idea that atoms are mostly empty space (a bad neighborhood). Both notions stem from a deep conviction that, despite everything we’ve learned, particles are really points with some position and momentum, rather than being wave functions that are spread out.
Consider a particle in a box, where we’ve drawn a line dividing the box into left and right sides. It has some wave function that is spread throughout the box. Let proposition P be “the particle is on the left side of the box,” and proposition Q be “the particle is on the right side of the box.” We might be tempted to say that both of these propositions are false, since the wave function stretches over both sides of the box. But the proposition “P or Q” has to be true, since the particle is in the box. In classical logic, we can’t have both P and Q be false but “P or Q” be true. So something fishy is going on.
What’s fishy is neither logic nor quantum mechanics but our casual disregard for the nature of quantum states when assigning truth values to the statements P and Q. These statements are neither true nor false; they’re just ill defined. There is no such thing as “the side of the box the particle is on.” If the wave function were concentrated entirely on one side of the box and exactly vanished on the other, we could get away with assigning truth values to P and Q; but in that case one would be true and the other would be false, and classical logic would be fine.
Despite the fact that classical logic is perfectly valid whenever it is properly applied, quantum mechanics has inspired more general approaches known as quantum logic, pioneered by John von Neumann and his collaborator Garrett Birkhoff. By starting with slightly different logical axioms from the standard ones, we can derive a set of rules obeyed by the probabilities implied by the Born rule in quantum mechanics. Quantum logic in this sense is both interesting and useful, but its existence does not invalidate the correctness of ordinary logic in appropriate circumstances.

Niels Bohr, in an attempt to capture what makes quantum theory so unique, proposed the concept of complementarity. The idea is that there can be more than two ways of looking at a quantum system, each of them equally valid, but with the property that you can’t employ them simultaneously. We can describe the wave function of a particle in terms of either position or momentum, but not both at the same time. Similarly, we can think of electrons as exhibiting either particle-like or wave-like properties, just not at the same time.
Nowhere is this feature made more evident than in the famous double-slit experiment. This experiment wasn’t actually performed until the 1970s, long after it was proposed. It wasn’t one of those surprising experimental results that theorists had to invent a new way of thinking in order to understand, but rather a thought experiment (suggested in its original form by Einstein during his debates with Bohr, and later popularized by Richard Feynman in his lectures to Caltech undergraduates) meant to show the dramatic implications of quantum theory.
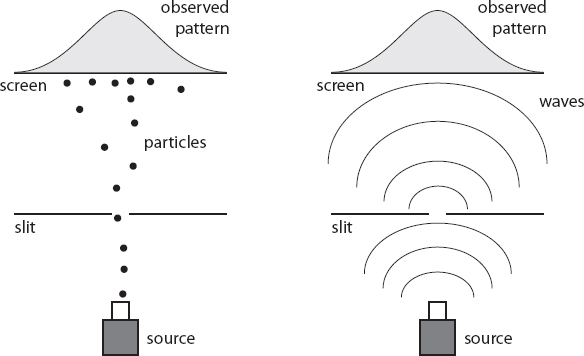
The idea of the experiment is to home in on the distinction between particles and waves. We start with a source of classical particles (maybe a pellet gun that tends to spray in somewhat unpredictable directions), shoot them through a single thin slit, then detect them at a screen on the other side of the slit. Mostly the particles will pass right through, with perhaps very slight deviations if they bump up against the sides of the slit. So what we see at the detector is a pattern of individual points where we detect the particles, arranged in more or less a slit-like pattern.
We could also do the same thing with waves, for example, by placing the slit in a tub of water and creating waves that pass through it. When the waves pass through, they spread out in a semicircular pattern before eventually reaching the screen. Of course, we don’t observe particle-like points when the water wave hits the screen, but let’s imagine we have a special screen that lights up with a brightness that depends on the amplitude the waves reach at any particular point. They will be brightest at the point of the screen that is closest to the slit, and gradually fade as we get farther away.
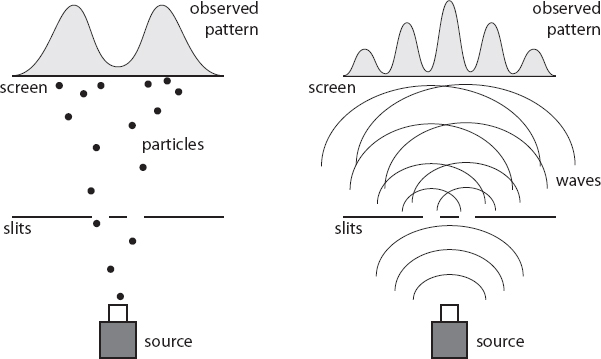
Now let’s do the same thing, but with two slits in the way rather than just one. The particle case isn’t that much different; as long as our source of particles is sufficiently random that particles pass through both slits, what we’ll see on the other side is two lines of points, one for each slit (or one thick line, if the slits themselves are sufficiently close together). But the wave case is altered in an interesting way. Waves can oscillate downward as well as upward, and two waves oscillating in opposite directions will cancel each other out—a phenomenon known as interference. So the waves pass through both slits at once, emanating outward in semicircles, but then set up an interference pattern on the other side. As a result, if we observe the amplitude of the resultant wave at the final screen, we don’t simply see two bright lines; rather, there will be a bright line in the middle (closest to both slits), with alternating dark/bright regions that gradually fade to either side.
So far, that’s the classical world we know and love, where particles and waves are different things and everyone can easily distinguish between them. Now let’s replace our pellet gun or wave machine with a source of electrons, in all their quantum-mechanical glory. There are several twists on this setup, each with provocative consequences.
First consider just a single slit. In this case the electrons behave just as if they were classical particles. They pass through the slit, then are detected by the screen on the other side, each electron leaving a single particle-like mark. If we let numerous electrons through, their marks are scattered around a central line in the image of the slit that they passed through. Nothing funny yet.
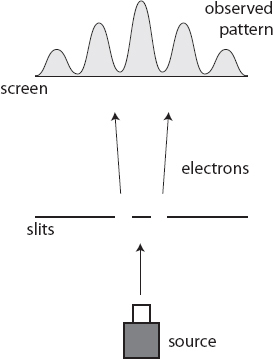
Now let’s introduce two slits. (The slits have to be very close together for this to work, which is one reason it took so long for the experiment to actually be carried out.) Once again, electrons pass through the slits and leave individual marks on the screen on the other side. However, their marks do not clump into two lines, as the classical pellets did. Rather, they form a series of lines: a high-density one in the middle, surrounded by parallel lines with gradually fewer marks, each separated by dark regions with almost no marks at all.
In other words, electrons going through two slits leave what is unmistakably an interference pattern, just like waves do, even though they hit the screen with individual marks just like particles. This phenomenon has launched a thousand unhelpful discussions about whether electrons are “really” particles or waves, or are sometimes particle-like and other times wave-like. One way or another, it’s indisputable that something went through both slits as the electrons traveled to the screen.
At this point this is no surprise to us. The electrons passing through the slits are described by a wave function, which just like our classical wave will go through both slits and oscillate up and down, and therefore it makes sense that we see interference patterns. Then when they hit the screen they are being observed, and it’s at that point they appear to us as particles.
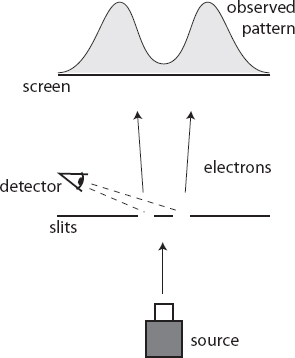
Let’s introduce one additional wrinkle. Imagine that we set up little detectors at each slit, so we can tell whether an electron goes through it. That will settle this crazy idea that an electron can travel through two slits once and for all.
You should be able to figure out what we see. The detectors don’t measure half of an electron going through each of the two slits; they measure a full electron going through one, and nothing through the other, every time. That’s because the detector acts as a measuring device, and when we measure electrons we see particles.
But that’s not the only consequence of looking at the electron as it passes through the slits. At the screen, on the other side of the slits, the interference pattern disappears, and we are back to seeing two bands of marks made by the detected electrons, one for each slit. With the detectors doing their job, the wave function collapses as the electron goes through the slits, so we don’t see interference from a wave passing through both slits at once. When we’re looking at them, electrons behave like particles.
The double-slit experiment makes it difficult to cling to the belief that the electron is just a single classical point, and the wave function simply represents our ignorance about where that point is. Ignorance doesn’t cause interference patterns. There is something real about the wave function.

Wave functions may be real, but they’re undeniably abstract, and once we start considering more than one particle at a time they become hard to visualize. As we move forward with increasingly subtle examples of quantum phenomena in action, it will be very helpful to have a simple, readily graspable example we can refer to over and over. The spin of a particle—a degree of freedom in addition to its position or momentum—is just what we’re looking for. We have to think a bit about what spin means within quantum mechanics, but once we do, it will make our lives much easier.
The notion of spin itself isn’t hard to grasp: it’s just rotation around an axis, as the Earth does every day or a pirouetting ballet dancer does on their tiptoes. But just like the energies of an electron orbiting an atomic nucleus, in quantum mechanics there are only certain discrete results we can obtain when we measure a particle’s spin.
For an electron, for example, there are two possible measurement outcomes for spin. First pick an axis with respect to which we measure the spin. We always find that the electron is spinning either clockwise or counterclockwise when we look along that axis, and always at the same rate. These are conventionally referred to as “spin-up” and “spin-down.” Think of the “right-hand rule”: if you wrap the fingers of your right hand in the direction of rotation, your thumb will be pointing along the appropriate up/down axis.
A spinning electron is a tiny magnet, with north and south magnetic poles, much like the Earth; the spin axis points toward the north pole. One way of measuring the spin of a particular electron is to shoot it through a magnetic field, which will deflect the electron by a bit depending on how its spin is oriented. (As a technicality, the magnetic field has to be focused in the right way—spread out on one side, pinched tightly on the other—for this to work.)
If I told you that the electron had a certain total spin, you might make the following prediction for such an experiment: the electron would be deflected up if its spin axis were aligned with the external field, deflected down if its spin were aligned in the opposite direction, and deflected at some intermediate angle if its spin were somewhere in between. But that’s not what we see.
This experiment was first performed in 1922, by German physicists Otto Stern (an assistant to Max Born) and Walter Gerlach, before the idea of spin had been explicitly spelled out. What they saw was remarkable. Electrons are indeed deflected by passing through the magnetic field, but they either go up, or they go down; nothing in between. If we rotate the magnetic field, the electrons are still deflected in the direction of the field they pass through, either along or against it, but no intermediate values. The measured spin, like the energy of an electron orbiting an atomic nucleus, appears to be quantized.
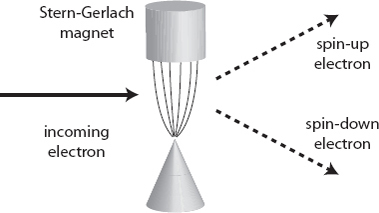
That seems surprising. Even if we’ve acclimated ourselves to the idea that the energy of an electron orbiting a nucleus only comes in certain quantized values, at least that energy seems like an objective property of the electron. But this thing we call the “spin” of the electron seems to give us different answers depending on how we measure it. No matter what particular direction we measure the spin along, there are only two possible outcomes we can obtain.
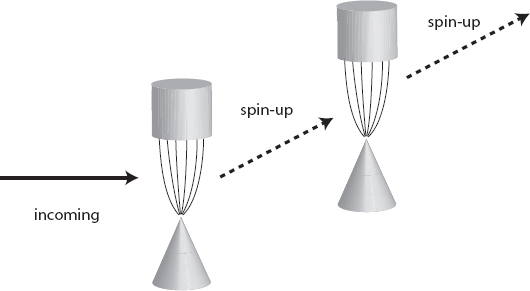
To make sure we haven’t lost our minds, let’s be clever and run the electron through two magnets in a row. Remember that the rules of textbook quantum mechanics tell us that if we get a certain measurement outcome, then measure the same system immediately again, we will always get the same answer. And indeed that’s what happens; if an electron is deflected upward by one magnet (and is therefore spin-up), it will always be deflected upward by a following magnet oriented in the same way.
What if we rotate one of the magnets by 90 degrees? So we’re splitting an initial beam of electrons into spin-up and spin-down as measured by a vertically oriented magnet, then taking the spin-up electrons and passing them through a horizontally oriented magnet. What happens then? Do they hold their breath and refuse to pass through, because they are vertically oriented spin-up electrons and we’re forcing them to be measured along a horizontal axis?
No. Instead, the second magnet splits the spin-up electrons into two beams. Half of them are deflected to the right (along the direction of the second magnet) and half of them are deflected to the left.
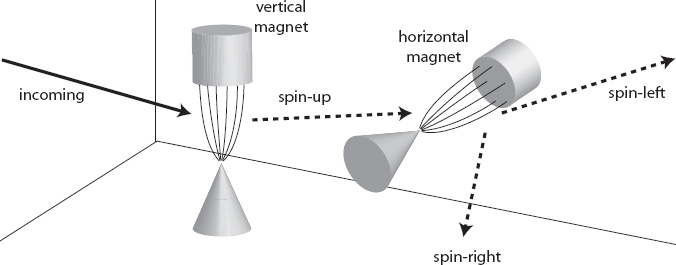
Madness. Our classical intuition makes us think that there is something called “the axis around which the electron is spinning,” and it makes sense (maybe) that the spin around that axis is quantized. But the experiments show that the axis around which the spin is quantized isn’t predetermined by the particle itself; you can choose any axis you like by rotating your magnet appropriately, and the spin will be quantized with respect to that axis.
What we’re bumping up against is another manifestation of the uncertainty principle. The lesson we learned was that “position” and “momentum” aren’t properties that an electron has; they are just things we can measure about it. In particular, no particle can have a definite value of both simultaneously. Once we specify the exact wave function for position, the probability of observing any particular momentum is entirely fixed, and vice versa.
The same is true for “vertical spin” and “horizontal spin.”* These are not separate properties an electron can have; they are just different quantities we can measure. If we express the quantum state in terms of the vertical spin, the probability of observing left or right horizontal spin is entirely fixed. The measurement outcomes we can get are determined by the underlying quantum state, which can be expressed in different but equivalent ways. The uncertainty principle expresses the fact that there are different incompatible measurements we can make on any particular quantum state.

Systems with two possible measurement outcomes are so common and useful in quantum mechanics that they are given a cute name: qubits. The idea is that a classical “bit” has just two possible values, say, 0 and 1. A qubit (quantum bit) is a system that has two possible measurement outcomes, say, spin-up and spin-down along some specified axis. The state of a generic qubit is a superposition of both possibilities, each weighted by a complex number, the amplitude for each alternative. Quantum computers manipulate qubits in the same way that ordinary computers manipulate classical bits.
We can write the wave function of a qubit as
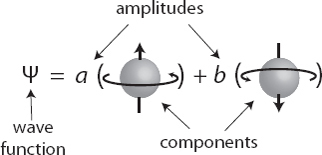
The symbols a and b are complex numbers, representing the amplitudes for spin-up and spin-down, respectively. The pieces of the wave function representing the different possible measurement outcomes, in this case spin-up/-down, are the “components.” In this state, the probability of observing the particle to be spin-up would be |a|2, and the probability for spin-down would be |b|2. If, for example, a and b were both equal to the square root of 1/2, the probability of observing spin-up or spin-down would be 1/2.
Qubits can help us understand a crucial feature of wave functions: they are like the hypotenuse of a right triangle, for which the shorter sides are the amplitudes for each possible measurement outcome. In other words, the wave function is like a vector—an arrow with a length and a direction.
The vector we’re talking about doesn’t point in a direction in real physical space, like “up” or “north.” Rather, it points in a space defined by all possible measurement outcomes. For a single spin qubit, that’s either spin-up or spin-down (once we choose some axis along which to measure). When we say “the qubit is in a superposition of spin-up and spin-down,” what we really mean is “the vector representing the quantum state has some component in the spin-up direction, and another component in the spin-down direction.”
It’s natural to think of spin-up and spin-down as pointing in opposite directions. I mean, just look at the arrows. But as quantum states, they are perpendicular to each other: a qubit that is completely spin-up has no component of spin-down, and vice versa. Even the wave function for the position of a particle is a vector, though we normally visualize it as a smooth function throughout space. The trick is to think of every point in space as defining a different component, and the wave function is a superposition of all of them. There are an infinite number of such vectors, so the space of all possible quantum states, called Hilbert space, is infinite-dimensional for the position of a single particle. That’s why qubits are so much easier to think about. Two dimensions are easier to visualize than infinite dimensions.
When there are only two components in our quantum state, as opposed to infinitely many, it can be hard to think of the state as a “wave function.” It’s not very wavy, and it doesn’t look like a smooth function of space. The right way to think about it is actually the other way around. The quantum state is not a function of ordinary space, it’s a function of the abstract “space of measurement outcomes,” which for a qubit only includes two possibilities. When the thing we observe is the location of a single particle, the quantum state assigns an amplitude to every possible location, which looks just like a wave in ordinary space. That’s the unusual case, however; the wave function is something more abstract, and when more than one particle is involved, it becomes hard to visualize. But we’re stuck with the “wave function” terminology. Qubits are great because at least the wave function has only two components.

This may seem like an unnecessary mathematical detour, but there are immediate payoffs to thinking about wave functions as vectors. One is explaining the Born rule, which says that the probability for any particular measurement outcome is given by its amplitude squared. We’ll dive into details later, but it’s easy to see why the idea makes sense. As a vector, the wave function has a length. You might expect that the length could shrink or grow over time, but it doesn’t; according to Schrödinger’s equation, the wave function just changes its “direction” while maintaining a constant length. And we can compute that length using Pythagoras’s theorem from high-school geometry.
The numerical value of the length of the vector is irrelevant; we can just pick it to be a convenient number, knowing that it will remain constant. Let’s pick it to be one: every wave function is a vector of length one. The vector itself is just like the hypotenuse of a right triangle, with the components forming the shorter sides. So from Pythagoras’s theorem, we have a simple relationship: the squares of the amplitudes add up to unity, |a|2 + |b|2 = 1.
That’s the simple geometric fact underlying the Born rule for quantum probabilities. Amplitudes themselves don’t add up to one, but their squares do. That is exactly like an important feature of probability: the sum of probabilities for different outcomes needs to equal one. (Something has to happen, and the total probability of all exclusive somethings adds up to unity.) Another rule is that probabilities need to be non-negative numbers. Once again, amplitudes squared fit the bill: amplitudes can be negative (or complex), but their squares are non-negative real numbers.
So even before thinking too hard, we can tell that “amplitudes squared” have the right properties to be the probabilities of outcomes—they are a set of non-negative numbers that always add up to one, because that’s the length of the wave function. This is at the heart of the whole matter: the Born rule is essentially Pythagoras’s theorem, applied to the amplitudes of different branches. That’s why it’s the amplitudes squared, not the amplitudes themselves or the square root of the amplitudes or anything crazy like that.
The vector picture also explains the uncertainty principle in an elegant way. Remember that spin-up electrons split fifty-fifty into right-and left-spinning electrons when they passed through a subsequent horizontal magnet. That suggests that an electron in a spin-up state is equivalent to a superposition of spin-right and spin-left electron states, and likewise for spin-down.

So the idea of being spin-left or spin-right isn’t independent from being spin-up or spin-down; any one possibility can be thought of as a superposition of the others. We say that spin-up and spin-down together form a basis for the state of a qubit—any quantum state can be written as a superposition of those two possibilities. But spin-left and spin-right form another basis, distinct but equally good. Writing it one way completely fixes the other way.
Think of this in vector terms. If we draw a two-dimensional plane with spin-up as the horizontal axis and spin-down as the vertical axis, from the above relations we see that spin-right and spin-left point at 45 degrees with respect to them. Given any wave function, we could express it in the up/down basis, but we could equally well express it in the right/left basis. One set of axes is rotated with respect to the other, but they are both perfectly legitimate ways of expressing any vector we like.
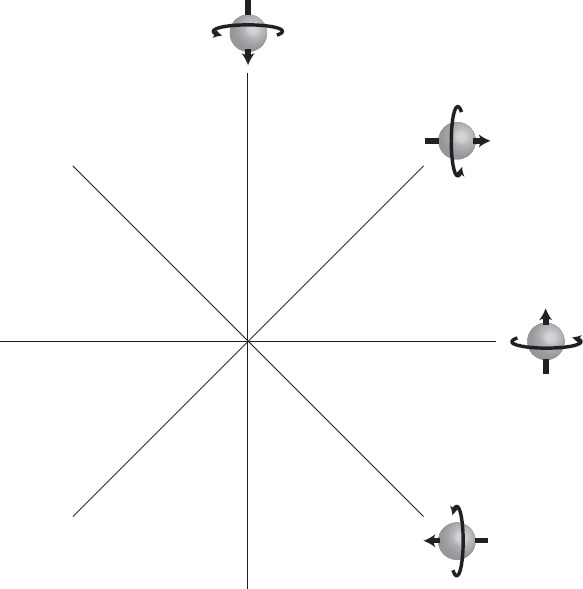
Now we can see where the uncertainty principle comes from. For a single spin, the uncertainty principle says that the state can’t have a definite value for the spin along the original axes (up/down) and the rotated axes (right/left) at the same time. This is clear from the picture: if the state is purely spin-up, it’s automatically some combination of spin-left and spin-right, and vice versa.
Just as there are no quantum states that are simultaneously localized in position and momentum, there are no states that are simultaneously localized in both vertical spin and horizontal spin. The uncertainty principle reflects the relationship between what really exists (quantum states) and what we can measure (one observable at a time).
* And for the third perpendicular direction, which we might call “forward spin,” though we didn’t measure that.