Popular discussions of the Einstein-Bohr debates often give the impression that Einstein couldn’t quite handle the uncertainty principle, and spent his time trying to invent clever ways to circumvent it. But what really bugged him about quantum mechanics was its apparent nonlocality—what happens at one point in space can seemingly have immediate consequences for experiments done very far away. It took him a while to codify his concerns into a well-formulated objection, and in doing so he helped illuminate one of the most profound features of the quantum world: the phenomenon of entanglement.
Entanglement arises because there is only one wave function for the entire universe, not separate wave functions for each piece of it. How do we know that? Why can’t we just have a wave function for every particle or field?
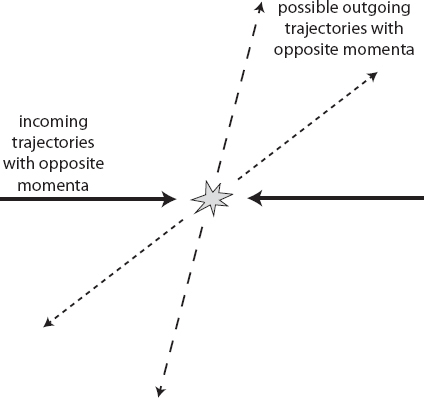
Consider an experiment in which we shoot two electrons at each other, moving with equal and opposite velocities. Because both have a negative electric charge, they will repel each other. Classically, if we were given the initial positions and velocities of the electrons, we could calculate precisely the directions into which each of them would scatter. Quantum-mechanically, all we can do is calculate the probability that they will each be observed on various paths after they interact with each other. The wave function of each particle spreads out in a roughly spherical pattern, until we ultimately observe it and pin down a definite direction in which it was moving.
When we actually do this experiment, and observe the electrons after they have scattered, we notice something important. Since the electrons initially had equal and opposite velocities, the total momentum was zero. And momentum is conserved, so the post-interaction momentum should also be zero. This means that while the electrons might emerge moving in various different directions, whatever direction one of them moves in, the other moves in precisely the opposite.

That’s funny, when you think about it. The first electron has a probability of scattering at various angles, and so does the second one. But if they each had a separate wave function, those two probabilities would be completely unrelated. We could imagine just observing one of the electrons, and measuring the direction in which it’s moving. The other one would be undisturbed. How could it know that it’s supposed to be moving in the opposite direction when we actually do measure it?
We’ve already given away the answer. The two electrons don’t have separate wave functions; their behavior is described by the single wave function of the universe. In this case we can ignore the rest of the universe, and just focus in on these two electrons. But we can’t ignore one of the electrons and focus in on the other; the predictions we make for observations of either one can be dramatically affected by the outcome of observations of the other. The electrons are entangled.
A wave function is an assignment of a complex number, the amplitude, to each possible observational outcome, and the square of the amplitude equals the probability that we would observe that outcome were we to make that measurement. When we’re talking about more than one particle, that means we assign an amplitude to every possible outcome of observing all the particles at once. If what we’re observing is positions, for example, the wave function of the universe can be thought of as assigning an amplitude to every possible combination of positions for all the particles in the universe.
You might wonder whether it’s possible to visualize something like that. We can do it for the simple case of a single particle that we imagine only moves along one dimension, say, an electron confined to a thin copper wire: we draw a line representing the position of the particle, and plot a function representing the amplitude for each position. (Generally we cheat even in this simple context by just plotting a real number rather than a complex number, but so be it.) For two particles confined to the same one-dimensional motion, we could draw a two-dimensional plane representing the positions of each of the two particles, and then do a three-dimensional contour plot for the wave function. Note that this isn’t one particle in two-dimensional space; it’s two particles, each on a one-dimensional space, so the wave function is defined on the two-dimensional plane describing both positions.
Because of the finite speed of light and a finite time since the Big Bang, we can see only a finite region of the cosmos, which we label “the observable universe.” There are approximately 1088 particles in the observable universe, mostly photons and neutrinos. That is a number much greater than two. And each particle is located in three-dimensional space, not just a one-dimensional line. How in the world are we supposed to visualize a wave function that assigns an amplitude to every possible configuration of 1088 particles distributed through three-dimensional space?
We’re not. Sorry. The human imagination wasn’t designed to visualize the enormously big mathematical spaces that are routinely used in quantum mechanics. For just one or two particles, we can muddle through; more than that, and we have to describe things in words and equations. Fortunately, the Schrödinger equation is straightforward and definite in what it says about how the wave function behaves. Once we understand what’s going on for two particles, the generalization to 1088 particles is just maths.

The fact that wave functions are so big can make thinking about them a little unwieldy. Happily we can cast almost everything interesting to say about entanglement into the much simpler context of just a few qubits.
Borrowing from a whimsical tradition in the literature on cryptography, quantum physicists like to consider two people named Alice and Bob who share qubits with each other. So let’s imagine two electrons, A belonging to Alice and B belonging to Bob. The spins of those two electrons constitute a two-qubit system, and are described by a corresponding wave function. The wave function assigns an amplitude to each configuration of the system as a whole, with respect to something we might observe about it, such as its spin in the vertical direction. So there are four possible measurement outcomes: both spins are up, both spins are down, A is up and B is down, and A is down and B is up. The state of the system is some superposition of these four possibilities, which are the basis states. Within each set of parentheses, the first spin is Alice’s, and the second is Bob’s.
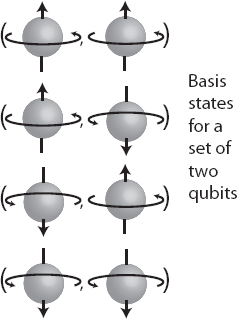
Just because we have two qubits, it doesn’t mean they are necessarily entangled. Consider a state that is simply one of the basis states, say, the one where both qubits are spin-up. If Alice measures her qubit along the vertical axis, she will always obtain spin-up, and likewise for Bob. If Alice measures her spin along the horizontal axis, she has a fifty-fifty chance of getting spin-right or spin-left, and again likewise for Bob. But in each case, we don’t learn anything about what Bob will see by learning what Alice saw. That’s why we can often casually speak of “the wave function of a particle,” even though we know better—when different parts of the system are unentangled with each other, it’s just as if they have their own wave functions.
Instead, let’s consider an equal superposition of two basis states, one with both spins up, and the other with both spins down:

If Alice measures her spin along the vertical axis, she has a fifty-fifty chance of getting spin-up or spin-down, and likewise for Bob. The difference now is that if we learn Alice’s outcome before Bob does his measurement, we know what Bob will see with 100 percent confidence—he’s going to see the same thing that Alice did. In the language of textbook quantum mechanics, Alice’s measurement collapses the wave function onto one of the two basis states, leaving Bob with a deterministic outcome. (In Many-Worlds language, Alice’s measurement branches the wave function, creating two different Bobs, each of whom will get a certain outcome.) That’s entanglement in action.

In the aftermath of the 1927 Solvay Conference, Einstein remained convinced that quantum mechanics, especially as interpreted by the Copenhagen school, did a very good job at making predictions for experimental outcomes, but fell well short as a complete theory of the physical world. His concerns were finally written up for publication in 1935 with his collaborators Boris Podolsky and Nathan Rosen, in a paper that is universally known as simply EPR. Einstein later said that the primary ideas had been his, Rosen had done the calculations, and Podolsky had done much of the writing.
EPR considered the position and momentum of two particles moving in opposite directions, but it’s easier for us to talk about qubits. Consider two spins that are in the entangled state written above. (It’s very easy to create such a state in the lab.) Alice stays home with her qubit, but Bob takes his and embarks on a long journey—say, he jumps in a rocket ship and flies to Alpha Centauri, four light-years away. The entanglement between two particles doesn’t fade away as they are moved apart; as long as neither Alice nor Bob measures the spins of their qubits, the overall quantum state will remain the same.
Once Bob arrives safely at Alpha Centauri, Alice finally does measure the spin of her particle, along an agreed-upon vertical axis. Before that measurement, we were completely unsure what such an observation would reveal for her spin, and likewise for Bob’s. Let’s suppose that Alice observes spin-up. Then, by the rules of quantum mechanics, we immediately know that Bob will also observe spin-up, whenever he gets around to doing a measurement.
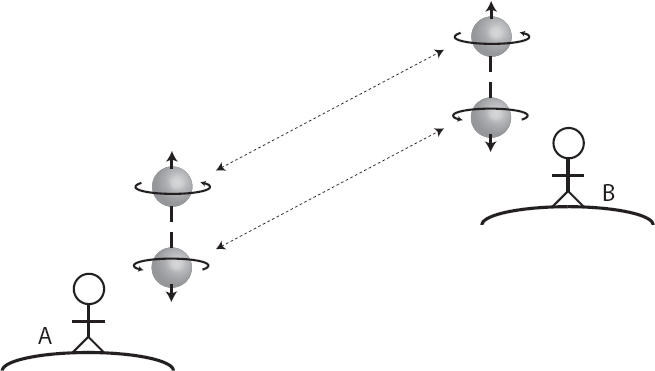
That’s weird. Thirty years earlier, Einstein had established the rules of the special theory of relativity, which says among other things that signals cannot travel faster than the speed of light. And yet here we’re saying that according to quantum mechanics, a measurement that Alice does here and now has an immediate effect on Bob’s qubit, even though it’s four light-years away. How does Bob’s qubit know that Alice’s has been measured, and what the outcome was? This is the “spooky action at a distance” that Einstein so memorably fretted about.
It’s not necessarily as bad as it seems. The first thing you might wonder about, upon being informed that quantum mechanics apparently sends influences faster than the speed of light, is whether or not we could take advantage of this phenomenon to communicate instantly across large distances. Can we build a quantum-entanglement phone, for which the speed of light is not a limitation at all?
No, we can’t. This is pretty clear in our simple example: if Alice measures spin-up, she instantly knows that Bob will also measure spin-up when he gets around to it. But Bob doesn’t know that. In order for him to know what the spin of his particle is, Alice has to send him her measurement result by conventional means—which are limited by the speed of light.
You might think there’s a loophole: What if Alice doesn’t just measure her qubit and find out a random answer, but rather forces her answer to be spin-up? Then Bob would also get spin-up. That would seem like information had been transmitted instantaneously.
The problem is that there’s no straightforward way to start with a quantum system that is in a superposition and measure it in such a way that we can force a particular answer. If Alice simply measures her spin, she’ll get up or down with equal probabilities, no ifs, ands, or buts. What Alice can do is to manipulate her spin before she measures it, forcing it to be 100 percent spin-up rather than in a superposition. For example, she can shoot a photon at her electron, with just the right properties that the photon leaves the electron alone if the electron was spin-up, and flips the electron to spin-up if it was spin-down. Now Alice’s original electron will definitely be measured to be spin-up. But that electron is also no longer entangled with Bob’s electron. Rather, the entanglement has been transferred to the photon, which is in a superposition of “left Alice’s electron alone” and “bumped into Alice’s electron.” Bob’s electron is completely unaffected, and he’s going to get spin-up or spin-down with fifty-fifty probability, so no information has been transmitted.
This is a general feature of quantum entanglement: the no-signaling theorem, according to which an entangled pair of particles cannot actually be used to transmit information between two parties faster than light. So quantum mechanics seems to be exploiting a subtle loophole, violating the spirit of relativity (nothing travels faster than the speed of light) while obeying the letter of the law (actual physical particles, and whatever useful information they might convey, cannot travel faster than the speed of light).

The so-called EPR paradox (which isn’t a paradox at all, just a feature of quantum mechanics) goes beyond simple worries about spooky action at a distance. Einstein aimed to show not only that quantum mechanics was spooky but that it couldn’t possibly be a complete theory—that there had to be some underlying comprehensive model for which quantum mechanics was simply a useful approximation.
EPR believed in the principle of locality—the physical quantities describing nature are defined at specific points in spacetime, not spread out all over the place, and they interact directly only with other quantities nearby, not at a distance. Said another way, given the speed-of-light restriction of special relativity, locality would seem to imply that nothing we can do to a particle at one location can instantaneously affect measurements we might perform on another particle very far away.
On the face of it, the fact that two widely separated particles can be entangled seems to imply that locality is violated in quantum mechanics. But EPR wanted to be a little more thorough, and establish that there wasn’t some clever work-around that would make everything seem local.
They suggested the following principle: if we have a physical system in a specified state, and there is a measurement we can do on that system such that we know with 100 percent certainty what the outcome will be, we associate an element of reality with that measurement outcome. In classical mechanics, the position and the momentum of each particle qualify as elements of reality. In quantum mechanics, if we have a qubit in a pure spin-up state, there is an element of reality corresponding to the spin in the vertical direction, but there need not be an element of reality corresponding to the horizontal spin, as we don’t know what we will get when we measure that. A “complete” theory, in the EPR formulation, is one in which every element of reality has a direct counterpart in the theory itself, and they argued that quantum mechanics couldn’t be complete by this criterion.
Let’s take Alice and Bob and their entangled qubits, and imagine that Alice has just measured the vertical spin of her particle, finding that it points upward. We now know that Bob will also measure spin-up, even if Bob doesn’t know it himself. So by EPR’s lights, there is an element of reality attached to Bob’s particle, saying that the spin is up. It’s not that this element of reality came into existence when Alice did her measurement, as Bob’s particle is very far away, and locality says that the element of reality must be located where the particle is; it must have been there all along.
But now imagine that Alice didn’t do the vertical-spin measurement at all, but instead measured the spin of her particle along the horizontal axis. Let’s say she measures spin-right for the particle. The entangled quantum state we started with ensures us that Bob will get the same result that Alice did, no matter what direction she chooses to measure her spin in. So we know that Bob would also measure spin-right, and by EPR’s lights there is—and was all along—an element of reality that says “spin-right for Bob’s qubit if it’s measured along the horizontal axis.”
There’s no way for either Alice’s particle or Bob’s to know ahead of time which measurement Alice was going to make. Hence, Bob’s qubit must come equipped with elements of reality guaranteeing that its spin would be up if measured vertically, and right if measured horizontally.
That’s exactly what the uncertainty principle says cannot happen. If the vertical spin is exactly determined, the horizontal spin is completely unknown, and vice versa, at least according to the conventional rules of quantum mechanics. There is nothing in the quantum formalism that can determine both a vertical spin and a horizontal spin at the same time. Therefore, EPR triumphantly conclude, there must be something missing—quantum mechanics cannot be a complete description of physical reality.
The EPR paper caused a stir that reached far beyond the community of professional physicists. The New York Times, having been tipped off by Podolsky, published a front-page story about the ideas. This outraged Einstein, who penned a stern letter that the Times published, in which he decried advance discussion of scientific results in the “secular press.” It’s been said that he never spoke to Podolsky again.

The response from professional scientists was also rapid. Niels Bohr wrote a quick reply to the EPR paper, which many physicists claimed resolved all the puzzles. What is less clear is precisely how Bohr’s paper was supposed to have achieved that; as brilliant and creative as he was as a thinker, Bohr was never an especially clear communicator, as he himself admitted. His paper was full of sentences like “in this stage there arises the essential problem of an influence on the precise conditions which define the possible types of prediction which regard the subsequent behavior of the system.” Roughly, his argument was that we shouldn’t go about attributing elements of reality to systems without taking into account how they are going to be observed. What is real, Bohr seems to suggest, depends not only on what we measure, but on how we choose to measure it.

Einstein and his collaborators laid out what they took to be reasonable criteria for a physical theory—locality, and associating elements of reality to deterministically predictable quantities—and showed that quantum mechanics was incompatible with them. But they didn’t conclude that quantum mechanics was wrong, just that it was incomplete. The hope remained alive that we would someday find a better theory that both was local and respected reality.
That hope was definitively squashed by John Stewart Bell, a physicist from Northern Ireland who worked at the CERN laboratory in Geneva, Switzerland. He became interested in the foundations of quantum mechanics in the 1960s, at a point in physics history when it was considered thoroughly disreputable to spend time thinking about such things. Today Bell’s theorem on entanglement is considered one of the most important results in physics.
The theorem asks us to once again consider Alice and Bob and their entangled qubits with aligned spins. (Such quantum states are now known as Bell states, although it was David Bohm who first conceptualized the EPR puzzle in these terms.) Imagine that Alice measures the vertical spin of her particle, and obtains the result that it is spin-up. We now know that if Bob measures the vertical spin of his particle, he will also obtain spin-up. Furthermore, by the ordinary rules of quantum mechanics we know that if Bob chooses to measure the horizontal spin instead, he will get spin-right and spin-left with fifty-fifty probability. We can say that if Bob measures the vertical spin, the correlation between his result and Alice’s will be 100 percent (we know exactly what he’ll get), whereas if he measures horizontal spin, there will be 0 percent correlation (we have no idea what he will get).
So what if Bob, growing bored all by himself in a spaceship orbiting Alpha Centauri, decides to measure the spin of his particle along some axis in between the horizontal and vertical? (For convenience imagine that Alice and Bob actually share a large number of entangled Bell pairs, so they can keep doing these measurements over and over, and we only care about what happens when Alice observes spin-up.) Then Bob will usually, but not always, observe the spin to be pointed along whatever direction is more closely aligned with the vertical “up.” In fact, we can do the maths: if Bob’s axis is at 45 degrees, exactly halfway between vertical and horizontal, there will be a 71 percent correlation between his results and Alice’s. (That’s one over the square root of two, if you’re wondering where the number comes from.)
What Bell showed, under certain superficially reasonable assumptions, is that this quantum-mechanical prediction is impossible to reproduce in any local theory. In fact, he proved a strict inequality: the best you can possibly do without some kind of spooky action at a distance would be to achieve a 50 percent correlation between Alice and Bob if their measurements were rotated by 45 degrees. The quantum prediction of 71 percent correlation violates Bell’s inequality. There is a distinct, undeniable difference between the dream of simple underlying local dynamics, and the real-world predictions of quantum mechanics.
I presume you are currently thinking to yourself, “Hey, what do you mean that Bell made superficially reasonable assumptions? Spell them out. I’ll decide for myself what I find reasonable and what I don’t.”
Fair enough. There are two assumptions behind Bell’s theorem in particular that one might want to doubt. One is contained in the simple idea that Bob “decides” to measure the spin of his qubit along a certain axis. An element of human choice, or free will, seems to have crept into our theorem about quantum mechanics. That’s hardly unique, of course; scientists are always assuming that they can choose to measure whatever they want. But really we think that’s just a convenient way of talking, and even those scientists are composed of particles and forces that themselves obey the laws of physics. So we can imagine invoking superdeterminism—the idea that the true laws of physics are utterly deterministic (no randomness anywhere), and furthermore that the initial conditions of the universe were laid down at the Big Bang in just precisely such a way that certain “choices” are never going to be made. It’s conceivable that one could invent a perfectly local superdeterministic theory that would mimic the predictions of quantum entanglement, simply because the universe was prearranged to make it appear that way. This seems unpalatable to most physicists; if you can delicately arrange your theory to do that, it can basically be arranged to do anything you want, and at that point why are we even doing physics? But some smart people are pursuing the idea.
The other potentially doubtable assumption seems uncontroversial at first glance: that measurements have definite outcomes. When you observe the spin of a particle, you get an actual result, either spin-up or spin-down along whatever axis you are measuring it with respect to. Seems reasonable, doesn’t it?
But wait. We actually know about a theory where measurements don’t have definite outcomes—austere, Everettian quantum mechanics. There, it’s simply not true that we get either up or down when we measure an electron’s spin; in one branch of the wave function we get up, in the other we get down. The universe as a whole doesn’t have any single outcome for that measurement; it has multiple ones. That doesn’t mean that Bell’s theorem is wrong in Many-Worlds; mathematical theorems are unambiguously right, given their assumptions. It just means that the theorem doesn’t apply. Bell’s result does not imply that we have to include spooky action at a distance in Everettian quantum mechanics, as it does for boring old single-world theories. The correlations don’t come about because of any kind of influence being transmitted faster than light, but because of branching of the wave function into different worlds, in which correlated things happen.
For a researcher in the foundations of quantum mechanics, the relevance of Bell’s theorem to your work depends on exactly what it is you’re trying to do. If you have devoted yourself to the task of inventing a new version of quantum mechanics from scratch, in which measurements do have definite outcomes, Bell’s inequality is the most important guidepost you have to keep in mind. If, on the other hand, you’re happy with Many-Worlds and are trying to puzzle out how to map the theory onto our observed experience, Bell’s result is an automatic consequence of the underlying equations, not an additional constraint you need to worry about moving forward.
One of the fantastic things about Bell’s theorem is that it turns the supposed spookiness of quantum entanglement into a straightforwardly experimental question—does nature exhibit intrinsically non-local correlations between faraway particles, or not? You’ll be happy to hear that experiments have been done, and the predictions of quantum mechanics have been spectacularly verified every time. There is a tradition in popular media of writing articles with breathless headlines like “Quantum Reality Is Even More Bizarre Than Previously Believed!” But when you look into the results they are actually reporting, it’s another experiment that confirms exactly what a competent quantum mechanic would have predicted all along using the theory that had been established by 1927, or at least by 1935. We understand quantum mechanics enormously better now than we did back then, but the theory itself hasn’t changed.
Which isn’t to say that the experiments aren’t important or impressive; they are. The problem with testing Bell’s predictions, for example, is that you are trying to make sure that the extra correlations predicted by quantum mechanics couldn’t have arisen due to some sneaky pre-existing classical correlation. How do we know whether some hidden event in the past secretly affected how we chose to measure our spin, or what the measurement outcome was, or both?
Physicists have gone to great lengths to eliminate these possibilities, and a cottage industry has arisen in doing “loophole-free Bell tests.” One recent result wanted to eliminate the possibility that an unknown process in the laboratory worked to influence the choice of how to measure the spin. So instead of letting a lab assistant choose the measurement, or even using a random-number generator sitting on a nearby table, the experiment made that choice based on the polarization of photons emitted from stars many light-years away. If there were some nefarious conspiracy to make the world look quantum-mechanical, it had to have been set up hundreds of years ago, when the light left those stars. It’s possible, but doesn’t seem likely.
It seems that quantum mechanics is right again. So far, quantum mechanics has always been right.