
The 1935 Einstein-Podolsky-Rosen (EPR) paper on quantum entanglement, and Niels Bohr’s response to it, were the last major public salvos in the Bohr-Einstein debates over the foundations of quantum mechanics. Bohr and Einstein had corresponded about quantum theory soon after Bohr proposed his model of quantized electron orbits in 1913, and their dispute came to a head at the 1927 Solvay Conference. In the popular retelling, Einstein would raise some objection to the rapidly coalescing Copenhagen consensus during conversations at the workshop with Bohr, who would spend the evening fretting about it, and then at breakfast Bohr would triumphantly present his rejoinder to the chastened Einstein. We are told that Einstein simply couldn’t come to grips with the fact of the uncertainty principle and the notion that God plays dice with the universe.
That’s not what happened. Einstein’s primary concerns were not with randomness but with realism and locality. His determination to salvage these principles culminated in the EPR paper and their argument that quantum mechanics must be incomplete. But by that time the public-relations battle had been lost, and the Copenhagen approach to quantum mechanics had been adopted by physicists worldwide, who then set about applying quantum mechanics to technical problems in atomic and nuclear physics, as well as the emerging fields of particle physics and quantum field theory. The implications of the EPR paper itself were largely ignored by the community. Wrestling with the confusions at the heart of quantum theory, rather than working on more tangible physics problems, began to be thought of as a somewhat eccentric endeavor. Something that could occupy the time of formerly productive physicists once they reached a certain age and were ready to abandon real work.
In 1933, Einstein left Germany and took a position at the new Institute for Advanced Study in Princeton, New Jersey, where he would remain until his death in 1955. His technical work after 1935 focused largely on classical general relativity and his search for a unified theory of gravitation and electromagnetism, but he never stopped thinking about quantum mechanics. Bohr would occasionally visit Princeton, where he and Einstein would carry on their dialogue.
John Archibald Wheeler joined the physics faculty at Princeton University, down the road from the Institute and Einstein, as an assistant professor in 1934. In later years Wheeler would become known as one of the world’s experts in general relativity, popularizing the terms “black hole” and “wormhole,” but in his early career he concentrated on quantum problems. He had briefly studied under Bohr in Copenhagen, and in 1939 he and Bohr published a pioneering paper on nuclear fission. Wheeler had great admiration for Einstein, but he venerated Bohr; as he would later put it, “Nothing has done more to convince me that there once existed friends of mankind with the human wisdom of Confucius and Buddha, Jesus and Pericles, Erasmus and Lincoln, than walks and talks under the beech trees of Klampenborg Forest with Niels Bohr.”
Wheeler made an impact on physics in a number of ways, one of which was in the mentoring of talented graduate students, including future Nobel laureates such as Richard Feynman and Kip Thorne. One of those students was Hugh Everett III, who would introduce a dramatically new approach to thinking about the foundations of quantum mechanics. We’ve already sketched his basic idea—the wave function represents reality, it evolves smoothly, and that evolution leads to multiple distinct worlds when a quantum measurement takes place—but now we have the tools to do it right.

Everett’s proposal, which eventually became his 1957 PhD thesis at Princeton, can be thought of as the purest incarnation of one of Wheeler’s favorite principles—that theoretical physics should be “radically conservative.” The idea is that a successful physical theory is one that has been tested against experimental data, but only in regimes that experimenters are actually able to reach. One should be conservative, in the sense that we should start with the theories and principles that are already established as successful, rather than arbitrarily introducing new approaches whenever new phenomena are encountered. But one should also be radical, in the sense that the predictions and implications of our theories should be taken seriously in regimes well outside where they have been tested. The phrases “we should start” and “should be taken seriously” are crucial here; of course new theories are warranted when old ones are shown to blatantly contradict the data, and just because a prediction is taken seriously doesn’t mean it shouldn’t be revised in light of new information. But Wheeler’s philosophy was that we should start prudently, with aspects of nature we believe we understand, and then act boldly, extrapolating our best ideas to the ends of the universe.
Part of Everett’s inspiration was the search for a theory of quantum gravity, which Wheeler had recently become interested in. The rest of physics—matter, electromagnetism, the nuclear forces—seems to fit comfortably within the framework of quantum mechanics. But gravity was (and remains) a stubborn exception. In 1915, Einstein proposed the general theory of relativity, according to which spacetime itself is a dynamical entity whose bends and warps are what you and I perceive as the force of gravity. But general relativity is a thoroughly classical theory, with analogues of position and momentum for the curvature of space-time, and no limits on how we might measure them. Taking that theory and “quantizing” it, constructing a theory of wave functions of space-time rather than particular classical spacetimes has proven difficult.

Hugh Everett III
(Courtesy of the Hugh Everett III Archive at the University of California, Irvine, and Mark Everett)
The difficulties of quantum gravity are both technical—calculations tend to blow up and give infinitely big answers—and also conceptual. Even in quantum mechanics, while you might not be able to say precisely where a certain particle is, the notion of “a point in space” is perfectly well defined. We can specify a location and ask what is the probability of finding the particle nearby. But if reality doesn’t consist of stuff distributed through space, but rather is a quantum wave function describing superpositions of different possible spacetimes, how do we even ask “where” a certain particle is observed?
The puzzles become worse when we turn to the measurement problem. By the 1950s the Copenhagen school was established doctrine, and physicists had made their peace with the idea of wave functions collapsing when a measurement occurred. They were even willing to go along with treating the measurement process as a fundamental part of our best description of nature. Or, at least, not to fret too much about it.
But what happens when the quantum system under consideration is the entire universe? Crucial to the Copenhagen approach is the distinction between the quantum system being measured and the classical observer doing the measuring. If the system is the universe as a whole, we are all inside it; there’s no external observer to whom we can appeal. Years later, Stephen Hawking and others would study quantum cosmology to discuss how a self-contained universe could have an earliest moment in time, presumably identified with the Big Bang.
While Wheeler and others thought about the technical challenges of quantum gravity, Everett became fascinated by these conceptual problems, especially how to handle measurement. The seeds of the Many-Worlds formulation can be traced to a late-night discussion in 1954 with fellow young physicists Charles Misner (also a student of Wheeler’s) and Aage Petersen (an assistant of Bohr’s, visiting from Copenhagen). All parties agree that copious amounts of sherry were consumed on the occasion.
Clearly, Everett reasoned, if we’re going to talk about the universe in quantum terms, we can’t carve out a separate classical realm. Every part of the universe will have to be treated according to the rules of quantum mechanics, including the observers within it. There will only be a single quantum state, described by what Everett called the “universal wave function” (and we’ve been calling “the wave function of the universe”).
If everything is quantum, and the universe is described by a single wave function, how is measurement supposed to occur? It must be, Everett reasoned, when one part of the universe interacts with another part of the universe in some appropriate way. That is something that’s going to happen automatically, he noticed, simply due to the evolution of the universal wave function according to the Schrödinger equation. We don’t need to invoke any special rules for measurement at all; things bump into each other all the time.
It’s for this reason that Everett titled his eventual paper on the subject “‘Relative State’ Formulation of Quantum Mechanics.” As a measurement apparatus interacts with a quantum system, the two become entangled with each other. There are no wave-function collapses or classical realms. The apparatus itself evolves into a superposition, entangled with the state of the thing being observed. The apparently definite measurement outcome (“the electron is spin-up”) is only relative to a particular state of the apparatus (“I measured the electron to be spin-up”). The other possible measurement outcomes still exist and are perfectly real, just as separate worlds. All we have to do is to courageously face up to what quantum mechanics has been trying to tell us all along.

Let’s be a little more explicit about what happens when a measurement is made, according to Everett’s theory.
Imagine that we have a spinning electron, which could be observed to be in states of either spin-up or spin-down with respect to some chosen axis. Before measurement, the electron will typically be in some superposition of up and down. We also have a measuring apparatus, which is a quantum system in its own right. Imagine that it can be in superpositions of three different possibilities: it can have measured the spin to be up, it can have measured the spin to be down, or it might not yet have measured the spin at all, which we call the “ready” state.
The fact that the measurement apparatus does its job tells us how the quantum state of the combined spin+apparatus system evolves according to the Schrödinger equation. Namely, if we start with the apparatus in its ready state and the spin in a purely spin-up state, we are guaranteed that the apparatus evolves to a pure measured-up state, like so:
The initial state on the left can be read as “the spin is in the up state, and the apparatus is in its ready state,” while the one on the right, where the pointer indicates the up arrow, is “the spin is in the up state, and the apparatus has measured it to be up.”
Likewise, the ability to successfully measure a pure-down spin implies that the apparatus must evolve from “ready” to “measured down”:

What we want, of course, is to understand what happens when the initial spin is not in a pure up or down state, but in some superposition of both. The good news is that we already know everything we need. The rules of quantum mechanics are clear: if you know how the system evolves starting from two different states, the evolution of a superposition of both those states will just be a superposition of the two evolutions. In other words, starting from a spin in some superposition and the measurement device in its ready state, we have:
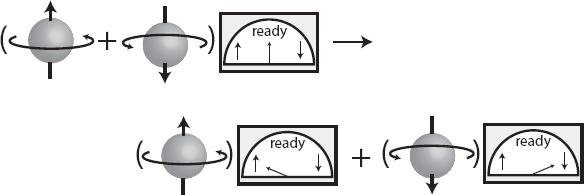
The final state now is an entangled superposition: the spin is up and it was measured to be up, plus the spin is down and it was measured to be down. At this point it’s not strictly correct to say “the spin is in a superposition” or “the apparatus is in a superposition.” Entanglement prevents us from talking about the wave function of the spin, or that of the apparatus, individually, because what we will observe about one can depend on what we observe about the other. The only thing we can say is “the spin+apparatus system is in a superposition.”
This final state is the clear, unambiguous, definitive final wave function for the combined spin+apparatus system, if all we do is evolve it according to the Schrödinger equation. This is the secret to Everettian quantum mechanics. The Schrödinger equation says that an accurate measuring apparatus will evolve into a macroscopic superposition, which we will ultimately interpret as branching into separate worlds. We didn’t put the worlds in; they were always there, and the Schrödinger equation inevitably brings them to life. The problem is that we never seem to come across superpositions involving big macroscopic objects in our experience of the world.
The traditional remedy has been to monkey with the fundamental rules of quantum mechanics in one way or another. Some approaches say that the Schrödinger equation isn’t always applicable, others say that there are additional variables over and above the wave function. The Copenhagen approach is to disallow the treatment of the measurement apparatus as a quantum system in the first place, and treat wave function collapse as a separate way the quantum state can evolve. One way or another, all of these approaches invoke contortions in order to not accept superpositions like the one written above as the true and complete description of nature. As Everett would later put it, “The Copenhagen Interpretation is hopelessly incomplete because of its a priori reliance on classical physics . . . as well as a philosophic monstrosity with a ‘reality’ concept for the macroscopic world and denial of the same for the microcosm.”
Everett’s prescription was simple: stop contorting yourself. Accept the reality of what the Schrödinger equation predicts. Both parts of the final wave function are actually there. They simply describe separate, never-to-interact-again worlds.
Everett didn’t introduce anything new into quantum mechanics; he removed some extraneous clunky pieces from the formalism. Every non-Everettian version of quantum mechanics is, as physicist Ted Bunn has put it, a “disappearing worlds” theory. If the multiple worlds bother you, you have to fiddle with either the nature of quantum states or their ordinary evolution in order to get rid of them. Is it worth it?

There’s a looming question here. We’re familiar with how wave functions represent superpositions of different possible measurement outcomes. The wave function of an electron can put it in a superposition of various possible locations, as well as in a superposition of spin-up and spin-down. But we were never tempted to say that each part of the superposition was a separate “world.” Indeed, it would have been incoherent to do so. An electron that is in a pure spin-up state with respect to the vertical axis is in a superposition of spin-up and spin-down with respect to the horizontal axis. So does that describe one world, or two?
Everett suggested that it is logically consistent to think of superpositions involving macroscopic objects as describing separate worlds. But at the time he was writing, physicists hadn’t yet developed the technical tools necessary to turn this into a complete picture. That understanding only came later, with the appreciation of a phenomenon known as decoherence. Introduced in 1970 by the German physicist Hans Dieter Zeh, the idea of decoherence has become a central part of how physicists think about quantum dynamics. To the modern Everettian, decoherence is absolutely crucial to making sense of quantum mechanics. It explains once and for all why wave functions seem to collapse when you measure quantum systems—and indeed what a “measurement” really is.
We know there is only one wave function, the wave function of the universe. But when we’re talking about individual microscopic particles, they can settle into quantum states where they are unentangled from the rest of the world. In that case, we can sensibly talk about “the wave function of this particular electron” and so forth, keeping in mind that it’s really just a useful shortcut we can employ when systems are unentangled with anything else.
With macroscopic objects, things aren’t that simple. Consider our spin-measuring apparatus, and let’s imagine we put it in a superposition of having measured spin-up and spin-down. The dial of the apparatus includes a pointer that is pointing either to Up or to Down. An apparatus like that doesn’t stay separate from the rest of the world. Even if it looks like it’s just sitting there, in reality the air molecules in the room are constantly bumping into it, photons of light are bouncing off of it, and so on. Call all that other stuff—the entire rest of the universe—the environment. In ordinary situations, there’s no way to stop a macroscopic object from interacting with its environment, even if very gently. Such interactions will cause the apparatus to become entangled with the environment, for example, because a photon would reflect off the dial if the pointer is in one position, but be absorbed by it if the pointer is pointing somewhere else.
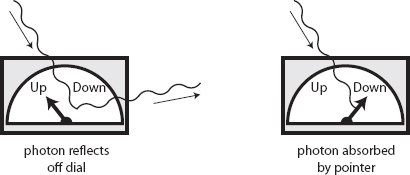
So the wave function we wrote down above, where an apparatus became entangled with a qubit, wasn’t quite the whole story. Putting the environment states in curly braces, we should have written
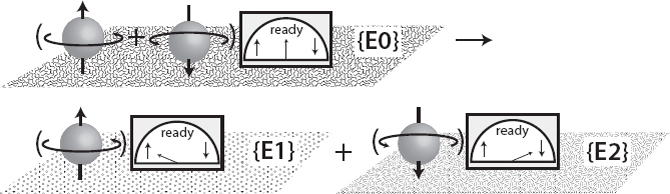
It doesn’t really matter what the environment states actually are, so we’ve portrayed them as different backgrounds labeled {E0}, {E1}, and {E2}. We don’t (and generally can’t) keep track of exactly what’s going on in the environment—it’s too complicated. It’s not going to just be a single photon that interacts differently with different parts of the apparatus’s wave function, it will be a huge number of them. Nobody can be expected to keep track of every photon or particle in a room.
That simple process—macroscopic objects become entangled with the environment, which we cannot keep track of—is decoherence, and it comes with universe-altering consequences. Decoherence causes the wave function to split, or branch, into multiple worlds. Any observer branches into multiple copies along with the rest of the universe. After branching, each copy of the original observer finds themselves in a world with some particular measurement outcome. To them, the wave function seems to have collapsed. We know better; the collapse is only apparent, due to decoherence splitting the wave function.
We don’t know how often branching happens, or even whether that’s a sensible question to ask. It depends on whether there are a finite or infinite number of degrees of freedom in the universe, which is currently an unanswered question in fundamental physics. But we do know that there’s a lot of branching going on; it happens every time a quantum system in a superposition becomes entangled with the environment. In a typical human body, about 5,000 atoms undergo radioactive decay every second. If every decay branches the wave function in two, that’s 25000 new branches every second. It’s a lot.

What makes a “world,” anyway? We just wrote down a single quantum state describing a spin, an apparatus, and an environment. What makes us say that it describes two worlds, rather than just one?
One thing you would like to have in a world is that different parts of it can, at least in principle, affect each other. Consider the following “ghost world” scenario (not meant as a true description of reality, just a colorful analogy): when living beings die, they all become ghosts. These ghosts can see and talk to one another, but they cannot see or talk to us, nor can we see or talk to them. They live on a separate Ghost Earth, where they can build ghost houses and go to their ghost jobs. But neither they nor their surroundings can interact with us and the stuff around us in any way. In this case it makes sense to say that the ghosts inhabit a truly separate ghost world, for the fundamental reason that what happens in the ghost world has absolutely no bearing on what happens in our world.
Now apply this criterion to quantum mechanics. We’re not interested in whether the spin and its measuring apparatus can influence each other—they obviously can. What we care about is whether one component of, say, the apparatus wave function (for example, the piece where the dial is pointing to Up) can possibly influence another piece (for example, where it’s pointing to Down). We’ve previously come across a situation just like this, where the wave function influences itself—in the phenomenon of interference from the double-slit experiment. When we passed electrons through two slits without measuring which one they went through, we saw interference bands on the final screen, and attributed them to the cancellation between the contribution to the total probability from each of the two slits. Crucially, we implicitly assumed that the electron didn’t interact and become entangled with anything along its journey; it didn’t decohere.
When instead we did detect which slit the electron went through, the interference bands went away. At the time we attributed this to the fact that a measurement had been performed, collapsing the electron’s wave function at one slit or another. Everett gives us a much more compelling story to tell.
What actually happened was that the electron became entangled with the detector as it moved through the slits, and then the detector quickly became entangled with the environment. The process is precisely analogous to what happened to our spin above, except that we’re measuring whether the electron went through the left slit L or the right slit R:
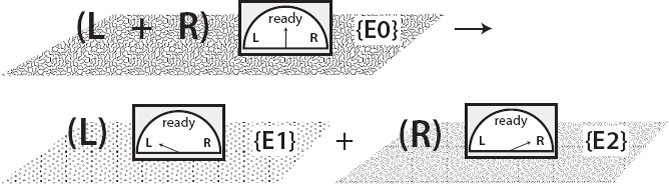
No mysterious collapsing; the whole wave function is still there, evolving cheerfully according to the Schrödinger equation, leaving us in a superposition of two entangled pieces. But note what happens as the electron continues on toward the screen. As before, the state of the electron at any given point on the screen will receive a contribution from what passed through slit L, and another contribution from what passed through slit R. But now those contributions won’t interfere with each other. In order to get interference, we need to be adding up two equal and opposite quantities:
1 + (-1) = 0.
But there is no point on the screen where we will find equal and opposite contributions to the electron’s wave function from the L and R slits, because passing through those slits entangled the electron with different states of the rest of the world. When we say equal and opposite, we mean precisely equal and opposite, not “equal and opposite except for that thing we’re entangled with.” Being entangled with different states of the detector and environment—being decohered, in other words—means that the two parts of the electron’s wave function can no longer interfere with each other. And that means they can’t interact at all. And that means they are, for all intents and purposes, part of separate worlds.* From the point of view of things entangled with one branch of the wave function, the other branches might as well be populated by ghosts.
The Many-Worlds formulation of quantum mechanics removes once and for all any mystery about the measurement process and collapse of the wave function. We don’t need special rules about making an observation: all that happens is that the wave function keeps chugging along in accordance with the Schrödinger equation. And there’s nothing special about what constitutes “a measurement” or “an observer”—a measurement is any interaction that causes a quantum system to become entangled with the environment, creating decoherence and a branching into separate worlds, and an observer is any system that brings such an interaction about. Consciousness, in particular, has nothing to do with it. The “observer” could be an earthworm, a microscope, or a rock. There’s not even anything special about macroscopic systems, other than the fact that they can’t help but interact and become entangled with the environment. The price we pay for such powerful and simple unification of quantum dynamics is a large number of separate worlds.

Everett himself wasn’t familiar with decoherence, so his picture wasn’t quite as robust and complete as the one we’ve painted. But his way of rethinking the measurement problem and offering a unified picture of quantum dynamics was compelling from the start. Even in theoretical physics, people do sometimes get lucky, hitting upon an important idea more because they were in the right place at the right time than because they were particularly brilliant. That’s not the case with Hugh Everett; those who knew him testify uniformly to his incredible intellectual gifts, and it’s clear from his writings that he had a thorough understanding of the implications of his ideas. Were he still alive, he would be perfectly at home in modern discussions of the foundations of quantum mechanics.
What was hard was getting others to appreciate those ideas, and that included his advisor. Wheeler was personally very supportive of Everett, but he was also devoted to his own mentor, Bohr, and was convinced of the basic soundness of the Copenhagen approach. He simultaneously wanted Everett’s ideas to get a wide hearing, and to ensure that they weren’t interpreted as a direct assault on Bohr’s way of thinking about quantum mechanics.
Yet Everett’s theory was a direct assault on Bohr’s picture. Everett himself knew it, and enjoyed illustrating the nature of this assault in vivid language. In an early draft of his thesis, Everett used the analogy of an amoeba dividing to illustrate the branching of the wave function: “One can imagine an intelligent amoeba with a good memory. As time progresses the amoeba is constantly splitting, each time the resulting amoebas having the same memories as the parent. Our amoeba hence does not have a life line, but a life tree.” Wheeler was put off by the blatantness of this (quite accurate) metaphor, scribbling in the margin of the manuscript, “Split? Better words needed.” Advisor and student were constantly tussling over the best way to express the new theory, with Wheeler advocating caution and prudence while Everett favored bold clarity.
In 1956, as Everett was working on finishing his dissertation, Wheeler visited Copenhagen and presented the new scenario to Bohr and his colleagues, including Aage Petersen. He attempted to present it anyway; by this time the wave-functions-collapse-and-don’t-ask-embarrassing-questions-about-exactly-how school of quantum theory had hardened into conventional wisdom, and those who accepted it weren’t interested in revisiting the foundations when there was so much interesting applied work to be done. Letters from Wheeler, Everett, and Petersen flew back and forth across the Atlantic, continuing when Wheeler returned to Princeton and helped Everett craft the final form of his dissertation. The agony of this process is reflected in the evolution of the paper itself: Everett’s first draft was titled “Quantum Mechanics by the Method of the Universal Wave Function,” and a revised version was called “Wave Mechanics Without Probability.” This document, later dubbed the “long version” of the thesis, wasn’t published until 1973. A “short version” was finally submitted for Everett’s PhD as “On the Foundations of Quantum Mechanics,” and eventually published in 1957 as “‘Relative State’ Formulation of Quantum Mechanics.” It omitted many of the juicier sections Everett had originally composed, including examinations of the foundations of probability and information theory and an overview of the quantum measurement problem, focusing instead on applications to quantum cosmology. (No amoebas appear in the published paper, but Everett did manage to insert the word “splitting” in a footnote added in proof while Wheeler wasn’t looking.) Furthermore, Wheeler wrote an “assessment” article that was published alongside Everett’s, which suggested that the new theory was radical and important, while at the same time attempting to paper over its manifest differences with the Copenhagen approach.
The arguments continued, without much headway being made. It is worth quoting from a letter Everett wrote to Petersen, in which his frustration comes through:
Lest the discussion of my paper die completely, let me add some fuel to the fire with . . . criticisms of the ‘Copenhagen interpretation.’ . . . I do not think you can dismiss my viewpoint as simply a misunderstanding of Bohr’s position. . . . I believe that basing quantum mechanics upon classical physics was a necessary provisional step, but that the time has come . . . to treat [quantum mechanics] in its own right as a fundamental theory without any dependence on classical physics, and to derive classical physics from it. . . .
Let me mention a few more irritating features of the Copenhagen Interpretation. You talk of the massiveness of macro systems allowing one to neglect further quantum effects (in discussions of breaking the measuring chain), but never give any justification for this flatly asserted dogma. [And] there is nowhere to be found any consistent explanation for this ‘irreversibility’ of the measuring process. It is again certainly not implied by wave mechanics, nor classical mechanics either. Another independent postulate?
But Everett decided not to continue the academic fight. Before finishing his PhD, he accepted a job at the Weapons Systems Evaluation Group for the US Department of Defense, where he studied the effects of nuclear weapons. He would go on to do research on strategy, game theory, and optimization, and played a role in starting several new companies. It’s unclear the extent to which Everett’s conscious decision to not apply for professorial positions was motivated by criticism of his upstart new theory, or simply by impatience with academia in general.
He did, however, maintain an interest in quantum mechanics, even if he never published on it again. After Everett defended his PhD and was already working for the Pentagon, Wheeler persuaded him to visit Copenhagen for himself and talk to Bohr and others. The visit didn’t go well; afterward Everett judged that it had been “doomed from the beginning.”
Bryce DeWitt, an American physicist who had edited the journal where Everett’s thesis appeared, wrote a letter to him complaining that the real world obviously didn’t “branch,” since we never experience such things. Everett replied with a reference to Copernicus’s similarly daring idea that the Earth moves around the sun, rather than vice versa: “I can’t resist asking: Do you feel the motion of the earth?” DeWitt had to admit that was a pretty good response. After mulling the matter over for a while, by 1970 DeWitt had become an enthusiastic Everettian. He put a great deal of effort into pushing the theory, which had languished in obscurity, toward greater public recognition. His strategies included an influential 1970 article in Physics Today, followed by a 1973 essay collection that included at last the long version of Everett’s dissertation, as well as a number of commentaries. The collection was called simply The Many-Worlds Interpretation of Quantum Mechanics, a vivid name that has stuck ever since.
In 1976, John Wheeler retired from Princeton and took up a position at the University of Texas, where DeWitt was also on the faculty. Together they organized a workshop in 1977 on the Many-Worlds theory, and Wheeler coaxed Everett into taking time off from his defense work in order to attend. The conference was a success, and Everett made a significant impression on the assembled physicists in the audience. One of them was the young researcher David Deutsch, who would go on to become a major proponent of Many-Worlds, as well as an early pioneer of quantum computing. Wheeler went so far as to propose a new research institute in Santa Barbara, where Everett could return to full-time work on quantum mechanics, but ultimately nothing came of it.
Everett died in 1982, age fifty-one, of a sudden heart attack. He had not lived a healthy lifestyle, overindulging in eating, smoking, and drinking. His son, Mark Everett (who would go on to form the band Eels), has said that he was originally upset with his father for not taking better care of himself. He later changed his mind: “I realize that there is a certain value in my father’s way of life. He ate, smoked and drank as he pleased, and one day he just suddenly and quickly died. Given some of the other choices I’d witnessed, it turns out that enjoying yourself and then dying quickly is not such a hard way to go.”
* The set of all branches of the wave function is different from what cosmologists often call “the multiverse.” The cosmological multiverse is really just a collection of regions of space, generally far away from one another, where local conditions look very different.