
One sunny day in Cambridge, England, Elizabeth Anscombe ran into her teacher, Ludwig Wittgenstein. “Why do people say,” Wittgenstein opened in his inimitable fashion, “that it was natural to think that the sun went round the earth, rather than that the earth turned on its axis?” Anscombe gave the obvious answer, that it just looks like the sun goes around the Earth. “Well,” Wittgenstein replied, “what would it have looked like if the Earth had turned on its axis?”
This anecdote—recounted by Anscombe herself, and which Tom Stoppard retold in his play Jumpers—is a favorite among Everettians. Physicist Sidney Coleman used to relate it in lectures, and philosopher of physics David Wallace used it to open his book The Emergent Multiverse. It even bears a family resemblance to Hugh Everett’s remark to Bryce DeWitt.
It’s easy to see why the observation is so relevant. Any reasonable person, when first told about the Many-Worlds picture, has an immediate, visceral objection: it just doesn’t feel like I personally split into multiple people whenever a quantum measurement is performed. And it certainly doesn’t look like there are all sorts of other universes existing parallel to the one I find myself in.
Well, the Everettian replies, channeling Wittgenstein: What would it feel and look like if Many-Worlds were true?
The hope is that people living in an Everettian universe would experience just what people actually do experience: a physical world that seems to obey the rules of textbook quantum mechanics to a high degree of accuracy, and in many situations is well approximated by classical mechanics. But the conceptual distance between “a smoothly evolving wave function” and the experimental data it is meant to explain is quite large. It’s not obvious that the answer we can give to Wittgenstein’s question is the one we want. Everett’s theory might be austere in its formulation, but there’s still a good amount of work to be done to fully flesh out its implications.
In this chapter we’ll confront a major puzzle for Many-Worlds: the origin and nature of probability. The Schrödinger equation is perfectly deterministic. Why do probabilities enter at all, and why do they obey the Born rule: probabilities equal amplitudes—the complex numbers the wave function associates with each possible outcome—squared? Does it even make sense to speak of the probability of ending up on some particular branch if there will be a future version of myself on every branch?
In the textbook or Copenhagen versions of quantum mechanics, there’s no need to “derive” the Born rule for probabilities. We just plop it down there as one of the postulates of the theory. Why couldn’t we do the same thing in Many-Worlds?
The answer is that even though the rule would sound the same in both cases—“probabilities are given by the wave function squared”—their meanings are very different. The textbook version of the Born rule really is a statement about how often things happen, or how often they will happen in the future. Many-Worlds has no room for such an extra postulate; we know exactly what will happen, just from the basic rule that the wave function always obeys the Schrödinger equation. Probability in Many-Worlds is necessarily a statement about what we should believe and how we should act, not about how often things happen. And “what we should believe” isn’t something that really has a place in the postulates of a physical theory; it should be implied by them.
Moreover, as we will see, there is neither any room for an extra postulate, nor any need for one. Given the basic structure of quantum mechanics, the Born rule is natural and automatic. Since we tend to see Born rule–like behavior in nature, this should give us confidence that we’re on the right track. A framework in which an important result can be derived from more fundamental postulates should, all else being equal, be preferred to one where it needs to be separately assumed.
If we successfully address this question, we will have made significant headway toward showing the world we would expect to see if Many-Worlds were true is the world we actually do see. That is, a world that is closely approximated by classical physics, except for quantum measurement events, during which the probability of obtaining any particular outcome is given by the Born rule.

The issue of probabilities is often phrased as trying to derive why probabilities are given by amplitudes squared. But that’s not really the hard part. Squaring amplitudes in order to get probabilities is a very natural thing to do; there weren’t any worries that it might have been the wave function to the fifth power or anything like that. We learned that back in Chapter Five, when we used qubits to explain that the wave function can be thought of as a vector. That vector is like the hypotenuse of a right triangle, and the individual amplitudes are like the shorter sides of that triangle. The length of the vectors equals one, and by Pythagoras’s theorem that’s the sum of the squares of all the amplitudes. So “amplitudes squared” naturally look like probabilities: they’re positive numbers that add up to one.
The deeper issue is why there is anything unpredictable about Everettian quantum mechanics at all, and if so, why there is any specific rule for attaching probabilities. In Many-Worlds, if you know the wave function at one moment in time, you can figure out precisely what it’s going to be at any other time, just by solving the Schrödinger equation. There’s nothing chancy about it. So how in the world is such a picture supposed to recover the reality of our observations, where the decay of a nucleus or the measurement of a spin seems irreducibly random?
Consider our favorite example of measuring the spin of an electron. Let’s say we start the electron in an equal superposition of spin-up and spin-down with respect to the vertical axis, and send it through a Stern-Gerlach magnet. Textbook quantum mechanics says that we have a 50 percent chance of the wave function collapsing to spin-up, and a 50 percent chance of it collapsing to spin-down. Many-Worlds, on the other hand, says there is a 100 percent chance of the wave function of the universe evolving from one world into two. True, in one of those worlds the experimenter will have seen spin-up and in the other they will have seen spin-down. But both worlds are indisputably there. If the question we’re asking is “What is the chance I will end up being the experimenter on the spin-up branch of the wave function?,” there doesn’t seem to be any answer. You will not be one or other experimenters; your current single self will evolve, with certainty, into both of them. How are we supposed to talk about probabilities in such a situation?
It’s a good question. To answer it, we have get a bit philosophical, and think about what “probability” really means.

You will not be surprised to learn that there are competing schools of thought on the issue of probability. Consider tossing a fair coin. “Fair” means that the coin will come up heads 50 percent of the time and tails 50 percent of the time. At least in the long run; nobody is surprised when you toss a coin twice and it comes up tails both times.
This “in the long run” caveat suggests a strategy for what we might mean by probability. For just a few coin tosses, we wouldn’t be surprised at almost any outcome. But as we do more and more, we expect the total proportion of heads to come closer to 50 percent. So perhaps we can define the probability of getting heads as the fraction of times we actually would get heads, if the coin were tossed an infinite number of times.
This notion of what we mean by probability is sometimes called frequentism, as it defines probability as the relative frequency of an occurrence in a very large number of trials. It matches pretty well with our intuitive notions of how probability functions when we toss coins, roll dice, or play cards. To a frequentist, probability is an objective notion, since it only depends on features of the coin (or whatever other system we’re talking about), not on us or our state of knowledge.
Frequentism fits comfortably with the textbook picture of quantum mechanics and the Born rule. Maybe you don’t actually send an infinite number of electrons through a magnetic field to measure their spins, but you could send a very large number. (The Stern-Gerlach experiment is a favorite one to reproduce in undergraduate lab courses for physics majors, so over the years quite a number of spins have been measured this way.) We can gather enough statistics to convince ourselves that the probability in quantum mechanics really is just the wave function squared.
Many-Worlds is a different story. Say we put an electron into an equal superposition of spin-up and spin-down, measure its spin, then repeat a large number of times. At every measurement, the wave function branches into a world with a spin-up result and one with a spin-down. Imagine that we record our results, labeling spin-up as “0” and spin-down as “1.” After fifty measurements, there will be a world where the record looks like
10101011111011001011001010100011101100011101000001.
That seems random enough, and to obey the proper statistics: there are twenty-four 0’s, and twenty-six 1’s. Not exactly fifty-fifty, but as close as we should expect.
But there will also be a world where every measurement returned spin-up, so that the record was just a list of fifty 0’s. And a world where all the spins were observed to be down, so the record was a list of fifty 1’s. And every other possible string of 0’s and 1’s. If Everett is right, there is a 100 percent probability that each possibility is realized in some particular world.
In fact, I’ll make a confession: there really are such worlds. The random-looking string above wasn’t something I made up to look random, nor was it created by a classical random-number generator. It was actually created by a quantum random-number generator: a gizmo that makes quantum measurements and uses them to generate random sequences of 0’s and 1’s. According to Many-Worlds, when I generated that random number, the universe split into 250 copies (that’s 1,125,899,906,842,624, or approximately 1 quadrillion), each of which carries a slightly different number.
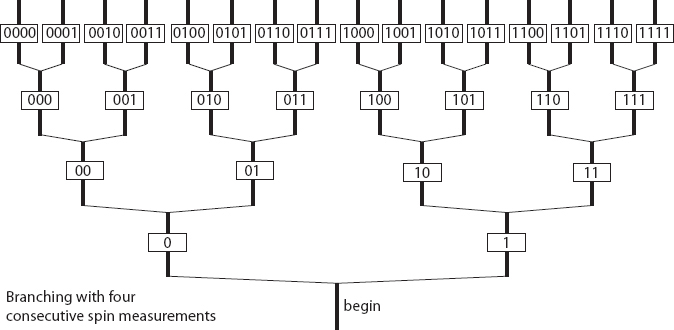
If all of the copies of me in all of those different worlds stuck with the plan of including the obtained number into the text of this book, that means there are over a quadrillion different textual variations of Something Deeply Hidden out there in the wave function of the universe. For the most part the variations will be minor, just rearranging some 0’s and 1’s. But some of those poor versions of me were the unlucky ones who got all 0’s or all 1’s. What are they thinking right now? Probably they thought the random-number generator was broken. They certainly didn’t write precisely the text I am typing at this moment.
Whatever I or the other copies of me might think about this situation, it’s quite different from the frequentist paradigm for probabilities. It doesn’t make too much sense to talk about the frequency in the limit of an infinite number of trials when every trial returns every result, just somewhere else in the wave function. We need to turn to another way of thinking about what probability is supposed to mean.

Fortunately, an alternative approach to probability exists, and long pre-dates quantum mechanics. That’s the notion of epistemic probability, having to do with what we know rather than some hypothetical infinite number of trials.
Consider the question “What is the probability that the Philadelphia 76ers will win the 2020 NBA Championship?” (I put a high value on that personally, but fans of other teams may disagree.) This isn’t the kind of event we can imagine repeating an infinite number of times; if nothing else, the basketball players would grow older, which would affect their play. The 2020 NBA Finals will happen only once, and there is a definite answer to who will win, even if we don’t know what it is. But professional oddsmakers have no qualms about assigning a probability to such situations. Nor do we, in our everyday lives; we are constantly judging the likelihood of different one-shot events, from getting a job we applied for to being hungry by seven p.m. For that matter we can talk about the probability of past events, even though there is a definite thing that happened, simply because we don’t know what that thing was—“I don’t remember what time I left work last Thursday, but it was probably between five p.m. and six p.m., since that’s usually when I head home.”
What we’re doing in these cases is assigning “credences”—degrees of belief—to the various propositions under consideration. Like any probability, credences must range between 0 percent and 100 percent, and your total set of credences for the possible outcomes of a specified event should add up to 100 percent. Your credence in something can change as you gather new information; you might have a degree of belief that a word is spelled a certain way, but then you go look it up and find out the right answer. Statisticians have formalized this procedure under the label of Bayesian inference, after Rev. Thomas Bayes, an eighteenth-century Presbyterian minister and amateur mathematician. Bayes derived an equation showing how we should update our credences when we obtain new information, and you can find his formula on posters and T-shirts in statistics departments the world over.
So there’s a perfectly good notion of “probability” that applies even when something is only going to happen once, not an infinite number of times. It’s a subjective notion, rather than an objective one; different people, in different states of knowledge, might assign different credences to the same outcomes for some event. That’s okay, as long as everyone agrees to follow the rules about updating their credences when they learn something new. In fact, if you believe in eternalism—the future is just as real as the past; we just haven’t gotten there yet—then frequentism is subsumed into Bayesianism. If you flip a random coin, the statement “The probability of the coin coming up heads is 50 percent” can be interpreted as “Given what I know about this coin and other coins, the best thing I can say about the immediate future of the coin is that it is equally likely to be heads or tails, even though there is some definite thing it will be.”
It’s still not obvious that basing probability on our knowledge rather than on frequencies is really a step forward. Many-Worlds is a deterministic theory, and if we know the wave function at one time and the Schrödinger equation, we can figure out everything that’s going to happen. In what sense is there anything that we don’t know, to which we can assign a credence given by the Born rule?
There’s an answer that is tempting but wrong: that we don’t know “which world we will end up in.” This is wrong because it implicitly relies on a notion of personal identity that simply isn’t applicable in a quantum universe.
What we’re up against here is what philosophers call our “folk” understanding of the world around us, and the very different view that is suggested by modern science. The scientific view should ultimately account for our everyday experiences. But we have no right to expect that the concepts and categories that have arisen over the course of pre-scientific history should maintain their validity as part of our most comprehensive picture of the physical world. A good scientific theory should be compatible with our experience, but it might speak an entirely different language. The ideas we readily deploy in our day-to-day lives emerge as useful approximations of certain aspects of a more complete story.
A chair isn’t an object that partakes of a Platonic essence of chairness; it’s a collection of atoms arranged in a certain configuration that makes it sensible for us to include it in the category “chair.” We have no trouble recognizing that the boundaries of this category are somewhat fuzzy—does a sofa count? What about a barstool? If we take something that is indubitably a chair, and remove atoms from it one by one, it gradually becomes less and less chairlike, but there’s no hard-and-fast threshold that it crosses to jump suddenly from chair to non-chair. And that’s okay. We have no trouble accepting this looseness in our everyday speech.
When it comes to the notion of “self,” however, we’re a little more protective. In our everyday experience, there’s nothing very fuzzy about our self. We grow and learn, our body ages, and we interact with the world in a variety of ways. But at any one moment I have no trouble identifying a specific person that is undeniably “myself.”
Quantum mechanics suggests that we’re going to have to modify this story somewhat. When a spin is measured, the wave function branches via decoherence, a single world splits into two, and there are now two people where I used to be just one. It makes no sense to ask which one is “really me.” Likewise, before the branching happens, it makes no sense to wonder which branch “I” will end up in. Both of them have every right to think of themselves as “me.”
In a classical universe, identifying a single individual as a person aging through time is generally unproblematic. At any moment a person is a certain arrangement of atoms, but it’s not the individual atoms that matter; to a large extent our atoms are replaced over time. What matters is the pattern that we form, and the continuity of that pattern, especially in the memories of the person under consideration.
The new feature of quantum mechanics is the duplication of that pattern when the wave function branches. That’s no reason to panic. We just have to adjust our notion of personal identity through time to account for a situation that we never had reason to contemplate over the millennia of pre-scientific human evolution.
As stubborn as our identity is, the concept of a single person extending from birth to death was always just a useful approximation. The person you are right now is not exactly the same as the person you were a year ago, or even a second ago. Your atoms are in slightly different locations, and some of your atoms might have been exchanged for new ones. (If you’re eating while reading, you might have more atoms now than you had a moment ago.) If we wanted to be more precise than usual, rather than talking about “you,” we should talk about “you at 5:00 p.m.,” “you at 5:01 p.m.,” and so on.
The idea of a unified “you” is useful not because all of these different collections of atoms at different moments of time are literally the same, but because they are related to one another in an obvious way. They describe a real pattern. You at one moment descend from you at an earlier moment, through the evolution of the individual atoms within you and the possible addition or subtraction of a few of them. Philosophers have thought this through, of course; Derek Parfit, in particular, suggested that identity through time is a matter of one instance in your life “standing in Relation R” to another instance, where Relation R says that your future self shares psychological continuity with your past self.
The situation in Many-Worlds quantum mechanics is exactly the same way, except that now more than one person can descend from a single previous person. (Parfit would have had no problem with that, and in fact investigated analogous situations featuring duplicator machines.) Rather than talking about “you at 5:01 p.m.,” we need to talk about “the person at 5:01 p.m. who descended from you at 5:00 p.m. and who ended up on the spin-up branch of the wave function,” and likewise for the person on the spin-down branch.
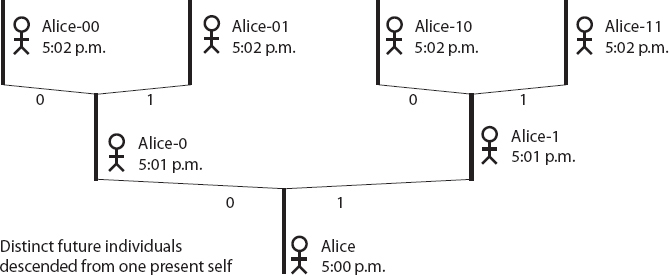
Every one of those people has a reasonable claim to being “you.” None of them is wrong. Each of them is a separate person, all of whom trace their beginnings back to the same person. In Many-Worlds, the life-span of a person should be thought of as a branching tree, with multiple individuals at any one time, rather than as a single trajectory—much like a splitting amoeba. And nothing about this discussion really hinges on what we’re talking about being a person rather than a rock. The world duplicates, and everything within the world goes along with it.

We’re now set up to confront this issue of probabilities in Many-Worlds. It might have seemed natural to think the proper question is “Which branch will I end up on?” But that’s not how we should be thinking about it.
Think instead about the moment immediately after decoherence has occurred and the world has branched. Decoherence is an extraordinarily rapid process, generally taking a tiny fraction of a second to happen. From a human perspective, the wave function branches essentially instantaneously (although that’s just an approximation). So the branching happens first, and we only find out about it slightly later, for example, by looking to see whether the electron went up or down when it passed through the magnetic field.
For a brief while, then, there are two copies of you, and those two copies are precisely identical. Each of them lives on a distinct branch of the wave function, but neither of them knows which one it is on.
You can see where this is going. There is nothing unknown about the wave function of the universe—it contains two branches, and we know the amplitude associated with each of them. But there is something that the actual people on these branches don’t know: which branch they’re on. This state of affairs, first emphasized in the quantum context by physicist Lev Vaidman, is called self-locating uncertainty—you know everything there is to know about the universe, except where you are within it.
That ignorance gives us an opening to talk about probabilities. In that moment after branching, both copies of you are subject to self-locating uncertainty, since they don’t know which branch they’re on. What they can do is assign a credence to being on one branch or the other.
What should that credence be? There are two plausible ways to go. One is that we can use the structure of quantum mechanics itself to pick out a preferred set of credences that rational observers should assign to being on various branches. If you’re willing to accept that, the credences you’ll end up assigning are exactly those you would get from the Born rule. The fact that the probability of a quantum measurement outcome is given by the wave function squared is just what we would expect if that probability arose from credences assigned in conditions of self-locating uncertainty. (And if you’re willing to accept that and don’t want to be bothered with the details, you’re welcome to skip the rest of this chapter.)
But there’s another school of thought, which basically denies that it makes sense to assign any definite credences at all. I can come up with all sorts of wacky rules for calculating probabilities for being on one branch of the wave function or another. Maybe I assign higher probability to being on a branch where I’m happier, or where spins are always pointing up. Philosopher David Albert has (just to highlight the arbitrariness, not because he thinks it’s reasonable) suggested a “fatness measure,” where the probability is proportional to the number of atoms in your body. There’s no reasonable justification for doing so, but who’s to stop me? The only “rational” thing to do, according to this attitude, is to admit that there’s no right way to assign credences, and therefore refuse to do so.
That is a position one is allowed to take, but I don’t think it’s the best one. If Many-Worlds is correct, we are going to find ourselves in situations of self-locating uncertainty whether we like it or not. And if our goal is to come up with the best scientific understanding of the world, that understanding will necessarily involve an assignment of credences in these situations. After all, part of science is predicting what will be observed, even if only probabilistically. If there were an arbitrary collection of ways to assign credences, and each of them seemed just as reasonable as the other, we would be stuck. But if the structure of the theory points unmistakably to one particular way to assign such credences, and that way is in agreement with our experimental data, we should adopt it, congratulate ourselves on a job well done, and move on to other problems.

Let’s say we buy into the idea that there could be a clearly best way to assign credences when we don’t know which branch of the wave function we’re on. Before, we mentioned that, at heart, the Born rule is just Pythagoras’s theorem in action. Now we can be a little more careful and explain why that’s the rational way to think about credences in the presence of self-locating uncertainty.
This is an important question, because if we didn’t already know about the Born rule, we might think that amplitudes are completely irrelevant to probabilities. When you go from one branch to two, for example, why not just assign equal probability to each, since they’re two separate universes? It’s easy to show that this idea, known as branch counting, can’t possibly work. But there’s a more restricted version, which says that we should assign equal probabilities to branches when they have the same amplitude. And that, wonderfully, turns out to be all we need to show that when branches have different amplitudes, we should use the Born rule.
Let’s first dispatch the wrong idea of branch counting before turning to the strategy that actually works. Consider a single electron whose vertical spin has been measured by an apparatus, so that decoherence and branching has occurred. Strictly speaking, we should keep track of the states of the apparatus, observer, and environment, but they just go along for the ride, so we won’t write them explicitly. Let’s imagine that the amplitudes for spin-up and spin-down aren’t equal, but rather we have an unbalanced state Ψ, with unequal amplitudes for the two directions.
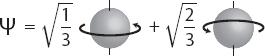
Those numbers outside the different branches are the corresponding amplitudes. Since the Born rule says the probability equals the amplitude squared, in this example we should have a 1/3 probability of seeing spin-up and a 2/3 probability of seeing spin-down.
Imagine that we didn’t know about the Born rule, and were tempted to assign probabilities by simple branch counting. Think about the point of view of the observers on the two branches. From their perspective, those amplitudes are just invisible numbers multiplying their branch in the wave function of the universe. Why should they have anything to do with probabilities? Both observers are equally real, and they don’t even know which branch they’re on until they look. Wouldn’t it be more rational, or at least more democratic, to assign them equal credences?
The obvious problem with that is that we’re allowed to keep on measuring things. Imagine that we agreed ahead of time that if we measured spin-up, we would stop there, but if we measured spin-down, an automatic mechanism would quickly measure another spin. This second spin is in a state of spin-right, which we know can be written as a superposition of spin-up and spin-down. Once we’ve measured it (only on the branch where the first spin was down), we have three branches: one where the first spin was up, one where we got down and then up, and one where we got down twice in a row. The rule of “assign equal probability to each branch” would tell us to assign a probability of 1/3 to each of these possibilities.
That’s silly. If we followed that rule, the probability of the original spin-up branch would suddenly change when we did a measurement on the spin-down branch, going from 1/2 to 1/3. The probability of observing spin-up in our initial experiment shouldn’t depend on whether someone on an entirely separate branch decides to do another experiment later on. So if we’re going to assign credences in a sensible way, we’ll have to be a little more sophisticated than simple branch counting.

Instead of simplistically saying “Assign equal probability to each branch,” let’s try something more limited in scope: “Assign equal probability to branches when they have equal amplitudes.” For example, a single spin in a spin-right state can be written as an equal superposition of spin-up and spin-down.
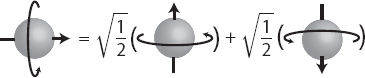
This new rule says we should give 50 percent credence to being on either the spin-up or spin-down branches, were we to observe the spin along the vertical axis. That seems reasonable, as there is a symmetry between the two choices; really, any reasonable rule should assign them equal probability.*
One nice thing about this more modest proposal is that no inconsistency arises with repeated measurements. Doing an extra measurement on one branch but not the other would leave us with branches that have unequal amplitudes again, so the rule doesn’t seem to say anything at all.
But in fact it’s way better than that. If we start with this simple equal-amplitudes-imply-equal-probabilities rule, and ask whether that is a special case of a more general rule that never leads to inconsistencies, we end up with a unique answer. And that answer is the Born rule: probability equals amplitude squared.
We can see this by returning to our unbalanced case, with one amplitude equal to the square root of 1/3 and the other equal to the square root of 2/3. This time we’ll explicitly include a second horizontal spin-right qubit from the start. At first, this second qubit just goes along for the ride.

Insisting on equal probability for equal amplitudes doesn’t tell us anything yet, since the amplitudes are not equal. But we can play the same game we did before, measuring the second spin along the vertical axis if the first spin is down. The wave function evolves into three components, and we can figure out what their amplitudes are by looking back at the decomposition of a spin-right state into vertical spins above. Multiplying the square root of 2/3 by the square root of 1/2 gives the square root of 1/3, so we get three branches, all with equal amplitudes.

Since the amplitudes are equal, we can now safely assign them equal probabilities. Since there are three of them, that’s 1/3 each. And if we don’t want the probability of one branch to suddenly change when something happens on another branch, that means we should have assigned probability 1/3 to the spin-up branch even before we did the second measurement. But 1/3 is just the square of the amplitude of that branch—exactly as the Born rule would predict.

There are a couple of lingering worries here. You may object that we considered an especially simple example, where one probability was exactly twice the other one. But the same strategy works whenever we can subdivide our states into the right number of terms so that all of the amplitudes are equal in magnitude. That works whenever the amplitudes squared are all rational numbers (one integer divided by another one), and the answer is the same: probability equals amplitude squared. There are plenty of irrational numbers out there, but as a physicist if you’re able to prove that something works for all rational numbers, you hand the problem to a mathematician, mumble something about “continuity,” and declare that your work here is done.
We can see Pythagoras’s theorem at work. It’s the reason why a branch that is bigger than another branch by the square root of two can split into two branches of equal size to the other one. That’s why the hard part isn’t deriving the actual formula, it’s providing a solid grounding for what probability means in a deterministic theory. Here we’ve explored one possible answer: it comes from the credences we have for being on different branches of the wave function immediately after the wave function branches.
You might worry, “But I want to know what the probability of getting a result will be even before I do the measurement, not just afterward. Before the branching, there’s no uncertainty about anything—you’ve already told me it’s not right to wonder which branch I’m going to end up on. So how do I talk about probabilities before the measurement is made?”
Never fear. You’re right, imaginary interlocutor, it makes no sense to worry about which branch you’ll end up on. Rather, we know with certainty that there will be two descendants of your present state, and each of them will be on a different branch. They will be identical, and they’ll be uncertain as to which branch they’re on, and they should assign credences given by the Born rule. But that means that all of your descendants will be in exactly the same epistemic position, assigning Born-rule probabilities. So it makes sense that you go ahead and assign those probabilities right now. We’ve been forced to shift the meaning of what probability is from a simple frequentist model to a more robust epistemic picture, but how we calculate things and how we act on the basis of those calculations goes through exactly as before. That’s why physicists have been able to do interesting work while avoiding these subtle questions all this time.
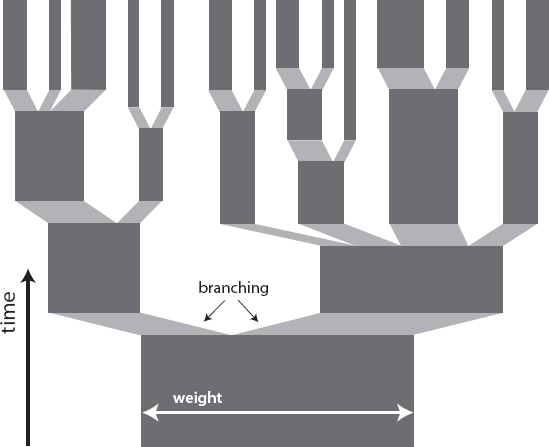
Intuitively, this analysis suggests that the amplitudes in a quantum wave function lead to different branches having a different “weight,” which is proportional to the amplitude squared. I wouldn’t want to take that mental image too literally, but it provides a concrete picture that helps us make sense of probabilities, as well as of other issues like energy conservation that we’ll talk about later.
Weight of a branch = |Amplitude of that branch|2
When there are two branches with unequal amplitudes, we say that there are only two worlds, but they don’t have equal weight; the one with higher amplitude counts for more. The weights of all the branches of any particular wave function always add up to one. And when one branch splits into two, we don’t simply “make more universe” by duplicating the existing one; the total weight of the two new worlds is equal to that of the single world we started with, and the overall weight stays the same. Worlds get thinner as branching proceeds.

This isn’t the only way to derive the Born rule in the Many-Worlds theory. A strategy that is even more popular in the foundations-of-physics community appeals to decision theory—the rules by which a rational agent makes choices in an uncertain world. This approach was pioneered in 1999 by David Deutsch (one of the physicists who had been impressed by Hugh Everett at the Texas meeting in 1977), and later made more rigorous by David Wallace.
Decision theory posits that rational agents attach different amounts of value, or “utility,” to different things that might happen, and then prefer to maximize the expected amount of utility—the average of all the possible outcomes, weighted by their probabilities. Given two outcomes A and B, an agent that assigns exactly twice the utility to B as to A should be indifferent between A happening with certainty and B happening with 50 percent probability. There are a bunch of reasonable-sounding axioms that any good assignment of utilities should obey; for example, if an agent prefers A to B and also prefers B to C, they should definitely prefer A to C. Anyone who goes through life violating the axioms of decision theory is deemed to be irrational, and that’s that.
To use this framework in the context of Many-Worlds, we ask how a rational agent should behave, knowing that the wave function of the universe was about to branch and knowing what the amplitudes of the different branches were going to be. For example, an electron in an equal superposition of spin-up and spin-down is going to travel through a Stern-Gerlach magnet and have its spin be measured. Someone offers to pay you $2 if the result is spin-up, but only if you promise to pay them $1 if the result is spin-down. Should you take the offer? If we trust the Born rule, the answer is obviously yes, since our expected payoff is 0.5($2) + 0.5(-$1) = $0.50. But we’re trying to derive the Born rule here; how are you supposed to find an answer knowing that one of your future selves will be $2 richer but another one will be $1 poorer? (Let’s assume you’re sufficiently well-off that gaining or losing a dollar is something you care about, but not life-changing.)
The manipulations are trickier here than in the previous case where we were explaining probabilities as credences in a situation of self-locating uncertainty, so we won’t go through them explicitly, but the basic idea is the same. First we consider a case where the amplitudes on two different branches are equal, and we show that it’s rational to calculate your expected value as the simple average of the two different utilities. Then suppose we have an unbalanced state like Ψ above, and I ask you to give me $1 if the spin is measured to be up and promise to give you $1 if the spin is down. By a bit of mathematical prestidigitation, we can show that your expected utility in this situation is exactly the same as if there were three possible outcomes with equal amplitudes, such that you give me $1 for one outcome and I give you $1 for the other two. In that case, the expected value is the average of the three different outcomes.
At the end of the day, a rational agent in an Everettian universe acts precisely as if they live in a nondeterministic universe where probabilities are given by the Born rule. Acting otherwise would be irrational, if we accept the various plausible-seeming axioms about what it means to be rational in this context.
One could stubbornly maintain that it’s not good enough to show that people should act “as if” something is true; it needs to actually be true. That’s missing the point a little bit. Many-Worlds quantum mechanics presents us with a dramatically different view of reality from an ordinary one-world view with truly random events. It’s unsurprising that some of our most natural-seeming notions are going to have to change along with it. If we lived in the world of textbook quantum mechanics, where wave-function collapse was truly random and obeyed the Born rule, it would be rational to calculate our expected utility in a certain way. Deutsch and Wallace have shown that if we live in a deterministic Many-Worlds universe, it is rational to calculate our expected utility in exactly the same way. From this perspective, that’s what it means to talk about probability: the probabilities of different events actually occurring are equivalent to the weighting we give those events when we calculate our expected utility. We should act exactly as if the probabilities we’re calculating apply to a single chancy universe; but they are still real probabilities, even though the universe is a little richer than that.
* There are more sophisticated arguments that such a rule follows from very weak assumptions. Wojciech Zurek has proposed a way of deriving such a principle, and Charles Sebens and I put forward an independent argument. We showed that this rule can be derived by insisting that the probabilities you assign for doing an experiment in your lab should be independent of the quantum state elsewhere in the universe.