
David Albert, now a philosophy professor at Columbia and one of the world’s leading researchers in the foundations of quantum mechanics, had a very typical experience as a graduate student who became interested in quantum foundations. He was in the PhD program in the physics department at Rockefeller University when, after reading a book by eighteenth-century philosopher David Hume on the relationship of knowledge and experience, he came to believe that what physics lacked was a good understanding of the quantum measurement problem. (Hume didn’t know about the measurement problem, but Albert connected dots in his head.) Nobody at Rockefeller in the late 1970s was interested in thinking along those lines, so Albert struck up a long-distance collaboration with the famous Israeli physicist Yakir Aharonov, resulting in several influential papers. But when he suggested submitting that work for his PhD thesis, the powers that be at Rockefeller were aghast. Under penalty of being kicked out of the program entirely, Albert was forced to write a separate thesis in mathematical physics. It was, as he recalled, “clearly being assigned because it was thought it would be good for my character. There was an explicitly punitive element there.”
Physicists have been very bad at coming to consensus about what the foundations of quantum mechanics actually are. But in the second half of the twentieth century, they did come to a remarkable degree of consensus on a related issue: whatever the foundations of quantum mechanics are, we certainly shouldn’t talk about them. Not while there was real work to be done, doing calculations and constructing new models of particles and fields.
Everett, of course, left academia without even trying to become a physics professor. David Bohm, who had studied and worked under Robert Oppenheimer in the 1940s, proposed an ingenious way of using hidden variables to address the measurement problem. But after a seminar in which another physicist explained Bohm’s ideas, Oppenheimer scoffed out loud, “If we cannot disprove Bohm, then we must agree to ignore him.” John Bell, who did more than anyone to illuminate the apparently nonlocal nature of quantum entanglement, purposefully hid his work on this subject from his colleagues at CERN, to whom he appeared as a relatively conventional particle theorist. Hans Dieter Zeh, who pioneered the concept of decoherence as a young researcher in the 1970s, was warned by his mentor that working on this subject would destroy his academic career. Indeed, he found it very difficult to publish his early papers, being told by journal referees that “the paper is completely senseless” and “quantum theory does not apply to macroscopic objects.” Dutch physicist Samuel Goudsmit, serving as the editor of Physical Review, put out a memo in 1973 explicitly banning the journal from even considering papers on quantum foundations unless they made new experimental predictions. (Had that policy been in place earlier, the journal would have had to reject the Einstein-Podolsky-Rosen paper, as well as Bohr’s reply.)
Yet, as these very stories make clear, despite a variety of hurdles put up in their way, a subset of physicists and philosophers nevertheless persevered in the effort to better understand the nature of quantum reality. The Many-Worlds theory, especially once the process of wave-function branching has been illuminated by decoherence, is one promising approach to answering the puzzles raised by the measurement problem. But there are others worth considering. They are worthwhile both because they might actually be right (which is always the best reason) and also because comparing the very different ways in which they work helps us to better appreciate quantum mechanics, no matter what our personal favorite approach happens to be.
An impressive number of alternative formulations of quantum theory have been proposed over the years. (The relevant Wikipedia article lists sixteen “interpretations” explicitly, along with a category for “other.”) Here we’ll consider three basic competitors to the Everett approach: dynamical collapse, hidden variables, and epistemic theories. While far from comprehensive, these serve to illustrate the basic strategies that people have taken.

The virtue of Many-Worlds is in the simplicity of its basic formulation: there is a wave function that evolves according to the Schrödinger equation. All else is commentary. Some of that commentary, such as the split into systems and their environment, decoherence, and branching of the wave function, is extremely useful, and indeed indispensable to matching the crisp elegance of the underlying formalism to our messy experience of the world.
Whatever your feelings might be about Many-Worlds, its simplicity provides a good starting point for considering alternatives. If you remain profoundly skeptical that there are good answers to the problem of probability, or are simply repulsed by the idea of all those worlds out there, the task you face is to modify Many-Worlds in some way. Given that Many-Worlds is just “wave functions and the Schrödinger equation,” a few plausible ways forward immediately suggest themselves: altering the Schrödinger equation so that multiple worlds never develop, adding new variables in addition to the wave function, or reinterpreting the wave function as a statement about our knowledge rather than a direct description of reality. All of these roads have been enthusiastically walked down.
We turn first to the possibility of altering the Schrödinger equation. This approach would seem to be squarely in the comfort zone of most physicists; almost before any successful theory has been established, theorists ask how they could play around with the underlying equations to make it even better. Schrödinger himself originally hoped that his equation would describe waves that naturally localized into blobs that behaved like particles when viewed from far away. Perhaps some modification of his equation could achieve that ambition, and even provide a natural resolution to the measurement problem without permitting multiple worlds.
This is harder than it sounds. If we try the most obvious thing, adding new terms like Ψ2 to the equation, we tend to ruin important features of the theory, such as the total set of probabilities adding up to one. This kind of obstacle rarely deters physicists. Steven Weinberg, who developed the successful model that unified the electromagnetic and weak interactions in the Standard Model of particle physics, proposed a clever modification of the Schrödinger equation that manages to maintain the total probability over time. It comes at a cost, however; the simplest version of Weinberg’s theory allows you to send signals faster than light between entangled particles, as opposed to the no-signaling theorem of ordinary quantum mechanics. This flaw can be patched, but then something even weirder occurs: not only are there still other branches of the wave function, but you can actually send signals between them, building what physicist Joe Polchinski dubbed an “Everett phone.” Maybe that’s a good thing, if you want to base your life choices on the outcome of a quantum measurement and then check in with your alternate selves to see which one turned out the best. But it doesn’t seem to be the way that nature actually works. And it doesn’t succeed in solving the measurement problem or getting rid of other worlds.
In retrospect this makes sense. Consider an electron in a pure spin-up state. That can equally well be expressed as an equal superposition of spin-left and spin-right, so that an observation along a horizontal magnetic field has a 50 percent chance of observing either outcome. But precisely because of that equality between the two options, it’s hard to imagine how a deterministic equation could predict that we would see either one or the other (at least without the addition of new variables carrying additional information). Something would have to break the balance between spin-left and spin-right.
We therefore have to think a bit more dramatically. Rather than taking the Schrödinger equation and gently tinkering with it, we can bite the bullet and introduce a completely separate way for wave functions to evolve, one that squelches the appearance of multiple branches. Plenty of experimental evidence assures us that wave functions usually obey the Schrödinger equation, at least when we’re not observing them. But maybe, rarely but crucially, they do something very different.
What might that different thing be? We seek to avoid the existential horror of multiple copies of the macroscopic world being described in a single wave function. So what if we imagined that wave functions undergo occasional spontaneous collapse, converting suddenly from being spread out over different possibilities (say, positions in space) to being relatively well localized around just one point? This is the key new feature of dynamical-collapse models, the most famous of which is GRW theory, after its inventors Giancarlo Ghirardi, Alberto Rimini, and Tullio Weber.
Envision an electron in free space, not bound to any atomic nucleus. According to the Schrödinger equation, the natural evolution of such a particle is for its wave function to spread out and become increasingly diffuse. To this picture, GRW adds a postulate that says at every moment there is some probability that the wave function will change radically and instantaneously. The peak of the new wave function is itself chosen from a probability distribution, the same one that we would have used to predict the position we would measure for the electron according to its original wave function. The new wave function is strongly concentrated around this central point, so that the particle is now essentially in one location as far as we macroscopic observers are concerned. Wave function collapses in GRW are real and random, not induced by measurements.
GRW theory is not some nebulous “interpretation” of quantum mechanics; it is a brand-new physical theory, with different dynamics. In fact, the theory postulates two new constants of nature: the width of the newly localized wave function, and the probability per second that the dynamical collapse will occur. Realistic values for these parameters are perhaps 10-5 centimeters for the width, and 10-16 for the probability of collapse per second. A typical electron therefore evolves for 1016 seconds before its wave function spontaneously collapses. That’s about 300 million years. So in the 14-billion-year lifetime of the observable universe, most electrons (or other particles) localize only a handful of times.
That’s a feature of the theory, not a bug. If you’re going to go messing around with the Schrödinger equation, you had better do it in such a way as to not ruin all of the wonderful successes of conventional quantum mechanics. We do quantum experiments all the time with single particles or collections of a few particles. It would be disastrous if the wave functions of those particles kept spontaneously collapsing on us. If there is a truly random element in the evolution of quantum systems, it should be incredibly rare for individual particles.
Then how does such a mild alteration of the theory manage to get rid of macroscopic superpositions? Entanglement comes to the rescue, much as it did with decoherence in Many-Worlds.
Consider measuring the spin of an electron. As we pass it through a Stern-Gerlach magnet, the wave function of the electron evolves into a superposition of “deflected upward” and “deflected downward.” We measure which way it went, for example, by detecting the deflected electron on a screen, which is hooked up to a dial with a pointer indicating Up or Down. An Everettian says that the pointer is a big macroscopic object that quickly becomes entangled with the environment, leading to decoherence and branching of the wave function. GRW can’t appeal to such a process, but something related happens.
It’s not that the original electron spontaneously collapses; we would have to wait for millions of years for that to become a likely event. But the pointer in the apparatus contains something like 1024 electrons, protons, and neutrons. All of these particles are entangled in an obvious way: they are in different positions depending on whether the pointer indicates Up or Down. Even though it’s quite unlikely that any specific particle will undergo spontaneous collapse before we open the box, chances are extremely good that at least one of them will—that should happen roughly 108 times per second.
You might not be impressed, thinking that we wouldn’t even notice a tiny subset of particles becoming localized in a macroscopic pointer. But the magic of entanglement means that if the wave function of just one particle is spontaneously localized, the rest of the particles with which that one is entangled will come along with it. If somehow the pointer did manage to avoid any of its particles localizing for a certain period of time, enough for it to evolve into a macroscopic superposition of Up and Down, that superposition would instantly collapse as soon as just one of the particles did localize. The overall wave function goes very rapidly from describing an apparatus pointing in a superposition of two answers to one that is definitively one or the other. GRW theory manages to make operational and objective the classical/quantum split that partisans of the Copenhagen approach are forced to invoke. Classical behavior is seen in objects that contain so many particles that it becomes likely that the overall wave function will undergo a series of rapid collapses.
GRW theory has obvious advantages and disadvantages. The primary advantage is that it’s a well-posed, specific theory that addresses the measurement problem in a straightforward way. The multiple worlds of the Everett approach are eliminated by a series of truly unpredictable collapses. We are left with a world that maintains the successes of quantum theory in the microscopic realm, while exhibiting classical behavior macroscopically. It is a perfectly realist account that doesn’t invoke any fuzzy notions about consciousness in its explanation of experimental outcomes. GRW can be thought of as Everettian quantum mechanics plus a random process that cuts off new branches of the wave function as they appear.
Moreover, it is experimentally testable. The two parameters governing the width of localized wave functions and the probability of collapse were not chosen arbitrarily; if their values were very different, they either wouldn’t do the job (collapses would be too rare, or not sufficiently localized) or they would already have been ruled out by experiment. Imagine we have a fluid of atoms in an incredibly low-temperature state, so that every atom is moving very slowly if at all. A spontaneous collapse of the wave function of any electron in the fluid would give its atom a little jolt of energy, which physicists could detect as a slight increase in the temperature of the fluid. Experiments of this form are ongoing, with the ultimate goal of either confirming GRW, or ruling it out entirely.
These experiments are easier said than done, as the amount of energy we’re talking about is very small indeed. Still, GRW is a great example to bring up when your friends complain that Many-Worlds, or different approaches to quantum mechanics more generally, aren’t experimentally testable. You test theories in comparison to other theories, and these two are manifestly different in their empirical predictions.
Among GRW’s disadvantages are the fact that, well, the new spontaneous-collapse rule is utterly ad hoc and out of step with everything else we know about physics. It seems suspicious that nature would not only choose to violate its usual law of motion at random intervals but do so in just such a way that we wouldn’t yet have been able to experimentally detect it.
Another disadvantage, one that has prevented GRW and related theories from gaining traction among theoretical physicists, is that it’s unclear how to construct a version of the theory that works not only for particles but also for fields. In modern physics, the fundamental building blocks of nature are fields, not particles. We see particles when we look closely enough at vibrating fields, simply because those fields obey the rules of quantum mechanics. Under some conditions, it’s possible to think of the field description as useful but not mandatory, and imagine that fields are just ways of keeping track of many particles at once. But there are other circumstances (such as in the early universe, or inside protons and neutrons) where the field-ness is indispensable. And GRW, at least in the simple version presented here, gives us instructions for how wave functions collapse that refers specifically to the probability per particle. This isn’t necessarily an insurmountable obstacle—taking simple models that don’t quite work and generalizing them until they do is the theoretical physicist’s stock-in-trade—but it’s a sign that these approaches don’t seem to fit naturally with how we currently think about the laws of nature.
GRW delineates the quantum/classical boundary by making spontaneous collapses very rare for individual particles, but very rapid for large collections. An alternative approach would be to make collapse occur whenever the system reached a certain threshold, like a rubber band breaking when it is stretched too far. A well-known example of an attempt along these lines was put forward by mathematical physicist Roger Penrose, best known for his work in general relativity. Penrose’s theory uses gravity in a crucial way. He suggests that wave functions spontaneously collapse when they begin to describe macroscopic superpositions in which different components have appreciably different gravitational fields. The criterion of “appreciably different” here turns out to be difficult to specify precisely; single electrons would not collapse no matter how spread-out their wave functions were, while a pointer is large enough to cause collapse as soon as it started evolving into different states.
Most experts in quantum mechanics have not warmed to Penrose’s theory, in part because they are skeptical that gravity should have anything to do with the fundamental formulation of quantum mechanics. Surely, they think, we can talk—and did, for most of the history of the subject—about quantum mechanics and wave-function collapse without considering gravity at all.
It’s possible that a precise version of Penrose’s criterion could be developed in which it is thought of as decoherence in disguise: the gravitational field of an object can be thought of as part of its environment, and if two different components of the wave function have different gravitational fields, they become effectively decohered. Gravity is an extremely weak force, and it will almost always be the case that ordinary electromagnetic interactions will cause decoherence long before gravity would. But the nice thing about gravity is that it’s universal (everything has a gravitational field, not everything is electrically charged), so at least this would be a way to guarantee that the wave function would collapse for any macroscopic object. On the other hand, branching when decoherence occurs is already part of the Many-Worlds approach; all that this kind of spontaneous-collapse theory would say is “It’s just like Everett, except that when new worlds are created, we erase them by hand.” Who knows? That might be how nature actually works, but it’s not a route that most working physicists are encouraged to pursue.

Since the very beginning of quantum mechanics, an obvious possibility to contemplate has been the idea that the wave function isn’t the whole story, but that there are also other physical variables in addition to it. After all, physicists were very used to thinking in terms of probability distributions from their experience with statistical mechanics, as it had been developed in the nineteenth century. We don’t specify the exact position and velocity of every atom in a box of gas, only their overall statistical properties. But in the classical view we take for granted that there is some exact position and velocity for each particle, even if we don’t know it. Maybe quantum mechanics is like that—there are definite quantities associated with prospective observational outcomes, but we don’t know what they are, and the wave function somehow captures part of the statistical reality without telling the whole story.
We know the wave function can’t be exactly like a classical probability distribution. A true probability distribution assigns probabilities directly to outcomes, and the probability of any given event has to be a real number between zero and one (inclusive). A wave function, meanwhile, assigns an amplitude to every possible outcome, and amplitudes are complex numbers. They have both a real and an imaginary part, either one of which could be either positive or negative. When we square such amplitudes we obtain a probability distribution, but if we want to explain what is experimentally observed, we can’t work directly with that distribution rather than keeping the wave function around. The fact that amplitudes can be negative allows for the interference that we see in the double-slit experiment, for example.
There’s a simple way of addressing this problem: think of the wave function as a real, physically existing thing (not just a convenient summary of our incomplete knowledge), but also imagine that there are additional variables, perhaps representing the positions of particles. These extra quantities are conventionally called hidden variables, although some proponents of this approach don’t like the label, as it’s these variables that we actually observe when we make a measurement. We can just call them particles, since that’s the case that is usually considered. The wave function then takes on the role of a pilot wave, guiding the particles as they move around. It’s like particles are little floating barrels, and the wave function describes waves and currents in the water that push the barrels around. The wave function obeys the ordinary Schrödinger equation, while a new “guidance equation” governs how it influences the particles. The particles are guided to where the wave function is large, and away from where it is nearly zero.
The first such theory was presented by Louis de Broglie, at the 1927 Solvay Conference. Both Einstein and Schrödinger were thinking along similar lines at the time. But de Broglie’s ideas were harshly criticized at Solvay, by Wolfgang Pauli in particular. From the records of the conference, it seems as if Pauli’s criticisms were misplaced, and de Broglie actually answered them correctly. But he was sufficiently discouraged by the reception that de Broglie abandoned the idea.
In a famous book from 1932, Mathematical Foundations of Quantum Mechanics, John von Neumann proved a theorem about the difficulty of constructing hidden-variable theories. Von Neumann was one of the most brilliant mathematicians and physicists of the twentieth century, and his name carried enormous credibility among researchers in quantum mechanics. It became standard practice, whenever anyone would suggest that there might be a more definite way to formulate quantum theory than the vagueness inherent in the Copenhagen approach, for someone to invoke the name of von Neumann and the existence of his proof. That would squelch any budding discussion.
In fact what von Neumann had proven was something a bit less than most people assumed (often without reading his book, which wasn’t translated into English until 1955). A good mathematical theorem establishes a result that follows from clearly stated assumptions. When we would like to invoke such a theorem to teach us something about the real world, however, we have to be very careful that the assumptions are actually true in reality. Von Neumann made assumptions that, in retrospect, we don’t have to make if our task is to invent a theory that reproduces the predictions of quantum mechanics. He proved something, but what he proved was not “hidden-variable theories can’t work.” This was pointed out by mathematician and philosopher Grete Hermann, but her work was largely ignored.
Along came David Bohm, an interesting and complicated figure in the history of quantum mechanics. As a graduate student in the early 1940s, Bohm became interested in left-wing politics. He ended up working on the Manhattan Project, but he was forced to do his work in Berkeley, as he was denied the necessary security clearance to move to Los Alamos. After the war he became an assistant professor at Princeton, and published an influential textbook on quantum mechanics. In that book he adhered carefully to the received Copenhagen approach, but thinking through the issues made him start wondering about alternatives.
Bohm’s interest in these questions was encouraged by one of the few figures who had the stature to stand up to Bohr and his colleagues: Einstein himself. The great man had read Bohm’s book, and summoned the young professor to his office to talk about the foundations of quantum theory. Einstein explained his basic objections, that quantum mechanics couldn’t be considered a complete view of reality, and encouraged Bohm to think more deeply about the question of hidden variables, which he proceeded to do.
All this took place while Bohm was under a cloud of political suspicion, at a time when association with Communism could ruin people’s careers. In 1949, Bohm had testified before the House Un-American Activities Committee, where he refused to implicate any of his former colleagues. In 1950 he was arrested in his office at Princeton for contempt of Congress. Though he was eventually cleared of all charges, the president of the university forbade him from setting foot on campus, and put pressure on the physics department to not renew his contract. In 1951, with support from Einstein and Oppenheimer, Bohm was eventually able to find a job at the University of São Paulo, and left for Brazil. That’s why the first seminar at Princeton to explain Bohm’s ideas had to be given by someone else.

None of this drama prevented Bohm from thinking productively about quantum mechanics. Encouraged by Einstein, he developed a theory that was similar to that of de Broglie, in which particles were guided by a “quantum potential” constructed from the wave function. Today this approach is often known as the de Broglie–Bohm theory, or simply Bohmian mechanics. Bohm’s presentation of the theory was a bit more fleshed out than de Broglie’s, especially when it came to describing the measurement process.
Even today you will sometimes hear professional physicists say that it’s impossible to construct a hidden-variable theory that reproduces the predictions of quantum mechanics, “because of Bell’s theorem.” But that’s exactly what Bohm did, at least for the case of non-relativistic particles. John Bell, in fact, was one of the few physicists who was extremely impressed by Bohm’s work, and he was inspired to develop his theorem precisely to understand how to reconcile the existence of Bohmian mechanics with the purported no-hidden-variables theorem of von Neumann.
What Bell’s theorem actually proves is the impossibility of reproducing quantum mechanics via a local hidden-variables theory. Such a theory is what Einstein had long been hoping for: a model that would attach independent reality to physical quantities associated with specific locations in space, with effects between them propagating at or below the speed of light. Bohmian mechanics is perfectly deterministic, but it is resolutely nonlocal. Separated particles can affect each other instantaneously.
Bohmian mechanics posits both a set of particles with definite (but unknown to us, until they are observed) positions, and a separate wave function. The wave function evolves exactly according to the Schrödinger equation—it doesn’t even seem to recognize that the particles are there, and is unaffected by what they are doing. The particles, meanwhile, are pushed around according to a guidance equation that depends on the wave function. However, the way in which any one particle is guided depends not just on the wave function but also on the positions of all the other particles that may be in the system. That’s the nonlocality; the motion of a particle here can depend, in principle, on the positions of other particles arbitrarily far away. As Bell himself later put it, in Bohmian mechanics “the Einstein-Podolsky-Rosen paradox is resolved in the way which Einstein would have liked least.”
This nonlocality plays a crucial role in understanding how Bohmian mechanics reproduces the predictions of ordinary quantum mechanics. Consider the double-slit experiment, which illustrates so vividly how quantum phenomena are simultaneously wave-like (we see interference patterns) and particle-like (we see dots on the detector screen, and interference goes away when we detect which slit the particles go through). In Bohmian mechanics this ambiguity is not mysterious at all: there are both particles and waves. The particles are what we observe; the wave function affects their motion, but we have no way of measuring it directly.
According to Bohm, the wave function evolves through both slits just as it would in Everettian quantum mechanics. In particular, there will be interference effects where the wave function adds or cancels once it reaches the screen. But we don’t see the wave function at the screen; we see individual particles hitting it. The particles are pushed around by the wave function, so that they are more likely to hit the screen where the wave function is large, and less likely to do so where it is small.
The Born rule tells us that the probability of observing a particle at a given location is given by the wave function squared. On the surface, this seems hard to reconcile with the idea that particle positions are completely independent variables that we can specify as we like. And Bohmian mechanics is perfectly deterministic—there aren’t any truly random events, as there are with the spontaneous collapses of GRW theory. So where does the Born rule come from?
The answer is that, while in principle particle positions could be anywhere at all, in practice there is a natural distribution for them to have. Imagine that we have a wave function and some fixed number of particles. To recover the Born rule, all we have to do is start with a Born rule–like distribution of those particles. That is, we have to distribute the positions of our particles so that the distribution looks like it was chosen randomly with probability given by the wave function squared. More particles where the amplitude is large, fewer particles where it is small.
Such an “equilibrium” distribution has the nice feature that the Born rule remains valid as time passes and the system evolves. If we start our particles in a probability distribution that matches what we expect from ordinary quantum mechanics, it will continue to match that expectation going forward. It is believed by many Bohmians that a non-equilibrium initial distribution will evolve toward equilibrium, just as a gas of classical particles in a box evolves toward an equilibrium thermal state; but the status of this idea is not yet settled. The resulting probabilities are, of course, about our knowledge of the system rather than about objective frequencies; if somehow we knew exactly what the particle positions were, rather than just their distribution, we could predict experimental outcomes exactly without any need for probabilities at all.
This puts Bohmian mechanics in an interesting position as an alternative formulation of quantum mechanics. GRW theory matches traditional quantum expectations usually, but also makes definite predictions for new phenomena that can be tested. Like GRW, Bohmian mechanics is unambiguously a different physical theory, not simply an “interpretation.” It doesn’t have to obey the Born rule if for some reason our particle positions are not in an equilibrium distribution. But it will obey the rule if they are. And if that’s the case, the predictions of Bohmian mechanics are strictly indistinguishable from those of ordinary quantum theory. In particular, we will see more particles hit the screen where the wave function is large, and fewer where it is small.
We still have the question of what happens when we look to see which slit the particle has gone through. Wave functions don’t collapse in Bohmian mechanics; as with Everett, they always obey the Schrödinger equation. So how are we supposed to explain the disappearance of the interference pattern in the double-slit experiment?
The answer is “the same way we do in Many-Worlds.” While the wave function doesn’t collapse, it does evolve. In particular, we should consider the wave function for the detection apparatus as well as for the electrons going through the slits; the Bohmian world is completely quantum, not stooping to an artificial split between classical and quantum realms. As we know from thinking about decoherence, the wave function for the detector will become entangled with that of an electron passing through the slit, and a kind of “branching” will occur. The difference is that the variables describing the apparatus (which aren’t there in Many-Worlds) will be at locations corresponding to one of these branches, and not the other. For all intents and purposes, it’s just like the wave function has collapsed; or, if you prefer, it’s just like decoherence has branched the wave function, but instead of assigning reality to each of the branches, the particles of which we are made are only located on one particular branch.
You won’t be surprised to hear that many Everettians are dubious about this kind of story. If the wave function of the universe simply obeys the Schrödinger equation, it will undergo decoherence and branching. And you’ve already admitted that the wave function is part of reality. The particle positions, for that matter, have absolutely no influence on how the wave function evolves. All they do, arguably, is point to a particular branch of the wave function and say, “This is the real one.” Some Everettians have therefore claimed that Bohmian mechanics isn’t really any different from Everett, it just includes some superfluous extra variables that serve no purpose but to assuage some anxieties about splitting into multiple copies of ourselves. As Deutsch has put it, “Pilot-wave theories are parallel-universe theories in a state of chronic denial.”
We won’t adjudicate this dispute right here. What’s clear is that Bohmian mechanics is an explicit construction that does what many physicists thought was impossible: to construct a precise, deterministic theory that reproduces all of the predictions of textbook quantum mechanics, without requiring any mysterious incantations about the measurement process or a distinction between quantum and classical realms. The price we pay is explicit nonlocality in the dynamics.

Bohm was hopeful that his new theory would be widely appreciated by physicists. This was not to be. In the emotionally charged language that so often accompanies discussions of quantum foundations, Heisenberg called Bohm’s theory “a superfluous ideological superstructure,” while Pauli referred to it as “artificial metaphysics.” We’ve already heard the judgment of Oppenheimer, who had previously been Bohm’s mentor and supporter. Einstein seems to have appreciated Bohm’s effort, but thought the final construction was artificial and unconvincing. Unlike de Broglie, however, Bohm didn’t bow to the pressure, and continued to develop and advocate for his theory. Indeed, his advocacy inspired de Broglie himself, who was still around and active (he died in 1987). In his later years de Broglie returned to hidden-variable theories, developing and elaborating his original model.
Even apart from the presence of explicit nonlocality and the accusation that the theory is just Many-Worlds in denial, there are other significant problems inherent in Bohmian mechanics, especially from the perspective of a modern fundamental physicist. The list of ingredients in the theory is undoubtedly more complicated than in Everett, and Hilbert space, the set of all possible wave functions, is as big as ever. The possibility of many worlds is not avoided by erasing the worlds (as in GRW), but simply by denying that they’re real. The way Bohmian dynamics works is far from elegant. Long after classical mechanics was superseded, physicists still intuitively cling to something like Newton’s third law: if one thing pushes on another, the second thing pushes back. It therefore seems strange that we have particles that are pushed around by a wave function, while the wave function is completely unaffected by the particles. Of course, quantum mechanics inevitably forces us to confront strange things, so perhaps this consideration should not be paramount.
More important, the original formulations of de Broglie and Bohm both rely heavily on the idea that what really exists are “particles.” Just as with GRW, this creates a problem when we try to understand the best models of the world that we actually have, which are quantum field theories. People have proposed ways of “Bohmizing” quantum field theory, and there have been some successes—physicists can be extremely clever when they want to be. But the results feel forced rather than natural. It doesn’t mean they are necessarily wrong, but it’s a strike against Bohmian theories when compared to Many-Worlds, where including fields or quantum gravity is straightforward.
In our discussion of Bohmian mechanics we referred to the positions of the particles, but not to their momenta. This hearkens back to the days of Newton, who thought of particles as having a position at every moment in time, and velocity (and momentum) as derived from that trajectory, by calculating its rate of change. More modern formulations of classical mechanics (well, since 1833) treat position and momentum on an equal footing. Once we go to quantum mechanics, this perspective is reflected in the Heisenberg uncertainty principle, in which position and momentum appear in exactly the same way. Bohmian mechanics undoes this move, treating position as primary, and momentum as something that derived from it. But it turns out that you can’t measure it exactly, due to unavoidable effects of the wave function on the particle positions over time. So at the end of the day, the uncertainty principle remains true in Bohmian mechanics as a practical fact of life, but it doesn’t have the automatic naturalness of theories in which the wave function is the only real entity.
There is a more general principle at work here. The simplicity of Many-Worlds also makes it extremely flexible. The Schrödinger equation takes the wave function and figures out how fast it will evolve by applying the Hamiltonian, which measures the different amounts of energy in different components of the quantum state. You give me a Hamiltonian, and I can instantly understand the Everettian version of its corresponding quantum theory. Particles, spins, fields, superstrings, doesn’t matter. Many-Worlds is plug-and-play.
Other approaches require a good deal more work than that, and it’s far from clear that the work is even doable. You have to specify not only a Hamiltonian but also a particular way in which wave functions spontaneously collapse, or a particular new set of hidden variables to keep track of. That’s easier said than done. The problem becomes even more pronounced when we move from quantum field theory to quantum gravity (which, remember, was one of Everett’s initial motivations). In quantum gravity the very notion of “a location in space” becomes problematic, as different branches of the wave function will have different spacetime geometries. For Many-Worlds that’s no problem; for alternatives it’s close to a disaster.
When Bohm and Everett were inventing their alternatives to Copenhagen in the 1950s, or Bell was proving his theorems in the 1960s, work on foundations of quantum mechanics was shunned within the physics community. That began to change somewhat with the advent of decoherence theory and quantum information in the 1970s and ’80s; GRW theory was proposed in 1985. While this subfield is still looked upon with suspicion by a large majority of physicists (for one thing, it tends to attract philosophers), an enormous amount of interesting and important work has been accomplished since the 1990s, much of it wide out in the open. However, it’s also safe to say that much contemporary work on quantum foundations still takes place in a context of qubits or non-relativistic particles. Once we graduate to quantum fields and quantum gravity, some things we could previously take for granted are no longer available. Just as it is time for physics as a field to take quantum foundations seriously, it’s time for quantum foundations to take field theory and gravity seriously.

In contemplating ways to eliminate the many worlds implied by a bare-bones version of the underlying quantum formalism, we have explored chopping off the worlds by a random event (GRW) or reaching some kind of threshold (Penrose) or picking out particular worlds as real by adding additional variables (de Broglie–Bohm). What’s left?
The problem is that the appearance of multiple branches of the wave function is automatic once we believe in wave functions and the Schrödinger equation. So the alternatives we have considered thus far either eliminate those branches or posit something that picks out one of them as special.
A third way suggests itself: deny the reality of the wave function entirely.
By this we don’t mean to deny the central importance of wave functions in quantum mechanics. Rather, we can use wave functions, but we might not claim that they represent part of reality. They might simply characterize our knowledge; in particular, the incomplete knowledge we have about the outcome of future quantum measurements. This is known as the “epistemic” approach to quantum mechanics, as it thinks of wave functions as capturing something about what we know, as opposed to “ontological” approaches that treat the wave function as describing objective reality. Since wave functions are usually denoted by the Greek letter Ψ (Psi), advocates of epistemic approaches to quantum mechanics sometimes tease Everettians and other wave-function-realists by calling them “Psi-ontologists.”
We’ve already noted that an epistemic strategy cannot work in the most naïve and straightforward way. The wave function is not a probability distribution; real probability distributions are never negative, so they can’t lead to interference phenomena such as we observe in the double-slit experiment. Rather than giving up, however, we can try to be a bit more sophisticated in how we think about the relationship between the wave function and the real world. We can imagine building up a formalism that allows us to use wave functions to calculate the probabilities associated with experimental outcomes, while not attaching any underlying reality to them. This is the task taken up by epistemic approaches.
There have been many attempts to interpret the wave function epistemically, just as there are competing collapse models or hidden-variable theories. One of the most prominent is Quantum Bayesianism, developed by Christopher Fuchs, Rüdiger Schack, Carlton Caves, N. David Mermin, and others. These days the label is typically shortened to QBism and pronounced “cubism.” (One must admit it’s a charming name.)
Bayesian inference suggests that we all carry around with us a set of credences for various propositions to be true or false, and update those credences when new information comes in. All versions of quantum mechanics (and indeed all scientific theories) use Bayes’s theorem in some version or another, and in many approaches to understanding quantum probability it plays a crucial role. QBism is distinguished by making our quantum credences personal, rather than universal. According to QBism, the wave function of an electron isn’t a once-and-for-all thing that everyone could, in principle, agree on. Rather, everyone has their own idea of what the electron’s wave function is, and uses that idea to make predictions about observational outcomes. If we do many experiments and talk to one another about what we’ve observed, QBists claim, we will come to a degree of consensus about what the various wave functions are. But they are fundamentally measures of our personal belief, not objective features of the world. When we see an electron deflected upward in a Stern-Gerlach magnetic field, the world doesn’t change, but we’ve learned something new about it.
There is one immediate and undeniable advantage of such a philosophy: if the wave function isn’t a physical thing, there’s no need to fret about it “collapsing,” even if that collapse is purportedly nonlocal. If Alice and Bob possess two particles that are entangled with each other and Alice makes a measurement, according to the ordinary rules of quantum mechanics the state of Bob’s particle changes instantaneously. QBism reassures us that we needn’t worry about that, as there is no such thing as “the state of Bob’s particle.” What changed was the wave function that Alice carries around with her to make predictions: it was updated using a suitably quantum version of Bayes’s theorem. Bob’s wave function didn’t change at all. QBism arranges the rules of the game so that when Bob does get around to measuring his particle, the outcome will agree with the prediction we would make on the basis of Alice’s measurement outcome. But there is no need along the way to imagine that any physical quantity changed over at Bob’s location. All that changes are different people’s states of knowledge, which after all are localized in their heads, not spread through all space.
Thinking about quantum mechanics in QBist terms has led to interesting developments in the mathematics of probability, and offers insight into quantum information theory. Most physicists, however, will still want to know: What is reality supposed to be in this view? (Abraham Pais recalled that Einstein once asked him whether he “really believed that the moon exists only when I look at it.”)
The answer is not clear. Imagine that we send an electron through a Stern-Gerlach magnet, but we choose not to look at whether it’s deflected up or down. For an Everettian, it is nevertheless the case that decoherence and branching has occurred, and there is a fact of the matter about which branch any particular copy of ourselves is on. The QBist says something very different: there is no such thing as whether the spin was deflected up or down. All we have is our degrees of belief about what we will see when we eventually decide to look. There is no spoon, as Neo learned in The Matrix. Fretting about the “reality” of what’s going on before we look, in this view, is a mistake that leads to all sorts of confusion.
QBists, for the most part, don’t talk about what the world really is. Or at least, as an ongoing research program, QBists have chosen not to dwell too much on the questions concerning the nature of reality about which the rest of us care so much. The fundamental ingredients of the theory are a set of agents, who have beliefs, and accumulate experiences. Quantum mechanics, in this view, is a way for agents to organize their beliefs and update them in the light of new experiences. The idea of an agent is absolutely central; this is in stark contrast to the other formulations of quantum theory that we’ve been discussing, according to which observers are just physical systems like anything else.
Sometimes QBists will talk about reality as something that comes into existence as we make observations. Mermin has written, “There is indeed a common external world in addition to the many distinct individual personal external worlds. But that common world must be understood at the foundational level to be a mutual construction that all of us have put together from our distinct private experiences, using our most powerful human invention: language.” The idea is not that there is no reality, but that reality is more than can be captured by any seemingly objective third-person perspective. Fuchs has dubbed this view Participatory Realism: reality is the emerging totality of what different observers experience.
QBism is relatively young as approaches to quantum foundations go, and there is much development yet to be done. It’s possible that it will run into insurmountable roadblocks, and interest in the ideas will fizzle out. It’s also possible that the insights of QBism can be interpreted as a sometimes-useful way of talking about the experiences of observers within some other, straightforwardly realist, version of quantum mechanics. And finally, it might be that QBism or something close to it represents a true, revolutionary way of thinking about the world, one that puts agents like you and me at the center of our best description of reality.
Personally, as someone who is quite comfortable with Many-Worlds (while recognizing that we still have open questions), this all seems to me like an incredible amount of effort devoted to solving problems that aren’t really there. QBists, to be fair, feel a similar level of exasperation with Everett: Mermin has said that “QBism regards [branching into many simultaneously existing worlds] as the reductio ad absurdum of reifying the quantum state.” That’s quantum mechanics for you, where one person’s absurdity is another person’s answer to all of life’s questions.

The foundations-of-physics community, which is full of smart people who have thought long and hard about these issues, has not reached a consensus on the best approach to quantum mechanics. One reason is that people come to the problem from different backgrounds, and therefore with different concerns foremost in their minds. Researchers in fundamental physics—particle theory, general relativity, cosmology, quantum gravity—tend to favor the Everett approach, if they deign to take a position on quantum foundations at all. That’s because Many-Worlds is extremely robust to the underlying physical stuff it is describing. You give me a set of particles and fields and what have you, and rules for how they interact, and it’s straightforward to fit those elements into an Everettian picture. Other approaches tend to be more persnickety, demanding that we start from scratch to figure out what the theory actually says in each new instance. If you’re someone who admits that we don’t really know what the underlying theory of particles and fields and spacetime really is, that sounds exhausting, whereas Many-Worlds is a natural easy resting place. As David Wallace has put it, “The Everett interpretation (insofar as it is philosophically acceptable) is the only interpretative strategy currently suited to make sense of quantum physics as we find it.”
But there is another reason, more based in personal style. Essentially everyone agrees that simple, elegant ideas are to be sought after as we search for scientific explanations. Being simple and elegant doesn’t mean an idea is correct—that’s for the data to decide—but when there are multiple ideas vying for supremacy and we don’t yet have enough data to choose among them, it’s natural to give a bit more credence to the simplest and most elegant ones.
The question is, who decides what’s simple and elegant? There are different senses of these terms. Everettian quantum mechanics is absolutely simple and elegant from a certain point of view. A smoothly evolving wave function, that’s all. But the result of these elegant postulates—a proliferating tree of multiple universes—is arguably not very simple at all.
Bohmian mechanics, on the other hand, is constructed in a kind of haphazard way. There are both particles and wave functions, and they interact through a nonlocal guidance equation that seems far from elegant. Including both particles and wave functions as fundamental ingredients is, however, a natural strategy to contemplate, once we have been confronted with the basic experimental demands of quantum mechanics. Matter acts sometimes like waves and sometimes like particles, so we invoke both waves and particles. GRW theory, meanwhile, adds a weird ad hoc stochastic modification to the Schrödinger equation. But it’s arguably the simplest, most brute-force way to physically implement the fact that wave functions appear to collapse.
There is a useful contrast to be drawn between the simplicity of a physical theory and the simplicity with which that theory maps onto reality as we observe it. In terms of basic ingredients, Many-Worlds is unquestionably as simple as it gets. But the distance between what the theory itself says (wave functions, Schrödinger equation) and what we observe in the world (particles, fields, spacetime, people, chairs, stars, planets) seems enormous. Other approaches might be more baroque in their underlying principles, but it’s relatively clear how they account for what we see.
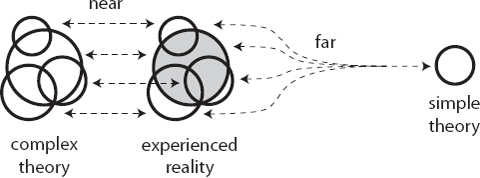
Both underlying simplicity and closeness to the phenomena are virtues in their own rights, but it’s hard to know how to balance them against each other. This is where personal style comes in. All of the approaches to quantum mechanics that we’ve considered face looming challenges as we contemplate developing them into rock-solid foundations for an understanding of the physical world. So each of us has to make a personal judgment about which of these problems will eventually be solved, and which will prove fatal for the various approaches. That’s okay; indeed, it’s crucial that different people come down differently on these judgments about how to move forward. That gives us the best chance to keep multiple ideas alive, maximizing the probability that we’ll eventually get things right.
Many-Worlds offers a perspective on quantum mechanics that is not only simple and elegant at its core but seems ready-made for adapting to the ongoing quest to understand quantum field theory and the nature of spacetime. That’s enough to convince me that I should learn to live with the annoyance of other copies of me being produced all the time. But if it turns out that an alternative approach answers our deepest questions more effectively, I’ll happily change my mind.