
Quantum field theory is able to successfully account for every experiment ever performed by human beings. When it comes to describing reality, it’s the best approach we have. It’s therefore extremely tempting to imagine that future physical theories will be set within the broad paradigm of quantum field theory, or perhaps small variations thereof.
But gravity, at least when it becomes strong, doesn’t seem to be well described by quantum field theory. So in this chapter we’ll ask whether we can make progress by attacking the problem from a different angle.
Following Feynman, physicists love to remind one another that nobody really understands quantum mechanics. Meanwhile, they have long lamented that nobody understands quantum gravity. Maybe these two lacks of understanding are related. Gravity, which describes the state of spacetime itself rather than just particles or fields moving within spacetime, presents special challenges when we try to describe it in quantum terms. Perhaps that shouldn’t be surprising, if we don’t think we fully understand quantum mechanics itself. It’s possible that thinking about the foundations of quantum theory—in particular, the Many-Worlds perspective that the world is just a wave function, and everything else emerges out of that—will shed new light on how curved spacetime emerges from quantum underpinnings.
Our self-appointed task is one of reverse engineering. Rather than taking classical general relativity and quantizing it, we will try to find gravity within quantum mechanics. That is, we will take the basic ingredients of quantum theory—wave functions, Schrödinger’s equation, entanglement—and ask under what circumstances we can obtain emergent branches of the wave function that look like quantum fields propagating in a curved spacetime.
Up to this point in the book, basically everything we’ve talked about is either well understood and established doctrine (such as the essentials of quantum mechanics), or at least a plausible and respectable hypothesis (the Many-Worlds approach). Now we’ve reached the edge of what is safely understood, and will be venturing out into uncharted territory. We’ll be looking at speculative ideas that might be important to understanding quantum spacetime and cosmology. But they might not be. Only years, possibly decades, of further investigation will reveal the answer with any confidence. By all means take these ideas as provocations to further thinking, and keep an eye on where the discussion goes in times to come, but keep in mind the intrinsic uncertainty that comes with wrestling with hard problems at the bleeding edge of our understanding.

Albert Einstein once mused to a colleague, “On quantum theory I use more brain grease than relativity.” But it was his contributions to relativity that made him an intellectual superstar.
Like “quantum mechanics,” “relativity” does not refer to a specific physical theory, but rather a framework within which theories can be constructed. Theories that are “relativistic” share a common picture of the nature of space and time, one in which the physical world is described by events happening in a single unified “spacetime.” Even before relativity, it was still possible to talk about spacetime in Newtonian physics: there is three-dimensional space, and one dimension of time, and to locate an event in the universe you have to specify both where the event is in space and when it occurs in time. But before Einstein, there wasn’t much motivation for combining them into a single four-dimensional concept. Once relativity came along, that became a natural step.
There are two big ideas that go under the name of “the theory of relativity,” the special theory and the general theory. Special relativity, which came together in 1905, is based on the idea that everyone measures light to travel at the same speed in empty space. Combining that insight with an insistence that there is no absolute frame of motion leads us directly to the idea that time and space are “relative.” Spacetime is universal and agreed upon by everyone, but how we divvy it up into “space” and “time” will be different for different observers.
Special relativity is a framework that includes many specific physical theories, all of which are dubbed “relativistic.” Classical electromagnetism, put together by James Clerk Maxwell in the 1860s, is a relativistic theory even though it was invented before relativity; the need to better understand the symmetries of electromagnetism was a driving force behind why relativity was invented in the first place. (Sometimes people misuse the word “classical” to include “non-relativistic,” but it’s better to reserve it to mean “non-quantum.”) Quantum mechanics and special relativity are 100 percent compatible with each other. The quantum field theories used in modern particle physics are relativistic to their cores.
The other big idea in relativity came ten years later, when Einstein proposed general relativity, his theory of gravity and curved spacetime. The crucial insight was that four-dimensional spacetime isn’t just a static background on which the interesting parts of physics take place; it has a life of its own. Spacetime can bend and warp, and does so in response to the presence of matter and energy. We grow up learning about the flat geometry described by Euclid, in which initially parallel lines remain parallel forever and the angles inside a triangle always add up to 180 degrees. Spacetime, Einstein realized, has a non-Euclidean geometry, in which these venerable facts are no longer the case. Initially parallel rays of light, for example, can be focused together while moving through empty space. The effects of this warping of geometry are what we recognize as “gravity.” General relativity came with numerous mind-stretching consequences, such as the expansion of the universe and the existence of black holes, though it has taken physicists a long time to appreciate what those consequences are.
Special relativity is a framework, but general relativity is a specific theory. Just like Newton’s laws govern the evolution of a classical system or the Schrödinger equation governs the evolution of a quantum wave function, Einstein derived an equation that governs the curvature of spacetime. As with Schrödinger’s equation, it’s fun to actually see Einstein’s equation written out, even if we don’t bother with all the details:
Rμν—(½)Rgμν = 8πGTμν
The maths behind Einstein’s equation is formidable, but the basic idea is simple, and was pithily summarized by John Wheeler: matter tells spacetime how to curve, and spacetime tells matter how to move. The left-hand side measures the curvature of spacetime, while the right-hand side characterizes energy-like quantities, including momentum, pressure, and mass.
General relativity is classical. The geometry of spacetime is unique, evolves deterministically, and can in principle be measured to arbitrary precision without disturbing it. Once quantum mechanics came along, it was perfectly natural to try to “quantize” general relativity, obtaining a quantum theory of gravity. Easier said than done. What makes relativity special is that it’s a theory of spacetime rather than a theory of stuff within spacetime. Other quantum theories describe wave functions that assign probabilities to observing things at definite, well-defined locations in space and moments in time. Quantum gravity, by contrast, will have to be a quantum theory of spacetime itself. That raises some issues.
Einstein, naturally, was one of the first to appreciate the problem. In 1936, he mused on the difficulty of even imagining how to apply the principles of quantum mechanics to the nature of spacetime:
Perhaps the success of the Heisenberg method points to a purely algebraical method of description of nature, that is to the elimination of continuous functions from physics. Then, however, we must also give up, by principle, the space-time continuum. It is not unimaginable that human ingenuity will some day find methods which will make it possible to proceed along such a path. At the present time, however, such a program looks like an attempt to breathe in empty space.
Here Einstein is contemplating Heisenberg’s approach to quantum theory, which you’ll remember provided a description in terms of explicit quantum jumps without trying to fill in the details about microscopic processes happening along the way. Similar worries persist if we switch to a more Schrödingerian point of view with wave functions. Presumably we would need a wave function that assigns amplitudes to different possible geometries of spacetime. But if we imagine, for example, two branches of such a wave function that describe different spacetime geometries, there is no unique way of specifying that two events in the two branches correspond to the “same” point in space-time. There is no unique map, in other words, between two different geometries.
Consider a two-dimensional sphere and torus. Imagine that a friend of yours picks out a point on a sphere, and then asks you to pick out “the same” point on the torus. You’d be stymied, and for good reason; there’s no way to do it.
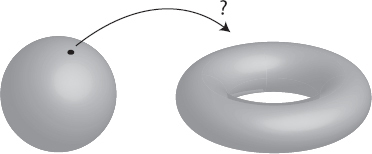
Apparently, spacetime can’t play the same central role in quantum gravity that it does in the rest of physics. There isn’t a single spacetime, there’s a superposition of many different spacetime geometries. We can’t ask what the probability might be to find an electron at a certain point in space, since there’s no objective way to specify which point we’re talking about.
Quantum gravity, then, comes with a set of conceptual issues that distinguish it from other quantum-mechanical theories. These issues can have important ramifications for the nature of our universe, including the question of what happened at the beginning, or if there was a beginning at all. We can even ask whether space and time are themselves fundamental, or if they emerge out of something deeper.

Just like the foundations of quantum mechanics, the field of quantum gravity was relatively ignored for decades as physicists concentrated on other things. Not completely; Hugh Everett was inspired to propose the Many-Worlds approach in part by thinking about the quantum theory of the entire universe, where gravity plays an important role, and his mentor, John Wheeler, worried about the problem for years. But even putting aside the conceptual issues, other obstacles got in the way of making serious progress on quantizing gravity.
A major roadblock is the difficulty of getting direct experimental data. Gravity is a very weak force; the electric repulsion between two electrons is about 1043 times stronger than their gravitational attraction. In any realistic experiment involving just a few particles, where we might expect quantum effects to be visible, the force of gravity is utterly negligible compared to other influences. We can imagine building a particle accelerator powerful enough to smash particles together at the Planck energy, where quantum gravity should become important. Unfortunately, if we simply scale up the technology in current machines, the resulting accelerator would have to be light-years in diameter. It’s not a feasible construction project at this time.
There are also technical problems with the theory itself, in addition to the conceptual ones just mentioned. General relativity is a classical field theory. The field involved is called the metric. (The symbol gμν in the middle of Einstein’s equation represents the metric, and the other quantities depend on it.) The word “metric” ultimately derives from the Greek metron, “something used to measure,” and that’s exactly what the metric field allows us to do. Given a path through space-time, the metric tells us the distance along that path. The metric essentially updates Pythagoras’s theorem, which works in flat Euclidean geometry but has to be generalized when spacetime is curved. Knowing the length of every curve suffices to fix the geometry of spacetime at every point.
Spacetime has a metric even in special relativity, or for that matter in Newtonian physics. But that metric is rigid, unchanging, and flat—the curvature of spacetime is zero at every point. The big insight of general relativity was to make the metric field into something that is dynamical and affected by matter and energy. We can attempt to quantize that field just as we would any other. Small ripples in the quantized gravitational field look like particles called gravitons, just like ripples in the electromagnetic field look like photons. Nobody has ever detected a graviton, and it’s possible that nobody ever will, since the gravitational force is so incredibly weak. But if we accept the basic principles of general relativity and quantum mechanics, the existence of gravitons is inevitable.
We can then ask what happens when gravitons scatter off each other or off other particles. Sadly, what we find is that the theory predicts nonsense, if it predicts anything at all. An infinite number of input parameters are needed to calculate any particular quantity of interest, so the theory has no predictive power. We can restrict our attention to an “effective” field theory of gravity, where by fiat we limit our attention to long wavelengths and low energies. That’s what allows us to calculate the gravitational field in the solar system, even in quantum gravity. But if we want a theory of everything, or at least a theory of gravity that is valid at all possible energies, we’re stuck. Something dramatic is called for.
The most popular contemporary approach to quantum gravity is string theory, which replaces particles by little loops or segments of one-dimensional “string.” (Don’t ask what the strings are made of—string stuff is what everything else is made of.) The strings themselves are incredibly small, so much so that they appear like particles when we observe them from a distance.
String theory was initially proposed to help understand the strong nuclear force, but that didn’t work out. One of the problems was that the theory inevitably predicts the existence of particles that look and behave exactly like gravitons. That was initially perceived as an annoyance, but pretty soon physicists thought to themselves, “Hmm, gravity actually exists. Maybe string theory is a quantum theory of gravity?” That turns out to be true, and even better there is a bonus: the theory makes finite predictions for all physical quantities, without needing an infinite number of input parameters. The popularity of strings exploded in 1984 when Michael Green and John Schwarz showed that the theory is mathematically consistent.
Today, string theory is the most pursued approach to exploring quantum gravity by a wide margin, although other ideas maintain their adherents. The second-most-popular approach is loop quantum gravity, which began as a way of directly quantizing general relativity by using a clever choice of variables—rather than looking at the curvature of spacetime at each point, we consider how vectors are rotated when they travel around closed loops in space. (If space is flat, they don’t rotate at all, while if space is curved, they can rotate by a lot.) String theory aspires to be a theory of all the forces and matter at once, while loop quantum gravity only aims at gravity itself. Unfortunately, the obstacles to gathering experimental data relevant to quantum gravity are equally formidable for all the alternatives, so we’re stuck not really knowing which approach (if any) is on the right track.
While string theory has been somewhat successful in dealing with the technical problems of quantum gravity, it hasn’t shed much light on the conceptual problems. Indeed, one way of thinking about different approaches within the quantum-gravity community is to ask how we should think about the conceptual side of things. A string theorist is likely to believe that if we take care of all the technical issues, the conceptual problems will eventually resolve themselves. Someone who thinks otherwise might be nudged toward loop quantum gravity or another alternative approach. When the data don’t point one way or the other, opinions tend to become deeply entrenched.
String theory, loop quantum gravity, and other ideas share a common pattern: they start with a set of classical variables, then quantize. From the perspective we’ve been following in this book, that’s a little backward. Nature is quantum from the start, described by a wave function evolving according to an appropriate version of the Schrödinger equation. Things like “space” and “fields” and “particles” are useful ways of talking about that wave function in an appropriate classical limit. We don’t want to start with space and fields and quantize them; we want to extract them from an intrinsically quantum wave function.
How can we find “space” within a wave function? We want to identify features of the wave function that resemble space as we know it, and in particular something that would correspond to a metric that defines distances. So let’s think about how distances show up in ordinary quantum field theory. For simplicity, let’s just think about distances in space; we’ll talk later about how time might enter into the game.
There’s one obvious place that distances show up in quantum field theory, which we’ve seen in the last chapter: in empty space, fields in different regions are entangled with each other, and regions that are far away are less entangled than ones that are nearby. Unlike “space,” the concept of “entanglement” is always available to us in any abstract quantum wave function. So perhaps we can get some purchase here, looking at the entanglement structure of states and using that to define distances. What we need is a quantitative measure of how entangled a quantum subsystem actually is. Happily, such a measure exists: it’s the entropy.
John von Neumann showed how quantum mechanics introduces a notion of entropy that parallels the classical definition. As explained by Ludwig Boltzmann, we start with a set of constituents that can mix together in various ways, like atoms and molecules in a fluid. The entropy is then a way of counting the number of ways those constituents can be arranged without changing the macroscopic appearance of the system. Entropy is related to ignorance: high-entropy states are those for which we don’t know much about the microscopic details of a system just from knowing its observable features.
Von Neumann entropy, meanwhile, is purely quantum mechanical in nature, and arises from entanglement. Consider a quantum system that is divided into two parts. It could be two electrons, or the quantum fields in two different regions of space. The system as a whole is described by a wave function, as usual. It has some definite quantum state, even if we can only predict measurement outcomes probabilistically. But as long as the two parts are entangled, there is only the one wave function for the whole thing, not a separate wave function for each part. The parts, in other words, are not in definite quantum states of their own.
Von Neumann showed that, for many purposes, the fact that entangled subsystems don’t have definite wave functions of their own is analogous to having a wave function, but we just don’t know what it is. Quantum subsystems, in other words, closely resemble the classical situation where there are many possible states that look macroscopically the same. And this uncertainty can be quantified into what we now call the entanglement entropy. The higher the entropy of a quantum subsystem, the more it’s entangled with the outside world.
Think about two qubits, one belonging to Alice and the other to Bob. It might be that they are unentangled, so each qubit has its own wave function, for example, an equal superposition of spin-up and spin-down. In that case, the entanglement entropy of each qubit is zero. Even if we can only predict measurement outcomes probabilistically, each subsystem is still in a definite quantum state.
But imagine that the two qubits are entangled, in an equal superposition of “both qubits are spin-up” and “both qubits are spin-down.” Alice’s qubit doesn’t have its own wave function, because it’s entangled with Bob’s. Indeed, Bob could perform a measurement of his spin, branching the wave function, so that now there are two copies of Alice, each of whom has a spin in a definite state. But neither copy of Alice knows which state that is; she’s in a state of ignorance, where the best she can do is say that there is a fifty-fifty chance her qubit is spin-up or spin-down. Note the subtle difference: Alice’s qubit is not in a quantum superposition where she doesn’t know what the measurement outcome will be; it’s in a state on each branch that will give a definite measurement outcome, but she doesn’t know which state it is. We therefore describe her qubit as having a nonzero entropy. Von Neumann’s idea was that we should ascribe a nonzero entropy to Alice’s qubit even before Bob measures his, because after all she doesn’t even know whether he’s done a measurement. That’s the entanglement entropy.

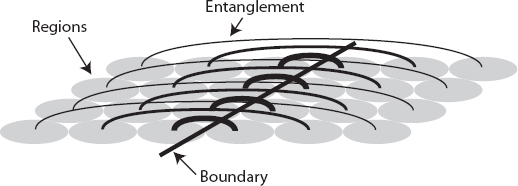
Let’s see how entanglement entropy appears in quantum field theory. Forgetting about gravity for a second, consider a region of empty space in the vacuum state, specified by a boundary separating inside the region from outside. Empty space is a richly textured place, full of quantum degrees of freedom that we can think of as modes of vibrating fields. The modes inside the region will be entangled with the modes outside, so the region has an entropy associated with it, even if the overall state is simply the vacuum.
We can even calculate what that entropy is. The answer is: infinity. This is a common complication with quantum field theory, that many questions of apparent physical relevance have seemingly infinite answers because there are an infinite number of possible ways for a field to vibrate. But just as we did for the vacuum energy in the last chapter, we can ask what happens when we impose a cutoff, allowing only modes longer than a certain wavelength. The resulting entropy is finite, and it turns out to be naturally proportional to the area of the region’s boundary. The reason isn’t hard to understand: field vibrations in one part of space are entangled with regions all over, but most of the entanglement is concentrated on nearby regions. The total entropy of a region of empty space depends on the amount of entanglement across the boundary, which is proportional to how big that boundary is—its area.
That’s an intriguing feature of quantum field theory. Pick out a region within empty space, and the entropy of that region is proportional to the area of its boundary. That relates on the one hand a geometric quantity, the area of a region, to a “matter” quantity, the entropy contained inside. It all sounds vaguely reminiscent of Einstein’s equation, which also connects geometry (the curvature of spacetime) to a matter quantity (energy). Are they somehow related?
They could be, as was pointed out in a provocative 1995 paper by Ted Jacobson, an ingenious physicist at the University of Maryland. In ordinary quantum field theory without gravity, entropy is proportional to area in the vacuum state, but in higher-energy states it doesn’t have to be. Jacobson postulated that there’s something special about gravity: when gravity is included, the entropy of a region is always proportional to its boundary area. That’s not at all what we would expect in quantum field theory, but maybe it happens once gravity enters the game. We can imagine that it might be the case, and see what happens.
What happens is pretty wonderful. Jacobson posited that the area of a surface is proportional to the entropy of the region it encloses. Area is a geometric quantity; we can’t calculate the area of a surface without knowing something about the geometry of the space it is a part of. Jacobson noted that we could relate the area of a very small surface to the same geometric quantity that appears on the left-hand side of Einstein’s equation. Meanwhile, entropy tells us something about “matter,” broadly construed; about the stuff that is living within spacetime. The concept of entropy originally arose within thermodynamics, where it was related to the heat leaving a system. And heat is a form of energy. Jacobson also argued that this entropy could be directly related to the energy term appearing on the right-hand side of Einstein’s equation. Through these maneuvers he was able to derive Einstein’s equation for general relativity, rather than directly postulating it, as Einstein did.
To say the same thing more directly, we consider a small region in flat spacetime. It has some entropy, because the modes inside the region are entangled with those outside. Now imagine changing the quantum state a little bit, so that we decrease the amount by which that region is entangled, and therefore decrease its entropy. In Jacobson’s picture, the area bounding our region changes in response, shrinking by a bit. And he shows that this response of the geometry of spacetime to a change in the quantum state is equivalent to Einstein’s equation of general relativity, relating curvature to energy.
This was the beginning of a surge of interest in what is now called “entropic” or “thermodynamic” gravity; other important contributions were made by Thanu Padmanabhan (2009) and Erik Verlinde (2010). The behavior of spacetime in general relativity can be thought of as simply the natural tendency of systems to move toward configurations of higher entropy.
This is a fairly radical change of perspective. Einstein thought in terms of energy, a definite quantity associated with particular configurations of stuff in the universe. Jacobson and others have argued that we can reach the same conclusions by thinking about entropy, a collective phenomenon that emerges from the mutual interaction of many small constituents of a system. This simple shift in focus might offer a crucial way forward in our quest to discover a fundamentally quantum theory of gravity.

Jacobson wasn’t himself proposing a theory of quantum gravity; he was pointing to a new way to derive Einstein’s equation for classical general relativity, with quantum fields acting as the source of energy. The appearance of words like “area” and “region of space” should indicate to us that the above discussion treated spacetime as a tangible, classical thing. But given the central role that entanglement entropy plays in his derivation, it’s natural to ask whether we might adapt the basic ideas to an approach that is more intrinsically quantum from the start, where space itself emerges from the wave function.
In Many-Worlds, a wave function is just an abstract vector living within the super-high-dimensional mathematical construct of Hilbert space. Usually we make wave functions by starting with something classical and quantizing it, which gives us an immediate handle on what the wave function is supposed to represent, the basic parts from which it is constructed. But here we don’t have any such luxury. All we have is the state itself and Schrödinger’s equation. We speak abstractly of “degrees of freedom,” but they aren’t the quantized version of any readily identifiable classical stuff—they are the quantum-mechanical essence out of which spacetime, and everything else, emerges. John Wheeler used to talk about the idea of “It from Bit,” suggesting that the physical world arose (somehow) out of information. These days, when entanglement of quantum degrees of freedom is the main focus, we like to talk about “It from Qubit.”
If we look back at the Schrödinger equation, it says that the rate at which the wave function changes with time is governed by the Hamiltonian. Remember that the Hamiltonian is a way of describing how much energy the system contains, and it’s a compact way of capturing all of the system’s dynamics. A standard feature of Hamiltonians in the real world is dynamical locality—subsystems interact with other subsystems only when they are next to each other, not when they are far away. Influences can travel through space, but only at speeds less than or equal to the speed of light. So an event at one particular moment only immediately affects what’s going on at its present location.
With the problem we’ve assigned to ourselves—how does space emerge from an abstract quantum wave function?—we don’t have the convenience of starting with individual parts and asking how they interact. We know what “time” means in this context—it’s right there in the Schrödinger equation, the letter t—but we don’t have particles, or fields, or even locations in a three-dimensional world. We’re caught breathing in empty space, and need to look for oxygen where we can find it.
Happily, this is a case where reverse engineering works quite well. Rather than starting with individual pieces of a system and asking how they interact, we can go the other way around: Given the system as a whole (the abstract quantum wave function) and its Hamiltonian, is there a sensible way to break it up into subsystems? It’s like buying sliced bread all your life, and then being handed an un-sliced loaf. There are many ways we could imagine slicing it; is there one particular way that’s clearly the best?
Yes, there is, if we believe that locality is an important feature of the real world. We can tackle the problem bit by bit, or qubit by qubit, at any rate.
A generic quantum state can be thought of as a superposition of a set of basis states with definite fixed energy. (Just like a generic state of a spinning electron can be thought of as a superposition of an electron that is definitely spin-up and one that is definitely spin-down.) The Hamiltonian tells us what the actual energy is for each possible definite-energy state. Given that list of possible energies, we can ask whether any particular way of dividing the wave function into subsystems implies that those subsystems interact “locally.” In fact, for a random list of energies, there won’t be any way of dividing the wave function into local subsystems, but for the right kind of Hamiltonian, there will be exactly one such way. Demanding that physics look local tells us how to decompose our quantum system into a collection of degrees of freedom.
In other words, we don’t need to start with a set of fundamental building blocks of reality, then stick them together to make the world. We can start with the world, and ask if there is a way to think about it as a collection of fundamental building blocks. With the right kind of Hamiltonian, there will be, and all of our data and experience of the world suggests that we do have the right kind of Hamiltonian. It’s easy to imagine possible worlds where the laws of physics weren’t local at all. But it’s hard to imagine what life would be like in such a world, or even whether life would be possible; the locality of physical interactions helps bring order to the universe.

We can begin to see how space itself emerges from the wave function. When we say that there’s a unique way of dividing up our system into degrees of freedom that interact locally with their neighbors, all we really mean is that each degree of freedom interacts with only a small number of other degrees of freedom. The notions of “local” and “nearest” aren’t imposed from the start—they pop out from the fact that these interactions are very special. The way to think about it isn’t “degrees of freedom interact only when they are nearby,” but rather “we define two degrees of freedom to be ‘nearby’ when they directly interact with each other, and ‘far away’ when they don’t.” A long list of abstract degrees of freedom has been knit together into a network, in which each degree of freedom is connected to a small number of other ones. This network forms the skeleton on which space itself is constructed.
That’s a start, but we want to do even more. When someone asks you how far apart two different cities are, they’re looking for something a bit more specific than “near” or “far.” They want an actual distance, and that’s what the metric on spacetime ordinarily lets us calculate. In our abstract wave function divided up into degrees of freedom, we haven’t yet constructed a full geometry, just a notion of near and far.
We can do better. Remember the intuition from vacuum states in quantum field theory that Jacobson used to derive Einstein’s equation: the entanglement entropy of a region of space is proportional to the area of its boundary. In our current context of a quantum state described in terms of abstract degrees of freedom, we don’t know what “area” is supposed to mean. But we do have entanglement between the degrees of freedom, and for any collection of them we can compute their entropy.
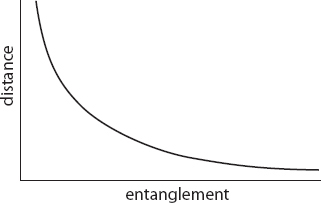
So once again following our reverse-engineering philosophy, we can define the “area” of a collection of degrees of freedom to be proportional to its entanglement entropy. In fact, we can assert this for every possible subset of degrees of freedom, assigning areas to every surface we can imagine drawing within our network. Happily, mathematicians long ago figured out that knowing the area of every possible surface in a region is enough to fully determine the geometry of that region; it’s completely equivalent to knowing the metric everywhere. In other words, the combination of (1) knowing how our degrees of freedom are entangled, and (2) postulating that the entropy of any collection of degrees of freedom defines an area of the boundary around that collection, suffices to fully determine the geometry of our emergent space.
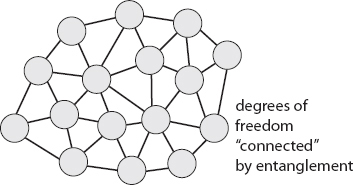
We can describe this construction in equivalent but slightly less formal terms. Pick out two of our spacetime degrees of freedom. They will generally have some entanglement between them. If they were modes of vibrating quantum fields in the vacuum state, we know exactly what that degree of entanglement would be: it would be high if they were nearby, and low if they were far away. Now we are simply thinking the other way around. If the degrees of freedom are highly entangled, we define them to be nearby, and the farther and farther away, the less entangled they are. A metric on space has emerged from the entanglement structure of the quantum state.
Thinking this way is a bit unusual, even for physicists, because we’re used to thinking of particles moving through space, while taking space itself for granted. As we know from the EPR thought experiment, two particles can be completely entangled no matter how far away they are; there’s no necessary relationship between entanglement and distance. Here, however, we’re not talking about particles but about the fundamental building-block degrees of freedom that make up space itself. Those aren’t entangled in any old way; they are strung together in a very specific structure.*
Now we can use Jacobson’s trick with entropy and area. Knowing the area of every surface in our network gives us a geometry, and knowing the entropy of each region tells us something about the energy in that region. I’ve been involved with this approach myself, in papers from 2016 and 2018 with my collaborators ChunJun (Charles) Cao and Spyridon Michalakis. Closely related ideas have been investigated by Tom Banks, Willy Fischler, Steve Giddings, and other physicists who are willing to contemplate the idea that spacetime isn’t fundamental, but emerges from the wave function.
We aren’t quite at the point where we can simply say, “Yes, this emergent geometry on space evolves with time in exactly the right way to describe a spacetime that obeys Einstein’s equation of general relativity.” That’s the ultimate goal, but we’re not there yet. What we can do is to specify a list of requirements under which that’s exactly what does happen. The individual requirements seem reasonable—things like “at long distances, physics looks like an effective quantum field theory”—but many of them remain unproven as yet, and so far the most rigorous results are available only in situations where the gravitational field is relatively weak. We don’t yet have a way of describing black holes or the Big Bang, though there are some promising ideas.
That’s life as a theoretical physicist. We don’t have all the answers, but let’s not lose sight of the overall ambition: starting from an abstract quantum wave function, we have a road map describing how space emerges, with a geometry fixed by quantum entanglement, and that geometry seems to obey the dynamical rules of general relativity. There are so many caveats and assumptions going into this proposal that it’s hard to know where to start listing them. But there seems to be a very real prospect that the route to understanding the universe lies not in quantizing gravity, but in finding gravity within quantum mechanics.

You may have noticed a tiny imbalance in this discussion. We’ve been asking how spacetime can emerge from entanglement in quantum gravity. But if we’re honest, we’ve really only looked at how space emerges; we’ve taken time for granted as something that comes along for the ride. And it’s possible that this approach is completely fair. Although relativity treats space and time as if they were on an equal footing, quantum mechanics generally does not. The Schrödinger equation, in particular, treats them very differently: it literally describes how the quantum state evolves with time. “Space” may or may not be part of that equation, depending on what system we’re looking at, but time is fundamental. It’s plausible that the symmetry between space and time that we’re familiar with from relativity isn’t built into quantum gravity, but emerges in the classical approximation.
It is nevertheless overwhelmingly tempting to wonder whether time, like space, might be emergent rather than fundamental, and whether entanglement might have anything to do with it. The answer is yes on both counts, although the details remain a little sketchy.
If we take the Schrödinger equation at face value, time seems to be right there in a fundamental way. Indeed, it immediately follows that the universe lasts eternally toward both the past and future, for almost all quantum states. You might think that this conflicts with the oft-repeated fact that the Big Bang was the beginning of our universe, but we don’t actually know that oft-repeated fact to be true. That’s a prediction of classical general relativity, not of quantum gravity. If quantum gravity operates according to some version of the Schrödinger equation, then for almost all quantum states, time runs from minus infinity in the past to plus infinity in the future. The Big Bang might be simply a transitional phase, with an infinitely old universe preceding it.
We have to say “almost all” in these statements because there is one loophole. The Schrödinger equation says that the rate of change of the wave function is driven by how much energy the quantum system has. What if we consider systems whose energy is precisely zero? Then all the equation says is that the system doesn’t evolve at all; time has disappeared from the story.
You might think it’s extremely implausible that the universe has exactly zero energy, but general relativity suggests you shouldn’t be so sure. Of course there seem to be energy-containing things all around us—stars, planets, interstellar radiation, dark matter, dark energy, and so on. But when you go through the maths, there is also a contribution to the energy of the universe from the gravitational field itself, which is generally negative. In a closed universe—one that wraps around on itself to form a compact geometry, like a three-dimensional sphere or torus, rather than stretching to infinity—that gravitational energy precisely cancels the positive energy from everything else. A closed universe has exactly zero energy, regardless of what’s inside.
That’s a classical statement, but there’s a quantum-mechanical analogue that was developed by John Wheeler and Bryce DeWitt. The Wheeler-DeWitt equation simply says that the quantum state of the universe doesn’t evolve at all as a function of time.
This seems crazy, or at least in flagrant contradiction to our observational experience. The universe certainly seems to evolve. This puzzle has been cleverly labeled the problem of time in quantum gravity, and it is where the possibility of emergent time might come to the rescue. If the quantum state of the universe obeys the Wheeler-DeWitt equation (which is plausible, but far from certain), time has to be emergent rather than fundamental.
One way that might work was suggested by Don Page and William Wootters in 1983. Imagine a quantum system consisting of two parts: a clock, and everything else in the universe. Imagine that both the clock and the rest of the system evolve in time as usual. Now take snapshots of the quantum state at regular intervals, perhaps once per second or once per Planck time. In any particular snapshot, the quantum state describes the clock reading some particular time, and the rest of the system in whatever configuration it was in at that time. That gives us a collection of instantaneous quantum states of the system.
The great thing about quantum states is that we can simply add them together (superposing them) to make a new state. So let’s make a new quantum state by adding together all of our snapshots. This new quantum state doesn’t evolve over time; it just exists, as we constructed it by hand. And there is no specific time reading on the clock; the clock subsystem is in a superposition of all the times at which we took snapshots. It doesn’t sound much like our world.
But here’s the thing: within that superposition of all the snapshots, the state of the clock is entangled with the state of the rest of the system. If we measure the clock and see that it reads some particular time, then the rest of the universe is in whatever state our original evolving system was caught in at precisely that time.

In other words, there’s not “really” time in the superposition state, which is completely static. But entanglement generates a relationship between what the clock reads and what the rest of the universe is doing. And the state of the rest of the universe is precisely what it would be if it were evolving as the original state did over time. We have replaced “time” as a fundamental notion with “what the clock reads in this part of the overall quantum superposition.” In that way, time has emerged from a static state, thanks to the magic of entanglement.
The jury remains out on whether the energy of the universe actually is zero, and therefore time is emergent, or it is any other number, such that time is fundamental. At the current state of the art, it makes sense to keep our options open and investigate both possibilities.
* In 2013, Juan Maldacena and Leonard Susskind suggested that we should think of entangled particles as being connected by a microscopic (and impossible-to-travel-through) wormhole in spacetime. This has been dubbed the “ER=EPR conjecture,” after two famous papers from 1935: one by Einstein and Nathan Rosen, where they introduced the concept of wormholes; and the other of course by Einstein, Rosen, and Boris Podolsky, where they discussed entanglement. How far such a suggestion can be taken is still unclear.