
Before Stephen Hawking’s death in 2018, he was the most famous living scientist in the world by a comfortable margin. That celebrity was entirely deserved; not only was Hawking a charismatic and influential public figure, and not only did he have an inspirational personal story, but his scientific contributions were incredibly significant in their own right.
Hawking’s greatest achievement was showing that, once we include the effects of quantum mechanics, black holes “ain’t so black,” as he liked to say. Black holes actually emit a steady stream of particles out into space, and those particles carry energy away from the black hole, causing it to shrink in size. This realization led both to profound insights (black holes have entropy) as well as unexpected puzzles (where does the information go when black holes form and then evaporate away?).
The fact that black holes radiate, and the implications of that surprising idea, are the single best clue we have about the nature of quantum gravity. Hawking didn’t first construct a full theory of quantum gravity and then use it to show that black holes radiate. Instead, he used a reasonable approximation, treating spacetime itself as classical, with dynamical quantum fields living on top of it. We hope that this is a reasonable approximation, anyway; but some of the puzzling aspects of Hawking’s insight have given us second thoughts. Forty-five years after Hawking’s original paper on the subject, trying to understand black-hole radiation is still one of the hottest topics in contemporary theoretical physics.
While that task is far from complete, one implication seems clear: the simple picture sketched in the last chapter, where space emerges from a set of entangled nearest-neighbor degrees of freedom, is probably not the entire story. It’s a very good story, and might be the right starting point for constructing a theory of quantum gravity. But it relies heavily on the idea of locality—what happens at one point in space can have an immediate effect only on points right next door. Black holes, to the extent that we understand them, seem to be indicating that nature is more subtle than that. In some circumstances the world looks like a collection of degrees of freedom interacting with their nearest neighbors, but when gravity becomes strong, that simple picture breaks down. Rather than being distributed throughout space, degrees of freedom squeeze together on a surface, and “space” is merely a holographic projection of the information contained therein.
Locality undoubtedly plays an important role in our everyday lives, but it seems like the fundamental nature of reality can’t quite be captured by a set of things happening at precise locations in space. Once again, what we have here is a job for the Many-Worlds approach to quantum mechanics. Other formulations take space as a given and work within it; the wave-function-first Everettian philosophy allows us to accept that space can appear fundamentally different depending on how we look at it, if it’s a useful concept at all. Physicists are still wrestling with the implications of this idea, but it’s already led us to some very interesting places indeed.
In general relativity, a black hole is a region of spacetime that is curved so dramatically that nothing can escape from it, not even light itself. The edge of the black hole, demarcating the inside from the outside, is the event horizon. According to classical relativity, the area of the event horizon can only grow, not shrink; black holes increase in size when matter and energy fall in, but cannot lose mass to the outside world.
Everyone thought that was true in nature until 1974, when Hawking announced that quantum mechanics changes everything. In the presence of quantum fields, black holes naturally radiate particles into their surroundings. Those particles have a blackbody spectrum, so every black hole has a temperature; more massive black holes are cooler, while very small black holes are incredibly hot. The formula for the temperature of a black hole’s radiation is engraved on Hawking’s gravestone in West-minster Abbey.
Particles radiated by a black hole carry away energy, causing the hole to lose mass and eventually evaporate away completely. While it would be nice to observe Hawking radiation in a telescope, it’s not going to happen for any of the black holes we know about. The Hawking temperature of a black hole the mass of the sun would be about 0.00000006 Kelvin. Any such signal would be swamped by other sources, such as the leftover microwave radiation from the Big Bang, which has a temperature of about 2.7 Kelvin. Even if such a black hole never grew by accreting matter and radiation, it will take over 1067 years for it to evaporate away completely.
There is a standard story that is told to explain why black holes emit radiation. I’ve told it, Hawking has told it, everyone tells it. It goes like this: according to quantum field theory, the vacuum is a bubbling stew of particles popping in and out of existence, typically in pairs consisting of one particle and one anti-particle. Ordinarily we don’t notice, but in the vicinity of a black hole event horizon, one of the particles can fall inside the hole and then never get out, while the other escapes to the outside world. From the perspective of someone watching from afar, the escaping particle has positive energy, so to balance the books the infalling particle must have negative energy, and the black hole shrinks in mass as it absorbs these negative-energy particles.
Given our wave-functions-first Everettian perspective, there’s a more accurate way to describe what’s happening. The particles-appearing-and-disappearing story is a colorful metaphor that often provides physical intuition, and this is definitely one of those cases. But what we really have is a quantum wave function of the fields near the black hole. And that wave function is not static; it evolves into something else, in this case a smaller black hole plus some particles traveling away from it in all directions. It’s not that different from an atom whose electrons have a bit of extra energy, and which therefore drop down to lower-energy states by emitting photons. The difference is that the atom eventually reaches a state of lowest possible energy and stays there, while the black hole (as far as we understand) just decays away entirely, exploding at the last second in a flash of high-energy particles.
The story of how black holes radiate and evaporate was derived by Hawking using the techniques of conventional quantum field theory, just in a curved spacetime of general relativity rather than a particle physicist’s usual no-gravity context. It’s not a genuinely quantum-gravity result; spacetime itself is treated classically, not as part of the quantum wave function. But nothing about the scenario actually seems to require deep knowledge of quantum gravity. As far as physicists can tell, Hawking radiation is a robust phenomenon. Whenever we do figure out quantum gravity, in other words, it should reproduce Hawking’s result.
That raises a problem, one that has become notorious within theoretical physics as the black hole information puzzle. Remember that quantum mechanics, in its Many-Worlds version, is a deterministic theory. Randomness is only apparent, arising from self-locating uncertainty when the wave function branches and we don’t know which branch we’re on. But in Hawking’s calculation, black-hole radiation seems not to be deterministic; it’s truly random, even without any branching. Starting from a precise quantum state describing matter that collapses to make a black hole, there is no way of computing the precise quantum state of the radiation into which it evaporates. The information specifying the original state seems to be lost.
Imagine taking a book—maybe the very one you are reading right now—and throwing it into a fire, letting it burn completely away. (Don’t worry, you can always buy more copies.) It might appear that the information contained in the book is lost in the flames. But if we turn on our physicist’s powers of thought-experiment ingenuity, we realize that this loss is only apparent. In principle, if we captured every bit of light and heat and dust and ash from the fire, and had perfect knowledge of the laws of physics, we could reconstruct exactly what went into the fire, including all the words on the pages of the book. It’ll never happen in the real world, but physics says it’s conceivable.
Most physicists think that black holes should be just like that: throw a book in, and the information contained in its pages should be secretly encoded in the radiation that the black hole emits. But this is not what happens, according to Hawking’s derivation of black-hole radiation; rather, the information in the book appears to be truly destroyed.
It’s possible, of course, that this implication is correct, that the information really is destroyed, and that black-hole evaporation is nothing like an ordinary fire. It’s not like we have any experimental input one way or the other. But most physicists believe that information is conserved, and that it really does get out somehow. And they suspect that the secret to getting it out lies in a better understanding of quantum gravity.
That’s easier said than done. One way of thinking about why black holes are supposed to be black in the first place is that in order to escape, you would have to be able to travel faster than light. Hawking radiation avoids that difficulty because it actually originates right outside the event horizon, not deep in the interior. But any book we throw inside does indeed plunge into the interior, with all its information intact. You might wonder whether the information is somehow copied onto the outgoing radiation as the book falls through the horizon, and carried out that way. Unfortunately that’s in contradiction with the basic principles of quantum mechanics; there is a result called the no-cloning theorem that says we can’t duplicate quantum information without destroying the original copy.
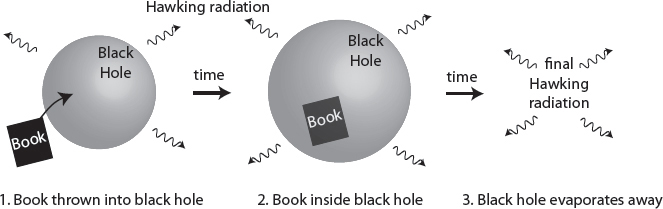
The other possibility seems to be that the book falls all the way in, but as it hits the singularity inside the black hole, its information is somehow transferred to the outgoing radiation at the horizon. Unfortunately, that would seemingly require faster-than-light communication. Or, equivalently, dynamical nonlocality—occurrences at one point in spacetime immediately influencing what happens some distance away. This kind of nonlocality is precisely what cannot happen, according to the ordinary rules of quantum field theory. This is a clue that those rules might have to be dramatically revised once quantum gravity becomes important.*
Hawking’s proposal that black holes radiate didn’t come out of the blue. It came in response to a suggestion from Jacob Bekenstein—who at the time was yet another graduate student of John Wheeler’s at Princeton—that black holes should have entropy.
One of the motivations behind Bekenstein’s idea was the fact that, according to classical general relativity, the area of a black hole’s event horizon can never decrease. That sounds suspiciously like the second law of thermodynamics, according to which the entropy of a closed system can never decrease. Inspired by this similarity, physicists constructed an elaborate analogy between the laws of thermodynamics and the behavior of black holes, according to which the mass of the black hole is like the energy of a thermodynamic system, and the area of the event horizon is like the entropy.
Bekenstein suggested that it was more than an analogy. The area of the event horizon isn’t just like the entropy, it is the entropy of the black hole, or at least proportional to it. Hawking and others scoffed at the suggestion at first—if black holes have entropy like conventional thermodynamic systems, they should also have a temperature, and then they should give off radiation! Motivated to disprove this ridiculous-sounding notion, Hawking ended up showing that it was all true. These days we refer to the entropy of a black hole as the Bekenstein-Hawking entropy.
One reason why this is such a provocative result is that classically, black holes don’t seem like things that should have entropy at all. They’re just regions of empty space. You get entropy when your system is made of atoms or other tiny constituents, which can be arranged in many different ways while maintaining the same macroscopic appearance. What are these constituents supposed to be for a black hole? The answer has to come from quantum mechanics.
It’s natural to presume that the Bekenstein-Hawking entropy of a black hole is a kind of entanglement entropy. There are some degrees of freedom inside the black hole, and they are entangled with the outside world. What are they?
We might first guess that the degrees of freedom are simply vibrational modes of the quantum fields inside the black hole. There are a couple of problems with that. For one thing, the real answer for the entropy of a region in quantum field theory was “infinity.” We could wrestle that down to a finite number by choosing to ignore very-small-wavelength modes, but that involved introducing an arbitrary cutoff on the energies of the field vibrations we were considering. The Bekenstein-Hawking entropy, on the other hand, is just a finite number, full stop. For another thing, the entanglement entropy in field theory should depend on exactly how many fields are involved—the electrons, quarks, neutrinos, and so forth. The formula for black-hole entropy that Hawking derived makes no mention of such things at all.
If we can’t simply attribute black-hole entropy to the quantum fields inside, the alternative is to imagine that spacetime itself is made of some quantum degrees of freedom, and the Bekenstein-Hawking formula measures the entanglement of the degrees of freedom inside the black hole with the degrees of freedom outside. If that sounds pretty vague, that’s because it is. We’re not precisely sure what these spacetime degrees of freedom are, or how they interact with one another. But the general principles of quantum mechanics should still be respected. If there’s entropy, and that entropy comes from entanglement, there must be degrees of freedom that can entangle with the rest of the world in many different ways, even if classical black holes are all featureless.
If this story is right, the number of degrees of freedom in a black hole isn’t infinite, but it is very large indeed. Our Milky Way galaxy contains a supermassive black hole at its center, associated with a radio source called Sagittarius A*. From observing how stars orbit around the hole, we can measure its mass to be 4 million times the mass of the sun. That corresponds to an entropy of 1090, which is greater than the entropy of all the known particles in the entire observable universe. The number of degrees of freedom in a quantum system has to be at least as large as its entropy, since that entropy comes precisely from those degrees of freedom being entangled with the outside world. So there must be at least 1090 degrees of freedom in the black hole.
While we tend to pay attention to the stuff we see in the universe—matter, radiation, and so on—almost all of the universe’s quantum degrees of freedom are invisible, doing nothing more than stitching spacetime together. In a volume of space roughly the size of an adult human, there must be at least 1070 degrees of freedom; we know that because that’s the entropy of a black hole that would fill such a volume. But there are only about 1028 particles in a person. We can think of a particle as a degree of freedom that has been “turned on,” while all the other degrees of freedom are peacefully “turned off” in the vacuum state. As far as quantum field theory is concerned, a human being or the center of a star isn’t all that different from empty space.

Maybe the fact that the entropy of a black hole is proportional to its area is just what we should expect. In quantum field theory it’s natural for regions of space to have an entropy proportional to their boundary area, and a black hole is just a region of space. But a problem lurks beneath the surface. It’s natural for a region of space in the vacuum state to have an entropy proportional to its boundary area. But a black hole isn’t part of the vacuum state; there’s a black hole there, and spacetime is noticeably curved.
Black holes have a very special property: they represent the highest-entropy states we can have in any given size region of space. This provocative fact was first noticed by Bekenstein, and later refined by Raphael Bousso. If you start from a region within the vacuum state and try to increase its entropy, you must also increase its energy. (Since you started in the vacuum, there’s nowhere for the energy to go but up.) As you keep throwing in entropy, the energy also increases. Eventually you have so much energy in a fixed region that the whole thing can’t help but collapse into a black hole. That’s the limit; you can’t fit any more entropy into a region than you would have if a black hole were there.
That conclusion is profoundly different from what we would expect in an ordinary quantum field theory without gravity. There, there is no limit on how much entropy we can fit in a region, because there’s also no limit on how much energy there can be. This reflects the fact that there are an infinite number of degrees of freedom in quantum field theory, even in a finite-sized region.
Gravity appears to be different. There is a maximum amount of energy and entropy that can fit into a given region, which seems to imply that there are only a finite number of degrees of freedom there. Somehow these degrees of freedom become entangled in the right way to stitch together into the geometry of spacetime. It’s not just black holes: every region of spacetime has a maximum entropy we could imagine fitting into it (the entropy that a black hole of that size would have), and therefore a finite number of degrees of freedom. It’s even true for the universe as a whole; because there is vacuum energy, the acceleration of space is expanding, and that means there is a horizon all around us that delineates the extent of the observable part of our cosmos. That observable patch of space has a finite maximum entropy, so there are only a finite number of degrees of freedom needed to describe everything we see or ever will see.
If this story is on the right track, it has an immediate, profound consequence for the Many-Worlds picture of quantum mechanics. A finite number of quantum degrees of freedom implies a finite-dimensional Hilbert space for the system as a whole (in this case, any chosen region of space). That in turn implies that there is some finite number of branches of the wave function, not an infinite number. That’s why Alice was cagey back in Chapter Eight about whether there are an infinite number of “worlds” in the wave function. In many simple models of quantum mechanics, including that of a fixed set of particles moving smoothly through space or any ordinary quantum field theory, Hilbert space is infinite-dimensional and there could potentially be an infinite number of worlds. But gravity seems to change things around in an important way. It prevents most of those worlds from existing, because they would describe too much energy being packed into a local region.
So maybe in the real universe, where gravity certainly exists, Everettian quantum mechanics only describes a finite number of worlds. The number Alice mentioned for the dimensionality of Hilbert space was 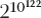 .
.
Now we can reveal where that number came from: it’s from calculating the entropy that our observable universe will have once it reaches maximum entropy, and working backward to find out how big Hilbert space needs to be to accommodate that much entropy. (The size of the observable universe is set by the vacuum energy, so the exponent 10122 is the ratio of the Planck scale to the cosmological constant, familiar from our discussion in Chapter Twelve.) Our confidence in the basic principles of quantum gravity isn’t strong enough to be absolutely sure that there are only a finite number of Everettian worlds, but it seems reasonable, and it certainly would make things much simpler.

The maximum-entropy nature of black holes also has an important consequence for quantum gravity. In classical general relativity, there’s nothing special about the interior region of a black hole, in between the event horizon and the singularity. There’s a gravitational field there, but to an infalling observer it otherwise looks like empty space. According to the story we told in the last chapter, the quantum version of “empty space” is something like “a collection of spacetime degrees of freedom entangled together in such a way as to form an emergent three-dimensional geometry.” Implicit in that description is that the degrees of freedom are scattered more or less uniformly throughout the volume of space we’re looking at. And if that were true, the maximum-entropy state of that form would have all of those degrees of freedom entangled with the outside world. The entropy would thus be proportional to the volume of the region, not the area of its boundary. What’s up?
There is a clue from the black hole information puzzle. The issue there was that there is no obvious way to transmit information from a book that has fallen into the black hole to the Hawking radiation emitted from the event horizon, at least not without signals moving faster than light. So what about this crazy idea: maybe all of the information about the state of the black hole—the “inside” as well as the horizon—can be thought of as living on the horizon itself, not buried in the interior. The black-hole state “lives,” in some sense, on a two-dimensional surface, rather than being stretched across a three-dimensional volume.
First developed by Gerard ’t Hooft and Leonard Susskind in the 1990s, based in part on a paper by Charles Thorn from 1978, this idea is known as the holographic principle. In an ordinary hologram, shining light on a two-dimensional surface reveals an apparently three-dimensional image. According to the holographic principle, the apparently three-dimensional interior of a black hole reflects information encoded on the two-dimensional surface of its event horizon. If this is true, maybe it’s not so hard to get information from the black hole to its outgoing radiation, because the information was always on the horizon to start with.
Physicists still haven’t settled on the precise meaning of holography for real-world black holes. Is it just a way of counting the number of degrees of freedom, or should we think that there is an actual two-dimensional theory living on the event horizon that describes the physics of the black hole? We don’t know, but there is a different context in which holography is very precise: the so-called AdS/CFT correspondence, proposed by Juan Maldacena in 1997. The “AdS” in the label stands for “anti–de Sitter space,” a hypothetical spacetime with no matter sources other than a negative vacuum energy (as opposed to the positive vacuum energy of our real world). “CFT” stands for conformal field theory, a particular kind of quantum field theory that can be defined on an infinitely faraway boundary of AdS. According to Maldacena, these two theories are secretly equivalent to each other. That’s extremely provocative, for a couple of reasons. First, the AdS theory includes gravity, while the CFT is an ordinary field theory that has no gravity at all. Second, the boundary of a spacetime has one fewer dimensions than the spacetime itself. If we consider four-dimensional AdS, for example, that is equivalent to a three-dimensional conformal field theory. You couldn’t ask for a more explicit example of holography in action.

Going into the details of AdS/CFT would require another book entirely. But it is worth mentioning that it is in this context that most modern research on the connection between spacetime geometry and quantum entanglement is being carried out. As noted by Shinsei Ryu, Tadashi Takayanagi, Mark Van Raamsdonk, Brian Swingle, and others in the early 2000s, there is a direct connection between entanglement in the boundary CFT and the resulting geometry in the AdS interior. Because AdS/CFT is relatively well defined as models of quantum gravity go, understanding this connection has been the target of a very intense effort over the past several years.
Alas, it’s not the real world. All of the fun of AdS/CFT comes from relating things in the interior, where gravity happens, to things on the boundary, where gravity is absent. But the existence of the boundary is very special to anti–de Sitter space, which relies on a negative vacuum energy. Our universe appears to have a positive vacuum energy, not a negative one.
There’s an old joke about the drunk who is looking under a lamppost for his lost keys. When someone asks if he’s sure he lost them there, he replies, “Oh no, I lost them somewhere else, but the light is much better over here.” In the quantum-gravity game, AdS/CFT is the world’s brightest lamppost. By studying it we’ve uncovered a large number of fascinating concepts that are useful to theoretical physicists, but there is no direct route to using that knowledge to understand why apples fall from trees, or other aspects of gravity in the space around us. It’s worth continuing the pursuit, but important to keep our eyes on the prize: understanding the world in which we actually live.

The implications of holography for real-world black holes are less clear than they are for the imaginary world of AdS/CFT. Are we saying that classical general relativity was completely wrong about the interior of a black hole appearing empty, and that in fact an infalling observer would smack into a holographic surface upon encountering the event horizon? We are not—at least, most adherents of holography aren’t saying that. Rather, they appeal to a related and equally startling idea, black-hole complementarity. It was proposed by Susskind and others, using terminology that intentionally recalls Bohr’s philosophy of quantum measurement.
The black-hole version of complementarity says that things are a little more nuanced than simply “the interior of a black hole looks like ordinary empty space” or “all the information about the black hole is encoded on the event horizon.” In fact both are true, but we can’t speak both languages at the same time. Or, as physicists are more likely to put it, they don’t simultaneously appear true to any single observer. To an observer falling through the event horizon, everything looks like normal empty space, while to an observer looking at the hole from far away, all of the information is spread across the horizon.
Even though this behavior is fundamentally quantum-mechanical, it does have a classical precursor. Think about what happens to a book (or a star, or whatever) when we throw it into a black hole in classical general relativity. From the book’s point of view, it just passes right into the interior. But the effect of spacetime warping is strong near the event horizon, so that’s not what an external observer would see. They would see the book appear to slow down as it approached the horizon, becoming redder and dimmer along the way. They wouldn’t ever see it cross; to someone far away, objects appear to be frozen in time as they approach the horizon, rather than plunging in. This led astrophysicists to develop a picture called the membrane paradigm, according to which we can model the physical properties of a black hole by imagining that there is a physical membrane at the horizon, with certain calculable properties such as temperature and electrical conductivity. The membrane paradigm was originally thought of as a convenient shortcut through which astrophysicists could simplify calculations involving black holes, but complementarity claims that external observers really do see black holes as if they were vibrating quantum membranes where the classical event horizon would be.
If you tend to think of spacetime as a fundamental thing, this might make no sense at all. Spacetime has some geometry, there’s nothing else to it. But quantum-mechanically it’s perfectly plausible; there’s a wave function of the universe, and different observations can reveal different things about it. It’s not that much different from saying that the number of particles in a state depends on how we observe it.
The world is a quantum state evolving in Hilbert space, and physical space emerges out of that. It shouldn’t come as a surprise that a single quantum state might exhibit different notions of position and locality depending on what kind of observations we perform on it. According to black-hole complementarity, there’s no such thing as “what the geometry of spacetime is,” or “where the degrees of freedom are”; you ask either what the quantum state is, or what is seen by some particular observer.
This sounds different from the picture we explored in the last chapter, where degrees of freedom were distributed in a network filling space, and became entangled to define an emergent geometry. But that picture was only meant to apply when gravity was weak, and black holes definitely do not qualify as weak. In the view presented in this chapter, there are still abstract degrees of freedom coming together to form spacetime, but “where they are located” depends on how they are being observed. Space itself is not fundamental; it’s just a useful way of talking from certain points of view.

Hopefully these last chapters have successfully conveyed the way in which Many-Worlds quantum mechanics might have significant implications for the long-standing problem of quantum gravity. To be honest, many physicists working on these problems don’t think of themselves as using Many-Worlds, though they are implicitly doing so. They certainly are not using hidden variables, or dynamical collapses, or an epistemic approach to quantum mechanics. When it comes to understanding how to quantize the universe itself, Many-Worlds seems to be the most direct path to take, if nothing else.
Is the picture we’ve sketched, where the entanglement between degrees of freedom somehow comes together to define the geometry of our approximately classical spacetime, actually on the right track? Nobody knows for sure. What seems clear, given the current state of our knowledge, is that both space and time could emerge from an abstract quantum state in the desired way—all the ingredients are there, and it’s not out of place to hope that a few more years of work will bring a much sharper picture into focus. If we train ourselves to discard our classical prejudices, and take the lessons of quantum mechanics at face value, we may eventually learn how to extract our universe from the wave function.
* It’s not completely agreed upon that infalling objects actually do travel deep into the interior of a black hole. In 2012 a group of physicists argued that, if information is going to escape from evaporating black holes without violating the basic tenets of quantum mechanics, something dramatic has to happen at the event horizon: not quiet, empty spacetime, as is usually assumed, but a blast of high-energy particles known as a firewall. Opinions about the firewall proposal are divided, as theorists continue to argue back and forth about the issue.