Aristotle’s Underlying Logic
1 Introduction
1.1 Aristotle’s commitment to reason and scientific understanding
The enlightenment thinkers of the ancient fifth century were natural heirs to the earlier thinkers who had aimed to replace mythopoeic and religious explanation of material phenomena with extensive observation and naturalistic explanation. With the advent of democracy and an increasing market economy there came a new spirit of inquiry, a new reliance on reasoned argumentation, and a new commitment to understanding nature. The aspirations of the enlightenment activists blossomed in the humanist ideals of scientific rationalism and political liberty, in profound philosophical inquiry into metaphysics, epistemology and ethics, and in artistic and cultural works of enduring value. These ancients condemned superstition in a way that recalls Hume’s exhortation to employ philosophy as “the sovereign antidote … against that pestilent distemper … to restore men to their native liberty”. We might recall Heraclitus’s own exhortation to listen to the logos, the aims of the Pythagorean mathêmatikoi, the nous of Anaxagoras, and the condemnation of superstition by Hippocrates in The Sacred Disease and Ancient Medicine. Sophocles especially captured this spirit in Antigone (332–375) where he has the Chorus sing that “there are many wonders, but nothing is more wonderful than a human being”. Indeed, Prometheus might well have been their patron saint, because, in providing humans with various technai, he affirmed optimism about their future. A principle underlying this optimism holds that human beings can understand themselves and nature sufficiently to govern their own destinies without the external and apparently capricious interventions of supernatural beings. These ancients embraced Kant’s dictum, expressed many centuries later, “Sapere aude!” — “Dare to know!”. Their steady strides in the second half of the fifth century toward consolidating and rationally organizing the sciences helped to bring the earlier inquiries to fruition and prepared the way for the enduring accomplishments of the later philosophers, scientists, and political theorists. Many high points mark the achievements of this enlightenment, but two stand out for their progressive humanist ambition. As Protagoras in relation to the social world developed a political technê that affirmed the teachability of virtue and citizenship and thus promoted an empowering democratic activism, so Hippocrates in relation to the natural world developed a medical technê that affirmed the intelligence of human beings to intervene in the workings of nature to preserve health and to prevent disease.
Aristotle, interestingly himself the son of a physician, is an exemplary fourth century heir to enlightenment trends in science and philosophy. He affirmed the principle that nature in its diversity and human beings in their complexity are comprehensible. In Metaphysics 1.2 he openly avows a humanist ideal kindred to that of Hippocrates in Ancient Medicine.1
The acquisition of this knowledge [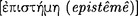 ] … [has been] regarded as not suited for man. … God alone may have this prerogative, and it is fitting that a man should seek only such knowledge as becomes him [and not, as the poets say, arouse the gods’ jealousy]. But we should not believe in divine jealousy; for it is proverbial that bards tell many lies, and we ought to regard nothing more worthy of honor than such knowledge.2 (982b28–983a7)
] … [has been] regarded as not suited for man. … God alone may have this prerogative, and it is fitting that a man should seek only such knowledge as becomes him [and not, as the poets say, arouse the gods’ jealousy]. But we should not believe in divine jealousy; for it is proverbial that bards tell many lies, and we ought to regard nothing more worthy of honor than such knowledge.2 (982b28–983a7)
Aristotle in the fourth century embraced the earlier enlightenment’s daring to know and its optimistic confidence in reason’s ability to establish objective knowledge. We can thus appreciate his exhortation in Nicomachean Ethics 10.7 that “we not follow the proverb-writers to ‘think mortal thoughts’ … Rather, as far as we can, we ought to strive to be immortal and to go to all lengths to live a life that expresses our supreme element” (1177b31–34). This supreme element consists precisely in the capacity of intellect by which human beings make both themselves and nature objects of contemplation.
Aristotle boldly began Metaphysics by affirming that “all men naturally desire to know”. He then traced the acquisition of knowledge from sensation through memory of the same thing and finally to art and science (epistêmê), which are produced through extensive experience.
Art [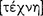 ] is born when out of many bits of information derived from experience there emerges a grasp of those similarities in view of which they are a unified whole. Thus, a man is experienced who knows that when Callias was ill of this disease he was helped by this medicine, and so for Socrates and for many others, one by one; but to have art is to grasp that all members of the group of those who are ill of this disease have been helped by this medicine.
] is born when out of many bits of information derived from experience there emerges a grasp of those similarities in view of which they are a unified whole. Thus, a man is experienced who knows that when Callias was ill of this disease he was helped by this medicine, and so for Socrates and for many others, one by one; but to have art is to grasp that all members of the group of those who are ill of this disease have been helped by this medicine.
Now experience [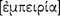 ] seems in no respect inferior to art in a situation in which something is to be done. … The reason is that experience, like action or production, deals with things severally as concrete individuals, whereas art deals with them generally. Thus, a physician does not cure species-man (except incidentally), but he cures Callias, Socrates, or some other individual with a proper name, each of whom happens to be a man. If, then, someone lacking experience, but knowing the general principles of the art, sizes up a situation as a whole, he will often, because he is ignorant of the individuals within that whole, miss the mark and fail to cure; for it is the individual that must be cured.
] seems in no respect inferior to art in a situation in which something is to be done. … The reason is that experience, like action or production, deals with things severally as concrete individuals, whereas art deals with them generally. Thus, a physician does not cure species-man (except incidentally), but he cures Callias, Socrates, or some other individual with a proper name, each of whom happens to be a man. If, then, someone lacking experience, but knowing the general principles of the art, sizes up a situation as a whole, he will often, because he is ignorant of the individuals within that whole, miss the mark and fail to cure; for it is the individual that must be cured.
Nevertheless, we believe that knowing and understanding 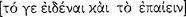 characterize art rather than experience. And so we take experts
characterize art rather than experience. And so we take experts  in an art to be wiser than men of mere experience; because wisdom presumably comes only with knowledge, and we believe that the experts can analyze and explain, whereas others cannot. Men of experience discern the fact “that”, but not the reason “why”. Hence we also hold master workmen [
in an art to be wiser than men of mere experience; because wisdom presumably comes only with knowledge, and we believe that the experts can analyze and explain, whereas others cannot. Men of experience discern the fact “that”, but not the reason “why”. Hence we also hold master workmen [ ] in each craft to be more valuable and discerning and wise than manual laborers [
] in each craft to be more valuable and discerning and wise than manual laborers [ ], because the former can discriminate the various factors relevant to the various effects produced; whereas the latter, like inanimate objects, produce effects, as fire burns, without knowing what they are doing. Inanimate objects produce their effects somehow by nature; and manual workers, by habit. Master workers are presumably wiser, then, not because they are practical, but because they have their reasons and can explain what they are doing [
], because the former can discriminate the various factors relevant to the various effects produced; whereas the latter, like inanimate objects, produce effects, as fire burns, without knowing what they are doing. Inanimate objects produce their effects somehow by nature; and manual workers, by habit. Master workers are presumably wiser, then, not because they are practical, but because they have their reasons and can explain what they are doing [ ] (981a5–981b6)
] (981a5–981b6)
Notwithstanding a class supremacy expressed here, it is evident that Aristotle was animated by a firm commitment to the centrality of reason in human life. Indeed, his many treatises on natural science, metaphysics, ethics and politics give expression to his commanding commitments to discovering truth and establishing knowledge. Thus, in spite of his frequent complaints about Socrates, Aristotle nevertheless embraced his teaching in Phaedo (89d) that “there is no worse sin than misology” and in Apology (38a) that “the unexamined life is not worth living for a human being”. The lessons of Nicornachean Ethics require a life of reason for realizing one’s humanity and achieving happiness. Human virtue consists in making excellent the soul’s deliberative and scientific faculties: practical wisdom 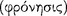 “is a state grasping the truth, involving reason [
“is a state grasping the truth, involving reason [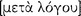 ], concerned with action about what is good and bad for a human being” (NE 6.5: 1140b4–6); and wisdom
], concerned with action about what is good and bad for a human being” (NE 6.5: 1140b4–6); and wisdom  “is understanding plus scientific knowledge [
“is understanding plus scientific knowledge [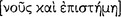 ] of the most honorable things” (NE 6.7: 1141a18–20; cf. Meta. 982a4–6). Human happiness requires a philosophic life. When we consider Aristotle’s bold statements in On the Soul 3.5 and 3.7 that “actual knowledge is identical with its object [
] of the most honorable things” (NE 6.7: 1141a18–20; cf. Meta. 982a4–6). Human happiness requires a philosophic life. When we consider Aristotle’s bold statements in On the Soul 3.5 and 3.7 that “actual knowledge is identical with its object [ ]” (430a19–20 & 431a1–2), we can more fully appreciate his exhortation in Nicomachean Ethics 10.7 that reaffirms the spirit of his inquiry in Metaphysics 1.2 not to bow to ignorance and inability, but always “to live a life that expresses our supreme dement”. Prometheus may have stolen for us fire from the hearth of the Olympians, but Aristotle aimed to secure for us a place at their table. In this connection, then, Aristotle’s logical investigations are among his enduring accomplishments toward realizing this end.
]” (430a19–20 & 431a1–2), we can more fully appreciate his exhortation in Nicomachean Ethics 10.7 that reaffirms the spirit of his inquiry in Metaphysics 1.2 not to bow to ignorance and inability, but always “to live a life that expresses our supreme dement”. Prometheus may have stolen for us fire from the hearth of the Olympians, but Aristotle aimed to secure for us a place at their table. In this connection, then, Aristotle’s logical investigations are among his enduring accomplishments toward realizing this end.
1.2 Previous interpretations
Until recently the difference between traditional or ‘Aristotelian’ logic and Aristotle’s own ancient logic had been blurred. This is similar to the blurring of a similar distinction between Christian religion and the teachings of Jesus, or the difference between various ‘Marxian’ philosophies and the teachings of Karl Marx. It is remarkable, for example, that for Aristotle in every syllogism the conclusion follows logically from the premisses. This contrasts with the usage of traditional logicians, who continue to speak of invalid syllogisms. For Aristotle this is a contradiction in terms, an oxymoron. In addition, Aristotle would never have tested the validity or invalidity of a syllogism according to rules of quality, quantity, and distribution. He had his own methods for establishing validity and invalidity. However, it was really not possible meaningfully to distinguish the historical logic of Aristotle from its later accretions and compare the two until modern logicians examined Aristotle’s syllogistic through the lens of mathematical logic — that is, until modern logicians turned their attention specifically to the formal aspects of deductive discourses apart from their subject matters. As a result, studies of Aristotle’s logic since the early 20th century have established his genius as a logician of considerable originality and insight. Indeed, we can now recognize many aspects of his logical investigations that are themselves modern, in the sense that modern logicians are making discoveries that Aristotle had already made or had anticipated. Perhaps the longevity of this oversight about the nature and accomplishments of his logical investigations is attributable to scholars not having recognized that Aristotle expressly treated the deduction process itself.
Jan Łukasiewicz initiated the reassessment of Aristotle’s syllogistic in the 1920s. He was followed by James W. Miller, I. M. Bochenski, and Günther Patzig among others. This reassessment culminated in the 1970s and 1980s with the works of John Corcoran, Timothy Smiley, and Robin Smith. These modern logicians used mathematical logic to model Aristotle’s logic and discovered a logical sophistication long overlooked by traditionalist logicians such as R. Whately, H. W. B. Joseph, J. N. Keynes, W. D. Ross, and R. M. Eaton. These traditionalists, whose modern origin can be traced to the Port Royal Logic, believe that Aristotle composed Prior Analytics as a logic manual for studying categorical arguments or syllogisms. They take a syllogism to be a fully interpreted premiss-conclusion argument whose validity or invalidity is determined by applying rules of quality, quantity, and distribution, all of which really only help to define a syllogism. However, traditionalists tend to conflate this sense of a syllogism with another sense when they take a syllogism also to be a relatively uninterpreted argument pattern whose instances are valid or invalid arguments.
Now, in spite of their equally criticizing traditionalist interpreters, mathematical logicians themselves tend to fall into two camps concerning Aristotle’s project in Prior Analytics. In fact, when modern logicians mathematically modeled Aristotle’s logic, they tacitly distinguished two tendencies in the traditionalist interpretation, the one treating what it believed were Aristotle’s axiomatic interests, the other treating Aristotle’s argumental interests. The axiomaticist interpretation by Łukasiewicz, Bochenski, Miller, and Patzig takes a syllogism to be a single, logically true conditional proposition, some of which are taken to be axioms. On this interpretation Prior Analytics contains an axiomatized deductive system with an implicit underlying propositional logic. Euclid’s Elements is an ancient analogue. The axiomaticists examine Aristotle’s syllogistic mathematically from a Frege-Russell view of logic as formal ontology. On the other hand, deductionists examine Aristotle’s logic mathematically from a Quinian view of logic as formal epistemology.3 The deductionist interpretation of Corcoran, Smiley, and Smith takes a syllogism to be a deduction, that is, to be a fully interpreted argumentation having a cogent chain of reasoning in addition to premisses and a conclusion. On this interpretation the number of premisses is not restricted to two. This interpretation sees Prior Analytics as having proof-theoretic interests relating to a natural deduction system. Interpretive lines, then, are drawn along what each view considers a syllogism to be and what each takes to be Aristotle’s accomplishment in Prior Analytics.
However, notwithstanding significant differences among modern interpretations, there are two striking similarities. (1) All three interpretations consider the process of reduction  treated in Prior Analytics A7 in virtually the same way. The various interpreters hold that reduction amounts to deduction of some syllogisms, taken as derived, from others, taken as primitive, to form a deductive system. In addition, they do not distinguish reduction from analysis
treated in Prior Analytics A7 in virtually the same way. The various interpreters hold that reduction amounts to deduction of some syllogisms, taken as derived, from others, taken as primitive, to form a deductive system. In addition, they do not distinguish reduction from analysis  . Aristotle, though, distinguished deduction from reduction and each of these from analysis. (2) The axiomaticists and deductionists equally consider Aristotle to have employed the method of counterargument to establish knowledge of invalidity in his treatment of syllogisms in Prior Analytics A4–6. However, Aristotle there used neither the method of counterargument nor the method of counterinterpretation. It is astonishing that such different interpretations of a syllogism could produce such similar views about the logical relationships among the syllogisms.
. Aristotle, though, distinguished deduction from reduction and each of these from analysis. (2) The axiomaticists and deductionists equally consider Aristotle to have employed the method of counterargument to establish knowledge of invalidity in his treatment of syllogisms in Prior Analytics A4–6. However, Aristotle there used neither the method of counterargument nor the method of counterinterpretation. It is astonishing that such different interpretations of a syllogism could produce such similar views about the logical relationships among the syllogisms.
In great measure, interpretive problems are attributable to scholars not having sufficiently recognized Aristotle’s acumen in distinguishing logical and metalogical discourses. Deductions are equally performed in different languages: (1) in an object language about a given subject matter and (2) in a metalanguage, which is used to model formal aspects of object language discourses relating to sentences, arguments, argumentations and deductions. Discourses in these categorially different languages may or may not use the same deduction system or the same logic terms with the same or different denotations. We distinguish an object language deduction from a metalogical deduction. Aristotle understood his syllogistic deduction system to function at both levels. In Prior Analytics he both studied his syllogistic logic and its applications and he used this logic in that study. Traditionalists, however, altogether missed Aristotle’s making this distinction by their conflating two senses of a syllogism and, consequently, they overlooked a syllogistic deduction process. Axiomaticists mistook a conditional sentence corresponding to a syllogism for the syllogism itself to confuse the two levels of discourse and thereby they lost sight of Aristotle’s principal concern with deduction. Still, they were correct to focus on his metalogical treatment of ‘syllogistic forms’, even if in their enthusiasm to apply mathematical logic to Aristotle’s work they mistakenly saw an axiomatized deductive system in Prior Analytics. Deductionists correctly focused attention on Aristotle’s concern with the process of deduction and a natural deduction system. However, in reacting to the axiomaticists, they did not take Aristotle as himself modeling object language discourses by means of a metalogical discourse. Nor, then, did they consider his metalogical discourse to be sufficiently formal for his having distinguished logical syntax from semantics. Deductionists modeled Aristotle’s logic but did not recognize Aristotle as himself providing an ancient model of an underlying logic with a formal language.
1.3 Aristotle’s project: to establish an underlying logic
Aristotle would have agreed with Alonzo Church that “(formal) logic is concerned with the analysis of sentences or of propositions and of proof with attention to the form in abstraction from the matter” (1956: 1; author’s emphasis). Thus, for Church the science of logic is a metalogical study of underlying logics (1956: 57–58). The difference between logic and metalogic is drawn between using a logic to process information about a given subject matter with a given object language and studying a logic or an underlying logic, which involves a language, a semantics, and a deduction system. Logicians use a metalanguage to study the formal aspects of an object language apart from its subject matter, often to study an underlying logic’s deduction system. Aristotle undertook just such a study in Prior Analytics. Indeed, part of Aristotle’s philosophical genius is to have established a formal logic, while at the same time making the study of logic scientific. He recognized that deductions about a given subject matter are topic specific and pertain to a given domain, say to geometry or to arithmetic or to biology, but that such deductions employ a topic neutral deduction system to establish knowledge of logical consequence.
In having a keen interest in epistemics, Aristotle shares with modern logicians the notion that central to the study of logic is examining the formal conditions for establishing knowledge of logical consequence — that logic, then, is a part of epistemology. He composed Prior Analytics and Posterior Analytics to establish a firm theoretical and methodological foundation for  (apodeiktikê epistêmê), or demonstrative knowledge (24a10–11). In Nicomachean Ethics 6, where he treated the intellectual excellences, Aristotle indicated the importance he attributed to demonstration (
(apodeiktikê epistêmê), or demonstrative knowledge (24a10–11). In Nicomachean Ethics 6, where he treated the intellectual excellences, Aristotle indicated the importance he attributed to demonstration ( [apodeixis]): “scientific knowledge, then, is a demonstrative state [
[apodeixis]): “scientific knowledge, then, is a demonstrative state [ ]” that constitutes an appropriate confidence in the results of deductive reasoning (1139b18–36; cf. Po.An.A2: 71b18–22). He saw his purpose in Prior Analytics precisely to establish confidence in the deduction process and particularly in his syllogistic deduction system. To accomplish this project he especially studied the formal or syntactic matter of deducibility. Aristotle thought of deduction as a kind of computational process. Indeed, the verb
]” that constitutes an appropriate confidence in the results of deductive reasoning (1139b18–36; cf. Po.An.A2: 71b18–22). He saw his purpose in Prior Analytics precisely to establish confidence in the deduction process and particularly in his syllogistic deduction system. To accomplish this project he especially studied the formal or syntactic matter of deducibility. Aristotle thought of deduction as a kind of computational process. Indeed, the verb  (sullogizesthai) used by Aristotle to denote the special kind of deduction process treated in Prior Analytics derives from mathematical calculation. His special concern, then, was to develop a deduction apparatus by which someone could decide in a strictly mechanical, or computational, manner which sentences are logical consequences of other sentences.
(sullogizesthai) used by Aristotle to denote the special kind of deduction process treated in Prior Analytics derives from mathematical calculation. His special concern, then, was to develop a deduction apparatus by which someone could decide in a strictly mechanical, or computational, manner which sentences are logical consequences of other sentences.
Aristotle’s promethean contribution to science and philosophy, then, concerns his study of the deduction process itself. He knew that a given sentence is either true or false; and he recognized this to be the case independent of a participant. He also knew from his familiarity with mathematical argumentation and dialectical reasoning that a given sentence either follows necessarily or does not follow necessarily from other given sentences; likewise, he recognized this to be the case independent of a participant. These are ontic matters having to do with being. In addition, Aristotle knew that the truth or falsity of a given sentence or the validity or invalidity of a given argument might not be known to one or another participant. Now, a given axiomatic science aims to establish knowledge about its proper subject matter (Po. An. A1: 71a1–11 & A3: 72b19–22). Since Aristotle took such a science to consist principally in the collection of sentences — definitions, axioms, theorems — of its extended discourse, the project of such a science is to decide which sentences pertaining to its subject matter are true, or theorems, and which sentences, for that matter, are false and not theorems. Procedures for deciding a sentence’s truth or falsity are epistemic matters having to do with knowing.
In respect of epistemics Aristotle recognized two ways to establish the truth of a given sentence: (1) by induction 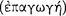 and (2) by deduction (Po.An.A1–2, EN 6.3 & Meta. 1.9: 992b30–993a1). In respect of an axiomatic science, while definitions and axioms, or first principles, are determined inductively and are not the result of a deductive process,4 its theorems are decided deductively. In the works of the Organon, particularly in Prior Analytics and Posterior Analytics, Aristotle treated the deductive method for establishing knowledge that a given sentence is true. This project requires two steps (Pr. An. A1: 25b28–31), which he treated separately in Prior Analytics and Posterior Analytics. In Posterior Analytics Aristotle treated the requirements for demonstrative science, a constituent part of which is demonstration. He writes in Posterior Analytics A2:
and (2) by deduction (Po.An.A1–2, EN 6.3 & Meta. 1.9: 992b30–993a1). In respect of an axiomatic science, while definitions and axioms, or first principles, are determined inductively and are not the result of a deductive process,4 its theorems are decided deductively. In the works of the Organon, particularly in Prior Analytics and Posterior Analytics, Aristotle treated the deductive method for establishing knowledge that a given sentence is true. This project requires two steps (Pr. An. A1: 25b28–31), which he treated separately in Prior Analytics and Posterior Analytics. In Posterior Analytics Aristotle treated the requirements for demonstrative science, a constituent part of which is demonstration. He writes in Posterior Analytics A2:
By a demonstration  I mean a scientific deduction
I mean a scientific deduction 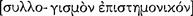 ; and by scientific I mean a deduction by possessing which we understand something … demonstrative understanding
; and by scientific I mean a deduction by possessing which we understand something … demonstrative understanding  in particular must proceed from items that are true and primitive and immediate and more familiar than and prior to and explanatory of the conclusions. There can be a deduction [
in particular must proceed from items that are true and primitive and immediate and more familiar than and prior to and explanatory of the conclusions. There can be a deduction [ (sullogisrnos)]even if these conditions are not met, but there cannot be a demonstration [
(sullogisrnos)]even if these conditions are not met, but there cannot be a demonstration [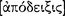 ] — for it will not bring about understanding [
] — for it will not bring about understanding [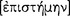 ]; in respect of a given subject matter]. (71b17–25; cf. Top. A1: 100a27–29)
]; in respect of a given subject matter]. (71b17–25; cf. Top. A1: 100a27–29)
Aristotle early distinguished deduction (sullogismos) from demonstration (apodeixis). In Prior Analytics A4 he stated that he would treat deduction before demonstration because it is more universal: “for [every] demonstration is a kind of deduction, but not every deduction is a demonstration” (25b30–31). In Posterior Analytics A2 (cf. Pr. An. B2–4) he determined this universality to consist in a deduction’s being possible even when the premiss sentences are not antecedently known to be true or even when they are false. Thus, one can know that the conclusion sentence of a given demonstration is true because (1) its premiss sentences are all true and (2) it is a deduction.
A deduction per se, then, establishes knowledge, not that the sentence that is the conclusion of a given argument is true, but only that it follows necessarily, or logically, from the sentences in a premiss-set. Aristotle made an important distinction in his logical investigations between epistemic concerns and ontic concerns. This is especially evident in Prior Analytics B1–4 where he treated the deducibility of true and false sentences from various combinations of true and false sentences taken as premisses. This distinction indicates an understanding of logical consequence that modern logicians will recognize. The confidence one acquires from a demonstration derives from knowing, as Aristotle often pointed out, that it is impossible for true sentences to imply a false sentence (Pr. An. B2–4). Given true sentences as premisses, established (initially) by means independent of deduction, one can be certain that the conclusion sentence of a demonstration also is true5 precisely because it is shown to be a logical consequence of other true sentences. In Prior Analytics Aristotle was especially concerned to determine which formal patterns of argumentation might be used to establish knowledge that a given sentence necessarily follows from other given sentences. In particular, he saw his project as determining “how every syllogism is generated” (25b26–31) by identifying which elementary argument patterns could serve as rules analogous to such patterns as modus ponens, modus tollens, and disjunctive syllogism for modern propositional logic.
Looking back, we see that mathematicians of the fourth century had been assiduously attending to axiomatizing geometry. This activity principally concerned condensing the entire wealth of geometric knowledge into small sets of definitions and axioms from which the theorems of geometry could be derived and set out as a long, extended discourse. Euclid’s Elements is an extant fruit of this activity. Except for identifying a small set of common notions 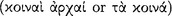 , these mathematicians were not concerned with studying the epistemic process underlying geometric discourse. They took geometry intuitively as an informal axiomatic system (Church 1956: 57) with an implicit underlying logic. The ancient mathematicians may have formalized the truths of geometry, but they hardly formalized the deductive method for processing the information already contained in its definitions and axioms.
, these mathematicians were not concerned with studying the epistemic process underlying geometric discourse. They took geometry intuitively as an informal axiomatic system (Church 1956: 57) with an implicit underlying logic. The ancient mathematicians may have formalized the truths of geometry, but they hardly formalized the deductive method for processing the information already contained in its definitions and axioms.
Undoubtedly Aristotle had participated in discussions, in the Academy and elsewhere, about axiomatizing geometry. He may have asked about deduction rules used to establish geometric theorems. Indications that he did include his attention to various proofs such as that of the incommensurability of the diagonal with the side of a square and those related to properties of triangles, and his frequent attention to the common notions of the mathematical sciences; there is also his curious mention of the middle term and syllogistic reasoning in connection with geometric demonstration (Po. An. A9: 76a4–10; A12: 77b27–28; cf. Pr. An. A35 & A24). Aristotle surely wondered how one could be assured in geometric demonstrations that a conclusion necessarily follows from premisses. This matter is all the more interesting in the case of longer, more involved demonstrations. Still, we cannot say that he undertook a metalogical study of geometric proof.
Perhaps it was Aristotle’s own insight or an implicit part of the philosophical discussion of the time that the axiomatization of geometry could serve in some way as a model for formalizing the non-mathematical sciences such as botany and zoology. Some such notion seems to have animated his scientific and logical investigations.6 Now, the actual project of establishing a given science’s definitions and axioms and then its theorems, which would conform to the criteria set out in Posterior Analytics A2, did not concern Aristotle in the Organon. This project lies outside the scope of logic. Rather, his preeminent concern there was to study deduction and demonstration per se: not with, that is, one or another distinct subject matter, but with the formal deduction process that has no similar subject matter. Aristotle in his logical investigations subordinated a concern with the what or the why and wherefore to focus on the that and the how. Thus, presupposing various axiomatic sciences with distinct domains, he took up the narrower and more poignant questions about the epistemic process of deriving theorems from axioms. Aristotle especially examined the deductive foundations of demonstration, that is, of demonstrative knowledge or axiomatic science.
The first chapters of Metaphysics 1 reveal Aristotle’s intellectual disposition toward scientific knowledge and signal the importance he attributed to metalogical study of deduction. In fact, Aristotle identified this task as a province proper only to philosophy. In Metaphysics 2.1 he writes that “philosophy is the science of truth  ” (993b20). And since “status in being governs status in truth
” (993b20). And since “status in being governs status in truth  ” (Meta. 2.1: 993b30–31), the philosopher’s project includes studying, not a particular part of being, but being-qua-being (
” (Meta. 2.1: 993b30–31), the philosopher’s project includes studying, not a particular part of being, but being-qua-being ( Meta. 4.1: 1003a21–26). “The philosopher must have within his province the first principles [
Meta. 4.1: 1003a21–26). “The philosopher must have within his province the first principles [ ] and primary factors of primary beings” (Meta. 4.2: 1003b17–19) and “be able to view things in a total way” (1004a34–1004b1). Accordingly, “it is not the geometer’s [nor any other specialist’s] business to answer questions about what contrariety is, or perfection, or being, or unity, or sameness, or diversity [or even, for that matter, about deduction rules]; for him these remain postulates [
] and primary factors of primary beings” (Meta. 4.2: 1003b17–19) and “be able to view things in a total way” (1004a34–1004b1). Accordingly, “it is not the geometer’s [nor any other specialist’s] business to answer questions about what contrariety is, or perfection, or being, or unity, or sameness, or diversity [or even, for that matter, about deduction rules]; for him these remain postulates [ ]” (Meta. 4.2: 1005a11–13; cf. 1005a31). Later in Metaphysics 4.3 Aristotle addressed the philosopher’s responsibility to examine certain axioms precisely because they refer to all of being — being-qua-being — and not just a part of being (1005a21–22).
]” (Meta. 4.2: 1005a11–13; cf. 1005a31). Later in Metaphysics 4.3 Aristotle addressed the philosopher’s responsibility to examine certain axioms precisely because they refer to all of being — being-qua-being — and not just a part of being (1005a21–22).
But it is clear that the axioms extend to all things as being (since they all have being in common); hence the theory of axioms [ ] also belongs to him who knows being as being. (1005a27–29)
] also belongs to him who knows being as being. (1005a27–29)
He is not writing about axioms special to a particular science, but about ontic principles that apply alike to all domains.
After indicating the limitations of the special sciences for examining these axioms, Aristotle writes that
the philosopher, who examines the most general features of primary being, must investigate also the principles of deductive reasoning [ ]. … So that he who gets the best grasp of beings as beings must be able to discuss the basic principles of all being
]. … So that he who gets the best grasp of beings as beings must be able to discuss the basic principles of all being  , and he is the philosopher. (1005b5-6-11; cf. Meta. 11.4)
, and he is the philosopher. (1005b5-6-11; cf. Meta. 11.4)
Immediately Aristotle cites the principle of non-contradiction as one of the principles “about which it is impossible to be mistaken” and writes, moreover, that such a principle that is “[necessary] in order to understand anything whatever cannot be an assumption  ” (1005b11–12 & 15–16): “It is impossible for the same thing at the same time to belong and not to belong
” (1005b11–12 & 15–16): “It is impossible for the same thing at the same time to belong and not to belong 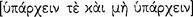 to the same thing and in the same respect” (1005b19–22). He states the principle here as an ontic principle,7 but he immediately relates it to demonstration, implicitly reminding us that being governs truth.
to the same thing and in the same respect” (1005b19–22). He states the principle here as an ontic principle,7 but he immediately relates it to demonstration, implicitly reminding us that being governs truth.
Hence, if contraries cannot at the same time belong to the same thing … and if an opinion [ ] stated in opposition to another opinion is directly contrary to it, then it is evidently absurd for the same man at the same time to believe the same thing to be and not to be; for whoever denies this would at the same time hold contrary opinions
] stated in opposition to another opinion is directly contrary to it, then it is evidently absurd for the same man at the same time to believe the same thing to be and not to be; for whoever denies this would at the same time hold contrary opinions  . It is for this reason that all who carry out a demonstration rest it on this as on an ultimate belief
. It is for this reason that all who carry out a demonstration rest it on this as on an ultimate belief  ; for this is naturally a foundation also of all other axioms [
; for this is naturally a foundation also of all other axioms [ ]. (1005b26–34)
]. (1005b26–34)
This passage ends Metaphysics 4.3. Much of the remainder of Metaphysics 4 is devoted to establishing the absurdity of rejecting the principle of non-contradiction for intelligible discourse. It is evident that Aristotle understood a philosopher’s responsibilities to include examining the principles of deductive reasoning. For Aristotle, studying the principles of being is simultaneously a study of the principles of thought. Logic, which he took to be a part of epistemology, is nevertheless grounded in the nature of being. Perhaps Aristotle appropriated Parmenides’ dictum that “thought and being are the same [ ]”, taking this to mean that truth and logical consequence, as they appear in thought, follow being.
]”, taking this to mean that truth and logical consequence, as they appear in thought, follow being.
Now, Aristotle writes in Metaphysics 11.4 that “taking equals from equals leaves equal remainders” is an example of a notion common to all quantitative being (1061b20–21). He had recognized that the common notions belonging to the mathematical sciences belonged equally to all and specially to none.8 And, although he never articulated a complete list of common notions for the non-mathematical sciences, nor for that matter in any systematic way for the mathematical sciences, he stated in Metaphysics 4 that the principles of contradiction and of the excluded middle are among the common notions applicable to all rational discourse. Aristotle noticed that the common notions relating to different branches of mathematics, while stipulative of magnitudes in general, do not stipulate any one domain, such as arithmetic or geometry, in particular. They generally do not specify any content however much they anticipate establishing relationships among magnitudes special to a mathematical science. They are topic neutral in this circumscribed sense, and, thus, they have a relative independence unlike lines, angles, or numbers. They are neither embedded in nor mentally inextricable from the objects of a particular science. This is not the case with a science’s principles. The common notions, then, may be taken in abstractum and treated on their own account irrespective of the subject matter of a given quantitative science.
These common notions, moreover, generally express formal relationships among magnitudes within a quantitative science and accordingly apply equally to a variety of different, quantitative domains. Because of their relative formality and their special universality, the common notions were applied as inference rules across the mathematical sciences. Their use in this epistemic manner is evident in Euclid’s Elements.9 Aristotle’s having recognized the common notions as principles of reasoning had profound consequences for the development of ancient logic. Understanding this and that Aristotle took a syllogism to fit an elementary argument pattern with only valid instances help to confirm the rule-nature of his statements in Prior Analytics A4–6 relating to when a syllogism comes about. In the case of Euclid’s common notions, two magnitudes remain incommensurable without there being a third, or middle, that unites them as extremes in a particular way — using a common notion makes this evident. An exactly analogous relationship applies in the case of the patterns of perfect or complete syllogisms, the  (teleioi sullogismoi), in Prior Analytics A4 in respect of relating substantive terms and making evident their connections. Aristotle’s manner of expressing the patterns of the syllogisms in sentences beginning with
(teleioi sullogismoi), in Prior Analytics A4 in respect of relating substantive terms and making evident their connections. Aristotle’s manner of expressing the patterns of the syllogisms in sentences beginning with  and
and  comports exactly with Euclid’s expressions of the common notions and suggests their similar rule-nature.10 Aristotle went on to express his rules using schematic letters where Euclid did not. Scholars have overlooked Aristotle’s written statements of the rules to see only their schematic representations. Consequently, they have not recognized this as part of his effort to model a logic. Accordingly, they missed this link to mathematics and thus they missed an important part of his theory of deduction.
comports exactly with Euclid’s expressions of the common notions and suggests their similar rule-nature.10 Aristotle went on to express his rules using schematic letters where Euclid did not. Scholars have overlooked Aristotle’s written statements of the rules to see only their schematic representations. Consequently, they have not recognized this as part of his effort to model a logic. Accordingly, they missed this link to mathematics and thus they missed an important part of his theory of deduction.
Finally in this connection, besides stating syllogistic deduction rules and his actually using the patterns of the teleioi sullogismoi as rules in Prior Analytics, Aristotle virtually stated his taking them formally as rules in Prior Analytics A30 (46a10–12/15). There he used the expression ‘the principles of deduction that we also encounter in Metaphysics 4.3 (1005b7). Aristotle did not refer here in Prior Analytics to the principles or axioms of a given science, but to the most general principles of all being as they are grasped in thought. And again, in this same connection, he used the expression ‘the principles of demonstrations
that we also encounter in Metaphysics 4.3 (1005b7). Aristotle did not refer here in Prior Analytics to the principles or axioms of a given science, but to the most general principles of all being as they are grasped in thought. And again, in this same connection, he used the expression ‘the principles of demonstrations in Metaphysics 3.2 (996b26). Indeed, throughout Metaphysics Aristotle used the following expressions as synonyms in referring to common notions, including the laws of non-contradiction and the excluded middle:
in Metaphysics 3.2 (996b26). Indeed, throughout Metaphysics Aristotle used the following expressions as synonyms in referring to common notions, including the laws of non-contradiction and the excluded middle:  (1061b18)
(1061b18) 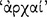 (996b26, 997a13)
(996b26, 997a13) (997a11, 13), and
(997a11, 13), and  (996b28, 997a21; see esp. Po. An. A10–11). Thus, we can see that a pattern of a syllogism is a relatively uninterpreted object. In fact, Aristotle treated each pattern exactly as a topic neutral rule of deduction in Prior Analytics A4–7 analogous to Euclid’s use of common notions in Elements. Perhaps the patterns of the four teleioi sullogismoi are Aristotle’s adaptation to the non-mathematical sciences of the common notions employed as deduction rules in the mathematical sciences.
(996b28, 997a21; see esp. Po. An. A10–11). Thus, we can see that a pattern of a syllogism is a relatively uninterpreted object. In fact, Aristotle treated each pattern exactly as a topic neutral rule of deduction in Prior Analytics A4–7 analogous to Euclid’s use of common notions in Elements. Perhaps the patterns of the four teleioi sullogismoi are Aristotle’s adaptation to the non-mathematical sciences of the common notions employed as deduction rules in the mathematical sciences.
1.4 The scope of this study
Our concern here is to present Aristotle’s system of logic while also revealing the mathematical sophistication of his logical investigations. Modern logicians believe that the possibility of mathematical logic, an important part of which involves generating models, consists in making a clear distinction between syntax and semantics. They also believe that the clear distinction between syntax and semantics resulted from borrowing symbolic notations from mathematical practice and then applying them to studies of deductive logics, but that earlier thinkers, lacking such notations, could not have made such distinctions. However, mathematical logic, considered as a discipline in general, has a formal and a material aspect. Its formal aspect has principally to do with the symbolic notations that have helped to illuminate underlying structural, or logical, features of deductive discourses. Yet, the substance of mathematical logic does not consist in its sophisticated notations, but in the problems logicians consider when studying underlying logics — that is, in particular, when they distinguish a logic’s syntax and its semantics and then ask questions about their relationships. Principal in this respect have been questions about a logic’s consistency, soundness, and completeness, which involve determining relationships between deducibility and logical consequence. A distinguishing feature of mathematical logic, then, consists precisely in these substantive matters.11 Remarkably, with only a rudimentary notation Aristotle considered just such mathematical matters in his concern to establish the practical, epistemic power of his logic for establishing scientific knowledge. In this connection we can grasp the revolution in the history and philosophy of logic — the “hypostatization of proof” — consolidated by Aristotle’s works on logic. “Prior Analytics is the earliest known work which treats proofs as timeless abstractions amenable to investigation similar to the investigations already directed toward numbers and geometrical figures” (Corcoran: personal communication). Thus, Prior Analytics is a proof-theoretic treatise on the deduction system of an underlying logic. Aristotle recognized the epistemic efficacy of certain elementary argument patterns, to wit, those of the syllogisms, and he formulated them as rules of natural deduction. Having raised important metalogical questions about the properties of his syllogistic deduction system, he successfully established a set of formal, epistemic conditions for recognizing logical necessity, and in this way he became the founder of formal logic.
Below we set out Aristotle’s underlying logic much as he himself did in the works of the Organon. We include Metaphysics among the treatises of his logical investigations. It is natural and not surprising that modern logicians and commentators, when treating Aristotle’s logic, focus principally on Prior Analytics: Prior Analytics is the most ‘logical’ of the treatises. In truth, the attraction of Prior Analytics has consisted in a scholar’s implicit recognition that Aristotle there treated the deduction system of an ancient underlying logic. We say ‘implicit’ because it was not until the studies of J. Corcoran and T. Smiley, and later those of R. Smith, that there is a growing explicit recognition that this is so. In any case, a deduction system is only one part of an underlying logic, which also contains a grammar and a semantics. Our contribution takes this recognition a little farther to hold that Aristotle intentionally aimed to develop an underlying logic along the lines of modernist thinking. This means that Aristotle invented a formal language to model his logic. However, since Aristotle did not set out his underlying logic in as systematic a manner as a modern logician, while, nevertheless, accomplishing much the same result, we employ the theoretical apparatus of modern mathematical logic to structure his account. With the aid of this template we show in Aristotle’s own words that he was concerned with exactly similar matters as a modern logician. We begin by presenting Aristotle’s treatment of the syntax and semantics of natural language in Categories, On Interpretation, and Metaphysics. These studies laid a foundation for his developing the formal language found in Prior Analytics for modeling axiomatic discourse. We then proceed to extract the syntax of sentence transformations leading to his establishing a set of deduction rules in Prior Analytics. Next we treat the logical methodology by which Aristotle established his deduction rules. We conclude with a statement of his understandings of “formal deducibility” and “logical consequence” and with a final section that summarizes four proof-theoretic accomplishments of his logical investigations.
1.5 Logic terminology
The following terminology assists in our study of Aristotle’s logic. We use Aristotle’s own terminology wherever it exists, which, interestingly, often corresponds exactly to ours. An argument is a two part system consisting in a set of sentences in the role of premisses and a single sentence in the role of conclusion; an argument is either valid or invalid. A sentence is either true or false. We sometimes use ‘conclusion’ elliptically for ‘sentence in the role of conclusion’ or ‘conclusion sentence’, and similarly for ‘premiss’. An argumentation is a three part system consisting in a chain of reasoning in addition to premisses and conclusion; an argumentation is either cogent, in which case it is a deduction, or fallacious, a fallacy. A sentence, an argument, and an argumentation are object language phenomena and domain specific. An argument pattern is a two part system consisting in a set of sentence patterns in the role of a premiss-set and a single sentence pattern in the role of a conclusion. A pattern is a metalinguistic object distinguishable from a form and is commonly represented schematically. An argument is said to fit, or to be an instance of, one or more argument patterns.12 A given argument pattern may have all valid instances, all invalid instances, or some valid and some invalid instances. An argument pattern is not properly valid or invalid, although logicians have used ‘valid’ in this connection, but we distinguish these category differences. An argument pattern with all valid instances is panvalid, that with all invalid instances is paninvalid, and that having instances of both is neutrovalid. We add that an elementary panvalid argument pattern is one having a simple premiss-set pattern whose epistemic value consists, in many cases, in its being quickly evident, or ‘evident through itself’, that its conclusion follows necessarily. An elementary argument pattern may be formulated in a corresponding sentence to express a rule of deduction. In addition, we follow G. Patzig (1968; cf. Rose 1968) to distinguish in Aristotle’s logic a concludent pattern of two sentences in the role of premisses, or a premiss-pair pattern, from an inconcludent premiss-pair pattern. A concludent pattern has a necessary result, that is, it results in a panvalid pattern all of whose instances are syllogisms, while an inconcludent pattern has no necessary result, that is, it cannot result in a panvalid pattern but only in a paninvalid pattern with only invalid argument instances.
In addition, we understand Aristotle to have considered a 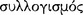 (sullogismos), which we translate by ‘syllogism’, to be a valid argument with only two premiss sentences, having only three terms, in one of three figures.13 A syllogism, then, is an elementary argument fitting a panvalid pattern. No syllogism is invalid. Aristotle saw his project in Prior Analytics to identify all such patterns, precisely because of their epistemic efficacy in the deduction process. We use the traditional names of the ‘syllogisms’ — ‘Barbara’, ‘Celarent’, etc.14 — to name patterns of syllogisms, just as ‘modus ponens’ names a kind of familiar pattern in propositional logic used in a deduction process. Still, these names do not signify instances of such patterns. Of course, ‘Barbara’ and ‘modus ponens’ also name deduction rules. However, in some cases — especially those pertaining to the teleioi sullogismoi, those in Sophistical Refutations, and those in Prior Analytics when Aristotle refers to a sullogismos as proving something — we translate ‘sullogismos’ by ‘deduction’. In these cases Aristotle recognized an epistemic process to occur in the mind of a participant who grasps that a given sentence is a logical consequence of other given sentences. Still, when he writes, in relation to a deduction process, that a syllogism arises (
(sullogismos), which we translate by ‘syllogism’, to be a valid argument with only two premiss sentences, having only three terms, in one of three figures.13 A syllogism, then, is an elementary argument fitting a panvalid pattern. No syllogism is invalid. Aristotle saw his project in Prior Analytics to identify all such patterns, precisely because of their epistemic efficacy in the deduction process. We use the traditional names of the ‘syllogisms’ — ‘Barbara’, ‘Celarent’, etc.14 — to name patterns of syllogisms, just as ‘modus ponens’ names a kind of familiar pattern in propositional logic used in a deduction process. Still, these names do not signify instances of such patterns. Of course, ‘Barbara’ and ‘modus ponens’ also name deduction rules. However, in some cases — especially those pertaining to the teleioi sullogismoi, those in Sophistical Refutations, and those in Prior Analytics when Aristotle refers to a sullogismos as proving something — we translate ‘sullogismos’ by ‘deduction’. In these cases Aristotle recognized an epistemic process to occur in the mind of a participant who grasps that a given sentence is a logical consequence of other given sentences. Still, when he writes, in relation to a deduction process, that a syllogism arises (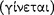 ), we understand him not to mean that a syllogism per se is a deduction, but that one’s arising during a deductive chain of reasoning signals making logical consequence evident, just as when a participant links given propositions and produces an instance of modus ponens signals logical consequence in propositional logic.
), we understand him not to mean that a syllogism per se is a deduction, but that one’s arising during a deductive chain of reasoning signals making logical consequence evident, just as when a participant links given propositions and produces an instance of modus ponens signals logical consequence in propositional logic.
Finally, we take treating patterns of sentences, patterns of arguments, and patterns of argumentations to constitute a large part of modeling a logic. Thus, for example, while there are numerous simple sentences in a given object language, each of them, nevertheless, consists in a subject and a predicate. Extracting this elementary pattern and representing it abstractly, or metalinguistically, is modeling a simple sentence — either by means of another sentence, using the language of the given object language (but, nevertheless, in the metalanguage), or by means of mathematical notation. In either case, a sentence is modeled and becomes an object of logical investigation. Thus, we take a formal language to be a model of one or another object language, with one or another degree of precision. In this way a logician can model arguments, deductions, and deduction systems better to study their respective properties and logical relationships.
2 Aristotle’s Ancient Model of an Underlying Logic
Aristotle knew that deductions about geometric objects are topic specific and that they employ a topic neutral deduction system, even if a participant uses that system implicitly. In Prior Analytics he turned his attention not to geometric or biological objects, nor even to geometric or biological discourses, but to the deduction apparatus used to make evident that a given categorical sentence necessarily follows from other given categorical sentences.15 Aristotle had observed a number of elementary argument patterns used in various object language discourses, some of which he recognized in their use always to result in something following necessarily, others of which he recognized in their use never to result in something following necessarily. He subsequently extracted these patterns for systematic examination. In Prior Analytics Aristotle modeled his syllogistic logic and presented the results of his investigating these patterns. In this connection, then, Prior Analytics is a scientific study of the syllogistic deduction system, which, taken together with Categories, On Interpretation, and parts of Metaphysics, comprises Aristotle’s treatment of an underlying logic.
The logic underlying cogent object language discourse accounts for that discourse’s coherence. While this discourse is itself topic specific as it treats objects of a given domain, its underlying logic is topic neutral and not bound to any one subject matter. The science of logic is devoted in great measure to modeling these underlying logics and consists in their study. To accomplish this study, a logician must not only model the deduction system of such discourse, but he/she must also model the object language itself, often with an aim to make such a language more precise. A logician’s principal concern is to extract and formalize (1) a grammar for the formation of sentences and their relationships and (2) a deduction system for sentence transformations. These are formal, syntactic concerns. A logician constructs a formal language to model one or more object language in respect of its structure. Such a formal language is taken to be uninterpreted, although hardly is such a formal language purely uninterpreted — often its logical constants are interpreted or have an implicit intended interpretation, as are what count as a sentence and an argument, etc. In any case, the ‘formulas’ or patterns for constructing and transforming sentences are relatively uninterpreted, as evidenced by the impossibility of assigning them meanings and truth-values (save for logics with identity and tautology). Thus, in modeling an underlying logic a logician also treats the semantics of sentences — establishing meaning and truth conditions — and of sentence transformations — establishing conditions of logical consequence.
Aristotle, then, invented an artificial language for two closely related purposes that embrace a modernist concern for modeling a logic. First, he wanted to develop a language (1) that conformed to his ontology of substance, a core of which is presented in Categories, and (2) that promoted a precision in scientific knowledge, a concern that he forcefully expressed in Metaphysics. Second, he wanted to model the underlying logic he developed as an epistemic instrument for scientific discourse both (1) to facilitate determining the properties of his logic and (2) to represent his logic for instructing others in its use. It is doubtful that Aristotle developed this artificial language to model natural language and more likely that he aimed to standardize scientific discourse and to model his logic. Aristotle invented four categorical sentence patterns, and he treated them as formal objects in order to establish certain of their properties and logical relationships. And while he did not represent his logic with a modern rigor and system, we can easily organize his own discourses according to a mathematical template without distortion to his meaning and intention. In this section we first consider Aristotle’s treatment of the grammars of natural language and his artificial language (§2.1), second, the semantics of his language (§2.2), and, third, the syntax of his deduction system (§2.3), While Aristotle treated the syntax of sentences in close relation to their semantics, he nevertheless sufficiently distinguished them so that we can treat them separately.
2.1 Aristotle’s metalinguistic study of grammar
To extract and represent his deduction system for analysis in Prior Analytics, and to prepare for its application to the various axiomatic sciences as a science is construed in Posterior Analytics, Aristotle undertook a systematic study of language. While the Sophists are perhaps his more immediate predecessors in this connection, Aristotle’s contributions firmly consolidated the early stages of linguistics as a special branch of learning. Efforts in this area are especially evident in Categories, On Interpretation, Metaphysics, Topics, Sophistical Refutations, and Rhetoric. In On Interpretation Aristotle treated the complexity of Greek grammar only generally as suited the purpose of his logical investigations. There he identified the simple sentence that predicates one thing of another thing as a proper object of logical analysis. By studying a natural language in these treatises Aristotle prepared the way to inventing the artificial language in Prior Analytics, perhaps the first artificial, or formal, language in the history of philosophy. And he accomplished this task without the aid of a sophisticated system of symbolic or mathematical notation. With his treatment of predication in Categories and Metaphysics in the background,16 we turn now to a part of the elementary grammar examined in On Interpretation.
The grammar of a natural language
In On Interpretation 1–4 Aristotle writes about sentence formation in a natural language, in this case in his own natural language. There he uses Greek to mention and to illustrate his observations about intelligible discourse that might apply in principle to any language (16a5–6). In this connection he intuitively takes Greek to be what modern logicians call a fully interpreted language. Nevertheless, he carefully focuses attention on its structural aspects apart from any meanings, except for purposes of illustration, that sentences might express about a subject matter. Indeed, although he does not have expressions for ‘natural language’, ‘object language’, and ‘metalanguage’, it is evident that in On Interpretation Aristotle intentionally objectifies aspects of language in general and does not study only the Greek language in particular. On Interpretation is a metalinguistic treatise in which Aristotle consciously examines certain syntactic and semantic aspects of language.
Aristotle treats sentence formation in a natural language as essentially consisting in combining 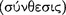 a noun
a noun  and a verb (
and a verb (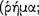 i.e., a predicate [16a9–18]) so as to produce a meaningful expression (phis
i.e., a predicate [16a9–18]) so as to produce a meaningful expression (phis ), a complete thought. Every sentence necessarily has these two basic components, neither of which by itself is sufficient.
), a complete thought. Every sentence necessarily has these two basic components, neither of which by itself is sufficient.
Every affirmative sentence [ ] consists in a noun and a verb, whether [determinate or] indeterminate. Unless there is also a verb, there is neither an affirmation nor a denial [
] consists in a noun and a verb, whether [determinate or] indeterminate. Unless there is also a verb, there is neither an affirmation nor a denial [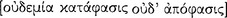 ]. (On Int. 10: 19b10–12; cf. Cat. 2: la16–19)17
]. (On Int. 10: 19b10–12; cf. Cat. 2: la16–19)17
In addition, Aristotle recognizes that the words making up a sentence must be concatenated or strung together in certain ways so as to bear meaning: “that the words are pronounced [merely] in succession [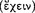 ] does not make them a unity [
] does not make them a unity [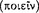 ]” (17a14).18 In On Interpretation 4 Aristotle defines ‘sentence’ as follows:
]” (17a14).18 In On Interpretation 4 Aristotle defines ‘sentence’ as follows:
A sentence [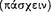 ] is meaningful speech [
] is meaningful speech [ ] — the parts of which, as expressed [separately] mean something as an expression but not as an affirmation [
] — the parts of which, as expressed [separately] mean something as an expression but not as an affirmation [ ]. I mean, for example, that ‘man’ means something, but [by itself] not that it is or is not; there will be an affirmation or a denial [only] if something is added [
]. I mean, for example, that ‘man’ means something, but [by itself] not that it is or is not; there will be an affirmation or a denial [only] if something is added [ ]. (16b26–28; cf. 10: 19b10–12)
]. (16b26–28; cf. 10: 19b10–12)
A noun and a verb by themselves may possess meaning, but by themselves they do not constitute a sentence, nor do they constitute a sentence merely by being strung together arbitrarily. Thus, from his notion of sentence in On Interpretation, we can extract Aristotle’s rule for the formation of a generic sentence in a natural language and express it as follows:
This rule identifies the broadest pattern of a sentence in a natural language. Aristotle’s syntax language specifies, abstractly, only nouns and verbs as its vocabulary, which are combined to form sentences according to this elementary rule. We might wish that Aristotle had expressed this rule with at least the modest precision here. However, Aristotle has neither a complete nor a complex set of syntax rules of sentence formation in On Interpretation. Still, it is evident from his treatment of this topic in his logical investigations that his understanding of the grammar of a natural language is richer than his lack of rigorously stated rules would indicate. And while this syntax rule is mixed with semantic notions, he nevertheless has identified here the basic pattern of a sentence in a natural language.
Aristotle continues his discussion of grammar in On Interpretation 4 by focusing his principal attention on the kinds of sentence that are subject to logical analysis. He excludes, for example, prayers; and we take him also to exclude imperatives, interrogatives, and exclamations (17a3–4). In Metaphysics 9.10, for example, he makes this point rather emphatically: “for an affirmation and a sentence are not the same [ ]” (1051b24–25). Accordingly, Aristotle considers only those kinds of sentence that are either true
]” (1051b24–25). Accordingly, Aristotle considers only those kinds of sentence that are either true  [alethês]) or false
[alethês]) or false 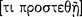 [pseudês]); or, as we express this nowadays, he considers only those sentences that have a truth-value (16a9–13). His explicit interest is only with the kind of sentence that expresses a proposition, namely, with the declarative sentence. He writes:
[pseudês]); or, as we express this nowadays, he considers only those sentences that have a truth-value (16a9–13). His explicit interest is only with the kind of sentence that expresses a proposition, namely, with the declarative sentence. He writes:
While every sentence [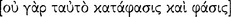 ] has meaning [
] has meaning [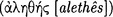 ], though not by nature but, as we observed, by convention
], though not by nature but, as we observed, by convention 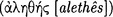 not every sentence is a declarative sentence [
not every sentence is a declarative sentence [ ], but [only those] to which being true or false belongs [
], but [only those] to which being true or false belongs [ ]. (16b33–17a3)
]. (16b33–17a3)
Aristotle uses 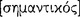 (apophansis) or ‘
(apophansis) or ‘ ’ (apophantikos logos) to denote the declarative sentence. A little later in his discussion he uses ‘
’ (apophantikos logos) to denote the declarative sentence. A little later in his discussion he uses ‘ ’ (kataphasis) and ‘
’ (kataphasis) and ‘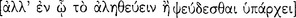 ’ (apophasis) to denote two species of declarative sentence, namely, affirmation and denial, respectively. He uses ‘
’ (apophasis) to denote two species of declarative sentence, namely, affirmation and denial, respectively. He uses ‘ ’ (logos), and sometimes ‘
’ (logos), and sometimes ‘ ’ (phasis), to denote the genus sentence, but he often uses ‘logos’ (among its other uses) interchangeably with ‘apophansis’. Thus, while a sentence consists in a noun and a verb, both of which are themselves meaningful sounds or expressions established by convention and not by nature,19 they do not necessarily express something true or false. Truth and falsity involve predication (16b7, 9–10), in particular for Aristotle, predicating one thing of another one thing by combining (
’ (phasis), to denote the genus sentence, but he often uses ‘logos’ (among its other uses) interchangeably with ‘apophansis’. Thus, while a sentence consists in a noun and a verb, both of which are themselves meaningful sounds or expressions established by convention and not by nature,19 they do not necessarily express something true or false. Truth and falsity involve predication (16b7, 9–10), in particular for Aristotle, predicating one thing of another one thing by combining ( ) or dividing (
) or dividing ( ). Thus, with his discussion in On Interpretation together with his fuller discussion of predication in Categories, Aristotle names as genuine objects of logical investigation only those sentences that involve predication so as to express a proposition.20
). Thus, with his discussion in On Interpretation together with his fuller discussion of predication in Categories, Aristotle names as genuine objects of logical investigation only those sentences that involve predication so as to express a proposition.20
Aristotle also recognizes a natural language to consist in both simple and compound sentences. Again, his logical investigation focuses on the simple sentence, and in On Interpretation 5 he anticipates his treatment of sentences in Prior Analytics.
One kind of declarative sentence [ ] is simple [
] is simple [ ], that is, it affirms or denies some one thing of another [
], that is, it affirms or denies some one thing of another [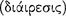 ], while the other is composite [
], while the other is composite [ ], that is, a sentence compounded [
], that is, a sentence compounded [ ] of [such] simple sentences. And [such] a simple sentence is a meaningful expression, concerning something belonging or not belonging [
] of [such] simple sentences. And [such] a simple sentence is a meaningful expression, concerning something belonging or not belonging [ ] in the different tenses. (17a20–24)
] in the different tenses. (17a20–24)
He states that “an affirmation and a denial are simple when they denote [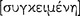 ] some one thing of one other, whether or not universally or of something universal [
] some one thing of one other, whether or not universally or of something universal [ ] (18a12–13). Again:
] (18a12–13). Again:
An affirmation [ ] is one that denotes [
] is one that denotes [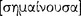 ] something of something. The subject [
] something of something. The subject [ ] is either a noun or a something not having a name [an indefinite noun], and what is affirmed must be one thing about one thing. (19b5–7)
] is either a noun or a something not having a name [an indefinite noun], and what is affirmed must be one thing about one thing. (19b5–7)
Thus, in On Interpretation Aristotle recognizes two kinds of sentence (logos), in particular, two species of declarative sentence, that express a proposition and that are, accordingly, proper subjects of logical analysis (Figure 1).

Figure 1
Aristotle succinctly defines each of these in On Interpretation 6: “an affirmation is a sentence affirming one thing of another; a denial a sentence denying one thing of another [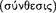 ]” (17a25–26). In this connection we can extract a second sentence formation rule for Aristotle, one pertaining especially to discursive discourse in a natural language and, following Aristotle, we restrict this rule to the simple sentence because it prepares us for his treatment of categorical sentences in Prior Analytics.
]” (17a25–26). In this connection we can extract a second sentence formation rule for Aristotle, one pertaining especially to discursive discourse in a natural language and, following Aristotle, we restrict this rule to the simple sentence because it prepares us for his treatment of categorical sentences in Prior Analytics.
Attributive ( ) predication produces an affirmation, privative (
) predication produces an affirmation, privative ( ) predication a denial, and such a denial always involves a negative operator (Pr. An. 51b31–35). We can represent the pattern of such a sentence graphically as follows (Figure 2).21
) predication a denial, and such a denial always involves a negative operator (Pr. An. 51b31–35). We can represent the pattern of such a sentence graphically as follows (Figure 2).21

Figure 2
Aristotle notes in On Interpretation 10: 20b1–12 that the general word order in natural Greek does not affect meaning: “nouns [subjects] and verbs [predicates] are interchangeable [ ] and express the same meaning [
] and express the same meaning [ ]” (20b1–2). He provides some examples to establish that interchanging the place of a noun and a verb does not generate two contradictions for a given sentence. He concludes by reaffirming his meaning: “Thus, by interchanging the noun and the verb an affirmation and a denial remain the same” (20b10–11), or, that is, express the same proposition.22
]” (20b1–2). He provides some examples to establish that interchanging the place of a noun and a verb does not generate two contradictions for a given sentence. He concludes by reaffirming his meaning: “Thus, by interchanging the noun and the verb an affirmation and a denial remain the same” (20b10–11), or, that is, express the same proposition.22
In Sophistical Refutations Aristotle poignantly emphasizes this point about the kind of predication specifically relating to the kind of discourse subject to logical analysis. There he focuses on sentences used in argumentation particularly as premisses. He writes in Sophistical Refutations 6, in connection with reducing all fallacies to ignoratio elenchi:
And since deduction is based on [declarative] sentences [taken as premisses] [ ], and refutation [
], and refutation [ ] is a deduction [
] is a deduction [ ], refutation will also be based on [such] sentences [
], refutation will also be based on [such] sentences [ ]. If, therefore, [such] a sentence [
]. If, therefore, [such] a sentence [ ] is a single predication about a single thing [
] is a single predication about a single thing [ ], clearly this fallacy [viz., treating many questions as one] also depends on ignorance of the nature of refutation; for what is not [such] a sentence appears to be one [
], clearly this fallacy [viz., treating many questions as one] also depends on ignorance of the nature of refutation; for what is not [such] a sentence appears to be one [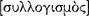 ]. (169a12–16)
]. (169a12–16)
Of course, here Aristotle uses ‘ ’ (protasis) to denote a sentence (logos, apophansis) used as the starting point for argumentation, that is, to denote a sentence in the role of a premiss. His discussion here comports exactly with his practice in Prior Analytics and with his definition of ‘protasis’ there.
’ (protasis) to denote a sentence (logos, apophansis) used as the starting point for argumentation, that is, to denote a sentence in the role of a premiss. His discussion here comports exactly with his practice in Prior Analytics and with his definition of ‘protasis’ there.
A premiss, then, is a sentence affirming or denying something about something [ ].23 (Pr. An. A1: 24a16–17; cf. On Int. 11: 20b22–25)
].23 (Pr. An. A1: 24a16–17; cf. On Int. 11: 20b22–25)
He also notes in Prior Analytics A1 that “a syllogistic premiss without qualification will be either the affirmation or the denial of one thing about another [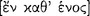 ]” (24a28–30). In Posterior Analytics A22 he writes that “one thing is predicated of one thing
]” (24a28–30). In Posterior Analytics A22 he writes that “one thing is predicated of one thing  ” (83b17–18; cf. Po.An. A2: 72a5–14).
” (83b17–18; cf. Po.An. A2: 72a5–14).
While in On Interpretation Aristotle provides rules for sentence formation in a natural language in a rather intuitive and, by modern standards, non-rigorous manner, he nevertheless is especially concerned there with syntactic matters. He even provides definitions of denial and affirmation that have a syntactic character, although, again, they are mixed with semantic notions, and he cites examples to bear out his meaning. He writes:
Whatever someone may affirm, it is possible as well to deny, and whatever someone may deny, it is possible as well to affirm. Thus, it is evident that each affirmative sentence has an opposite denial [ ], just as each denial has an [opposite] affirmative. (17a30–33)
], just as each denial has an [opposite] affirmative. (17a30–33)
Here Aristotle is particularly concerned with contradictories and not with contraries.
In this connection Aristotle provides in On Interpretation a rather syntactic rule for forming the negation, or contradictory, of a given affirmation. This rule is similar to that for forming an indefinite noun by prefixing ‘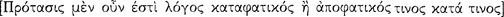 ’ (ou, ouk, oux) to the common noun.24 His example of negating a common noun is the following (16a29–30):
’ (ou, ouk, oux) to the common noun.24 His example of negating a common noun is the following (16a29–30):

In On Interpretation 10: 20a7–9 he states that the ‘ouk’ is attached to the noun and is not a part of the verb: “but the ‘not’ must be added to ‘man’  ”. Table 1 provides two sets of his examples of contradictories from On Interpretation 10, each having its one negation (contradictory) matched with its one given affirmation (19b14–19; cf. 19b27–29 & 19b38–20a1).
”. Table 1 provides two sets of his examples of contradictories from On Interpretation 10, each having its one negation (contradictory) matched with its one given affirmation (19b14–19; cf. 19b27–29 & 19b38–20a1).
Table 1

It is interesting to notice that Aristotle does not cite a partial privative sentence as the negation of a universal attributive sentence as is his customary practice when he treats contradictories in Prior Analytics. Here he prefixes an entire sentence with ‘ou’ in a syntactic way, and he does this both with the verb ‘to be’ and with transitive and intransitive verbs. Thus, for “ ” (“Every man is just”) in the above examples he could have used “
” (“Every man is just”) in the above examples he could have used “
 ” (“Some man is not just”) as its specific negation, but he did not.25 In this connection, then, we can formulate another rule of sentence formation having to do with negation as follows (Table 1):
” (“Some man is not just”) as its specific negation, but he did not.25 In this connection, then, we can formulate another rule of sentence formation having to do with negation as follows (Table 1):
Prefixing ‘ou’ in this way to form the negation, or contradictory, of a given sentence does not comport with ordinary Greek syntax, and thus it indicates an artifice on Aristotle’s part in his treatment of sentences in On Interpretation. We can take ‘not’ here to mean ‘it is not the case that …’.
Although Aristotle only addressed sentence formation in a natural language in On Interpretation, we can see him there having already anticipated the formal language found in Prior Analytics.
Aristotle on proposition
Whether Aristotle had taken a philosophical position, vis-à-vis the modern discussion, on whether or not propositions exist as ideal objects need not concern us here. Given his anti-platonic, materialist tendency this seems unlikely. However, if we take ‘proposition’ more loosely to denote the meaning of a declarative sentence, we can easily see that Aristotle made and worked with a distinction between a sentence, which is a linguistic object, and the meaning or proposition it expresses, which is a non-linguistic object. Both of these, of course, he distinguished from what a sentence denotes, which is a state of affairs  , that is, something that obtains or does not obtain in the world. This is evident from his treatment of sentences in On Interpretation and in Prior Analytics, when he used ‘apophansis’, and ‘logos apophantikos’, as well as ‘kataphasis’, ‘apophasis’, and ‘protasis’. None of these words properly translates as ‘proposition’ per se; but each can be understood to convey what ‘sentence expressing a proposition’ means. Aristotle recognized that two or more different sentences, whether of one’s own natural language or of different natural languages, might express the same proposition, as well as that the same sentence might express more than one proposition or have more than one meaning. In On Interpretation 1 he writes that words are “symbols of affections in the soul”
, that is, something that obtains or does not obtain in the world. This is evident from his treatment of sentences in On Interpretation and in Prior Analytics, when he used ‘apophansis’, and ‘logos apophantikos’, as well as ‘kataphasis’, ‘apophasis’, and ‘protasis’. None of these words properly translates as ‘proposition’ per se; but each can be understood to convey what ‘sentence expressing a proposition’ means. Aristotle recognized that two or more different sentences, whether of one’s own natural language or of different natural languages, might express the same proposition, as well as that the same sentence might express more than one proposition or have more than one meaning. In On Interpretation 1 he writes that words are “symbols of affections in the soul”  , that speech, and thus writing, is not the same for all peoples (16a3–6; cf. n19 above). He continues:
, that speech, and thus writing, is not the same for all peoples (16a3–6; cf. n19 above). He continues:
But all the mental affections themselves  , of which these words are primarily signs
, of which these words are primarily signs  , are the same for everyone, [just] as are the objects
, are the same for everyone, [just] as are the objects  of which those affections are likenesses
of which those affections are likenesses  . (16a6–8)
. (16a6–8)
Perhaps his claim here about the whole of mankind is a bit sweeping. Nevertheless, he clearly indicates here his distinguishing very different linguistic objects as expressing the same meaning or expressing the same proposition — that peculiar, non-linguistic thing that is grasped by a human being in thought.26
Aristotle makes much the same point in On Interpretation 14, although there in relation to considering what count as genuine contraries.
Is an affirmation  contrary to a denial
contrary to a denial  or contrary to another affirmation
or contrary to another affirmation 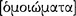 ? Is the sentence
? Is the sentence  “Every man is just” contrary to “No man is just”? or to “Every man is unjust”? For example, “Callias is just”, “Not – Callias is just”, “Callias is unjust”. Which of these sentences are contraries?
“Every man is just” contrary to “No man is just”? or to “Every man is unjust”? For example, “Callias is just”, “Not – Callias is just”, “Callias is unjust”. Which of these sentences are contraries?
For if the expression corresponds with things in the mind, and it is the opinion of the contrary that is contrary, for example, that “Every man is just” [is contrary to] “Every man is unjust”, then the same thing must hold of our expressed affirmations as well  . But if it is not the case that the opinion of the contrary is not the contrary, then neither will one affirmation be the contrary to another
. But if it is not the case that the opinion of the contrary is not the contrary, then neither will one affirmation be the contrary to another  ; but the above mentioned denial will be the contrary
; but the above mentioned denial will be the contrary  . And so, one must inquire which opinion is contrary to a false opinion, whether the opinion of the true denial or the contrary opinion. [On taking ‘good’ and ‘bad’ in sentences and thought.] (23a27–23b2)
. And so, one must inquire which opinion is contrary to a false opinion, whether the opinion of the true denial or the contrary opinion. [On taking ‘good’ and ‘bad’ in sentences and thought.] (23a27–23b2)
Aristotle here fusses with a notion of logical equivalence while considering different sentences and their meanings. He takes up this matter in virtually the same way in Prior Analytics A46. In any case, this shows that he distinguished a sentence, here taken as a formal object, from its meaning or content.
Aristotle specifically addresses the topic of a given sentence having more than one meaning in On Interpretation 8. To establish a point of contrast he first mentions some sentences in which each word has only one meaning (18a12–17). He then cites an instance of a sentence in which a given word is artificially designated as having more than one meaning. He writes:
If one word  has two meanings, which do not combine to make one, the affirmation itself is not one
has two meanings, which do not combine to make one, the affirmation itself is not one  . If, for instance, you give the name ‘garment’ alike to a horse and a man, then it follows that “garment is white” would not be one but two affirmations, nor would “garment is not white” be one denial but two. (18a18–21)
. If, for instance, you give the name ‘garment’ alike to a horse and a man, then it follows that “garment is white” would not be one but two affirmations, nor would “garment is not white” be one denial but two. (18a18–21)
Surely this treatment of the topic not only indicates his making a clear distinction between a sentence and the proposition it expresses, but it also strikingly rings of his experimenting with a notion of reinterpretation familiar to modern logicians. This is not to claim that Aristotle is a model-theoretic logician. Still, it is evident that in this case Aristotle has retained the word ‘garment’ but reinterpreted it twice. And while his example is elementary and serves as an illustration, he might just as easily have reinterpreted an entire sentence. In this connection it is worth noticing that Aristotle regularly used the definite neuter article  (inflected as appropriate in the context of his exposition) as moderns use quotation marks to mention a word or an expression or even to mention an entire sentence.
(inflected as appropriate in the context of his exposition) as moderns use quotation marks to mention a word or an expression or even to mention an entire sentence.
The matter of a given sentence expressing more than one proposition occupied Aristotle’s attention in Sophistical Refutations, where his discussion is considerably more developed than has customarily been acknowledged. Surely recognizing a given sentence as having more than one meaning is evidence of making a distinction between its syntax and its semantics. Sophistical Refutations is replete with such examples, especially, for instance, where Aristotle treated ambiguity and equivocation.27
We can now turn to Aristotle’s model of the grammar of the formal language of the underlying logic depicted in Prior Analytics. His notation there is quite elementary: he employed only upper case Greek letters as schematic placeholders for terms in categorical sentences. And he never provided abbreviations for his logical constants. Nevertheless, he specifically treated sentence patterns and their logical relationships in a genuinely syntactic manner.
The grammar of Aristotle’s formal language
In respect of the theory of predicating of substance outlined in Categories, as treated also in Metaphysics and Topics, and that underlies his notion of predication in Prior Analytics, Aristotle understood there to be four ways that an attribute or property  (see Top. 1.5:102a18–30 on
(see Top. 1.5:102a18–30 on 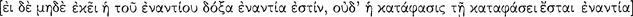 ) — can be related (or belong) to a substance or subject
) — can be related (or belong) to a substance or subject  or
or  (Table 2).
(Table 2).
Table 2
Kinds of substance attribution
These attributions involve ontic relationships that exist independent of a knower: they obtain or they do not obtain. Aristotle referred to such matters generally as  (pragmata; singular pragma), or states of affairs, facts, and he used
(pragmata; singular pragma), or states of affairs, facts, and he used  to be [the case]” — and
to be [the case]” — and  not to be [the case]” — to qualify them (cf. on his using
not to be [the case]” — to qualify them (cf. on his using  and
and  in this connection). From these facts about existence Aristotle conceived four ways that a human being could express — that is, predicate (
in this connection). From these facts about existence Aristotle conceived four ways that a human being could express — that is, predicate ( ) — these substance/attribute relationships linguistically. In the process he invented four logical constants to capture these relationships — and he explicitly named each, although without an expression for ‘logical constant’, in Prior Analytics A4: 26b30–33 (cf. A23: 40b23–26). Thus, corresponding to the four ontic relationships above, there are four possible predications of a subject by a participant (3).
) — these substance/attribute relationships linguistically. In the process he invented four logical constants to capture these relationships — and he explicitly named each, although without an expression for ‘logical constant’, in Prior Analytics A4: 26b30–33 (cf. A23: 40b23–26). Thus, corresponding to the four ontic relationships above, there are four possible predications of a subject by a participant (3).
Table 3

Correspondingly, there are four categorical sentence patterns that Aristotle used throughout his logical investigations in Prior Analytics. His most commonly used schematic representations of the four categorical sentences are represented in Table 4.
Table 4

Concerning any categorical sentence AB, then, A can be taken, or predicated, of B in four ways. ‘A’ and ‘B’ here are schematic letters that hold places for terms, or non-logical constants. The four kinds of sentence involve the four kinds of predication, which themselves reflect the four ontic relationships.28 Aristotle thought of a categorical sentence as having a special pattern that distinguishes it from other kinds of sentence, namely, from those of natural Greek. Moreover, he thought of each of the four kinds of categorical sentence as itself fitting a special pattern. This is most evident in his treating the syllogisms and non-syllogisms in Prior Analytics A4–6. Thus, we can extract Aristotle’s syntax rule, according to his formal grammar, for forming a simple categorical sentence in a given object language pertaining to a given domain and express it as follows.
This rule identifies the pattern of a categorical sentence in Aristotle’s formal language. Aristotle’s expression for ‘non-logical constant’ is  . The term in the first position is called the predicate term
. The term in the first position is called the predicate term  , the term in the second position is called the subject term
, the term in the second position is called the subject term  . In natural Greek it is customary, but not a strict practice (On Int. 20b1–12), to place the subject of a sentence before the predicate/verb. But in Prior Analytics we see that Aristotle quite deliberately placed the predicate term before the logical constant, which acts as a verb, and then place the subject term after the logical constant. In addition, the logical constants themselves are rather artificial constructions aimed to reproduce linguistically what he took to be conditions of being, as in Categories and Metaphysics. It is evident that Aristotle thought of a categorical sentence as formally constructed by concatenating, stringing or combining, a predicate term (or non-logical constant) with a logical constant with a subject term (or non-logical constant) strictly in this order.
. In natural Greek it is customary, but not a strict practice (On Int. 20b1–12), to place the subject of a sentence before the predicate/verb. But in Prior Analytics we see that Aristotle quite deliberately placed the predicate term before the logical constant, which acts as a verb, and then place the subject term after the logical constant. In addition, the logical constants themselves are rather artificial constructions aimed to reproduce linguistically what he took to be conditions of being, as in Categories and Metaphysics. It is evident that Aristotle thought of a categorical sentence as formally constructed by concatenating, stringing or combining, a predicate term (or non-logical constant) with a logical constant with a subject term (or non-logical constant) strictly in this order.
We might also extract two additional categorical sentence formation rules that have a rather more semantic character, but which nevertheless bear on the logical pattern of a sentence.
The two non-logical constants in every categorical sentence are not identical.29
This seems to be Aristotle’s practice, at least, for the most part. There is a passage in Prior Analytics A36 that confirms this (CSFR3).
For we state this without qualification about them all: that terms must always be put in accordance with the cases of the nouns  … (48b40–41; see 48b39–49a2; cf. Pr. An. A39–40).
… (48b40–41; see 48b39–49a2; cf. Pr. An. A39–40).
Conversion otherwise would seem unintelligible. According to modern standards, we might also formulate a fourth rule, which is surely implicit in Aristotle’s thinking.
There is no analogous, strong syntax rule for forming the negation, or contradictory, of a given affirmative sentence in Prior Analytics as there is at places in On Interpretation. However, in Prior Analytics A46 he holds that denials require the use of a negative operator.
Consequently, it is evident that ‘is not-good’ is not the denial [ ] of ‘is good’. If, therefore, ‘affirmation’ or ‘denial’
] of ‘is good’. If, therefore, ‘affirmation’ or ‘denial’  is true about every single <predicate>, then if ‘is not-good’ is not a denial, it is evident that it must be a sort of affirmation
is true about every single <predicate>, then if ‘is not-good’ is not a denial, it is evident that it must be a sort of affirmation  . But there is a denial of every affirmation
. But there is a denial of every affirmation 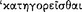 , and, therefore, the denial of this affirmation is ‘is not not-good’. (51b31–35).
, and, therefore, the denial of this affirmation is ‘is not not-good’. (51b31–35).
For Aristotle a genuine denial, as distinguished from an affirmation, involves a negative operator, whether as an adverb attached to a verb (predicate), or as a pronominal adjective attached to a non-logical constant (or as part of the logical constant).30
We can represent Aristotle’s thinking on sentence formation as prescribed in his formal language as follows (Figure 3):

Figure 3
Now, in Prior Analytics, as contrasted with his treatment of sentence formation in On Interpretation, Aristotle fixed the word order in a sentence. The order of the constituent parts of a categorical sentence does not change as it might in a natural language. The syntax of a categorical sentence is strict since its use is anticipated in the syllogistic deduction process, and this process requires precision.
In connection with treating language formally, Aristotle frequently writes of ‘taking’  or ‘not taking’ A of B in one of four ways. He writes, for example, about predicating in general that it is necessary to take something of something:
or ‘not taking’ A of B in one of four ways. He writes, for example, about predicating in general that it is necessary to take something of something:  (Pr. An. A23: 40b31). He often uses ‘AB’, or similar expressions, to indicate any categorical sentence (Pr. An. A25: 42b6). This way of addressing predication tends to treat a sentence as uninterpreted, although, of course for Aristotle, not completely. A categorical sentence may be understood to express taking one term about another term as a formal matter. This is especially the case in Prior Analytics A23, which is an especially proof-theoretic chapter (§5.1). Moreover, he often writes in the same manner about taking sentences of one or another pattern, for example, as starting points of argumentation. In addition, he often uses the word
(Pr. An. A23: 40b31). He often uses ‘AB’, or similar expressions, to indicate any categorical sentence (Pr. An. A25: 42b6). This way of addressing predication tends to treat a sentence as uninterpreted, although, of course for Aristotle, not completely. A categorical sentence may be understood to express taking one term about another term as a formal matter. This is especially the case in Prior Analytics A23, which is an especially proof-theoretic chapter (§5.1). Moreover, he often writes in the same manner about taking sentences of one or another pattern, for example, as starting points of argumentation. In addition, he often uses the word  (problêma) to indicate, not a particular sentence with a particular meaning, but to refer to each of the four kinds of categorical sentence. Consider in Prior Analytics A4 where he uses ‘problêma’ to indicate a sentence pattern:
(problêma) to indicate, not a particular sentence with a particular meaning, but to refer to each of the four kinds of categorical sentence. Consider in Prior Analytics A4 where he uses ‘problêma’ to indicate a sentence pattern:
All the problêmata are proved through this figure  . (26b30–31; cf. A27: 43a16–19, A28: 44a36–37, & A29: 45a36–38)
. (26b30–31; cf. A27: 43a16–19, A28: 44a36–37, & A29: 45a36–38)
‘Problêmata’ here does not refer to problems in a given domain as he uses this word in, for example, Problems and elsewhere, but to the four kinds of categorical sentence: it is used purely in reference to a formal object. We see that Aristotle’s formal language, at least in respect of sentences, while not a purely uninterpreted object (as in string theory), is nevertheless sufficiently formal to exemplify the defining structures or patterns of categorical sentences.31 This indicates that Aristotle took his logical (formal or artificial) language represented in Prior Analytics to be a syntactic object for the purpose of defining an underlying logic.
Aristotle also considered the relationship of negation in a somewhat syntactic manner, notwithstanding that his semantics is just below the surface. He writes in On Interpretation that whatever can be affirmed can also be denied, whatever denied can be affirmed, and that each attributive sentence and each privative sentence has its own opposite (17a30–33). This is all formal. In On Interpretation 7 he recognized two kinds of sentence that are opposites  : contradictories
: contradictories 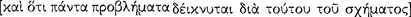 and contraries
and contraries  . This corresponds exactly with what he writes in Metaphysics 5.10 on contrariety in things. In On Interpretation 7 he defines contradictories in a loosely syntactic manner as follows:
. This corresponds exactly with what he writes in Metaphysics 5.10 on contrariety in things. In On Interpretation 7 he defines contradictories in a loosely syntactic manner as follows:
Now, I call an affirmation  contradictorily opposed
contradictorily opposed  to a denial
to a denial  when what the one denotes
when what the one denotes  universally and the other not universally. (17b16–18)
universally and the other not universally. (17b16–18)
And then he provides some examples
“Every man is white” [to] “Not every man is white”  and “No man is white” [to] “Some man is white”
and “No man is white” [to] “Some man is white”  . (17b18–20)
. (17b18–20)
This definition is used throughout Prior Analytics. Aristotle models these sentences as shown in Table 5.
Table 5

The following two syntactic relationships hold between these different sentences:
1. Whenever a sentence fitting the pattern AaB is taken, then a sentence fitting the pattern AoB cannot be taken; and whenever a sentence fitting the pattern AoB is taken, then a sentence fitting the pattern AaB cannot be taken.
2. Whenever a sentence fitting the pattern AeB is taken, then a sentence fitting the pattern AiB cannot be taken; and whenever a sentence fitting the pattern AiB is taken, then a sentence fitting the pattern AeB cannot be taken.
Here Aristotle leaves the schematic letters uninterpreted — or unsubstituted — and asserts the formal, logical relationships that exist between sentences fitting such patterns. In fact, from his text on contradictories (cited above), we can extract Aristotle’s rule for their formation and express it as follows.
Contradictory formation rule
The contradictory of a given sentence, whether attributive or privative, is formed by retaining the predicate and subject terms (non-logical constants) as given and replacing the logical constants as follows:
1. In the case of a universal attributive sentence, the universal attributive logical constant is replaced by the partial privative logical constant.
2. In the case of a universal privative sentence, the universal privative logical constant is replaced by the partial attributive logical constant.
3. In the case of a partial attributive sentence, the partial attributive logical constant is replaced by the universal privative logical constant.
4. In the case of a partial privative sentence, the partial privative logical constant is replaced by the universal attributive logical constant.
In On Interpretation 7 Aristotle defines contraries in a loosely syntactic manner in the following way:
His example is the following:
Of course, in both contradictory sentences and contrary sentences, the subject terms and the predicate terms in the one are the same in the other. Aristotle indicated this a little earlier in On Interpretation 7:
Now if someone states universally of a universal that something belongs or does not belong  , there will be contraries. (17b3–5)
, there will be contraries. (17b3–5)
Perhaps he states this more emphatically in On Interpretation 14: “for contraries are among things that differ most in respect of the same thing  ” (23b22–23); and again in Categories 11: “the nature of contraries is to belong to the same thing, either in species or in genus
” (23b22–23); and again in Categories 11: “the nature of contraries is to belong to the same thing, either in species or in genus 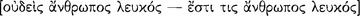 ” (14a15–16). In On Interpretation 6: 17a33–37 (34–35) he writes on contradictories that: “I mean opposites
” (14a15–16). In On Interpretation 6: 17a33–37 (34–35) he writes on contradictories that: “I mean opposites  that [affirm and deny] the same thing of the same thing
that [affirm and deny] the same thing of the same thing  and not ambiguously
and not ambiguously  ”. This definition is also used throughout Prior Analytics. Aristotle models these sentences as in Table 6.
”. This definition is also used throughout Prior Analytics. Aristotle models these sentences as in Table 6.
Table 6

The following syntactic relationships hold between the different sentences:
1. Whenever a sentence fitting the pattern AaB is taken, then a sentence fitting the pattern AeB cannot be taken.
2. And whenever a sentence fitting the pattern AeB is taken, then a sentence fitting the pattern AaB cannot be taken.
We can extract a formation rule for contraries analogous to that for contradictories from Aristotle’s text (cited above) and express it as follows.
The contrary of a given sentence, whether attributive or privative, is formed by retaining the predicate and subject terms as given and replacing the universal logical constants as follows:
1. In the case of a universal attributive sentence by replacing the universal attributive logical constant with the universal privative logical constant.
2. In the case of a universal privative sentence by replacing the universal privative logical constant with the universal attributive logical constant.
What Aristotle writes in On Interpretation and in Categories corresponds exactly with what he does and with what he writes in Prior Analytics B15 about the formal relationships among categorical sentences.
I say that verbally  there are four 〈pairs of〉 opposite sentences
there are four 〈pairs of〉 opposite sentences  , to wit: ‘to every’
, to wit: ‘to every’  〈is opposed〉 to ‘to no’
〈is opposed〉 to ‘to no’  ; and ‘to every’
; and ‘to every’  〈is opposed〉 to ‘not to every’
〈is opposed〉 to ‘not to every’  ; and ‘to some’
; and ‘to some’  〈is opposed〉 to ‘to no’
〈is opposed〉 to ‘to no’  ; and ‘to some’
; and ‘to some’  〈is opposed〉 to ‘not to some’
〈is opposed〉 to ‘not to some’  . In truth, however, there are three, for ‘to some’ and ‘not to some’ are only opposites verbally. Of these, I call the universal sentences contraries (‘to every’ is contrary to ‘to none’, as, for example, ‘every science is good’
. In truth, however, there are three, for ‘to some’ and ‘not to some’ are only opposites verbally. Of these, I call the universal sentences contraries (‘to every’ is contrary to ‘to none’, as, for example, ‘every science is good’ 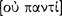 is contrary to ‘no science is good’
is contrary to ‘no science is good’  ) and the other pairs of sentences opposites [sc., contradictories]. (63b23–30)
) and the other pairs of sentences opposites [sc., contradictories]. (63b23–30)
Aristotle’s concern for argumentational skill and logical syntax
The syntactic character of Aristotle’s treatment of opposition is all the more assured when we place his logical investigations in the context of his concern with argumentation, as it pertains to both axiomatic discourse and disputational discourse. Aristotle was eminently occupied in Sophistical Refutations and Topics with equipping his students with argumentational skills that they could employ quickly and with facility and keenness. These two treatises surely served as student handbooks. Perhaps his introduction to Topics exemplifies this concern.
The purpose of the present treatise is to discover a method  by which we shall be able to reason deductively
by which we shall be able to reason deductively 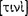 from generally accepted opinions about any problem set before us and shall ourselves, when sustaining an argumentation, avoid saying anything self-contradictory
from generally accepted opinions about any problem set before us and shall ourselves, when sustaining an argumentation, avoid saying anything self-contradictory  .32 (100a18–21; cf. Top.1. 2)
.32 (100a18–21; cf. Top.1. 2)
Aristotle did not have his students memorize certain texts — a set of specific, stock speeches — to acquire this skill, as was a common practice at the time. Rather, he expected them to become familiar with the structural — formal or syntactic — aspects of cogent and fallacious reasoning. In effect, Aristotle aimed to have his students become accomplished logicians. His formal interests are especially evident in his closing remarks in Sophistical Refutations 34. He writes, in connection with remarking that his logical investigations are entirely new:
For the training given by the paid teachers of eristic argumentation resembled the pedagogy of Gorgias. For some of them required their students to learn by heart speeches that were either rhetorical or consisted of questions and answers, in which both sides thought that the rival argumentations were for the most part included. Hence the teaching that they gave to their students was rapid but unscientific  ; for they conceived that they could train their students by imparting to them not an art but the results of an art … he has helped to supply his need but has not imparted an art
; for they conceived that they could train their students by imparting to them not an art but the results of an art … he has helped to supply his need but has not imparted an art  to him. … [While there was much information available having to do with rhetoric] whereas regarding deductive reasoning
to him. … [While there was much information available having to do with rhetoric] whereas regarding deductive reasoning  we had absolutely no earlier work to quote but were for a long time laboring at tentative researches. (183b36–184b3)33
we had absolutely no earlier work to quote but were for a long time laboring at tentative researches. (183b36–184b3)33
Aristotle also took up developing argumentational skills in Prior Analytics, especially at A24–46, the chapters that follow the formal representation of his deduction system. He was particularly concerned in these chapters with developing an individual’s ability to establish 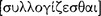 or to destroy
or to destroy  an argumentation.34 This theme is wholly consonant with his treatment of argumentation in Sophistical Refutations and Topics. Indeed, the title of his works on formal logic,
an argumentation.34 This theme is wholly consonant with his treatment of argumentation in Sophistical Refutations and Topics. Indeed, the title of his works on formal logic,  a topic specially treated in Prior Analytics A45 — signifies his concern with the formal aspects of argumentation. Analysis
a topic specially treated in Prior Analytics A45 — signifies his concern with the formal aspects of argumentation. Analysis 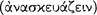 is a process of transforming one syllogism in any one figure into another syllogism of another figure if both syllogisms prove the same problêma (§6.2). Aristotle aimed to promote his students’ facility with reasoning syllogistically to establish and to refute arguments by studying the logical relationships among sentence patterns and among patterns of elementary arguments. This is analogous to a modern logician’s studying the formal relationships among the rules of propositional logic.
is a process of transforming one syllogism in any one figure into another syllogism of another figure if both syllogisms prove the same problêma (§6.2). Aristotle aimed to promote his students’ facility with reasoning syllogistically to establish and to refute arguments by studying the logical relationships among sentence patterns and among patterns of elementary arguments. This is analogous to a modern logician’s studying the formal relationships among the rules of propositional logic.
Aristotle’s mathematical disposition toward the study of grammar
In On Interpretation Aristotle treated sentences in natural languages metalinguistically. His practice there is much the same, although without the complexity, as that of a modern grammarian whose natural language is, say, English, and who writes an English grammar. Aristotle used Greek to mention Greek as this grammarian would use English to mention English. However, Aristotle went considerably farther than a grammarian in his treating the syntactic aspects of a language because he thought of his linguistic investigations as laying an epistemological — or formal — foundation for various axiomatic sciences, the apodeiktikai epistêmai. As a logician formalizing a deduction system, Aristotle continued in Prior Analytics to develop a formal grammar where a grammarian of a natural language might leave off in On Interpretation.
Aristotle always took Greek, whether explicitly or implicitly, as the background language for discourse in any specialized domain. In this connection, we might say that Aristotle took Greek as his master language, although he never formulated the matter using just such an expression. Still, he recognized that each of the special axiomatic sciences was equipped, or ought to be equipped, with its own specialized terminology, or vocabulary, appropriate to its domain. Aristotle indicated his having a notion of a specialized vocabulary in Metaphysics 4.2. There he wrote about using terminology across sciences and thus indicated, albeit negatively, that each science has its own terminology.
For a term belongs to different sciences, not merely because it is used in many ways, but when its definition can be referred neither to a single subject matter nor to a common ground. (1004a24–25)
That Aristotle had a clear notion of universe of discourse, although, again, without an equivalent expression in Greek, is evident from his treatment of the genus of a given science in Posterior Analytics A7, 9–10, 28.35 This notion is poignantly expressed also in Metaphysics 10.4: “a single science covers a single genus and therefore deals with the complete differences in that genus” (1055a31–32).36 Perhaps Posterior Analytics A7 (cf. A8–10) expresses his notion of universe of discourse most plainly.
Thus you cannot prove anything by crossing from another kind — for example, something geometrical by arithmetic. There are three things involved in demonstrations: one, what is being demonstrated, or the conclusion  (this is what holds of some kind in itself); one, the axioms
(this is what holds of some kind in itself); one, the axioms  (axioms are the items from which the demonstrations proceed); third, the underlying kind
(axioms are the items from which the demonstrations proceed); third, the underlying kind 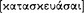 whose attributes
whose attributes  — that is, the items incidental to it in itself — the demonstrations make plain.
— that is, the items incidental to it in itself — the demonstrations make plain.
Now the items from which the demonstrations proceed may be the same  ; but where the kinds are different
; but where the kinds are different  , as with arithmetic and geometry, you cannot attach arithmetical demonstrations to what is incidental to magnitudes — unless magnitudes are numbers. … Arithmetical demonstrations always contain the kind with which the demonstrations are concerned, and so too do all other demonstrations. Hence the kind must be the same, either simpliciter or in some respect, if a demonstration is to cross
, as with arithmetic and geometry, you cannot attach arithmetical demonstrations to what is incidental to magnitudes — unless magnitudes are numbers. … Arithmetical demonstrations always contain the kind with which the demonstrations are concerned, and so too do all other demonstrations. Hence the kind must be the same, either simpliciter or in some respect, if a demonstration is to cross  . That it is impossible otherwise is plain; for the extremes and the middle terms must come from the same kind
. That it is impossible otherwise is plain; for the extremes and the middle terms must come from the same kind  , since if they do not hold in themselves, they will be incidentals.37
, since if they do not hold in themselves, they will be incidentals.37
For this reason you cannot prove by geometry that there is a single science of contraries, nor even that two cubes make a cube. (Nor can you prove by any other science what pertains to a different science, except when they are so related to one another that the one falls under the other — as, for example, optics is related to geometry and harmonics to arithmetic.) Nor indeed anything that holds of lines not as lines and as depending on the principles proper to them — for example, whether straight lines are the most beautiful of lines, or whether they are contrarily related to curved lines; for these things hold of lines not in virtue of their proper kind but rather in virtue of something common. (75a38–75b20)
Not only has Aristotle indicated his notion of universe of discourse in relation to a genus, but he has also indicated that he worked with a notion of category mistake. This matter also is treated in Sophistical Refutations.
That different scientific domains are distinguished in one or another discourse is an important part of Aristotle’s discussion of fallacious reasoning in Sophistical Refutations. There he treats a kind of fallacious reasoning that violates the boundaries of different domains. In Sophistical Refutations 8: 169b20–23 he remarks that a sophistical refutation, while it is usually a spurious deduction of the contradictory of a given sentence, might, nevertheless, be a genuine deduction (i.e., a refutation) but one that is not germane to the subject matter under discussion. The deductive reasoning while genuine “only seems to be, but is really not, germane to the subject at hand  ”. In Sophistical Refutations 9 Aristotle draws a distinction between the function of a scientist and that of a dialectician, or, that is, of a logician. In this connection he writes about demonstrations and refutations special to a given science.
”. In Sophistical Refutations 9 Aristotle draws a distinction between the function of a scientist and that of a dialectician, or, that is, of a logician. In this connection he writes about demonstrations and refutations special to a given science.
So we shall need to have scientific knowledge of everything; for some refutations will depend on the principles of geometry and their conclusions, others on those of medicine, and others on those of the other sciences. Moreover, spurious refutations  also are among things which are infinite [as are, perhaps, the sciences and their demonstrations (170a22–23)]; for every art has a spurious proof peculiar to it, geometry a geometrical proof and medicine a medical proof. By ‘peculiar to an art’
also are among things which are infinite [as are, perhaps, the sciences and their demonstrations (170a22–23)]; for every art has a spurious proof peculiar to it, geometry a geometrical proof and medicine a medical proof. By ‘peculiar to an art’ 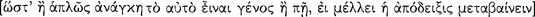 I mean ‘in accordance with the principles of that art’
I mean ‘in accordance with the principles of that art’  . (170a27–34)
. (170a27–34)
Aristotle returns to this matter in force in Sophistical Refutations 11, where he treats the discipline of logic as the dialectical art of the deductive principles common to all intelligible, cogent discourse. He also distinguishes the sophist from the eristic in respect of their motives (171b29–34). In this connection he establishes a clear notion of universe of discourse.
Then there are those spurious deductions that do not accord with the method of inquiry peculiar to the subject yet seem to accord with the art concerned. For false geometrical figures are not contentious (for the resultant fallacies accord with the subject-matter of the art), and the same is the case with any figure illustrating something which is true, for example, Hippocrates’ figure or the squaring of the circle by means of lunules. … [Bryson’s method of squaring is sophistical because it does not accord with the subject-matter.] … And so any merely apparent deduction on these topics is a contentious argumentation, and any deduction that merely appears to accord with the subject-matter  , even though it be a genuine deduction, is a contentious argumentation [because it only appears to accord with the subject-matter]. (171b11–22)
, even though it be a genuine deduction, is a contentious argumentation [because it only appears to accord with the subject-matter]. (171b11–22)
A little later in this discussion Aristotle provides some examples to illustrate his meaning.
For example, the squaring of the circle by means of lunules is not contentious, whereas Bryson’s method is contentious. It is not proper to transfer the former outside the sphere of geometry because it is based on principles that are special to geometry  , whereas the latter can be used against many disputants, namely, all those who do not know what is possible and what impossible in any particular case; for it will always be applicable. And the same is true of the way in which Antiphon used to square the circle. Or, again, if someone were to deny that it is better to take a walk after dinner because of Zeno’s argumentation, it would not be a medical argument; for it is of a general application. (172a2–9)
, whereas the latter can be used against many disputants, namely, all those who do not know what is possible and what impossible in any particular case; for it will always be applicable. And the same is true of the way in which Antiphon used to square the circle. Or, again, if someone were to deny that it is better to take a walk after dinner because of Zeno’s argumentation, it would not be a medical argument; for it is of a general application. (172a2–9)
It is evident, then, that Aristotle recognized there to be any number of special sciences, each with its own domain and topical sub-language, each of which is a fragment of a whole, or master, language.
Aristotle’s focus shifts from a general concern with grammar, as in On Interpretation, to a more specialized concern with language and grammar in Prior Analytics and Posterior Analytics and in Metaphysics. There language is treated (1) as modified from natural language according as its universe of discourse is delimited and specialized and (2) as more rigorously formalized for the purposes of precision and deduction. Aristotle’s emphasis on the simple sentence in On Interpretation repays him well in Prior Analytics where he treats his deduction system with more rigor. His linguistic and argumentational analyses in On Interpretation, and in Sophistical Refutations and Topics, provided the foundation for his formulating the simple grammar of the artificial language in Prior Analytics.
Now, while Aristotle seemed always to have natural language in the background when he undertook his logical investigations, his thinking was surely disposed toward constructing an artificial language. And while he surely did not work with a fully uninterpreted calculus, he nevertheless had already moved toward developing a notion of a precise scientific language for extended deductive discourse in each of the special axiomatic sciences. And here he developed some stringent requirements for intelligible discourse. In particular, in Metaphysics 11.5 he expressed a requirement that in scientific discourse one word have one meaning, and if it were to have more than one meaning this should be made patently clear. He treats this topic there in conjunction with treating the law of non-contradiction in the following way:
Those, therefore, who are to communicate with one another by way of argumentation  must have some common understanding. … Each word must therefore be intelligible
must have some common understanding. … Each word must therefore be intelligible  and indicate something definite, not many things, but only one
and indicate something definite, not many things, but only one  ; and if it has more than one meaning it must be made plain in which of these the word is being used. He, therefore, who says that “this is and is not” denies what he affirms, with the consequence that he declares the word to signify what it does not signify; but this is absurd. Consequently, if “this is” signifies something, it is absurd to assert truly its contradictory.
; and if it has more than one meaning it must be made plain in which of these the word is being used. He, therefore, who says that “this is and is not” denies what he affirms, with the consequence that he declares the word to signify what it does not signify; but this is absurd. Consequently, if “this is” signifies something, it is absurd to assert truly its contradictory.
Accordingly, if a word signifies something, and this is truly asserted, this [connection] must be necessary; but what necessarily is cannot ever not be; and so opposite sentences concerning the same thing cannot be true together … [again] opposite sentences concerning the same thing can never be true together. (1062a11–23)38
Aristotle’s scientific languages eschew the ambiguity that abounds in natural languages. Surely his concern for a precise syntax is a reflex of his concern for scientific precision. Again, we have the testimony of Sophistical Refutations to make Aristotle’s case; this point is especially evident there when Aristotle treats fallacious reasoning involving ambiguity and equivocation as well as making many questions into one.
In connection with his study of logic, then, what he writes in Metaphysics and in Sophistical Refutations can be taken as a move toward developing a logically perfect language, albeit restricted in its scope to a specific, delimited domain. Nevertheless, Aristotle’s impulse and that of a modern logician are correspondingly the same when their respective focuses are on the deduction process. Now, of course, each of these scientific languages is a topical sub-language of a given master language, in this case Greek, and as such each is an object, if not a natural, language. We might think of this as natural Greek departmentalized; or, rather, that the languages of mathematics and biology, for example, are specialized topical sub-languages with a tailored Greek as their mode of expression. In any case, Aristotle’s requirements for scientific discourse, in connection with his syllogistic logic, indicate that his treatment of language in On Interpretation, Prior Analytics, Metaphysics, Sophistical Refutations, and even Categories is (1) thoroughly metalinguistic and, thus, (2) especially occupied with syntax. Aristotle aimed to formalize scientific discourse, not only with a polished deduction system, but also with precisely formulated linguistic requirements concerning both its syntactic and semantic dimensions.
Aristotle’s formal language is not strictly an uninterpreted calculus awaiting an interpretation as a modern logician understands this matter. Its vocabulary consists only in (1) four fully interpreted logical constants and (2) a number of schematic (upper case Greek) letters that function purely as metalinguistic placeholders for terms in categorical (or predicational) sentences. These schematic letters, however, are generally uninterpreted in a way familiar to modern logicians; but they are not variables.39 There are no genuine variables, whether bound or free, ranging over individuals in a given domain in Aristotle’s formal language. Indeed, there is no need for variables, since the system lacks quantification theory and works with patterns appropriate to a term logic. Nor, then, are there any non-logical constants in his formal language. Non-logical constants pertain to a given universe of discourse along with its object language. Again, there is no need for any non-logical constants. His formal language does not anticipate quantification and the existence of variables in a given object language.
It may be that considerations of natural language underlay Aristotle’s thinking when he constructed his artificial language. However that may be, where a natural language has sentences, and this holds of an interpreted language or an interpretation of a formal language, Aristotle’s formal language does not have sentences per se, but only formalized sentence patterns. A sentence possesses a truth-value; a sentence pattern does not. Indeed, just as with a modern formal language, Aristotle’s artificial language is not strictly a language, since it contains no true or false sentences. So, while his language is interpreted in respect of its logical constants, it is not a fully interpreted object in respect of (1) its not being bound to a particular universe of discourse and (2) its having schematic letters holding places for terms that anticipate a given universe of discourse. In respect of the first point, his language is formally applicable to every domain but is itself specific to none — it is topic neutral. And in respect of the second point, ‘term’ is a metalinguistic name for a formal part of a categorical sentence, that part which is filled by a non-logical constant, a name or substantive. Aristotle’s definition of ‘term’  in Prior Analytics A1 is consonant with his practice.
in Prior Analytics A1 is consonant with his practice.
I call that a term into which a premiss may be broken up, that is, both that which is predicated and that of which it is predicated (whether or not ‘is’ or ‘is not’ is added or divides them). (24b16–18)
There are no terms in Aristotle’s formal language, only schematic letters holding places for non-logical constants (terms); and, of course, a schematic letter is not itself a term. The word ‘term’  exists in Aristotle’s metalanguage. In addition, there are no logically true sentences in Aristotle’s syntax language.40 Thus, there are absolutely no truth-conditions for sentence patterns in Aristotle’s formal language. In principle, this is exactly the case with modern logics, save for a logic involving identity and tautology. Aristotle had genuinely syntactic concerns, although, again, without the sophistication and rigor of a modern mathematical logician, but, nevertheless, with an intelligence sufficient for having accomplished many of the same results as a modern logician. Aristotle’s formal language is entirely a metalogical (metalinguistic) device used to objectify and exemplify, to explicate, and to study his logic, and, moreover, it was conceived by him to be applicable equally to all the axiomatic or axiomatizable sciences.41
exists in Aristotle’s metalanguage. In addition, there are no logically true sentences in Aristotle’s syntax language.40 Thus, there are absolutely no truth-conditions for sentence patterns in Aristotle’s formal language. In principle, this is exactly the case with modern logics, save for a logic involving identity and tautology. Aristotle had genuinely syntactic concerns, although, again, without the sophistication and rigor of a modern mathematical logician, but, nevertheless, with an intelligence sufficient for having accomplished many of the same results as a modern logician. Aristotle’s formal language is entirely a metalogical (metalinguistic) device used to objectify and exemplify, to explicate, and to study his logic, and, moreover, it was conceived by him to be applicable equally to all the axiomatic or axiomatizable sciences.41
2.2 Truth conditions for object language sentences
In relation to establishing truth conditions for sentences, it is customary for a modern logician to speak about ‘giving an interpretation’ of a formal language. In this respect, then, a modern logician would (1) specify a non-empty domain as a universe of discourse, (2) specify the meanings of all logical constants, (3) establish definitions of ‘true’ and ‘false’, and (4) establish conditions under which a given interpreted sentence is either true or false. However, in connection with truth conditions, Aristotle did not employ a modern system of interpretations and reinterpretations; he seemed not to work with model-theoretic notions. Thus, we do not find him saying that “a given sentence is true under a given interpretation”. Aristotle, however, does use a method of substituting non-logical constants for schematic letters in categorical sentence patterns. And we do witness him establish meanings for his logical constants and truth conditions for sentences, categorical or otherwise. Above we treated their syntax and now we treat their semantics, principally focussing on categorical sentences.
Since the four categorical sentence patterns are not themselves sentences possessing a truth-value, we might wonder what conditions Aristotle required to produce a categorical sentence according to his definition of ‘logos’ or ‘apophansis’, that is, beyond his sentence formation rules. It is immediately apparent that he would specify a universe of discourse — that is, he would introduce genuine non-logical constants, or, what amounts to the same thing, he would apply his formal language to a given domain. The following passage from Posterior Analytics A10 establishes that this is so.
Every demonstrative science  is concerned with three things: [1] what it posits to exist
is concerned with three things: [1] what it posits to exist 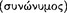 (these items constitute the kind
(these items constitute the kind 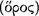 of which it studies the attributes
of which it studies the attributes  which hold of it in itself); [2] the so-called common axioms
which hold of it in itself); [2] the so-called common axioms  , that is, the primitives from which its demonstrations proceed; and [3] thirdly, the attributes
, that is, the primitives from which its demonstrations proceed; and [3] thirdly, the attributes  where it assumes what each of them means
where it assumes what each of them means  . (76b11–16)
. (76b11–16)
Aristotle also provided meanings for his logical constants. In addition, he defined ‘truth’ and ‘falsity’, which he understood to pertain to sentences, and he provided the conditions under which a given sentence is true or false. We can take his discussions, particularly in Posterior Analytics, on the genus of a science as evidence of the requirement that a non-empty domain be specified. In this section we examine his definitions of the logical constants, his definitions of ‘true’ and ‘false’, and the conditions under which a sentence is true or false. There also is a section on Aristotle’s notion of existential import and a final note on his intensional notion of truth. We begin with a brief statement on the importance he attributed to meaning.
Aristotle on meaning in general
Aristotle gave special attention to the matter of meaning in various treatises. In connection with semantics in general, he defined ‘having a meaning’ in relation to intelligible discourse in Metaphysics 4.4, concerning the principle of non-contradiction, in the following, rather stipulative, way:
Suppose ‘man’ has the meaning ‘two-footed animal’. By ‘having a meaning’  I mean this: if ‘man’ is ‘two-footed animal’, then if anything is a man, its ‘being two-footed’ will be what its ‘being a man’ is. (1006a31–34)
I mean this: if ‘man’ is ‘two-footed animal’, then if anything is a man, its ‘being two-footed’ will be what its ‘being a man’ is. (1006a31–34)
Aristotle recognized that the meanings assigned to words, and the words, or meaningful sounds themselves, are conventions. Accordingly, he expected those engaged in intelligible discourse to agree that one word have one meaning, or if many meanings that this be made clear: “let us suppose … that a word has a meaning and one specific meaning  ” (Meta. 4.4: 1006b12–13; cf. Meta. 11.5: 1062a11–23). Moreover, he made absolutely clear that we not confuse a word with its denotation.
” (Meta. 4.4: 1006b12–13; cf. Meta. 11.5: 1062a11–23). Moreover, he made absolutely clear that we not confuse a word with its denotation.
As to having a meaning, what we insist on is that the meaning is not the object referred to [itself] (since then ‘musical’ and ‘white’ and ‘man’ could have a single meaning or referent, and all would be one, and those terms would be synonymous). [What we mean is that] it will not be possible to be and not to be the same thing  , except ambiguously; for example, if we call a ‘man’ what others were to call a ‘non-man’. The question is not whether the same thing can at the same time be and not be a man in name, but in fact
, except ambiguously; for example, if we call a ‘man’ what others were to call a ‘non-man’. The question is not whether the same thing can at the same time be and not be a man in name, but in fact 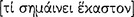 . (1006b15–22)
. (1006b15–22)
Aristotle took up this matter throughout most of Metaphysics 4.4, where he was careful to state the necessity for clear definition and meaning in connection with the law of non-contradiction. He wrote that “to signify its being means that its being is not something else” (1007a26–27); and “there must, accordingly, be some meaning in the sense of indicating a thing’s being” (1007b16–17). Here again Aristotle expected that words be used carefully and precisely in order better to reflect in thought what exists independently of thought. Then, later in Metaphysics 4.7 he wrote that
basic to all these argumentations [viz., eristic argumentations] are definitions. And definition  arises out of the necessity of stating what we mean; for the sentence of which the word is a sign becomes a definition
arises out of the necessity of stating what we mean; for the sentence of which the word is a sign becomes a definition  . (1012a21–24)
. (1012a21–24)
Then, in connection with meaning in relation to truth and falsity, Aristotle wrote in Metaphysics 4.8:
Against all such argumentations, however, it must be asked [as at Meta. 4.4: 1006a18–22] … not that something is or is not, but that something has meaning  ; so that we must converse on the basis of definition
; so that we must converse on the basis of definition  by grasping what falsity and truth mean. (1012b5–8)
by grasping what falsity and truth mean. (1012b5–8)
We shall treat truth and falsity more fully below, but note here that Aristotle is quite clear about the importance of establishing meaning42 and about the relationship between meaning and existence.43
Defining the logical constants
Aristotle provides some explicit definitions of his logical constants in Prior Analytics and elsewhere. On ‘belonging to every’ and ‘belonging to no’ he writes in Prior Analytics A1: “I call ‘belonging to every’ or ‘to none’ universal” (24a18). He adds:
For one thing to be in another as a whole is the same as for one thing to be predicated of every one of another. We use the expression ‘predicated of every’ when none of the subject can be taken of which the other term cannot be said, and we use ‘predicated of none’ likewise. (24b26–30)
In Posterior Analytics A4 he writes on universal predication in much the same way:
I say that something holds of every case if it does not hold of some cases and not of others, nor at some times and not at others. For example, if animal holds of every man, then if it is true to call this a man, it is true to call him an animal too; and if he is now the former, he is the latter too. (73a28–31; cf. A4: 73b25–74a3 on ‘holding universally’ 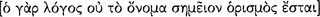 )
)
In On Interpretation 7 he defines ‘predicating universally’ indirectly, when he identifies some sentences as indeterminate. He writes:
It is necessary when asserting 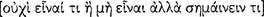 as either belonging or not belonging
as either belonging or not belonging  sometimes to something universal
sometimes to something universal  sometimes to an individual
sometimes to an individual  . Now, if someone states universally of a universal that something belongs or does not belong, there will be contrary sentences
. Now, if someone states universally of a universal that something belongs or does not belong, there will be contrary sentences 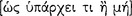 . I mean by stating universally of the universal, for example, “Every man is white” and “No man is white”. (17b1–6)
. I mean by stating universally of the universal, for example, “Every man is white” and “No man is white”. (17b1–6)
In Prior Analytics A1 when he treats ‘belonging to some’ and ‘not belonging to some’ Aristotle writes in a rather eclipsed manner: “I call ‘belonging to some’, ‘belonging not to some’, or ‘belonging not to every’ partial  ” (24a18–19). He seems to have taken their meanings as evident to his audience. In addition, Aristotle takes ‘belonging to some’ in two ways, implicitly in On Interpretation 7 but rather more explicitly in Prior Analytics. (1) In its determinate
” (24a18–19). He seems to have taken their meanings as evident to his audience. In addition, Aristotle takes ‘belonging to some’ in two ways, implicitly in On Interpretation 7 but rather more explicitly in Prior Analytics. (1) In its determinate  meaning, ‘some’ means, as in ‘A belongs to some B’, that ‘some Bs are A’ and ‘some Bs are not A’ but not that ‘possibly all Bs are A’. The determinateness of a sentence pertains to its having only one meaning. A participant knows that, of a given kind, some indeed have and some indeed do not have a given property. (2) In its indeterminate
meaning, ‘some’ means, as in ‘A belongs to some B’, that ‘some Bs are A’ and ‘some Bs are not A’ but not that ‘possibly all Bs are A’. The determinateness of a sentence pertains to its having only one meaning. A participant knows that, of a given kind, some indeed have and some indeed do not have a given property. (2) In its indeterminate  meaning, ‘some’ means ‘at least one, possibly all’. Here a participant does not know, in the case of ‘A belongs to some B’, whether some Bs are not A or every B is an A. He writes in Prior Analytics A1 that
meaning, ‘some’ means ‘at least one, possibly all’. Here a participant does not know, in the case of ‘A belongs to some B’, whether some Bs are not A or every B is an A. He writes in Prior Analytics A1 that
I call belonging or not belonging without a universal or partial indeterminate  as, for example, “The science of contraries is the same” or “Pleasure is not a good”. (24a19–22)
as, for example, “The science of contraries is the same” or “Pleasure is not a good”. (24a19–22)
Again, an indeterminate sentence is ambiguous. Aristotle does not usually cite a partial sentence, that is, one specifically using a partial logical constant, to identify indeterminateness. Rather, he usually cites a general sentence, such as “Men are white” or “Pleasure is good”. In such cases he remarks that while ‘men’ is used universally, the sentence is indeterminate: it could mean “Some men are white” and “Some men are not white” or “All men are white” (On Int. 7: 17a38–17b16). There he indicates the indeterminateness of “Man is white” and “Man is not white”. He notes that
the universal ‘man’ is not used universally in the sentence. For the word ‘every’ does not signify the universal but that it is taken universally  .44 (17b11–12)
.44 (17b11–12)
This matter is clearly stated in Prior Analytics A27 where he counterposes a sentence being determinate to its being indeterminate. There Aristotle comments on developing argumentational skills and instructs his students to select things that follow the subject as a whole since “a syllogism is through universal premisses”. He continues this thought and thereby clarifies the meaning of ‘indeterminate’:
Now, if it is indeterminate  , it is unclear
, it is unclear  whether the premiss is universal
whether the premiss is universal  , whereas if it is determinate this is evident
, whereas if it is determinate this is evident  . (43b14–15; cf. Pr. An. A4: 26b21–25)
. (43b14–15; cf. Pr. An. A4: 26b21–25)
He also reveals his understanding when he establishes the inconcludence of a few patterns of premiss pairs by “proving it from the indeterminate”. In Prior Analytics A4, in connection with showing that a pair of premisses — the major a universal attributive or privative, the minor a partial privative — does not result in a syllogism, Aristotle notes that this must be established from the indeterminate. He writes:
Moreover, since “B does not belong to some C” is indeterminate, that is, it is true if B belongs to none as well as if it does not belong to every (because it does not belong to some), … (26b14–16; cf. Pr. An. A5: 27b16–23)
In this way, then, Aristotle defined his logical constants.
Finally, in this connection, Aristotle distinguishes variously between kinds of declarative sentence (apophansis). There are, first, the affirmation (kataphasis) and the denial (apophasis). Using Aristotle’s terminology developed in Prior Analytics, we can take a kataphasis to be a positive, or attributive  , sentence and an apophasis as a negative, or privative
, sentence and an apophasis as a negative, or privative  , sentence that uses a negative operator. Second, a sentence can be singular
, sentence that uses a negative operator. Second, a sentence can be singular  , partial, or particular
, partial, or particular  , or universal
, or universal  . The first of these determinations usually captures the quality of a sentence, the second its quantity. Third, a sentence can be either determinate (
. The first of these determinations usually captures the quality of a sentence, the second its quantity. Third, a sentence can be either determinate ( ) or indeterminate (
) or indeterminate ( ), as we noted above. These distinctions are more sharply defined in Prior Analytics than they are in On Interpretation, but the two works are generally in accord on these sentential determinations.45 We shall examine the kinds of sentence more fully when we treat their truth-values in relation to the matter of existential import.
), as we noted above. These distinctions are more sharply defined in Prior Analytics than they are in On Interpretation, but the two works are generally in accord on these sentential determinations.45 We shall examine the kinds of sentence more fully when we treat their truth-values in relation to the matter of existential import.
Defining truth and falsity
In On Interpretation 9 Aristotle treats the notions of truth and falsity especially in relation to examining contrary and contradictory sentences. There he provides definitions of ‘true’  and ‘false’
and ‘false’  that accord exactly with Alfred Tarski’s treatment of the topic in “The concept of truth in formalized languages”.46 Aristotle writes:
that accord exactly with Alfred Tarski’s treatment of the topic in “The concept of truth in formalized languages”.46 Aristotle writes:
For, if it is true to assert  that something is white or not white, then it is necessarily
that something is white or not white, then it is necessarily 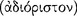 white or not white. And if it is
white or not white. And if it is  white or not white, it was true to affirm or deny it
white or not white, it was true to affirm or deny it  . And, if it is not [in fact] white
. And, if it is not [in fact] white 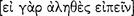 , then to say that it is will be false
, then to say that it is will be false  ; if to say that it is will be false
; if to say that it is will be false  , then it is not white
, then it is not white  . And so, it is necessary that the affirmation or the denial be true
. And so, it is necessary that the affirmation or the denial be true  . (18a39–18b4)
. (18a39–18b4)
The upshot of this discussion is to affirm that every declarative sentence is either true or false and that “the truth of sentences consists in corresponding with states of affairs 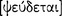 ” (19a32–33). In Categories 12 Aristotle writes in much the same vein, but he states the case somewhat more strongly when he addresses various meanings of ‘prior’.
” (19a32–33). In Categories 12 Aristotle writes in much the same vein, but he states the case somewhat more strongly when he addresses various meanings of ‘prior’.
The existence of a man is reciprocal in relation to the true sentence about him as it follows from there being [such] a man  . For if a man exists, then the sentence asserting
. For if a man exists, then the sentence asserting  that a man exists will be true
that a man exists will be true  . And conversely, if the sentence asserting
. And conversely, if the sentence asserting  that a man exists is true
that a man exists is true  , then the man exists. The true sentence
, then the man exists. The true sentence  , however, is in no way the cause of the [given] state of affairs
, however, is in no way the cause of the [given] state of affairs 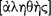 ; and yet the state of affairs
; and yet the state of affairs  seems somehow to be the cause of the truth of the sentence
seems somehow to be the cause of the truth of the sentence 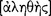 . For a sentence is called true or false as the state of affairs exists or does not exist
. For a sentence is called true or false as the state of affairs exists or does not exist  . (14b14–22)
. (14b14–22)
Aristotle is quite clear about distinguishing a sentence pattern from a sentence, and a sentence from its denotation, or state of affairs, or even from its sense or meaning. Again, we have ample evidence of this topic treated more fully throughout Sophistical Refutations and Rhetoric.
We can supplement what Aristotle writes on truth and falsity in these works with what he writes in Metaphysics 4.7–8 in connection with his discussion of the laws of non-contradiction and excluded middle.
Aristotle, then, is quite clear about ‘truth’ and ‘falsity’ applying to sentences (logoi) and not to states of affairs (pragmata), which he characterized using  , or ‘being [the case]’, and
, or ‘being [the case]’, and  , or ‘not being [the case]’. However, Aristotle sometimes uses the words ‘alêthês’ and ‘pseudos’ in relation to pragmata where we would prefer using ‘is the case’ and ‘is not the case’ and thus would avoid making a category mistake. Consider, for example, what he writes in Metaphysics 5.12 where he defines ‘possibility’ [
, or ‘not being [the case]’. However, Aristotle sometimes uses the words ‘alêthês’ and ‘pseudos’ in relation to pragmata where we would prefer using ‘is the case’ and ‘is not the case’ and thus would avoid making a category mistake. Consider, for example, what he writes in Metaphysics 5.12 where he defines ‘possibility’ [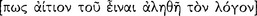 ] and ‘impossibility’ [
] and ‘impossibility’ [ ]. (Here we transliterate, rather than translate, and mark in bold face, the Greek for ‘true’ and ‘false’ to objectify Aristotle’s meanings.)
]. (Here we transliterate, rather than translate, and mark in bold face, the Greek for ‘true’ and ‘false’ to objectify Aristotle’s meanings.)
[In the case where ‘impossibility’ means the opposite of ‘possibility’, the impossible is] the contrary of what is necessarily alêthês [ ]: that the diagonal of a square is commensurable with its side is impossible, because that is something pseudos [
]: that the diagonal of a square is commensurable with its side is impossible, because that is something pseudos [ ], and its direct contrary, incommensurability, is not only alêthês [
], and its direct contrary, incommensurability, is not only alêthês [ ] but also necessary; that it is commensurable is, therefore, not only pseudos [
] but also necessary; that it is commensurable is, therefore, not only pseudos [ ] but also necessarily pseudos [
] but also necessarily pseudos [ ]. On the other hand, the contrary of this, the “possible”, holds when it is not necessary for its contrary to be pseudos [
]. On the other hand, the contrary of this, the “possible”, holds when it is not necessary for its contrary to be pseudos [ ]: it is possible for a man to be seated, for it is not of necessity pseudos [
]: it is possible for a man to be seated, for it is not of necessity pseudos [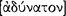 ] that he is not seated. The possible, then, means: (1) what is not of necessity pseudos [
] that he is not seated. The possible, then, means: (1) what is not of necessity pseudos [ ]; (2) what is alêthês [
]; (2) what is alêthês [ ]; (3) what may be alêthês [
]; (3) what may be alêthês [ ]. (1019b23–33)
]. (1019b23–33)
It is not uncommon for Aristotle, and he suggests that it is a common practice, to use ‘alêthês’ and ‘pseudês’ to refer to both sentences (logoi) and states of affairs (pragmata). In fact, he explicitly makes this point in Metaphysics 9.10 where he remarks that being and nonbeing are commonly assessed according to the ‘true’ or the ‘false’, that is, by using the words ‘alêthês’ and ‘pseudês’. He writes:
This use depends on things being combined or dissociated [ ]; so that he who thinks that what is dissociated is dissociated, and what is combined is combined, holds the truth, whereas he whose thought is contrary to the state of affairs is in error [
]; so that he who thinks that what is dissociated is dissociated, and what is combined is combined, holds the truth, whereas he whose thought is contrary to the state of affairs is in error [ ]. When, therefore, is there or is there not what is called truth or falsity?
]. When, therefore, is there or is there not what is called truth or falsity?
We must inquire into what we mean by this. For it is not because we truly [ ] hold you to be white that you are white; but it is because you are white that we who assert this speak truly [
] hold you to be white that you are white; but it is because you are white that we who assert this speak truly [ ]. (1051b2–9)
]. (1051b2–9)
Here he uses ‘alêthês’ and ‘pseudês’ to mean true and false in relation to sentences. He also frequently uses, as he does here, the verbs  and
and  . Continuing later in this same passage he writes:
. Continuing later in this same passage he writes:
As to “being” [ ] in the sense of the true [
] in the sense of the true [ ] and “not being” [
] and “not being” [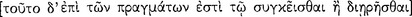 ] in the sense of the false [
] in the sense of the false [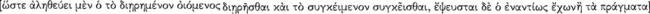 ], there are two cases: in one case there is truth [
], there are two cases: in one case there is truth [ ] if the combination [
] if the combination [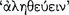 ] [
] [ ] exists, and falsity [
] exists, and falsity [ ] if there is a dissociation [
] if there is a dissociation [ ]; in the other case, however, whatever is, is as it is, or it is not at all. Here truth is the knowledge of these things [
]; in the other case, however, whatever is, is as it is, or it is not at all. Here truth is the knowledge of these things [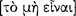 ]. (1051b33–1052a2)
]. (1051b33–1052a2)
Aristotle also makes much the same point succinctly in Metaphysics 5.29.
The “false” [ ] refers (1) to a state of affairs as not the case [
] refers (1) to a state of affairs as not the case [ ]: and this, on the one hand, because it is not put together or cannot be put together. … States of affairs [
]: and this, on the one hand, because it is not put together or cannot be put together. … States of affairs [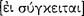 ] then are said to be not the case [
] then are said to be not the case [ ] whether because they themselves are not or because the appearance derived from them is of something that is not.
] whether because they themselves are not or because the appearance derived from them is of something that is not.
Next, (2) a false account, in so far as it is false, is the account of things that are not. Hence, every account is false which is an account of something other than that of which it is true [ ]; for example, an account of a circle is false of a triangle.47 (1024b17–19, 24–28)
]; for example, an account of a circle is false of a triangle.47 (1024b17–19, 24–28)
We encounter an analogue of this ambiguity in English, where ‘true’ and ‘false’ have a range of meanings, including the genuine and the spurious. We might be inclined to accuse Aristotle of making a category mistake, and perhaps there are cases where he slips. However, it is obvious here that Aristotle does not commit a category mistake, but that he uses the same word with two meanings corresponding to the two contexts. He does not confuse a sentence (logos or apophansis) with a corresponding state of affairs (pragma), although we might wish that he had always used different expressions to distinguish their being or not being. Thus, in relation to states of affairs (pragmata), we could properly translate ‘alêthês’ by ‘is the case’ and ‘pseudês’ by ‘is not the case’.
Again, Aristotle is quite clear about pragmata either being or not being, obtaining or not obtaining. This is something ontic. He affirms, in one sense, that combination and division are mental acts, in particular, acts of predicating one thing of another either attributively or privatively, which are participant relative. In Metaphysics 6.4 he writes:
Now, being [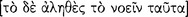 ] in the sense of being true and nonbeing [
] in the sense of being true and nonbeing [ ] in the sense of being false are concerned with union [
] in the sense of being false are concerned with union [ ] and division [
] and division [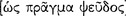 ] and, taken together, with the relation of contradictories [
] and, taken together, with the relation of contradictories [ ]. For there is truth when an affirmation corresponds to a combination in beings and when a denial corresponds to a dissociation among beings; whereas there is error [or nonbeing] when the opposite relations hold [
]. For there is truth when an affirmation corresponds to a combination in beings and when a denial corresponds to a dissociation among beings; whereas there is error [or nonbeing] when the opposite relations hold [ ]. (1027b18–23)
]. (1027b18–23)
A little later in this same passage he remarks that “the false and the true are not in things [ ], as if the good were true and the bad were forthwith false; but they are in thought [
], as if the good were true and the bad were forthwith false; but they are in thought [ ]” (1027b25–27). We could not ask him to be more clear. He adds, nevertheless:
]” (1027b25–27). We could not ask him to be more clear. He adds, nevertheless:
However, since unification and separation are in thought and not in things, ‘being’ in this sense differs from ‘being’ in the chief sense. For to predicate or deny what something is, or that it is of some sort, or that it is so much, or the like requires thinking [ ]. (1027b29–33)
]. (1027b29–33)
And thoughts become ‘materialized’, or expressed, by means of sentences. Aristotle makes this point at Metaphysics 4.7 as follows:
Still, every concept and thought is expressed either as an affirmation or a negation [ ]; this is clear from the definition [
]; this is clear from the definition [ ] of truth and falsity. When a sentence either asserts or denies, it expresses either truly or falsely [
] of truth and falsity. When a sentence either asserts or denies, it expresses either truly or falsely [ ].48 (1012a2–4).
].48 (1012a2–4).
The distinctions that modern logicians believe themselves to have invented were surely anticipated, if not invented, by Aristotle in ancient times. Categories helps to make this even more evident.
Aristotle’s treatment of truth conditions in Categories
In Categories, as he sharpens the distinction between a sentence and its denotation, Aristotle defines truth and falsity by affirming that a sentence is not a substance (ousia). In Metaphysics he makes it clear that a substance, or a subject (hupokeimenon), maintains the same identity and yet admits of contrary qualities. In this connection he defines contraries, or contrariety, in Metaphysics 10.4 as they pertain to substance.49
Since things which differ may be more or less different, there is a greatest difference; this I call contrariety [ ]. We can show inductively that contrariety is the greatest difference. … Hence the distance between extremes is a maximum, and this constitutes the relation of contrariety. … From these considerations, then, it is clear that contrariety is perfect difference.50 (1055a3–6, 9–10, 16–17)
]. We can show inductively that contrariety is the greatest difference. … Hence the distance between extremes is a maximum, and this constitutes the relation of contrariety. … From these considerations, then, it is clear that contrariety is perfect difference.50 (1055a3–6, 9–10, 16–17)
A given individual, then, at one time might be warm or good and at another time cold or bad, but he/she cannot be both warm and cold or good and bad at the same time in the same respect. For Aristotle a substance has a capacity for contraries, but does not itself change identity. In Categories 5 he discusses the mistake of thinking that a sentence (logos) or an opinion ([doxa]), which is expressed by a sentence, admits of contrariety. He writes that
the same sentence [ ] appears to be both true and false. For example, if the sentence “Someone sits” is true, but if he rises, the same sentence becomes false. And likewise with opinions [
] appears to be both true and false. For example, if the sentence “Someone sits” is true, but if he rises, the same sentence becomes false. And likewise with opinions [ ]. For if someone believes truly the sentence “Someone sits”, then upon the person rising he will believe falsely if he still holds the same opinion about him [
]. For if someone believes truly the sentence “Someone sits”, then upon the person rising he will believe falsely if he still holds the same opinion about him [ ]. (4a23–28)
]. (4a23–28)
Aristotle continues here to remark that whenever a substance admits of contrary qualities it is due to a change within itself. However, in the case of a sentence (logos) and an opinion (doxa) each
remains in itself unaltered in any and every respect; but it is because of a change in the fact [ ] that the contrary applies to them. For the sentence “Someone sits” remains the same; but according to changing conditions [
] that the contrary applies to them. For the sentence “Someone sits” remains the same; but according to changing conditions [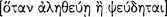 ] it becomes at one time true and at another time false. As with sentences, so too with opinions [
] it becomes at one time true and at another time false. As with sentences, so too with opinions [ ]. (4a34–4b2)
]. (4a34–4b2)
At 4b2–6 Aristotle asserts that it is the special property (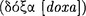 ) of substance to admit of changes (
) of substance to admit of changes ( ) within itself, but that opinions and sentences do not admit of such changes. He next forcefully states that anyone maintaining that a sentence admits of contrary qualifications is speaking nonsense.
) within itself, but that opinions and sentences do not admit of such changes. He next forcefully states that anyone maintaining that a sentence admits of contrary qualifications is speaking nonsense.
It is not because a sentence and an opinion [ ] take on contrary qualities that they are said to take on contraries, but because of what has happened to something else. For it is because the fact is or is not that case [
] take on contrary qualities that they are said to take on contraries, but because of what has happened to something else. For it is because the fact is or is not that case [ ] that a sentence [
] that a sentence [ ] is called true or false, and not that it can itself receive contrary qualities. For absolutely nothing [
] is called true or false, and not that it can itself receive contrary qualities. For absolutely nothing [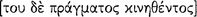 ] can alter either a sentence or an opinion, and so, since they cannot receive contraries nothing changes in them. (4b6–13)
] can alter either a sentence or an opinion, and so, since they cannot receive contraries nothing changes in them. (4b6–13)
Only substances can admit of such changes (4b13–14). Here again Aristotle affirms the difference between a sentence and the state of affairs denoted by the sentence as he treats truth and falsity. In Categories 10 he develops this distinction with even more precision.
Nor is what underlies [ ] an affirmation and a denial an affirmation and a denial. An affirmation [
] an affirmation and a denial an affirmation and a denial. An affirmation [ ] is an affirmative sentence [
] is an affirmative sentence [ ], a denial [
], a denial [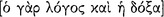 ] is a denying sentence [
] is a denying sentence [ ]. But what underlies [
]. But what underlies [ ] either an affirmation or a denial is not a sentence [
] either an affirmation or a denial is not a sentence [ ]. Still, these things are said to be opposed to each other as affirmation and denial; there is the same manner of opposition. For just as an affirmation is opposed to a denial — for example, “Someone sits” and “Someone does not sit” — so are opposed the things that underlie each sentence [
]. Still, these things are said to be opposed to each other as affirmation and denial; there is the same manner of opposition. For just as an affirmation is opposed to a denial — for example, “Someone sits” and “Someone does not sit” — so are opposed the things that underlie each sentence [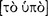 ] — the sitting and the not sitting. (12b5–16)
] — the sitting and the not sitting. (12b5–16)
As Aristotle had distinguished a word and its object, here he distinguishes a sentence from what it expresses. He clearly grasps the difference between a sentence and its denotation. Later in this same discussion in Categories 10 he turns to a position he treats in On Interpretation 7:
It is evident that affirmations and denials are opposed in none of those ways we have already treated. For only in relation to [contradictory] sentences is it always necessary for one to be true the other to be false. With contraries it is not always necessary for one to be true the other false, nor with relatives, nor with possession, nor with privation. For example, health and sickness are contraries, but neither the one nor the other is either true or false; likewise with the relatives the double and the half. Nor are privation and possession such as sight and blindness. Generally, nothing that is said without combination is either true or false [ ]. All the opposites just treated are said without combination [
]. All the opposites just treated are said without combination [ ]. (13a37–13b12)
]. (13a37–13b12)
Thus, Aristotle distinguishes a sentence from its denotation, and he establishes that the truth or falsity of a given sentence, which are ontic determinations, depends upon correspondence with the states of affairs or facts, which also are ontic matters, denoted by the sentence as being the case  .51
.51
Truth-values of contradictory and contrary sentences
In Metaphysics 5.10 Aristotle defines ‘opposite’ (antikeimenon) as having a variety of meanings: contradiction, contrariety, correlation, privation, possession. What he writes there about being corresponds exactly with what he writes in On Interpretation 7 having to do with contradictory and contrary sentences. In Metaphysics 10.4 he states of substance that “the primary form of contrariety [ ] is that between a positive state and a privation [
] is that between a positive state and a privation [ ]” (1055a33–34).52 He continues there to distinguish contradiction from contrariety as follows:
]” (1055a33–34).52 He continues there to distinguish contradiction from contrariety as follows:
Opposition [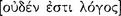 ] may take the form of contradiction [
] may take the form of contradiction [ ] or of privation [
] or of privation [ ] or of contrariety [
] or of contrariety [ ] or of relation [
] or of relation [ ]. The first of these is contradiction, and contradiction admits of no intermediate, whereas contraries do; it is clear that contradictories and contraries are not the same. (1055a38–1055b3)
]. The first of these is contradiction, and contradiction admits of no intermediate, whereas contraries do; it is clear that contradictories and contraries are not the same. (1055a38–1055b3)
Aristotle defines ‘contrary’ and ‘contradictory’ in Prior Analytics B15: 63b23–30 in a way that exactly comports with what he writes in On Interpretation, but in Prior Analytics in relation to the logical constants.
I say that verbally there are four <pairs of> opposite sentences [ ], to wit: [1] ‘to every’ and ‘to no’, [2] ‘to every’ and ‘not to every’, [3] ‘to some’ and ‘to no’, and [4] ‘to some’ and ‘not to some’. In truth, however, there are three, for ‘to some’ and ‘not to some’ are only opposites verbally. Of these, I call the universal sentences contraries [
], to wit: [1] ‘to every’ and ‘to no’, [2] ‘to every’ and ‘not to every’, [3] ‘to some’ and ‘to no’, and [4] ‘to some’ and ‘not to some’. In truth, however, there are three, for ‘to some’ and ‘not to some’ are only opposites verbally. Of these, I call the universal sentences contraries [ ] (‘to every’ is contrary to ‘to none’, as, for example, “Every science is good” is contrary to “No science is good”) and the other pairs of sentences opposites [
] (‘to every’ is contrary to ‘to none’, as, for example, “Every science is good” is contrary to “No science is good”) and the other pairs of sentences opposites [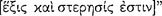 ]. (63b23–30)
]. (63b23–30)
Only opposites cannot belong to the same thing at the same time. According to the principle of opposition, both opposites obtaining at the same time is impossible (Meta. 10.5: 1055b37–1056a3). When he turns in On Interpretation 7 to treat sentences, he states that “the denial … must deny the same thing the affirmation affirms of the same thing” (17b39–40).53 And there also he makes this point about contraries: “but what constitutes sentences as contrary is having two contrary meanings, not having two contrary subjects” (23b6–7). And, “it is impossible for opposite sentences [ ] to be true about the same thing” (21b17–18). In fact, when one of a pair of contradictories is true the other is necessarily false. This is not the case with contraries where both might be false, but not both true. In On Interpretation 7 he writes:
] to be true about the same thing” (21b17–18). In fact, when one of a pair of contradictories is true the other is necessarily false. This is not the case with contraries where both might be false, but not both true. In On Interpretation 7 he writes:
But I call the universal affirmation [ ] and the universal denial [
] and the universal denial [ ] contrarily opposite … Hence, these cannot be true together, but it is possible that their opposites [i.e., sub-contraries] can be true of the same thing. (17b20–26)
] contrarily opposite … Hence, these cannot be true together, but it is possible that their opposites [i.e., sub-contraries] can be true of the same thing. (17b20–26)
Among the relationships Aristotle understands to exist between categorical sentences are two pairs of contradictories and one pair of contraries, all of which he employs in his deduction system. Now, rather than grasping some syntactic relationships among categorical sentences as taking a given sentence and then as a result being able or not able to take another sentence, Aristotle treats their semantic relationships as follows.
1. If a sentence fitting the pattern AaB is true, then a sentence fitting the pattern AoB is necessarily false; if a sentence fitting the pattern AaB is false, then a sentence fitting the pattern AoB is necessarily true.
If a sentence fitting the pattern AoB is true, then a sentence fitting the pattern AaB is necessarily false; if a sentence fitting the pattern AoB is false, then a sentence fitting the pattern AaB is necessarily true.
2. If a sentence fitting the pattern AeB is true, then a sentence fitting the pattern AiB is necessarily false; if a sentence fitting the pattern AeB is false, then a sentence fitting the pattern AiB is necessarily true.
If a sentence fitting the pattern AiB is true, then a sentence fitting the pattern AeB is necessarily false; if a sentence fitting the pattern AiB is false, then a sentence fitting the pattern AeB is necessarily true.
For contraries:
1. If a sentence fitting the pattern AaB is true, then a sentence fitting the pattern AeB is necessarily false; but if a sentence fitting the pattern AaB is false, then a sentence fitting the pattern AeB is not necessarily true but might be false.
2. If a sentence fitting the pattern AeB is true, then a sentence fitting the pattern AaB is necessarily false; but if a sentence fitting the pattern AeB is false, then a sentence fitting the pattern AaB is not necessarily true but might be false.
Aristotle states all this in so many words, although not as rigorously, and it is obviously an important part of his treatment of sentences in Prior Analytics. This position is explicitly treated in On Interpretation and it is used throughout his analyses in Prior Analytics, notably there in relation to conversion (A2: 25a17–19) and to his treating reductio proofs (e.g., those of Baroco in A5: 27a30–27b3 and of Bocardo in A6: 28b17–20).
Aristotle on existential import
Aristotle noticed some difficulty concerning the semantics of some sentences, particularly indeterminate sentences and those having to do with future events (On. Int. 9).54 Still, his considerations of these matters in On Interpretation (6, 7–8, 9–11, 12, 13) seem well resolved. He reaffirms that every sentence is either true or false, although determining this in one or another case may be difficult or sometimes impossible. Modern logicians, however, seem more puzzled by considerations of existence, and they fear that Aristotle’s logic leads to peculiar violations of the square of opposition, particularly in relation to contradictories.55 However, this matter was not especially troubling to Aristotle. In Categories 10 he addresses this matter in the following way.
It is evident that affirmations and denials are opposed in none of those ways we have already treated. For only in relation to [contradictory] sentences is it always necessary for one to be true the other to be false. With contraries it is not always necessary for one to be true the other false, nor with relatives, nor with possession, nor with privation. For example, health and sickness are contraries, but neither the one nor the other is either true or false; likewise with the relatives the double and the half. Nor are privation and possession such as sight and blindness. Generally, nothing that is said without combination is either true or false [ ]. All the opposites just treated are said without combination [
]. All the opposites just treated are said without combination [ ].
].
However, it might seem that some such thing follows in the case of contraries said with combination [ ] — [as in] the sentence “Socrates is ill” is contrary to “Socrates is well”. Yet, even in these cases it is not always necessary that one sentence be true and the other be false. For, if Socrates exists, one is true and the other is false; but if Socrates does not exist, both [sentences] are false. For neither will the sentence “Socrates is ill” nor the sentence “Socrates is well” be true if Socrates himself does not exist.
] — [as in] the sentence “Socrates is ill” is contrary to “Socrates is well”. Yet, even in these cases it is not always necessary that one sentence be true and the other be false. For, if Socrates exists, one is true and the other is false; but if Socrates does not exist, both [sentences] are false. For neither will the sentence “Socrates is ill” nor the sentence “Socrates is well” be true if Socrates himself does not exist.
As for affirmations and denials [ ], if [the subject] does not exist, then neither sentence is true. But if [the subject] exists, even then one or the other will not always be true. The sentence “Socrates has sight” is the opposite of the sentence “Socrates is blind” [in the sense in which ‘opposite’ is applied] to privation and possession. For, if he [viz., Socrates] exists, it is not necessary that the one sentence be true and the other false (since until the time when it is natural for him to have sight both sentences are false). While if Socrates does not exist then both sentences are false: both “He has sight” and “He is blind”.
], if [the subject] does not exist, then neither sentence is true. But if [the subject] exists, even then one or the other will not always be true. The sentence “Socrates has sight” is the opposite of the sentence “Socrates is blind” [in the sense in which ‘opposite’ is applied] to privation and possession. For, if he [viz., Socrates] exists, it is not necessary that the one sentence be true and the other false (since until the time when it is natural for him to have sight both sentences are false). While if Socrates does not exist then both sentences are false: both “He has sight” and “He is blind”.
However, concerning affirmation and negation [i.e., contradictories] the one will always be false the other true whether or not [the subject] exists. For take the sentence “Socrates is ill” and the sentence “Socrates is not ill”, if he exists it is evident that the one or the other must be true or false. It is the same if he does not exist. If Socrates exists, the sentence [expressing] that he is sick is false, but the sentence [expressing] that he is not sick is true. Thus, it is characteristic [ ] of these only — sentences opposed as affirmation and denial [viz., contradictories] — that the one is always true and the other always false in all cases will hold of those opposites only which are in the same sense opposed as affirmative and negative sentences. (13a37–13b35)
] of these only — sentences opposed as affirmation and denial [viz., contradictories] — that the one is always true and the other always false in all cases will hold of those opposites only which are in the same sense opposed as affirmative and negative sentences. (13a37–13b35)
We cite here again a passage from Categories 12 where he writes about truth and falsity.
The existence of a man is reciprocal in relation to the true sentence about him as it follows from there being [such] a man [ ]. For if a man exists, then the sentence [
]. For if a man exists, then the sentence [ ] asserting that a man exists will be true. And conversely, if the sentence asserting that a man exists is true, then the man exists. The true sentence, however, is in no way the cause of the [given] state of affairs [
] asserting that a man exists will be true. And conversely, if the sentence asserting that a man exists is true, then the man exists. The true sentence, however, is in no way the cause of the [given] state of affairs [ ]; and yet the state of affairs [
]; and yet the state of affairs [ ] seems somehow to be the cause of the truth of the sentence. For a sentence is called true or false as the state of affairs exists or does not exist. (14b14–22)
] seems somehow to be the cause of the truth of the sentence. For a sentence is called true or false as the state of affairs exists or does not exist. (14b14–22)
Aristotle affirms that the truth or falsity of a given sentence depends, first and foremost, upon whether what it expresses corresponds to a given state of affairs. In this connection, then, it depends upon whether the objects denoted by the subject exist or do not exist, whether what is asserted is the case or is not the case. The cause, or ground, of the truth of a sentence is the state of affairs it denotes. This notion is underwritten by his notion of substance. “Were there no individuals existing of whom it could thus be affirmed, it could not be affirmed of the species; and were there no primary substance, nothing else could so much as exist” (Cat. 5: 2a38–2b1). Aristotle has remarked in what way existence is the cause of a sentence being true (Meta. 4.7: 1011b23–29).
With what he writes in Categories 10 and 12 and elsewhere on truth and falsity, we can make sense of the semantics of the various sentences that Aristotle treats concerning their existential import. In general, in the case of existence, a sentence is true or false as, respectively, the state of affairs denoted by the sentence is the case or is not the case; in these cases there are no empty classes. In the case of non-existence, no affirmation is true because it affirms something to be the case that is not the case, and every privative, that is, every sentence with a negative operator, is true because it truly expresses what is not the case.
Below we set out Aristotle’s semantics according as he considers sentences to be: (1) singular  , universal
, universal  , or partial
, or partial  ; (2) attributive
; (2) attributive  or privative
or privative  — affirmative [positive] or negative: an affirmation
— affirmative [positive] or negative: an affirmation  or a denial
or a denial 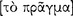 (3) determinate
(3) determinate  or indeterminate
or indeterminate  (4) having a subject that exists or having a subject that does not exist. Aristotle understands an opposite
(4) having a subject that exists or having a subject that does not exist. Aristotle understands an opposite  of a given affirmative sentence to be either (1) a contrary
of a given affirmative sentence to be either (1) a contrary  , which may or may not involve a negative operator, or (2) a contradictory
, which may or may not involve a negative operator, or (2) a contradictory  , which always involves a negative operator. In our treatment of sentences below we always take a sentence to be a simple sentence according to Aristotle’s stipulation in his formal language.
, which always involves a negative operator. In our treatment of sentences below we always take a sentence to be a simple sentence according to Aristotle’s stipulation in his formal language.
The singular sentence
A singular sentence predicates, attributively or privatively, one thing of a particular this, a primary substance  , and this particular is not predicable of anything else (On Int. 7: 17a38–17b1; Cat. 5: 2a11–14; Pr. An. A27: 43a25–29, 39–40). Every singular sentence is determinate. The opposite of a given attributive singular sentence is either its contrary or its contradictory. A contrary of an attributive singular sentence does not have a negative operator and is always another attributive singular sentence (sc. an affirmation). Since, for Aristotle, every denial involves a negative operator, there are no privative contraries in the case of singular sentences. Using a negative operator
, and this particular is not predicable of anything else (On Int. 7: 17a38–17b1; Cat. 5: 2a11–14; Pr. An. A27: 43a25–29, 39–40). Every singular sentence is determinate. The opposite of a given attributive singular sentence is either its contrary or its contradictory. A contrary of an attributive singular sentence does not have a negative operator and is always another attributive singular sentence (sc. an affirmation). Since, for Aristotle, every denial involves a negative operator, there are no privative contraries in the case of singular sentences. Using a negative operator  in the case of an attributive singular sentence, either adverbially as attached to a verb, or logical constant, or as prefixing an entire sentence, always results in the contradictory of the given singular sentence. Prior Analytics treats singular sentences only incidentally. Moreover, Prior Analytics does not prefix a given sentence with ‘ou’ to produce its negation. Table 7 represents Aristotle’s thinking on the semantics of singular sentences.56
in the case of an attributive singular sentence, either adverbially as attached to a verb, or logical constant, or as prefixing an entire sentence, always results in the contradictory of the given singular sentence. Prior Analytics treats singular sentences only incidentally. Moreover, Prior Analytics does not prefix a given sentence with ‘ou’ to produce its negation. Table 7 represents Aristotle’s thinking on the semantics of singular sentences.56
Table 7

The universal sentence
A universal sentence predicates, attributively or privatively, one thing of every or of no member of a given kind, a secondary substance  . Every universal sentence is determinate. The opposite of a given attributive universal sentence is either its contrary or its contradictory. A contrary of an attributive universal sentence might or might not involve a negative operator, as in both On Interpretation and Prior Analytics. The negative operator in these cases appears as a pronominal adjective modifying the subject (or as part of the logical constant, which nevertheless modifies the subject). The contradictory of a given universal attributive sentence involves a negative operator in both On Interpretation and Prior Analytics. The negative operator in these cases might appear as prefixing an entire sentence, as in On Interpretation but not in Prior Analytics, or adverbially as attached to a verb as part of the logical constant. Table 8 represents Aristotle’s thinking on the semantics of universal sentences.
. Every universal sentence is determinate. The opposite of a given attributive universal sentence is either its contrary or its contradictory. A contrary of an attributive universal sentence might or might not involve a negative operator, as in both On Interpretation and Prior Analytics. The negative operator in these cases appears as a pronominal adjective modifying the subject (or as part of the logical constant, which nevertheless modifies the subject). The contradictory of a given universal attributive sentence involves a negative operator in both On Interpretation and Prior Analytics. The negative operator in these cases might appear as prefixing an entire sentence, as in On Interpretation but not in Prior Analytics, or adverbially as attached to a verb as part of the logical constant. Table 8 represents Aristotle’s thinking on the semantics of universal sentences.
Table 8
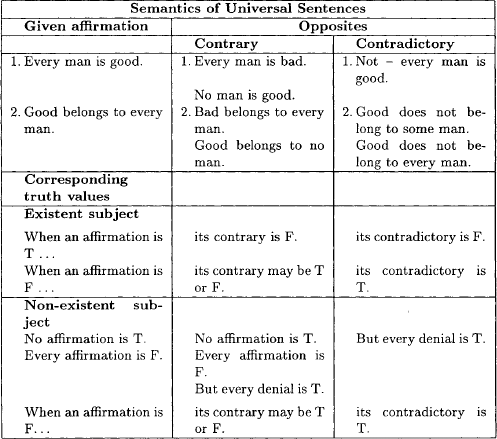
The partial sentence
A partial sentence predicates, attributively or privatively, one thing of some or of not every member of a given kind. Here there are instances of both determinate and indeterminate sentences. General sentences, for example, “Man is white” or “Pleasure is good”, lack a universal quantifier and thus can be interpreted as denoting both some and all; their meaning is not determinate but ambiguous.
The opposite of a given determinate partial attributive sentence is either its sub-contrary (as modern logicians name it) or its contradictory. A sub-contrary of a given partial attributive sentence might, as in both On Interpretation and Prior Analytics, or it might not involve a negative operator. The negative operator in the case of a sub-contrary appears adverbially as attached to a verb, or as part of a logical constant. The contradictory of a given partial attributive sentence involves a negative operator in both On Interpretation and Prior Analytics. The negative operator in the case of a contradictory may appear as a pronominal adjective as part of the logical constant, or as merely modifying the subject, or as prefixing an entire sentence as in On Interpretation. Table 9 represents Aristotle’s thinking on the semantics of partial sentences.57
Table 9
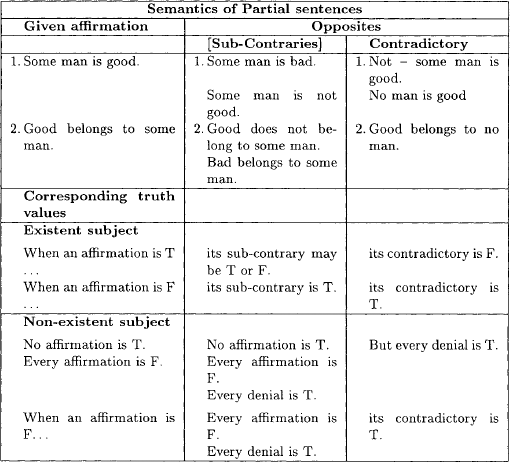
Denying a given privative sentence does not seem to have been treated by Aristotle in either On Interpretation or Prior Analytics, although there are suggestions in On Interpretation. Because he lacks a notion of double negation, or, at least, it seems, a strong notion of double negation, Aristotle does not treat denying a privative sentence save for reverting to its already given affirmation. This is particularly true in Prior Analytics, where he does not negate an entire sentence with ‘ou’ as in On Interpretation. Rather, there he begins with an affirmation, then provides its contradictory, and then looks back at the original affirmation to obtain the contradictory of the negation: he does not, then, negate the negation to obtain its own contradictory. As he remarked at different places, each affirmation has its own, one negation, each negation its own, one affirmation — and he takes them as pairs.
Finally, in respect of existential import, according to his definitions of true and false, Aristotle holds that “to deny what is or to affirm what is not is false, whereas to affirm what is and to deny what is not are true; so that any sentence that anything is or is not states either truly or falsely” (Meta. 4.7: 1011b26–28). This notion is again poignantly expressed in Metaphysics 5.7:
‘Being’ [ ] means [
] means [ ] the ‘true’ when something is the case and ‘not being’ [
] the ‘true’ when something is the case and ‘not being’ [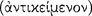 ] <means> the ‘not true’ but the ‘false’ when something is not the case; likewise for affirmation and denial [
] <means> the ‘not true’ but the ‘false’ when something is not the case; likewise for affirmation and denial [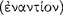 ]; for example, that “Socrates is musical” means that this is the case <but we know that this sentence is false>, or that “Socrates is non-white” means that this is the case <but, again, we know that this state of affairs is not the case>. But that “the diagonal <of the square> is not commensurate <with the side>” means that this is not the case <and this, of course, is not the case, and so the sentence is true>. (1017a31–35)
]; for example, that “Socrates is musical” means that this is the case <but we know that this sentence is false>, or that “Socrates is non-white” means that this is the case <but, again, we know that this state of affairs is not the case>. But that “the diagonal <of the square> is not commensurate <with the side>” means that this is not the case <and this, of course, is not the case, and so the sentence is true>. (1017a31–35)
Thus, for Aristotle, every sentence affirming something of a non-existent subject is false because it affirms, incorrectly, something to be the case that is not the case. In addition, every sentence denying — that is, using a negative operator — something of a non-existent subject is true because it affirms, correctly, something not to be the case that indeed is not the case. The correspondence, or non-correspondence as the case may be, of thought to being is foundational in Aristotle’s thinking about truth and falsity. Now, when we turn back to On Interpretation 6, just after where he writes that an affirmation states something of something, a denial denies something of something, we can better understand Aristotle’s meaning.
Now it is possible to state of what does belong that it does not belong, of what does not belong that it does belong, of what does belong that it does belong, and of what does not belong that it does not belong [ ]. (17a26–29)
]. (17a26–29)
When someone asserts of what does not belong, or is not the case, that it does not belong, or is not the case, he/she speaks truly.
Truth-value: an extensional or intensional determination?
Considering the meanings Aristotle assigns to his logical constants might lead one to believe that the truth-value of a categorical sentence is determined extensionally. Recall, for example, that he defines ‘belonging to every’ by writing that “for one thing to be in another as a whole …”. This suggests his taking the application of the universal attributive logical constant extensionally with respect to non-empty domains. However, Aristotle continues this statement by writing that “…is the same as for one thing to be predicated of every one of another”, or “to hold in every case”. His writing here seems shy of an extensional determination.
Now, while interpreting the relationship of terms in a categorical sentence as that between classes, or even of sets, has been fruitful, this interpretation, nevertheless, does not reproduce Aristotle’s own understanding. It has become a common practice to define the truth of a categorical sentence in this way as follows (using traditional expressions; ‘A’ and ‘B’ are placeholders).
“Every A is a B” is true iff the extension of A is entirely included in the extension of B.
“No A is B” is true iff the extension of A is disjoint with the extension of B.
“Some A is B” is true iff the extension of A intersects with the extension of B.
“Some A is not B” is true iff the extension of A is not entirely included in the extension of B.
Perhaps in some cases Aristotle did envisage terms to relate extensionally as classes. Nevertheless, this interpretation does not take into account Aristotle’s notions of attribution and privation, which pertain to things (pragmata), and his notions of predicating of and not predicating of, which pertain to sentences (apophanseis). Underlying his theory of predication in Categories, On Interpretation, and in Prior Analytics is his theory of substance in Categories and Metaphysics. Briefly, for Aristotle attribution is ontic and independent of a participant, while predication is intentional or linguistic and participant dependent. Predicating is an activity of a human being reflecting in thought what exists or does not exist outside of thought. For Aristotle, insofar as he considers matters of logic, thought follows being. And his notion of substance (ousia) is precisely that in which properties (pathêmata) inhere or do not inhere. A substance, whether primary or secondary, has or does not have one or another property. This explains Aristotle’s use of ‘huparchein’ in the logical constants.
In order better to grasp term relationships and to see Aristotle as not determining truth extensionally, we might consider his objection to platonic forms. For Plato, an individual person’s being two-footed, for example, is just his participation in the transcendent form ‘two-footedness’. Aristotle, rejecting the reality of such transcendent forms and their putative explanatory value, rather thought of an individual person’s being two-footed as his having this property or attribute — as this characteristic inhering in, or as immanent in, a subject. A sentence expressing this relationship would be attributive. To express the notion of a horse, on the other hand, as not having rationality would be privative. Aristotle treats attribution, in so far as a human expresses attribution in thought by means of sentences, rather fully in Categories as well as at places in Metaphysics.
Since his theory of substance underlies his theory of predication, we ought rather to say that truth for Aristotle is determined intensionally (or, perhaps, ‘possessionally’), remembering his correspondence notion of knowledge. Thus, (using his sentential expressions) we have the following (see n17):
“A belongs to every B” is true iff every individual B has property A.
“A belongs to no B” is true iff no individual B has property A.
“A belongs to some B” is true iff some individual B has property A.
“A does not belong to some B” is true iff some individual B does not have property A.
Aristotle uses ‘hupokeimenon’ to refer to the subject of a categorical sentence, and he uses ‘pathê’ or ‘idion’ to refer to a property attributable or not attributable to a subject. ‘Pathê’ contains a notion of ‘affect’, and surely not a notion of ‘class’, but of something ‘happening to’ an individual this. Indeed, again, this is just his meaning of the categories (Cat. 4). If we add, as Aristotle sometimes did, that property A is essential and not accidental to subject B, then we understand him to mean that having property A, or being A, is just what it means to be B. We again cite a passage from Metaphysics tersely to illustrate his thinking.
Suppose ‘man’ has the meaning ‘two-footed animal’. By ‘having a meaning’ I mean this: if ‘man’ is ‘two-footed animal’, then if anything is a man, its ‘being two-footed’ will be what its ‘being a man’ is. (1006a31–34)
Thus, we can take the following expressions of the universal attributive logical constant (and the corresponding sentence patterns) to be generally equivalent in meaning for Aristotle.
2.3 The deduction system of Aristotle’s underlying logic
In Prior Analytics Aristotle turned his attention away from object language discourses and toward objectifying the formal deduction apparatus used to establish scientific theorems. He was especially concerned to determine “how every syllogism is generated” (25b26–31). He refers here to the elements of syllogistic reasoning, which consist in elementary two-premiss valid arguments — the syllogisms — that, when chained together, make up longer syllogistic (deductive) discourses. Aristotle’s project was to identify all the panvalid patterns of such elementary arguments. In this way he explicitly treated deduction rules and their logical relationships in Prior Analytics. These rules include both the one-premiss conversion rules and the two-premiss syllogism rules. He accomplished this by exhaustively treating each and every possible argument pattern relating to both the one-premiss and two-premiss rules: (1) those patterns of arguments having a premiss-set of just one categorical sentence with only two different terms — the conversions; and (2) those patterns of arguments having a premiss-set of just two categorical sentences with only three different terms — the syllogisms. Aristotle limited his study of multi-premiss arguments to their two-premiss patterns because two categorical sentences, taken together, have ‘the fewest number of terms and premisses through which something different than what was initially taken follows necessarily’.58 The syllogisms, then, are the building blocks of longer deductive discourses.
We have thus far examined the grammar of categorical sentences as Aristotle treated this matter with the artifice of his formal language. We have also treated their semantics. We turn now to the syntactic matter of generating, or transforming, sentences from given categorical sentences according to stipulated rules. This defines the deduction system of Aristotle’s underlying logic. Briefly, the deduction system as presented in Prior Analytics A1–2, 4–6 consists in the following (Table 10:
Table 10
Aristotle’s deduction system
Below we extract the rules Aristotle used for forming one-premiss arguments and the three corresponding conversion rules and his rules for forming two-premiss arguments and the corresponding syllogism rules.
The one-premiss conversion rules
In Prior Analytics A2 Aristotle treats converting ( conversion:
conversion:  ) the predicate and subject terms of categorical sentences to extract certain deduction rules. To do this he treats each of the four kinds of categorical sentence metalogically; that is, he treats at one time, say, all universal privative sentences, by treating the one sentence pattern that they all fit. Aristotle models an object language conversion as an elementary one-premiss argument pattern — where a given sentence is in the role of premiss and its conversion is in the role of conclusion. In this way, without considering object language arguments but only their patterns, he determines which sentences logically convert with respect to terms and which do not by establishing that the argument pattern that they fit is panvalid. Aristotle determines that of the four kinds of categorical sentence three logically convert and thus their panvalid argument patterns can serve as deduction rules. Interestingly, he first states each of the three conversion rules in a sentence (25a5–13), as we would expect a rule to be expressed. Moreover, he treats the conversions in Prior Analytics A2 exactly as he does the syllogism rules in Prior Analytics A4–6 (§3.2 and n68). Aristotle assumes his reader’s familiarity with converting, since he does not define conversion per se: he takes it as obvious that conversion involves changing the places of the subject and predicate terms in a given categorical sentence while leaving its logical constant unchanged (save for per accidens conversion). Aristotle considers these formal transformations to be deduction rules because something different than what is initially taken is established to follow necessarily in each instance. Their being universal in this respect underlies their rule nature.
) the predicate and subject terms of categorical sentences to extract certain deduction rules. To do this he treats each of the four kinds of categorical sentence metalogically; that is, he treats at one time, say, all universal privative sentences, by treating the one sentence pattern that they all fit. Aristotle models an object language conversion as an elementary one-premiss argument pattern — where a given sentence is in the role of premiss and its conversion is in the role of conclusion. In this way, without considering object language arguments but only their patterns, he determines which sentences logically convert with respect to terms and which do not by establishing that the argument pattern that they fit is panvalid. Aristotle determines that of the four kinds of categorical sentence three logically convert and thus their panvalid argument patterns can serve as deduction rules. Interestingly, he first states each of the three conversion rules in a sentence (25a5–13), as we would expect a rule to be expressed. Moreover, he treats the conversions in Prior Analytics A2 exactly as he does the syllogism rules in Prior Analytics A4–6 (§3.2 and n68). Aristotle assumes his reader’s familiarity with converting, since he does not define conversion per se: he takes it as obvious that conversion involves changing the places of the subject and predicate terms in a given categorical sentence while leaving its logical constant unchanged (save for per accidens conversion). Aristotle considers these formal transformations to be deduction rules because something different than what is initially taken is established to follow necessarily in each instance. Their being universal in this respect underlies their rule nature.
Aristotle does not explicitly state any general syntax rules for forming premiss-sets or for forming premiss-conclusion arguments. Still, in this connection he tends to be more explicit in the case of the syllogisms than in the case of the conversions. In any case, we can easily extract from his practice of treating conversion in Prior Analytics the following conversion premiss formation rules.
This rule could be generalized for any one-premiss argument.
The following are one-premiss argument formation rules implicit in Aristotle’s treatment of conversion.
A one-premiss conversion argument consists in one and only one categorical sentence in the role of premiss and one and only one categorical sentence in the role of conclusion.
The logical constant in the conclusion sentence is the same as the logical constant in the premiss sentence.59
The non-logical constant in the predicate position in the conclusion sentence is the same as the non-logical constant in the subject position in the premiss sentence, and the non-logical constant in the subject position in the conclusion sentence is the same as the non-logical constant in the predicate position in the premiss sentence.
We can now turn to the three conversion rules Aristotle established in Prior Analytics A2.
CR1–CR3 below are Aristotle’s statements of the three deduction rules involving conversion. Our formulations of his statements using a modern notation exactly reproduce Aristotle’s meaning, both in his manner of expression in Prior Analytics and in his using them there. In the boxes below, the texts of Aristotle’s models appear on the left, our modern representation of the panvalid argument patterns on the right.60 We treat Aristotle’s logical methodology for establishing the conversion rules below (§3.1).
| “First, then, let premiss AB be universally privative” (25a14): | e simple conversion |
| “Now, if A belongs to none of the Bs, then neither will B belong to any of the As.” (25a15–16) | 1. AeB ∴ BeA |
This can be expressed syntactically as: whenever AeB is taken then BeA can be taken. Thus, a sentence fitting the pattern BeA logically follows from a given sentence fitting the pattern AeB. Aristotle treats the e conversion first.
| On the universal attributive: | a conversion per accidens |
| “And if A belongs to every B, then B will [necessarily] belong to some A” (25a17–18) | 1. AaB ∴ BiA |
This can be expressed syntactically as: whenever AaB is taken then BiA can be taken. Thus, a sentence fitting the pattern BiA logically follows from a given sentence fitting the pattern AaB.
| On the partial attributive: | i simple conversion |
| “And similarly if the premiss is partial: if A belongs to some of the Bs, then necessarily B belongs to some of the As” (25a20–21) | 1. AiB ∴ BiA |
This can be expressed syntactically as: whenever AiB is taken then BiA can be taken. Thus, a sentence fitting the pattern BiA logically follows from a given sentence fitting the pattern AiB. Aristotle remarks that the partial privative sentence does not convert: “…but the privative premiss need not [convert]” (25a12–13).
We might wish that Aristotle had stated each rule more rigorously. Nevertheless, it is evident that he construes these conversions to be rules and that he treats them syntactically. And, although he is quick to provide an example to help illustrate his thinking in each case,61 his doing so no more subverts his syntactic analysis and configuration than does providing a counterargument subvert this for a modern logician. Moreover, as we show below in relation to the syllogisms (§3.2), it is evident from his discourse in A2 that Aristotle thinks of these transformations as metalogical patterns of arguments whose premiss-sets are single sentences.
The two-premiss syllogism rules
Aristotle noted that two premisses with three different terms is the fewest number by which someone could deduce a sentence that is neither (1) a repetition nor (2) a conversion. Accordingly, to fulfill his principal concern in Prior Analytics, he demonstrated which of these elementary two-premiss argument patterns have only valid argument instances and which elementary patterns have only invalid argument instances. The results of his study, particularly in Prior Analytics A4–7, serve as elements, or principles — in particular, as deduction rules — in his deduction system. Aristotle thought of syllogistic reasoning as progressively linking the conclusions of two premiss arguments — to wit, the syllogisms — until a final conclusion (theorem) is reached. Here again we extract his syntactic two-premiss deduction rules before taking up his logical methodology (§3.2).
In order systematically to extract all possible panvalid patterns of two-premiss categorical arguments, Aristotle considered in Prior Analytics A4–6 every possible arrangement of any two of the four kinds of categorical sentence with three different terms. Working with a notion of ‘form’ of argument that is genuinely syntactic, he systematically treated patterns of two protaseis (sentences), or premiss-pair patterns, and their corresponding argument patterns, and he treated neither premisses nor arguments per se. To do this he treated each premiss-pair pattern metalogically; that is, he treated at one time, say, all such patterns of two universal attributive sentences in a given figure, by treating the one premiss-pair pattern that they all fit in that figure. Aristotle modeled an object language syllogism as an elementary two-premiss argument pattern — where two given sentences are in the role of premises and one sentence is in the role of conclusion. In this way, without considering object language arguments but only their patterns, he determined which argument patterns are panvalid and which are not panvalid. Thus, any argument fitting a panvalid pattern is valid; its validity might be recognized by virtue of its fitting such a pattern. Aristotle determined that 14 such premise-pair patterns are concludent and thus that at least one corresponding argument pattern is panvalid and can thereby serve as a deduction rule. Aristotle first states each of the syllogism rules in a sentence, as we would expect a rule to be expressed. He then treats each of the argument patterns schematically, that is, he models each as a two-premiss argument pattern to determine its panvalidity. Arguments are introduced (1) to establish that certain premise-pair patterns are inconcludent and (2) to serve as instances of panvalid argument patterns or of paninvalid argument patterns.
We take Aristotle at his word when he states, on numerous occasions in both Prior Analytics and Posterior Analytics, that “every demonstration [ ] and every deduction [
] and every deduction [ ] will be through only three terms … it will also be from two premisses [or intervals] and no more, for three terms are two premises” (Pr. An. A25: 42a30–33; cf. Pr. An. A25: 41b36–37 and Po. An. A19: 81b10 & A25: 86b7–8 among many other passages). From this statement and his practice throughout, we can extract his rules for syllogistic62 premise-pair formation as follows.
] will be through only three terms … it will also be from two premisses [or intervals] and no more, for three terms are two premises” (Pr. An. A25: 42a30–33; cf. Pr. An. A25: 41b36–37 and Po. An. A19: 81b10 & A25: 86b7–8 among many other passages). From this statement and his practice throughout, we can extract his rules for syllogistic62 premise-pair formation as follows.
Aristotle provides additional text in Prior Analytics A23 that confirms our taking him to have such a rigid rule. We shall refer to this text again when we treat Aristotle’s notion of deducibility (§5.1).
Now, if someone should have to deduce A of B, either as belonging or as not belonging, then it is necessary for him to take something about something. If, then, A should be taken about B, then the initial thing will have been taken. But if A should be taken about C, and C about nothing nor anything else about it, nor some other thing about A, then there will be no syllogism, for nothing results of necessity through a single thing having been taken about one other. Consequently, another premiss must be taken in addition. If, then, A is taken about something else, or something else about it or about C, then nothing prevents there being a syllogism, but it will not be in relation to B through the premisses taken. Nor when C is taken to belong to something else, that to another thing, and this to something else, but it is not connected to B: there will not be a syllogism in relation to B in this way either. (40b30–41a2)
Aristotle makes it abundantly clear that taking three terms in two sentences is possible in only three ways. He established this implicitly in Prior Analytics A4–6, but he makes this explicitly part of his argumentation in A23 where he effectively treats deducibility and the completeness of his logic. He writes there that “every demonstration and every deduction must necessarily come about through the three figures” (41b1–3; cf. 40b19–22 & A28: 44b6–8, 19–20). His fuller statement at A23 follows:
For, in general, we said that there cannot ever be any syllogism of one thing about another without some middle term having been taken which is related in some way to each according to the kinds of predications. For a syllogism, without qualification, is from premises; a syllogism in relation to this term is from premisses in relation to this term; and a syllogism of this term in relation to that is through premisses of this term in relation to that. And it is impossible to take a premiss in relation to B without either predicating or rejecting anything of it, or again to get a syllogism of A in relation to B without taking any common term, but <only> predicating or rejecting certain things separately of each of them. As a result, something must be taken as a middle term for both which will connect the predications, since the syllogism will be of the term in relation to that. If, then, it is necessary to take some common term in relation to both, and if this is possible in three ways (for it is possible to do so by predicating A of C and C of B, or by predicating C of both A and B, or by predicating both A and B of C), and these ways are the figures stated, then it is evident that every syllogism must come about through some one of these figures. (41a2–18)
Thus, we can extract three additional syllogistic premiss formation rules.
The two categorical sentences in a syllogistic premiss-set consist in three different non-logical constants (terms).
Aristotle nowhere states SPFR4 in rule fashion, but it is evident from his treatment of the premise-pair patterns throughout Prior Analytics A4–6 that he consciously works with such a rule of premiss formation.
The salient feature of his exposition in this connection is the crucial role he attributes to the middle term. He makes this quite emphatic in Prior Analytics A28:
It is also clear that one must take things which are the same, not things which are different or contrary, as the terms selected for the investigation. This is because, in the first place, the examination is for the sake of the middle term, and one must take as middle something the same, not something different. (44b38–45a1; cf. A29: 45b36–46a2)
Again, there is a rule of the middle term for taking pairs of sentences as premisses to form syllogistic arguments: “there cannot ever be any syllogism of one thing about another without some middle term having been taken which is related in some way to each according to the kinds of predications” (A23: 41a2–4). This, of course, is a theme highly resonant in Posterior Analytics A & B, and this might best be captured as follows from Posterior Analytics B4: “A deduction proves something of something through the middle term [ ]” (91a14–15). Aristotle recognized three possible positions for the term shared by each of the categorical sentences in a syllogistic premise-set. He called this the middle term, and he named three figures, “first”, “second”, and “third”. Accordingly, he had three rules for constructing a syllogistic premise-set for each of the three figures (
]” (91a14–15). Aristotle recognized three possible positions for the term shared by each of the categorical sentences in a syllogistic premise-set. He called this the middle term, and he named three figures, “first”, “second”, and “third”. Accordingly, he had three rules for constructing a syllogistic premise-set for each of the three figures (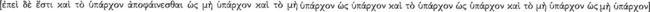 singular
singular  ). While he names the first figure at the end of Prior Analytics A4 (26b33) Aristotle defines it at the beginning. And thus we have his rule for forming a first figure syllogistic premise-set.
). While he names the first figure at the end of Prior Analytics A4 (26b33) Aristotle defines it at the beginning. And thus we have his rule for forming a first figure syllogistic premise-set.
Aristotle’s rule for forming a second figure syllogistic premiss-set is the following:
When the same thing belongs to all of one term and to none of the other, or to all of each or none of each, I call such a figure the second. In it, I call that term the middle which is predicated of both and call those of which this is predicated extremes; the major extreme is the one lying next to the middle, while the minor extreme is the one farther from the middle. The middle is placed outside the extremes and is first in position. (26b34–39)
Aristotle’s rule for forming a third figure syllogistic premiss-set is the following:
If one term belongs to all and another to none of the same thing, or if they both belong to all or none of it, I call such a figure the third. By the middle in it I mean that term of which they are both predicated, and by extremes the things predicated; by major extreme I mean the one farther from the middle and by minor the one closer. The middle is placed outside the extremes and is last in position. (28a10–15)
Thus, there are only three syntactic arrangements of middle (or common) terms, called the three figures: “[1] by predicating A of C and C of B, or [2] by predicating C of both A and B, or [3] by predicating both A and B of C” (41a15–16). In the context of his logical investigations in Prior Analytics A4–6, we can state a rule implicit in his treatment of the syllogisms.
Thus far we have represented Aristotle’s rules for forming premise-sets of syllogistic arguments. He also has syntax rules for forming syllogistic premise-conclusion (P-c) arguments, that is, in particular, rules concerning the relationships of terms (1) to each other in the conclusion of a syllogistic argument in relation to (2) those in the premise-set in connection with each figure. His rules involve taking sentences to form P-c arguments consisting of a set of two sentences — call them protaseis (premises) — and a single sentence — call this the  (sumperasma), or conclusion. These rules anticipate the rules of syllogistic inference.
(sumperasma), or conclusion. These rules anticipate the rules of syllogistic inference.
A two-premiss syllogistic argument consists in two and only two categorical sentences in the role of premisses and one and only one categorical sentence in the role of conclusion.
Any of the four logical constants can appear in each of the three categorical sentences composing a syllogistic argument.
Each syllogistic argument consists in three and only three different non-logical constants (terms); no non-logical constant appears twice in a categorical sentence in a syllogistic argument.
Of the two different non-logical constants in the conclusion sentence, the one appears once in one of the two premiss sentences, the other once in the other premiss sentence.
In the first figure the predicate term of the conclusion is the term predicated of the middle term in the premiss-set; the subject term of the conclusion is the term in the premiss-set of which the middle term is predicated.
In the second figure the predicate term of the conclusion is the subject term of the first or major premiss; the subject term in the conclusion is the subject term of the second or minor premiss.
In each figure, the predicate term of the conclusion both is the major term and its presence identifies the major premiss of a syllogistic argument; the subject term of the conclusion both is the minor term and its presence identifies the minor premiss of a syllogistic argument. These rules compass syllogistic P-c argument formation for Aristotle in Prior Analytics. Thus, we can set out the patterns of the three figures as follows, using our abbreviations of Aristotle’s logical constants for convenience (Table 11.63
Table 11

Aristotle understood that the order of a given set of two categorical sentences taken as premisses does not affect their implying a given categorical sentence taken as a conclusion. Premiss order is not important for logical consequence. On occasion he reversed the order in which he presented the two sentence patterns in the premisses when he considered them in Prior Analytics A4–6.64 This shows that he understood this to be so. Nevertheless, in order to treat his premise-pair patterns systematically, he treated them as ordered pairs in the framework of his strict syllogistic syntax. Here the premiss order matters significantly (1) for systematically treating all possible combinations (sc. patterns) of two categorical sentences in the role of premisses and (2) for relating terms in the conclusion to those in the premises. In general, he first treated the universal sentences as premises, then combinations of universal and partial sentences, and finally combinations of partial sentences.
Now, of the 192 possible combinations of syllogistic premises, Aristotle identified 14 that result in syllogisms when terms are substituted for the placeholders.65 As he did with the one-premiss conversion rules, he did with the two-premiss syllogistic rules. He first provided a sentence stating the rule before he represented it schematically, and then he provided a metalogical proof of its panvalidity. Below we provide Aristotle’s texts in Prior Analytics that model his 14 two-premiss syllogism rules, our modern notation to the right.66
| Barbara (25b37–39) | 1. AaB |
| For if A is predicated of every B and B of every C, it is necessary for A to be predicated of every C. | 2. BaC ∴ AaC |
| Celarent (25b40–26a2) | 1. AeB 2. BaC |
| Similarly, if A is predicated of no B and B of every C, it is necessary that A will belong to no C. | ∴ AeC |
If one of the terms is universal and the other is partial in relation to the remaining term, then when the universal is put in relation to the major extreme (whether this is positive or privative) and the partial is put in relation to the minor extreme (which is positive), then there will necessarily be a complete syllogism. (26a17–20) 1ai
| Darii (26a23–25) | 1. AaB 2. BiC |
| For let A belong to every B and B to some C. …it is necessary for A to belong to some C. | ∴ AiC |
If one of the terms is universal and the other is partial in relation to the remaining term, then when the universal is put in relation to the major extreme (whether this is positive or privative) and the partial is put in relation to the minor extreme (which is positive), then there will necessarily be a complete syllogism. (26a17–20) 1ei
| Ferio (26a25–27) | 1. AeB 2. BiC |
| And if A belongs to no B and B to some C, then it is necessary for A not to belong to some C. | ∴ AoC |
| Cesare (27a5–9) | 1. MeN 2. MaX |
| For let M be predicated of no N but to every X. …so that N belongs to no X. | ∴ NeX |
| Camestres (27a9–14) | 1. MaN 2. MeX |
| Next, if M belongs to every N but to no X, then neither will N belong to any X. | ∴ NeX |
If the middle is universal only in relation to one term, then when it is universal in relation to the major extreme (whether positively or privatively) but partially with respect to the minor and oppositely to the universal … then it is necessary for the privative partial syllogism to come about. (27a26–32) 2ei
| Festino (27a32–36) | 1. MeN 2. MiX |
| For if M belongs to no N and to some X, it is necessary for N not to belong to some X. | ∴ NoX |
If the middle is universal only in relation to one term, then when it is universal in relation to the major extreme (whether positively or privatively) but partially with respect to the minor and oppositely to the universal … then it is necessary for the privative partial syllogism to come about. (27a26–32) 2ao
| Baroco (27a36–27b1) | 1. MaN 2. MoX |
| Next, if M belongs to every N but does not belong to some X, it is necessary for N not to belong to some X. | ∴ NoX |
| Darapti (27a17–26) | 1. PaS 2. RaS |
| When both P and R belong to every S, it results of necessity that P will belong to some R. | ∴ PiR |
| Felapton (28a26–30) | 1. PeS 2. RaS |
| And if R belongs to every S but P to none, then there will be a deduction that P of necessity does not belong to some R. | ∴ PoR |
| Disamis (28b7–11) | 1. PiS 2. RaS |
| For if R belongs to every S and P to some, then it is necessary for P to belong to some R. | ∴ PiR |
| Datisis (28b11–15) | 1. PaS 2. RiS |
| Next, if R belongs to some S and P to every S, then it is necessary for P to belong to some R. | ∴ PiR |
| Bocardo (28b17–20) | 1. PoS 2. RaS |
| For if R belongs to every S and P does not belong to some, then it is necessary for P not to belong to some R. | ∴ PoR |
Having now set out Aristotle’s deduction system, we turn to examine the logical, or metalogical, methodology by which he established these deduction rules.
 (17b20–21)
(17b20–21) . (17b21–22)
. (17b21–22)
 premiss necessarily converts [with respect to its terms], though not universally but in part” (25a7–9).
premiss necessarily converts [with respect to its terms], though not universally but in part” (25a7–9).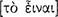 must convert partially [with respect to its terms]” (25a10–11).
must convert partially [with respect to its terms]” (25a10–11).