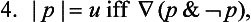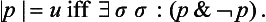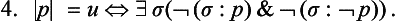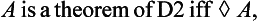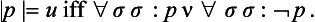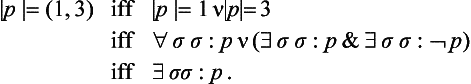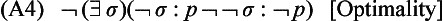Indian Logic
1 Argumentation within Dialectic and Debate: Pragmatic Criteria for Good Argumentation
1.1 Early dialogues: information-seeking, interrogation and cross-checking
The intellectual climate of ancient India was vibrant, and bristled with controversy. Debates were held on a great variety of matters, philosophical, scientific and theological. Quite soon, the debates became formal affairs, with reputations at stake and matters of importance in the balance. Already in the Brhad ra
ra yaka Upani
yaka Upani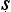 ad (c. 7th century BCE), we find the sage Y
ad (c. 7th century BCE), we find the sage Y jñavalkya being quizzed by the king’s priestly entourage on tricky theological puzzles:
jñavalkya being quizzed by the king’s priestly entourage on tricky theological puzzles:
Once when Janaka, the king of Videha, was formally seated, Y jñvalkya came up to him. Janaka asked him: ‘Y
jñvalkya came up to him. Janaka asked him: ‘Y jñvalkya, why have you come? Are you after cows, or discussion about subtle truths?’ He replied: ‘Both, your majesty.’ (BU 4.1.1).
jñvalkya, why have you come? Are you after cows, or discussion about subtle truths?’ He replied: ‘Both, your majesty.’ (BU 4.1.1).
What followed was a question-answer type dialogue in which Janaka interrogated the sage, not only to solicit information but to test Y jñavalkya’s mettle. The sage had earlier granted Janaka a wish, and the wish he chose was the freedom to ask any question at will. Y
jñavalkya’s mettle. The sage had earlier granted Janaka a wish, and the wish he chose was the freedom to ask any question at will. Y jñavalkya was not to be released from this wish until he had fully satisfied Janaka’s probing inquiry:
jñavalkya was not to be released from this wish until he had fully satisfied Janaka’s probing inquiry:
[Janaka] ‘Here, sire, I’ll give you a thousand cows! But you’ll have to tell me more than that to get yourself released!’ At this point Y jñvalkya became alarmed, thinking: ‘The king is really sharp! He has flushed me out of every cover.’ (BU 4.3.33–4).
jñvalkya became alarmed, thinking: ‘The king is really sharp! He has flushed me out of every cover.’ (BU 4.3.33–4).
It is in fact a characteristic of the earliest recorded debates that they take the form of question-answer dialogues. As a form of debate, the goal of a question-answer dialogue is not restricted merely to one party soliciting information from another, for there are, as this dialogue shows, elements too of testing out one’s opponent and cross-checking what he says. A particularly important early question-answer dialogue is the Milinda-pañha, or Questions of King Milinda. It records the encounter between a Buddhist monk N gasena and Milinda, also known as Menander, an Indo-Bactrian king who ruled in the part of India that had fallen under Greek influence at the time of Alexander’s Indian campaign. The document dates from around the first century CE, although Milinda’s reign was 155–130 BCE. At the outset, N
gasena and Milinda, also known as Menander, an Indo-Bactrian king who ruled in the part of India that had fallen under Greek influence at the time of Alexander’s Indian campaign. The document dates from around the first century CE, although Milinda’s reign was 155–130 BCE. At the outset, N gasena insists that their dialogue is conducted as scholarly debate and not merely by royal declaration1 —
gasena insists that their dialogue is conducted as scholarly debate and not merely by royal declaration1 —
King Milinda said: Reverend Sir, will you discuss with me again?
N gasena: If your Majesty will discuss (v
gasena: If your Majesty will discuss (v da) as a scholar, well, but if you will discuss as a king, no.
da) as a scholar, well, but if you will discuss as a king, no.
Milinda: How is it then that scholars discuss?
N gasena: When scholars talk a matter over one with another, then is there a winding up, an unravelling, one or other is convicted of error, and he then acknowledges his mistake; distinctions are drawn, and contra-distinctions; and yet thereby they are not angered. Thus do scholars, O King, discuss.
gasena: When scholars talk a matter over one with another, then is there a winding up, an unravelling, one or other is convicted of error, and he then acknowledges his mistake; distinctions are drawn, and contra-distinctions; and yet thereby they are not angered. Thus do scholars, O King, discuss.
Milinda: And how do kings discuss?
N gasena: When a king, your Magesty, discusses a matter, and he advances a point, if any one differ from him on that point, he is apt to fine him, saying “Inflict such and such a punishment upon that fellow!” Thus, your Magesty, do kings discuss.
gasena: When a king, your Magesty, discusses a matter, and he advances a point, if any one differ from him on that point, he is apt to fine him, saying “Inflict such and such a punishment upon that fellow!” Thus, your Magesty, do kings discuss.
Milinda: Very well. It is as a scholar, not as a king, that I will discuss. (MP 2.1.3).
V da, the type of dialogue N
da, the type of dialogue N gasena depicts as that of the scholar, is one in which there are two parties. Each defends a position with regard to the matter in hand; there is an ‘unravelling’ (nibbe
gasena depicts as that of the scholar, is one in which there are two parties. Each defends a position with regard to the matter in hand; there is an ‘unravelling’ (nibbe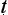 hanam; an unwinding, an explanation) and a disambiguation of the positions of both — a process of revealing commitments, presumptions and faulty argument; there is also a ‘winding up’ ending in the censure (niggaho; Skt. nigraha) of one party, a censure based on reasons he himself will acknowledge (pa
hanam; an unwinding, an explanation) and a disambiguation of the positions of both — a process of revealing commitments, presumptions and faulty argument; there is also a ‘winding up’ ending in the censure (niggaho; Skt. nigraha) of one party, a censure based on reasons he himself will acknowledge (pa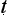 ikamman; ‘re-action’, rejoinder). This is a species of the persuasion dialogue, a ‘conversational exchange where one party is trying to persuade the other part that some particular proposition is true, using arguments that show or prove to the respondent that the thesis is true’2. Indeed, it would seem to be the species that has come to be known as the critical discussion, a persuasion dialogue in which the conflict is resolved ‘only if somebody retracts his doubt because he has been convinced by the other party’s argumentation or if he withdraws his standpoint because he has realized that his argumentation cannot stand up to the other party’s criticism’3. Not every persuasion dialogue need end in one party recognising defeat, for an important function of the general persuasion dialogue is to be maieutic, helping each side to clarify the nature of their commitments and the presuppositions upon which their positions depend.4 In the to-and-fro of such a dialogue, each party is allowed to retract earlier commitments, as it becomes clear what the consequences of such a commitment would be. This maieutic, clarificatory function of a dialogue is perhaps what N
ikamman; ‘re-action’, rejoinder). This is a species of the persuasion dialogue, a ‘conversational exchange where one party is trying to persuade the other part that some particular proposition is true, using arguments that show or prove to the respondent that the thesis is true’2. Indeed, it would seem to be the species that has come to be known as the critical discussion, a persuasion dialogue in which the conflict is resolved ‘only if somebody retracts his doubt because he has been convinced by the other party’s argumentation or if he withdraws his standpoint because he has realized that his argumentation cannot stand up to the other party’s criticism’3. Not every persuasion dialogue need end in one party recognising defeat, for an important function of the general persuasion dialogue is to be maieutic, helping each side to clarify the nature of their commitments and the presuppositions upon which their positions depend.4 In the to-and-fro of such a dialogue, each party is allowed to retract earlier commitments, as it becomes clear what the consequences of such a commitment would be. This maieutic, clarificatory function of a dialogue is perhaps what N gasena intends when he speaks of an ‘unravelling’, and it seems clearer still in his characterisation of ‘investigation’ (vik
gasena intends when he speaks of an ‘unravelling’, and it seems clearer still in his characterisation of ‘investigation’ (vik ra) as a ‘threshing-out’:
ra) as a ‘threshing-out’:
Milinda: What is the distinguishing characteristic, N gasena, of reflection (vitakka)?
gasena, of reflection (vitakka)?
N gasena: The effecting of an aim.
gasena: The effecting of an aim.
Milinda: Give me an illustration.
N gasena: It is like the case of a carpenter, great king, who fixes in a joint a well-fashioned piece of wood. Thus it is that the effecting of an aim is the mark of reflection.
gasena: It is like the case of a carpenter, great king, who fixes in a joint a well-fashioned piece of wood. Thus it is that the effecting of an aim is the mark of reflection.
Milinda: What is the distinguishing characteristic, N gasena, of investigation (vik
gasena, of investigation (vik ra)?
ra)?
N gasena: Threshing out again and again.
gasena: Threshing out again and again.
Milinda: Give me an illustration.
N gasena: It is like the case of the copper vessel, which, when it is beaten into shape, makes a sound again and again as it gradually gathers shape. The beating into shape is to be regarded as reflection and the sounding again and again as investigation. Thus it is, great king, that threshing out again and again is the mark of investigation.
gasena: It is like the case of the copper vessel, which, when it is beaten into shape, makes a sound again and again as it gradually gathers shape. The beating into shape is to be regarded as reflection and the sounding again and again as investigation. Thus it is, great king, that threshing out again and again is the mark of investigation.
So it is through reflection and argumentation that the parties to an investigation together thrash out a position. N gasena tells us very little about the sort of argumentation that is appropriate, and we can learn little more about argument within persuasion dialogues from the Questions of King Milinda (although Milinda’s repeated request to be given an illustration is suggestive of the importance that would later be attached to the citation of illustrative examples in good argumentation; see §1.3 below). And yet there is still something to learn. For the dialogue of the Questions of King Milinda is not, contrary to N
gasena tells us very little about the sort of argumentation that is appropriate, and we can learn little more about argument within persuasion dialogues from the Questions of King Milinda (although Milinda’s repeated request to be given an illustration is suggestive of the importance that would later be attached to the citation of illustrative examples in good argumentation; see §1.3 below). And yet there is still something to learn. For the dialogue of the Questions of King Milinda is not, contrary to N gasena’s initial statement, a straighforwardly scholarly debate, but proceeds instead with his being interrogated at the hands of Milinda. Ostensibly Milinda wishes to be informed as to the answer to a range of thorny ethical and metaphysical questions, but his questioning is not so innocent, and at times he seems intent on entrapping N
gasena’s initial statement, a straighforwardly scholarly debate, but proceeds instead with his being interrogated at the hands of Milinda. Ostensibly Milinda wishes to be informed as to the answer to a range of thorny ethical and metaphysical questions, but his questioning is not so innocent, and at times he seems intent on entrapping N gasena in false dichotomies and leading questions. So it is said of him:
gasena in false dichotomies and leading questions. So it is said of him:
Master of words and sophistry ( ī), clever and wise
ī), clever and wise
Milinda tried to test great N gasena’s skill.
gasena’s skill.
Leaving him not, again and yet again,
Milinda here is significantly described as a ‘master of sophistry’ or ī, a practitioner of the dialogue form known as vi
ī, a practitioner of the dialogue form known as vi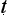 a
a
 , a ‘refutation-only’ type of dialogue in which the opponent defends no thesis of his own but is set only on refuting that of the proponent (see §1.4). The implication here is that such dialogues are essentially eristic. And it is, in particular, the eristic use of questioning that Milinda is a master of. Questions need not be innocent requests for information; they can also be disguised arguments. To reply to the question ‘When did you stop cheating on your tax returns?’ at all, affirmatively or negatively, is already to commit oneself to the ‘premise’ of the question, that one has indeed been cheating on one’s tax returns. In the intellectual climate of ancient India, when interrogative dialogue was common-place, it was very well known that questions can be used to entrap the unwitting, and counter-strategies were invented to avoid entrapment. The Buddha himself was well aware that replying to a yes-no question can commit one to a proposition, whatever answer one gives, and his solution, famously, was to refuse to answer. Thus when asked a series of ten leading questions — is the soul is eternal? is it non-eternal? etc. — the Buddha declined to offer a reply. For any reply would commit him, against his wish, to the existence of souls. In the Questions of King Milinda, we see N
, a ‘refutation-only’ type of dialogue in which the opponent defends no thesis of his own but is set only on refuting that of the proponent (see §1.4). The implication here is that such dialogues are essentially eristic. And it is, in particular, the eristic use of questioning that Milinda is a master of. Questions need not be innocent requests for information; they can also be disguised arguments. To reply to the question ‘When did you stop cheating on your tax returns?’ at all, affirmatively or negatively, is already to commit oneself to the ‘premise’ of the question, that one has indeed been cheating on one’s tax returns. In the intellectual climate of ancient India, when interrogative dialogue was common-place, it was very well known that questions can be used to entrap the unwitting, and counter-strategies were invented to avoid entrapment. The Buddha himself was well aware that replying to a yes-no question can commit one to a proposition, whatever answer one gives, and his solution, famously, was to refuse to answer. Thus when asked a series of ten leading questions — is the soul is eternal? is it non-eternal? etc. — the Buddha declined to offer a reply. For any reply would commit him, against his wish, to the existence of souls. In the Questions of King Milinda, we see N gasena experimenting with a different technique to avoid entrapment. To some of Milinda’s more devious yes-no questions, instead of refusing to reply at all, N
gasena experimenting with a different technique to avoid entrapment. To some of Milinda’s more devious yes-no questions, instead of refusing to reply at all, N gasena replies ‘Both yes and no’! To others he replies ‘Neither yes nor no’! For example:
gasena replies ‘Both yes and no’! To others he replies ‘Neither yes nor no’! For example:
Milinda: He who is born, N gasena, does he remain the same or become another?
gasena, does he remain the same or become another?
N gasena: Neither the same nor another.
gasena: Neither the same nor another.
Milinda: Give me an illustration.
N gasena: Now what do you think, O king? You were once a baby, a tender thing, and small in size, lying flat on your back. Was that the same as you who are now grown up?
gasena: Now what do you think, O king? You were once a baby, a tender thing, and small in size, lying flat on your back. Was that the same as you who are now grown up?
Milinda: No. That child was one, I am another.
N gasena: If you are not that child, it will follow that you have had neither mother nor father, no! nor teacher. You cannot have been taught either learning, or behaviour, or wisdom. … Suppose a man, O king, were to light a lamp, would it burn the night through?
gasena: If you are not that child, it will follow that you have had neither mother nor father, no! nor teacher. You cannot have been taught either learning, or behaviour, or wisdom. … Suppose a man, O king, were to light a lamp, would it burn the night through?
N gasena: Now, is it the same flame that burns in the first watch of the night, Sir, and in the second?
gasena: Now, is it the same flame that burns in the first watch of the night, Sir, and in the second?
N gasena: Or the same that burns in the second watch and the third?
gasena: Or the same that burns in the second watch and the third?
N gasena: Then there is one lamp in the first watch, and another in the second, and another in the third?
gasena: Then there is one lamp in the first watch, and another in the second, and another in the third?
Milinda: No. The light comes from the same lamp all the night through.
N gasena: Just so, O king, is the continuity of a person or thing maintained. One comes into being, another passes away; and the rebirth is, as it were, simultaneous. Thus neither as the same nor as another does a man go on to the last phase of his self-consciousness. (MP 2.2.1)
gasena: Just so, O king, is the continuity of a person or thing maintained. One comes into being, another passes away; and the rebirth is, as it were, simultaneous. Thus neither as the same nor as another does a man go on to the last phase of his self-consciousness. (MP 2.2.1)
The ‘premise’ of the question, that to change is to cease to be, is very effectively refuted with a ‘neither yes nor no’ reply. N gasena first makes Milinda acknowledge that, with this as the background premise, answering either ‘yes’ or ‘no’ leads to an absurdity. For if he is strictly identical to the child, then he must share that child’s properties; and if he is different, then he cannot. Having exposed the false premise, N
gasena first makes Milinda acknowledge that, with this as the background premise, answering either ‘yes’ or ‘no’ leads to an absurdity. For if he is strictly identical to the child, then he must share that child’s properties; and if he is different, then he cannot. Having exposed the false premise, N gasena, rejects it in favour of the view that persistence through time requires not strict identity but causal continuity. Here is a different kind of example:
gasena, rejects it in favour of the view that persistence through time requires not strict identity but causal continuity. Here is a different kind of example:
Milinda: Does memory, N gasena, always arise subjectively, or is it stirred up by suggestion from outside?
gasena, always arise subjectively, or is it stirred up by suggestion from outside?
N gasena: Both the one and the other.
gasena: Both the one and the other.
Milinda: But does not that amount to all memory being subjective in origin, and never artificial?
N gasena: If, O king, there were no artificial (imparted) memory, then artisans would have no need of practice, or art, or schooling, and teachers would be useless. But the contrary is the case.
gasena: If, O king, there were no artificial (imparted) memory, then artisans would have no need of practice, or art, or schooling, and teachers would be useless. But the contrary is the case.
Here the question’s hidden premise is that memories are caused either wholly by what goes on in the mind or wholly by factors external to it, and the ‘both yes and no’ reply makes plain that what ought to be said is that memories are wholly caused either by what goes on in the mind or by factors external to it, but not caused wholly by one or the other. Again, subsidiary argumentation exposes the absurdity in replying with an unqualified ‘yes’ or an unqualified ‘no’. It was perhaps in recognition of the tactical importance of such ‘neither yes nor no’ and ‘both yest and no’ replies that it became a common-place that there are four possible ways of responding to any question of the yes-no type, an idea that was systematised in the work of N g
g rjuna (§1.4). What we see very clearly in the Questions of King Milinda is a sophisticated early appreciation of the pragmatics of interogative dialogues.
rjuna (§1.4). What we see very clearly in the Questions of King Milinda is a sophisticated early appreciation of the pragmatics of interogative dialogues.
1.2 On balance and fairness in the conduct of dialogue: The Kath vatthu
vatthu
The Kath vatthu or Points of Controversy (circa third century BCE) is a book about method. It describes, for the benefit of adherents to various Buddhist schisms, the proper method to be followed in conducting a critical discussion into an issue of doctrinal conflict. Recent scholarship has largely focussed on the question of the extent to which there is, in the Kath
vatthu or Points of Controversy (circa third century BCE) is a book about method. It describes, for the benefit of adherents to various Buddhist schisms, the proper method to be followed in conducting a critical discussion into an issue of doctrinal conflict. Recent scholarship has largely focussed on the question of the extent to which there is, in the Kath vatthu, an ‘anticipation’ of results in propositional logic.5 For, while it is true that the formulation of arguments there is term logic rather than propositional, and true also that the propositional rules are nowhere formulated in the abstract, the codified argumentation clearly exploits manipulations that trade on the definition of material implication, on contraposition, and on at least one of modus tollens, modus ponens and reductio ad absurdum. The preoccupation with this question of anticipation, assumes, however, a methodology for the interpretation of Indian logic that suffers a number of serious disadvantages. For, first, in presupposing that the only matter of interest is the extent to which a given text displays recognition of principles of formal logic, the methodology fails to ask what it was that the authors themselves were trying to do, and in consequence, is closed to the possibility that these texts contribute to logical studies of a different kind. And second, in supposing that arguments have to be evaluated formally, the important idea that there are informal criteria for argument evaluation is neglected. In fact, the Kath
vatthu, an ‘anticipation’ of results in propositional logic.5 For, while it is true that the formulation of arguments there is term logic rather than propositional, and true also that the propositional rules are nowhere formulated in the abstract, the codified argumentation clearly exploits manipulations that trade on the definition of material implication, on contraposition, and on at least one of modus tollens, modus ponens and reductio ad absurdum. The preoccupation with this question of anticipation, assumes, however, a methodology for the interpretation of Indian logic that suffers a number of serious disadvantages. For, first, in presupposing that the only matter of interest is the extent to which a given text displays recognition of principles of formal logic, the methodology fails to ask what it was that the authors themselves were trying to do, and in consequence, is closed to the possibility that these texts contribute to logical studies of a different kind. And second, in supposing that arguments have to be evaluated formally, the important idea that there are informal criteria for argument evaluation is neglected. In fact, the Kath vatthu offers a particularly clear example of a text whose richness and interest lies elsewhere than in its anticipation of deductive principles and propositional laws. As a meticulous analysis of the argumentation properly to be used in the course of a dialogue of a specific type, its concern is with the pragmatic account of argument evaluation, the idea that arguments have to be evaluated as good or bad with regard to their contribution towards the goals of the dialogue within which they are embedded. The leading concern of the Kath
vatthu offers a particularly clear example of a text whose richness and interest lies elsewhere than in its anticipation of deductive principles and propositional laws. As a meticulous analysis of the argumentation properly to be used in the course of a dialogue of a specific type, its concern is with the pragmatic account of argument evaluation, the idea that arguments have to be evaluated as good or bad with regard to their contribution towards the goals of the dialogue within which they are embedded. The leading concern of the Kath vatthu is with issues of balance and fairness in the conduct of a dialogue, and it recommends a strategy of argumentation which guarrantees that both parties to a point of controversy have their arguments properly weighed and considered. It is important, in the normative framework of the Kath
vatthu is with issues of balance and fairness in the conduct of a dialogue, and it recommends a strategy of argumentation which guarrantees that both parties to a point of controversy have their arguments properly weighed and considered. It is important, in the normative framework of the Kath vatthu, that there is a distinction between the global aim of the dialogue as a whole — here to rehearse in an even-handed manner all the considerations that bear upon an issue of dispute, to clarify what is at stake even if no final resolution is achieved — and the local aim of each participant — to advocate the stance they adopt with regard to that issue by supplying arguments for it and attacking the arguments of the other parties.
vatthu, that there is a distinction between the global aim of the dialogue as a whole — here to rehearse in an even-handed manner all the considerations that bear upon an issue of dispute, to clarify what is at stake even if no final resolution is achieved — and the local aim of each participant — to advocate the stance they adopt with regard to that issue by supplying arguments for it and attacking the arguments of the other parties.
A dialogue conducted in accordance with the prescribed method of the Kath vatthu is called a v
vatthu is called a v dayutti. The goal of a v
dayutti. The goal of a v dayutti is the reasoned examination (yutti; Skt. yukti) of a controversial point in and through a noneristic dialogue (v
dayutti is the reasoned examination (yutti; Skt. yukti) of a controversial point in and through a noneristic dialogue (v da). The dialogue is highly structured, and is to be conducted in accordance with a prescribed format of argumentation. There is a given point at issue, for example, whether ‘a person is known in the sense of a real and ultimate fact’ (i.e. whether persons are conceived of as metaphysically irreducible), whether there are such things as morally good and bad actions, and so, in general, whether A is B. A dialogue is now divided into eight sub-dialogies or ‘openings’ (a
da). The dialogue is highly structured, and is to be conducted in accordance with a prescribed format of argumentation. There is a given point at issue, for example, whether ‘a person is known in the sense of a real and ultimate fact’ (i.e. whether persons are conceived of as metaphysically irreducible), whether there are such things as morally good and bad actions, and so, in general, whether A is B. A dialogue is now divided into eight sub-dialogies or ‘openings’ (a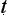
 hamukha). These correspond to eight attitudes it is possible to adopt with regard to the point at issue. So we have:
hamukha). These correspond to eight attitudes it is possible to adopt with regard to the point at issue. So we have:
The introduction of an explicit quantification over times, places and objects serves to determine an attitude of proponent and respondent to the point of controversy. If the issue in question is, for example, whether lying is immoral, the clarification would be as to whether that proposition is to be maintained or denied, and in either case, whether absolutely, or only as relativised in some way to circumstances, times or agents. So an opening thesis here is by definition a point at issue together with an attitude towards it.
Each such ‘opening’ now proceeds as an independent dialogue, and each is divided into five stages: the way forward (anuloma), the way back (pa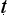 ikamma), the refutation (niggaha), the application (upanayana), and the conclusion (niggamana). In the way forward, the proponent solicits from the respondent their endorsement of a thesis, and then tries to argue against it. In the way back, the respondent turns the tables, soliciting from the proponent their endorsement of the counter-thesis, and then trying argue against it. In the refutation, the respondent, continuing, seeks to refutes the argument that the proponent had advanced against the thesis. The application and conclusion repeat and reaffirm that the proponent’s argument against the respondent’s thesis is unsound, while the respondent’s argument against the proponent’s counter-thesis is sound.
ikamma), the refutation (niggaha), the application (upanayana), and the conclusion (niggamana). In the way forward, the proponent solicits from the respondent their endorsement of a thesis, and then tries to argue against it. In the way back, the respondent turns the tables, soliciting from the proponent their endorsement of the counter-thesis, and then trying argue against it. In the refutation, the respondent, continuing, seeks to refutes the argument that the proponent had advanced against the thesis. The application and conclusion repeat and reaffirm that the proponent’s argument against the respondent’s thesis is unsound, while the respondent’s argument against the proponent’s counter-thesis is sound.
It is significant to note that there is here no pro-argumentation, either by the respondent for the thesis or by the proponent for the counter-thesis. There is only contra-argumentation, and that in two varieties. The respondent, in the ‘way back’, supplies an argument against the proponent’s counter-thesis, and in the refutation stage, against the proponent’s alleged argument against the thesis. So we see here a sharp distinction between three types of argumentation — pro argumention, argumentation that adduces reasons in support of one’s thesis, counter argumenation — argumentation that adduces reasons against the counter-thesis, and defensive argumentation, argumentation that defends against counter-arguments directed against one’s thesis. The respondent, having been ‘attacked’ in the first phase, ‘counter-attacks’ in the second phase, ‘defends’ against the initial attack in the third, and ‘consolidates’ the counter-attack and the defence in the fourth and fifth. The whole pattern of argumentation, it would seem, is best thought of as presumptive, that is, as an attempt to switch a burden of proof that is initially even distributed between the two parties. The respondent tries to put the burden of proof firmly onto the proponent, by arguing against the proponent while countering any argument against herself. The fact that the respondent does not offer any pro argumentation in direct support of the thesis means that the whole pattern of argumentation is technically ab ignorantium; that is, argumentation of the form “I am right because not proved wrong”. But ab ignorantium reasoning is not always fallacious; indeed, it is often of critical importance in swinging the argument in one’s favour in the course of a dialogue (see §1.5).
In the first stage, the way forward, the proponent elicits from the respondent an endorsement of a thesis, and then sets out to reason against it. Not any form of reasoning is allowed; indeed the Kath vatthu prescribes a very specific method of counter-argumentation. Thus:
vatthu prescribes a very specific method of counter-argumentation. Thus:
I The Way Forward
Therav din: Is the soul (puggala) known as a real and ultimate fact?
din: Is the soul (puggala) known as a real and ultimate fact?
Therav din: Is the soul known in the same way as a real and ultimate fact is known?
din: Is the soul known in the same way as a real and ultimate fact is known?
[2] Puggalav din: No, that cannot be truly said.
din: No, that cannot be truly said.
Therav din: Acknowledge your refutation (niggaha):
din: Acknowledge your refutation (niggaha):
[3] If the soul be known as a real and ultimate fact, then indeed, good sir, you should also say, the soul is known in the same way as any other real and ultimate is known.
[4] That which you say here is false, namely, that we should say, “the soul is known as a real and ultimate fact”, but we should not say, “the soul is known in the same way as any other real and ultimate fact is known.”
[5] If the later statement cannot be admitted, then indeed the former statement should not be admitted either.
[6] In affirming the former, while denying the latter, you are wrong.
The respondent, here a puggalav din or believer in the existence of personal souls, is asked to endorse the thesis. The proponent then attempts to draw out an implication of that thesis, an implication more over to which the puggalav
din or believer in the existence of personal souls, is asked to endorse the thesis. The proponent then attempts to draw out an implication of that thesis, an implication more over to which the puggalav din will not be willing to give his consent. Here the thesis that persons are thought of as metaphysically irreducible elements of the world is held to imply that knowledge of persons is knowledge of the same kind as that of other types of thing. The puggalav
din will not be willing to give his consent. Here the thesis that persons are thought of as metaphysically irreducible elements of the world is held to imply that knowledge of persons is knowledge of the same kind as that of other types of thing. The puggalav din, will perhaps want to draw an epistemological distinction between empirical knowledge of external objects and self-knowledge, and so will not endorse this derived proposition. And now the proponent, in a fresh wave of argumentation, demonstrates that it is inconsistent for the puggalav
din, will perhaps want to draw an epistemological distinction between empirical knowledge of external objects and self-knowledge, and so will not endorse this derived proposition. And now the proponent, in a fresh wave of argumentation, demonstrates that it is inconsistent for the puggalav din to endorse the thesis but not the derived consequence. So a counter-argument has three components: the initial thesis or thapan
din to endorse the thesis but not the derived consequence. So a counter-argument has three components: the initial thesis or thapan (Skt. sth
(Skt. sth pan
pan ), the derived implication or p
), the derived implication or p pan
pan , and the demonstration of inconsistency or ropan
, and the demonstration of inconsistency or ropan .
.
It is in the ropan that there seems to be an ‘anticipation’ of propositional logic. Of the four steps of the ropan
that there seems to be an ‘anticipation’ of propositional logic. Of the four steps of the ropan , the first, from [3] to [4], looks like an application of the definition of material implication or its term-logical equivalent:
, the first, from [3] to [4], looks like an application of the definition of material implication or its term-logical equivalent:
Notice here that an effect of soliciting from the respondent a ‘no’ in answer to the proponent’s second question is that the negation is external and not internal. Thus, we have ‘¬(C is D)’ rather than ‘(C is ¬ D)’. This what one needs in the correct definition of material implication.
The second step, from [4] to [5], looks like a derivation of the contraposed version of the conditional, a derivation that depends on the stated definition of the conditional. From that definition, and assuming that ‘&’ is commutative, it follows that
The final step now is an application of modus ponens. So what we have is:
| [1] (A is B) | premise |
| [2] ¬(C is D) | premise |
| [3] (A is B) → (C is D) | additional premise? |
| [4] ¬((A is B)&¬(C is D)) | 3, defn. of → |
| [5] ¬(C is D) → ¬(A is B) | 4, defn. of → |
| [6] ¬(A is B) | 2, 5, MP |
This is how Matilal6 reconstructs the ropan stage of argumentation. Earlier, Bochenski7 recommended a variant in which steps [3] and [4] “together constitute a kind of law of contraposition or rather a modus tollendo tollens in a term-logical version”. Still another alternative is to see step [3] as a piece of enthymematic reasoning from the premise already given, rather than as the introduction of an additional premise. In other words, the ‘if…then’ in [3] is to be understood to signify the logical consequence relation rather than material implication. Then step [4] negates the premise in an application of reductio ad absurdum. That is:
stage of argumentation. Earlier, Bochenski7 recommended a variant in which steps [3] and [4] “together constitute a kind of law of contraposition or rather a modus tollendo tollens in a term-logical version”. Still another alternative is to see step [3] as a piece of enthymematic reasoning from the premise already given, rather than as the introduction of an additional premise. In other words, the ‘if…then’ in [3] is to be understood to signify the logical consequence relation rather than material implication. Then step [4] negates the premise in an application of reductio ad absurdum. That is:
| [1,2] (A is B) & ¬(C is D) | premise |
| [3] (C is D) | 1 + 2, enthymematic derivation |
| [4] ¬((A is B) & ¬(C is D)) | 1 + 2,3; RAA |
| [5] ¬(C is D) → ¬(A is B) | 4, defn. of → |
| [6] ¬((A is B) & ¬(C is D)) | 5, defn. of → |
This reconstuction seems more in keeping with the overall pattern of argumentation — to take the respondent’s thesis and derive from it consequences the respondent will not endorse, and thereby to argue against the thesis (and it preserves the repetition of the original). Here again we see that the form of argumentation in the Kath vatthu is better understood if we bear in mind the function it is intended to serve within a dialogue context.
vatthu is better understood if we bear in mind the function it is intended to serve within a dialogue context.
The same dialogue context is normative, in the sense that it gives the grounds for evaluating any actual instance of such argumentation as good or bad. It seems possible to understand the ‘way forward’ in terms of certain concepts from the theory of argumenation. Hamblin introduced the idea that each participant in a dialogue has a ‘commitment store’, a set of propositions to which they commit themselves in the course of the dialogue, primarily by asserting them directly.8 In Hamblin’s model, the commitments of each party are on public display, known to every participant in the dialogue. In order to represent the fact that this is very often not the case, Walton9 employs a distinction between open or ‘light-side’ commitments, and veiled or ‘dark-side’ commitments. The veiled commitments of a participant are not on public view, and might not be known even to that participant themselves: but perhaps the participant trades on them in making certain kinds of dialogue move. Indeed, it is part of what Walton10 calls the ‘maieutic’ role of dialogue to make explicit the veiled commitments of the participants, a process of clarification that is valuable even if it does not lead to the issue at stake being decided in favour of one party or the other.11
Something of this sort is what is being described in the initial stages of the ‘way forward’. Steps [1] and [2] elicit from the respondent an explicit and open commitment to the propositions ‘A is B’ and ‘¬ (C is D)’. ¿ From the respective assertion and denial, these become parts of her explicit commitment store. But next, though the enthymematic argumentation that constitutes the p pan
pan or stage [3], it is made clear that the respondent has a veiled commitment to the proposition ‘C is D’. For this is shown to follow from propositions in the explicit commitment store of the respondent. Finally, the ropan
or stage [3], it is made clear that the respondent has a veiled commitment to the proposition ‘C is D’. For this is shown to follow from propositions in the explicit commitment store of the respondent. Finally, the ropan stage of reasoning reveals this newly explosed commitment to be inconsistent with the respondent’s other explicit commitments. The overall effect is to force the respondent into a position where she must retract at least one of the propositions to which she has committed herself. Indeed, we can say that such a retraction is the primary goal of the way forward. The primary aim is not to disprove the thesis, but to force a retraction of commitment. So when we evaluate the argumentation used in this part of the dialogue, it is to be evaluated as good or bad with reference to how well it succeeds in forcing such a retraction, and not simply or only or even in terms of its deductive or inductive soundness. The strategic problem here is how to persuade the respondent to accept some proposition that is meant ultimately to be used to force a retraction, and the type of strategy being recommended is the one Walton calls that of “separating”, where “two or more propositions are proved separately and then eventually put together in an argument structure that is used to prove one’s own thesis or argue against an opponent’s”.12 In setting out the reasoning in this way, the intention of the author of the Kath
stage of reasoning reveals this newly explosed commitment to be inconsistent with the respondent’s other explicit commitments. The overall effect is to force the respondent into a position where she must retract at least one of the propositions to which she has committed herself. Indeed, we can say that such a retraction is the primary goal of the way forward. The primary aim is not to disprove the thesis, but to force a retraction of commitment. So when we evaluate the argumentation used in this part of the dialogue, it is to be evaluated as good or bad with reference to how well it succeeds in forcing such a retraction, and not simply or only or even in terms of its deductive or inductive soundness. The strategic problem here is how to persuade the respondent to accept some proposition that is meant ultimately to be used to force a retraction, and the type of strategy being recommended is the one Walton calls that of “separating”, where “two or more propositions are proved separately and then eventually put together in an argument structure that is used to prove one’s own thesis or argue against an opponent’s”.12 In setting out the reasoning in this way, the intention of the author of the Kath vatthu is not to imply that precisely this sequence of arguments is sound. What is being shown is the form that any counter-argument should take. It is a description, in generic terms, of the strategic resources open to the proponent, and serves rather as a blue-print for any actual v
vatthu is not to imply that precisely this sequence of arguments is sound. What is being shown is the form that any counter-argument should take. It is a description, in generic terms, of the strategic resources open to the proponent, and serves rather as a blue-print for any actual v dayutti dialogue.
dayutti dialogue.
At this point in the sub-dialogue that is the first opening, then, the burden of proof seems to lie squarely with the respondent, the puggalav din, who is being pressured into the uncomfortable position of having to retract his stated thesis. The remaining four phases of the first opening are a summary of the strategic resources open to the respondent to recover his position, and indeed to turn the tables against the proponent. First, the way back. This is a phase of counter attact, in which the respondent uses parallel reasoning to force the proponent too into a position of retraction with regard to the counter-thesis.
din, who is being pressured into the uncomfortable position of having to retract his stated thesis. The remaining four phases of the first opening are a summary of the strategic resources open to the respondent to recover his position, and indeed to turn the tables against the proponent. First, the way back. This is a phase of counter attact, in which the respondent uses parallel reasoning to force the proponent too into a position of retraction with regard to the counter-thesis.
II The Way Back
Puggalav din: Is the soul not known as a real and ultimate fact?
din: Is the soul not known as a real and ultimate fact?
[1] Therav din: No, it is not known.
din: No, it is not known.
Puggalav din: Is it not known in the same way as any real and ultimate fact is known?
din: Is it not known in the same way as any real and ultimate fact is known?
[2] Therav din: No, that cannot be truly said.
din: No, that cannot be truly said.
Puggalav din: Acknowledge the rejoinder (pa
din: Acknowledge the rejoinder (pa ikamma):
ikamma):
[3] If the soul is not known as a real and ultimate fact, then indeed, good sir, you should also say: it is not known in the same way as any other real and ultimate fact is known.
[4] That which you say is false, namely, that we should say “the soul is not known as a real and ultimate fact”, but we should not say “it is not known in the same way as any other real and ultimate fact is known”.
[5] If the latter statement cannot be admitted, then indeed the former statement should not be admitted either.
[6] In affirming the former while denying the latter, you are wrong.
At the end of the ‘way back’, if the respondent’s arguments have gone well, the proponent has been pressed in the direction of retracting his commitment to the counter-thesis. If the respondent were to leave matters here, however, he would have failed in the global aim of the ‘opening’. The aim of the opening is to shift the burden of proof decisively onto the proponent. After the second stage in the opening, however, the burden of proof is again symmetrically distributed among the parties to the dialogue — both are in a position of being pressed to retract their respective commitment. So, in the third phase, the respondent seeks, in a defensive move, to diffuse the argument of the proponent that is forcing this retraction. Again, the cited reasoning is schematic, it indicates a general strategy the details of which must be worked out differently in each specific case. The distinction being drawn is the one between counter-argument, and defensive repost, a distinction that makes sense only within the normative framework of a dialogical exchange.
The first opening in the v dayutti has rehearsed the best argumentation that available against someone whose attitude towards the point at issue is one of unqualified affirmation. Remember, however the global aim of a v
dayutti has rehearsed the best argumentation that available against someone whose attitude towards the point at issue is one of unqualified affirmation. Remember, however the global aim of a v dayutti — to be the form of dialogue most conducive to a balanced examination of the best arguments, both for and against. It is the function now of the second opening to rehearse the best argumentation against someone whose attitude towards the point at issue is one of unqualified denial, and of the subsequent openings to do likewise with respect to attitudes of qualified affirmation and denial. Even at the end of the dialogue, there may be no final resolution, but an important maieutic function has been served — the clarification of the commitments entailed by each position, of their best strategies and forms of argumentation. So, indeed, it is as a rich account of presumptive reasoning in dialogue, and not so much for its ‘anticipations’ of formal logic, that the Kath
dayutti — to be the form of dialogue most conducive to a balanced examination of the best arguments, both for and against. It is the function now of the second opening to rehearse the best argumentation against someone whose attitude towards the point at issue is one of unqualified denial, and of the subsequent openings to do likewise with respect to attitudes of qualified affirmation and denial. Even at the end of the dialogue, there may be no final resolution, but an important maieutic function has been served — the clarification of the commitments entailed by each position, of their best strategies and forms of argumentation. So, indeed, it is as a rich account of presumptive reasoning in dialogue, and not so much for its ‘anticipations’ of formal logic, that the Kath vatthu makes a rewarding object of study.
vatthu makes a rewarding object of study.
1.3 Case-based reasoning, extrapolation and inference from sampling: The Ny yasūtra
yasūtra
It was Henry Colebrooke13 who first brought Indian logic to the attention of the English philosophical world, announcing in a famous lecture to the Royal Asiatic Society in 1824 his discovery of what he called the ‘Hindu Syllogism’. Colebrooke’s ‘discovery’ consisted in fact in a translation of an ancient Indian treatise called the Ny yasūtra. It dates from around the 1st or 2nd century AD, and is said to be the work of Gautama Ak
yasūtra. It dates from around the 1st or 2nd century AD, and is said to be the work of Gautama Ak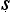 ap
ap da. Scholars are now inclined to regard it as the amalgamation of two earlier works on philosophical method, one a treatise on the rules and principles of debate, the other a discussion of more general issues in epistemology and metaphysics. In a section on the proper way for a debater to set out their argument, the Ny
da. Scholars are now inclined to regard it as the amalgamation of two earlier works on philosophical method, one a treatise on the rules and principles of debate, the other a discussion of more general issues in epistemology and metaphysics. In a section on the proper way for a debater to set out their argument, the Ny yasūtra prescribes a five-step schema for well-formed argument, and it is this schema that Colebrooke identified as the Indian syllogism. We now know much much more than Colebrooke about the historical development of Indian logic. He, for instance, was unaware of the informal logic and anticipations of propositional calculus in the Kath
yasūtra prescribes a five-step schema for well-formed argument, and it is this schema that Colebrooke identified as the Indian syllogism. We now know much much more than Colebrooke about the historical development of Indian logic. He, for instance, was unaware of the informal logic and anticipations of propositional calculus in the Kath vatthu (§1.2) or the theories of the Buddhists Vasubandhu, Di
vatthu (§1.2) or the theories of the Buddhists Vasubandhu, Di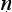 n
n ga and Dharmakīrti on formal criteria for inference (§§2.1–5). And scholars had yet to learn the complexities of the later logical school of Navya-Ny
ga and Dharmakīrti on formal criteria for inference (§§2.1–5). And scholars had yet to learn the complexities of the later logical school of Navya-Ny ya (§§4.1–3), with its intriguing treatment of negation, logical consequence and quantification, and even, as Daniel Ingalls has shown in his pioneering book entitled Materials for the Study of Navya-Ny
ya (§§4.1–3), with its intriguing treatment of negation, logical consequence and quantification, and even, as Daniel Ingalls has shown in his pioneering book entitled Materials for the Study of Navya-Ny ya Logic, the formulation of De Morgan’s Laws.14 Nevertheless, in spite of Colebrooke’s lack of acquaintance with the historical context, he and those who followed him were right to see the Ny
ya Logic, the formulation of De Morgan’s Laws.14 Nevertheless, in spite of Colebrooke’s lack of acquaintance with the historical context, he and those who followed him were right to see the Ny yasūtra as a treatise of fundamental importance in Indian logical thinking, and I would like to pick up and continue the thread of their discussion. I want to argue that the Ny
yasūtra as a treatise of fundamental importance in Indian logical thinking, and I would like to pick up and continue the thread of their discussion. I want to argue that the Ny asūtra begins a transformation in Indian thinking about logic. And this in two inter-related respects: in the beginnings of a shift of interest away from the place of argumentation within dialectic and debate and towards a greater concern with the more formal properties of sound inference; and in a parallel and correlated shift from case-based to rule-governed accounts of logical reasoning. I will discuss each of these in turn.
asūtra begins a transformation in Indian thinking about logic. And this in two inter-related respects: in the beginnings of a shift of interest away from the place of argumentation within dialectic and debate and towards a greater concern with the more formal properties of sound inference; and in a parallel and correlated shift from case-based to rule-governed accounts of logical reasoning. I will discuss each of these in turn.
In the Ny yasūtra, there is a more systematic discussion of the categories and methods of debate than in earlier debating manuals. Three kinds of debate are distinguished: good or honest debate (v
yasūtra, there is a more systematic discussion of the categories and methods of debate than in earlier debating manuals. Three kinds of debate are distinguished: good or honest debate (v da), tricky or bad debate (jalpa) and a refutation-only debate (vi
da), tricky or bad debate (jalpa) and a refutation-only debate (vi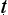 a
a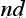
 ):
):
Good debate (v da) is one in which there is proof and refutation of thesis and antithesis based on proper evidence (pram
da) is one in which there is proof and refutation of thesis and antithesis based on proper evidence (pram
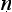 a) and presumptive argumentation (tarka), employing the five-step schema of argumentation, and without contradicting any background or assumed knowledge (siddh
a) and presumptive argumentation (tarka), employing the five-step schema of argumentation, and without contradicting any background or assumed knowledge (siddh nta).
nta).
Tricky debate (jalpa) is one in which, among the features mentioned before, proof and refutation exploit such means as quibbling (chala), false rejoinders (j ti), and any kind of clincher or defeat situation (nigrahasth
ti), and any kind of clincher or defeat situation (nigrahasth na).
na).
Refutation-only debate (vi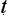 a
a
 ) is one in which no counter-thesis is proven. (NS 1.2.1–3).
) is one in which no counter-thesis is proven. (NS 1.2.1–3).
Here is our first reference to the Indian five-step inference pattern. It is a schema for proper argumentation among disputants who are engaged in an honest, friendly, noneristic, and balanced debate (v da). In the dialectical context in which such arguments are embedded, a proponent attempts to prove a thesis and to refute the counter-thesis of the opponent, both parties drawing upon a shared body of background knowledge and received belief, and using properly accredited methods for the acquisition and consideration of evidence. The aim of each participant in the dialogue is not victory but a fair assessment of the best arguments for and against the thesis. In Indian logic, v
da). In the dialectical context in which such arguments are embedded, a proponent attempts to prove a thesis and to refute the counter-thesis of the opponent, both parties drawing upon a shared body of background knowledge and received belief, and using properly accredited methods for the acquisition and consideration of evidence. The aim of each participant in the dialogue is not victory but a fair assessment of the best arguments for and against the thesis. In Indian logic, v da represents an ideal of fair-minded and respectful discourse. By contrast, in a tricky debate (jalpa), underhanded debating tactics are allowed, and the aim is to win at all costs and by any means necessary. The third kind of debate, the refutation-only debate (vi
da represents an ideal of fair-minded and respectful discourse. By contrast, in a tricky debate (jalpa), underhanded debating tactics are allowed, and the aim is to win at all costs and by any means necessary. The third kind of debate, the refutation-only debate (vi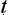 a
a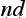
 ), is the variety of dialogue preferred by the sceptics — to argue against a thesis without commitment to any counter-thesis. It is not entirely clear whether this is a type of good or tricky debate. We might conjecture, however, that if dialectic is a rough kin of v
), is the variety of dialogue preferred by the sceptics — to argue against a thesis without commitment to any counter-thesis. It is not entirely clear whether this is a type of good or tricky debate. We might conjecture, however, that if dialectic is a rough kin of v da, and sophistic of jalpa, then the Socratic elenchus could be regarded as a species of vi
da, and sophistic of jalpa, then the Socratic elenchus could be regarded as a species of vi a
a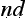
 , which is not, therefore, an entirely disreputable method of debate.
, which is not, therefore, an entirely disreputable method of debate.
The aim, in a good debate between friends, is the assessment of the best arguments for or against the thesis. And that leads to the question: how are arguments to be assessed or evaluated? Are the criteria for assessment formal, to do only with the form of the argument schema itself; or are they informal, pragmatic criteria, according to which arguments have to be evaluated as good or bad with regard to their contribution towards the goals of the dialogue within which they are embedded?
With this question in mind, let us look at the five-step proof pattern. The proper formulation of an argument is said to be in five parts: tentative statement of the thesis to be proved (pratijñ ); citation of a reason (hetu); mention of an example (ud
); citation of a reason (hetu); mention of an example (ud hara
hara a); application of reason and example to the case in hand (upanaya); final assertion of the thesis (nigamana). An unseen fire is inferred to be present on the mountain, on the basis of a plume of smoke; just as the two have been found associated in other places like the kitchen. The terms used here are defined in a series of admittedly rather gnomic utterances (NS 1.1.34–39):
a); application of reason and example to the case in hand (upanaya); final assertion of the thesis (nigamana). An unseen fire is inferred to be present on the mountain, on the basis of a plume of smoke; just as the two have been found associated in other places like the kitchen. The terms used here are defined in a series of admittedly rather gnomic utterances (NS 1.1.34–39):
1.1.32. ‘the parts [of an argument scheme] are thesis, reason, example, application and conclusion’
1.1.33. ‘the thesis is a statement of that which is to be proved’
1.1.34. ‘the reason is that which proves what is to be proven in virtue of a similarity with the example’ (ud hara
hara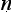 as
as dharmy
dharmy t s
t s dhyas
dhyas dhana
dhana hetu
hetu ).
).
1.1.35. ‘again, in virtue of a dissimilarity’ (tath vaidharmy
vaidharmy t).
t).
1.1.36. ‘the example is an illustration which, being similar to that which is to be proved, has its character’ (s dhyas
dhyas dharmy
dharmy t taddharmabh
t taddharmabh vī d
vī d
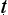
 nta ud
nta ud hara
hara am).
am).
1.1.37. ‘or else, being opposite to it, is contrary’ (tadviparyay d v
d v viparītam).
viparītam).
1.1.38. ‘the application to that which is to be proved is a drawing in together (upasa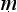 h
h ra) “this is so” or “this is not so,” depending on the example’ (ud
ra) “this is so” or “this is not so,” depending on the example’ (ud hara
hara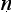
 pek
pek as tathety upasa
as tathety upasa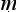 h
h ro na tatheti v
ro na tatheti v s
s dhyasyopanaya
dhyasyopanaya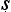 ).
).
1.1.39. ‘the conclusion is a restatement of the thesis as following from the statement of the reason’ (hetvapade
 t pratijñ
t pratijñ y
y
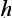 punarvacana
punarvacana nigamanam).
nigamanam).
The basic idea is that an object is inferred to have one (unobserved) property on the grounds that it has another, observed, one — “there is fire on the mountain because there is smoke there”. The most distinctive aspect of the schema, though, is the fundamental importance given to the citation of an example, a single case said either to be similar or else dissimilar to the case in hand. Suppose I want to persuade you that it is about to rain. I might reason as follows: “Look, it is going to rain (thesis). For see that large black cloud (reason). Last time you saw a large black cloud like that one (example), what happened? Well, its the same now (application). It is definitely going to rain (conclusion).”
Let us try to unpick the Ny yasūtra definitions. Suppose we let ‘F’ denote the property that serves as the reason here (hetu), ‘G’ the property whose presence we are seeking to infer (s
yasūtra definitions. Suppose we let ‘F’ denote the property that serves as the reason here (hetu), ‘G’ the property whose presence we are seeking to infer (s dhya), ‘a’ the new object about which we are trying to decide if it is G or not (pak
dhya), ‘a’ the new object about which we are trying to decide if it is G or not (pak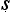 a), and ‘b’ the cited example (ud
a), and ‘b’ the cited example (ud hara
hara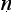 a). Then we seem to have a pair of schematic inferences, one based on similarity, the other on dissimilarity:
a). Then we seem to have a pair of schematic inferences, one based on similarity, the other on dissimilarity:


The counter-proof follows the same pattern, proving the counter-thesis (¬Ga) by means of a different reason and example:

The five-step schema was interpreted in a particular way by V tsy
tsy yana, the first commentator on the Ny
yana, the first commentator on the Ny yasūtra. His interpretation is largely responsible for shaping the direction Indian logic was later to take. At the same time, it was an interpretation that made the citation of an example essentially otiose. V
yasūtra. His interpretation is largely responsible for shaping the direction Indian logic was later to take. At the same time, it was an interpretation that made the citation of an example essentially otiose. V tsy
tsy yana was, in effect, to transform Indian logic, away from what it had been earlier, namely a theory of inference from case to case on the basis of resemblance, and into a rule-governed account in which the citation of cases has no significant role.
yana was, in effect, to transform Indian logic, away from what it had been earlier, namely a theory of inference from case to case on the basis of resemblance, and into a rule-governed account in which the citation of cases has no significant role.
Let us then consider first V tsy
tsy yana’s interpretation. What V
yana’s interpretation. What V tsy
tsy yana says is that the similarity between a and b just consists in their sharing the reason property F. The basic pattern of inference is now: a is like b [both are F]; GbGa. Or else: a is unlike b [one is F and the other isn’t]; ¬Gb Ga. Writing it out as before, what we have is:
yana says is that the similarity between a and b just consists in their sharing the reason property F. The basic pattern of inference is now: a is like b [both are F]; GbGa. Or else: a is unlike b [one is F and the other isn’t]; ¬Gb Ga. Writing it out as before, what we have is:

In a counterproof, a is demonstrated to be similar in some other respect to some other example, one that lacks the property G:

Thus, for example, a proof might be: the soul is eternal because it is uncreated, like space. And the counterproof might be: the soul is non-eternal because it is perceptible, like a pot.
The proposal is that if a resembles b, and b is G, then a can be inferred to be G too. But there is an obvious difficulty, which is that mere resemblance is an insufficient ground. Admittedly, the soul and space are both uncreated, but why should that give us any grounds for transferring the property of being eternal from one to the other? The respect in which the example and the case in hand resemble one another must be relevant to the property whose presence is being inferred. This is where the idea of a ‘false proof’ or ‘false rejoinder’ (j ti) comes in. Any argument that, while in the form of the five-step schema, fails this relevance requirement is called a ‘false proof’ and the Ny
ti) comes in. Any argument that, while in the form of the five-step schema, fails this relevance requirement is called a ‘false proof’ and the Ny yasūtra has a whole chapter (chapter 5) classifying and discussing them. A ‘false rejoinder’ is defined in this way:
yasūtra has a whole chapter (chapter 5) classifying and discussing them. A ‘false rejoinder’ is defined in this way:
NS 1.2.18 ‘a j ti is an objection by means of similarity and dissimilarity’ (s
ti is an objection by means of similarity and dissimilarity’ (s dharymavaidharmy
dharymavaidharmy bh
bh
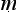 pratyavasth
pratyavasth na
na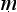 j
j ti
ti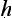 ).
).
It appears to be admissible to transfer the property ‘rain-maker’ from one black cloud to another black cloud, but not from a black cloud to a white cloud. It appears to be admissible to transfer the property ‘has a dewlap’ from one cow to another cow, but not from one four-legged animal (a cow) to another (a horse). It is clear what now needs to be said. The argument is good if there exists a general relationship between the reason F and the property being proved G, such that the latter never occurs without the former.
It is the Buddhist logician Di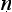 n
n ga (480–540 CE) who seems to have been the first to make this explicit (see also §2.2). According to him, a reason must satisfy three conditions. Define a ‘homologue’ (sapak
ga (480–540 CE) who seems to have been the first to make this explicit (see also §2.2). According to him, a reason must satisfy three conditions. Define a ‘homologue’ (sapak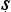 a) as an object other than a that possesses G, and a ‘heterologue’ (vipak
a) as an object other than a that possesses G, and a ‘heterologue’ (vipak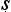 a) as an object other than a that does not possess G. Then Di
a) as an object other than a that does not possess G. Then Di n
n ga’s three conditions on a good reason are:
ga’s three conditions on a good reason are:
Condition [3] asserts, in effect, that F never occurs without G, and this, together with [1] that F occurs in a, implies of course that G occurs in a. In effect, the citation of an example in the original Ny yasūtra formula has been transformed into a statement of a general relationship between F and G. There remains only a vestigial role for the example in condition [2], which seems to insist that there be an instance of F other than a which is also G.
yasūtra formula has been transformed into a statement of a general relationship between F and G. There remains only a vestigial role for the example in condition [2], which seems to insist that there be an instance of F other than a which is also G. n
n ga is worried about the soundness of inferences based on a reason which is a property unique to the object in hand; for example, the inference “sound is eternal because it is audible”. For if this is sound, then why not the counter-argument “sound is non-eternal because it is audible”? And yet there are many inferences like this that are sound, so it seems to be a mistake to exclude them all. In fact condition [2] soon came to be rephrased in a way that made it logically equivalent to [3], namely as saying that F occur only in homologues (eva ‘only’ is used here as a quantifier). In asking for the respect in which the example and the new case must resemble each other, for the presence of G in the example to be a reason for inferring that G is present in the new case, we are led to give the general relationship that any such respect must bear to G, and that in turn makes citation of an example otiose. The five-step schema becomes:
ga is worried about the soundness of inferences based on a reason which is a property unique to the object in hand; for example, the inference “sound is eternal because it is audible”. For if this is sound, then why not the counter-argument “sound is non-eternal because it is audible”? And yet there are many inferences like this that are sound, so it seems to be a mistake to exclude them all. In fact condition [2] soon came to be rephrased in a way that made it logically equivalent to [3], namely as saying that F occur only in homologues (eva ‘only’ is used here as a quantifier). In asking for the respect in which the example and the new case must resemble each other, for the presence of G in the example to be a reason for inferring that G is present in the new case, we are led to give the general relationship that any such respect must bear to G, and that in turn makes citation of an example otiose. The five-step schema becomes:
| [thesis] | Ga |
| [reason] | because F |
| [example] | where there is F, there is G; for example, b. |
| [application] | Fa |
| [conclusion] | Ga |
It is the five-step argument pattern so transformed that has suggested to Colebrooke and other writers on Indian logic a comparison with an Aristotelian syllogism in the first figure, Barbara. We simply re-write it in this form:
This assimilation seems forced in at least two respects. First, the conclusion of the Ny yasūtra demonstration is a singular proposition. In Aristotle’s system, on the other hand, it is always either a universal proposition with ‘all’ or ‘no’, or a particular proposition with ‘some’. Second, and relatedly, the role of the ‘minor term’ is quite different: in the Indian schema, it indicates a locus for property-possession, while in Aristotle, the relation is ‘belongs to’. Again, in reducing the Indian pattern to an Aristotelian syllogism, the role of the example, admittedly by now rather vestigial, is made to disappear altogether.
yasūtra demonstration is a singular proposition. In Aristotle’s system, on the other hand, it is always either a universal proposition with ‘all’ or ‘no’, or a particular proposition with ‘some’. Second, and relatedly, the role of the ‘minor term’ is quite different: in the Indian schema, it indicates a locus for property-possession, while in Aristotle, the relation is ‘belongs to’. Again, in reducing the Indian pattern to an Aristotelian syllogism, the role of the example, admittedly by now rather vestigial, is made to disappear altogether.
A rather better reformulation of the five-step schema is suggested by Stanisław Schayer,15 who wants to see the Indian ‘syllogism’ as really a proof exploiting two rules of inference:
| [thesis] | Ga | There is fire on a (= on this mountain). |
| [reason] | Fa | There is smoke on a. |
| [‘example’] | (x)(Fx → Gx) | For every locus x: if there is smoke in x then there is fire in x. |
| [application] | Fa → Ga | This rule also applies for x = a. |
| [conclusion] | Ga | Because the rule applies to x = a and the statement Ga is true, the statement Fa is true. |
Two inference rules are in play here — a rule of substitution, allowing us to infer from ‘(x)ζx’ to ‘ζa’, and a rule of separation, allowing us to infer from ‘θ → ϕ’ and ‘θ’ to ‘ϕ’. Schayer thereby identifies the Indian syllogism with a proof in a natural deduction system:
We have seen how the Ny yasūtra model of good argumentation came to be transformed and developed by later writers in the Indian tradition in the direction of a formal, rule-governed theory of inference, and how writers in the West have interpreted what they have called the Indian ‘syllogism’. I suggested at the beginning that we might try to interpret the Ny
yasūtra model of good argumentation came to be transformed and developed by later writers in the Indian tradition in the direction of a formal, rule-governed theory of inference, and how writers in the West have interpreted what they have called the Indian ‘syllogism’. I suggested at the beginning that we might try to interpret the Ny ya model along different lines altogether, seeing it an early atttempt at what is now called ‘case-based reasoning’. Case-based reasoning begins with one or more prototypical exemplars of a category, and reasons that some new object belongs to the same category on the grounds that it resembles in some appropriate and context determined manner one of the exemplars. Models of case-based reasoning have been put forward for medical diagnostics and legal reasoning, and some have been implemented in artificial intelligence models. It has been shown, for example, that training a robot to solve problems by having it retrieve solutions to stored past cases, modifying them to fit the new circumstances, can have great efficiency gains over seeking solutions through the application of first principles. Perhaps something like this underlies a lot of the way we actually reason, and perhaps it was as an attempt to capture this type of reasoning that we should see the ancient logic of the Ny
ya model along different lines altogether, seeing it an early atttempt at what is now called ‘case-based reasoning’. Case-based reasoning begins with one or more prototypical exemplars of a category, and reasons that some new object belongs to the same category on the grounds that it resembles in some appropriate and context determined manner one of the exemplars. Models of case-based reasoning have been put forward for medical diagnostics and legal reasoning, and some have been implemented in artificial intelligence models. It has been shown, for example, that training a robot to solve problems by having it retrieve solutions to stored past cases, modifying them to fit the new circumstances, can have great efficiency gains over seeking solutions through the application of first principles. Perhaps something like this underlies a lot of the way we actually reason, and perhaps it was as an attempt to capture this type of reasoning that we should see the ancient logic of the Ny yasūtra and indeed of the medical theorist Caraka.16. In this model, a perceived association between symptoms in one case provides a reason for supposing there to be an analogous association in other, resembling cases. The physician observing a patient A who has, for example, eaten a certain kind of poisonous mushroom, sees a number of associated symptoms displayed, among them F and G, say. He or she now encounters a second patient B displaying a symptom at least superficially resembling F. The physician thinks back over her past case histories in search of cases with similar symptoms. She now seeks to establish if any of those past cases resembles B, and on inquiry into B’s medical history, discovers that B too has consumed the same kind of poisonous mushroom. These are her grounds for inferring that B too will develop the symptom G, a symptom that had been found to be associated with F in A. A common etiology in the two cases leads to a common underlying disorder, one that manifests itsself in and explains associations between members of a symptom-cluster.
yasūtra and indeed of the medical theorist Caraka.16. In this model, a perceived association between symptoms in one case provides a reason for supposing there to be an analogous association in other, resembling cases. The physician observing a patient A who has, for example, eaten a certain kind of poisonous mushroom, sees a number of associated symptoms displayed, among them F and G, say. He or she now encounters a second patient B displaying a symptom at least superficially resembling F. The physician thinks back over her past case histories in search of cases with similar symptoms. She now seeks to establish if any of those past cases resembles B, and on inquiry into B’s medical history, discovers that B too has consumed the same kind of poisonous mushroom. These are her grounds for inferring that B too will develop the symptom G, a symptom that had been found to be associated with F in A. A common etiology in the two cases leads to a common underlying disorder, one that manifests itsself in and explains associations between members of a symptom-cluster.
Can we find such a model of the informal logic of case-based reasoning in the Ny yasūtra? Consider again NS 1.1.34. It said that ‘the reason is that which proves what is to be proved in virtue of a similarity with the example.’ On our reading, what this says is that a similarity between the symptom F in the new case and a resembling symptom F′ in the past-case or example is what grounds the inference. And NS 1.1.34 says that ‘the example is something which, being similar to that which is to be proved, has its character’. Our reading is that the old case and the new share something in their circumstances, like having eaten the same kind of poisonous mushroom, in virtue of which they share a ‘character’, an underlying disorder that expains the clustering of symptoms. So the five-step demonstration is now:
yasūtra? Consider again NS 1.1.34. It said that ‘the reason is that which proves what is to be proved in virtue of a similarity with the example.’ On our reading, what this says is that a similarity between the symptom F in the new case and a resembling symptom F′ in the past-case or example is what grounds the inference. And NS 1.1.34 says that ‘the example is something which, being similar to that which is to be proved, has its character’. Our reading is that the old case and the new share something in their circumstances, like having eaten the same kind of poisonous mushroom, in virtue of which they share a ‘character’, an underlying disorder that expains the clustering of symptoms. So the five-step demonstration is now:
| [thesis] | Ga | |
| [reason] | Fa | F is similar to F′ in b. |
| [example] | b | exhibits the same underlying structure as a, because it resembles a. |
| [application] | a is the same as b with respect to G. | |
| [conclusion] | Ga |
Let us see if this pattern fits examples of good inference taken from a variety of early Indian logical texts. One pattern of inference, cited in the Ny yasūtra, is causal-predictive: Seeing the ants carrying their eggs, one infers that it will rain; seeing a full and swiftly flowing river, one infers that it has been raining; seeing a cloud of smoke, one infers the existence of an unseen fire. Presumably the idea is that one has seen other ants carrying their eggs on a past occasion, and on that occasion it rained. The inference works if, or to the exent that, we have reasons for thinking that those ants and these share some unkown capacity, a capacity that links detection of the imment arrival of rain with the activity of moving their eggs. The pattern is similar in another kind of inference, inference from sampling: Inferring from the salty taste of one drop of sea water that the whole sea is salty; inferring that all the rice is cooked on tasting one grain. The assumption again is that both the sampled grain of rice and any new grain share some common underlying structure, a structure in virtue of which they exhibit the sydromes associated with being cooked, and a structure whose presence in both is indicated by their being in the same pan, heated for the same amount of time, and so forth.
yasūtra, is causal-predictive: Seeing the ants carrying their eggs, one infers that it will rain; seeing a full and swiftly flowing river, one infers that it has been raining; seeing a cloud of smoke, one infers the existence of an unseen fire. Presumably the idea is that one has seen other ants carrying their eggs on a past occasion, and on that occasion it rained. The inference works if, or to the exent that, we have reasons for thinking that those ants and these share some unkown capacity, a capacity that links detection of the imment arrival of rain with the activity of moving their eggs. The pattern is similar in another kind of inference, inference from sampling: Inferring from the salty taste of one drop of sea water that the whole sea is salty; inferring that all the rice is cooked on tasting one grain. The assumption again is that both the sampled grain of rice and any new grain share some common underlying structure, a structure in virtue of which they exhibit the sydromes associated with being cooked, and a structure whose presence in both is indicated by their being in the same pan, heated for the same amount of time, and so forth.
I will make two final comments about these patterns of case-based reasoning. First, it is clear that background knowledge is essentially involved. As the Ny yasūtra stresses in its definition of a good debate, both parties in a debate much be able to draw upon a commonly accepted body of information. Such knowledge gets implicated in judgements about which similarities are indicative of common underlying disorders, and which are not. Second, in such reasoning the example does not seem to be redundant or eliminable in favour of a general rule. For although there always will be a general law relating the underlying disorder with its cluster of symptoms, the whole point of this pattern of reasoning is that the reasoner need not be in a position to know what the underlying disorder is, and so what form the general law takes. In conclusion, while the history of logic in India shows a strong tendency towards formalisation, the logic of ancient India tried to model informal patterns of reasoning from cases that are increasingly becoming recognised as widespread and representative of the way much actual reasoning takes place.
yasūtra stresses in its definition of a good debate, both parties in a debate much be able to draw upon a commonly accepted body of information. Such knowledge gets implicated in judgements about which similarities are indicative of common underlying disorders, and which are not. Second, in such reasoning the example does not seem to be redundant or eliminable in favour of a general rule. For although there always will be a general law relating the underlying disorder with its cluster of symptoms, the whole point of this pattern of reasoning is that the reasoner need not be in a position to know what the underlying disorder is, and so what form the general law takes. In conclusion, while the history of logic in India shows a strong tendency towards formalisation, the logic of ancient India tried to model informal patterns of reasoning from cases that are increasingly becoming recognised as widespread and representative of the way much actual reasoning takes place.
1.4 Refutation-only dialogue: vita

We have already seen how ‘refutation-only’ debate is defined in the Ny yasūtra:
yasūtra:
For the Naiy yika, to argue thus is to argue in a purely negative and destructive way. Here one has no goal other than to undermine one’s opponent. People who use reason in this way are very like the sceptics and unbelievers of the epics. V
yika, to argue thus is to argue in a purely negative and destructive way. Here one has no goal other than to undermine one’s opponent. People who use reason in this way are very like the sceptics and unbelievers of the epics. V tsy
tsy yana claims indeed that to use reason in this way is virtually self-defeating:
yana claims indeed that to use reason in this way is virtually self-defeating:
A vait
 ika is one who employs destructive criticism. If when questioned about the purpose [of so doing], he says ‘this is my thesis’ or ‘this is my conclusion,’ he surrenders his status as a vait
ika is one who employs destructive criticism. If when questioned about the purpose [of so doing], he says ‘this is my thesis’ or ‘this is my conclusion,’ he surrenders his status as a vait
 ika. If he says that he has a purpose, to make known the defects of the opponent, this too will is the same. For if he says that there is one who makes things known or one who knows, or that there is a thing by which things are made known or a thing made known, then he surrenders his status as a vait
ika. If he says that he has a purpose, to make known the defects of the opponent, this too will is the same. For if he says that there is one who makes things known or one who knows, or that there is a thing by which things are made known or a thing made known, then he surrenders his status as a vait
 ika.17
ika.17
Vi a
a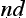
 is the sceptic’s use of argumentation, and it is a familiar move to attempt to argue that scepticism is self-defeating. In India, it is the M
is the sceptic’s use of argumentation, and it is a familiar move to attempt to argue that scepticism is self-defeating. In India, it is the M dhyamika Buddhist N
dhyamika Buddhist N g
g rjuna (circa first century CE) who is most closely associated with the theoretical elaboration of refutation-only argumentation, through the method of ‘four-limbed refutation’ (catu
rjuna (circa first century CE) who is most closely associated with the theoretical elaboration of refutation-only argumentation, through the method of ‘four-limbed refutation’ (catu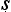 ko
ko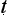 i) and the allied technique of presumptive reasoning (prasa
i) and the allied technique of presumptive reasoning (prasa ga; tarka). In the next section, I will show how this latter technique became a device for shifting the burden of proof onto one’s opponent. First, I will examine the method of ‘four-limbed’ refutation in the context of N
ga; tarka). In the next section, I will show how this latter technique became a device for shifting the burden of proof onto one’s opponent. First, I will examine the method of ‘four-limbed’ refutation in the context of N g
g rjuna’s wider philosophical project.
rjuna’s wider philosophical project.
Reasoning, for N g
g rjuna, is the means by which one ‘steps back’ from common sense ways of understanding to a more objective view of the world. Reason is a mode of critical evaluation of one’s conceptual scheme. A more objective understanding is one in which one understands that things are not necessarily as they appear. It is a view from which one can see how and where one’s earlier conceptions are misleading. One learns not to trust one’s perceptions when a large object far away looks small, or a stick half submerged in water looks bent, and in learning this one exercises a mode of self-critical reason. So too a rational person learns not to trust their conceptions when they presuppose the existence of independent, self-standing objects. From the vantage point of an objective view, it is easy to see that one’s old conceptions had false presuppositions. The real trick, however, is to be able to expose those presuppositions while still ‘within’ the old conception, and so to lever oneself up to a more objective view. This levering-up-from-within requires a new way of reasoning: N
rjuna, is the means by which one ‘steps back’ from common sense ways of understanding to a more objective view of the world. Reason is a mode of critical evaluation of one’s conceptual scheme. A more objective understanding is one in which one understands that things are not necessarily as they appear. It is a view from which one can see how and where one’s earlier conceptions are misleading. One learns not to trust one’s perceptions when a large object far away looks small, or a stick half submerged in water looks bent, and in learning this one exercises a mode of self-critical reason. So too a rational person learns not to trust their conceptions when they presuppose the existence of independent, self-standing objects. From the vantage point of an objective view, it is easy to see that one’s old conceptions had false presuppositions. The real trick, however, is to be able to expose those presuppositions while still ‘within’ the old conception, and so to lever oneself up to a more objective view. This levering-up-from-within requires a new way of reasoning: N g
g rjuna’s celebrated prasa
rjuna’s celebrated prasa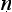 ga-type rationality. It is a self-critical rationality which exposes as false the existential presuppositions on which one’s present conceptions are based. The same method can equally well be used to expose the false presuppositions on which one’s dialectical opponents’ views are based, and for this reason the whole technique is strongly maieutic, in the sense defined earlier.
ga-type rationality. It is a self-critical rationality which exposes as false the existential presuppositions on which one’s present conceptions are based. The same method can equally well be used to expose the false presuppositions on which one’s dialectical opponents’ views are based, and for this reason the whole technique is strongly maieutic, in the sense defined earlier.
A simple example will illustrate the kind of reasoning N g
g rjuna thinks is needed if one is to expose the presuppositions of one’s conceptual scheme from within. A non-compound monadic concept ‘F’ has the following application-condition: it applies only to things which are F. It is therefore a concept whose application presupposes that there is a condition which divides the domain into two. For our purposes, the condition can be thought of either as ‘belonging to the class of Fs’ or ‘possessing the property being-F’. Now take an arbitrary object, a, from some antecedently specified domain. There are apparently two possibilities for a: either it falls under the concept, or else it is not. That is, the two options are:
rjuna thinks is needed if one is to expose the presuppositions of one’s conceptual scheme from within. A non-compound monadic concept ‘F’ has the following application-condition: it applies only to things which are F. It is therefore a concept whose application presupposes that there is a condition which divides the domain into two. For our purposes, the condition can be thought of either as ‘belonging to the class of Fs’ or ‘possessing the property being-F’. Now take an arbitrary object, a, from some antecedently specified domain. There are apparently two possibilities for a: either it falls under the concept, or else it is not. That is, the two options are:
Suppose that one can disprove both of these options. How one would try to do this will vary from case to case depending on the individual concept under scrutiny. But if one is able to disprove (I) and to disprove (II), then the concept in question can have no application-condition. The presupposition for the application of the concept, that there is a condition (class, property) effecting a division within the domain, fails. A later M dhyamika master18expresses the idea exactly:
dhyamika master18expresses the idea exactly:
When neither existence nor nonexistence presents itself before the mind, then, being without objective support (nir lambana) because there is no other way, [the mind] is still.
lambana) because there is no other way, [the mind] is still.
Sentences are used to make statements, but if the statement so made is neither true nor false, then, because there is no third truth-value, the statement must be judged to lack content.19
N g
g rjuna’s developed strategy involves a generalization. A generalization is needed because many if not most of the concepts under scrutiny are relational rather than monadic; centrally: causes, sees, moves, desires. When a concept is relational, there are four rather than two ways for its application-condition to be satisfied (see Figure 1, page 332):
rjuna’s developed strategy involves a generalization. A generalization is needed because many if not most of the concepts under scrutiny are relational rather than monadic; centrally: causes, sees, moves, desires. When a concept is relational, there are four rather than two ways for its application-condition to be satisfied (see Figure 1, page 332):
(I) R relates a only to itself
(II) R relates a only to things other than itself
(III) R relates a both to itself and to things other than itself
As an illustration of the four options, take R to the square-root relation √, and the domain of objects to be the set of real numbers. Then the four possibilities are exemplified by the numbers 0, 4, 1 and −1 respectively. For √0 = 0, √4 = 2 and also −2, √1 = 1 and also −1, while finally −1 does not have a defined square root among the real numbers. The list of four options is what is called in Madhyamaka a catu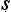 ko
ko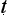 i.
i.
Everything is thus, not thus, both thus and not thus, or neither thus nor not thus. That is the Buddha’s [provisional] instruction. [Mūlamadhyanakaka=arik , MK 18.8]
, MK 18.8]
Some say that suffering (du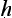 kha) is self-produced, or produced from another, or produced from both, or produced without a cause. [MK 12.11
kha) is self-produced, or produced from another, or produced from both, or produced without a cause. [MK 12.11
Since every factor in existence (dharma) are empty, what is finite and what is infinite? What is both finite and infinite? What is neither finite nor infinite? [MK 25.22]
It is easy to see that the four options are mutually exclusive and jointly exhaustive. For the class of objects to which R relates a is either (IV) the empty set ∅ or, if not, then either (I) it is identical to {a}, or (II) it excludes {a}, or (III) it includes {a}. Not every relation exhibits all four options. (I) not exhibited if R is anti-reflexive. (II) is not exhibited if R is reflexive and bijective. (IV) is not exhibited if R is defined on every point in the domain. Note in particular that if R is the identity relation, then neither (III) nor (IV) are exhibited, not (III) because identity is transitive, and not (IV) because identity is reflexive. Indeed, options (III) and (IV) are not exhibited whenever R is an equivalence (transitive, symmetric, and reflexive) relation.
or, if not, then either (I) it is identical to {a}, or (II) it excludes {a}, or (III) it includes {a}. Not every relation exhibits all four options. (I) not exhibited if R is anti-reflexive. (II) is not exhibited if R is reflexive and bijective. (IV) is not exhibited if R is defined on every point in the domain. Note in particular that if R is the identity relation, then neither (III) nor (IV) are exhibited, not (III) because identity is transitive, and not (IV) because identity is reflexive. Indeed, options (III) and (IV) are not exhibited whenever R is an equivalence (transitive, symmetric, and reflexive) relation.
The next step in the ‘refutation-only’ strategy is to construct subsidiary ‘disproofs’, one for each of the four options. Although there is no pre-determined procedure for constructing such disproofs, by far the most commonly used method is to show that the option in question has some unacceptable consequence (prasa ga). I will examine this method in detail in §1.5. A major dispute for later M
ga). I will examine this method in detail in §1.5. A major dispute for later M dhyamikas was over what sort of reasoning is permissible in the four subsidiary disproofs, the proofs that lead to the rejection of each of the four options. It is a difficult question to answer, so difficult indeed that it led, at around 500 AD, to a fission within the school of Madhyamaka. The principal group (Pr
dhyamikas was over what sort of reasoning is permissible in the four subsidiary disproofs, the proofs that lead to the rejection of each of the four options. It is a difficult question to answer, so difficult indeed that it led, at around 500 AD, to a fission within the school of Madhyamaka. The principal group (Pr sa
sa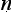 gika, headed by Buddhap
gika, headed by Buddhap lita) insisted that only prasa
lita) insisted that only prasa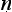 ga-type, ‘presupposition-negating’ reasoning is admissible. This faction is the more conservative and mainstream, in the sense that their teaching seems to be in keeping with N
ga-type, ‘presupposition-negating’ reasoning is admissible. This faction is the more conservative and mainstream, in the sense that their teaching seems to be in keeping with N g
g rjuna’s own method of reasoning. The important later M
rjuna’s own method of reasoning. The important later M dhyamika masters Candrakīrti and Ś
dhyamika masters Candrakīrti and Ś ntideva defended this view. A splinter faction, however, (Sv
ntideva defended this view. A splinter faction, however, (Sv tantrika, headed by Bh
tantrika, headed by Bh vaviveka) allowed ‘independent’ inference or inductive demonstration into the disproofs. Perhaps this was done so that the inferential methods developed by
vaviveka) allowed ‘independent’ inference or inductive demonstration into the disproofs. Perhaps this was done so that the inferential methods developed by n
n ga (§2.2) could be deployed in establishing the M
ga (§2.2) could be deployed in establishing the M dhyamika’s doctrinal position. Clearly, the fewer restrictions one places on the type of reasoning one permits oneself to use, the greater are the prospects of successfully finding arguments to negate each of the four options. On the other hand, we have seen that the citation of paradigmatic examples is essential to this type of reasoning (§1.3), and it is hard to see how one could be entitled to cite examples in support of one’s argument, when the very conception of those examples is in question.
dhyamika’s doctrinal position. Clearly, the fewer restrictions one places on the type of reasoning one permits oneself to use, the greater are the prospects of successfully finding arguments to negate each of the four options. On the other hand, we have seen that the citation of paradigmatic examples is essential to this type of reasoning (§1.3), and it is hard to see how one could be entitled to cite examples in support of one’s argument, when the very conception of those examples is in question.
The effect of the four subsidiary disproofs is to establish that none of the four options obtains:20
Neither from itself nor from another, nor from both, nor without a cause, does anything whatever anywhere arise. [MK 1.1]
One may not say that there is emptiness, nor that there is non-emptiness. Nor that both, nor that neither exists; the purpose for so saying is only one of provisional understanding. [MK 22.11]
The emptiness of the concept in question is now deduced as the final step in the process. For it is a presupposition of one of the four options obtaining that the concept does have an application-condition (a class of classes or relational property). If all four are disproved, then the presupposition itself cannot be true. When successful, the procedure proves that the concept in question is empty, null,  ūnya. This is N
ūnya. This is N g
g rjuna’s celebrated and controversial ‘prasa
rjuna’s celebrated and controversial ‘prasa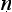 ga-type’ rational inquiry, a sophisticated use of rationality to annul a conceptual scheme.
ga-type’ rational inquiry, a sophisticated use of rationality to annul a conceptual scheme.
A statement is truth-apt if it is capable of being evaluated as either true or false. When N g
g rjuna rejects each of the four options, he is rejecting the claim that a statement of the form ‘aRb’ is truth-apt, since the four options exhaust the possible ways in which it might be evaluated as true. But if the statements belonging to a certain discourse are not truth-apt, then the discourse cannot be part of an objective description of the world (a joke is either funny or unfunny, but it cannot be evaluated as true or false.) The prasa
rjuna rejects each of the four options, he is rejecting the claim that a statement of the form ‘aRb’ is truth-apt, since the four options exhaust the possible ways in which it might be evaluated as true. But if the statements belonging to a certain discourse are not truth-apt, then the discourse cannot be part of an objective description of the world (a joke is either funny or unfunny, but it cannot be evaluated as true or false.) The prasa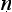 ga negates a presupposition for truth-aptness and so for objective reference.
ga negates a presupposition for truth-aptness and so for objective reference.
N g
g rjuna applies the procedure in an attempt to annul each of the concepts that are the basic ingredients of our common-sense scheme. In each case, his method is to identify a relation and prove that none of the four options can obtain. On closer inspection, it turns out that his argumentation falls into two basic patterns.21 One pattern is applied to any concept involving the idea of an ordering or sequence, especially the concept of a causal relation, of a temporal relation and of a proof relation. The paradigm for this argument is N
rjuna applies the procedure in an attempt to annul each of the concepts that are the basic ingredients of our common-sense scheme. In each case, his method is to identify a relation and prove that none of the four options can obtain. On closer inspection, it turns out that his argumentation falls into two basic patterns.21 One pattern is applied to any concept involving the idea of an ordering or sequence, especially the concept of a causal relation, of a temporal relation and of a proof relation. The paradigm for this argument is N g
g rjuna’s presentation of a paradox of origin (chapter 1), which serves as model for his analysis of causation (chapter 8), the finitude of the past and future (chapter 11), and suffering (chapter 12). The argument seeks to establish that a cause can be neither identical to, nor different from, the effect. If nothing within the domain is uncaused, then the four options for the realization of a causal relation are foreclosed.
rjuna’s presentation of a paradox of origin (chapter 1), which serves as model for his analysis of causation (chapter 8), the finitude of the past and future (chapter 11), and suffering (chapter 12). The argument seeks to establish that a cause can be neither identical to, nor different from, the effect. If nothing within the domain is uncaused, then the four options for the realization of a causal relation are foreclosed.
The other pattern of argumentation in N g
g rjuna is essentially grammatical. When a relational concept is expressed by a transitive verb, the sentence has an Agent and a Patient (the relata of the relation). For example, “He sees the tree,” “He goes to the market,” “He builds a house.” The idea of the grammatical argument is that one can exploit features of the deep case structure of such sentences in order to prove that the Patient can be neither identical to the Agent, nor include it, nor exclude it, and that there must be a Patient. N
rjuna is essentially grammatical. When a relational concept is expressed by a transitive verb, the sentence has an Agent and a Patient (the relata of the relation). For example, “He sees the tree,” “He goes to the market,” “He builds a house.” The idea of the grammatical argument is that one can exploit features of the deep case structure of such sentences in order to prove that the Patient can be neither identical to the Agent, nor include it, nor exclude it, and that there must be a Patient. N g
g rjuna uses this pattern of argumentation in constructing a paradox of motion (MK, chapter 2), and this chapter serves as a model for his analysis of perception (chapter 3), composition (chapter 7), fire (chapter 10), and of bondage and release (chapter 16). Indeed, the same pattern of argument seems to be applicable whenever one has a concept which involves a notion of a single process extended in time. What exactly these arguments show and how well they succeed is a matter of debate, but what we have seen is the elaboration of a sophisticated sceptical strategy of argumentation, based on the idea of ‘refutation-only’ dialogue.
rjuna uses this pattern of argumentation in constructing a paradox of motion (MK, chapter 2), and this chapter serves as a model for his analysis of perception (chapter 3), composition (chapter 7), fire (chapter 10), and of bondage and release (chapter 16). Indeed, the same pattern of argument seems to be applicable whenever one has a concept which involves a notion of a single process extended in time. What exactly these arguments show and how well they succeed is a matter of debate, but what we have seen is the elaboration of a sophisticated sceptical strategy of argumentation, based on the idea of ‘refutation-only’ dialogue.
1.5 Presumptive argumentation (tarka) and burden-of-proof shifting
Indian logicians developed a theory of what they call ‘suppositional’ or ‘presumptive’ argumentation (tarka). It is a theory about the burden of proof and the role of presumption, about the conditions under which even inconclusive evidence is sufficient for warranted belief. As we have already seen, it is a style of reasoning that is regarded as permissible within a well-conducted dialogue (v da; see §1.3). In the canonical and early literature, tarka is virtually synonymous with reasoned thinking in general. The free-thinkers so derided in the epics were called t
da; see §1.3). In the canonical and early literature, tarka is virtually synonymous with reasoned thinking in general. The free-thinkers so derided in the epics were called t rkikas or ‘followers of reason’. Even later on, when the fashion was to adorn introductory surveys of philosophy with such glorious names as The Language of Reason (Tarkabh
rkikas or ‘followers of reason’. Even later on, when the fashion was to adorn introductory surveys of philosophy with such glorious names as The Language of Reason (Tarkabh
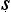
 , Mok
, Mok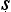
 karagupta), Immortal Reason (Tark
karagupta), Immortal Reason (Tark m
m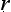 ta, Jagadī
ta, Jagadī a), Reason’s Moonlight (Tarkakaumudī, Laug
a), Reason’s Moonlight (Tarkakaumudī, Laug k
k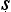 i Bh
i Bh skara), it was usual to confer on a graduate of the medieval curriculum an honorific title like Master or Ford of Reason (tarkav
skara), it was usual to confer on a graduate of the medieval curriculum an honorific title like Master or Ford of Reason (tarkav gī
gī a, tarkatīrtha). Such a person is a master in the art of evidence and the management of doubt, knowing when to accept the burden of proof and also when and how to deflect it.
a, tarkatīrtha). Such a person is a master in the art of evidence and the management of doubt, knowing when to accept the burden of proof and also when and how to deflect it.
Extrapolative inference (anum na, see §1.3) rests on the knowledge of universal generalisations, and it is the possibility of such knowledge that the most troubling forms of scepticism call into question. How can one be entitled to believe that something is true of every member of a domain without inspecting each member individually? How does one cope with the ineliminable possibility that an unperceived counterexample exists in some distant corner of the domain? The difficulty here is with the epistemology of negative existentials. The Buddhist
na, see §1.3) rests on the knowledge of universal generalisations, and it is the possibility of such knowledge that the most troubling forms of scepticism call into question. How can one be entitled to believe that something is true of every member of a domain without inspecting each member individually? How does one cope with the ineliminable possibility that an unperceived counterexample exists in some distant corner of the domain? The difficulty here is with the epistemology of negative existentials. The Buddhist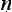 n
n ga formulates the extrapolation relation as a ‘no counterexample’ relation. For him, x extrapolates y just in case there is no x without y (y-avina x-abh
ga formulates the extrapolation relation as a ‘no counterexample’ relation. For him, x extrapolates y just in case there is no x without y (y-avina x-abh va). The Navya-Ny
va). The Navya-Ny ya logicians prefer a different negative existential condition, one derived from the reflexivity and transitivity of the extrapolation relation. Given transitivity, if x extrapolates y then, for any z, if y extrapolates z, so does x. The converse of this conditional holds too, given that the extrapolation relation is reflexive (proof: let z = y). So let us define an ‘associate condition’ (up
ya logicians prefer a different negative existential condition, one derived from the reflexivity and transitivity of the extrapolation relation. Given transitivity, if x extrapolates y then, for any z, if y extrapolates z, so does x. The converse of this conditional holds too, given that the extrapolation relation is reflexive (proof: let z = y). So let us define an ‘associate condition’ (up dhi) as a property which is extrapolated by y but not x. Then x extrapolates y just in case there is no associate condition.22 One can infer fire from smoke but not smoke from fire, for there is an associate condition, dampness-of-fuel, present wherever smoke is but not wherever fire is. Tinkering with the definition, though, does not affect the epistemological problem; it remains the one of proving a nonexistence claim.
dhi) as a property which is extrapolated by y but not x. Then x extrapolates y just in case there is no associate condition.22 One can infer fire from smoke but not smoke from fire, for there is an associate condition, dampness-of-fuel, present wherever smoke is but not wherever fire is. Tinkering with the definition, though, does not affect the epistemological problem; it remains the one of proving a nonexistence claim.
Presumptive argumentation, tarka, is a device for appropriating a presumptive right — the right to presume that one’s own position is correct even without conclusive evidence in its support. One is, let us imagine, in a state of doubt as to which of two hypotheses A and B is true. A and B are exclusive (at most one is true) but not necessarily contradictory (both might be false). Technically, they are in a state of ‘opposition’ (virodha).23 The doubt would be expressed by an exclusive disjunction in the interrogative – Is it that A or that B? Uncertainty initiates inquiry, and at the beginning of any inquiry the burden of proof is symmetrically distributed among the alternative hypotheses. A piece of presumptive argumentation shifts the burden of proof by adducing a prima facie counterfactual argument against one side. The form of the argument is the same in all cases. It is that one alternative, supposed as true, would have a consequence in conflict with some set of broadly defined constraints on rational acceptability. The existence of such an argument gives one the right to presume that the other alternative is true, even though one has no conclusive proof of its truth, and even though the logical possibility of its being false remains open. In the psychologized language of the Ny ya logician, a suppositional argument is a ‘blocker’ (b
ya logician, a suppositional argument is a ‘blocker’ (b dhaka) to belief in the supposed alternative, and an ‘eliminator’ (nirvartaka) of doubt. The Naiy
dhaka) to belief in the supposed alternative, and an ‘eliminator’ (nirvartaka) of doubt. The Naiy yika V
yika V caspati (9th century) comments:24
caspati (9th century) comments:24
Even if, following a doubt, there is a desire to know [the truth], the doubt still remains after the desire to know [has come about]. This is the situation intended for the application of presumptive argumentation. Of two theses, one should be admitted as known when the other is rejected by the reasoning called ‘suppositional.’ Thus doubt is suppressed by the application of presumptive argumentation to its subject matter… A means of knowing is engaged to decide a question, but when there is a doubt involving its opposite, the means of knowing fails [in fact] to engage. But the doubt concerning the opposite is not removed as such by the undesired consequence. What makes possible its removal is the means of knowing.
V caspati stresses that a thesis is not itself proved by a suppositional demonstration that the opposite has undesired consequences; one still needs evidence corroborating the thesis. But there is now a presumption in its favour, and the burden of proof lies squarely with the opponent. Presumptive argumentation ‘supports’ one’s means of acquiring evidence but it not itself a source of evidence. It role is to change the standard of evidence required for proof in the specific context.
caspati stresses that a thesis is not itself proved by a suppositional demonstration that the opposite has undesired consequences; one still needs evidence corroborating the thesis. But there is now a presumption in its favour, and the burden of proof lies squarely with the opponent. Presumptive argumentation ‘supports’ one’s means of acquiring evidence but it not itself a source of evidence. It role is to change the standard of evidence required for proof in the specific context.
A radical sceptical hypothesis is a proposition inconsistent with ordinary belief but consistent with all available evidence for it. The aim of the radical sceptic is to undermine our confidence that our beliefs are justified, to introduce doubt. The Ny ya logicians’ response to scepticism is not to deny that there is a gap between evidence and belief, or to deny the logical possibility of the sceptical hypothesis. It is to draw a distinction between two kinds of doubt, the reasonable and the reasonless. A doubt is reasonable only when both alternatives are consistent with all the evidence and the burden of proof is symmetrically distributed between them. One paradigmatic example is the case of seeing in the distance something that might be a person or might be a tree-stump. Udayana gives the epistemology of such a case: it is a case in which one has knowledge of common aspects but not of specific distinguishing features. What we can now see is that the example gets its force only on the assumption that there is a level epistemic playing field, with both hypotheses carrying the same prima facie plausibility. Presumptive argumentation has the potential to break the impasse — imagine, for example, that the unidentified lump is just one of ten in an orderly row not there an hour ago. The perceptual evidence remains the same, but the burden of proof is on anyone who wants to maintain in this situation that the lump is a stump.
ya logicians’ response to scepticism is not to deny that there is a gap between evidence and belief, or to deny the logical possibility of the sceptical hypothesis. It is to draw a distinction between two kinds of doubt, the reasonable and the reasonless. A doubt is reasonable only when both alternatives are consistent with all the evidence and the burden of proof is symmetrically distributed between them. One paradigmatic example is the case of seeing in the distance something that might be a person or might be a tree-stump. Udayana gives the epistemology of such a case: it is a case in which one has knowledge of common aspects but not of specific distinguishing features. What we can now see is that the example gets its force only on the assumption that there is a level epistemic playing field, with both hypotheses carrying the same prima facie plausibility. Presumptive argumentation has the potential to break the impasse — imagine, for example, that the unidentified lump is just one of ten in an orderly row not there an hour ago. The perceptual evidence remains the same, but the burden of proof is on anyone who wants to maintain in this situation that the lump is a stump.
The other paradigm is knowledge of extrapolation relations. The problem here is that the thesis is one of such high generality that the burden of proof is already heavily against it! How can a few observations of smoke with fire ground a belief that there is fire whenever there is smoke? Suppositional argument has a different supportive role here. Its function is to square the scales, to neutralise the presumption against the belief in generality. It does so by finding prima facie undesirable consequences in the supposition that an associate condition or counterexample exists. Then sampling (observation only of confirmatory instances in the course of a suitably extensive search for counterexamples), though still weak evidence, can tilt the scale in its favour.
A presumptive argument moves from conjecture to unacceptable consequence. Modern writers often identify it with the medieval technique of reductio ad absurdum, but in fact its scope is wider. The ‘unacceptable consequence’ can be an out-and-out contradiction but need not be so. For we are not trying to prove that the supposition is false, but only to shift the burden of proof onto anyone who would maintain it. And for this it is enough simply to demonstrate that the supposition comes into conflict with some well-attested norm on rationality. Udayana, the first to offer any systematic discussion, does not even mention contradiction as a species of unacceptable consequence. He says25 that presumptive argumentation is of five types –
2. mutual dependence (itaretar
 raya)
raya)
3. cyclical dependence (cakraka)
The last of these is really just the generic case, what distinguishes presumptive argumentation in general. The first four form a tight logical group. If the supposition is the proposition A, then the four types of unacceptable consequence are (1) proving A from A, (2) proving A from B, and B from A, (3) proving A from B, B from C, and C from A — or any higher number of intermediate proof steps eventually leading back to A, and (4) proving A from B, B from C, C from D,…, without end. So what presumptive argumentation must show is that the supposition is ungrounded, its proof being either regressive or question-begging.
Two points are noteworthy about Udayana’s list. First, rational unacceptability bears upon the proof adduced for the supposition, not the supposition itself. The underlying implication is that one has the right to presume that one’s thesis is correct if one can find fault with the opponent’s proof of the antithesis. Principles of this sort are familiar from discussion of the informal logic of arguments from ignorance in which one claims entitlement to assert A on the grounds that it is not known (or proved) that ¬A.26 In general such a claim must be unfounded – it amounts to the universal appropriation of a presumptive right in all circumstances.
The second point to notice about Udayana’s list, however, is that it is very narrow. Udayana places strict constraints on what will count as an unacceptable consequence, constraints which are more formal than broadly rational. Conflict with other well-attested belief is not mentioned, for instance. Udayana severely limits the scope of presumptive argumentation. His motive, perhaps, is to disarm the sceptic. For presumptive argumentation is the favoured kind of reasoning of the sceptic-dialecticians (and indeed the term Udayana uses is prasa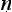 ga, the same term N
ga, the same term N g
g rjuna had used for his dialectical method). Sceptics typically will want to loosen the conditions on what constitutes an unacceptable consequence of a supposition, so that the scope for refutation is expanded. So what Udayana seems to be saying is that one does indeed have the right to presume that one’s thesis is correct when the argument for the counter-thesis commits a fallacy of a particularly gross type — not mere conflict with other beliefs but formal lack of foundation. If the best argument for the antithesis is that bad, then one has a prima facie entitlement to one’s thesis.
rjuna had used for his dialectical method). Sceptics typically will want to loosen the conditions on what constitutes an unacceptable consequence of a supposition, so that the scope for refutation is expanded. So what Udayana seems to be saying is that one does indeed have the right to presume that one’s thesis is correct when the argument for the counter-thesis commits a fallacy of a particularly gross type — not mere conflict with other beliefs but formal lack of foundation. If the best argument for the antithesis is that bad, then one has a prima facie entitlement to one’s thesis.
Śrīhar a (c. AD 1140) is an Advaita dialectician, a poet and a sceptic.27 He expands the notion of unacceptable consequence, noticing several additional types unmentioned by Udayana.28 One is ‘self-contradiction’ (vy
a (c. AD 1140) is an Advaita dialectician, a poet and a sceptic.27 He expands the notion of unacceptable consequence, noticing several additional types unmentioned by Udayana.28 One is ‘self-contradiction’ (vy gh
gh ta). It was Udayana himself29 who analysed the notion of opposition as noncompossibility, and cited as examples the statements “My mother is childless,” “I am unable to speak”, and “I do not know this jar to be a jar.” In the first instance, the noncompossibility is in what the assertion states, in the second it is in the speech-act itself, while in the third the propositional attitude self-ascription is self-refuting (a case akin to the Cartesian impossibility of thinking that one is not thinking).
ta). It was Udayana himself29 who analysed the notion of opposition as noncompossibility, and cited as examples the statements “My mother is childless,” “I am unable to speak”, and “I do not know this jar to be a jar.” In the first instance, the noncompossibility is in what the assertion states, in the second it is in the speech-act itself, while in the third the propositional attitude self-ascription is self-refuting (a case akin to the Cartesian impossibility of thinking that one is not thinking).
Another refutation-exacting circumstance is the one called ‘recrimination’ (pratibandī). This is a situation in which one’s opponent accuses one of advancing a faulty proof, when his own proof suffers exactly the same fault! There is a disagreement about what this state of equifallaciousness does to the burden of proof. The practice of Naiy yikas is to take the circumstance as tilting the balance against the opponent – the opponent discredits himself in pressing an accusation without seeing that it can be applied with equal force to his own argument. But Śrīhar
yikas is to take the circumstance as tilting the balance against the opponent – the opponent discredits himself in pressing an accusation without seeing that it can be applied with equal force to his own argument. But Śrīhar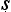 a quotes with approval Kum
a quotes with approval Kum rila’s assertion that “all things being equal, where the same fault afflicts both positions one should not be censured [and not the other]”.30
rila’s assertion that “all things being equal, where the same fault afflicts both positions one should not be censured [and not the other]”.30
Śrīhar a, the sceptic, would like to see both parties refuted by this circumstance. The same point underlies his mention as an unacceptable consequence the circumstance of ‘lack of differential evidence’ (vinigaman
a, the sceptic, would like to see both parties refuted by this circumstance. The same point underlies his mention as an unacceptable consequence the circumstance of ‘lack of differential evidence’ (vinigaman viraha), when thesis and antithesis are in the same evidential situation. Again, what we see is a jostling with the burden of proof. Here Śrīhar
viraha), when thesis and antithesis are in the same evidential situation. Again, what we see is a jostling with the burden of proof. Here Śrīhar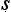 a is saying that absence of differential evidence puts a burden of proof on both thesis and antithesis — doubt itself refutes. It is the sceptic’s strategy always to seek to maximise the burden of proof, and so to deny that anyone ever has the right to presume their position to be correct. That is, as Stanisław Schayer observed a long time ago, a difference between the tarka of the Naiy
a is saying that absence of differential evidence puts a burden of proof on both thesis and antithesis — doubt itself refutes. It is the sceptic’s strategy always to seek to maximise the burden of proof, and so to deny that anyone ever has the right to presume their position to be correct. That is, as Stanisław Schayer observed a long time ago, a difference between the tarka of the Naiy yika and the prasa
yika and the prasa ga of a sceptic like Śrīhar
ga of a sceptic like Śrīhar a or N
a or N g
g rjuna.31 For the latter, the demonstration that a thesis has an allegedly false consequence does not commit the refuter to an endorsement of the antithesis. N
rjuna.31 For the latter, the demonstration that a thesis has an allegedly false consequence does not commit the refuter to an endorsement of the antithesis. N g
g rjuna wants to maintain instead that thesis and antithesis share a false existential precommitment.
rjuna wants to maintain instead that thesis and antithesis share a false existential precommitment.
Simplicity (laghutva) is, Śrīhar a considers and the Naiy
a considers and the Naiy yikas agree, a ceteris paribus preference-condition. Of two evidentially equivalent and otherwise rationally acceptable theses, the simpler one is to be preferred. The burden of proof lies with someone who wishes to defend a more complex hypothesis when a simpler one is at hand. The Ny
yikas agree, a ceteris paribus preference-condition. Of two evidentially equivalent and otherwise rationally acceptable theses, the simpler one is to be preferred. The burden of proof lies with someone who wishes to defend a more complex hypothesis when a simpler one is at hand. The Ny ya cosmological argument appeals to simplicity when it infers from the world as product to a single producer rather than a multiplicity of producers. Here too the role of the simplicity consideration is to affect the burden of proof, not itself to prove. Cohen and Nagel32 make a related point when they diagnose as the ‘fallacy of simplism’ the mistake of thinking that “of any two hypotheses, the simpler is the true one.” In any case, simplicity can be a product not of the content of a hypothesis but only of its mode of presentation — the distinction is made by the Naiy
ya cosmological argument appeals to simplicity when it infers from the world as product to a single producer rather than a multiplicity of producers. Here too the role of the simplicity consideration is to affect the burden of proof, not itself to prove. Cohen and Nagel32 make a related point when they diagnose as the ‘fallacy of simplism’ the mistake of thinking that “of any two hypotheses, the simpler is the true one.” In any case, simplicity can be a product not of the content of a hypothesis but only of its mode of presentation — the distinction is made by the Naiy yikas themselves.33 And it is hard to see how it can be rational to prefer one hypothesis to another only because it is simpler in form.
yikas themselves.33 And it is hard to see how it can be rational to prefer one hypothesis to another only because it is simpler in form.
We have assumed that the rival hypotheses are both empirically adequate, that is to say, they are both consistent with all known facts. Śrīhar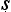 a mentions an unacceptable consequence involving empirical evidence (utsarga). It is an objection to the usual idea that if there is empirical evidence supporting one hypothesis but not the other, then the first is confirmed. Śrīhar
a mentions an unacceptable consequence involving empirical evidence (utsarga). It is an objection to the usual idea that if there is empirical evidence supporting one hypothesis but not the other, then the first is confirmed. Śrīhar a’s sceptical claim is that a hypothesis must be considered refuted unless it is conclusively proved; nonconclusive empirical evidence does nothing to affect this burden of proof. Likewise, he says, a hypothesis must be considered refuted if it is incapable of being proved or disproved — this at least seems to be the import of the unacceptable consequence he calls ‘impertinence’ (anucitya) or ‘impudence’ (vaiy
a’s sceptical claim is that a hypothesis must be considered refuted unless it is conclusively proved; nonconclusive empirical evidence does nothing to affect this burden of proof. Likewise, he says, a hypothesis must be considered refuted if it is incapable of being proved or disproved — this at least seems to be the import of the unacceptable consequence he calls ‘impertinence’ (anucitya) or ‘impudence’ (vaiy tya).
tya).
Other varieties of suppositional refutation have been suggested along lines similar to the ones we have reviewed. Different authors propose different sets of criteria for rational nonacceptance. What we have seen is that there is, in the background, a jostling over the weight and place of the burden of proof. The sceptic presses in the direction of one extreme — that a thesis can be considered refuted unless definitively proven. The constructive epistemologist tries to press in the direction of the opposite extreme — that a thesis can be considered proved unless definitively disproved. The truth lies somewhere in between, and it is the role of presumptive argumentation to locate it.
2 Buddhist Contributions in Indian Logic: Formal Criteria for Good Argumentation
2.1 The doctrine of the triple condition (trairūpya)
The Buddhist logician n
n ga (c. 480–540 AD) recommends a fundamental restructuring of the early Ny
ga (c. 480–540 AD) recommends a fundamental restructuring of the early Ny ya analysis of reasoned extrapolation and inference. Recall that analysis. It is an inference from likeness and unalikeness. In the one case, some object is inferred to have the target property on the grounds that it is ‘like’ a paradigmatic example. The untasted grain of rice is inferred to be cooked on the grounds that it is in the same pan as a test grain which is found to be cooked. In the other case, the object is inferred to have the target property on the grounds that it is ‘unlike’ an example lacking the target property. Likeness and unalikeness are matters of sharing or not sharing some property, the reason-property or evidence grounding the inference. Examples are either ‘positive’ — having both the reason and the target property, or ‘negative’ — lacking both. Extrapolation is the process of extrapolating a property from one object to another on the basis of a likeness or unalikeness between them.
ya analysis of reasoned extrapolation and inference. Recall that analysis. It is an inference from likeness and unalikeness. In the one case, some object is inferred to have the target property on the grounds that it is ‘like’ a paradigmatic example. The untasted grain of rice is inferred to be cooked on the grounds that it is in the same pan as a test grain which is found to be cooked. In the other case, the object is inferred to have the target property on the grounds that it is ‘unlike’ an example lacking the target property. Likeness and unalikeness are matters of sharing or not sharing some property, the reason-property or evidence grounding the inference. Examples are either ‘positive’ — having both the reason and the target property, or ‘negative’ — lacking both. Extrapolation is the process of extrapolating a property from one object to another on the basis of a likeness or unalikeness between them.
The difficulty is that not every such extrapolation is rational or warranted. The extrapolation of a property from one object to another is warranted only when the two objects are relevantly alike or relevantly unalike. That two objects are both blue does not warrant an extrapolation of solidity from one to the other; neither can we infer that they are different in respect to solidity because they are of different colours. What one needs, then, is a theory of relevant likeness or unalikeness, a theory, in other words, of the type of property (the reason property) two objects must share if one is to be licensed to extrapolate another property (the target property) from one to the other.
This is exactly what n
n ga gives in his celebrated theory of the ‘reason with three characteristics’ (trairūpya).
ga gives in his celebrated theory of the ‘reason with three characteristics’ (trairūpya). n
n ga’s thesis is that relevant likeness is an exclusion relation. Two objects are relevantly alike with respect to the extrapolation of a property S just in case they share a property excluded from what is other than S. In other words, a reason property H for the extrapolation of a target property S is a property no wider in extension than S (assuming that ‘non’ is such that H∩ nonS = ∅
ga’s thesis is that relevant likeness is an exclusion relation. Two objects are relevantly alike with respect to the extrapolation of a property S just in case they share a property excluded from what is other than S. In other words, a reason property H for the extrapolation of a target property S is a property no wider in extension than S (assuming that ‘non’ is such that H∩ nonS = ∅ iff H ⊆ S). Here is the crucial passage in the Pram
iff H ⊆ S). Here is the crucial passage in the Pram
 a-samuccaya, or Collection on Knowing:
a-samuccaya, or Collection on Knowing:
The phrase [from II lb] “through a reason that has three characteristics” must be explained.
[A proper reason must be] present in the site of inference and in what is like it and absent in what is not [II 5cd].
The object of inference is a property-bearer qualified by a property. After observing [the reason] there, either through perception or through inference, one also establishes in a general manner [its] presence in some or all of the same class. Why is that? Because the restriction is such that [the reason] is present only in what is alike, there is no restriction that it is only present. But in that case nothing is accomplished by saying that [the reason] is “absent in what is not”. This statement is made in order to determine that [the reason], absent in what is not [like the site of inference], is not in what is other than or incompatible with the object of inference. Here then is the reason with three characteristics from which we discern the reason-bearer.
Di n
n ga’s important innovation is to take the notions of likeness and unalikeness in extrapolation to be relative to the target property rather than the reason property. Two objects are ‘alike’ if they both have, or both lack, the target property. Two objects are ‘unalike’ if one has and the other lacks the target property. We want to know if our object — the ‘site’ of the inference — has the target property or not. What we do know is that our object has some other property, the reason property. So what is the formal feature of that reason property, in virtue of which its presence in our object determines the presence or absence of the target property? The formal feature,
ga’s important innovation is to take the notions of likeness and unalikeness in extrapolation to be relative to the target property rather than the reason property. Two objects are ‘alike’ if they both have, or both lack, the target property. Two objects are ‘unalike’ if one has and the other lacks the target property. We want to know if our object — the ‘site’ of the inference — has the target property or not. What we do know is that our object has some other property, the reason property. So what is the formal feature of that reason property, in virtue of which its presence in our object determines the presence or absence of the target property? The formal feature, n
n ga claims, is that the reason property is present only in what is alike and absent in whatever is unalike our object.
ga claims, is that the reason property is present only in what is alike and absent in whatever is unalike our object.
This can happen in one of two ways. It happens if the reason property is absent from everything not possessing the target property and present only in things possessing the target property. Then we can infer that our object too possesses the target property. It can also happen if the reason property is absent from everything possessing the target property and present only in things not possessing the target property. Then we can infer that our object does not possess the target property.
Call the class of objects which are like the site of the inference the ‘likeness class’, and the class of objects unlike the site the ‘unlikeness class’ ( n
n ga’s terms aresapak
ga’s terms aresapak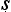 a and vipak
a and vipak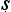 a). Interpreters have traditionally taken the likeness class to be the class of objects which possess the target property, and the unlikeness class to be the class of objects which do not possess the target property. I read
a). Interpreters have traditionally taken the likeness class to be the class of objects which possess the target property, and the unlikeness class to be the class of objects which do not possess the target property. I read n
n ga differently. I take his use of the terms ‘likeness’ and ‘unlikeness’ here at face-value, and identify the likeness class with the class of things in the same state vis-à-vis the target property as the site of the inference. We do not know in advance what that state is, but neither do we need to. The pattern of distribution of the reason property tells us what we can infer – that the site has the target property, that it lacks it, or that we can infer nothing. My approach has several virtues, chief among which is that it preserves the central idea of likeness as a relation between objects rather than, as with the traditional interpretation, referring to a property of objects. I think it also avoids many of the exegetical problems that have arisen in the contemporary literature with regard to
ga differently. I take his use of the terms ‘likeness’ and ‘unlikeness’ here at face-value, and identify the likeness class with the class of things in the same state vis-à-vis the target property as the site of the inference. We do not know in advance what that state is, but neither do we need to. The pattern of distribution of the reason property tells us what we can infer – that the site has the target property, that it lacks it, or that we can infer nothing. My approach has several virtues, chief among which is that it preserves the central idea of likeness as a relation between objects rather than, as with the traditional interpretation, referring to a property of objects. I think it also avoids many of the exegetical problems that have arisen in the contemporary literature with regard to n
n ga’s theory.
ga’s theory.
One of the traditional problems is whether the site of the inference is included in the likeness class or not.34 If the likeness class is the class of objects possessing the target property, then to include it seems to beg the question the inference is trying to resolve: does the site have that property or not. But to exclude it implies that the union of the likeness and unlikeness classes does not exhaust the universe (the site cannot, for obvious reasons, be unlike itself). So one is left with two disjoint domains, and an apparently insuperable problem of induction – how can correlations between the reason property and the target property in one domain be any guide to their correlation in another, entirely disjoint, domain?35
If we take n
n ga’s appeal to the idea of likeness at face-value, however, the problem simply does not arise. The site of the inference is in the likeness class on the assumption that likeness is a reflexive relation — but that begs no question, for we do not yet know whether the likeness class is the class of things which possess the target property, or the class of things which do not possess it. It is the class of things which are in the same state vis-à-vis the target property as the inferential site itself. We can, if needs be, refer to objects ‘like the site but not identical to it;’ or we can take likeness to be nonreflexive, and refer instead, if needs be, to ‘the site and objects like it’ — but this is a matter only of labelling, with no philosophical interest.
ga’s appeal to the idea of likeness at face-value, however, the problem simply does not arise. The site of the inference is in the likeness class on the assumption that likeness is a reflexive relation — but that begs no question, for we do not yet know whether the likeness class is the class of things which possess the target property, or the class of things which do not possess it. It is the class of things which are in the same state vis-à-vis the target property as the inferential site itself. We can, if needs be, refer to objects ‘like the site but not identical to it;’ or we can take likeness to be nonreflexive, and refer instead, if needs be, to ‘the site and objects like it’ — but this is a matter only of labelling, with no philosophical interest.
Another of the traditional problems with n
n ga’s account is an alleged logical equivalence between the second and third conditions.36 The second condition states that the reason property be present only in what is alike.37 The third condition states that it be absent in what is not. But if it is present only in what is alike, it must be absent in what is not; and if it is absent in what is not alike, it must be present only in what is. Now it is clear that
ga’s account is an alleged logical equivalence between the second and third conditions.36 The second condition states that the reason property be present only in what is alike.37 The third condition states that it be absent in what is not. But if it is present only in what is alike, it must be absent in what is not; and if it is absent in what is not alike, it must be present only in what is. Now it is clear that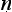 n
n ga’s reason for inserting the particle only into his formula is to prevent a possible misunderstanding. The misunderstanding would be that of taking the second condition to assert that the reason property must be present in all like objects. That would be too strong a condition, ruling out any warranted inferences in which the reason property is strictly narrower than the target. On account of the meaning of the particle only, we can see that it is also one of the two readings of the statement:
ga’s reason for inserting the particle only into his formula is to prevent a possible misunderstanding. The misunderstanding would be that of taking the second condition to assert that the reason property must be present in all like objects. That would be too strong a condition, ruling out any warranted inferences in which the reason property is strictly narrower than the target. On account of the meaning of the particle only, we can see that it is also one of the two readings of the statement:
where the particle only is inserted into the predicate position.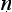 n
n ga eliminates this unwanted reading of the second condition, but he does so in a disastrous way. He eliminates it by inserting the particle into the subject position:
ga eliminates this unwanted reading of the second condition, but he does so in a disastrous way. He eliminates it by inserting the particle into the subject position:
The reason this is disastrous is that it makes the second condition logically equivalent to the third. Notice, however, that when only is in predicate position, there are still two readings. The reading one needs to isolate is the second of these two readings:
That is, the reason is present in some of what is alike.
Accordingly, the theory is this. The extrapolation of a property S to an object is grounded by the presence in that object of any property X such that X excludes nonS but not S. A reason property for S is any member of the class
The clause ‘but not S’ (the second of n
n ga’s three conditions) has a clear function now. It is there to rule out properties which exclude both nonS and S. Such properties are properties ‘unique’ to the particular object which is the site of the inference, and
ga’s three conditions) has a clear function now. It is there to rule out properties which exclude both nonS and S. Such properties are properties ‘unique’ to the particular object which is the site of the inference, and n
n ga does not accept as warranted any extrapolation based on them. I will look at his motives in the next section.
ga does not accept as warranted any extrapolation based on them. I will look at his motives in the next section.
Reason properties are nonempty subsets of the properties whose extrapolation they ground. If two objects are ‘alike’ in sharing a property, and one has a second property of wider extension than the first, then so does the second. Inductive extrapolation, in effect, is grounded in the contraposed universal generalisation “where the reason, so the target.” A difficult problem of induction remains – how can one come to know, or justifiably believe, that two properties stand in such a relation without surveying all their instances? n
n ga has no adequate answer to this problem (but see [Tuske, 1998; Peckhaus, 2001]). Dharmakīrti,
ga has no adequate answer to this problem (but see [Tuske, 1998; Peckhaus, 2001]). Dharmakīrti, n
n ga’s brilliant reinterpreter, does. His answer is that when the relation between the two properties is one of causal or metaphysical necessity, the observation of a few instances is sufficient to warrant our belief that it obtains (§2.3).
ga’s brilliant reinterpreter, does. His answer is that when the relation between the two properties is one of causal or metaphysical necessity, the observation of a few instances is sufficient to warrant our belief that it obtains (§2.3). n
n ga, however, is not interested in such questions. For him, the hard philosophical question is that of discovering the conditions for rational extrapolation. It is another issue whether those conditions can ever be known to obtain.
ga, however, is not interested in such questions. For him, the hard philosophical question is that of discovering the conditions for rational extrapolation. It is another issue whether those conditions can ever be known to obtain.
To sum up, n
n ga’s three conditions on the reason are:
ga’s three conditions on the reason are:

If we take these conditions to be independent, it follows that there are exactly seven kinds of extrapolative inferential fallacy — three ways for one of the conditions to fail, three ways for two conditions to fail, and one way for all three conditions to fail. So the new theory puts the concept of a fallacy on a more formal footing. A fallacy is no longer an interesting but essentially ad hoc maxim on reasoned argument. It is now a formal failing of the putative reason to stand in the correct extrapolation-grounding relation. One way for the reason to fail is by not attaching to the site at all, thereby failing to ground any extrapolation of other properties to it. This is a failure of the first condition. Another way for the reason to fail is by ‘straying’ onto unlike objects, thereby falsifying the third condition. The presence of one property cannot prove the presence of another if it is sometimes present where the other one is not. (It can, however, prove the absence of the other if it is only present where the other is not — and then the absence of the first property is a proof of the presence of the second.) We might then think of the third condition as a ‘no counter-example’ condition, a counter-example to the extrapolation-warranting relation of subsumption being an object where the allegedly subsumed property is present along with the absence of its alleged subsumer. An extrapolation is grounded just as long as there are no counterexamples.
2.2 Di n
n ga’s ‘wheel of reasons’ (hetucakra)
ga’s ‘wheel of reasons’ (hetucakra)
In addition to his Pram
 a-samuccaya,
a-samuccaya, n
n ga wrote another, very brief text on logic, the Wheel of Reasons, or Hetucakranir
ga wrote another, very brief text on logic, the Wheel of Reasons, or Hetucakranir aya.
aya. n
n ga’s aim here is to classify all the different types of argument which fit into the general schema 〈p has s because it has h〉, and to give an example of each. It is here that he applies his theory of a triple-conditioned sign to show when an inference is sound or unsound, and the kinds of defect an inferential sign can suffer from. Hence, it leads to a classification of fallacious and non-fallacious inferences.
ga’s aim here is to classify all the different types of argument which fit into the general schema 〈p has s because it has h〉, and to give an example of each. It is here that he applies his theory of a triple-conditioned sign to show when an inference is sound or unsound, and the kinds of defect an inferential sign can suffer from. Hence, it leads to a classification of fallacious and non-fallacious inferences.
The ‘wheel’ or ‘cycle’ is in fact a 3 by 3 square, giving nine inference types. n
n ga derives the square as follows. A ‘homologue’ (sapak
ga derives the square as follows. A ‘homologue’ (sapak a) is defined as any object (excluding the locus of the inference) which is possesses the inferrable property, s. Now, a putative inferential sign, h, might be either (i) present in every homologue, (ii) present in only some of the homologues but not in others, or (iii) present in no homologue. Suppose we let ‘sp’ stand for the class of homologues. Then we can represent these three possibilities as ‘sp+’, ‘sp±’, and ‘sp-’ respectively. The same three possibilities are also available with respect to the class of heterologues (objects, excluding the locus, which do not possess the inferred property, s). We can denote these by ‘vp+’, ‘vp±’, and ‘vp-’ respectively. Thus, ‘vp+’ means that every member of vp (every heterologue) possesses the sign property, h, etc. Now since any putative inferential sign must either be present in all, some or no homologue, and also in either all, some or no heterologue, there are just nine possibilities (Figure 2):
a) is defined as any object (excluding the locus of the inference) which is possesses the inferrable property, s. Now, a putative inferential sign, h, might be either (i) present in every homologue, (ii) present in only some of the homologues but not in others, or (iii) present in no homologue. Suppose we let ‘sp’ stand for the class of homologues. Then we can represent these three possibilities as ‘sp+’, ‘sp±’, and ‘sp-’ respectively. The same three possibilities are also available with respect to the class of heterologues (objects, excluding the locus, which do not possess the inferred property, s). We can denote these by ‘vp+’, ‘vp±’, and ‘vp-’ respectively. Thus, ‘vp+’ means that every member of vp (every heterologue) possesses the sign property, h, etc. Now since any putative inferential sign must either be present in all, some or no homologue, and also in either all, some or no heterologue, there are just nine possibilities (Figure 2):
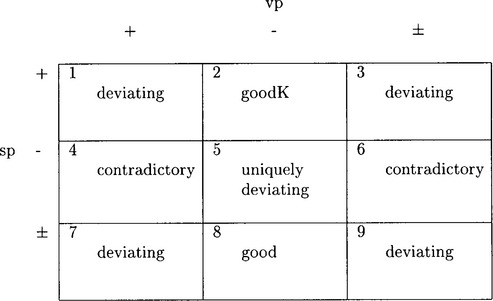
Figure 2
Why does n
n ga say that only 2 and 8 are cases of a good inferential sign? Recall the three conditions on a good sign. The first is that the inferential sign must be present in the locus of inference. This is taken for granted in the wheel. The second states that the inferential sign should be present in some (at least one) homologous case. In other words, a good sign is one for which either ‘sp+’ or ‘sp±’. Thus the second condition rules out 4, 5 and 6. Similarly, the third condition states that the inferential sign should be absent from any heterologous case, i.e. that ‘vp-’. This rules out 1, 4, 7 and 3, 6, 9. So only 2 and 8 represent inferential signs which meet all three conditions and generate good inferences. Note here that the third condition alone is sufficient to rule out every fallacious case except 5. Hence, seeing why
ga say that only 2 and 8 are cases of a good inferential sign? Recall the three conditions on a good sign. The first is that the inferential sign must be present in the locus of inference. This is taken for granted in the wheel. The second states that the inferential sign should be present in some (at least one) homologous case. In other words, a good sign is one for which either ‘sp+’ or ‘sp±’. Thus the second condition rules out 4, 5 and 6. Similarly, the third condition states that the inferential sign should be absent from any heterologous case, i.e. that ‘vp-’. This rules out 1, 4, 7 and 3, 6, 9. So only 2 and 8 represent inferential signs which meet all three conditions and generate good inferences. Note here that the third condition alone is sufficient to rule out every fallacious case except 5. Hence, seeing why n
n ga considers ‘type-5’ inferences to be unsound will reveal why he considered the second of the three conditions to be necessary (see below).
ga considers ‘type-5’ inferences to be unsound will reveal why he considered the second of the three conditions to be necessary (see below).
 n
n ga next gives an illustration of each of the nine possibilities. They can be tabulated, as in Figure 3.
ga next gives an illustration of each of the nine possibilities. They can be tabulated, as in Figure 3.
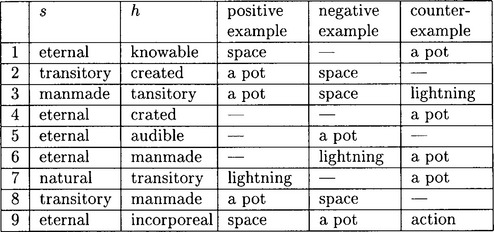
Figure 3
In each case, the locus of the inference is sound. Note that wherever possible, n
n ga cites both a ‘positive confirming example’, i.e. an object where both h and s are present, as well as a negative confirming example’, i.e. an object where neither h nor s is present. Both support the inference. He also cites, where relevant, a ‘counter-example’, i.e. a case where h is present but s is absent. The existence of a counter-example undermines the inference. Let us look at four representative cases.
ga cites both a ‘positive confirming example’, i.e. an object where both h and s are present, as well as a negative confirming example’, i.e. an object where neither h nor s is present. Both support the inference. He also cites, where relevant, a ‘counter-example’, i.e. a case where h is present but s is absent. The existence of a counter-example undermines the inference. Let us look at four representative cases.
Case 2: A warranted inference. This inference reads: Sound is transitory, because it is created, e.g. a pot; space. Intuitively, this inference is sound, because the reason-property, createdness, is present only in places where the inferred property, transitoriness, is also present. Hence createdness is a good sign of transitoriness. The inference is supported first by an example where both are present, a pot, and second by an example where neither are present, space.
Case 3: ‘deviating’ (asiddha). This inference reads: Sound is manmade, because it is transitory, e.g. a pot; space. Intuitively, this inference is unsound, because the reason-property, transitoriness, is present in places where the inferred property, manmade, is absent. The counterexample cited is lightning — transitory but not manmade. Because we can find such a counter-example, the inferential sign is said to ‘deviate’ from the inferred property. Deviating inferences are ones which satisfy the second condition but fail the third.
Case 6: ‘contradictory’ (viruddha). The inference reads: Sound is eternal, because it is manmade, e.g. lightning. The sign here fails both conditions 2 and 3 — there is no case of a thing which is eternal and manmade, but there is a counter-example, for instance, a pot, which is manmade but non-eternal. Such an inference is called ‘contradictory’ because we can in fact infer to the contrary conclusion, namely that sound is non-eternal because it is manmade. We can do this because in the contrary inference, the homologous and heterologous domains are switched round.
Case 5: ‘specific’ (as dh
dh ra
ra a). Sound is eternal, because it is audible, e.g. a pot. The first point to notice is that there are no counter-examples to this inference, for there are no examples, outside the ‘locus’ domain of sounds, of an audible thing which is non-eternal. This is because there are no audible things other than sounds! Hence the third condition seems to be satisfied trivially. The characteristic of type-5 inferences is that the reason-property is ‘unique’ to the locus. According to
a). Sound is eternal, because it is audible, e.g. a pot. The first point to notice is that there are no counter-examples to this inference, for there are no examples, outside the ‘locus’ domain of sounds, of an audible thing which is non-eternal. This is because there are no audible things other than sounds! Hence the third condition seems to be satisfied trivially. The characteristic of type-5 inferences is that the reason-property is ‘unique’ to the locus. According to n
n ga, such inferences are unsound, and the reason is that they fail the second condition – there is no homologue, i.e. an eternal thing other than sound, which is also audible.
ga, such inferences are unsound, and the reason is that they fail the second condition – there is no homologue, i.e. an eternal thing other than sound, which is also audible.
But this just restates the characteristic feature of such inferences, it doesn’t explain why they are unsound. Some modern authors argue that the significance of the second condition is more epistemological, than logical: the second condition implies that there must be a positive supporting example, and without such an example the inference, even if sound, carries no conviction. n
n ga might, however, have had a more formal or logical reason for rejecting type-5 inferences. The universal rule here is “Whatever is audible, apart from sound, is eternal”. Now if a universal rule of the form ‘(∀x)(Fx → Gx)’ is made true by there being no Fs, then so is the rule ‘(∀x)(Fx → not-Gx)’ Hence, we could equally infer that sound is non-eternal because it is audible! This resembles the fault which the Ny
ga might, however, have had a more formal or logical reason for rejecting type-5 inferences. The universal rule here is “Whatever is audible, apart from sound, is eternal”. Now if a universal rule of the form ‘(∀x)(Fx → Gx)’ is made true by there being no Fs, then so is the rule ‘(∀x)(Fx → not-Gx)’ Hence, we could equally infer that sound is non-eternal because it is audible! This resembles the fault which the Ny ya called ‘prakara
ya called ‘prakara asama’ or ‘indecisive’
asama’ or ‘indecisive’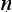 n
n ga, it seems, wants to avoid this by saying that ‘(∀x)(Fx → Gx)’ is true only if there is at least one F, which leads to the second condition.
ga, it seems, wants to avoid this by saying that ‘(∀x)(Fx → Gx)’ is true only if there is at least one F, which leads to the second condition.
Let us consider the argument from specifics further. I have said that an extrapolation-grounding property is a nonempty subproperty — a property narrower in extension than the property being extrapolated, and resident at least in the object to which that property is being extrapolated. The sweet smell of a lotus is a ground for extrapolating that it has a fragrance; its being a blue lotus is a ground for extrapolating its being a lotus. Extrapolation is a move from the specific to the general, from species to genus, from conjunction to conjunct. Extrapolation is a move upwards in the hierarchy of kinds. This model of extrapolation works well in most cases, but what happens at the extremes? The extreme in one direction is a most general property of all, a property possessed by everything. Existence or ‘reality’, if it is a property, is a property like this, and the theory entails that existence is always extrapolatable — the inference ‘a is, because a is F’ is always warranted. n
n ga’s theory faces a minor technical difficulty here. Since everything exists, then everything is ‘like’ the site of the inference (in the same state as the site with respect to existence), and the unlikeness class is empty. So
ga’s theory faces a minor technical difficulty here. Since everything exists, then everything is ‘like’ the site of the inference (in the same state as the site with respect to existence), and the unlikeness class is empty. So n
n ga has to be able to maintain that his third condition — absence of the reason property in every unlike object — is satisfied when there are no unlike objects. The universal quantifier must have no existential import. His innovative distinction between inference ‘for oneself’ (sv
ga has to be able to maintain that his third condition — absence of the reason property in every unlike object — is satisfied when there are no unlike objects. The universal quantifier must have no existential import. His innovative distinction between inference ‘for oneself’ (sv rth
rth num
num na) and inference ‘for others’ (par
na) and inference ‘for others’ (par rth
rth num
num na) is a help here. It is the distinction between the logical preconditions for warranted extrapolation and the debate-theoretic exigencies of persuasion. While it might be useful, even necessary, to be able to cite a supporting negative example if one’s argument is to carry conviction and meet the public norms on believable inference, there is no corresponding requirement that the unlikeness class be nonempty if an extrapolation is to be warranted.
na) is a help here. It is the distinction between the logical preconditions for warranted extrapolation and the debate-theoretic exigencies of persuasion. While it might be useful, even necessary, to be able to cite a supporting negative example if one’s argument is to carry conviction and meet the public norms on believable inference, there is no corresponding requirement that the unlikeness class be nonempty if an extrapolation is to be warranted.
What happens at the other extreme? Extrapolation is a move from the more specific to the less specific, and the limit is the case when the reason property is entirely specific to the site of the inference. There is no doubt but that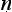 n
n ga thinks that extrapolation breaks down at this limit. He calls such reason properties ‘specific indeterminate’ (as
ga thinks that extrapolation breaks down at this limit. He calls such reason properties ‘specific indeterminate’ (as dh
dh ra
ra
 naik
naik ntika), and classifies them as bogus-reasons. Indeed it is the entire function of his second condition to rule out such properties. That is why the second condition insists that the reason property must be present in an object like the site. This condition is an addition to the first, that the reason property be present in the site — it demands that the reason be present in some other object like but not identical to the site.
ntika), and classifies them as bogus-reasons. Indeed it is the entire function of his second condition to rule out such properties. That is why the second condition insists that the reason property must be present in an object like the site. This condition is an addition to the first, that the reason property be present in the site — it demands that the reason be present in some other object like but not identical to the site. n
n ga’s example in the Collection on Knowing [II 7d] is:
ga’s example in the Collection on Knowing [II 7d] is:
| [Thesis] | Sound is noneternal. |
| [Reason] | Because it is audible. |
In the Wheel of Reasons [5cd–7a], he gives another example:
| [Thesis] | Sound is eternal. |
| [Reason] | Because it is audible. |
What is the difference? In fact, the difference between these two examples holds the key to what n
n ga thinks is wrong. The property audibility, something specific to sound, does not determine whether sound is eternal or noneternal. In either case, audibility is absent from what is unlike sound (because it is unique to sound) but also from what is like sound (except for sound itself). This symmetry in the distribution of the reason property undermines its capacity to discriminate between truth and falsity. To put it another way, if we take the universal quantifier to range over everything except the site of the inference, sound, then it is true both that everything audible is eternal and that everything audible is noneternal – both are true only because there are no audibles in the range of the quantifier.
ga thinks is wrong. The property audibility, something specific to sound, does not determine whether sound is eternal or noneternal. In either case, audibility is absent from what is unlike sound (because it is unique to sound) but also from what is like sound (except for sound itself). This symmetry in the distribution of the reason property undermines its capacity to discriminate between truth and falsity. To put it another way, if we take the universal quantifier to range over everything except the site of the inference, sound, then it is true both that everything audible is eternal and that everything audible is noneternal – both are true only because there are no audibles in the range of the quantifier.
This seems to be n
n ga’s point, but it is not very satisfactory. Sound is either eternal or noneternal, and so audibility is a subproperty of one or the other. One and only one of the above universal quantifications is true when the quantifier is unrestricted. In any case, just why is it that we should not reason from the specific properties of a thing? We do it all the time. Historical explanations are notoriously singular — unrepeated historical events are explained by specific features of their context.
ga’s point, but it is not very satisfactory. Sound is either eternal or noneternal, and so audibility is a subproperty of one or the other. One and only one of the above universal quantifications is true when the quantifier is unrestricted. In any case, just why is it that we should not reason from the specific properties of a thing? We do it all the time. Historical explanations are notoriously singular — unrepeated historical events are explained by specific features of their context.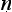 n
n ga, it seems, is like the follower of the deductive-nomological model in insisting on repeatability as a criterion of explanation. What about mundane cases like this one: the radio has stopped because I have unplugged it? Being unplugged by me is a property specific to the radio, and yet the form of the explanation seems unapproachable. Perhaps, however, what one should say is that the explanatory property is ‘being unplugged’, and not ‘being unplugged by me’, and the explanation rests on the generalisation ‘whenever a radio is unplugged, it stops.’ So then the restriction is not to any property specific to the site, but only to those which are not merely tokens of some more general explanatory property. And yet there are still intuitively rational but specific inferences — that salt is soluble because it has a certain molecular structure, that helium is inert because it has a certain atomic number, flying creatures fly because they have wings. Why shouldn’t the specific properties of a thing be implicated in inferences of its other properties?
ga, it seems, is like the follower of the deductive-nomological model in insisting on repeatability as a criterion of explanation. What about mundane cases like this one: the radio has stopped because I have unplugged it? Being unplugged by me is a property specific to the radio, and yet the form of the explanation seems unapproachable. Perhaps, however, what one should say is that the explanatory property is ‘being unplugged’, and not ‘being unplugged by me’, and the explanation rests on the generalisation ‘whenever a radio is unplugged, it stops.’ So then the restriction is not to any property specific to the site, but only to those which are not merely tokens of some more general explanatory property. And yet there are still intuitively rational but specific inferences — that salt is soluble because it has a certain molecular structure, that helium is inert because it has a certain atomic number, flying creatures fly because they have wings. Why shouldn’t the specific properties of a thing be implicated in inferences of its other properties?
What we see here is n
n ga’s adherence to a strictly inductivist model of extrapolation. The specific property audibility does not ground an extrapolation of eternality or noneternality because there can be no inductive evidence for the extrapolation. Inductive evidence takes the form of objects in the likeness and unlikeness classes known to have or not to have the reason. One might think that one does have at least ‘negative’ evidence, for one knows that audibility is absent from any object in the unlikeness class. So why can one not infer from the fact that audibility is absent in unlike objects that it must be present in like objects? The answer is that one can indeed make that inference, but it does not get one very far. For we must recall again the way these classes are defined – as classes of objects like or unlike the site with respect to eternality. We do not know whether the site is eternal or noneternal, and in consequence we do not know whether unlike things are things which are noneternal or eternal. So while we have plenty of examples of eternal inaudibles and noneternal inaudibles, we still do not know which are the ‘alike’ ones and which the ‘unalike’.
ga’s adherence to a strictly inductivist model of extrapolation. The specific property audibility does not ground an extrapolation of eternality or noneternality because there can be no inductive evidence for the extrapolation. Inductive evidence takes the form of objects in the likeness and unlikeness classes known to have or not to have the reason. One might think that one does have at least ‘negative’ evidence, for one knows that audibility is absent from any object in the unlikeness class. So why can one not infer from the fact that audibility is absent in unlike objects that it must be present in like objects? The answer is that one can indeed make that inference, but it does not get one very far. For we must recall again the way these classes are defined – as classes of objects like or unlike the site with respect to eternality. We do not know whether the site is eternal or noneternal, and in consequence we do not know whether unlike things are things which are noneternal or eternal. So while we have plenty of examples of eternal inaudibles and noneternal inaudibles, we still do not know which are the ‘alike’ ones and which the ‘unalike’.
The explanation of salt’s solubility by its specific molecular structure exemplifies a quite different model of explanation. It is a theoretical explanation resting on the postulates of physical chemistry. It is from theory, not from observation, that one infers that having an NaCl lattice structure is a subproperty of being soluble. Similarly, within the context of suitable theories about the nature of sound and secondary qualities, one might well be able to infer from sound’s being audible to its being noneternal.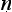 n
n ga, in spite of his brilliance and originality, could not quite free himself from the old model of inference from sampling. His inclusion of the second condition was a concession to this old tradition. He should have dropped it. Later Buddhists, beginning with Dharmakīrti, did just that – they effectively dropped the second condition by adopting the reading of it that makes it logically equivalent to the third.
ga, in spite of his brilliance and originality, could not quite free himself from the old model of inference from sampling. His inclusion of the second condition was a concession to this old tradition. He should have dropped it. Later Buddhists, beginning with Dharmakīrti, did just that – they effectively dropped the second condition by adopting the reading of it that makes it logically equivalent to the third.
 Din
Din ga’s insistence that any acceptible inference should be accompanied by both positive and negative supporting examples provoked the Naiy
ga’s insistence that any acceptible inference should be accompanied by both positive and negative supporting examples provoked the Naiy yika Uddyotakara to criticise and expand the Wheel. Uddyotakara points out that there are sound patterns of inference in which either the class of homologues or the class of heterologues is empty. These he calls the ‘universally negative’ (kevala-vyatikekin) and ‘universally positive’ (keval
yika Uddyotakara to criticise and expand the Wheel. Uddyotakara points out that there are sound patterns of inference in which either the class of homologues or the class of heterologues is empty. These he calls the ‘universally negative’ (kevala-vyatikekin) and ‘universally positive’ (keval nvayin) inferences. We now have a wheel with sixteen possible cases (Figure 4):
nvayin) inferences. We now have a wheel with sixteen possible cases (Figure 4):
Figure 4
Here, ‘o’ means that the class (sp or vp) is empty. An example of a sound ‘universally positive’ inference might be: “This exists because I can see it”. There are no heterologues, because there are no things which do not exist, and so there are no negatively supporting examples. Nevertheless, we should recognise the acceptibility such an inference. Examples of ‘universally negative’ inferences are more difficult to find. The later Ny ya link such inferences with their theory of definition, considering such examples as “Cows are distinct from non-cows, because they have dewlap’. There are no objects which are distinct from non-cows except for cows, and hence no homologues. But the inference might have significance, for it tells us that the property of having dewlap serves to distinguish cows from non-cows, and hence can be used as a definition of cowhood38.
ya link such inferences with their theory of definition, considering such examples as “Cows are distinct from non-cows, because they have dewlap’. There are no objects which are distinct from non-cows except for cows, and hence no homologues. But the inference might have significance, for it tells us that the property of having dewlap serves to distinguish cows from non-cows, and hence can be used as a definition of cowhood38.
2.3 Arguments from effect, essence and non-observation
Dharmakīrti (AD 600–660) offers a substantive account of the conditions under which the observation of a sample warrants extrapolation. His claim is that this is so if the reason property is one of three types: an ‘effect’ reason (k rya-hetu), a natural reason (svabh
rya-hetu), a natural reason (svabh va-hetu), or a reason based on nonobservation (anupalabdhi-hetu).39.
va-hetu), or a reason based on nonobservation (anupalabdhi-hetu).39.
In each case, the presence of the reason in some sense necessitates the presence of the target. An effect-reason is a property whose presence is causally necessitated by the presence of the target property – for example, inferring that the mountain has fire on it, because of smoke above it. The reason-target relation is a causal relation. Clearly one can, and later philosophers40 indeed did, extend this to cover other species of causal inference, such as cases when reason and target are both effects of a common cause. The generalisation ‘night follows day’ is true, not because day causes night but because both day and night are caused by the rotation of the earth. An example often cited is the inference of lemon-colour from lemon-taste, when both are products of the same cause, viz. the lemon itself. Still another example is the inference of ashes from smoke: ashes and smoke are both effects of fire. Such an inference has two steps. First, fire is inferred from smoke; second, ash is inferred from fire. The second step, in which we infer an effect from its cause, is possible only because ash is a necessary effect of fire.
A natural reason is one whose presence metaphysically necessitates that of the target property, for example the inference that something is a tree because it is a  i
i
 ap
ap (a species of tree). Dharmakīrti appears to regard the law “all
(a species of tree). Dharmakīrti appears to regard the law “all  i
i
 ap
ap s are trees” as necessarily true, even if its truth has to be discovered by observation, and thus to anticipate the idea that there are a posteriori necessities.41 He states, surprisingly, that the reason-target relation in such inferences is the relation of identity. Why? Perhaps his idea is that the two properties being-a-
s are trees” as necessarily true, even if its truth has to be discovered by observation, and thus to anticipate the idea that there are a posteriori necessities.41 He states, surprisingly, that the reason-target relation in such inferences is the relation of identity. Why? Perhaps his idea is that the two properties being-a- i
i
 ap
ap and being-a-tree are token-identical, for the particular tree does not have two distinct properties, being-a-
and being-a-tree are token-identical, for the particular tree does not have two distinct properties, being-a- i
i
 ap
ap and a separate property being-a-tree, any more than something which weighs one kilogramme has two properties, having-weight and having-weight-one-kilogramme. The properties as types are distinct, but their tokens in individual objects are identical. Trope-theoretically, the point can easily be understood. The very same trope is a member of two properties, one wider in extension than the other, just as the class of blue tropes is a subset of the class of colour tropes. But a blue object does not have two tropes – one from the class of blue tropes and one from the class of colour tropes. It is the self-same trope.
and a separate property being-a-tree, any more than something which weighs one kilogramme has two properties, having-weight and having-weight-one-kilogramme. The properties as types are distinct, but their tokens in individual objects are identical. Trope-theoretically, the point can easily be understood. The very same trope is a member of two properties, one wider in extension than the other, just as the class of blue tropes is a subset of the class of colour tropes. But a blue object does not have two tropes – one from the class of blue tropes and one from the class of colour tropes. It is the self-same trope.
Is absence of evidence evidence of absence? According to Dharmakīrti, nonobservation sometimes proves absence: my failure to see an object, when all the conditions for its perception are met, is grounds for an inference that it is not here. The pattern of argument such inferences exemplify was known to the medievals as argumentum ad ignorantiam, or an ‘argument from ignorance.’ The pattern occurs whenever one infers that p on the grounds that there is no evidence that p is false. Dharmakīrti states that the argument depends on the object’s being perceptible, i.e. that all the conditions for its perception (other than its actual presence) are met in the given situation. Douglas Walton, in a major study of arguments from ignorance,42 claims that they depend for their validity on an implicit conditional premise — if p were false, p would be known to be false. The characteristics of an argument from ignorance are then a ‘lack-of-knowledge’ premise — it is not known that not-p, and a ‘search’ premise — if p were false, it would be known that not-p. The underlying hidden premise mentioned by Dharmakīrti seems to be exactly the one Walton gives: if the object were here, one would see it. The necessity here is subjunctive. The argument has a presumptive status – one has a right to presume the conclusion to be true to the extent that one has searched for and failed to find counter-evidence. It is this idea that is strikingly absent in n
n ga. Warranted extrapolation depends not on the mere nonobservation of counterexamples, but on one’s failing to find them in the course of a suitably extensive search.
ga. Warranted extrapolation depends not on the mere nonobservation of counterexamples, but on one’s failing to find them in the course of a suitably extensive search.
In each of the three cases, the universal relation between reason and target is a relation not of coincidence but of necessity – causal, metaphysical or subjunctive. Dharmakīrti’s solution to the problem of induction, then, is to claim that observation supports a generalisation only when that generalisation is lawlike or necessary. In this, I think he anticipates the idea that the distinction between lawlike and accidental generalisations is that only the former support the counterfactual ‘if the reason property were instantiated here, so would be the target property’. In such a context, let us note, the observation of even a single positive example might sometimes be sufficient to warrant the extrapolation: I infer that any mango is sweet having tasted a single mango; I infer that any fire will burn having once been burnt.
Extrapolation is warranted when the reason-target is lawlike, but it does not follow that the extrapolator must know that it is lawlike. What Dharmakīrti has succeeded in doing is to describe the conditions under which extrapolation works — the conditions under which one’s actions, were they to be in accordance with the extrapolation, would meet with success. It is a description of the type of circumstance in which extrapolation is rewarded (i.e. true — if, as it seems, Dharmakīrti has a pragmatic theory of truth43). As to how, when or whether one can know that one is in such a circumstance, that is another problem altogether and not one that Dharmakīrti has necessarily to address. For a general theory of rationality issues in conditions of the form ‘in circumstances C, it is rational to do ϕ’ or ‘in circumstances C, it is rational to believe p’. And this is precisely the form Dharmakīrti’s conditions take.
2.4 The Jaina reformulation of the triple condition
 n
n ga had argued that there are three marks individually necessary and jointly sufficient for the warranted extrapolation from reason to target (§2.2). They are (1) that the reason be present in the site of the extrapolation, (2) that the reason be present (only) in what is similar to the target, and (3) that the reason be absent in what is dissimilar to the target. The second of these conditions is, arguably, equivalent to the third, which asserts that the reason property is absent when the target property is absent. That was supposed to capture the idea of a ‘no counterexample’ condition, according to which an extrapolation is warranted just in case there is nothing in which the reason is present but not the target. What happens to this account if one allows, as the Jaina logicians do, that a property and its absence be compossible in a single object?44 What happens is that the three marks cease to be sufficient for warranted extrapolation. In particular, the third mark no longer captures the idea behind the ‘no counterexample’ condition. For now the absence of the reason property in a place where the target is absent does not preclude its presence there too! So the third mark can be satisfied and yet there still be counterexamples — cases of the presence of the reason together with the absence of the target.
ga had argued that there are three marks individually necessary and jointly sufficient for the warranted extrapolation from reason to target (§2.2). They are (1) that the reason be present in the site of the extrapolation, (2) that the reason be present (only) in what is similar to the target, and (3) that the reason be absent in what is dissimilar to the target. The second of these conditions is, arguably, equivalent to the third, which asserts that the reason property is absent when the target property is absent. That was supposed to capture the idea of a ‘no counterexample’ condition, according to which an extrapolation is warranted just in case there is nothing in which the reason is present but not the target. What happens to this account if one allows, as the Jaina logicians do, that a property and its absence be compossible in a single object?44 What happens is that the three marks cease to be sufficient for warranted extrapolation. In particular, the third mark no longer captures the idea behind the ‘no counterexample’ condition. For now the absence of the reason property in a place where the target is absent does not preclude its presence there too! So the third mark can be satisfied and yet there still be counterexamples — cases of the presence of the reason together with the absence of the target.
The Jainas indeed claim that the three marks are neither necessary nor sufficient for warranted extrapolation. Their response is to substitute for the three marks a new, single, mark. It is clear that if the presence and absence of a property are compossible, then a distinction needs to be drawn between absence and nonpresence. The first is consistent with the presence of the property; the second is not. Early post- n
n ga Jainas like Akala
ga Jainas like Akala ka and Siddhasena described the new mark in quasi-Buddhistic terms, as ‘no presence without’ (a-vin
ka and Siddhasena described the new mark in quasi-Buddhistic terms, as ‘no presence without’ (a-vin -bh
-bh va) — i.e. no presence of the reason without the target. Thus Akala
va) — i.e. no presence of the reason without the target. Thus Akala ka:45
ka:45
An extrapolation is a cognition of what is signified from a sign known to have the single mark of no presence without the target (s dhy
dhy vin
vin bh
bh va). Its result is blocking and other cognitions.
va). Its result is blocking and other cognitions.
The relata of the causality and identity relations cannot be cognised without the suppositional knowledge (tarka) of their being impossible otherwise, [which is] the proof that this is the single mark even without those relations. Nor is a tree the own-nature (svabh va) or the effect (k
va) or the effect (k rya) of such things as shade. And there is no disagreement here.
rya) of such things as shade. And there is no disagreement here.
There is an obvious reference to and criticism of Dharmakīrti here,46 and also a mention of the important idea, which we have already discussed, that presumptive argumentation (tarka) is what gives us knowledge of the universal generalisations grounding extrapolations. The crucial difference from the Buddhists is in the meaning of ‘no presence’. For the Jainas, it has to stand for nonpresence and not for absence. That led them to reformulate the reason-target relation as a relation of necessitation. Siddhasena:
The mark of a reason is ‘being impossible otherwise’ (anyath nupannatva) [Ny
nupannatva) [Ny y
y vat
vat ra 22].
ra 22].
V dideva Sūri gives the developed Jaina formulation:
dideva Sūri gives the developed Jaina formulation:
A reason has a single mark, ‘determined as impossible otherwise’. It does not have three marks, for fallacies are then still possible [Pram
 anayatatt
anayatatt lok
lok la
la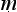 k
k ra 3.11–12].
ra 3.11–12].
The idea is that the reason cannot be present if the target is not. It is impossible for the reason to be present otherwise than if the target is present. The presence of the reason necessitates the presence of the target.
I said that n
n ga’s three marks are, for the Jainas, neither necessary nor sufficient. They are not sufficient because they permit extrapolation when the reason is both present and absent, and the target nonpresent. On what grounds are they thought not to be necessary? The theory of extrapolation as developed first by the early Naiy
ga’s three marks are, for the Jainas, neither necessary nor sufficient. They are not sufficient because they permit extrapolation when the reason is both present and absent, and the target nonpresent. On what grounds are they thought not to be necessary? The theory of extrapolation as developed first by the early Naiy yikas and then by
yikas and then by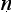 n
n ga has a built-in simplifying assumption. The assumption is that extrapolation is always a matter of inferring from the presence of one property in an object to the presence of a second property in that same object. But that assumption excludes many intuitively warranted extrapolations. The main examples considered by the Jainas are; (i) the
ga has a built-in simplifying assumption. The assumption is that extrapolation is always a matter of inferring from the presence of one property in an object to the presence of a second property in that same object. But that assumption excludes many intuitively warranted extrapolations. The main examples considered by the Jainas are; (i) the  aka
aka a star-group will rise because k
a star-group will rise because k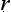 ttik
ttik star-group has risen; (ii) the sun is above the horizon because the earth is in light; (iii) there is a moon in the sky because there is a moon in the water.
star-group has risen; (ii) the sun is above the horizon because the earth is in light; (iii) there is a moon in the sky because there is a moon in the water.
These examples are said to prove that the first of
 ga’s three marks, that the reason property is present in the site, is not a necessary condition on warranted extrapolation. And yet, while it is certainly desirable to broaden the reach of the theory to cover new patterns of extrapolative inference, it is not very clear what these examples show. What is the underlying generalisation? What are the similar and dissimilar examples? In the first case, the extrapolation seems to be grounded in the universal generalisation ‘whenever the k
ga’s three marks, that the reason property is present in the site, is not a necessary condition on warranted extrapolation. And yet, while it is certainly desirable to broaden the reach of the theory to cover new patterns of extrapolative inference, it is not very clear what these examples show. What is the underlying generalisation? What are the similar and dissimilar examples? In the first case, the extrapolation seems to be grounded in the universal generalisation ‘whenever the k ttik
ttik arises, so too does the
arises, so too does the  aka
aka a.’ But then there is indeed a single site of extrapolation — the present time. The inference is: the
a.’ But then there is indeed a single site of extrapolation — the present time. The inference is: the  aka
aka a will rise now because k
a will rise now because k ttik
ttik has now risen. A similar point could be made about the second example. There seems indeed to be an implicit temporal reference in both of the first two cases, an extrapolation grounded in a universal generalisation over times.
has now risen. A similar point could be made about the second example. There seems indeed to be an implicit temporal reference in both of the first two cases, an extrapolation grounded in a universal generalisation over times.
The third case is more convincing, yet here too one might try to discern a common site. For the true form of the extrapolation is: the moon is in the sky because it is reflected in the water, an extrapolation grounded in a universal generalisation of the form ‘objects cause their own reflections’. Certainly, however, there are patterns of extrapolation for which the ‘single site’ condition does not hold. If, for example, one can find a universal generalisation of the form ‘∀x∃y(Fx → Gy)’, then from ‘∃xFx’ one can infer ‘∃xGx’. Perhaps this is the pattern of extrapolation the Jainas intend to exemplify with their example of a sky-moon and a water-moon. If so, it is represents an important criticism of a simplifying, but in the end also restricting, assumption in the classical theory of extrapolation.
3 Jaina Contributions in Indian Logic: the Logic of Assertion
3.1 Rationality and Consistency
What is the rational response when confronted with a set of propositions each of which we have some reason to accept, and yet which taken together form an inconsistent class? This was, in a nutshell, the problem addressed by the Jaina logicians of classical India, and the solution they gave is, I think, of great interest, both for what it tells us about the relationship between rationality and consistency, and for what we can learn about the logical basis of philosophical pluralism. The Jainas claim that we can continue to reason in spite of the presence of inconsistencies, and indeed construct a many-valued logical system tailored to the purpose. My aim in this chapter is to offer an interpretation of that system and to try to draw out some of its philosophical implications.
There was in classical India a great deal of philosophical activity. Over the years, certain questions came to be seen as fundamental, and were hotly contested. Are there universals? Do objects endure or perdure? Are there souls, and, if so, are they eternal or non-eternal entities? Do there exist wholes over and above collections of parts? Different groups of philosophers offered different answers to these and many other such questions, and each, moreover, was able to supply plausible arguments in favour of their position, or to offer a world-view from which their particular answers seemed true. The body of philosophical discourse collectively contained therefore, a mass of assertions and contradictory counter-assertions, behind each of which there lay a battery of plausible arguments. Such a situation is by no means unique to philosophical discourse. Consider, for instance, the current status of physical theory, which comprises two sub-theories, relativity and quantum mechanics, each of which is extremely well supported, and yet which are mutually inconsistent. The same problem is met with in computer science, where a central notion, that of putting a query to a data-base, runs into trouble when the data-base contains data which is inconsistent because it is coming in from many different sources. For another example of the general phenomenon under discussion, consider the situation faced by an investigator using multiple-choice questionnaires, when the answers supplied in one context are in conflict with those supplied in another. Has the interrogee said ‘yes’ or ‘no’ to a given question, when they said ‘yes’ under one set of conditions but ‘no’ under another? Do their answers have any value at all, or should we simply discard the whole lot on account of its inconsistency? Perhaps the most apposite example of all is the case of a jury being presented with the evidence from a series of witnesses. Each witness, we might suppose, tells a consistent story, but the total evidence presented to the jury might itself well be inconsistent.
The situation the Jainas have in mind is one in which a globally inconsistent set of propositions, the totality of philosophical discourse, is divided into subsets, each of which is internally consistent. Any proposition might be supported by others from within the same subset. At the same time, the negation of that proposition might occur in a distinct, though possibly overlapping subset, and be supported by other propositions within it. Each such consistent sub-set of a globally inconsistent discourse, is what the Jainas call a “standpoint” (naya). A standpoint corresponds to a particular philosophical perspective.
Let us say that a proposition is arguable if it is assertible within some standpoint, i.e. if it is a member of a mutually supporting consistent set of propositions. The original problem posed was this: what is the rational reaction to a class of propositions, each of which is, in this sense, arguable, yet which is globally inconsistent? It seems that there are three broad types of response. The first, which I will dub doctrinalism, is to say that it will always be possible, in principle, to discover which of two inconsistent propositions is true, and which is false. Hence our reaction should be to reduce the inconsistent set to a consistent subset, by rejecting propositions which, on close examination, we find to be unwarranted. This is, of course, the ideal in philosophical debate, but it is a situation we are rarely if ever in. The problem was stipulated to be one such that we cannot decide, as impartial observers, which of the available standpoints, if any, is correct. If doctrinalism were the only option, then we would have no choice but to come down in favour of one or other of the standpoints, basing our selection, perhaps on historical, cultural, or sociological considerations, but not on logical ones.
A second response is that of scepticism. Here the idea is that the existence both of a reason to assert and a reason to reject a proposition itself constitutes a reason to deny that we can justifiably either assert or deny the proposition. A justification of a proposition can be defeated by an equally plausible justification of its negation. This sceptical reaction is at the same time a natural and philosophically interesting one, and indeed has been adopted by some philosophers, notably N g
g rjuna in India and the Pyrrhonic sceptics as reported by Sextus Empiricus. Sextus, indeed states as the first of five arguments for scepticism, that philosophers have never been able to agree with one another, not even about the criteria we should use to settle controversies.
rjuna in India and the Pyrrhonic sceptics as reported by Sextus Empiricus. Sextus, indeed states as the first of five arguments for scepticism, that philosophers have never been able to agree with one another, not even about the criteria we should use to settle controversies.
The third response is that of pluralism, and this is the response favoured by the Jainas. The pluralist finds some way conditionally to assent to each of the propositions, and she does so by recognising that the justification of a proposition is internal to a standpoint. In this way, the Jainas try “to establish a rapprochement between seemingly disagreeing philosophical schools”47, thereby avoiding the dogmatism or “one-sidedness” from which such disagreements flow. Hence another name for their theory was anek ntav
ntav da, the doctrineζ of “non-one-sidedness”.48
da, the doctrineζ of “non-one-sidedness”.48
In spite of appearances to the contrary, the sceptic and the pluralist have much in common. For although the sceptic rejects all the propositions while the pluralist endorses all of them, they both deny that we can solve the problem by privileging just one position, i.e. by adopting the position of the doctrinalist. (It seems, indeed, that scepticism and pluralism developed in tandem in India, both as critical reactions to the system-based philosophical institutions.) Note too that both are under pressure to revise classical logic. For the sceptic, the problem is with the law of excluded middle, the principle that for all p, either p or ¬p. The reason this is a problem for the sceptic is that she wishes to reject each proposition p without being forced to assent to its negation ¬p. The pluralist, on the other hand, has trouble with a different classical law, the law of non-contradiction, that for all p, it is not the case both that p and that ¬p, for she wishes to assent both to the proposition p and to its negation. While a comparative study of the two responses, sceptical and pluralist, would be of interest, I will here confine myself to developing the version of pluralism developed by the Jainas, and discussing the extent to which their system becomes paraconsistent. It is very often claimed that the Jainas ‘embrace’ inconsistency, but I will be arguing that this is not so, that we can understand their system by giving it a less strongly paraconsistent reading.
3.2 Jaina seven-valued logic
The Jaina philosophers support their pluralism by constructing a logic in which there are seven distinct semantic predicates (bha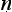 gī), which, since they attach to sentences, we might think of as truth-values (for a slightly different interpretation, see Ganeri 2001, chapter 5). I will first set out the system following the mode of description employed by the Jainas themselves, before attempting to reconstruct it in a modern idiom. I will follow here the twelfth century author V
gī), which, since they attach to sentences, we might think of as truth-values (for a slightly different interpretation, see Ganeri 2001, chapter 5). I will first set out the system following the mode of description employed by the Jainas themselves, before attempting to reconstruct it in a modern idiom. I will follow here the twelfth century author V dideva Sūri (1086–1169 A.D.), but similar descriptions are given by many others, including Prabh
dideva Sūri (1086–1169 A.D.), but similar descriptions are given by many others, including Prabh candra, Malli
candra, Malli sena and Samantabhadra. This is what V
sena and Samantabhadra. This is what V dideva Sūri says (Pram
dideva Sūri says (Pram
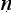 a-naya-tattv
a-naya-tattv lok
lok la
la
 ra
ra , chapter 4, verses 15–21):49
, chapter 4, verses 15–21):49
The seven predicate theory consists in the use of seven claims about sentences, each preceded by “arguably” or “conditionally” (sy t), [all] concerning a single object and its particular properties, composed of assertions and denials, either simultaneously or successively, and without contradiction. They are as follows:
t), [all] concerning a single object and its particular properties, composed of assertions and denials, either simultaneously or successively, and without contradiction. They are as follows:
1. Arguably, it (i.e. some object) exists (sy d asty eva). The first predicate pertains to an assertion.
d asty eva). The first predicate pertains to an assertion.
2. Arguably, it does not exist (sy n n
n n sty eva). The second predicate pertains to a denial.
sty eva). The second predicate pertains to a denial.
3. Arguably, it exists; arguably, it doesn’t exist (sy d asty eva sy
d asty eva sy n n
n n sty eva). The third predicate pertains to successive assertion and denial.
sty eva). The third predicate pertains to successive assertion and denial.
4. Arguably, it is ‘non-assertible’ (sy d avaktavyam eva). The fourth predicate pertains to a simultaneous assertion and denial.
d avaktavyam eva). The fourth predicate pertains to a simultaneous assertion and denial.
5. Arguably, it exists; arguably it is non-assertible (sy d asty eva sy
d asty eva sy d avaktavyam eva). The fifth predicate pertains to an assertion and a simultaneous assertion and denial.
d avaktavyam eva). The fifth predicate pertains to an assertion and a simultaneous assertion and denial.
6. Arguably, it doesn’t exist; arguably it is non-assertible (sy n n
n n sty eva sy
sty eva sy d avaktavyam eva). The sixth predicate pertains to a denial and a simultaneous assertion and denial.
d avaktavyam eva). The sixth predicate pertains to a denial and a simultaneous assertion and denial.
7. Arguably, it exists; arguably it doesn’t exist; arguably it is non-assertible (sy d asty eva sy
d asty eva sy n n
n n sty eva sy
sty eva sy d avaktavyam eva). The seventh predicate pertains to a successive assertion and denial and a simultaneous assertion and denial.
d avaktavyam eva). The seventh predicate pertains to a successive assertion and denial and a simultaneous assertion and denial.
The structure here is simple enough. There are three basic truth-values, true (t), false (f), and non-assertible (u). There is also some means of combining basic truth-values, to form four further compound values, which we can designate tf, tu, fu and tfu. There is a hint too that the third basic value is itself somehow a product of the first two, although by some other means of combination – hence the talk of simultaneous and successive assertion and denial. Thus, in Jaina seven valued logic, all the truth-values are thought to be combinations in some way or another of the two classical values.
There is, however, a clear risk that the seven values in this system will collapse trivially into three. For if the fifth value, tu, means simply “true and true-and-false”, how is it distinct from the fourth value, u, “true-and-false”? No reconstruction of the Jaina system can be correct if it does not show how each of the seven values is distinct. The way forward is to pay due attention to the role of the conditionalising operator “arguably” (sy t). The literal meaning of “sy
t). The literal meaning of “sy t” is “perhaps it is”, the optative form of the verb “to be”. The Jaina logicians do not, however, use it in quite its literal sense, which would imply that no assertion is not made categorically, but only as a possibility-claims. Instead, they use it to mean “from a certain standpoint” or “within a particular philosophical perspective”. This is the Jaina pluralism: assertions are made categorically, but only from within a particular framework of supporting assertions. If we let the symbol “∇” represent “sy
t” is “perhaps it is”, the optative form of the verb “to be”. The Jaina logicians do not, however, use it in quite its literal sense, which would imply that no assertion is not made categorically, but only as a possibility-claims. Instead, they use it to mean “from a certain standpoint” or “within a particular philosophical perspective”. This is the Jaina pluralism: assertions are made categorically, but only from within a particular framework of supporting assertions. If we let the symbol “∇” represent “sy t’, then the Jaina logic is a logic of sentences of the form “∇p”, a logic of conditionally justified assertions. As we will see, it resembles other logics of assertion, especially the ones developed by Ja
t’, then the Jaina logic is a logic of sentences of the form “∇p”, a logic of conditionally justified assertions. As we will see, it resembles other logics of assertion, especially the ones developed by Ja kowski50 and Rescher51
kowski50 and Rescher51
The first three of the seven predications now read as follows:
In other words, p is true iff it is arguable that p. We are to interpret this as saying that there is some standpoint within which p is justifiably asserted. We can thus write it as
where “σ: p” means that p is arguable from the standpoint σ For the second value we may similarly write,
The third value is taken by those propositions whose status is controversial, in the sense that they can be asserted from some standpoints but their negations from others. These are the propositions which the Jainas are most concerned to accommodate. Thus
I.e.
or again
This way of introducing a new truth-value, by combining two others, may seem a little odd. I think, however, that we can see the idea behind it if we approach matters from another direction. Let us suppose that every standpoint is such that for any given proposition, either the proposition or its negation is assertible from within that standpoint. Later, I will argue that the Jainas did not want to make this assumption, and that this is what lies behind their introduction of the new truth-value “non-assertible”. But for the moment let us make the assumption, which is tantamount to supposing that every standpoint is ‘optimal’, in the sense that for any arbitrary proposition, it either supplies grounds for accepting it, or else grounds for denying it. There are no propositions about which an optimal standpoint is simply indifferent. Now, with respect to the totality of actual optimal standpoints, a proposition can be in just one of three states: either it is a member of every optimal standpoint, or its negation is a member of every such standpoint, or else it is a member of some, and its negation of the rest. If we number these three states, 1, 2 and 3, and call the totality of all actual standpoints, Σ, then the value of any proposition with respect to Σ is either 1, 2 or 3. The values 1, 2 and 3 are in fact the values of a three-valued logic, which we can designate M3. There is a correspondence between this logic and the system introduced by the Jainas (J3, say). The idea, roughly is that a proposition has the value ‘true’ iff it either has the value 1 or 3, it has the value ‘false’ iff it either has the value 2 or 3, and it has the value ‘tf’ iff it has the value 3. Hence the three values introduced by the Jainas represent, albeit indirectly, the three possible values a proposition may take with respect to the totality of optimal standpoints.
Before elaborating this point further, we must find an interpretation for the Jainas’ fourth value “non-assertible”. Bharucha and Kamat offer the following analysis of the fourth value:
The fourth predication consists of affirmative and negative statements made simultaneously. Since an object X is incapable of being expressed in terms of existence and non-existence at the same time, even allowing for Sy d, it is termed ‘indescribable’. Hence we assign to the fourth predication … the indeterminate truth-value I and denote the statement corresponding to the fourth predication as (p&¬p).52
d, it is termed ‘indescribable’. Hence we assign to the fourth predication … the indeterminate truth-value I and denote the statement corresponding to the fourth predication as (p&¬p).52
Bharucha and Kamat’s interpretation is equivalent to
that is
Thus, for Bharucha and Kamat, the Jaina system is paraconsistent because it allows for standpoints in which contradictions are justifiably assertible. This seems to me to identify the paraconsistent element in the Jaina theory in quite the wrong place. For while there may be certain sentences, such as the Liar, which can justifiably be both asserted and denied, this cannot be the case for the wide variety of sentences which the Jainas have in mind, sentences like “There exist universals” and so on. Even aside from such worries, the current proposal has a technical defect. For what now is the fifth truth-value, tu? If Bharucha and Kamat are right then it means that there is some standpoint from which ‘p’ can be asserted, and some from which ‘p&¬p’ can be asserted. But this is logically equivalent to u itself. The Bharucha and Kamat formulation fails to show how we get to a seven-valued logic.
Another proposed interpretation is due to Matilal. Taking at face-value the Jainas’ elaboration of the fourth value as meaning “simultaneously both true and false”, he says
the direct and unequivocal challenge to the notion of contradiction in standard logic comes when it is claimed that the same proposition is both true and false at the same time in the same sense. This is exactly accomplished by the introduction of the [fourth] value – “Inexpressible”, which can also be rendered as paradoxical.53
Matilal’s intended interpretation seems thus to be
Matilal’s interpretation is a little weaker than Bharucha and Kamat, for he does not explicitly state that the conjunction ‘p&¬p’ is asserted, only that both conjuncts are. Admittedly, the difference between Matilal and Bharucha and Kamat is very slight, and indeed only exists if we can somehow make out the claim that both a proposition and its negation are assertible without it being the case that their conjunction is. For example, we might think that the standpoint of physical theory can be consistently extended by including the assertion that gods exists, and also by including the assertion that gods do not exist. It would not follow that one could from any standpoint assert the conjunction of these claims. Yet whether there is such a difference between Matilal’s position and that of Bharucha and Kamat is rather immaterial, since Matilal’s proposal clearly suffers from the precisely the same technical defect as theirs, namely the lack of distinctness between the fourth and fifth values.
Tere is another interpretation, one which gives an intuitive sense to the truth-value “non-assertible”, sustains the distinctness of each of the seven values, but does not require us to abandon the assumption that standpoints are internally consistent. Recall that we earlier introduced the idea of an optimal standpoint, by means of the assumption that for every proposition, either it or its negation is justifiably assertible from within the standpoint. Suppose we now retract that assumption, and allow for the existence of standpoints which are just neutral about the truth or falsity of some propositions. We can then introduce a new value as follows:
Neither the proposition nor its negation is assertible from the standpoint. For example, neither the proposition that happiness is a virtue nor its negation receives any justification from the standpoint of physical theory. We have, in effect, rejected a commutativity rule, that if it not the case that ‘p’ is assertible from a standpoint σ then ‘¬p’ is assertible from σ and vice versa [¬(σ: p) ⇔ (σ: ¬p)]. Our new truth-value, u, is quite naturally called “non-assertible”, and it is clear that the fifth value, tu, the conjunction of t with u, is not equivalent simply with u. The degree to which the Jaina system is paraconsistent is, on this interpretation, restricted to the sense in which a proposition can be tf, i.e. both true and false because assertible from one standpoint but deniable from another. It does not follow that there are standpoints from which contradictions can be asserted.
Why have so many writers on Jaina logic have felt that Jaina logic is paraconsistent in the much stronger sense. The reason for this belief is the account which some of the Jainas themselves give of the meaning of their third basic truth-value, “non-assertible”. As we saw in the passage from V dideva Sūri, some of them say that a proposition is non-assertible iff it is arguably both true and false simultaneously, as distinct from the truth value tf, which is successively arguably true and arguably false. We are interpreting the Jaina distinction between successive and simultaneous combination of truth-values in terms of a scope distinction with the operator “arguably”. One reads “arguably (t&f)”, the other “(arguably t) & (arguably f)” If this were the correct analysis of the fourth truth-value, then Jaina logic would indeed be strongly paraconsistent, for it would be committed to the assumption that there are philosophical positions in which contradictions are rationally assertible. Yet while such an interpretation is, on the face of it, the most natural way of reading V
dideva Sūri, some of them say that a proposition is non-assertible iff it is arguably both true and false simultaneously, as distinct from the truth value tf, which is successively arguably true and arguably false. We are interpreting the Jaina distinction between successive and simultaneous combination of truth-values in terms of a scope distinction with the operator “arguably”. One reads “arguably (t&f)”, the other “(arguably t) & (arguably f)” If this were the correct analysis of the fourth truth-value, then Jaina logic would indeed be strongly paraconsistent, for it would be committed to the assumption that there are philosophical positions in which contradictions are rationally assertible. Yet while such an interpretation is, on the face of it, the most natural way of reading V dideva Sūri’s elaboration of the distinction between the third and fourth values, it if far from clear that the Jaina pluralism really commits them to paraconsistency in this strong form. Their goal is, to be sure, to reconcile or synthesise mutually opposing philosophical positions, but they have no reason to suppose that a single philosophical standpoint can itself be inconsistent. Internal consistency was, in classical India, the essential attribute of a philosophical theory, and a universally acknowledged way to undermine the position of one’s philosophical opponent was to show that their theory contradicted itself. The Jainas were as sensitive as anyone else to allegations that they were inconsistent, and strenuously denied such allegations when made. I have shown that it is possible to reconstruct Jaina seven-valued logic in a way which does not commit them to a strongly paraconsistent position.
dideva Sūri’s elaboration of the distinction between the third and fourth values, it if far from clear that the Jaina pluralism really commits them to paraconsistency in this strong form. Their goal is, to be sure, to reconcile or synthesise mutually opposing philosophical positions, but they have no reason to suppose that a single philosophical standpoint can itself be inconsistent. Internal consistency was, in classical India, the essential attribute of a philosophical theory, and a universally acknowledged way to undermine the position of one’s philosophical opponent was to show that their theory contradicted itself. The Jainas were as sensitive as anyone else to allegations that they were inconsistent, and strenuously denied such allegations when made. I have shown that it is possible to reconstruct Jaina seven-valued logic in a way which does not commit them to a strongly paraconsistent position.
The interpretation I give to the value “non-assertible” is quite intuitive, although it does not mean “both true and false simultaneously”. My interpretation, moreover, is supported by at least one Jaina logician, Prabh candra. Prabh
candra. Prabh candra, who belongs to the first part of the ninth century C.E., is one of the few Jainas directly to address the question of why there should be just seven values. What he has to say is very interesting:
candra, who belongs to the first part of the ninth century C.E., is one of the few Jainas directly to address the question of why there should be just seven values. What he has to say is very interesting:
(Opponent:) Just as the values ‘true’ and ‘false’, taken successively, form a new truth-value ‘true-false’, so do the values ‘true’ and ‘true-false’. Therefore, the claim that there are seven truth-values is wrong.
(Reply:) No: the successive combination of ‘true’ and ‘true-false’ does not form a new truth-value, because it is impossible to have ‘true’ twice. … In the same way, the successive combination of ‘false’ and ‘true-false’ does not form a new truth-value.
(Opponent:) How then does the combination of the first and the fourth, or the second and the fourth, or the third and the fourth, form a new value?
(Reply:) It is because, in the fourth value “non-assertible”, there is no grasp of truth or falsity. In fact, the word “non-assertible” does not denote the simultaneous combination of truth and falsity. What then? What is meant by the truth-value “non-assertible” is that it is impossible to say which of ‘true’ and ‘false’ it is.54
This passage seems to support the interpretation offered above. When talking about the “law of non-contradiction” in a deductive system, we must distinguish between two quite different theses: (a) the thesis that “¬(p&¬p)” is a theorem in the system, and (b) the thesis that it is not the case that both ‘p’ and ‘¬p’ are theorems. The Jainas are committed to the first of these theses, but reject the second. This is the sense in which it is correct to say that the Jainas reject the “law of non-contradiction”.
I showed earlier that when we restrict ourselves to optimal standpoints, the total discourse falls into just one of three possible states with respect to each system. The Jainas have a seven-valued logic because, if we allow for the existence of non-optimal standpoints, standpoints which are just neutral with respect to some propositions, then, for each proposition, p say, the total discourse has exactly seven possible states. They are as follows:
1. p is a member of every standpoint in Σ.
2. ¬p is a member of every standpoint in Σ.
3. p is a member of some standpoints, and ¬p is a member of the rest.
4. p is a member of some standpoints, the rest being neutral.
5. ¬p is a member of some standpoints, the rest being neutral.
6. p is neutral with respect to every standpoint.
7. p is a member of some standpoints, ¬p is a member of some other standpoints, and the rest are neutral.
Although Jainas do not define the states in this way, but rather via the possible combinations of the three primitive values, t, f and u, it is not difficult to see that the two sets map onto one another, just as they did before. Thus t = (1, 3, 4, 7), f = (2, 3 5, 7), tf = (3, 7), and so on.
Using many-valued logics in this way, it should be noted, does not involve any radical departure from classical logic. The Jainas stress their commitment to bivalence, when they try to show, as V dideva Sūri did above, that the seven values in their system are all products of combining two basic values. This reflects, I think, a commitment to bivalence concerning the truth-values of propositions themselves. The underlying logic within each standpoint is classical, and it is further assumed that each standpoint or participant is internally consistent. The sometimes-made suggestion55 that sense can be made of many-valued logics if we interpret the assignment of non-classical values to propositions via the assignment of classical values to related items is reflected here in the fact that the truth-value of any proposition p (i.e. |p|) has two values, the status of p with respect to standpoint σ (‘|p|σ’) derivatively has three values, and the status of p with respect to a discourse Σ (‘|p|Σ’), as we have just seen, has seven.
dideva Sūri did above, that the seven values in their system are all products of combining two basic values. This reflects, I think, a commitment to bivalence concerning the truth-values of propositions themselves. The underlying logic within each standpoint is classical, and it is further assumed that each standpoint or participant is internally consistent. The sometimes-made suggestion55 that sense can be made of many-valued logics if we interpret the assignment of non-classical values to propositions via the assignment of classical values to related items is reflected here in the fact that the truth-value of any proposition p (i.e. |p|) has two values, the status of p with respect to standpoint σ (‘|p|σ’) derivatively has three values, and the status of p with respect to a discourse Σ (‘|p|Σ’), as we have just seen, has seven.
Consider again the earlier example of a jury faced with conflicting evidence from a variety of witnesses. The Jainas wouldn’t here tell us ‘who dun it’, for they don’t tell us the truth-value of any given proposition. What they give us is the means to discover patterns in the evidence, and how to reason from them. For example, if one proposition is agreed on by all the witnesses, and another is agreed on by some but not others, use of the Jaina system will assign different values to the two propositions. The Jainas, as pluralists, do not try to judge which of the witnesses is lying and which is telling the truth; their role is more like that of the court recorder, to present the totality of evidence in a maximally perspicuous form, one which still permits deduction from the totality of evidence.
So far so good. But there is another worry now, one which strikes at the very idea of using a many-valued logic as the basis for a logic of discourse. For, when we come to try and construct truth-tables for the logical constants in such a logic, we discover that the logic is not truth-functional. That is to say, the truth-value of a complex proposition such as ‘p&q’, is not a function solely of the truth-values of the constituent propositions ‘p’ and ‘q’. To see this, and to begin to find a solution, I shall need briefly to describe the work of the Polish logician, Ja kowski, who was the founder of discursive logics in the West, and whose work, in motivation at least, provides the nearest contemporary parallel to the Jaina theory.
kowski, who was the founder of discursive logics in the West, and whose work, in motivation at least, provides the nearest contemporary parallel to the Jaina theory.
3.3 Ja kowski and the Jainas
kowski and the Jainas
Philosophical discourse is globally inconsistent, since there are many propositions to which some philosophers assent while others dissent. The Jainas therefore develop a logic of assertions-made-from-within-a-particular-standpoint, and note that an assertion can be both arguably true, i.e. justified by being a member of a consistent philosophical position, and at the same time be arguably false, if its negation is a member of some other consistent philosophical standpoint. This move is quite similar to that of the founder of inconsistent logics, Ja kowski, who developed a “discussive logic” in which a proposition is said to be ‘discussively true’ iff it is asserted by some member of the discourse.
kowski, who developed a “discussive logic” in which a proposition is said to be ‘discussively true’ iff it is asserted by some member of the discourse.
Ja kowski motivates his paper “Propositional Calculus for Contradictory Deductive Systems” with two observations. The first is that
kowski motivates his paper “Propositional Calculus for Contradictory Deductive Systems” with two observations. The first is that
any vagueness of the term a can result in a contradiction of sentences, because with reference to the same object X we may say that “X is a” and also “X is not a”, according to the meanings of the term a adopted for the moment,
the second is that
the evolution of the empirical sciences is marked by periods in which the theorists are unable to explain the results of experiments by a homogeneous and consistent theory, but use different hypotheses, which are not always consistent with one another, to explain the various groups of phenomena.56
He then introduces an important distinction between two properties of deductive systems. A deductive system is said to be contradictory if it includes pairs of theorems A and ¬A which contradict each other. It is over-complete, on the other hand, if every well-formed formula is a theorem of the system. In classical logic, these two properties are conflated; hence the slogan “anything follows from a contradiction”. The problem to which Ja kowski addresses himself, therefore, is that of constructing a non-classical system which is contradictory but not over-complete. In classical logic, given two contradictory theses A, ¬A, we may deduce first that A&¬A, using the &-introduction or Adjunction Rule, A, B → A&B. Then, since A&¬A iff B&¬B for any arbitrary A and B, and since B¬B → B from &:-elimination or Simplification, A&B → A, it follows that B. More clearly:
kowski addresses himself, therefore, is that of constructing a non-classical system which is contradictory but not over-complete. In classical logic, given two contradictory theses A, ¬A, we may deduce first that A&¬A, using the &-introduction or Adjunction Rule, A, B → A&B. Then, since A&¬A iff B&¬B for any arbitrary A and B, and since B¬B → B from &:-elimination or Simplification, A&B → A, it follows that B. More clearly:
| 1. | A, ¬A | |
| 2. | A&¬A, | from 1 by Adjunction. |
| 3. | A&¬A iff B&¬B, | for any arbitrary A and B. |
| 4. | B&¬B → B, | by Simplification. |
| 5. | A&¬A → B, | from 3 and 4. |
| 6. | B, | from 2 and 5 by Modus Ponens.  |
To get an inconsistent (contradictory but not over-complete) system, at least one step in this sequence must be broken. In Ja kowskiapos;s new system, ‘discursive logic’, it is the Adjunction Rule which no longer holds. Ja
kowskiapos;s new system, ‘discursive logic’, it is the Adjunction Rule which no longer holds. Ja kowski considers the system in which many different participants makes assertions, each thereby contributing information to a single discourse. The best example, perhaps, is one already given, the evidence presented to a jury by witnesses at a trial. Ja
kowski considers the system in which many different participants makes assertions, each thereby contributing information to a single discourse. The best example, perhaps, is one already given, the evidence presented to a jury by witnesses at a trial. Ja kowski then introduces the notion of discursive assertion, such that a sentence is discursively asserted if it is asserted by one of the participants in the discourse, and he notes that the operator “it is asserted by someone that…” is a modal operator for the semantics of which it should be possible to use an existing modal logic. Thus
kowski then introduces the notion of discursive assertion, such that a sentence is discursively asserted if it is asserted by one of the participants in the discourse, and he notes that the operator “it is asserted by someone that…” is a modal operator for the semantics of which it should be possible to use an existing modal logic. Thus
where D2 is Ja kowski’s two-valued discursive logic, and “
kowski’s two-valued discursive logic, and “ ” is the operator “someone asserts that…”. For some reason, Ja
” is the operator “someone asserts that…”. For some reason, Ja kowski chooses a strong modal system, S5, to give the semantics of this operator, but this is surely a mistake. The reason is that the S5 modal principle ‘A →
kowski chooses a strong modal system, S5, to give the semantics of this operator, but this is surely a mistake. The reason is that the S5 modal principle ‘A →  A’ does not seem to hold for a discursive system, since there will be truths which no-one asserts. It would not be difficult, however, to use a weaker modal system than S5, for example S20 or S3 which lack the above principle, as the basis for D2. (The characteristic axiom of S40, ‘
A’ does not seem to hold for a discursive system, since there will be truths which no-one asserts. It would not be difficult, however, to use a weaker modal system than S5, for example S20 or S3 which lack the above principle, as the basis for D2. (The characteristic axiom of S40, ‘
 A →
A →  A’, does not seem to hold in a discursive system: it can be assertible from some standpoint that there is another standpoint in which p is assertible without there being such a standpoint). The point to note is that, in most modal systems, the Adjunction Rule fails, since it does not follow that the conjunction A&B is possible, even if A is possible and B is separately possible. And this too, is what we would expect from the discursive operator, for one participant may assert A, and another B, without there being anyone who asserts the conjunction. Ja
A’, does not seem to hold in a discursive system: it can be assertible from some standpoint that there is another standpoint in which p is assertible without there being such a standpoint). The point to note is that, in most modal systems, the Adjunction Rule fails, since it does not follow that the conjunction A&B is possible, even if A is possible and B is separately possible. And this too, is what we would expect from the discursive operator, for one participant may assert A, and another B, without there being anyone who asserts the conjunction. Ja kowski therefore arrives at a system which is contradictory, since both A and ¬A can be theses, but, because it is non-adjunctive, is not over-complete.
kowski therefore arrives at a system which is contradictory, since both A and ¬A can be theses, but, because it is non-adjunctive, is not over-complete.
3.4 The Logical Structure of the Jaina System
The parallels in motivation between Ja kowski’s discursive logic, and the Jaina system are unmistakable. There is, however, an important difference, to which I alluded earlier. Modal logics are not truth-functional; one cannot, for example, deduce the truth-value of ‘
kowski’s discursive logic, and the Jaina system are unmistakable. There is, however, an important difference, to which I alluded earlier. Modal logics are not truth-functional; one cannot, for example, deduce the truth-value of ‘ (A&B)’ from the truth-values of ‘
(A&B)’ from the truth-values of ‘ A’ and ‘
A’ and ‘ B’. And it seems for the same reason that a discursive logic cannot be truth-functional either. Suppose, for example, that we have two propositions A, and B, both of which are assertible from (possibly distinct) standpoints, and hence both true in the Jaina system. What is the truth-value of A&B? It seems that this proposition could be either true, false, or both.
B’. And it seems for the same reason that a discursive logic cannot be truth-functional either. Suppose, for example, that we have two propositions A, and B, both of which are assertible from (possibly distinct) standpoints, and hence both true in the Jaina system. What is the truth-value of A&B? It seems that this proposition could be either true, false, or both.
It is possible to offer a defence of the Jaina position here. For simplicity, let us restrict ourselves to the Jaina system with only optimal standpoints and just three truth-values. If my suggested defence works here, its extension to the full Jaina system J7, would not be especially problematic. Consider again the three-valued logic, M3, whose values were defined as follows:
These correspond to the three possible states of a totality of optimal standpoints. When we try to construct the truth-table for conjunction in such a system, we find that it is non-truth-functional. Thus, consider the truth-value of ‘p&q’, when |p| = |q| = 3. Here, |p&q| might itself be 3, but it might also be 2. Thus, the truth-value of the conjunction is not uniquely determined by those of its conjuncts. What is uniquely determined, however, is that the truth-value belongs to the class (2, 3). To proceed, we can appeal to an idea first introduced by N. Rescher in his paper “Quasi-truth-functional systems of propositional logic”.57 A quasi-truth-functional logic is defined there as one in which “some connectives are governed by many-valued functions of the truth-values of their variables”. The entries in the truth-table of such a logic are typically not single truth-values but sets of values. It is clear that the system set up just now is, in this, sense, quasi-truth-functional. Now, as Rescher himself points out, a quasi-truth-functional logic will always be equivalent to a multi-valued strictly truth-functional system. The idea, roughly, is that we can treat a class of truth-values as constituting a new truth-value. Typically, if the quasi-truth-functional system has n truth-values, its strictly truth-functional equivalent will have 2n − 1 values (Rescher notes that “in the case of a three-valued (T, F, I) quasi-truth-functional system we would need seven truth-values, to represent: T, F, I, (T, F), (T, I), (F, I), (T, F, I)” but argues that there are special reasons entailing that for a two-valued quasi-truth-functional system we need four rather than three values.). The seven-valued system which results in this way from the three-valued logic sketched above has, in fact, been studied notably by Moffat58. I will therefore call it M7. An initially tempting idea is to identify the Jaina system J7 with M7. This, however, will only work if the fourth value, u, is defined thus:
For then ‘tu’ in the Jaina system will be identical with ‘1’ in the Moffat system, etc. This is, however, not an interpretation which receives any textual support.
Instead, let us observe that there is a close connection between M7 and the restricted Jaina system, J3. For note that the value (1, 3) in M7 is such that
Thus (1, 3) in M7 is just the value ‘true’ in J3. Similarly, (1, 2) in M7 is just the value ‘false’ in J3. Thus, although J3 is not strictly truth-functional, its truth-tables are embedded in those of the Moffat logic, M7.
It is presumably possible to find a quasi-truth-functional system whose truth-tables embed those of J7, the full Jaina system, in an entirely analogous way. Thus, although the loss of Adjunction means that the Jaina logic J7, is not truth-functional, its truth-table is embedded in a suitable quasi-functional system. The lack of truth-functionality is not, after all, a fatal flaw in the Jaina approach.
3.5 Axiomatisation of the Jaina System
We have shown that it is possible to use many-valued truth-tables to formalise the Jaina system. This was, in effect, the approach of the Jaina logicians themselves. Yet it would surely be much better to proceed by axiomatising the modal standpoint operator, ∇. Once again we look to Rescher59. His work on what he calls “assertion logics” is an extension of the work of Ja kowski. Rescher introduces a system A1, with the following axiomatic basis:
kowski. Rescher introduces a system A1, with the following axiomatic basis:
| (A1) | (∃p)σ: p | [Nonvacuousness] |
| (A2) | (σ: p & σ: q) ⊃ σ: (p & q) | [Conjunction] |
| (A3) | ¬σ: (p & ¬p) | [Consistency] |
| (R) | If p  q, then σ: p q, then σ: p  σ: q σ: q |
[Commitment] |
Note that one effect of the rule (R) is to ensure that the notion captured is not merely explicit assertion but ‘commitment to assert’, for (R) states that from a standpoint one may assert anything entailed by another of the assertions. I believe that the Jainas would accept each of the axioms (A1) to (A3). Bharucha and Kamat, it may be noted, would reject (A3), while Matilal, as I have represented him, would reject (A2). I have already argued that these claims are mistaken. In particular, with regard to (A2), although it is true that the Jainas reject Adjunction, what this means is that assertions made from within different standpoints cannot be conjoined, not that assertions made within the same standpoint cannot be conjoined.
We now introduce the modal standpoint operator, ∇ “arguably”, via the definition:
and add the axioms of S30 or some other suitable modal system.
Rescher defines some further systems by adding further axioms, none of which, I think, the Jainas would accept. For example, he defines A2 by adding to A1 the axiom that anything asserted by everyone is true [(∀σ)σ: p ⊃ p]. There is no reason to suppose the Jainas commit themselves to this. The system J3, however, is distinguished by the new axiom (A4):
Rescher too proposes a “three-valued approach” to assertion logic, via the notion of ‘the truth status of the assertion p with respect to an assertor’, written ‘|p|σ’, and the definitions:
and he shows that using the axioms of A1, we can derive a quasi-truth-functional logic for this system. These are not quite the Jaina values, as introduced earlier, for they do not quantify over standpoints or assertors. It is clear, however, that the Jaina system is of the same type as a modalised Rescher assertion logic. Their innovation is to introduce three truth-values via the definitions given before (|p|Σ = t iff (∃σ)(σ: p);[|p|Σ = f iff (∃σ)(σ: ¬p); and |p|Σ = u iff (∃σ)(¬(Σ: p)&¬(Σ: ¬p)), where ‘|p|Σ’ stands for ‘the status of the assertion p with respect to the total discourse Σ’). It is this attempt to take a many-valued approach to the modalised, rather than the unmodalised, version of assertion logic which generates the extra complexity of the Jaina system. I have already noted that, since the axiom “p ⊃ ∇p” is lacking, the modal structure of the system will be no stronger than that of S30 Yet in principle there seems no reason to think that the Jaina system cannot in this way be given an axiomatic basis.
3.6 Pluralism, Syncretism, and the Many-faceted View of Reality
The Jainas avoid dogmatism and a one-sided view of the world simply by noting that assertions are only justified in the background of certain presuppositions or conditions. It is perfectly possible for an assertion to be justified given one set of presuppositions, and for its negation to be justified given another different set. The Jainas’ ingenuity lies in the skill with which they developed a logic of discourse to make more precise this natural idea. However, they also went beyond this, for they added that every standpoint reveals a facet of reality, and that, to get a full description of the world, what we need to do is to synthesise the various standpoints. As Matilal puts it, “The Jainas contend that one should try to understand the particular point of view of each disputing party if one wishes to grasp completely the truth of the situation. The total truth … may be derived from the integration of all different viewpoints”.60 But is this further step, the step from pluralism to syncretism, a coherent step to take? In particular, how is it possible to integrate inconsistent points of view? The point is made by Priest and Routley, who, commenting on the Jaina theory, state that “…such a theory risks trivialization unless some (cogent) restrictions are imposed on the parties admitted as having obtained partial truth — restrictions of a type that might well be applied to block amalgamations leading to violations of Non-Contradiction”.61
Perhaps we can understand the Jaina position as follows. The so-called ‘integration’ of two points of view, σ1 and σ2, does not mean the creation of some new standpoint, which is the combination of the first two. For this would lead to the formation of inconsistent standpoints unless implausible constraints were placed on what can constitute a standpoint. Instead, what it means is that, if p is assertible from some standpoint σ1, then this fact, that p is assertible from σ1, can itself be asserted from σ2 and every other standpoint. In this way, each disputant can recognise the element of truth in the other standpoints, by making explicit the presuppositions or conditions under which any given assertion is made.
If correct, this idea has an interesting consequence. In moving from pluralism to syncretism, the Jainas commit themselves to the claim that we are led to a complete account of reality by integrating of all the different points of view. It follows from this that every true proposition must be asserted within some standpoint, i.e. “p ⊃ (∃σ)(σ: p) or “p ⊃ ∇p”. Hence the move from pluralism to syncretism is a move from a logic of assertibility based on S30 or weaker to one based on S3 or stronger.
To conclude, we have seen how the Jainas developed a plausible and interesting logic of philosophical discourse, how they did not (or need not) commit themselves to the strongly paraconsistent position normally attributed to them, and how, as they strengthened their position from one of pluralism to one of syncretism, they had also to strengthen correspondingly the modal logic underlying the operator “sy t’.
t’.

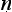 opanayanigaman
opanayanigaman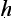 ).
).
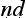

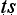 aprasa
aprasa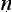 ga)
ga)