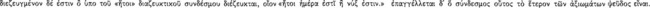7 The Conditional Axiōma
The conditional axiōma, according to Chrysippus and Diogenes the Babylonian, is constructed from two axiōmata by means of the connective ‘if‘ 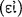 (DL 7.71). Of the two constituent axiōmata, the one signified by the sentence placed immediately after the connective is called the ‘antecedent’ and ‘first’
(DL 7.71). Of the two constituent axiōmata, the one signified by the sentence placed immediately after the connective is called the ‘antecedent’ and ‘first’ 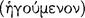 , whereas the other is called the ‘consequent’ and ‘second’
, whereas the other is called the ‘consequent’ and ‘second’  (AM 8.110).112 The connective ‘if’ seems to ‘promise’ or ‘guarantee’
(AM 8.110).112 The connective ‘if’ seems to ‘promise’ or ‘guarantee’ 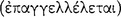 that the consequent ‘follows’
that the consequent ‘follows’ 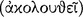 the antecedent (AM 8.111; DL 7.71); hence, the relationship of ‘following’
the antecedent (AM 8.111; DL 7.71); hence, the relationship of ‘following’  between its antecedent and consequent is evidently the characteristic property of the conditional axiōma. Since the conditional axiōma is, after all, an axiōma, it might be expected that for any particular conditional axiōma, one could give an account of the presentation to which it corresponds, and of the pragma which is the content of the presentation. A passage of Sextus Empiricus, which we intend to quote presently, provides a clue to the psychological aspects of this relationship. However, since the context in which this passage occurs is a discussion of the Stoic doctrine of signs, it might be useful to give a short summary of this teaching.
between its antecedent and consequent is evidently the characteristic property of the conditional axiōma. Since the conditional axiōma is, after all, an axiōma, it might be expected that for any particular conditional axiōma, one could give an account of the presentation to which it corresponds, and of the pragma which is the content of the presentation. A passage of Sextus Empiricus, which we intend to quote presently, provides a clue to the psychological aspects of this relationship. However, since the context in which this passage occurs is a discussion of the Stoic doctrine of signs, it might be useful to give a short summary of this teaching.
According to Sextus Empiricus, the Stoics define the sign  as a true antecedent axiōma in a sound conditional, capable of revealing
as a true antecedent axiōma in a sound conditional, capable of revealing  the consequent (AM 8.245; 250; PH 2.104).113 Sextus reports that signs were distinguished between those which are ‘indicative’
the consequent (AM 8.245; 250; PH 2.104).113 Sextus reports that signs were distinguished between those which are ‘indicative’  , and those which are ‘commemorative’
, and those which are ‘commemorative’  (AM 8.151). An indicative sign is said to indicate ‘that which is naturally non-evident’
(AM 8.151). An indicative sign is said to indicate ‘that which is naturally non-evident’  , and is never observed in conjunction with the thing signified (8.154). The soul, for example, is naturally non-evident, and its existence is supposed to be indicated by bodily motions (8.155). A commemorative sign, on the other hand, signifies what is ‘temporarily non-evident’
, and is never observed in conjunction with the thing signified (8.154). The soul, for example, is naturally non-evident, and its existence is supposed to be indicated by bodily motions (8.155). A commemorative sign, on the other hand, signifies what is ‘temporarily non-evident’  , and is sometimes observed in conjunction with what is signified; hence, the perception of the sign brings to mind what is often perceived along with it but is momentarily unperceived. For example, since smoke is often observed in conjunction with fire, it is taken as a commemorative sign of fire even though the fire itself is unperceived (8.151-52).
, and is sometimes observed in conjunction with what is signified; hence, the perception of the sign brings to mind what is often perceived along with it but is momentarily unperceived. For example, since smoke is often observed in conjunction with fire, it is taken as a commemorative sign of fire even though the fire itself is unperceived (8.151-52).
7.1 Akolouthia: psychological aspects
The connection between the doctrine of signs and the notion of ‘following’  is spelled out by Sextus Empiricus in a passage which records the Stoic reply to several criticisms levelled at the theory of signs by the Skeptics.
is spelled out by Sextus Empiricus in a passage which records the Stoic reply to several criticisms levelled at the theory of signs by the Skeptics.
[The Stoics] say that it is not with respect to uttered speech  that man differs from the irrational animals—for crows and jays and parrots utter articulate sounds, but with respect to internal discourse
that man differs from the irrational animals—for crows and jays and parrots utter articulate sounds, but with respect to internal discourse 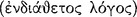 . Nor [does man differ from the irrational animals] with respect to the simple presentations (for they also form such presentations), but with respect to the ‘inferential’
. Nor [does man differ from the irrational animals] with respect to the simple presentations (for they also form such presentations), but with respect to the ‘inferential’  114 ανδ ‘ζoμπoσιτιoναλ’
114 ανδ ‘ζoμπoσιτιoναλ’ 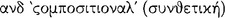 presentations, because of which he immediately possesses the conception
presentations, because of which he immediately possesses the conception  of ‘following’
of ‘following’ 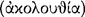 , and through the conception of following he apprehends the notion
, and through the conception of following he apprehends the notion  of sign
of sign 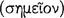 ; for sign itself is such as this: ‘If this, then this’. Therefore it follows that sign also exists in accordance with the nature and constitution of man (AM 8.275-77).
; for sign itself is such as this: ‘If this, then this’. Therefore it follows that sign also exists in accordance with the nature and constitution of man (AM 8.275-77).
We interpret this passage as follows. The faculty of forming presentations from our conceptions and complex presentations from simpler ones is part of the nature and constitution of human beings. This faculty is itself founded on our capacity for ‘internal discourse’, which makes possible the ‘inferential’ and ‘compositional’ thought necessary for the production of such presentations. Thus, we differ from the irrational animals, for they do not possess this faculty for producing presentations, but must rely solely on their senses for the data from which presentations are formed. Moreover, because of this capacity for constructing inferential and compositional presentations, we also possess the conception of ‘following’, and since the relationship between the sign and what it reveals can be represented as a conditional axiōma, it is through the conception of following, that we understand the notion of sign.
Of immediate interest in this text is the statement that we possess the conception of akolouthia because of our ability to form inferential and compositional presentations. There is little indication in the passage as to how this capacity is supposed to produce the conception of following. It may be possible, however, to work out an interpretation by considering some clear examples of akolouthia from Sextus Empiricus’ discussion of the theory of signs, and by keeping in mind the quotation of Aëtius concerning the acquisition of conceptions and preconceptions, as well as the texts of Diogenes Laërtius and Sextus Empiricus concerning the ways of producing complex conceptions.115 Our conjecture is that the ‘inferential’ and ‘compositional’ presentations are those from which the conceptions of general conditionals are inscribed on the soul. Furthermore, we would suggest that it is the totality of conceptions of general conditionals from which the conception of following arises.
Consider, then, some examples of signs mentioned by Sextus Empiricus. The following are commemorative signs: smoke is a sign of fire and a scar a sign of a previous wound (AM 8.152-53; PH 2.102). A punctured heart is a sign of immanent death (AM 8.153). Lactation is a sign of conception (AM 8.252; PH 2.106) and a bronchial discharge is a sign of a lung wound (AM 8.252-53). In these examples, according to Sextus, the sign often appears together with what it indicates, and hence, when the latter is not evident, the sign is able to reveal it because we remember that they occur together, for instance, that a punctured heart results in death (AM 8.152-53). But it would seem to be implicit in the passage quoted above that a certain degree of prior conceptual development must take place before one acquires the conception of sign, and so understands one state of affairs as a sign of another states of affairs.
This development, as Sextus indicates, no doubt begins by one’s noticing that certain types of presentations seem to occur together as a sequence. Thus a presentation of a man who has been wounded in the heart will be followed after some period of time by a presentation of the same man having died. The pragmata which are the contents of these presentations may be represented respectively by the complex {This man, to be wounded in the heart} and the complex {This man, to die}. They would be spoken respectively as the axiōmata This man is wounded in the heart and This man has died (cf. AM 8.254). Given some number of similar situations and supposing the capacity for ‘inferential’ and compositional’ thought—perhaps along with certain conceptions and preconceptions already established, for example, general conceptions of causality—one might produce a non-sensory presentation of a causal connection between these types of events.116 The content of this presentation would be a complex pragma, and the components of this complex pragma may be represented as follows: the first constituent will be the pragma {Someone, to be wounded in the heart}, followed by, say, an arrow to represent the connection,117 followed by the pragma {That one, to die}. Finally, the whole complex will be enclosed in braces. Thus the representation will be constructed as follows:
The axiōma which is this pragma spoken as an assertion might be represented in a similar manner, although it may contain certain constituents such as temporal elements not present in the representation of the pragma. The axiōma, then, might be represented as follows:
Taking the particle ‘if ‘ as the connective which seems to provide the most natural way to signify the arrow, the sentence which signifies this axiōma will be the sentence ‘If someone is wounded in the heart, that one will die’. This sentence which signifies a generalised conditional axiōma
as the connective which seems to provide the most natural way to signify the arrow, the sentence which signifies this axiōma will be the sentence ‘If someone is wounded in the heart, that one will die’. This sentence which signifies a generalised conditional axiōma  might be seen as expressing a law-like relationship between those situations in which someone is wounded in the heart and those situations in which that person dies of the wound. No doubt this could be viewed as a relationship of ‘following’ or ‘consequence’ in the causal sequence of events, and given a similar analysis of the causal relationships between other states of affairs, it seems probable that a general conception of following would be developed; moreover, one might plausibly assume that the relationship of following conceived to obtain between events in the causal nexus would be carried over to the axiōmata. In any case, there is no doubt that the Stoics viewed the relationship of akolouthia as one which holds between axiōmata as well as between events in the causal nexus.
might be seen as expressing a law-like relationship between those situations in which someone is wounded in the heart and those situations in which that person dies of the wound. No doubt this could be viewed as a relationship of ‘following’ or ‘consequence’ in the causal sequence of events, and given a similar analysis of the causal relationships between other states of affairs, it seems probable that a general conception of following would be developed; moreover, one might plausibly assume that the relationship of following conceived to obtain between events in the causal nexus would be carried over to the axiōmata. In any case, there is no doubt that the Stoics viewed the relationship of akolouthia as one which holds between axiōmata as well as between events in the causal nexus.
A difficulty with this interpretation is that for most of the examples cited from Sextus Empiricus, the direction of the relationship between the sign and what it indicates, or between the antecedent and consequent of the parallel conditional axiōma, is not the same as the direction of the causal sequence. For example, a scar is said to be a sign of a previous wound. The general conditional axiōma might be expressed by the sentence ‘If anyone has a scar, that one has had a wound’. According to the interpretation so far, having a wound would follow from having a scar, but clearly, the direction of akolouthia with respect to the causal sequence is from the occurrence of the wound to the formation of the scar. So it is obvious that some adjustment must be made in this account of the development of the conception of akolouthia.
Previously, we quoted A.A. Long ([1971, p. 46]: see page 425) to the effect that since the Stoics assumed that events occurred according to a strict causal nexus, they perhaps assigned to logic as its major function the task of making possible predictions about the future from considerations of what follows from present events. On this assumption, one might expect that they would have concentrated at first on examples in which the direction of akolouthia coincided for the causal sequence and the relationship of following in the conditional axiōma, and so stressed the development of the conception of following as we have interpreted it above. But of course, they would also have been interested in drawing out the present consequences of past actions or events, especially with respect to allocating responsibility in the sphere of ethics. Hence, the following relationship between the antecedent and consequent of a conditional axiōma need not always proceed from cause to effect as does the following relationship of the parallel causal sequence. And not the least consideration would be those instances of following between the parts of a conditional axiōma which do not correspond to instances of following in the causal nexus: in other words, conditional axiōmata matching logical connections. Nevertheless, it is not implausible to suppose that the conception of following as it relates to axiōmata had its basis in a preoccupation with the kinds of examples which involve reasoning from cause to effect.
There are not so many examples of indicative signs occurring in the text as there are of commemorative signs, but here are two: bodily movement is a sign of the presence of the soul (AM 8.155) and sweat flowing through the skin the sign of the existence of intelligible pores (AM 8.306). For the Stoics, the first example would be a straightforward instance of a causal relationship. The presence of the cause, however, must be inferred from the existence of the effect, hence acquiring the conception of the relationship between them will depend entirely on already established conceptions and preconceptions, and on the capacity for inferential and compositional thought. The relationship in the second example is not obviously a causal relationship, but seems to be a strictly logical. Yet acquiring the conception of the following relationship between these states of affairs would also seem to depend on previously acquired conceptions and preconceptions, such as theories about surfaces and the flow of fluids, as well as on inferential and compositional thought.
7.2 Pragmata spoken as conditionals
Suppose that someone utters the sentence ‘If Dion is walking, Dion is moving’.118 What is the nature of the pragma signified by this utterance and of the presentation which has this pragma as content? Apparently, the utterance of this sentence will induce a presentation in the mind of the hearer, the content of which will be a complex pragma. The components of this complex pragma may be represented as follows: the first constituent will be the pragma {Dion, to walk}, followed by, say, an arrow to represent the relation of akolouthia,119 followed by the pragma {Dion, to move}. Finally, the whole complex will be enclosed in braces. Thus the representation will be constructed as follows:
As we indicated in the previous section, the axiōma, that is, the pragma spoken, will be represented by the construction
The information conveyed by the axiōma and apprehended in the pragma is that any situation in which Dion is walking will be one in which Dion is moving; moreover, this information is communicated regardless of whether there ever is any real situation in which Dion is walking.
Similarly, the utterance of the sentence ‘If Dion was walking about in Athens at noon yesterday, he was not on the Isthmus at noon yesterday’ will induce a presentation which has as content the pragma which may be represented by the complex:
What the axiōma conveys is that the existence of the situation in which Dion was walking about in Athens at noon yesterday, rules out the existence of the situation in which Dion was on the Isthmus at noon yesterday.120 We shall see in the sequel that the standard criterion for the sound conditional axiōma, that is, one for which the consequent follows from the antecedent, is a reflection of the kind of relationship that holds between these situations. This relationship might also have been signified by a sentence constructed with the connective ‘not both … and … ’, but it may be that Chrysippus wished to reserve this connective to signify contingent relationships between states of affairs.121
Each of the conditional axiōmata in these examples will be sound 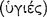 or true
or true 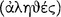 if and only if the consequent axiōma follows from the antecedent axiōma, which is to say, if and only if it is the case that the pragma signified by the consequent sentence follows from the pragma signified by the antecedent sentence. How would someone know that this relation holds? In the first example, if one were to have the conception of the general conditional axiōma If anything is walking, that thing is moving, and were to know that the relation holds for the general conditional, then it seems clear that one would know that it holds for the particular conditional. It is probably important that this conception could, in principle, be acquired by experience, although it is probably more likely that it would be taught. It could be acquired by experience because in Stoicism something walking possesses an attribute which is identifiable as a certain configuration or mixture of the pneuma with the individually qualified substrate; moreover, something moving also has an attribute identifiable in the same manner. Thus one could find out through direct experience that anything which possessed one attribute also possessed the other, and in this way come to have the conception of the general conditional. In the other example, one would rely on the conception of the general conditional
if and only if the consequent axiōma follows from the antecedent axiōma, which is to say, if and only if it is the case that the pragma signified by the consequent sentence follows from the pragma signified by the antecedent sentence. How would someone know that this relation holds? In the first example, if one were to have the conception of the general conditional axiōma If anything is walking, that thing is moving, and were to know that the relation holds for the general conditional, then it seems clear that one would know that it holds for the particular conditional. It is probably important that this conception could, in principle, be acquired by experience, although it is probably more likely that it would be taught. It could be acquired by experience because in Stoicism something walking possesses an attribute which is identifiable as a certain configuration or mixture of the pneuma with the individually qualified substrate; moreover, something moving also has an attribute identifiable in the same manner. Thus one could find out through direct experience that anything which possessed one attribute also possessed the other, and in this way come to have the conception of the general conditional. In the other example, one would rely on the conception of the general conditional
It is unclear how the acquisition of this conception would be explained. It may be that it would be classified as a preconception  . In any event, knowing that the relation holds for the particular conditional would seem to require knowing that it holds for the general conditional.
. In any event, knowing that the relation holds for the particular conditional would seem to require knowing that it holds for the general conditional.
8 Semantics and Inference
The foundation of the Stoic system of inference was the so-called ‘indemonstrables’ 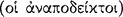 , a set of five basic argument types which are attributed to Chrysippus by several sources (AM 8.223; DL 7.79; Galen inst. log. 34–35), although there is some controversy whether they actually originated with him. Their origin has been ascribed to the Peripatetic philosopher Theophrastus by both Prantl and Zeller,122 but it has been argued by Boche
, a set of five basic argument types which are attributed to Chrysippus by several sources (AM 8.223; DL 7.79; Galen inst. log. 34–35), although there is some controversy whether they actually originated with him. Their origin has been ascribed to the Peripatetic philosopher Theophrastus by both Prantl and Zeller,122 but it has been argued by Boche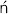 ski123 and others124 that this claim is doubtful. On the other hand, there is some indication that arguments of this sort were discussed by Aristotle and his followers. In the Prior Analytics at 50a 16–50b 4, Aristotle discusses arguments from agreement
ski123 and others124 that this claim is doubtful. On the other hand, there is some indication that arguments of this sort were discussed by Aristotle and his followers. In the Prior Analytics at 50a 16–50b 4, Aristotle discusses arguments from agreement  and arguments by reduction to the impossible
and arguments by reduction to the impossible 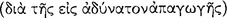 .125 He says that many other arguments are concluded from hypothesis, and these he promises to consider and distinguish in the sequel. But, as Alexander of Aphrodisias points out (in an. pr. 390.1), Aristotle never did fulfil this promise. Alexander conjectures, however, that perhaps Aristotle was speaking of certain arguments from hypothesis mentioned by Theophrastus and Eudemus and some others of his followers (390.2–3). These include ‘arguments by connection’
.125 He says that many other arguments are concluded from hypothesis, and these he promises to consider and distinguish in the sequel. But, as Alexander of Aphrodisias points out (in an. pr. 390.1), Aristotle never did fulfil this promise. Alexander conjectures, however, that perhaps Aristotle was speaking of certain arguments from hypothesis mentioned by Theophrastus and Eudemus and some others of his followers (390.2–3). These include ‘arguments by connection’  , which are also called ‘conditional’
, which are also called ‘conditional’ 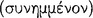 or ‘hypothetical by an additional premiss’
or ‘hypothetical by an additional premiss’  , ‘arguments by separation’
, ‘arguments by separation’ 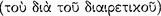 , also called ‘disjunctive’
, also called ‘disjunctive’ and ‘arguments from a negated conjunction’
and ‘arguments from a negated conjunction’  (390.3–6). In another place, Alexander attributes this alternative terminology to ‘the younger philosophers’ or neōteroi
(390.3–6). In another place, Alexander attributes this alternative terminology to ‘the younger philosophers’ or neōteroi 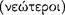 , and there is no doubt that this is Stoic terminology. The terms
, and there is no doubt that this is Stoic terminology. The terms  ,
,  , and are attested as Stoic in numerous places. The term
, and are attested as Stoic in numerous places. The term  is attested by Sextus Empiricus (PH 2.202) and by Galen (inst. log. 17.1), and the term
is attested by Sextus Empiricus (PH 2.202) and by Galen (inst. log. 17.1), and the term  by Sextus (AM 8.413) and by Diogenes Laërtius (7.76). According to Kieffer [1964, p. 66], the terms ‘argument by connection’
by Sextus (AM 8.413) and by Diogenes Laërtius (7.76). According to Kieffer [1964, p. 66], the terms ‘argument by connection’  and ‘argument by separation’
and ‘argument by separation’  are not found in Aristotle’s works. Kieffer [1964, p. 67] cites Boche
are not found in Aristotle’s works. Kieffer [1964, p. 67] cites Boche ski’s argument (La Logique de Thu)ophraste 108) that since these terms are Peripatetic but not Aristotelian, they likely were coined by Theophrastus and Eudemus. All in all it would seem to be rather unclear to what extent these philosophers advanced the study of hypothetical arguments. If indeed they were responsible for this terminology, then perhaps, as the Kneales suggest [Kneale and Kneale, 1962a, p. 105], its existence is an indication that they made some headway in the analysis of such arguments. On the other hand, we have the testimony of Boethius that neither Theophrastus nor Eudemus carried the investigation into the hypothetical syllogisms much further than where Aristotle left off (Graeser Die logischen Fragmente des Theophrast, fr. 29).
ski’s argument (La Logique de Thu)ophraste 108) that since these terms are Peripatetic but not Aristotelian, they likely were coined by Theophrastus and Eudemus. All in all it would seem to be rather unclear to what extent these philosophers advanced the study of hypothetical arguments. If indeed they were responsible for this terminology, then perhaps, as the Kneales suggest [Kneale and Kneale, 1962a, p. 105], its existence is an indication that they made some headway in the analysis of such arguments. On the other hand, we have the testimony of Boethius that neither Theophrastus nor Eudemus carried the investigation into the hypothetical syllogisms much further than where Aristotle left off (Graeser Die logischen Fragmente des Theophrast, fr. 29).
A general description of the indemonstrables would be that they are arguments with two premisses of which the ‘major’, called ‘tropikon’  , is either a conditional, a disjunction, or a negated conjunction, and the minor, called ‘proslēpsis’
, is either a conditional, a disjunction, or a negated conjunction, and the minor, called ‘proslēpsis’  , is a categorical. If the major is a conditional, then the minor is either its antecedent, in which case the conclusion is its consequent, or it is the negation of the consequent, in which case the conclusion is the negation of the antecedent. If the major is a disjunction, then either the minor is one of the disjuncts, in which case the conclusion is the negation of the other disjunct, or it is the negation of one of the disjuncts, in which case the conclusion is the other disjunct itself. If the major is a negated conjunction, then the minor is one of the conjuncts and the conclusion is the negation of the other conjunct. The indemonstrables were often represented by the Stoics as they are below, that is, as schemata having ordinal numbers as variables:126
, is a categorical. If the major is a conditional, then the minor is either its antecedent, in which case the conclusion is its consequent, or it is the negation of the consequent, in which case the conclusion is the negation of the antecedent. If the major is a disjunction, then either the minor is one of the disjuncts, in which case the conclusion is the negation of the other disjunct, or it is the negation of one of the disjuncts, in which case the conclusion is the other disjunct itself. If the major is a negated conjunction, then the minor is one of the conjuncts and the conclusion is the negation of the other conjunct. The indemonstrables were often represented by the Stoics as they are below, that is, as schemata having ordinal numbers as variables:126
(I) If the first, the second; but the first; therefore, the second.
(II) If the first, the second; but not the second; therefore, not the first.
(III) Not both the first and the second; but the first; therefore, not the second.
(IV) Either the first or the second; but the first; therefore, not the second.
(V) Either the first or the second; but not the first; therefore, the second.
In what follows we intend to consider mainly those arguments having a conditional axiōma as the major premiss, its antecedent as minor premiss, and its consequent as conclusion, which is to say, those arguments exemplifying schema (I) in the above list.
8.1 The sound conditional
In this section we consider several topics concerning the character of the Stoic conditional. These questions would seem to have a bearing on one’s view of the role of the conditional in the Stoic system of inference and on one’s view of Stoic logic in general. These topics are: (1) the debate over the criterion for a sound conditional, (2) the question whether there was a standard criterion for the Old Stoa, and (3) an account of the notion of conflict  which appears in the criterion attributed to Chrysippus.
which appears in the criterion attributed to Chrysippus.
The controversy
It is well known to students of ancient logic that in the fourth century B.C. a controversy prevailed among various ‘dialecticians’127 as to the proper criterion for a sound conditional 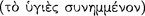 128Although this dispute is mentioned briefly by Cicero in Academica 2.143, our information comes mainly from the writings of Sextus Empiricus. At 8.108 in Adversus Mathematicos, Sextus outlines the Stoic characterisation of the conditional axiōma.129 The conditional, according to the Stoics, is a non-simple axiōma whose parts are joined by the connective ‘if’
128Although this dispute is mentioned briefly by Cicero in Academica 2.143, our information comes mainly from the writings of Sextus Empiricus. At 8.108 in Adversus Mathematicos, Sextus outlines the Stoic characterisation of the conditional axiōma.129 The conditional, according to the Stoics, is a non-simple axiōma whose parts are joined by the connective ‘if’ 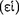 . The part preceding this connective is called the ‘antecedent’ or ‘first’
. The part preceding this connective is called the ‘antecedent’ or ‘first’  , whereas the other is called ‘consequent’ or ‘second’
, whereas the other is called ‘consequent’ or ‘second’ 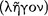 . Such an axiōma “seems to promise that its second component follows consequently on its first” (AM 8.111), and if this promise is carried through so that the consequent does indeed ‘follow’ the antecedent, then the conditional is true
. Such an axiōma “seems to promise that its second component follows consequently on its first” (AM 8.111), and if this promise is carried through so that the consequent does indeed ‘follow’ the antecedent, then the conditional is true 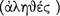 , but if not, then it is false
, but if not, then it is false  (AM 8.112).
(AM 8.112).
Note that in these passages where he is discussing the controversy on conditionals (AM 8.112–17; PH 2.110–12), Sextus appears to use 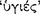 (sound) and
(sound) and  (true) as though they were synonymous. In the glossary of Stoic Logic, Mates claims that, according to Stoic usage, these terms are interchangeable ([Mates, 1953], 132). Jonathan Barnes states that the conditional “If p then q” is
(true) as though they were synonymous. In the glossary of Stoic Logic, Mates claims that, according to Stoic usage, these terms are interchangeable ([Mates, 1953], 132). Jonathan Barnes states that the conditional “If p then q” is  iff it is true.” On the other hand, he also writes that “of course,
iff it is true.” On the other hand, he also writes that “of course,  does not mean ‘true’” ([Barnes, 1980], 169n11). It seems possible that there is an ambiguity in Sextus’ use of the adjective
does not mean ‘true’” ([Barnes, 1980], 169n11). It seems possible that there is an ambiguity in Sextus’ use of the adjective  , which, given that he is reporting on Stoic doctrine, one might assume to be a reflection of an ambiguity in Stoic usage. Sextus seems for the most part to represent the Stoics as using this term to describe a statement expressing an axiōma the content of which correctly represents ‘the way things are’. For example, he reports in one place that the definite axiōma ‘This man is sitting’ or ‘This man is walking’ is true
, which, given that he is reporting on Stoic doctrine, one might assume to be a reflection of an ambiguity in Stoic usage. Sextus seems for the most part to represent the Stoics as using this term to describe a statement expressing an axiōma the content of which correctly represents ‘the way things are’. For example, he reports in one place that the definite axiōma ‘This man is sitting’ or ‘This man is walking’ is true  whenever the person indicated by the demonstrative is actually sitting or walking (8.100).130 On the other hand, there is some evidence to suggest that in the passages cited above (AM 8.112–17; PH 2.110–12), he may also use the term
whenever the person indicated by the demonstrative is actually sitting or walking (8.100).130 On the other hand, there is some evidence to suggest that in the passages cited above (AM 8.112–17; PH 2.110–12), he may also use the term  in the sense of ‘genuine’ or ‘real’.
in the sense of ‘genuine’ or ‘real’.
First, there is the evident fact that he seems to use  interchangeably. But, as Barnes has pointed out,
interchangeably. But, as Barnes has pointed out, 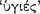 does not mean ‘true’ in the sense of a correct representation of the ‘way things are’. On the other hand, according to other sources on Stoic logical theory, it does appear in certain contexts to mean ‘genuine’ or ‘proper’. Consider, for example, the following dilemma set out by Aulus Gellius (2.7.6–10):
does not mean ‘true’ in the sense of a correct representation of the ‘way things are’. On the other hand, according to other sources on Stoic logical theory, it does appear in certain contexts to mean ‘genuine’ or ‘proper’. Consider, for example, the following dilemma set out by Aulus Gellius (2.7.6–10):
A father’s command is either honourable or base;
if his command is honourable, it is not to be obeyed merely because it
is his order, but because it is right that it be done;
if his command is base, it is not to be obeyed because what is wrong
Gellius rejects this argument on the basis that the leading premiss “cannot be considered what the Greeks call a sound and proper  disjunctive proposition.” (2.7.21). He claims that it requires the additional disjunct “or are neither honourable nor base” in order to be considered a genuine Stoic disjunction. Gellius’ motivation here seems to be a reflection of his claim at 16.8.12–14 that the disjuncts of a Stoic disjunction must exhaust the alternatives.
disjunctive proposition.” (2.7.21). He claims that it requires the additional disjunct “or are neither honourable nor base” in order to be considered a genuine Stoic disjunction. Gellius’ motivation here seems to be a reflection of his claim at 16.8.12–14 that the disjuncts of a Stoic disjunction must exhaust the alternatives.
Sextus himself makes the same claim at AM 8.434 where he includes an argument invalid because of deficiency in his classification of invalid Stoic arguments.131 Here Sextus writes that in the following argument the disjunctive premiss is deftcient:
In order to be  , according to Sextus, the disjunctive premiss ought to read as follows: ‘Wealth is either a good or an evil or indifferent’. In both this example and in Gellius’ example, the etymological derivation from the sense of
, according to Sextus, the disjunctive premiss ought to read as follows: ‘Wealth is either a good or an evil or indifferent’. In both this example and in Gellius’ example, the etymological derivation from the sense of  as ‘sound’ to its sense as ‘complete’ or ‘having the required characteristics’ would seem to be clear. Moreover, since that which is incomplete could not be a proper exemplar of its kind, the derivation to its sense as ‘genuine’ also seems clear.
as ‘sound’ to its sense as ‘complete’ or ‘having the required characteristics’ would seem to be clear. Moreover, since that which is incomplete could not be a proper exemplar of its kind, the derivation to its sense as ‘genuine’ also seems clear.
At AM 8.111–112, Sextus writes that a conditional proposition “seems to promise” that its consequent follows 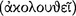 from its antecedent. Moreover, he adds that such a proposition is
from its antecedent. Moreover, he adds that such a proposition is  just in case this promise is fulfilled. Since a conditional proposition which lacked this characteristic could not be a proper Stoic conditional, one might suppose that a conditional is also therefore
just in case this promise is fulfilled. Since a conditional proposition which lacked this characteristic could not be a proper Stoic conditional, one might suppose that a conditional is also therefore  when this promise is fulfilled. Now inasmuch as
when this promise is fulfilled. Now inasmuch as 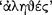 can be used in the sense of ‘genuine’ or ‘real’, it is possible, therefore, that Sextus uses both
can be used in the sense of ‘genuine’ or ‘real’, it is possible, therefore, that Sextus uses both  and
and 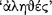 in that sense. This would explain why he uses them interchangeably, even though
in that sense. This would explain why he uses them interchangeably, even though 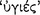 does not mean ‘true’ in the sense of a correct representation. However, a conditional proposition which was ‘sound’ or ‘true’ in the sense of ‘genuine’—which is to say that its consequent follows from its antecedent—could not help but be ‘true’ in the derivative sense that it would correctly represent the real connections between the states of affairs represented in the antecedent and consequent.
does not mean ‘true’ in the sense of a correct representation. However, a conditional proposition which was ‘sound’ or ‘true’ in the sense of ‘genuine’—which is to say that its consequent follows from its antecedent—could not help but be ‘true’ in the derivative sense that it would correctly represent the real connections between the states of affairs represented in the antecedent and consequent.
To return to Sextus’ account, it would seem to be agreed among the dialecticians that a conditional axiōma is sound whenever the consequent ‘follows’ from the antecedent. The disagreement arises, however, over the question of a criterion to determine when this relation of following holds. At AM 8.112, Sextus sets up the dispute as follows:
Now on the one hand all the dialecticians assert in common that the conditional proposition is sound whenever its consequent follows its antecedent. On the other hand, concerning when and how it follows they are at odds with one another, and set forth conflicting criteria for the notion of ‘following’.132
The most valuable discussion of the controversy over the criterion for a sound conditional is presented by Sextus in the passage at PH 2.110–12, wherein he outlines the four distinct and competing accounts. In this presentation Sextus apparently orders these definitions from the weakest to the strongest, in each case citing an example which is allowed by the next weaker interpretation, but which is rejected by the one under discussion.
Sextus begins by summarising the position of Diodorus Cronus of the Dialectical School and the conflicting position of his pupil, Philo the Dialectician.133 He attributes the first account to Philo, and states that according to this version, a conditional is sound whenever it is not the case that the antecedent is true and the consequent false (PH 2.110, cf. AM 8.113). In the passage at AM 8.113, Sextus presents what is in effect a truth table for the Philonian conditional. According to this summary, there are three combinations of truth values for the components of the conditional which make it sound and one which makes it false. These assignments correspond to the assignments in the truth table for the material conditional (cf. AM 8.245); consequently, there is general agreement among modern logicians that Philo’s definition amounts to a definition of the material conditional (cf. Mates [1953, p. 44]; Boche ski [Boche
ski [Boche ski, 1963, p. 89]). The second definition cited by Sextus is ascribed to the Diodorus Cronus. According to Diodorus, a sound conditional is one which neither was capable nor is capable of having a true antecedent and a false consequent (PH 2.110; cf. AM 8.115). Mates has argued cogently that a sound Diodorian conditional is an always true Philonian conditional ([Mates, 1953], 44–46).
ski, 1963, p. 89]). The second definition cited by Sextus is ascribed to the Diodorus Cronus. According to Diodorus, a sound conditional is one which neither was capable nor is capable of having a true antecedent and a false consequent (PH 2.110; cf. AM 8.115). Mates has argued cogently that a sound Diodorian conditional is an always true Philonian conditional ([Mates, 1953], 44–46).
Sextus attributes the third version of the correct criterion to those who advance the view that there must be a ‘connexion’ or ‘coherence’ 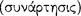 between the antecedent and consequent of a sound conditional. According to this view, a conditional proposition is sound whenever the contradictory
between the antecedent and consequent of a sound conditional. According to this view, a conditional proposition is sound whenever the contradictory  134
134 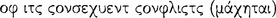
 with its antecedent (PH 2.111). Unlike the first two cases, this definition is not linked by Sextus to the name of any particular philosopher. Recently, however, several authors (e.g., Kneale and Kneale [1962a], 129; Gould [1970], 76; Mueller [1978], 20) have cited a passage in Cicero (De Faro, 12) as evidence that the ‘connection’ view is that of Chrysippus. We shall refer to this definition of a sound conditional as the ‘connexivist view’, in accordance with its attribution by Sextus to “those who introduce connexion.”135
with its antecedent (PH 2.111). Unlike the first two cases, this definition is not linked by Sextus to the name of any particular philosopher. Recently, however, several authors (e.g., Kneale and Kneale [1962a], 129; Gould [1970], 76; Mueller [1978], 20) have cited a passage in Cicero (De Faro, 12) as evidence that the ‘connection’ view is that of Chrysippus. We shall refer to this definition of a sound conditional as the ‘connexivist view’, in accordance with its attribution by Sextus to “those who introduce connexion.”135
The fourth definition, according to Sextus, is advocated by “those who introduce ‘implication’  .” It states that in a sound conditional the consequent must be ‘potentially contained’
.” It states that in a sound conditional the consequent must be ‘potentially contained’ 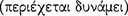 in the antecedent (PH 2.112). According to Mates ([1953], 49), this fourth definition cited by Sextus is not discussed by any other ancient sources, nor has its ancestry been attributed to any particular philosopher. In addition, with such a dearth of information, it has been little discussed by modern commentators. Martha Kneale has suggested that this may even be a Peripatetic view (Kneale and Kneale [1962a], 29). Long and Sedley, on the other hand, think that it may not be Significantly different from the connexion account ([Long and Sedley, 1990], 1.211). In any event, this version does not bear the name of any ancient philosopher, nor has a name been adopted as a consequence of its modern interpretations, as in the case of the connexivist thesis. More recently, however, Michael J. White has speculated that the motivation for this fourth type of conditional is somewhat akin to the ideas put forward in roodern relevant logics (White [1986, pp. 9–14]; hence we might call this fourth view the ‘relevantist’ view. However, since White’s speculations are somewhat tenuous, and since the philosophers who propose the definition invoke the notion of the virtual ‘inclusion’ or ‘containment’ of the consequent in the antecedent, it would seem better to call this fourth view the ‘inclusion’ or ‘containment’ criterion.
in the antecedent (PH 2.112). According to Mates ([1953], 49), this fourth definition cited by Sextus is not discussed by any other ancient sources, nor has its ancestry been attributed to any particular philosopher. In addition, with such a dearth of information, it has been little discussed by modern commentators. Martha Kneale has suggested that this may even be a Peripatetic view (Kneale and Kneale [1962a], 29). Long and Sedley, on the other hand, think that it may not be Significantly different from the connexion account ([Long and Sedley, 1990], 1.211). In any event, this version does not bear the name of any ancient philosopher, nor has a name been adopted as a consequence of its modern interpretations, as in the case of the connexivist thesis. More recently, however, Michael J. White has speculated that the motivation for this fourth type of conditional is somewhat akin to the ideas put forward in roodern relevant logics (White [1986, pp. 9–14]; hence we might call this fourth view the ‘relevantist’ view. However, since White’s speculations are somewhat tenuous, and since the philosophers who propose the definition invoke the notion of the virtual ‘inclusion’ or ‘containment’ of the consequent in the antecedent, it would seem better to call this fourth view the ‘inclusion’ or ‘containment’ criterion.
As an example of a conditional which is sound according to Philo’s criterion, Sextus cites the following: ‘If it is day, I converse’. This conditional is sound, he says, when in fact it is day and the subject is conversing (PH 2.110). And indeed, if Philo’s definition is the analogue of the material conditional, it would also be sound whenever either it is not day or the subject is conversing. But Sextus tells us that according to Diodorus this conditional is false  ,136 since it is obviously capable of having a true antecedent and false consequent whenever it is in fact day, but the subject remains silent (PH 2.110). As is the case with each of the critiques offered by Sextus, one has to consider the possibility that this objection was not in fact put forward by Diodorus but was contrived by Sextus himself for exegetical reasons. It was noted above that in presenting these definitions of a sound conditional Sextus’ intention seems to have been to order them from the weakest to the strongest, one definition being stronger than another just in case an example can be found which is rejected as being a sound by the former, but which is accepted by the latter. Martha Kneale [1962a, p. 129]) has pointed out that if Sextus did so arrange them, then it cannot be assumed that these criteria were actually conceived in the order presented. But even if one cannot make this assumption, it seems to us that one can put forward an account of the development of the controversy which is at least partially along the lines of Sextus’ arrangement.
,136 since it is obviously capable of having a true antecedent and false consequent whenever it is in fact day, but the subject remains silent (PH 2.110). As is the case with each of the critiques offered by Sextus, one has to consider the possibility that this objection was not in fact put forward by Diodorus but was contrived by Sextus himself for exegetical reasons. It was noted above that in presenting these definitions of a sound conditional Sextus’ intention seems to have been to order them from the weakest to the strongest, one definition being stronger than another just in case an example can be found which is rejected as being a sound by the former, but which is accepted by the latter. Martha Kneale [1962a, p. 129]) has pointed out that if Sextus did so arrange them, then it cannot be assumed that these criteria were actually conceived in the order presented. But even if one cannot make this assumption, it seems to us that one can put forward an account of the development of the controversy which is at least partially along the lines of Sextus’ arrangement.
For one thing, it is unclear why chronological priority should be a factor in the debate between Diodorus and Philo. Since these philosophers were teacher and pupil, then regardless of which definition was put forward first, it seems plausible to suppose that it was Diodorus himself who articulated the objections to Philo’s account and put forward the counter-example. In addition, since several modern commentators agree that the connexion view can be attributed to Chrysippus, it seems feasible that this criterion was formulated later than both the Diodorian and the Philonian definitions; moreover, it seems quite reasonable to suppose that it was Chrysippus who raised the objections to the Diodorian view. On the other hand, it would be somewhat more difficult to substantiate Sextus’ ordering of the connexion and inclusion accounts, the reason being that there is no confirmation other than Sextus’ own testimony to support the hypothesis that the inclusion criterion was formulated after the connexion account. Nor is there any other evidence to support his version of the inclusionist objections to the connexivist criterion. Hence, in contrast to Kneale’s assumption that “we can take it that the objections mentioned by Sextus were in fact put forward at some time” [Kneale and Kneale, 1962a, p. 129], we would urge that one not take his account of the debate between the inclusionists and the connexivists for granted.
The conditional presented by Sextus as being sound according to Diodorus’ criterion but not sound according to the connexion criterion is the following: ‘If it is not the case that atomic elements of existents are without parts, then atomic elements of existents are without parts’137 (ПH 2.111). T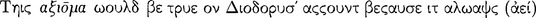
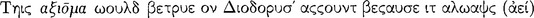 138 begins with the false clause ‘It is not the case that atomic elements of existents are without parts’ and ends with the true clause ‘atomic elements of existents are without parts’; hence, it never was capable, nor is it capable of beginning with a true antecedent and ending with a false consequent (PH 2.111). It seems clear that the axiōma ‘Atomic elements of existents are without parts’ is conceptually or analytically true, and hence necessary. What is more relevant, however, is that it would count as a necessary proposition according to the versions of necessity of both Diodorus and Chrysippus. The definition of Diodorus is worded as follows: “The necessary is that which being true, will not be false” (necessarium, quod cum verum sit non erit falsum) (Boethius in de interp. 234); whereas that of Chrysippus is worded thus: “The necessary is that which being true does not admit of being false, or admits of being false but is prevented by external factors from being false” (DL 7.75).139 It is evident that on either account of necessity, Diodorus’ criterion for a sound conditional will make the counter-example sound merely by the fact that the consequent is necessary or that the antecedent is impossible, since either circumstance is sufficient to insure that the conditional never was capable, nor is capable, of having a true antecedent and a false consequent. Thus it seems plain why Diodorus’ definition would be rejected by someone who thinks that a sound conditional requires a connexion or coherence between the antecedent and consequent, for clearly his criterion would permit a conditional to be sound even though there is no connection whatever between its parts.
138 begins with the false clause ‘It is not the case that atomic elements of existents are without parts’ and ends with the true clause ‘atomic elements of existents are without parts’; hence, it never was capable, nor is it capable of beginning with a true antecedent and ending with a false consequent (PH 2.111). It seems clear that the axiōma ‘Atomic elements of existents are without parts’ is conceptually or analytically true, and hence necessary. What is more relevant, however, is that it would count as a necessary proposition according to the versions of necessity of both Diodorus and Chrysippus. The definition of Diodorus is worded as follows: “The necessary is that which being true, will not be false” (necessarium, quod cum verum sit non erit falsum) (Boethius in de interp. 234); whereas that of Chrysippus is worded thus: “The necessary is that which being true does not admit of being false, or admits of being false but is prevented by external factors from being false” (DL 7.75).139 It is evident that on either account of necessity, Diodorus’ criterion for a sound conditional will make the counter-example sound merely by the fact that the consequent is necessary or that the antecedent is impossible, since either circumstance is sufficient to insure that the conditional never was capable, nor is capable, of having a true antecedent and a false consequent. Thus it seems plain why Diodorus’ definition would be rejected by someone who thinks that a sound conditional requires a connexion or coherence between the antecedent and consequent, for clearly his criterion would permit a conditional to be sound even though there is no connection whatever between its parts.
Note that the rejection of the counter-example cited in the previous section can be generalised by stating that the connexivist criterion renders false any conditional in which the antecedent and consequent are contradictories. This characteristic property of the connexivist view of implication is stated by Storrs McCall as follows: “[N]o proposition connexively implies or is implied by its own negation, since it is never incompatible with its own double negation, nor is its own negation incompatible with itself” [McCall, 1966, p. 415]. According to McCall, “this connexive property of propositions was known to Aristotle” [McCall, 1966, p. 415]. In the Prior Analytics Aristotle argues that “it is impossible that the same thing should be necessitated by the being and by the not-being of the same thing” (57b3). If it is supposed, for example, that if A is white, then necessarily B is great, and if A is not white, then necessarily B is great, then “it follows of necessity that if B is not great, then B itself is great; but this is impossible”  (57b13). Consequently, McCall dubs this property, which he represents in Polish notation as NCNpp, ‘Aristotle’s Thesis’ ([McCall, 1966], 415).140
(57b13). Consequently, McCall dubs this property, which he represents in Polish notation as NCNpp, ‘Aristotle’s Thesis’ ([McCall, 1966], 415).140
As an instance of a conditional sound according to the connexivist criterion, Sextus puts forward the example ‘If it is day, it is day’ (PH 2.111). This conditional is connexively sound since obviously every proposition must be in conflict with its own contradictory. Sextus claims that on the inclusion view this proposition and every such ‘duplicated’  conditional would be false, the reason being that “it is not feasible that any object should be included in itself” (PH 2.112). Sextus does not give an example of a conditional sound according to the inclusion criterion, and the reason may be, as is suggested by Michael J. White, that “it would ill accord with his purpose of producing suspension of belief … with respect to all accounts to leave the reader with the impression that [this] last account … is correct” [White, 1986, p. 10]. White also suggests that Sextus “gives the impression of having to strain a bit” [White, 1986, p. 10] in his attempt to show that the aforementioned connexivist paradigm would be false according to the inclusion view. As he expresses the point, this rather “literal-minded” interpretation of
conditional would be false, the reason being that “it is not feasible that any object should be included in itself” (PH 2.112). Sextus does not give an example of a conditional sound according to the inclusion criterion, and the reason may be, as is suggested by Michael J. White, that “it would ill accord with his purpose of producing suspension of belief … with respect to all accounts to leave the reader with the impression that [this] last account … is correct” [White, 1986, p. 10]. White also suggests that Sextus “gives the impression of having to strain a bit” [White, 1986, p. 10] in his attempt to show that the aforementioned connexivist paradigm would be false according to the inclusion view. As he expresses the point, this rather “literal-minded” interpretation of 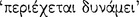 does nothing to convince one that these conditionals were indeed rejected by the inclusion view.141
does nothing to convince one that these conditionals were indeed rejected by the inclusion view.141
It is of interest in this regard to note some comments which have been recorded concerning the relationship between the connexion and inclusion conditionals. The remark of Long and Sedley to the effect that they may not differ significantly from one another has already been mentioned above. Add to this the comments of Martha Kneale that “the difference between them was small” and that “the objection which the partisans of implication brought against the theory of connexion is not of a fundamental kind” (Kneale and Kneale [1962a, p. 134]), as well as the observation of Mates that “the fourth type of implication seems to be a restricted type of Chrysippean implication” [Mates, 1953, p. 49], and there seems to be reason enough to concur with White’s doubts about the accuracy of Sextus’ report concerning the relationship between these two accounts of implication. Given these doubts, one is tempted to speculate that the order of appearance between the connexion and inclusion definitions may have been the reverse of Sextus’ arrangement. If so, then it may be that Chrysippus saw a need for more precision than that afforded by the inclusion definition, and thus formulated the connexion account in response to that perception.
The standard Stoic conditional
There are several reasons to suppose that from Chrysippus on, the connexivist account was the standard doctrine of the Old Stoa concerning the criterion for a sound conditional. First, there is some textual evidence in Diogenes Laërtius. At 7.71, in recording the Stoic account of non-simple axiōmata, Diogenes reports that according to Chrysippus in his Dialectics and Diogenes of Babylon in his Art of Dialectic, a conditional is a non-simple axiōma constructed by means of the connective ‘if’ 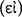 , such that this connective promises that the consequent follows
, such that this connective promises that the consequent follows  the antecedent. Later, at 7.73, he attests that according to the Stoic criterion, a true
the antecedent. Later, at 7.73, he attests that according to the Stoic criterion, a true  conditional is one in which the contradictory of the consequent conflicts
conditional is one in which the contradictory of the consequent conflicts  with the antecedent. Now although this version of a sound conditional is not actually attributed to Chrysippus and Diogenes of Babylon, the juxtaposition of these passages would seem to indicate a connection. In any case, there is further indirect textual support afforded by the passage of Cicero at De fato 12. We have already mentioned that this passage has been cited by several modern commentators as providing strong evidence that the connection or coherence criterion was the account accepted by Chrysippus.142
with the antecedent. Now although this version of a sound conditional is not actually attributed to Chrysippus and Diogenes of Babylon, the juxtaposition of these passages would seem to indicate a connection. In any case, there is further indirect textual support afforded by the passage of Cicero at De fato 12. We have already mentioned that this passage has been cited by several modern commentators as providing strong evidence that the connection or coherence criterion was the account accepted by Chrysippus.142
Although the testimony of Cicero and Diogenes Laërtius would appear to be sufficient to establish that Chrysippus propounded the connection doctrine for a sound implication, it does not focus any light on the question as to what criterion Zeno and Kleanthes supported. Indeed, the information available in the texts would seem to be inadequate to establish any certainty in this regard. However, there are some passages in which Sextus Empiricus attributes the Philonian criterion to ‘the Stoics’ or to ‘the Dogmatists’, and these remarks are taken by at least one writer to indicate that Zeno adopted Philo’s definition of a sound conditional [Rist, 1978, p. 391]. Since Zeno and Philo were contemporaries and both students of Diodorus Cronus, this is a plausible conjecture. On the other hand, there is nothing specific in these passages to link the Philonian criterion to Zeno, and in fact, there is room for some doubt concerning Sextus’ attribution of this definition to the Stoics.
As a sceptic Sextus was out to discredit the views of all the so-called ‘dogmatic philosophers’. With respect to the Stoics this would have involved, among other things, showing their logical system to be useless as a means of making inferences or providing demonstrations. Thus it is significant that in those passages where he attributes the Philonian definition to the Stoics, Sextus then invokes this alleged characteristic in an attack on some aspect of the Stoic theory of inference. For example, consider the passages at PH 2.104 and at AM 8.244 where he assails the Stoic doctrine of signs.143 According to Sextus, the Stoics define the sign as an antecedent axiōma in a sound conditional, capable of revealing  the consequent (AM 8.245; PH 2.104). Since there are three possible combinations of truth values for a sound conditional,144 the Stoics further stipulate that the sign will be the antecedent of a sound conditional which begins with a true axiōma and ends with a true axiōma (AM 8.248–50; PH 2.106). Clearly, nothing in this definition of a sign commits the Stoics to the Philonian criterion for a sound conditional; however, Sextus claims that this is the criterion they accept (AM 8.247; PH 2.105). In proceeding with his criticism, Sextus points out that, according to the Stoics, the thing signified
the consequent (AM 8.245; PH 2.104). Since there are three possible combinations of truth values for a sound conditional,144 the Stoics further stipulate that the sign will be the antecedent of a sound conditional which begins with a true axiōma and ends with a true axiōma (AM 8.248–50; PH 2.106). Clearly, nothing in this definition of a sign commits the Stoics to the Philonian criterion for a sound conditional; however, Sextus claims that this is the criterion they accept (AM 8.247; PH 2.105). In proceeding with his criticism, Sextus points out that, according to the Stoics, the thing signified  is either ‘pre-evident’
is either ‘pre-evident’  or ‘non-evident’
or ‘non-evident’  (AM 8.265; PH 2.116). But if pre-evident, then “it will not admit of being signified, nor will it be signified by anything, but will be perceived of itself” (AM 8.267). On the other hand, if it is non-evident, then it cannot be known that it is true, since if it were known, it would then be pre-evident (AM 8.267). Hence, although the truth-value of the antecedent is known to be true, that of the consequent is necessarily uncertain. Therefore, the truth-value of the conditional is uncertain, since the truth-value of the consequent must be known in order to determine the truth value of the conditional (AM 8.268). Hence the Stoic account of a sign is useless, since the soundness of a conditional with a non-evident consequent is indeterminate (AM 8.268).
(AM 8.265; PH 2.116). But if pre-evident, then “it will not admit of being signified, nor will it be signified by anything, but will be perceived of itself” (AM 8.267). On the other hand, if it is non-evident, then it cannot be known that it is true, since if it were known, it would then be pre-evident (AM 8.267). Hence, although the truth-value of the antecedent is known to be true, that of the consequent is necessarily uncertain. Therefore, the truth-value of the conditional is uncertain, since the truth-value of the consequent must be known in order to determine the truth value of the conditional (AM 8.268). Hence the Stoic account of a sign is useless, since the soundness of a conditional with a non-evident consequent is indeterminate (AM 8.268).
At AM 8.449, using a similar strategy, Sextus attacks the Stoic argument schemata, and in particular, the first indemonstrable.145 He intends to show that an argument having this schema cannot in fact be a demonstrative argument, and hence, is of no use in demonstrating a conclusion. According to the Stoics, a demonstrative argument  is an argument which is conclusive
is an argument which is conclusive  , has true premisses and a true conclusion, and deduces a non-evident conclusion from pre-evident premisses (PH 2.140; AM 8.422). Starting with this definition, Sextus proceeds roughly as follows (AM 8.449–52). Given any argument for which the premisses are pre-evident, the conclusion is either pre-evident and known, or it is non-evident and unknown. If the conclusion is pre-evident and known, then according to the definition of a demonstrative argument, such an argument is not demonstrative. On the other hand, if the conclusion if non-evident and unknown, then the truth value of the conditional premiss is indeterminate. For the antecedent of this conditional is the minor premiss of the argument, which is pre-evident and known to be true, while the consequent is the conclusion of the argument, which we are assuming to be non-evident and unknown. Hence, since it cannot be determined whether the premisses are true, it cannot be determined that the argument is demonstrative; therefore, in either case, the argument is not demonstrative. But if it is not demonstrative, then it is of no practical use as a means of inference.
, has true premisses and a true conclusion, and deduces a non-evident conclusion from pre-evident premisses (PH 2.140; AM 8.422). Starting with this definition, Sextus proceeds roughly as follows (AM 8.449–52). Given any argument for which the premisses are pre-evident, the conclusion is either pre-evident and known, or it is non-evident and unknown. If the conclusion is pre-evident and known, then according to the definition of a demonstrative argument, such an argument is not demonstrative. On the other hand, if the conclusion if non-evident and unknown, then the truth value of the conditional premiss is indeterminate. For the antecedent of this conditional is the minor premiss of the argument, which is pre-evident and known to be true, while the consequent is the conclusion of the argument, which we are assuming to be non-evident and unknown. Hence, since it cannot be determined whether the premisses are true, it cannot be determined that the argument is demonstrative; therefore, in either case, the argument is not demonstrative. But if it is not demonstrative, then it is of no practical use as a means of inference.
As Ian Mueller points out [Mueller, 1978, p. 23], if the truth-functional interpretation of the conditional is taken as the Stoic criterion, then no defence against Sextus’ argument can be mustered on behalf of the first indemonstrable. On the other hand, if the connexion interpretation (or the inclusion interpretation) were taken as the Stoic definition, then Sextus’ argument would fail. It should be obvious that the ascription of either the connexion criterion or the inclusion criterion to the Stoics would, in addition to blocking Sextus’ criticism of the indemonstrables, also nullify his objection, discussed above, to the Stoic doctrine of signs. With respect to the criticism of the indemonstrables, Mueller expresses the point thus:
There is no way out of this situation, a fact that strongly suggests that Sextus’ insistence on applying the truth-functional interpretation to the conditional represents an argumentative device rather than an accurate reflection of standard Stoic doctrine. If the first premise of an undemonstrable argument expresses a stronger than truth-functional connection between its component propositions, there is no reason why the first premise can not be established independently of the conclusion [Mueller, 1978, p. 23].
Mueller goes on to point out that the ascription of a strong interpretation to the Stoic conditional “means that philosophically a great deal of weight must be placed on the knowledge of necessary connections between propositions” [Mueller, 1978, p. 23]. It seems to us, however, that although Mueller’s point is correct, his putting the matter in this way is somewhat misleading. Although we will not argue for the point here, we would suggest that it is because their view places a great deal of philosophical weight on a knowledge of necessary connections between axiōmata that one ought to ascribe a strong interpretation of the conditional to the Stoics, and not the reverse.
A further point mentioned by Mueller is that many of the criticisms put forward by Sextus in the course of his writings are directed against the possibility of there being such knowledge of necessary connections as the Stoics suppose [Mueller, 1978, p. 23]. However, since it is not our intention here to defend Stoic doctrines from the objections of Sextus Empiricus and other critics, these criticisms are not a concern. What is of concern is to minimise the effects of Sextus’ claim that the Stoics adopted the Philonian criterion for a sound conditional. One of these effects, as has already been noted above, is Rist’s conjecture that it was Zeno himself who opted for the Philonian view. Clearly this conjecture is at odds with the interpretation we intend to put forward; we take it, however, that what has been said about Sextus’ motives in ascribing the Philonian conditional to the Stoics is sufficient to cast some doubt on his claim, and hence, to render Rist’s conjecture doubtful as well.
There is yet another passage which would seem to indicate that the Stoics chose the Philonian interpretation for the conditional. This passage occurs in Diogenes Laërtius, and hence, since Diogenes does not write in a polemical tone, one cannot in this case invoke the sort of argument used against Sextus’ attribution. There are, however, some doubts which can be raised against this ascription as well. The passage in question is at 7.81. Here Diogenes says that according to the Stoics:
The true follows from the true, as, for example, ‘It is light’ from ‘It is day’; and the false, from the false, for example, ‘It is dark’ from the false ‘It is night’; and the true from the false, for example, ‘The earth exists’ from ‘The earth flies’; but the false does not follow from the true, for from ‘The earth exists’, ‘The earth flies’ does not follow.
The difficulty with taking this passage as an indication the Stoics adopted the Philonian conditional (e.g. Mates [1953, 44n14]) is that one is immediately confronted with an inconsistency in Diogenes’ account of Stoic logic. For at DL 7.73, he reports that, according to Stoic theory, a true conditional is one in which the contradictory of the consequent conflicts with the antecedent. This criterion is precisely the definition of a sound conditional which Sextus described as the one put forward by “those who introduce ‘connexion’ (PH 2.111).146 So if one takes the passage at DL 7.81 to indicate that the Stoics adopted the Philonian conditional, then it appears that the account from which Diogenes got his information is inconsistent, since it attests to the adoption by the Stoics of two incompatible definitions of a sound or true conditional. One possibility, of course, is that these different views were predominant at different periods in the history of the Stoic school. However, according to Hicks (DL 7.38nb), the source for the entire doxography on the Stoics from DL 7.49 to DL 7.83 is Diocles of Magnesia, a scholar of the first century B.C. considered by Mates “to have a fair knowledge of Stoic logic” [Mates, 1953, p. 9]. Consequently, one would expect that the account given in these passages would be fairly unified; moreover, one would also expect that if criteria from different periods were included in this doxography, some mention would have been made of the fact. Given these considerations, we would suggest that rather than suppose an inconsistency in Diogenes’ source, one take the connexivist definition as the standard Stoic criterion for the period covered by this doxography and look for some other interpretation to explain the passage at DL 7.81.
Such an interpretation might be suggested by considering the examples introduced by Diogenes in this passage. It seems to us that the examples of a sound conditional which he cites are all conditionals which would be sound according to the connexivist criterion (and also, perhaps, according to the inclusion criterion). For instance, he illustrates the true-true case with the conditional ‘If it is day, it is light’, and the false-false case with ‘If it is night, it is dark’. It seems plausible that the Stoics might have taken the contradictory of the consequent in these conditionals to be in conflict with the antecedent on the grounds that these states of affairs are related by a necessary causal sequence. Diogenes exemplifies the false-true case with ‘If the earth flies, the earth exists’, and for this example it is feasible that the Stoics might have invoked conceptual grounds to argue that the contradictory of the consequent would conflict with the antecedent. What we have in mind, then, is that the passage quoted above can be interpreted as a demonstration of the point that it is possible for a sound conditional to have either a true antecedent and true consequent, or a false antecedent and false consequent, or a false antecedent and true consequent. And in order to facilitate this demonstration, the Stoics naturally presented examples of conditionals which they took to be sound according to the connexivist criterion, since they adopted the connexivist definition as their criterion for a sound conditional, as we are informed at DL 7.73. For the case in which the antecedent is true and the consequent false, which is to say, for the case where the conditional is not sound, Diogenes gives the example ‘If the earth exists, the earth flies’. It would seem that the Stoics might again appeal to conceptual considerations in order to say that in this example the contradictory of the consequent does not conflict with the antecedent; moreover, since this criterion determines an unsound conditional (DL 7.73), they could also say on connexivist grounds that this conditional is not sound.
We have already suggested that, given the Stoic definition of a sign, Zeno’s interest in the doctrine of signs would afford him reason to take a stance with respect to the criterion for a sound conditional (see page 407). And we have also put forward the view that the purpose of logic for Zeno’s wise man is to allow him to make correct judgements about the connections between particular states of affairs on the basis of his knowledge of the general causal principles governing such connections (see page 422). Hence, we take it that Zeno’s interest in signs is a manifestation of his general concern to draw out the implications of one’s actions in accordance with the natural sequence of events. And since Zeno identified the natural sequence of causation, which he called heimarmenē with the logos or rational principle of the universe (DL 7.149), and since he also identified the logos itself with ‘necessity’ (Lactanius, Tertullianis SVF 1.160), our understanding is that he saw these causal connections as necessary in the sense implied by these identifications. Moreover, we propose that he chose the conditional construction as the syntactical representation of these connections because such representation is suggestive of the causal sequence of events. Hence, the Stoic use of the particle  is technical and already implies a strong interpretation of the conditional since it presupposes a necessary connection between the antecedent and consequent (see page 423).
is technical and already implies a strong interpretation of the conditional since it presupposes a necessary connection between the antecedent and consequent (see page 423).
Therefore, it seems unlikely to us that Zeno would have adopted the view of either Philo or Diodorus, for on either of these conceptions a conditional may be sound even though there is no connection between its parts. Moreover, if the invention of the connexion view can be attributed to Chrysippus, then it seems evident that Zeno could not have opted for this definition since it would not have been available to him. One might conjecture that he proposed an account of his own, and if this were the case, then plausibly he introduced the inclusion criterion.On the other hand, it is possible that he put forward a version which is completely unrecorded, although it seems to us that this alternative is not so plausible as the first one. In any event, although we shall pursue the matter no further in this work, it would be of interest to explore the possibility that the inclusion definition of a sound conditional was the criterion with which Zeno worked.
Consequence and conflict
The view of Mates and others notwithstanding, it would appear to be an open question how one is to understand the use of the verb 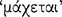 in the passages where it is used in the definition of a sound conditional by Sextus Empiricus (PH 2.111) and Diogenes Laërtius (7.73; 77). The consensus among these commentators is that it should be understood as ‘is incompatible’ where ‘incompatible “is used in its ordinary sense,” which is to say, in the sense that two “incompatible propositions cannot both be true, i.e., their conjunction is logically false” [Mates, 1953, p. 48]. On this view, then, a valid argument, according to the connexivists, is such that it is not logically possible for both the contradictory of the conclusion and the conjunction of the premisses to be simultaneously true. But even leaving aside the difficulty of determining the Stoics’ understanding of ‘logical possibility’,147 there remain some etymological questions as to whether one ought to accept this account as accurately reflecting the intension of
in the passages where it is used in the definition of a sound conditional by Sextus Empiricus (PH 2.111) and Diogenes Laërtius (7.73; 77). The consensus among these commentators is that it should be understood as ‘is incompatible’ where ‘incompatible “is used in its ordinary sense,” which is to say, in the sense that two “incompatible propositions cannot both be true, i.e., their conjunction is logically false” [Mates, 1953, p. 48]. On this view, then, a valid argument, according to the connexivists, is such that it is not logically possible for both the contradictory of the conclusion and the conjunction of the premisses to be simultaneously true. But even leaving aside the difficulty of determining the Stoics’ understanding of ‘logical possibility’,147 there remain some etymological questions as to whether one ought to accept this account as accurately reflecting the intension of 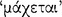 in Stoic terminology.
in Stoic terminology.
To forestall possible objections to putting an etymological cast on the problem, it would be useful to consider Mates’ criticism of Philip De Lacy for the latter’s use of “weaving together” as a translation of the Greek term 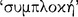 , which is standardly translated as ‘conjunction’.
, which is standardly translated as ‘conjunction’.
 the technical term for conjunction, should not be translated as “weaving together.” There is no virtue in employing etymological translations for technical terms, since a term becomes technical precisely by being dissociated from its etymological and other connotations and associated unambiguously with its denotation [Mates, 1953, 92n24].
the technical term for conjunction, should not be translated as “weaving together.” There is no virtue in employing etymological translations for technical terms, since a term becomes technical precisely by being dissociated from its etymological and other connotations and associated unambiguously with its denotation [Mates, 1953, 92n24].
Doubtless one can agree that it is never virtuous and perhaps always somewhat fanciful to translate a technical term by summoning forth its etymological origins. But it does not follow that in attempting to understand a term, the technical meaning of which is either unclear or controversial, one ought to ignore its semantic history.
In the present case, there are those who believe that ‘incompatibility’ designates a non-truth-functional relation which exists between propositions.148 They would criticise Mates’ and those who agree with him on the grounds that, according to his characterisation, it would turn out that an impossible proposition would be incompatible with any proposition, even itself. This result is not in accord with their logical intuitions. The relation which Mates describes is, on their view, more aptly designated as incompossibility.149 What is relevant to this controversy, however, is the question of how the Stoics understood the meaning of 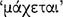 which, as has been noted, is standardly translated as ‘incompatible’. It is here that one can look to etymology for assistance.
which, as has been noted, is standardly translated as ‘incompatible’. It is here that one can look to etymology for assistance.
The primary meaning for  , the infinitive form of the verb, is to fight or to battle or to war. Now, one would hardly want to translate the term
, the infinitive form of the verb, is to fight or to battle or to war. Now, one would hardly want to translate the term 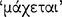 in a logical context as ‘fights’ or ‘battles’ or ‘wars’. To the modern logician, not only do they seem somewhat fatuous as a description of a relation between propositions, but also they seem rather out of place in a logic treatise. Nevertheless, these renderings would seem to reflect more faithfully the etymology of
in a logical context as ‘fights’ or ‘battles’ or ‘wars’. To the modern logician, not only do they seem somewhat fatuous as a description of a relation between propositions, but also they seem rather out of place in a logic treatise. Nevertheless, these renderings would seem to reflect more faithfully the etymology of  than does the translation ‘is incompatible’, at least where the latter is understood as Mates understands it. Probably ‘conflicts’ is just the right compromise. It is bloodless enough for a logic book, yet it remains faithful to the etymological origins of the Greek term, more so, it would seem, than ‘is incompatible’.
than does the translation ‘is incompatible’, at least where the latter is understood as Mates understands it. Probably ‘conflicts’ is just the right compromise. It is bloodless enough for a logic book, yet it remains faithful to the etymological origins of the Greek term, more so, it would seem, than ‘is incompatible’.
Now with this translation in mind, consider the thesis that the Stoics understood this notion of conflict in terms of ‘incompossibility’, where this term is taken in the sense that two propositions are incompossible just in case it is not possible that they both be true. It has been pointed out that, according to this characterisation, it is a sufficient condition for two propositions to be incompossible if one of them is necessarily false. Hence, the propositions ‘All triangles have four sides’ and ‘Chrysippus is the greatest of Stoic logicians’ would be incompossible. Would the Stoics have considered these propositions to be in any sense ‘in conflict’? It is difficult to see how anyone would suppose them so. On the other hand, consider the propositions ‘All triangles have four sides’ and ‘All triangles have five sides’. These propositions are clearly incompossible because both are impossible, but it is also clear that they are related in such a way that if one is affirmed, then the other must be denied. This relation, moreover, is independent of the truth values or the modal status of the individual propositions. It is this sort of relation which the critics of Mates’ view appear to have in mind as the proper meaning of the term ‘incompatibility’. And, one might assume, it is also what they would expect that the Stoics had in mind when the latter spoke of propositions or states of affairs being ‘in conflict’.
8.2 The conditional and inference
Validity and conditionalisation
The so-called principle of conditionalisation is presented in several places by Sextus Empiricus as a Stoic criterion for a valid argument.150 As it is framed by the Stoics, this canon states that an argument is conclusive151  : PH 2.137) or true (
: PH 2.137) or true ( : AM 8.417): that is, the conditional which has the conjunction of the premisses as antecedent and the conclusion of the argument as consequent. As an example, Sextus presents the following case at PH 2.137. The argument
: AM 8.417): that is, the conditional which has the conjunction of the premisses as antecedent and the conclusion of the argument as consequent. As an example, Sextus presents the following case at PH 2.137. The argument
has as its corresponding conditional the following:
The application of the principle here is the assertion that since the corresponding conditional is sound, the argument is valid. According to Sextus’ account at AM 8.111–12, it was agreed among the ‘dialecticians’ that a conditional axiōma is sound whenever its consequent axiōma ‘follows’ its antecedent axiōma. Hence, to say that (2) is sound is just to say that its consequent, which corresponds to the conclusion of (1), indeed follows its antecedent, which corresponds to the conjunction of the premisses of (1). It seems evident that if the Stoics wished to attribute such a property to a valid argument, then they must have assumed that the relation of ‘following’  , which they took to be the relation holding between the antecedent and consequent in a sound conditional, was the same relation holding between the premisses and conclusion of a valid argument (cf. PH 2.113).
, which they took to be the relation holding between the antecedent and consequent in a sound conditional, was the same relation holding between the premisses and conclusion of a valid argument (cf. PH 2.113).
Taking into account the debate over the sound conditional discussed in Section 8.1, as well as the principle of conditionalisation, one would expect that there would have been recorded as many distinct conceptions of a valid argument as there were accounts of a sound conditional. This does not, however, seem to be the case. Other than the conditionalisation principle itself, there appears to be no mention in the fragments of a criterion for a valid argument except the one implied by Diogenes Laërtius at 7.77. In this passage Diogenes presents the following characterisation of an invalid argument.
And of arguments some are conclusive (valid) and some inconclusive (invalid). Inconclusive are those in which the contradictory of the conclusion does not conflict with the conjunction of the premisses.152
Although it is not explicitly stated, this characterisation would seem to imply that a valid argument is one in which the contradictory of the conclusion is in conflict with the conjunction of the premisses.
In addition to the above account which implies a criterion for a valid argument, Diogenes also reports the following Stoic criterion for a sound conditional.
So, then, the true conditional axiōma is one in which the contradictory of the consequent conflicts with the antecedent, as in this example: ‘If it is day, it is light’ (DL 7.73).153
It is evident that the criterion for a sound conditional described in the passage at DL 7.77 is identical to the one which Sextus Empiricus reports at PH 2.111. This is the criterion proposed by “those who introduce ‘connexion’ or ‘coherence’  ” as a condition on the relation of following between the antecedent and consequent of a sound conditional. It was mentioned earlier that this standard has been ascribed by several modern commentators to Chrysippus himself (see page 479). In light of his influence on the development of Stoic logic, it is probable that if this ‘connexivist’ view was indeed the one he advocated, then it would have been the one accepted by the Stoa.
” as a condition on the relation of following between the antecedent and consequent of a sound conditional. It was mentioned earlier that this standard has been ascribed by several modern commentators to Chrysippus himself (see page 479). In light of his influence on the development of Stoic logic, it is probable that if this ‘connexivist’ view was indeed the one he advocated, then it would have been the one accepted by the Stoa.
The formulation of the connexivist criterion leaves no doubt that its adoption would commit the Stoics to a strong interpretation of the criterion for a sound conditional axiōma. Thus it seems plausible that for the Stoics the term  expressed a real connection or coherence between the antecedent and consequent, and, in some sense, a necessary relation between them. Since the conditionalisation principle implies that the same relationship holds between the premisses and conclusion of a valid argument, we can infer that such a connexion obtained between them as well.
expressed a real connection or coherence between the antecedent and consequent, and, in some sense, a necessary relation between them. Since the conditionalisation principle implies that the same relationship holds between the premisses and conclusion of a valid argument, we can infer that such a connexion obtained between them as well.
Now in accordance with the conditionalisation principle, the ubiquitous Stoic example
would be valid just in case the following conditional were sound:
And in accordance with the description of a sound conditional given by Diogenes Laërtius at 7.73, (4) would be sound just in case the contradictory of its consequent were in conflict with its antecedent. Thus, in conformity with the conditionalisation principle and the description of a sound conditional presented by Diogenes, (3) would be valid just in case the contradictory of its conclusion were in conflict with the conjunction of its premisses. This would seem to suggest that the characterisation of a valid argument given by Diogenes at 7.77 is derived from an application of the connexivist notion of a sound conditional to the principle of conditionalisation.
There are, however, difficulties with this proposal. The first objection is that there are the passages in Sextus Empiricus (PH 2.104; AM 8.245) which seem to indicate that the Stoics adopted the Philonian account of a sound conditional (cf. [Mates, 1953, p. 43]). A further objection is that both Mates [1953, p. 60, 75] and Boche ski [1963, p. 97] cite passages at PH 2.137 and AM 8.415 to support the thesis that the conditionalisation principle required a ‘Diodorean-true’ conditional. The views of the Dialecticians Philo and Diodorus have been discussed earlier (see page 479), however, a brief summary of their views might be in order for the present. According to Philo, then, a conditional is sound whenever it does not have a true antecedent and false consequent (PH 2.110; AM 8.113). According to Diodorus, on the other hand, a conditional is sound if it neither was capable nor is capable of having a true antecedent and false consequent (PH 2.110; AM 8.115).
ski [1963, p. 97] cite passages at PH 2.137 and AM 8.415 to support the thesis that the conditionalisation principle required a ‘Diodorean-true’ conditional. The views of the Dialecticians Philo and Diodorus have been discussed earlier (see page 479), however, a brief summary of their views might be in order for the present. According to Philo, then, a conditional is sound whenever it does not have a true antecedent and false consequent (PH 2.110; AM 8.113). According to Diodorus, on the other hand, a conditional is sound if it neither was capable nor is capable of having a true antecedent and false consequent (PH 2.110; AM 8.115).
In replying to the first objection one probably cannot deny that the texts appear to support the view that the Philonian account gained some measure of acceptance among the Stoics. One might point out that acceptance of this account was by no means unanimous, as the passage at AM 8.245 indicates. And even if this was the view chosen by many Stoics, the debate continued.154 If it were the case that they did opt for the Philonian criterion, then one would expect that applications of the conditionalisation principle would reflect that fact. But we believe that a more telling reply would be to point out the inconsistencies in Sextus’ various reports. First, the adoption of the Philonian truth conditions would seem to be in conflict with the reported wide acceptance of the doctrine that an argument is valid when and only when its corresponding conditional is sound. Since there is no necessity in the relation between the antecedent and consequent of a sound Philonian conditional, it is hard to see how such a conditional could underwrite the validity of its corresponding argument. Against this reply, one might propose, as Josiah B. Gould does [Gould, 1974, p. 160], that the advocates of the Philonian view perhaps invoked the Diodorian truth conditions in applications of the conditionalisation principle. One might point to those passages cited by Mates and Boche ski wherein it appears that the Stoics had the Diodorean conditional in mind when they framed this principle. This approach, however, has its own problems. This interpretation of the texts mentioned above would seem to be inconsistent with the account of the criteria for invalidity referred to by Sextus at PH 2.146–51 and AM 8.429–34.
ski wherein it appears that the Stoics had the Diodorean conditional in mind when they framed this principle. This approach, however, has its own problems. This interpretation of the texts mentioned above would seem to be inconsistent with the account of the criteria for invalidity referred to by Sextus at PH 2.146–51 and AM 8.429–34.
In this account Sextus reports that the Stoics deemed an argument invalid according to a list of four criteria. These are: having premisses and conclusion which are incoherent with one another, having redundant premisses, being propounded in an invalid form, and having a deficient premiss. A problem arises when one attempts to square the first criterion on this list with the proposal that the principle of conditionalisation required a Diodorean-sound conditional. As a consequence of this proposal, an argument such as the following would appear to be valid:
One would be committed to judge (5) as valid if the following, which is its corresponding conditional, were Diodorean-sound:
(6) If (wheat is being sold in the market, and if Dion is walking, then he is moving), then the elements of existents are without parts.
But (5) could not be considerd valid according to the criterion which prohibits incoherent 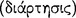 arguments from being valid. The problem, therefore, is that if the principle of conditionalisation requires a Diodorean-sound conditional and if (6) were Diodorean-sound, then (5) would be valid, contrary to the criterion for invalidity mentioned above. On the other hand, if this criterion for invalidity were to prevail, then (5) could not be valid and the conditionalisation principle could not require a Diodorean-sound conditional, provided that (6) is Diodorean-sound. Thus, if (6) is Diodorean-sound and (5) is not valid, then it is not clear that one ought to accept the thesis that the principle of conditionalisation requires a Diodorean-sound conditional.
arguments from being valid. The problem, therefore, is that if the principle of conditionalisation requires a Diodorean-sound conditional and if (6) were Diodorean-sound, then (5) would be valid, contrary to the criterion for invalidity mentioned above. On the other hand, if this criterion for invalidity were to prevail, then (5) could not be valid and the conditionalisation principle could not require a Diodorean-sound conditional, provided that (6) is Diodorean-sound. Thus, if (6) is Diodorean-sound and (5) is not valid, then it is not clear that one ought to accept the thesis that the principle of conditionalisation requires a Diodorean-sound conditional.
Now it is apparent that Diodorus would have been committed to the soundness of (6) merely because of the modal status of its consequent, for according to Sextus Empiricus (PH 2.111), Diodorus would deem the following conditional to be sound.
(7) If it is not the case that the elements of existents are without parts, then the elements of existents are without parts.
It was determined earlier (see page 481) that the consequent of this conditional would have been considered necessarily true according to the Diodorean view of necessity. Hence, the corresponding conditional of (5) would be Diodorean-sound merely because, according to Diodorus, its consequent could have been neither false nor false. That is, (6) neither was nor is capable of having a true antecedent and a false consequent, since it neither was nor is capable of having a false consequent. It would seem apparent, then, that (6) is Diodorean-sound. It is not clear, therefore, that one need accept the contention that the principle of conditionalisation requires a Diodorean-sound conditional.
In view of the foregoing arguments, neither of the objections considered is decisive against the proposal that the connexivist standard was the criterion for a sound conditional which prevailed in the early Stoa. The formulation of this account, which was put forward by “those who introduce ‘connexion’ or ‘coherence’” as a condition on the relation of following between the components of a sound conditional, would seem clearly to have committed the Stoics to a strong interpretation of the relationship between the antecedent and consequent of a conditional axiōma. Thus the Stoics would seem to have understood the term ‘to follow’ 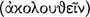 as expressing a necessary relation, in the appropriate sense of necessary, not only between the antecedent and consequent of a sound conditional, but also, as a result of the connection between a valid argument and its corresponding conditional, between the premisses and conclusion of a valid argument.
as expressing a necessary relation, in the appropriate sense of necessary, not only between the antecedent and consequent of a sound conditional, but also, as a result of the connection between a valid argument and its corresponding conditional, between the premisses and conclusion of a valid argument.
General conditionals
According to Josiah Gould, as we have seen, Chrysippus thought that one could generalise on the observed relations between different types of states of affairs or events and express these generalisations as conditional statements [Gould, 1970, pp. 200–201]: see page 426). What is required, then, is an account of such general conditionals, and clearly the relationship between singular and general conditionals will need to be sorted out. Unfortunately, there are very few examples of such general conditionals in the extant texts; however, the few that there are would seem to be sufficient to indicate the pattern. An example occurring in Cicero is as follows” “If anyone (quis) was born at the rising of the dogstar, he will not die at sea” (De fato 12). Another example occurs in Sextus Empiricus where he informs us that, according to the writers on logic, “the definition ‘Man is a rational, mortal animal’, although differing in its construction, is the same in meaning as the universal 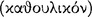 ‘If something
‘If something  is a man, that thing
is a man, that thing  is a rational, mortal animal’” (AM 11.8). Other examples are available, but the pattern for the general conditional seems apparent. Evidently, the subject of the antecedent clause is expressed by an indefinite pronoun, and though it is not clear in the Latin example, the Greek example would seem to indicate that the subject of the consequent clause having anaphoric reference to the subject of the antecedent clause is also an indefinite pronoun.155
is a rational, mortal animal’” (AM 11.8). Other examples are available, but the pattern for the general conditional seems apparent. Evidently, the subject of the antecedent clause is expressed by an indefinite pronoun, and though it is not clear in the Latin example, the Greek example would seem to indicate that the subject of the consequent clause having anaphoric reference to the subject of the antecedent clause is also an indefinite pronoun.155
Now consider the example of a singular conditional from AM 8.305 and what we might call its ‘associated’ general conditional, the latter being constructed on the pattern determined above. The singular conditional is If Dion is walking, Dion is moving, and the associated general conditional would be If someone is walking, he (or that one) is moving. In his paper “Stoic Use of Logic,” William H. Hay has suggested that what we have here is, in effect, a universally quantified conditional and an instantiation of it [Hay, 1969, 151n22]. If this assessment is correct, then it would evidently imply not only that the Stoics used general conditionals in place of statements using ‘all’,156 as well as employing a rule of instantiation for deriving singular conditionals from general ones, but also that their logic cannot be viewed on this account as simply a logic of propositions. The suggestion expressed by Hay raises a difficulty which is communicated by Charles Kahn in the following dilemma:
Either Stoic logic is based solely on the propositional connectives, and then it is epistemically sterile … Or else it involves generalized conditionals and a rule of instantiation, but then it is defective as logic since we are left without any account of the quantified conditional [Kahn, 1969, p. 164].
Now we believe that what Khan has in mind here in setting out the first horn of this dilemma is a propositional logic with a classical truth-functional interpretation of the propositional connectives. It is worth noting that the classical interpretation of the connectives is only one of many possible interpretations which might be assigned to them; hence, given an appropriate interpretation, a propositional logic need not be so barren as Kahn envisages. In any case, it seems evident that Stoic logic was not a classical propositional logic, and could not, therefore, be viewed as ‘epistemically sterile’ on the assumption that it was; moreover, it also seems clear that the Stoics themselves did not consider their logic to be so. Thus, we would reject the first horn of the dilemma. As for the other horn, we find it difficult to agree that the Stoic system was ‘defective’ as logic because it lacks an account of the quantified conditional. Kahn writes that “it is time to return to a more adequate view of Stoic logic within the context of their theory of language, their epistemology, their ethical psychology, and the general theory of nature” [Kahn, 1969, p. 159]. This suggestion would seem to imply that Stoic logic be assessed on it own terms and not as an attempt at constructing a modern formal system. In putting forth his criticism, Kahn seems to be ignoring his own reproach. At any rate, it may be that one can give an account of general conditionals which justifies the inference from general conditionals to singular or particular conditionals, and do so without invoking universal quantifiers and a rule of instantiation.
A general conditional, as has been noted above, seems to be signified by a conditional sentence having an indefinite pronoun in the subject position of the antecedent and an indefinite pronoun having anaphoric reference to the subject of the antecedent. It seems evident that the general conditional would be true just in case every associated particular conditional which has either a demonstrative pronoun or a name in the subject position, is true. Thus the general conditional may have been viewed as the conjunction of its associated particular conditionals. If the Stoics were to have allowed the inference of the conjuncts of a conjunction without an explicit rule of conjunction elimination, then this might explain why they seem to have supposed that one could infer the particular conditional from the general conditional without a rule of universal elimination.
9 Form in Stoic Logic
Over the long history of what is referred to as Stoicism, there was no doubt much unrecorded even unnoticed variability in metalogical doctrine. No doubt many distinctions which we now take for granted were ‘beneath the level of specificity of their intentions’. Nor is there any reason to suppose that the Stoics surpassed twentieth-century philosophers in their awareness of the degree of indeterminacy of their adopted theoretical language, or of their prospects for success. And no doubt, their approach consisted, to some extent, in talking in order to find out what they were talking about. So there might be little point in looking for a mathematically precise account of their doctrines, even if the historical records were much more complete than they are. In fact their intellectual environment was so different from our own as to have long since rendered their semantic space largely inaccessible to us. We simply cannot reconstruct, let alone reproduce, the effects that their theoretical vocabulary could have been counted upon to have. The best we can hope for is an illusion of precise positive understanding. We can, however, take some precautions against particular misunderstandings of their project. More specifically, and for all likely purposes, most usefully, we can take account of ways in which their logical culture and methods differed from our own, and take due note of the superficiality of apparent similarities between their approach and ours. Positively, we can give more reliable shape to Stoic logical theory by using our own richer notational resources to approximate their conceptions and engage their subject matter. And we can try to triangulate their position by considering what theoretical resources lay nearly within their reach.
In this section we illustrate the difficulties by a detailed consideration of the Stoic notion of  (disjunction) in relation to the question as to whether Stoic logic can be regarded as formal in the twentieth-century use of the word.
(disjunction) in relation to the question as to whether Stoic logic can be regarded as formal in the twentieth-century use of the word.
9.1 First blush
The superficial similarities of the indemonstrables to a set of natural deductive rules may tempt the unwary to a reconstruction in the language of twentieth-century formal systems, to define the elements of the language, the atoms, the connectives, the well-formed formulae, and then to introduce the rules for extending proofs. This would be to suppose that the Stoics viewed the connective vocabulary of the indemonstrables as having uniform logical status. A closer examination would reveal that the supposition was unwarranted. They seem to have been interested in vocabulary whose correspondents had, for them, some degree of physical éclat. So they were more interested in disjunctions than conjunctions, and more interested in conditionals, than in negations. In fact, although there seems to have been some unclarity on this score, their focus was primariy upon relationships, conflict and consequence, for example, and only secondarily upon the vocabulary that was used to distinguish them.
A related temptation would be to suppose that because a connective would admit an introduction or an elimination rule that coincides with an indemonstrable, that must have been the connective that the Stoics had in mind. Consider first the accepted doctrine that indemonstrables [IV] and [V] rely upon the exclusive disjunction of
I. M. Boche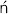 ski:
ski:
… out of the fourth and fifth indemonstrables which were fundamental in Stoic logic, we see that exclusive disjunction (matrix ‘0110’) was meant. ([Boche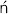 ski, 1963], 91)
ski, 1963], 91)
W. and M. Kneale (on Galen’s remark that ‘Either it is day or it is night’ is equivalent to ‘If it is not day it is night’):
Possibly his expression is loose and he means to say that the disjunctive statement is equivalent to the biconditional ‘It is not day, if and only if, it is night’. For the assertion of such an equivalence would indeed be in keeping with the Stoic doctrine of disjunction, provided always that the conditional is understood to convey necessary connection. ([Kneale and Kneale, 1962b], 162)
Benson Mates:
Two basic types of disjunction were recognized by the Stoics: exclusive and inclusive. Exclusive disjunction 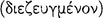 was most used, and is the only type of disjunction which occurs in the five fundamental inference-schemas of Stoic propositional logic. ([Mates, 1953], 51)
was most used, and is the only type of disjunction which occurs in the five fundamental inference-schemas of Stoic propositional logic. ([Mates, 1953], 51)
Łukasiewicz:
It is evident from the fourth syllogism that disjunction is conceived of as an exclusive ‘either-or’ connective. ([Łukasiewicz, 1967], 74)
‘The first or the second’ is true if and only if exactly one of the first and the second is true. (In modern logic it is customary to use ‘or’ inclusively, and hence to substitute ‘at least’ for ‘exactly’ in the truth conditions for disjunction. The fourth indemonstrable argument shows that disjunction is exclusive in the Stoic system.) ([Mueller, 1978], 16)
9.2 Some evidencea
All of these authors cite ancient sources for this account, among them, Cicero, Gellius, Galen, Sextus Empiricus and Diogenes Laërtius. Their accounts are the following:
There are several other methods used by the logicians, which consist of propositions disjunctively connected: Either this or that is true; but this is true, therefore that is not. Similarly either this or that is true; but this is not, therefore that is true. These conclusions are valid because in a disjunctive statement not more than one [disjunct] can be true.157
Gellius:
There is another form which the Greeks call  and we call disiunctum. For example: ‘Pleasure is good or evil or it is neither good nor evil.’ Now all statements which are contrasted ought to be opposed to each other, and their opposites, which the Greeks call
and we call disiunctum. For example: ‘Pleasure is good or evil or it is neither good nor evil.’ Now all statements which are contrasted ought to be opposed to each other, and their opposites, which the Greeks call  , ought also to be opposed. Of all statements which are contrasted, one ought to be true and the rest false.158
, ought also to be opposed. Of all statements which are contrasted, one ought to be true and the rest false.158
Galen:
… the disjunctives have one member only true, whether they be composed of two simple propositions or of more than two.159
… for the true disjunctive announces that one of its clauses is true, but the other or others false or false and contradictory.160
Diogenes Laërtius:
A disjunction is [a proposition] conjoined by means of the disjunctive conjunction ‘either’ 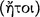 . For example, ‘Either it is day or it is night.’ This conjunction declares that one or the other of the propositions is false.161
. For example, ‘Either it is day or it is night.’ This conjunction declares that one or the other of the propositions is false.161
9.3 The question of arity
The first point to attend to is that three of the five authors admit disjunctions of more than two disjuncts, while two illustrate the construction with two-member disjunctions. No great importance is attached to this by the commentators, and it is unclear whether none of them thinks it significant. There need, of course, be no great importance in the fact that the earliest and the latest of the sources quoted above define disjunction specifically with reference to two-termed disjunctions. In Diogenes’ example, it may only be because the illustration is two-termed that the last comment is framed as it is. It is reasonable to surmise that neither Cicero nor Diogenes Laërtius would have precluded three-term or four-term disjunctions, and that their account would coincide with those of Gellius, Galen and Sextus Empiricus, according to which, in the three-term case, the disjunction is true if and only if exactly one of its disjuncts is true. Since none of the modern commentators explicitly addresses the issue of arity, one might have assumed that that is their view of the matter as well. Boche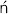 ski [1970, p. 91] mentions the greater generality of Stoic conjunction ‘the [conjunctive] functor was defined by the truth-table ‘1110’ [sic] as our logical product (only an indeterminate number of arguments was meant)’, and one may assume that his omission of the corresponding remark about
ski [1970, p. 91] mentions the greater generality of Stoic conjunction ‘the [conjunctive] functor was defined by the truth-table ‘1110’ [sic] as our logical product (only an indeterminate number of arguments was meant)’, and one may assume that his omission of the corresponding remark about  is an oversight. But some explain three-member disjunctions as though they nested a two-member disjunction. Commenting on the form:
is an oversight. But some explain three-member disjunctions as though they nested a two-member disjunction. Commenting on the form:
Either the first or the second or the third; but not the first; and not the second; therefore the third
which Sextus attributes to Chrysippus, the Kneales [1962a, p. 167] surmise:
Here, it seems, we must think of the words ‘ the second or the third’ as bracketed together in the disjunctive premiss; for the conclusion can then be obtained by two applications of indemonstrable 5. If this procedure is correct, the disjunction may be as long as we please, since the conclusion can always be proved by a number of applications of the same indemonstrable.
But though bracketing will have the required effect in the case of the fifth indemonstrable, its effect will be quite other in the case of the fourth; for correctly inferring from the truth of the first disjunct the falsity of the disjunction of the second and third will not then let us infer the falsity of the third from the truth of the second: the disjunction of the second and the third may be false because both the second and the third disjuncts are true. The conclusion must be that although we can in isolated instances treat three-term disjunctions as nestings, nevertheless if we are to give a unified account of Stoic disjunction, we may never understand three-term disjunctions as understanding the second and third to be implicitly bracketed. Brackets are simply not permitted. If this arity-free account is the correct and most general account of the Stoic notion of disjunction, several observations may be made: first that were we to symbolise such a connective it would be unambiguous and natural to do so in prefix notation as:
where the subscript σ serves to make the Stoic connection explicit. For the 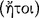 of Greek, like the ‘or’ of English, is not specifically a binary connective, and the Stoic practice of representing sentences by nominals (
of Greek, like the ‘or’ of English, is not specifically a binary connective, and the Stoic practice of representing sentences by nominals (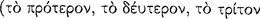 , the first, the second, the third) tends to mask the distinction which, when in a philosophical set of mind, we implicitly make in English between, say, a list of three nominals composed with ‘or’ and a three-term disjunctive sentence. In the former case, we do not, indeed cannot think of the or-list of two of the names as forming a new name and that disjoined to the third. In ordinary English we are not required to think of the or-composition of three sentences in this way either. No rules of well-formedness force us to parse a three-clause sentence composed with ‘or’ into a two-clause sentence one of whose clauses is a disjunction. Except for the exclusivity, the Stoic construction
, the first, the second, the third) tends to mask the distinction which, when in a philosophical set of mind, we implicitly make in English between, say, a list of three nominals composed with ‘or’ and a three-term disjunctive sentence. In the former case, we do not, indeed cannot think of the or-list of two of the names as forming a new name and that disjoined to the third. In ordinary English we are not required to think of the or-composition of three sentences in this way either. No rules of well-formedness force us to parse a three-clause sentence composed with ‘or’ into a two-clause sentence one of whose clauses is a disjunction. Except for the exclusivity, the Stoic construction

alternatively,

is more like the syntax of ordinary Greek than the modern symbolization
is like the syntax of ordinary English, since to repeat the ‘either’ to express the inner parenthesis would be stilted and unidiomatic. Now, to be sure, we could abbreviate a modern n-term exclusive disjunction analogously by:
since exclusive disjunction is an associative operation. But although the ambiguity is not vicious, we would normally understand such a formula as associated to the left or to the right, since is a binary connective, and well-formedness requires it. That modern exclusive disjunction is a binary truth-function and that the Stoic notion had no fixed arity should not be lost sight of when comparing the two. It will serve to remind us that the truth conditions of the two constructions are not in general the same, a fact upon which none of the modern commentators seems to have remarked. Consider as example the exclusive disjunction:
is a binary connective, and well-formedness requires it. That modern exclusive disjunction is a binary truth-function and that the Stoic notion had no fixed arity should not be lost sight of when comparing the two. It will serve to remind us that the truth conditions of the two constructions are not in general the same, a fact upon which none of the modern commentators seems to have remarked. Consider as example the exclusive disjunction:
When it is disambiguated into, say:
it becomes evident that since the second disjunction is false (since both of its disjuncts are true) and the first disjunct is true, the whole disjunction is true in spite of (or rather because of) the fact that all its disjuncts are true. The Stoic disjunction:
is false, since more than one of its disjuncts are true. Since Stoic disjunction has no fixed arity, it would be suitable to regard it as a kind of restricted propositional quantifier, having, in prefix notation, the reading
Since exclusive disjunction is commutative and associative, a quantifier reading would be suitable for it as well. But as a simple induction will demonstrate, its quantificational rendering would be:
The two kinds of disjunction will, of course, coincide on the two-clause case, but will coincide for no n-clause case for n < 2. A three-clause exclusive disjunction, for example, will be true if and only if either exactly one or exactly three clauses are true, as will a four-clause exclusive disjunction. A five- or six-clause exclusive disjunction will be true if and only if either exactly one or exactly three or exactly five disjuncts are true, and so on.
A valid Stoic disjunction of two terms would disjoin a sentence α with a sentence equivalent to the negation of α. A true n-term Stoic disjunction would disjoin n finite state descriptions. As an example, imagine the formulation of a row of a truth table, that is, the effect of conjoining propositional variables or negations of propositional variables accordingly as l’s or 0’s appear under them in that row. A valid Stoic disjunction in m independent variables would be equivalent to the 2m-term disjunction of the formulations of the rows of a table displaying all possible combinations of their truth values. Particularly if, as some of the early sources suggest, the Stoic notion of disjunction was that of an intensional operation, a sentence of the form

given such a technical use of  would assert that the four sentences bore to one another a relationship akin to the relationship of the formulations of rows of a two-variable truth table:
would assert that the four sentences bore to one another a relationship akin to the relationship of the formulations of rows of a two-variable truth table:

As a consequence of this, if we seriously adopt the view that the disjunction that Chrysippus had in mind in the fourth indemonstrable is the present day 0110 disjunction, then the Stoics really had at least two different kinds of disjunction represented by the same piece of notation in their logical system. And having come this far, we could admit no grounds for regarding the disjunction of the fifth indemonstrable as anything but a third sort, namely 1110 disjunction. The more plausible account would be that they had one sort of disjunction in mind, namely, the disjunction of no fixed arity which happens to resemble 0110 disjunction in the two-term case.
9.4 The consequences for their idea of form
The standard notion of form as applied to propositional argument schemata follows these lines: let F be the set of sentences of a language L and S an argument schema expressed with constants of the language L and metalogical variables of the metalanguage ranging over F. Then the argument form Fs associated with S is the set of arguments which can be generated from S by uniform substitution of sentences of F for metalogical variables in S. This notion of form depends upon a fixed meaning for the constants of L. In the propositional case, for example, we assume that ¬, ∧, ∨, → and so on do not change their meanings as we uniformly substitute sentences for the metalogical variables flanking them. We do not account ‘α therefore α or β’ an invalid form because from the sentence ‘You may go or you may stay’ it follows that you may stay. We say rather that ‘You may go; therefore you may go or you may stay’ is not of the form ‘α therefore α or β’. We might retreat, if pressed, to the claim that they share grammatical but not logical form. Or we might admit the argument to the form but insist that the conclusion must then be understood as a disjunction, from which ‘You may stay’ does not follow. It seems certain that the Stoics never articulated a notion of argument form in these or equivalent terms. But, if we are to take into account the totality of evidence from early sources, according to which  was understood in something like the quantificational reading outlined earlier, and the generally held view that they gave to the particle
was understood in something like the quantificational reading outlined earlier, and the generally held view that they gave to the particle 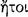 a technical meaning accordingly, then the Stoic schema [IV]:
a technical meaning accordingly, then the Stoic schema [IV]:

is insufficiently general to capture the inferential force of the connective  in their technical sense. The three-term σ-disjunction is not obtainable from the two-term σ-disjunction by substitution of a two-term σ-disjunction for one of the original disjuncts. Some such schema as:
in their technical sense. The three-term σ-disjunction is not obtainable from the two-term σ-disjunction by substitution of a two-term σ-disjunction for one of the original disjuncts. Some such schema as:
would be required. So if the Stoic notion of disjunction was as general as the early commentators suggest, and we are to judge their conjectured position by standards of any rigour, then we must conclude that their understanding of the role of the fourth indemonstrable schema was something other than that of specifying a form in the substitutional sense of the word. Notably it is only the fourth indemonstrable that straightforwardly gives rise to such a problem of reinterpretation, since the other logical connections exhibited in the earlier indemonstrable schemata, viz. if … then … and not both … and … represent specifically binary connections, at least for the Stoics, and at least so far as the evidence tells us. Of these, only not both … and … readily admits of generalization to the n-ary case, and there is nothing in the sources to guide us in choosing between the generalization to At most one of the following is true and the generalization to Not all of the following are true, interpretations which again coincide only in the two-term case. If we suppose that they took conjunction seriously as a logical connection, perhaps the second is the more natural; for there is nothing to require the translation of the initial 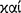 as both except in the two-term case. Even here a slightly dissimilar case would arise if we tried to construct the generalized schema. For in the two-term case, the connective not both … and … coincides in sense with the Sheffer stroke, which, since it is not an associative operation, cannot, in the n-term case, be straightforwardly thought of quantificationally. The sentence:
as both except in the two-term case. Even here a slightly dissimilar case would arise if we tried to construct the generalized schema. For in the two-term case, the connective not both … and … coincides in sense with the Sheffer stroke, which, since it is not an associative operation, cannot, in the n-term case, be straightforwardly thought of quantificationally. The sentence: would mean something like:
would mean something like:
There would, however, remain the problem that the third indemonstrable schema:
is insufficiently general in form to define the class of arguments which the general account of conjunction would license.
Now it is unfortunately convenient to treat Stoic logic, however fragmentary and indirect our understanding of it, as a product of the same general understanding of the issues that we ourselves are able to bring to bear. In this frame of mind, we are apt to see our scholarly task as one of rational reconstruction in the light of that general understanding. In such a frame of mind, we might well agree with Josiah Gould [1970, p. 83] that
it is clear in each of our fragments that the author intends the adjective ‘undemonstrated’ to qualify what we would today call ‘argument forms.’
and that the examples given are
what we would today call substitution instances. [Gould, 1974, p. 84]
Better to ask of the fragmentary information available to us, what stage the Stoics’ general understanding might have reached, allowing the relics of their doctrines a reasonable degree of tentativeness without assuming that their approach, had it only succeeded, would have been our own. This is, admittedly, a delicate task, not least because we cannot know whether we have succeeded in it. But the approach permits us, as need arises, to say ‘They did not foresee this difficulty’ rather than ‘This view creates a difficulty on the modern understanding and must therefore not be attributed to them.’ As an exercise, one might ask whether, on the evidence, the Stoics had hit upon something like our notion of logical form. If they had, well and good, but if they had not, then we ought not to suppose that all of the indemonstrables were regarded as formally valid or correct schemata in any single sufficiently well-defined sense of ‘formal’ to be of use. We would not be compelled, as we are by the contrary assumption, to assert of them that their use of  in the fourth and fifth indemonstrables was a technical one according to which it meant what is meant by 0110 disjunction. As we have seen, unless they meant different things by
in the fourth and fifth indemonstrables was a technical one according to which it meant what is meant by 0110 disjunction. As we have seen, unless they meant different things by  in different contexts, 0110 disjunction is not what they meant anyway, even if there is something, in the relevant respects determinate, that they did mean. In spite of what we have said about the notion of form, there is no harm in applying the word formal to the Stoics’ work. By some standards, it is not informal and by those standards we may therefore call it formal where that is the contrast intended; and we may therefore distinguish their uses of
in different contexts, 0110 disjunction is not what they meant anyway, even if there is something, in the relevant respects determinate, that they did mean. In spite of what we have said about the notion of form, there is no harm in applying the word formal to the Stoics’ work. By some standards, it is not informal and by those standards we may therefore call it formal where that is the contrast intended; and we may therefore distinguish their uses of 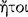 and
and  in formal contexts from their uses of them in merely expository ones, where by this we mean just to distinguish the ceremonial from the everyday.
in formal contexts from their uses of them in merely expository ones, where by this we mean just to distinguish the ceremonial from the everyday.
10 The Linguistic Evidence
Was there something that  and
and 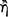 meant? What is the evidence? Quite apart from the remarks of the early commentators, there is the evidence provided by the Greek and Latin languages themselves. It is an urban myth that there is an exclusive sense of or in English, and a suburban myth that Latin lexically marked the distinction between 1110 and 0110 disjunctions by vel and aut. It is unclear when these myths first arose. We have been unable to find them in any sources earlier than the twentieth century. It is true that the Latin commentators used aut … aut … to convey the Stoic use of
meant? What is the evidence? Quite apart from the remarks of the early commentators, there is the evidence provided by the Greek and Latin languages themselves. It is an urban myth that there is an exclusive sense of or in English, and a suburban myth that Latin lexically marked the distinction between 1110 and 0110 disjunctions by vel and aut. It is unclear when these myths first arose. We have been unable to find them in any sources earlier than the twentieth century. It is true that the Latin commentators used aut … aut … to convey the Stoic use of 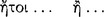 , but we must not place too much weight upon this. It was the best choice on grounds quite separate from the fictional one that aut corresponded to exclusive ‘or’. We should recall that in the course of explaining the truth conditions of what he takes to be the Stoic notion of
, but we must not place too much weight upon this. It was the best choice on grounds quite separate from the fictional one that aut corresponded to exclusive ‘or’. We should recall that in the course of explaining the truth conditions of what he takes to be the Stoic notion of  , Gellius uses aut in a long disjunctive antecedent clause of a conditional which is transparently intended to abbreviate a conjunction of conditionals:
, Gellius uses aut in a long disjunctive antecedent clause of a conditional which is transparently intended to abbreviate a conjunction of conditionals:
… si aut nihil omnium verum aut omnia plurave quam unum vera erunt, cut quae disjuncta sunt non pugnabunt, cut quae opposita eorum sunt contraria inter sese no erunt, tune id disjunctum mendacium est … Noctes Atticae 16.8.14.
(…i f none of them is true, or all or more than one are true, or the contrasted things do not conflict, or those opposed are not contrary, then it is a false disjunction …)
Evidently the choice of Latin vocabulary in which to cast the connective of the fourth and fifth indemonstrables was not dictated by the need to convey exclusivity formally. Had no Megarian or Stoic ever dreamt of the fourth indemonstrable, the most suitable Latin translation of the fifth indemonstrable and for the regimentation of ordinary language arguments of the corresponding grammatical cast, would nevertheless have used aut. There is no reason to suppose that the mere use of aut, independently of ancillary discussion and explanation of what it was intended to convey, would have made the formal correctness of the fourth indemonstrable, or of particular instances of it, transparent to Roman commentators.
Greek, like Latin, possessed no special connective by which 0110 disjunction was distinguished from 1110 disjunction. The ‘logical’ sense of 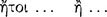 and its variants was essentially that of either … or …; like either … or …, its use was indifferent as to the number of terms joined and as between exclusive and non-exclusive fillings; any additional imposition of an exclusive reading was through emphasis and intonation. In particular the use of
and its variants was essentially that of either … or …; like either … or …, its use was indifferent as to the number of terms joined and as between exclusive and non-exclusive fillings; any additional imposition of an exclusive reading was through emphasis and intonation. In particular the use of  as an auxiliary had no special role as an indicator of exclusivity, that particle being a compound of
as an auxiliary had no special role as an indicator of exclusivity, that particle being a compound of  meaning variously or or than, and the enclitic τoι an etymological cousin of the second person singular pronoun. Its ordinary use was emphatic, akin to the use in English of now surely or in Welsh English of Look you. Galen reports
meaning variously or or than, and the enclitic τoι an etymological cousin of the second person singular pronoun. Its ordinary use was emphatic, akin to the use in English of now surely or in Welsh English of Look you. Galen reports 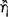 as an alternative to
as an alternative to  in Stoic usage, although he himself uses the latter exclusively in the context of the indemonstrables [Frede, 1974, pp. 93-4], Certainly the use of
in Stoic usage, although he himself uses the latter exclusively in the context of the indemonstrables [Frede, 1974, pp. 93-4], Certainly the use of  in ordinary non-philosophical written Greek was uncommon by contrast with some philosophical writing and there is evidence that the philosophers have pressed into use a construction normally reserved as a spoken form. Thus Denniston [1954, p. 553]:
in ordinary non-philosophical written Greek was uncommon by contrast with some philosophical writing and there is evidence that the philosophers have pressed into use a construction normally reserved as a spoken form. Thus Denniston [1954, p. 553]:
 (often
(often 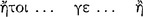 ) is common in Plato and Aristotle. It is difficult to say what degree of vividness τoι retains here. On the one hand, Thucydides confines
) is common in Plato and Aristotle. It is difficult to say what degree of vividness τoι retains here. On the one hand, Thucydides confines 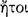 , like simple τoι, to speeches … this suggests that he felt τoι as vivid in the combination. On the other, the frequency of
, like simple τoι, to speeches … this suggests that he felt τoι as vivid in the combination. On the other, the frequency of 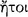 in the matter-of-fact style of Aristotle suggests that for him τoι did nothing more than emphasize the disjunction.
in the matter-of-fact style of Aristotle suggests that for him τoι did nothing more than emphasize the disjunction.
B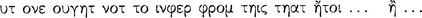 is more common than
is more common than  in Aristotle and Plato, or that either of them set aside the former for uses which prefigured the Stoic use. Neither is by any means true. In particular, Aristotle uses
in Aristotle and Plato, or that either of them set aside the former for uses which prefigured the Stoic use. Neither is by any means true. In particular, Aristotle uses  in the overwhelming majority of cases, and in many which would have provided excellent examples of disjunction for the Stoics:
in the overwhelming majority of cases, and in many which would have provided excellent examples of disjunction for the Stoics:
(A premiss then is a sentence affirming or denying something of something. This is either universal or particular or indefinite.)
(… he has proved that the diagonal is either commensurate or incommensurate)
and others where, if his understanding of the meaning of  anticipated the Stoic use of it, we would expect
anticipated the Stoic use of it, we would expect  :
:
On the other hand, Aristotle’s uses of  , either give no evidence that he was after a distinction that anticipated the Stoics’, or else provide evidence that he had no such intention. Thus, when in the course of explaining kinds of contrariety he denies that everybody must be black or white, he uses
, either give no evidence that he was after a distinction that anticipated the Stoics’, or else provide evidence that he had no such intention. Thus, when in the course of explaining kinds of contrariety he denies that everybody must be black or white, he uses  … :
… :
but the reason for denying this is that there are intermediates between white and black, namely all the other colours. It is in any case used here between predicates and not between whole sentences.
The relative scarcity of  as opposed to
as opposed to  in the logical setting does not of course indicate that the Stoics gave the word
in the logical setting does not of course indicate that the Stoics gave the word 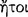 any special technical sense as distinct from a technical use. The thesis that it has a special sense is forced upon us only if we also adopt the view that their enterprise was a formal one in the substitutional sense. We have already seen that on any straightforward interpretation, it was not. A more plausible guess would be that that combination gradually gained favour in general philosophical practice and presented itself to the philosophical innovator, perhaps Theophrastus, casting about for suitably perspicuous notation as a construction already set apart for special philosophical applications. Compare the current use of It is not the case that .… Again, it need hardly be said that there was no special intensional sense of
any special technical sense as distinct from a technical use. The thesis that it has a special sense is forced upon us only if we also adopt the view that their enterprise was a formal one in the substitutional sense. We have already seen that on any straightforward interpretation, it was not. A more plausible guess would be that that combination gradually gained favour in general philosophical practice and presented itself to the philosophical innovator, perhaps Theophrastus, casting about for suitably perspicuous notation as a construction already set apart for special philosophical applications. Compare the current use of It is not the case that .… Again, it need hardly be said that there was no special intensional sense of 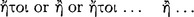 in ordinary Greek, the necessity or contingency of a disjunction being entirely determined by its disjuncts. But insofar as intended exclusivity can be conveyed by emphasis, the intention is conveyed more easily with more syllables than with fewer. And on that score
in ordinary Greek, the necessity or contingency of a disjunction being entirely determined by its disjuncts. But insofar as intended exclusivity can be conveyed by emphasis, the intention is conveyed more easily with more syllables than with fewer. And on that score  is more emphatic than
is more emphatic than 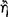 . Greek, like Latin and, come to that, like English, had a great variety of connectives all of which could receive translation as or, but whose significance in discourse is best understood by immersion in the literature in which they occur. Like sive … sive … of Latin, Greek had
. Greek, like Latin and, come to that, like English, had a great variety of connectives all of which could receive translation as or, but whose significance in discourse is best understood by immersion in the literature in which they occur. Like sive … sive … of Latin, Greek had  which was common as a conjunctively distributive connective in the antecedents of conditional constructions. Homeric Greek sometimes has τε in place of a second
which was common as a conjunctively distributive connective in the antecedents of conditional constructions. Homeric Greek sometimes has τε in place of a second 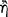 , and
, and  , in place of a second
, in place of a second  . Aeschylus sometimes answers
. Aeschylus sometimes answers  with
with  . But Greek was in general more fluid in its use of particles than Latin. There are recorded instances of
. But Greek was in general more fluid in its use of particles than Latin. There are recorded instances of  where
where  would be expected; and there are idioms in which
would be expected; and there are idioms in which  occurs with the sense of
occurs with the sense of 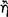 , as in
, as in
In general, the use of particular particles in the Greek of the last several centuries of the old era varied, not only over time, but from author to author, even from work to work, and particularly from genre to genre.162 As a symptom of this greater fluidity, there is evident a larger freedom in the use of particles in abbreviative constructions, especially favouring the use of constructions relying upon superficial grammatical ellipsis over those requiring (or rather, as our thesis demands, at least capable of receiving) a truth-functional logical transformation. The use of or constructions in if-clauses to force a conjunctive reading is reinforced by the availability of a non-elliptical reading for an antecedent in and, particularly in a language which, like Latin, is less subtly variable than Greek in its use of particles,. In Greek, for whatever reason, this tension between grammatical ellipsis and logical transformation was less insistent than in Latin, so that when the context demands it, an if-clause occurrence of  more readily accedes to a conjunctively distributive reading. And one finds
more readily accedes to a conjunctively distributive reading. And one finds  sometimes following
sometimes following 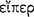 and grammatically absorbed by it, producing something akin to if even …, as one finds them in the opposite order having the sense of even if.… The logical particles whose English counterparts we have been taught to think of as, to extend Ryle’s colourful metaphor, importantly combat-ready, lived altogether more easily in one another’s company.
and grammatically absorbed by it, producing something akin to if even …, as one finds them in the opposite order having the sense of even if.… The logical particles whose English counterparts we have been taught to think of as, to extend Ryle’s colourful metaphor, importantly combat-ready, lived altogether more easily in one another’s company.
Any attempt to construct a useful formal system that still retains a connection with the inferential practices that have inspired it cannot but sacrifice non-logical distinctions, and the logic of the Stoics, arising as it did out of a language so fluid in its particulate usages as the Greek of their period, was not to be excepted. The abstraction of the logically essential into a simplified vocabulary was part of the task, but refining their very conception of the task and what was essential to it was all a part of the same continuing academic enterprise. As modern logic has no distinct notation for whether … or …, letting if … or … do the work, and as Roman logicians did not retain sive … sive … or tum … tum, so Greek logicians shed  as they did the distinction between the suppositive negating adverb
as they did the distinction between the suppositive negating adverb 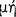 and the absolute
and the absolute 
 since the retention of
since the retention of  in negated if-clauses would complicate conditionalization of arguments of the form of the second indemonstrable. In any case, however much greater fluidity there may have been, and however much simplified the account of logical connection, it remains true that the role of
in negated if-clauses would complicate conditionalization of arguments of the form of the second indemonstrable. In any case, however much greater fluidity there may have been, and however much simplified the account of logical connection, it remains true that the role of  in Greek was preponderantly aggregative or agglomerative. And the role of
in Greek was preponderantly aggregative or agglomerative. And the role of  was preponderantly separative, as that of either … or … is in English. Its ordinary understanding was certainly such as to support an inference schema such as the fifth indemonstrable. But the use of
was preponderantly separative, as that of either … or … is in English. Its ordinary understanding was certainly such as to support an inference schema such as the fifth indemonstrable. But the use of  in the fourth indemonstrable goes beyond simplification. For, as we have noted, there was, in Greek as in Latin and English, no or word that indicated exclusive disjunction. If the Stoics intended that the fourth indemonstrable should be understood formally in the substitutional sense, they could not have counted upon that formal correctness being evident from the ordinary understanding of its logical vocabulary, as they could have in the case of the first, second, third and fifth. Consider, for example, a remark of Sextus:
in the fourth indemonstrable goes beyond simplification. For, as we have noted, there was, in Greek as in Latin and English, no or word that indicated exclusive disjunction. If the Stoics intended that the fourth indemonstrable should be understood formally in the substitutional sense, they could not have counted upon that formal correctness being evident from the ordinary understanding of its logical vocabulary, as they could have in the case of the first, second, third and fifth. Consider, for example, a remark of Sextus:

… the disjunction has one of its clauses true, since if both are true or both are false, the whole will be false. (SE AM 8.283)
 is not to be understood ‘in an exclusive sense’, in spite of the exclusiveness of its disjuncts, but rather in the ordinary sense which makes the conditional in whose antecedent it occurs elliptical for, or at least equivalent to, a conjunction of conditionals. The inequivalence of the conditional having an exclusive disjunctive antecedent (in modern notation),
is not to be understood ‘in an exclusive sense’, in spite of the exclusiveness of its disjuncts, but rather in the ordinary sense which makes the conditional in whose antecedent it occurs elliptical for, or at least equivalent to, a conjunction of conditionals. The inequivalence of the conditional having an exclusive disjunctive antecedent (in modern notation),
and the corresponding conjunction of conditionals
has consequences elsewhere. On a purely syntactic/semantic understanding of  by which it would mean just declarative sentences joined by
by which it would mean just declarative sentences joined by 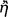 understood in the technical 0110 sense, that inequivalence would make it difficult to square the fondness for the dilemma, which was ubiquitous from pre-Socratic through Hellenistic writings, with the general acceptance of the principle of conditionalisation, which was generally accepted by the Stoics. Now the ordinary application of conditionalisation as a test of validity would conjoin the premisses in the if-clause of a conditional, having the conclusion as then-clause. Presumably, in the particular application, an argument involving dilemma would yield a pair of conditionals whose validity would then be considered. The difficulty lies in the fact that the conditional
understood in the technical 0110 sense, that inequivalence would make it difficult to square the fondness for the dilemma, which was ubiquitous from pre-Socratic through Hellenistic writings, with the general acceptance of the principle of conditionalisation, which was generally accepted by the Stoics. Now the ordinary application of conditionalisation as a test of validity would conjoin the premisses in the if-clause of a conditional, having the conclusion as then-clause. Presumably, in the particular application, an argument involving dilemma would yield a pair of conditionals whose validity would then be considered. The difficulty lies in the fact that the conditional
might be necessarily true because both α and β were necessarily true and α ∨σ β therefore necessarily false, but both conjuncts of
false because γ was false. On those grounds alone, it is unlikely that  was a simple syntactic/semantic item in the Stoic conception of logic.
was a simple syntactic/semantic item in the Stoic conception of logic.
10.1 Cicero’s clanger
There is further evidence of this tension between the normal use of  and the Stoic use of it in the fact that there is a greater confusion sown in the accounts of
and the Stoic use of it in the fact that there is a greater confusion sown in the accounts of 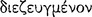 than there is in the accounts of the other connections. If the fourth indemonstrable was intended as a formally admitted schema in the substitutional sense, the difficulty can only have been one of understanding a new technical sense being lent to the grammatical form
than there is in the accounts of the other connections. If the fourth indemonstrable was intended as a formally admitted schema in the substitutional sense, the difficulty can only have been one of understanding a new technical sense being lent to the grammatical form  It cannot be confidently rejected that Cicero, whose faux pas in his Topica still costs him invitations, was among the victims of the confusion.
It cannot be confidently rejected that Cicero, whose faux pas in his Topica still costs him invitations, was among the victims of the confusion.
At least it must be said that a formal reading by which the fourth indemonstrable does represent a new technical use of  ought to dispose us more charitably toward Cicero’s curious augmentation, in top. 13.57 of the standard five indemonstrables. Cicero claims there, so far as we know erroneously, that there was a Stoic indemonstrable the Latin form of which would have been:
ought to dispose us more charitably toward Cicero’s curious augmentation, in top. 13.57 of the standard five indemonstrables. Cicero claims there, so far as we know erroneously, that there was a Stoic indemonstrable the Latin form of which would have been:
When the indemonstrables are understood formally, this would seem on first hearing to represent a truly resounding logical clanger. Since the indemonstrables are almost universally regarded as formal, this estimation has been the conventional view.163 There is no independent evidence that any Stoic logician ever included this kind of argument in his list of indemonstrables. On this point, we take it that Cicero was merely wrong. But could there have been such a kind of argument? If we are right about what inferences could be justified by reference to the meaning of  in Greek, and if the indemonstrables are formal, then the use of
in Greek, and if the indemonstrables are formal, then the use of  in the fourth indemonstrable forces an exclusive reading which did not exist in the natural language. For there, the nearest we have to an exclusive
in the fourth indemonstrable forces an exclusive reading which did not exist in the natural language. For there, the nearest we have to an exclusive 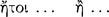 is the use of
is the use of  with exclusive alternatives. But then the analogous technical use of not both … and … would force a reading according to which from the falsity of one element the truth of the other would follow. Indeed, anyone whose understanding of Stoic logic was indirect and conjectural, and whose knowledge of Greek was not, might well have considered that given the eccentric character of the fourth indemonstrable, the Stoics could be expected to have a corresponding dual eccentricity of the sort embodied in Cicero’s argument. It is true that the use of not both … and … never implies by itself that both sentences cannot be false, but neither is there a use of or that implies by itself that both sentences cannot be true. However, there are uses of not both … and … with sentences which cannot both be false, just as there are uses of or with sentences which cannot both be true. Understood as a formal theory, there is nothing more eccentric about Cicero’s supplement than there is about the undoubtedly Stoic fourth indemonstrable. But suppose for the sake of argument that Cicero’s addition were to be found extensively in Stoic logical writings and attributed, say, to Chrysippus. Any historian of Stoic logic finding himself unwilling to accept that indemonstrable as merely representing a technical usage, ought to feel no more willingness to accept, on those terms, the Stoics’ eccentric use of ‘or’ in the fourth.
with exclusive alternatives. But then the analogous technical use of not both … and … would force a reading according to which from the falsity of one element the truth of the other would follow. Indeed, anyone whose understanding of Stoic logic was indirect and conjectural, and whose knowledge of Greek was not, might well have considered that given the eccentric character of the fourth indemonstrable, the Stoics could be expected to have a corresponding dual eccentricity of the sort embodied in Cicero’s argument. It is true that the use of not both … and … never implies by itself that both sentences cannot be false, but neither is there a use of or that implies by itself that both sentences cannot be true. However, there are uses of not both … and … with sentences which cannot both be false, just as there are uses of or with sentences which cannot both be true. Understood as a formal theory, there is nothing more eccentric about Cicero’s supplement than there is about the undoubtedly Stoic fourth indemonstrable. But suppose for the sake of argument that Cicero’s addition were to be found extensively in Stoic logical writings and attributed, say, to Chrysippus. Any historian of Stoic logic finding himself unwilling to accept that indemonstrable as merely representing a technical usage, ought to feel no more willingness to accept, on those terms, the Stoics’ eccentric use of ‘or’ in the fourth.
Make the parallel more explicit. The formalist historian claims that the Stoics used 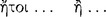 technically to mean Either … or … and not both … and … In ordinary Greek, its meaning comprehended the former conjunct but not the latter. If Cicero were right, there would be a second pill to swallow: that the Stoics used Not both A and B technically to mean the same thing. In ordinary Greek, its meaning comprehended the latter but not the former. Even on a formalist rendering, the mistake ought to seem on reflection no great logical howler. But when we consider, as we shall, the notion that the indemonstrables were not formally intended, we may also entertain among others, the possibility that Cicero’s error represents at worst a merely historical error or a badly worded description, a wrong but not unreasonable reconstruction from memory of something he had read or heard from Diodotus or Philo.164 But again, on a non-formalist construal, especially given our more less comprehensive ignorance of the teachings of minor Stoic teachers, it could well be an accurate recollection of something taught him (however erroneously) by Diodotus. It would not have been an impossible kind of argument, on a non-formalist view, for a Stoic to have noted. Consider what textbooks of this age say about aut.
technically to mean Either … or … and not both … and … In ordinary Greek, its meaning comprehended the former conjunct but not the latter. If Cicero were right, there would be a second pill to swallow: that the Stoics used Not both A and B technically to mean the same thing. In ordinary Greek, its meaning comprehended the latter but not the former. Even on a formalist rendering, the mistake ought to seem on reflection no great logical howler. But when we consider, as we shall, the notion that the indemonstrables were not formally intended, we may also entertain among others, the possibility that Cicero’s error represents at worst a merely historical error or a badly worded description, a wrong but not unreasonable reconstruction from memory of something he had read or heard from Diodotus or Philo.164 But again, on a non-formalist construal, especially given our more less comprehensive ignorance of the teachings of minor Stoic teachers, it could well be an accurate recollection of something taught him (however erroneously) by Diodotus. It would not have been an impossible kind of argument, on a non-formalist view, for a Stoic to have noted. Consider what textbooks of this age say about aut.
10.2 The question of form
So we return to the question whether the Stoics regarded the indemonstrables as formally correct schemata in anything like the modern understanding of formal correctness. The evidence is clouded and there are many imponderables. We do not know with certainty to what extent the technical vocabulary,  , validus,
, validus,  and so on had been freed from its etymological roots for Galen or Sextus, or with certainty what points of terminology and doctrine remained a matter of controversy into the Christian era. We do not know with what exactitude the logical vocabulary was defined by Chrysippus or others. But it would not be too pessimistic at least to lower our estimations of their capacity for logical description. As we have seen, the standard substitutional notion of valid form does not adequately account for the Stoic account of disjunction in inference, since it does not accommodate connectives of no fixed arity. A relaxed, descriptive notion of valid form might come closer to theirs. The difference is this: a substitution account presents a schema and (perhaps implicitly) a rule of uniform substitution, or asserts that for every pair of sentences a and b, such and such a conclusion may be inferred from such and such premisses. Arguments of the same form retain the syncategorematic vocabulary and repeat sentences in the same pattern as the repetition of metalogical variables in the schema. One might say that the substitutional account stands for an abstract syntactic description applicable to any argument of the form. What we shall call a descriptive account would give an explicit description, saying what belongs in each premiss, and what in the conclusion, perhaps illustrating by a schema, or an example. Of the fourth indemonstrable it might say: ‘An argument of the fourth type has a diezeugmenonic major premiss etc.’ and mention that a diezeugmenonic sentence is of the grammatical form:
and so on had been freed from its etymological roots for Galen or Sextus, or with certainty what points of terminology and doctrine remained a matter of controversy into the Christian era. We do not know with what exactitude the logical vocabulary was defined by Chrysippus or others. But it would not be too pessimistic at least to lower our estimations of their capacity for logical description. As we have seen, the standard substitutional notion of valid form does not adequately account for the Stoic account of disjunction in inference, since it does not accommodate connectives of no fixed arity. A relaxed, descriptive notion of valid form might come closer to theirs. The difference is this: a substitution account presents a schema and (perhaps implicitly) a rule of uniform substitution, or asserts that for every pair of sentences a and b, such and such a conclusion may be inferred from such and such premisses. Arguments of the same form retain the syncategorematic vocabulary and repeat sentences in the same pattern as the repetition of metalogical variables in the schema. One might say that the substitutional account stands for an abstract syntactic description applicable to any argument of the form. What we shall call a descriptive account would give an explicit description, saying what belongs in each premiss, and what in the conclusion, perhaps illustrating by a schema, or an example. Of the fourth indemonstrable it might say: ‘An argument of the fourth type has a diezeugmenonic major premiss etc.’ and mention that a diezeugmenonic sentence is of the grammatical form:
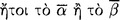
(not ‘a diezeugmenonic sentence is any sentence of the grammatical form
The class of valid arguments of that descriptive form would be the class of arguments satisfying the description, which might but might not coincide with the class of arguments obtained by uniform substitution in the illustrating schema. In the case of arguments with a diezeugmenonic major premiss, presumably the two notions would not coincide if the understood arity of disjunction were variable. If the distinction between the two notions of form were never explicitly stated, it is credible that discussions would sometimes vaguely have assumed the one and sometimes vaguely the other.
In the case of the fourth indemonstrable, a substitution account would offer the schema:
A rule of substitution would license any argument obtained by substituting an occurrence of some declarative sentence A for every occurrence of a and an occurrence of some declarative sentence B for every occurrence of β as an argument of the form of the schema. Alternatively, a substitution account would say:
A descriptive account of [IV] (for the general case) would be this: ‘From a disjunction together with one of its disjuncts, the negation of any distinct disjunct may be inferred.’ What constitutes an argument of this description depends upon what is meant by disjunction, but we may say that the simplest argument of this kind would of be the form:
Now if, in addition, our notion of disjunction had as its foundation the notion of a relationship between states of affairs or situations such that exactly one of them must obtain (and only derivatively of a string of sentences alleging such states, separated by or), rather than simply any string of sentences separated by or, the puzzle about the technical meaning of  would be less perplexing. Indeed there would be no puzzle. Both the fourth and fifth indemonstrables would represent valid kinds of argument, and the schemata presented would represent the forms of the simplest arguments of this kind. Why Either … or … ? It is the obvious connective, since it permits the construction of a true sentence out of contradictories and, in any case, the Either … or … construction is the one in which these contradictory alternatives are naturally contemplated. That the fifth indemonstrable is justifiable solely on the basis of the meaning of or and the fourth only on the basis of the particularities of its arguments, on such an account, does not matter. It is relevant only in the presence of convincing evidence that they had in mind a substitutional notion of form. That is precisely what is lacking.
would be less perplexing. Indeed there would be no puzzle. Both the fourth and fifth indemonstrables would represent valid kinds of argument, and the schemata presented would represent the forms of the simplest arguments of this kind. Why Either … or … ? It is the obvious connective, since it permits the construction of a true sentence out of contradictories and, in any case, the Either … or … construction is the one in which these contradictory alternatives are naturally contemplated. That the fifth indemonstrable is justifiable solely on the basis of the meaning of or and the fourth only on the basis of the particularities of its arguments, on such an account, does not matter. It is relevant only in the presence of convincing evidence that they had in mind a substitutional notion of form. That is precisely what is lacking.
The evidence suggesting the less finely tuned notion of validity is by no means unequivocal. The clearest case of a descriptive presentation of the indemonstrables is that of Ioannes Philoponous in his Scholia to Ammonius:
The disjunctive syllogism proceeds on the basis of complete incompatibles.165
But all of the early sources give, more or less, a descriptive account of the fourth and fifth indemonstrables. Cicero, who gives barely more than schemata, feels it necessary to add the comment that ‘these conclusions are valid because in a disjunctive statement not more than one (disjunct) can be true’, a remark more significant for having seemed necessary than for what it says. Much that is otherwise puzzling is less so on the view that their notion of validity had, at least not yet, become fixed upon a substitution account. If the notion of disjunction was the descriptive one, meaning essentially sentences in a certain relation, every disjunction which was  or validus in the more etymological sense of ‘proper’ or ‘sound’ would also be
or validus in the more etymological sense of ‘proper’ or ‘sound’ would also be  or validus in the derivative sense of true, even in the further derivative sense of valid. This would explain Gellius’ rejection of the premiss
or validus in the derivative sense of true, even in the further derivative sense of valid. This would explain Gellius’ rejection of the premiss
on the grounds that it is not what the Greeks call ‘a sound and regular disjunction’  . (Gellius Noctes Atticae 2.7.21) It would justify Favorinus’ response to Bias’ dilemma, that its major premiss (You will marry either a beautiful or an ugly woman) was not a proper disjunction (iustum disiunctivum), since it was not inevitable that one of the two opposites be true, which must be the case in a disjunctive proposition. (Noctes Atticae 5.11.8) On the substitution account, the truth or falsity of a premiss ought not to affect validity. On the descriptive account, particularly in the case of a disjunctive premiss, its falsity cannot but affect at least the question whether it is of the particular valid kind, since if it is false, it is not a genuine disjunction. There are other, similar instances, as for example Sextus’ rejection of the argument:
. (Gellius Noctes Atticae 2.7.21) It would justify Favorinus’ response to Bias’ dilemma, that its major premiss (You will marry either a beautiful or an ugly woman) was not a proper disjunction (iustum disiunctivum), since it was not inevitable that one of the two opposites be true, which must be the case in a disjunctive proposition. (Noctes Atticae 5.11.8) On the substitution account, the truth or falsity of a premiss ought not to affect validity. On the descriptive account, particularly in the case of a disjunctive premiss, its falsity cannot but affect at least the question whether it is of the particular valid kind, since if it is false, it is not a genuine disjunction. There are other, similar instances, as for example Sextus’ rejection of the argument:
on the grounds that the first premiss does not state an exhaustive disjunction of the possibilities.166. These’extra-logical considerations’ [Gould, 1974, pp. 165-66] and this ‘serious confusion between a disjunction and a true disjunction’ [Mates, 1953, pp. 52–53] have puzzled earlier modern commentators. But if the specification of form was thought of as being given descriptively rather than substitutionally, so that the distinction between disjunction and true disjunction was not present, then the inexhaustiveness of the major premiss would debar justification by reference to [V] as the incompleteness of conflict would debar justification by reference to [IV]. And notice the restricted claim Sextus Empiricus is, on one occasion, content to allow himself about the nature of disjunction:
The true disjunction declares that one of its clauses is true, but the other or others false or false and contradictory.
It is a curious restriction if the distinction between a disjunction and a true disjunction is an important one.
Again, Galen’s discussion of the distinction between  and
and  makes it clear that he at least does not understand the claims of the fourth and fifth indemonstrables according to a substitution sense of validity. For he recognised what could be called paradisjunctive syllogism as a distinct type of syllogism, while evidently not regarding it as exhibiting a distinct form. Having given an account of Chrysippus’ classification of the indemonstrables, he remarks:
makes it clear that he at least does not understand the claims of the fourth and fifth indemonstrables according to a substitution sense of validity. For he recognised what could be called paradisjunctive syllogism as a distinct type of syllogism, while evidently not regarding it as exhibiting a distinct form. Having given an account of Chrysippus’ classification of the indemonstrables, he remarks:
In syllogisms of this sort i.e., disjunctive and hypothetical, the major premisses determine the minor; for neither in the disjunctive do more than two additional premisses occur nor in the conditional, while in the case of incomplete conflict 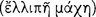 it is possible to make one additional assumption only. (Institutio Logica 7.1)
it is possible to make one additional assumption only. (Institutio Logica 7.1)
But when earlier he discusses the distinction between complete and incomplete conflict, a single multi-termed sentence does duty for both.
For ‘Dion is walking’ is one simple proposition, and also ‘Dion is sitting’; and ‘Dion is lying down’ is one proposition, and so, too, ‘He is running,’ and ‘He is standing still,’ but out of all of them is made a disjunctive proposition, as follows: ‘Dion is either walking or is sitting or is lying down or is running or is standing still’; whenever a proposition is formed in this way any one member is in incomplete conflict with another, but taken all together they are in complete conflict with one another, since it is necessary that one of them must be true and the others not. (Institutio Logica 5.2)
Notice that as an example of conflict, Galen’s is a good one in its listing states that cannot simultaneously obtain, but a bad one in providing a list that is not, as Galen suggests, genuinely exhaustive. (Dion might be crouching or signalling.) From an inferential point of view, its inexhaustiveness is unimportant, since given the truth of the disjunction it follows, solely in consequence of the meaning of the particle  , that if one of the disjuncts is false, then one of the others is true.
, that if one of the disjuncts is false, then one of the others is true.
Ian Mueller, in his discussion of the possible non-truth-functional status of the Stoic sentential combinations says
We cannot be sure about ‘or,’ but I suspect that a disjunction was taken to be true only if the disjuncts were mutually exclusive and exhaustive of the alternatives. [Mueller, 1978, p. 20]
It is a more plausible conjecture that what was meant by ‘disjunction’ was what would be called ‘true disjunction’ on a substitution interpretation, that in the case of disjunction, the etymological sense of ‘sound’ suggesting the correct internal relationships among parts, was not absent from the understanding of 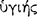 . In an application to a very simple object, this sense would be tantamount to ‘true’ in the sense of ‘genuine’. (For in a sufficiently simple kind of object, little in the way of internal relationships can fail before the object is not merely defective of the kind, but no longer an instance of the kind.) No disjunction that was true in the sense of ‘genuine’ could fail to be true in the sense of ‘representative of how things are’. Now to say this is not to say that they were confused between form and content as we imagine we understand the distinction. It is to say that the boundary between the two had not yet been clearly drawn, let alone drawn where, at least in propositional logic, we now draw it. In fact, we can go further. For one need only read De Morgan’s Cambridge lectures to see how far much of the philosophical establishment as recently as the nineteenth century was from grasping our present understanding of form. The resistance from Sir William Hamilton and his followers to the liberation of the idea of logical form from the shackles of Kantianism was one of the most serious academic obstacles that De Morgan had to surmount in getting his logical ideas accepted. One could argue that that struggle for liberation was one of the major contributions of nineteenth century logic. And the battle will not be certifiably won until the day when logic textbooks no longer call 1110 disjunctions exclusive on the grounds that their disjuncts are incompatible. It is therefore a serious matter to suppose that the Stoics were in full possession of the notion, particularly when the historical evidence indicates so clearly that their conception of the nature and place of logic were fundamentally different from that of twentieth century theorists.
. In an application to a very simple object, this sense would be tantamount to ‘true’ in the sense of ‘genuine’. (For in a sufficiently simple kind of object, little in the way of internal relationships can fail before the object is not merely defective of the kind, but no longer an instance of the kind.) No disjunction that was true in the sense of ‘genuine’ could fail to be true in the sense of ‘representative of how things are’. Now to say this is not to say that they were confused between form and content as we imagine we understand the distinction. It is to say that the boundary between the two had not yet been clearly drawn, let alone drawn where, at least in propositional logic, we now draw it. In fact, we can go further. For one need only read De Morgan’s Cambridge lectures to see how far much of the philosophical establishment as recently as the nineteenth century was from grasping our present understanding of form. The resistance from Sir William Hamilton and his followers to the liberation of the idea of logical form from the shackles of Kantianism was one of the most serious academic obstacles that De Morgan had to surmount in getting his logical ideas accepted. One could argue that that struggle for liberation was one of the major contributions of nineteenth century logic. And the battle will not be certifiably won until the day when logic textbooks no longer call 1110 disjunctions exclusive on the grounds that their disjuncts are incompatible. It is therefore a serious matter to suppose that the Stoics were in full possession of the notion, particularly when the historical evidence indicates so clearly that their conception of the nature and place of logic were fundamentally different from that of twentieth century theorists.
Finally, when the matter is viewed in this light, one is tempted to speculate that it was precisely their preoccupation with the dilemma both as a form of argument and as a paradigm of moral predicament which fixed the attention of the later Peripatetics and the Stoics upon inference patterns such as [IV], as having a fundamental place in a codification of academic inferential practice. If this were true it would not be surprising that they would wish to exclude as improper those disjunctions of which both disjuncts could be true, for these are the just the instances which would defeat conditionalisation of dilemmas. Since the substitution account of validity would not rule out such disjunctions and a descriptive account would, the descriptive account seems on that score to be the more likely candidate for the Stoic conception of validity.
11 What Stoic Disjunction May Have Been
We have concentrated upon disarming the prejudices which might suggest that they introduced a technical sense of  and aut … aut … or relied upon senses of those constructions already present in Greek and Latin. But we have allowed, without comment, anachronistic terminology such as ‘proposition’ to creep into our account (albeit only descriptively) which might itself create the false impression that the Stoics had some such notion in common with us. It would in particular be a serious misunderstanding to suppose that the Stoics had in their notion of a lekton a notion corresponding to the Fregean proposition. It is precisely in the nature of the lekton that most recent commentators have found grounds for denying the earlier assumption that the nature of Stoic logic could be well enough understood by comparison with modern calculi. Their arguments, to which may be added the arguments given here against the application to their work of a substitutional notion of logical form, have drawn their premisses from quite a different source, namely the nature of the relationship between Stoic logic and Stoic epistemology and physics.
and aut … aut … or relied upon senses of those constructions already present in Greek and Latin. But we have allowed, without comment, anachronistic terminology such as ‘proposition’ to creep into our account (albeit only descriptively) which might itself create the false impression that the Stoics had some such notion in common with us. It would in particular be a serious misunderstanding to suppose that the Stoics had in their notion of a lekton a notion corresponding to the Fregean proposition. It is precisely in the nature of the lekton that most recent commentators have found grounds for denying the earlier assumption that the nature of Stoic logic could be well enough understood by comparison with modern calculi. Their arguments, to which may be added the arguments given here against the application to their work of a substitutional notion of logical form, have drawn their premisses from quite a different source, namely the nature of the relationship between Stoic logic and Stoic epistemology and physics.
One account which forcefully presents Stoic logic in a non-formalist interpretation, is due to Claude Imbert [1980]. She takes as her point of departure the Stoic notion of 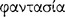 , usually translated as ‘presentation’, taken up as an alternative to Aristotle’s theory of imitation and applied to the art of Alexandria. It is through an understanding of the nature of
, usually translated as ‘presentation’, taken up as an alternative to Aristotle’s theory of imitation and applied to the art of Alexandria. It is through an understanding of the nature of  and their relationship to the major premisses of the indemonstrables that we understand why Stoic logic is conceptually incomparable with modern calculi.
and their relationship to the major premisses of the indemonstrables that we understand why Stoic logic is conceptually incomparable with modern calculi.
The conclusion of a Stoic syllogism is inferred from other sentences which translate natural signs apprehended in presentations, and which never presuppose the existence of transcendent forms or universals … Every logical structure rests on the possibility of translating presentations into discursive sequences, and each sequence must exhaust the scientific content latent in its presentation. Inference thus depends on a rhetorical function which maps utterances (lekta) on to contents of presentations (phantasia). [Imbert, 1980, pp. 187–88]
The transition from impression, which all animals have, to a presentation characteristic of human apprehension, depends upon the capacity to grasp connections among the contents of experience. Complex utterances, hypothetical, conjunctive and disjunctive, represent three ways of grasping connections. The one which concerns us here is the way which corresponds to the disjunctive proposition: the recognition of alternative exclusive possibilities. The use of the language of  in this connection is suggestive, in one respect, of Aristotle’s use of the same term in De Anima where it designates an activity characteristic of common (as distinct from particular) sense. And other evidence has suggested to some commentators that the ideas of the logical connections were originally a Peripatetic innovation.167 Finally, a full understanding of the Stoic preoccupation with what appears to the present day philosopher as a rather specialized and arcane notion of disjunction cannot neglect its connection with a theme which recurs as a leitmotif in one form or another throughout the history of Greek philosophy. The
in this connection is suggestive, in one respect, of Aristotle’s use of the same term in De Anima where it designates an activity characteristic of common (as distinct from particular) sense. And other evidence has suggested to some commentators that the ideas of the logical connections were originally a Peripatetic innovation.167 Finally, a full understanding of the Stoic preoccupation with what appears to the present day philosopher as a rather specialized and arcane notion of disjunction cannot neglect its connection with a theme which recurs as a leitmotif in one form or another throughout the history of Greek philosophy. The  of the Stoics is a late practical refinement of the notion of the conflict of opposites, which can be traced through Heracleitus’ doctrines of the unity of opposites to Anaximander’s doctrine of the generation of opposites from the undifferentiated
of the Stoics is a late practical refinement of the notion of the conflict of opposites, which can be traced through Heracleitus’ doctrines of the unity of opposites to Anaximander’s doctrine of the generation of opposites from the undifferentiated  , and is to be found in the central images of the mythic cosmogony of Hesiod. For the Stoics, it was at the heart of their ethics, physics and logic, and its recognition was a necessary constituent of the rational unity to be made of the conduct of human affairs and the operations of nature. We can construct a simplified model that realizes some such conception as the one they seem to have had in mind. According to such a picture, each succeeding state of the world makes some atomic sentences true and the rest false. So each moment of time may be thought of as a function or rule which takes sentences to truth values. Coming to an understanding of the intelligent character of the world amounts to grasping the principles by which these functions are selected in their turn. And in a poetic or spiritual frame of mind, we might imagine such rules as competing for selection and thus, since they represent incompatible assignments of truth-values, we might imagine them as being in conflict. Moreover, the image comes equally to mind of nature selecting its way among these competing functions according to some rational principle. In the sphere of individual action, the notion will readily suggest itself to us that in minute part we each bear some responsibility through our choices for the successive states of the universe. The apprehension of the distinctness of these state-functions within the subdomain of alternatives presented to us would, in this admittedly fanciful reconstruction, correspond to the apprehension of
, and is to be found in the central images of the mythic cosmogony of Hesiod. For the Stoics, it was at the heart of their ethics, physics and logic, and its recognition was a necessary constituent of the rational unity to be made of the conduct of human affairs and the operations of nature. We can construct a simplified model that realizes some such conception as the one they seem to have had in mind. According to such a picture, each succeeding state of the world makes some atomic sentences true and the rest false. So each moment of time may be thought of as a function or rule which takes sentences to truth values. Coming to an understanding of the intelligent character of the world amounts to grasping the principles by which these functions are selected in their turn. And in a poetic or spiritual frame of mind, we might imagine such rules as competing for selection and thus, since they represent incompatible assignments of truth-values, we might imagine them as being in conflict. Moreover, the image comes equally to mind of nature selecting its way among these competing functions according to some rational principle. In the sphere of individual action, the notion will readily suggest itself to us that in minute part we each bear some responsibility through our choices for the successive states of the universe. The apprehension of the distinctness of these state-functions within the subdomain of alternatives presented to us would, in this admittedly fanciful reconstruction, correspond to the apprehension of  . Like the rows of a truth table, or the items of a menu, they would be represented as mutually exclusive alternatives; were we to articulate them, it would most naturally take the form of a string of alternatives separated by ‘or’: this set of atoms true or that or the other.…
. Like the rows of a truth table, or the items of a menu, they would be represented as mutually exclusive alternatives; were we to articulate them, it would most naturally take the form of a string of alternatives separated by ‘or’: this set of atoms true or that or the other.…
Now this fancy is an anachronism, though the Stoics seemed to recognize something like the possibilities represented by the rows of a truth table. But if we cannot understand the Stoic use of or in other terms than those of twentieth century logical theory, it would be less misleading to bring the notion of  into the light of such simple-hearted model-theoretic ideas than to associate it with the substitutional idea of a particular logical form.
into the light of such simple-hearted model-theoretic ideas than to associate it with the substitutional idea of a particular logical form.
As much as one might wish to complain to the Stoics that there are connections, such as non-exclusive alternatives, which are not provided for in their scheme, such objections are not to the present point, for what we have wanted is an explanation of the Stoic use of  which accords with the evident fact that their technical use does not constitute a technical meaning. Understood as representing the most succinct way in which we reflect in utterance the connection between exclusive alternatives viewed as such, the use is surely unobjectionable. The fact that we, and for that matter, the Greeks, had other less succinct ways of reflecting such connections and as well used the same connective for non-exclusive alternatives is neither here nor there. In any case, when such alternatives confront us, a complete analysis of the possibilities will always yield exclusive alternands, namely, those corresponding to the three 1’s of the truth table of ∨. If α and β present themselves to us as non-exclusive alternatives, our choice, when fully and analytically apprehended, is seen to be among the three exclusive alternatives: pursuing both α and β, pursuing α but not β, and pursuing β but not α. Though the origins were different and the motives, the method need not be thought entirely unlike Boole’s. For he too took exclusivity, even the same arity-free idea of exclusivity, to be centrally important to his representation, but the exclusivity was constructed out of a non-exclusive disjunctive use of or.
which accords with the evident fact that their technical use does not constitute a technical meaning. Understood as representing the most succinct way in which we reflect in utterance the connection between exclusive alternatives viewed as such, the use is surely unobjectionable. The fact that we, and for that matter, the Greeks, had other less succinct ways of reflecting such connections and as well used the same connective for non-exclusive alternatives is neither here nor there. In any case, when such alternatives confront us, a complete analysis of the possibilities will always yield exclusive alternands, namely, those corresponding to the three 1’s of the truth table of ∨. If α and β present themselves to us as non-exclusive alternatives, our choice, when fully and analytically apprehended, is seen to be among the three exclusive alternatives: pursuing both α and β, pursuing α but not β, and pursuing β but not α. Though the origins were different and the motives, the method need not be thought entirely unlike Boole’s. For he too took exclusivity, even the same arity-free idea of exclusivity, to be centrally important to his representation, but the exclusivity was constructed out of a non-exclusive disjunctive use of or.
12 Stoic Disjunction as a Hyper-Relation
It is important to bear in mind that before the nineteenth century, logical theorists, though they spoke of form (as distinct from content) thought of logical connection in relational rather than formal terms. The character and status of the items between which the relations were thought to obtain varied through the history of the subject, but the relational character can be said to have persisted without challenge at least until George Boole’s temporal semantics for the connectives, and in some branches of logic, notably Idealist logic, to have persisted as explicit doctrine well into the twentieth century. The 1929 symposium on negation (Mabbott et al. 1929) might be said to mark its final departure from academic philosophical logic. We can, however, capture the character of Stoic disjunction in the recent language of coherence measures.
Let Σ be a set of sentences. Then the coherence level of Σ, λ(Σ) = min ξ: ∃π ∈ Πξ(Σ): ⩝c ∈ π, c ⩝ ⊥, if that limit exists; else λ(Σ) = ∞.
Thus, for example, λ({p, ¬p}) = 2; λ({p ∧ q, p ∧ ¬q,¬ p ∧ q, ¬p ∧ ¬q}) = 4; λ({⊥ }) = ∞ and so on.
Let Σ be a set of sentences. Then the coherence dilution of Σ, δ(Σ) = min ξ: ∃Δ ⊆ Σ |Δ| = ξ, and Δ  ⊥, if such a subset exists; else Δ(Σ) = ∞.
⊥, if such a subset exists; else Δ(Σ) = ∞.
Thus, for example, δ({p ∧ ¬p} = δ({⊥} = 1; δ({p ∧q, p ∧ ¬q, ¬p ∧ q, ¬p ∧ ¬q}) = 2; δ({α, α → β, β → γ, γ → ζ, ¬ζ}) = 5; δ({p}) = ∞ and so on.
Again, maximum dilution is illustrated by the modest believer, whose only mistaken belief is that at least one of his beliefs is false. No proper subset of his beliefs is inconsistent, yet the set as a whole is.
Then a set-representation of an n-term Stoic disjunction can be given as the set Σ = {σ1,…,σn} of its disjunctions where Σ satisfies:
The weaker Stoic notion of paradisjunction can be given a set-representation that weakens the dilution requirement to
Now it would not have taken the Stoics beyond the resources available to them to have introduced a measure on paradisjunctions representing the maximum number of disjuncts that could be true. Such a measure would indirectly have yielded a measure of dilution of incoherence capable of independent study. As an example, consider the set
Σ is a set representative of a paradisjunction: one of its elements must be true but all of them can be. On the other hand, the conflict among the elements of ¬[Σ] is less diffuse than among the negated disjuncts of a Stoic disjunction. If the ideal is the absence of conflict, evidently more dilute conflict is better than less. Thus the notion that inference should preserve dilution is in the logical spirit of Stoicism. We conclude with the observation that a system of inference that (a) permitted only dilution-preserving inferences, and (b) took those inferences Σ ∴ α as correct for which the dilution of Σ ∪ {α} was greater than the dilution of Σ ∪ {¬α} would satisfy connexivist constraints on inference corresponding to the theses of Aristotle and Boethius discussed earlier (page 482). Such a system was nearly within reach of the Stoics, and would constitute a natural extension of their logical theory.
cl975-. 2 volumes. Anderson, Alan Ross, Belnap, Nuel D., Jr., Entailment: the logic of relevance and necessity. Princeton UP: Delhi, 1975.
Barnes, Jonathan. Proof destroyed. In: Schofield, et al, eds. Doubt and Dogmatism. Princeton, N.J.: Clarendon; 1980:81–161.
New Brunswick Barnes, Jonathan, Theophrastus and hypothetical syllogistic. Fortenbaugh William W., et al, eds., eds. Theophrastus of Eresus: On His Life and Work. 1985.
Boche ski, I.M. Ancient Formal Logic. Oxford: North-Holland; 1963.
ski, I.M. Ancient Formal Logic. Oxford: North-Holland; 1963.
1961 Boche ski, I.M., A History of Formal Logic. Ivo, Thomas, eds. 2nd edition. Chelsea: Amsterdam, 1970.
ski, I.M., A History of Formal Logic. Ivo, Thomas, eds. 2nd edition. Chelsea: Amsterdam, 1970.
Rpt. (with corrections) 1966 Denniston, J.D. The Greek Particles, 2nd edition. New York: Clarendon Press; 1954.
Elgi, Urs. Stoic syntax and semantics. In: Brunschwig Jacques, ed. Les Stoïciens et leur logique. Oxford: Librairie Philosophique J. Vrin; 1978:54–135.
Frede, Michael. Die stoische Logik. Paris: Vandenhoeck and Ruprecht; 1974.
Frede, Michael. The original notion of cause. In: Essays in Ancient Philosophy. U of Minnesota Press: Göttingen, 1987:125–150. Schofield, Malcolm, et al. Doubt and Dogmatism. Minneapolis: Clarendon; 1980:216–249.
Frede, Michael. The origins of traditional grammar. In: Essays in Ancient Philosophy. U of Minnesota Press, 1987:338–359. Butts, R.E., Hintikka, J. Historical and Philosophical Dimensions of Logic, Methodology, and Philosophy of Science. Minneapolis: Reidel; 1977:51–79.
Frede, Michael. Principles of stoic grammar. In: Essays in Ancient Philosophy. U of Minnesota Press, 1987:301–337. Rist, J.M. The Stoics. Minneapolis: U of California Press; 1978:27–75.
Frede, Michael. Stoic vs. aristotelian syllogistic. In: Essays in Ancient Philosophy. U of Minnesota Press; 1987:99–124.Archiv für Geschichte der Philosophic. 1956;volume 56.
Frede, Michael. Stoics and skeptics on clear and distinct impressions. In: Essays in Ancient Philosophy. Minneapolis: U of Minnesota Press; 1987:151–176. Burnyeat, Miles. The Sceptical Tradition. U of California: Minneapolis, 1983 [First published in].
Gould, Josiah B. The Philosophy of Chrysippus. State U of New York Press; 1970.
Gould, Josiah B. Deduction in stoic logic. In: Corcoran John, ed. Ancient Logic and Its Modern Interpretations. Albany: D. Reidel; 1974:68–151.
Graeser, Andreas. The stoic categories. In: Brunschwig Jacques, ed. Les Stoïciens et leur logique. Dordrecht: Librairie Philosophique J. Vrin; 1978:199–221.
Graeser, Andreas. The stoic theory of meaning. In: Rist J.M., ed. The Stoics. Paris: U of California Press; 1978:77–100.
Hay, W.H. Stoic use of logic. Archiv für Geschichte der Philosophic. 1969;51:57–145.
Hurst, Martha. Implication in the fourth century b.c. Mind. 1935;44:95–484.
Imbert, Claude. Theorie de la representation et doctrine logique. In: Brunschwig Jacques, ed. Les Stoïciens et leur logique. Berkeley: Librairie Philosophique J. Vrin; 1978:49–223.
translated by Jonathan barnes Imbert, Claude. Stoic logic and alexandrian poetics. In: Schofield Malcolm, et al, eds. Doubt and Dogmatism. Paris: Clarendon; 1980:182–216.
Inwood, Brad. Ethics and Human Action in Early Stoicism. Oxford: Clarendon; 1985.
Kahn, Charles H. Stoic logic and stoic logos. Archiv für Geschichte der Philosophie. 1969;51:72–158.
Kerferd, Georg. The problem of synkatathesis and katalēpsis in stoic doctrine. In: Brunschwig Jacques, ed. Les Stoïciens et leur logique. Oxford: Librairie Philosophique J. Vrin; 1978:72–251.
Kerferd, Georg. What does the wise man know. In: Rist J.M., ed. The Stoics. Paris: U of California Press, 1978.
Kieffer John Spangler, ed. Galen’s Institution Logica. Berkeley: Johns Hopkins, 1964.
Kirk G.S., ed. Heraclitus: The Cosmic Fragments. Baltimore: Cambridge UP, 1962.
Reprinted (with corrections, new as paperback) 1988. Kneale, William, Kneale, Martha. The Development of Logic. Cambridge: Clarendon; 1962.
Reprinted (with corrections, new as paperback) 1988. Kneale, William, Kneale, Martha. The Development of Logic. Oxford: Clarendon; 1962.
1987 Long, A.A., Sedley, D.N., The Hellenistic Philosophers [2 volumes]. Cambridge UP: Oxford, 1990.
Long, A.A. Language and thought in stoicism. In: Long A.A., ed. Problems in Stoicism. Cambridge: Athlone; 1971:75–113.
Long, A.A. Hellenistic Philosophy, 2nd edition. London: U of California Press; 1986.
Oxford Lukasiewicz, Jan, On the history of the logic of propositions. McCall Storrs, ed., eds. Polish Logic: 1920–1939. 1967:67–87.
Mates, Benson. Stoic Logic. Berkeley: U of California Press; 1953.
McCall, Storrs. Connexive implication. The Journal of Symbolic Logic. 1966;31:33–415.
Mueller, Ian. An introduction to stoic logic. In: Rist J.M., ed. The Stoics. Berkeley and Los Angeles: U of California Press; 1978:1–26.
Nelson, Everett J. Intensional relations. Mind. 1930;39:53–440.
Reesor, Margaret E. The stoic concept of quality. American Journal of Philology. 1954;75:40–58.
Reesor, Margaret E. The Nature of Man in Early Stoic Philosophy. Berkeley: Duckworth; 1989.
Rpt. in Long 1971, 38-57 Rist, J.M. Categories and their uses. In: Rist J.M, ed. Stoic Philosophy. London: Cambridge UP; 1969:72–152.
Rist, J.M. The criterion of truth. In: Rist J.M., ed. Stoic Philosophy. Cambridge UP; 1969:51–133.
Rist, J.M. Stoic Philosophy. Cambridge UP; 1969.
Rist, J.M. Zeno and the origins of stoic logic. In: Brunschwig Jacques, ed. Les Stoïciens et leur logique. Librairie Philosophique J. Vrin; 1978:387–400.
Sambursky, S. Physics of the Stoics. Paris: Routledge and Kegan Paul; 1959.
Sandbach, F.H. Ennoia and prolepsis. In: Long A.A., ed. Problems in Stoicism. London: Athlone; 1971:22–37.Classical Quarterly. 1930;volume 24:45–51.
Sandbach, F.H. Phantasia kataleptike. In: Long A.A., ed. Problems in Stoicism. London: Athlone; 1971:9–21.
Sandbach, F.H. The Stoics. London: Chatto and Windus; 1975.
Sandbach, F.H. Aristotle and the stoics. In: Supplementary volume 10 of The Cambridge Philological Society. London: Cambridge UP; 1985.
Searle, John R. Speech Acts. Cambridge UP; 1969.
Sedley, David, Diodorus Cronus and hellenistic philosophy. Proceedings of the Cambridge Philological Society, volume 1977;23:74–120.
Stopper, M.R. Schizzi pirroniani. Phronesis. 1983;28:97–265.
Watson, Gerard. The Stoic Theory of Knowledge. Cambridge: Queen’s U; 1966.
Supplementary volume White, Nicholas, The role of physics in stoic ethics. Spindel Conference 1984-Recovering the Stoics. The Southern Journal of Philosophy. Dept. of Philosophy, Memphis State U: Belfast, 1985.
White, Michael J. The fourth account of conditionals in Sextus Empiricus. History and Philosophy of Logic. 1986;7:1–14.
Trans. Oswald J. Reichel Zeller, E., The Stoics, Epicurean and Sceptics [revised edition]. Russell and Russell, 1962..Die Philosophic der Griechen. 1879;vol. 3.
1Geschichte der Logik im Abendlande, 1.404. Translated by Mates [1953, p. 87].
2The fourth syllogism may be represented by the schema ‘α or β but α therefore, not β’, and the fifth by the schema ‘α or β but not α therefore, β’.
3Łukasiewicz [1967, p. 74]; Boche ski [1963, p. 91]; Mates [1953, p. 51]; Kneale and Kneale [1962a, p. 148]; Gould [1970, p. 72].
ski [1963, p. 91]; Mates [1953, p. 51]; Kneale and Kneale [1962a, p. 148]; Gould [1970, p. 72].
4Mates [1953, p. 52]; Boche ski [1963, p. 91].
ski [1963, p. 91].
5cf. Aulus Gellius Noctes Atticae. 16.8.13–14; Galen inst. log. 12; PH 2.191.
6The ‘arity’ of a binary operator is 2; that of a ternary operator, 3; of a quaternary operator, 4; and so on.
7Sextus Empiricus (circa A.D. 200) was a Greek physician and sceptic philosopher who succeeded Herodotus of Tarsus as head of the Sceptic School. Sextus’ critique of Stoic philosophical doctrine is covered in a series of eleven books under the general title of Adversus Mathematicos (abbreviated AM), and a series of three books under the title Outlines of Pyrrhonism (abbreviated PH). Stoic logical doctrine is contained for the most part in Books 7 and 8 of AM and in Book 2 of PH. Physical tenets are covered in Books 9 and 10 of AM and in Book 3 of PH. Ethical teachings are criticised in Book 11 of AM and in Book 3 of PH. Sextus’ account of Stoic Philosophy is probably one of the most extensive of the ancient commentaries. However, because of it polemic nature, its value is perhaps less than it might been.
8After Sextus Empiricus, Diogenes Laërtius (circa A.D. 200–250?) provides the next most extensive account of Stoic doctrine. Much of what he writes on the Stoics corroborates what is written by Sextus Empiricus, but in contrast to the latter’s account, Diogenes’ report has the advantage that it is not in the least polemical. It is fortunate that in Book 7 of Lives and Opinions of Eminent Philosophers, the section in which he covers the Stoic School, Diogenes draws on a handbook written by Diocles of Magnesia. His account of Stoic logic, therefore, is widely considered to be reliable. Since he is not in general considered a reliable source, it might have been otherwise.
9We have relied on the commentaries of Benson Mates [1953, pp. 86–90] and I. M. Boche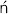 ski [1963, pp. 6–8]; [1963, pp. 5–6] for an assessment of Prantl’s contribution to the history of Stoic logic.
ski [1963, pp. 6–8]; [1963, pp. 5–6] for an assessment of Prantl’s contribution to the history of Stoic logic.
10Critique of Pure Reason, Unabridged Edition. Translated by Norman Kemp Smith. Macmillan, 1929. New York: St. Martin’s Press, 1965.
11See, for example, A. A. Long, [1986, p. 115]; Jonathan Barnes, Oxford History of the Classical World, p. 368.
12Much of the information on the lives and doctrines of the early Stoics come from Diogenes Laërtius’ Lives and Opinions of Eminent Philosophers. However, we have also relied heavily on Reichel’s Stoics, Epicurians, and Sceptics, which is translated from the third volume of Zeller’s Die Philosophie der Griechen, as well as on Long’s Hellenistic Philosophy, on Long and Sedley’s The Hellenistic Philosophers, on Sandbach’s The Stoics, on Rist’s Stoic Philosophy, and on Barnes’ article in The Oxford History of the Classical World, pp. 365–85.
It is evident from Diogenes account that there was some dispute concerning the important dates in Zeno’s life. By way of reconciling this problem, we will report the alternatives which Long and Zeller suggest to be the most reliable.
13Sandbach: “… Citium, once a Greek colony, was [at the time of Zeno’s birth] predominantly Phoenician in language, in institutions, and perhaps in population. Zeno’s contemporaries who called him a Phoenician may have been justified in so doing, but he must be imagined as growing up in an environment where Greek was important” [Sandbach, 1975, p. 20].
14Andreas Graeser, for example, in his Die logischen Fragmente des Theophrast assumes that Zeno was a pupil of Theophrastus (44).
15Cf. F.H. Sandbach’s reference “the striking absence of explicit evidence that the early Stoics took an interest in the work of Aristotle or of his following in the Peripatos” [Sandbach, 1985, p. 55].
16This view is expressed by Sandbach in his concluding paragraph [Sandbach, 1985, p. 55], and evidence for it is well-documented throughout his monograph.
17Sandbach’s explanation of this term is as follows: “… Aristotle did write some works, now lost, of which some were dialogues, intended for a wider public than the students who were attached to his school. Later scholars, and probably Aristotle himself, referred to these as ‘exoteric”’ [Sandbach, 1985, p. 1].
18Axiōmata are somewhat akin to propositions, but differ in some important ways. For a discussion see section 6 on page 463.
19For the details on this debate, see Section 8.1.
20It should be noted in passing that it cannot be assumed that either Sextus Empiricus, or any other late commentator or doxographer, in using the term ‘hoi dialektikoi’, is referring specifically to the Dialectical School. Sedley points out at least two reasons for supposing that this is so: first, the term ‘dialektikos’, was commonly used to designate anyone who used the method of argumentation from which the Dialectical School got its name, that is, the method of putting an argument in the form of question and answer (75; cf. DL 2.106); moreover, to quote Sedley, “by the time of Chrysippus, in the late third century, [dialektikos] is the standard term for ‘logician”’ [Sedley, 1977, p. 75]. Now since the Stoics were recognised for their logical acumen above and beyond any rival school, it seems more likely that when Sextus refers to ‘hoi dialektikoi’, for the most part, he means the Stoics.
21The Greek text is in Stobaeus Eclogae Physicae et Ethicae, vol. 1, page 25, line 12 to page 27, line 4. The text is translated in Long and Sedley [1990, 1.326-327]. There is also a translation in somewhat more archaic (poetical?) language in Sandbach [1975, pp. 110–111].
22The term protasis  is used in Sextus Empiricus to refer to the major premiss of a categorical syllogism (PH 2.164; 195). Galen seems here to be extending the use of this term to refer to the major premiss of a Stoic hypothetical syllogism as well. Thus it would be interchangeable with the term lēmma
is used in Sextus Empiricus to refer to the major premiss of a categorical syllogism (PH 2.164; 195). Galen seems here to be extending the use of this term to refer to the major premiss of a Stoic hypothetical syllogism as well. Thus it would be interchangeable with the term lēmma  , which, according to Diogenes Laërtius, the Stoics used to refer to the major premiss of an argument (DL 7.76).
, which, according to Diogenes Laërtius, the Stoics used to refer to the major premiss of an argument (DL 7.76).
23In his commentary on this section of the Institutio, Kieffer provides the following explanation: “Galen’s point in calling the major premiss in a hypothetical syllogism determinative of the minor is that the minor premiss is either one of the members of the hypothetical major or its contradictory” ([Kieffer, 1964], 92). Thus in the case where the major premiss of the hypothetical syllogism is a conditional, the minor premiss will be either the antecedent of the conditional (as in modus ponens) or the negation of the consequent (as in modus tollens). Note that ‘hypothetical syllogism’ here covers any syllogism which is not categorical, and for the Stoics this includes not only syllogisms with a conditional as major premiss but also those with either a disjunctive or a negated conjunction.
24For a more complete account of the Stoic argument schemata called the ‘indemonstrables’, see page 474.
25cf. Boethius in de interp. 234.22–26: quod aut est aut erit. As Benson Mates points out, Boethius in this passage also gives definitions of the related terms ‘impossible’, ‘necessary’, and ‘non-necessary’, and based on the construction of these other definitions, one can conjecture that the above definition of the possible was “slightly elliptical.” The full definition should have been ‘that which is or will be true’ [Mates, 1953, p. 37].
26According to Zeller, the view of most writers was that Chrysippus was born at Soli in Cilicia; however, since his father emigrated to Soli from Tarsus, it is possible that Chrysippus was born there instead ([Zeller, 1962], 45n5).
27Here, and in Plutarch’s De Stoicorum repugnantiis at 1036c, as well as in Epictetus’ The Discourses at 1.27.15–21, the term  seems to have the meaning ‘common experience’; on the other hand, in Diogenes Laërtius at 7.59 it would appear to mean ‘ordinary language’, and in De Stoicorum repugnantiis at 1048a, to mean ‘common use of language’ (cf. the entry in Liddel and Scott, II.2).
seems to have the meaning ‘common experience’; on the other hand, in Diogenes Laërtius at 7.59 it would appear to mean ‘ordinary language’, and in De Stoicorum repugnantiis at 1048a, to mean ‘common use of language’ (cf. the entry in Liddel and Scott, II.2).
28This thesis is put forward by J.M. Rist in his essay “Cynicism and Stoicism” which appears as Chapter 4 of his Stoic Philosophy.
29The terms which Long and Sedley render as ‘happiness’ and ‘unhappiness’ are 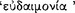 (eudaimonia) and
(eudaimonia) and  (kakodaimonia) respectively. Now although these are standard translations, it has been suggested that they fail to capture the notion which they are intended to express. Sandbach has the following to say on this point:
(kakodaimonia) respectively. Now although these are standard translations, it has been suggested that they fail to capture the notion which they are intended to express. Sandbach has the following to say on this point:
eudaimonia, although something experienced by the man who is eudaimōn, is (perhaps primarily) something objective, that others can recognise—having a good lot in life … Thus the Stoics did not attempt to describe eudaimonia as a subjective feeling, but identified it with such things as ‘living a good life’, ‘being virtuous’, or ‘good calculation in the choice of things that possess value’ … For the Stoic, who confines the word ‘good’ to the morally good, it is consistent that a good life is a morally good life and the well-being indicated by eudaimonia is unaffected by what is morally indifferent, however acceptable [Sandbach, 1975, p. 41].
In another place Long himself renders eudaimonia as ‘self-fulfilment’ ([Long, 1971], 104), a translation which probably better comprehends the meaning, although still not completely.
30The doctrine of the Academy would appear to go back to Plato himself, for in Laws 661a–d, he has the Athenian say that things such as health, beauty, wealth, and acute sensibility all are to be counted as goods, but only in the possession of the just and virtuous; in the possession of one who is not so, however, all these things are rather evils than goods.
31In the third sense, according to Diogenes, “value is the worth set by an appraiser, which should be fixed according to experience of the facts, as, for example, wheat is said to be exchanged for barley plus a mule (DL 7.105).
32Long and Sedley note that in De finibus 3.17 and 20–21, Cicero “envisages five progressive stages, each of which is represented as performance of ‘proper functions’ as these could evolve for a human being” [Long and Sedley, 1990, 1.368]. Edelstien and Kidd, on the other hand, stresses De finibus 4.39 where Cicero gives a threefold division of ta kata physin (Posidonius I: the Fragments 155). It seems to us that there is a clear relationship between this division of ta kata physin and the five stages of ta kathēkonta as they are summarised at de fin. 3.20, wherein the first two stages of ta kathēkonta, i.e. “to preserve oneself in one’s natural constitution” and “to retain those things which are in accordance with nature and to repel those that are the contrary,” are associated with the first division of ta kata physin; the second two stages, i.e. “choice conditioned by reasoned action” and “such choice becoming a fixed habit,” with the second division; and the last stage, i.e. “choice fully rationalised and in accordance with nature,” with the third division. Hence in our presentation we have exploited this relationship by merging these categorisations into one three-fold differentiation.
33So Sandbach: “What Zeno was probably afraid of was that what might be dignified with the name of acts of will might in fact be acts of whim and caprice. Since virtue itself seemed so difficult to understand or describe, the danger of this was very real indeed. That is why so many of the Cynics give the impression of being merely irresponsible exhibitionists” [Sandbach, 1975, p. 71].
34E.g., Cicero de fin. 3.33; Seneca epist. 120.4. See also Long [1986], 199–205.
35See Sandbach’s discussion in The Stoics, [Sandbach, 1975, pp. 53–55].
36For a more extensive explication of this problem, see Kerferd’s article in Rist 1978: “What Does the Wise Man Know?” [Kerferd, 1978b]. See also the article by Nicholas White, “The Role of Physics in Stoic Ethics,” Southern Journal of Philosophy: Recovering the Stoics, Spindel Conference: 1984 (1985): 57–74. White takes the view that “we are not in a position to be sure why the early Stoics thought that detailed physical and cosmological theory … would be required by their ethics” [White, 1985, p. 72]. Although White grants the plausibility of the premiss that they might have held such a view, he argues that any actual arguments for it, or explanations of it, are lacking [White, 1985, p. 72].
37At the end of his summary of Stoic logic Diogenes has this to say: “The reason why the Stoics adopt these views in logic is to give the strongest possible confirmation to their claim that the wise man is always a dialectician. For all things are observed through study conducted in discourses, whether they belong to the domain of physics or equally that of ethics (DL 7.83).
Compare: “[T]he Stoics, who define dialectic as the science of speaking well, taking speaking well to consist in saying what is true and what is fitting, and regarding this as a distinguishing characteristic of the philosopher, use [the term ‘dialectic’] of philosophy at its highest. For this reason, only the wise man is a dialectician in their view” (Alexander in top. 1.8–14).
38Contrary to some interpretations (e.g., Kerferd [1978a, p. 260]; Watson [1966, pp. 47–48], we take it that although every lekton belongs to the class of sēmainomena, not every sēmainomenon is a lekton. Proper names and common nouns, for example, are sēmainonta which signify ‘individual qualities’  and ‘common qualities’
and ‘common qualities’  respectively (DL 7.58). Since qualities for the Stoics are corporeal, and since lekta are incorporeal, it is evident that both individual qualities and common qualities are sēmainomena which are not lekta.
respectively (DL 7.58). Since qualities for the Stoics are corporeal, and since lekta are incorporeal, it is evident that both individual qualities and common qualities are sēmainomena which are not lekta.
39In some places (e.g., PH 2.137, 146) Sextus uses  , whereas at other places (e.g., AM 8.429) he uses
, whereas at other places (e.g., AM 8.429) he uses  and
and  . Hence, as Mates indicates in his glossary ([Mates, 1953], 132–36), these terms appear to be interchangeable. Diogenes Laërtius, however, in his discussion of arguments from 7.77–79 uses
. Hence, as Mates indicates in his glossary ([Mates, 1953], 132–36), these terms appear to be interchangeable. Diogenes Laërtius, however, in his discussion of arguments from 7.77–79 uses 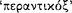 exclusively for ‘conclusive’ and
exclusively for ‘conclusive’ and  for ‘inconclusive’.
for ‘inconclusive’.
40See page 477 for a discussion of the use of 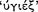 and
and 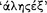 in these contexts.
in these contexts.
41It is unlikely that by ‘dialectician’ here Sextus is referring exclusively to a member of the Dialectical School of which Diodorus Cronus and Philo were members. He is probably using it as a synonym for ‘logician’ (see footnote 20, page 408).
42See Section 8.1 for a discussion of the four views.
43Long and Sedley have commented that the containment view “may not differ significantly” from the conflict view (1.211). We intend to explore this possibility.
44
 .
.
45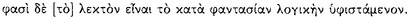 .
.
46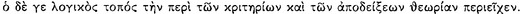 .
.
47According to Rist, “the overwhelming body of evidence that we shall consider [concerning the Stoic criterion of truth] suggests that the normal Stoic answers to the question What is the criterion of truth? are either Recognition  , or Recognizable Presentation
, or Recognizable Presentation 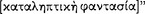 ” [Rist, 1969b, p. 133].
” [Rist, 1969b, p. 133].
48Sextus Empiricus AM 7.230; Aëtius SVF 2.54. Sextus uses the term 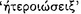 , which we have rendered as ‘alteration’ or ‘modification’ (cf. Bury). In the corresponding passage, Aëtius uses ‘gpa’joc’, which might be rendered ‘affection’ (cf. Long and Sedley [1990, 1.237]).
, which we have rendered as ‘alteration’ or ‘modification’ (cf. Bury). In the corresponding passage, Aëtius uses ‘gpa’joc’, which might be rendered ‘affection’ (cf. Long and Sedley [1990, 1.237]).
49This expanded definition was put forward in order to forestall certain objections that not all modifications of the psychē could be presentations.
50Nemesius SVF 1.143; Chalcidius SVF 2.879; DL 7.110.
51 : Nemesius SVF 2.39.22.
: Nemesius SVF 2.39.22.
52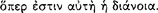 .
.
53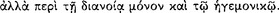 .
.
54 . In his Alexander of Aphrodisias on Stoic Physics, Robert B. Todd discusses the Stoic theory of total blending as it is reported by Alexander in De mixtione.
. In his Alexander of Aphrodisias on Stoic Physics, Robert B. Todd discusses the Stoic theory of total blending as it is reported by Alexander in De mixtione.
55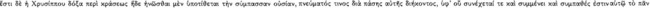 (Alexander de mixtione 216.14–17).
(Alexander de mixtione 216.14–17).
56Zeno’s corresponding argument is also recorded by Chalcidius (SVF 1.138). cf. Tertullian (SVF 1.137).
57One fragment seems to indicate that not only presentation, but also assent  , impulse
, impulse 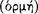 , and reason
, and reason 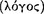 are qualities of the psych (Iamblichus de anima, apud Stobaeus eclog. 1.368.12–20; cf. AM 7.237), and qualities, according to the Stoics, are corporeal (SVF 2.376–98).
are qualities of the psych (Iamblichus de anima, apud Stobaeus eclog. 1.368.12–20; cf. AM 7.237), and qualities, according to the Stoics, are corporeal (SVF 2.376–98).
58Aristocles SVF 1.98; Chalcidius 293, L & S 44E; Galen hist. phil., DDG 608; DL 7.134. One reading of DL 7.134 (Suidas) has it that the archai are  )(incorporeal). The reading of the codices, however, has it that they are
)(incorporeal). The reading of the codices, however, has it that they are  (corporeal). Long and Sedley prefer the reading
(corporeal). Long and Sedley prefer the reading  [1990, 2.226], their reasons being (1) that this interpretation is supported by other texts, and (2) the corporeality of the principles follows by implication from the Stoic view that only bodies are capable of acting and being acted upon [Long and Sedley, 1990, 1.273–74]. But since the active principle is explicitly identified with God (DL 7.134), then it would seem to follow that God (or the gods) is corporeal.
[1990, 2.226], their reasons being (1) that this interpretation is supported by other texts, and (2) the corporeality of the principles follows by implication from the Stoic view that only bodies are capable of acting and being acted upon [Long and Sedley, 1990, 1.273–74]. But since the active principle is explicitly identified with God (DL 7.134), then it would seem to follow that God (or the gods) is corporeal.
59AM 8.194;275;3.25;DL 7.53. Sandbach [1971a, p. 26] translates ‘metabasis’ in DL 7.53 as ‘inference’.
60For example, Plutarch de comm. not. 1085e; Galen SVF 2.377; 410; Simplicius in cat. 271.20; in phys. 509.9. Long and Sedley argue indexLong, A. A.that “the corporeality of qualities is one of many Stoic theses implied by the corporeality of the principles” [Long and Sedley, 1990, 1.274] (see 432, footnote 58).
61 (AM 8.409).
(AM 8.409).
62Aëtius plac. 4.11.1–4, DDG 400 = SVF 2.83. The translation is that of Long and Sedley [1990, 1.238]. According to Sandbach, “the claim that reason is made up in the first seven years is surprising and conflicts with all other sources, which give 14 as the age when it is established. … Au)’tius seems to have confused the beginning of the growth of reason in the first seven years of life with its completion round about the age of fourteen” [Sandbach, 1985, 80n118]. Jamblichus, for example, reports that “the Stoics say that reason is not immediately implanted, but is assembled later from sense perceptions and presentations about the fourteenth year” (de anima, apud Stobaeus eclog. 1.317.20). cf. Inwood: “Reason … begins to be acquired at or about the age of seven and is ‘completely acquired’ at or about the age of fourteen” [Inwood, 1985, p. 72].
63We are rendering 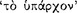 that which is real’ or ‘reality’ rather than as ‘the real object’. We will argue in the sequel that although the Stoics took “objective particulars” as their “fundamental existents” (cf. Long [1971, p. 75]), they nevertheless thought that reality consists not only in such objective particulars, but also in the properties and relations of these objects.
that which is real’ or ‘reality’ rather than as ‘the real object’. We will argue in the sequel that although the Stoics took “objective particulars” as their “fundamental existents” (cf. Long [1971, p. 75]), they nevertheless thought that reality consists not only in such objective particulars, but also in the properties and relations of these objects.
64We follow several authors in translating 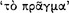 as ‘the state of affairs: e.g., Long [1971, 107n10]; Long and Sedley [1990, 1.195, 202]; Reesor [1989, Ch. 3]. The term certainly can have this meaning in ordinary Greek; it seems evident, however, that the Stoics gave it a technical meaning in the context of their semantic theory. We take it that in this context the term referred to a semantic structure which corresponded in structure either to a real state of affairs, or to a mooted state of affairs.
as ‘the state of affairs: e.g., Long [1971, 107n10]; Long and Sedley [1990, 1.195, 202]; Reesor [1989, Ch. 3]. The term certainly can have this meaning in ordinary Greek; it seems evident, however, that the Stoics gave it a technical meaning in the context of their semantic theory. We take it that in this context the term referred to a semantic structure which corresponded in structure either to a real state of affairs, or to a mooted state of affairs.
65For similar commentary on Sextus’ example, see Long and Sedley [1990, 2.197]; Long [1971, p. 77 and 107n11]; Frede [1987b, p. 349]. Kerferd, on the other hand, argues that the conclusion that ‘Dion’ signifies a lekton is straightforward in spite of the many passages suggesting that only axiōmata are true or false [Kerferd, 1978a, pp. 260–61]. He does not mention the difficulty posed by Diogenes’ passage which says that names signify corporeal qualities, not incorporeal lekta.
66Long and Sedley translate 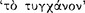 as ‘the name-bearer’. For an explanation and discussion of this translation, see Long and Sedley [1990], 1.201 and 2.197. In an earlier work, Long translated
as ‘the name-bearer’. For an explanation and discussion of this translation, see Long and Sedley [1990], 1.201 and 2.197. In an earlier work, Long translated 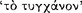 as ‘the object of reference’ [Long, 1971, p. 76, 107n9]. For Michael Frede’s interpretation, see his [1987b, pp. 349–50].
as ‘the object of reference’ [Long, 1971, p. 76, 107n9]. For Michael Frede’s interpretation, see his [1987b, pp. 349–50].
68Note that in English, the axiōma is mentioned by setting of the corresponding sentence in single quotation marks. In the Greek, it is often mentioned by similar means—usually with double quotation marks, and examples are often introduced by the term 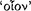 , with or without quotation marks. Also, the axiōma is sometimes mentioned by nominalising the corresponding sentence by means of the definite article. Hence, the axiōma which we represent in English as ‘Dion is walking’, may be represented in the Greek as
, with or without quotation marks. Also, the axiōma is sometimes mentioned by nominalising the corresponding sentence by means of the definite article. Hence, the axiōma which we represent in English as ‘Dion is walking’, may be represented in the Greek as  . At any rate, the same means are used to mention sentences, both in English and in the Greek, respectively, and it would appear that some ancient commentators, as well as some recent translators, do not always keep the distinction in mind.
. At any rate, the same means are used to mention sentences, both in English and in the Greek, respectively, and it would appear that some ancient commentators, as well as some recent translators, do not always keep the distinction in mind.
69It is evident that the Stoics thought that the attribute ‘walking’ is real when possessed by someone or something, even though they also thought that the predicate ‘walking’ is incorporeal (see footnote 84, page 448).
70“As physical events are transmitted by nearby action, either through direct contact of bodies or by the pneuma, this must be true also for cause-effect relations. Contiguity is therefore an essential attribute of causality, and causes are bodies acting upon other bodies either in spatial contact with them or through the medium of the pneuma” (Sambursky [1959, p. 53]).
71 .
.
72Hick’s note here is somewhat misleading. He writes that “Direct Predicate” answers to our Active Verb, ‘Predicate Reversed’ to our Passive” (DL 7.63 note a). This seems to point out a fairly fundamental misunderstanding of the concept of a lekton in Stoic semantics. As lekta, predicates are incorporeal, verbs are parts of speech, and as such, are corporeal. A verb 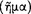 , according to Diogenes the Babylonian, is a part of speech signifying an uncombined predicate (DL 7.58).
, according to Diogenes the Babylonian, is a part of speech signifying an uncombined predicate (DL 7.58).
73A Compare the definition given by Sextus at PH 2.104:
Compare the definition given by Sextus at PH 2.104: 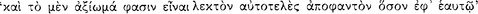 . These descriptions differ on in that Sextus has ‘lekton’ instead of ‘pragma’. And Aulus Gellius reports that he found this definition of the axiōma in his Greek books:
. These descriptions differ on in that Sextus has ‘lekton’ instead of ‘pragma’. And Aulus Gellius reports that he found this definition of the axiōma in his Greek books: 
74For further discussion of the difficulties in rendering this passage, see Frede [1974, pp. 38–40]; Long and Sedley [1990, 2.204–05]; and Margaret Reesor [1989 pp. 46–48].
75This book, called Logical Inquiries (λOγIKωN ZHTHMATωN), is included in the collection by von Arnim as Fragment 2.298a. For an interesting view on the content of these writings and on the possible similarity of the Stoic theory to those of modern theorists in the logic of imperatives: see Inwood’s Ethics and Human Action in Early Stoicism, [Inwood, 1985]
76 .
.
77The presentations of children, for example, are not rational until they have accumulated a certain stock of conceptions (e.g., see footnote 62, page 433), but since they apparently do have presentations, surely one can speak of ‘that which is presented’ in such presentations.
78 . My justification for inserting
. My justification for inserting  into the text here is twofold: first, there is the passage at 7.65 where Diogenes describes the axiōma as a
into the text here is twofold: first, there is the passage at 7.65 where Diogenes describes the axiōma as a 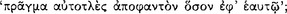 ; second, in the passages from 7.66–68, there are the instances of
; second, in the passages from 7.66–68, there are the instances of  occurring in similar grammatical constructions in the descriptions of the other types of lekta. For the translation in these contexts of
occurring in similar grammatical constructions in the descriptions of the other types of lekta. For the translation in these contexts of  as ‘state of affairs’, see Long, ([1971], 107n10; Long and Sedley, [1990], 1.195, 202; Reesor, [1989, Ch. 3].
as ‘state of affairs’, see Long, ([1971], 107n10; Long and Sedley, [1990], 1.195, 202; Reesor, [1989, Ch. 3].
79See Margaret Reesor’s comments on the Stoic notion of speaking as ‘speaking a pragma’ (state of affairs) [Reesor, 1989, pp. 33–34].
81As it is used in the phrase ‘mode of assertion’, the term ‘assertion’ should be understood as neutral among the various illocutionary acts.
82See page 433 for a discussion of how rationality is completed from our preconceptions  , and see page 434 for a discussion of how more complex conceptions might be produced from these primary conceptions.
, and see page 434 for a discussion of how more complex conceptions might be produced from these primary conceptions.
83Contrast Graeser, [1978b, p. 8]: “[The Stoics] insisted that there holds no isomorphic correlation between thought on the one hand and things-that-are on the other. … [They] implied that ontological analysis is bound to be subjective, or rather functional, in that it is man’s mind that superimposes its concepts on reality.” It seems to us, however, that if someone believed that the same logos which structures reality is also immanent in our minds, then one would expect them also to believe in some sort of isomorphism between thought and reality. But then Graeser seems to take what Long and Sedley refer to as a “variant reading” [Long and Sedley, 1990, 1.274] of Diogenes Laërtius 7.134 as evidence that the logos itself is incorporeal [Graeser, 1978b, p. 99]. He mentions Posidonius as possibly holding such a view [Graeser, 1978b, p. 99]. This may be so. However, as Long and Sedley have argued [1990, 1.274], this cannot be the view of the Old Stoa.
84According to Stobaeus, Chrysippus held that even predicates are real, but only those which are actual attributes  . He says that “walking”
. He says that “walking” 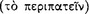 is real
is real 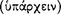 for me when I am walking, but it is not real when I have lain down or am sitting down” (eclog. 1.106.18–20).
for me when I am walking, but it is not real when I have lain down or am sitting down” (eclog. 1.106.18–20).
Seneca records a dispute between Kleanthes and his pupil Chrysippus about the nature of walking. According to Kleanthes walking is breath (spiritus = pneuma) extending from the hēgemonikon (principalis = hēgemonikon) to the feet, whereas, according to Chrysippus, it is the hēgemonikon itself (epist. 113.23). Leaving aside the question of how the dispute turned out, it seems apparent that whatever else they meant by the term ‘walking’, both Kleanthes and Chrysippus thought that they were talking about something corporeal, for in Stoic doctrine both the pneuma and the hēgemonikon are bodies (SVF 2.879). But since there is no doubt that they conceived of predicates as being incorporeal, they clearly could not have been referring to the predicate {walking} by their use in this context of the term ‘walking’.
85It seems apparent that the Stoics used the nominalised infinitive verb to signify a predicate. For example, at AM 9.211, Sextus reports that according to the Stoics, “the scalpel is corporeal, and the flesh is corporeal, but the predicate ‘to be cut’ is incorporeal” 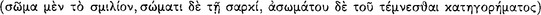 (cf. Clement strom. 8.9.30.3). Although it may seem more natural to render the nominalised infinitive by a gerund, for example, ‘walking’ rather than ‘to walk’, it is not always the simplest representation, particularly in the case of complex predicates. Note that a finite verb seems to be the signification of an incomplete predicate. So at 7.63 Diogenes Laërtius says that the verb
(cf. Clement strom. 8.9.30.3). Although it may seem more natural to render the nominalised infinitive by a gerund, for example, ‘walking’ rather than ‘to walk’, it is not always the simplest representation, particularly in the case of complex predicates. Note that a finite verb seems to be the signification of an incomplete predicate. So at 7.63 Diogenes Laërtius says that the verb  (He/she writes) signifies an incomplete predicate (see the next section for further discussion of incomplete predicates).
(He/she writes) signifies an incomplete predicate (see the next section for further discussion of incomplete predicates).
86Mates [1953], 16–17; Kneale & Kneale [1962a], 144, 148; Watson [1966], 47–49; Graeser [1978b], 91; Sandbach [1975], 96.
87For example Mates [1953, p. 19]; Gould [1970, 70n1].
88Note that ‘effatum’, ‘enuntiatum’, and ‘dictum’ are Latin translations of  (cf. Cicero acad. 2.95 [effatum]; de fato 19.28 [enuntiatum = enuntiatio]).
(cf. Cicero acad. 2.95 [effatum]; de fato 19.28 [enuntiatum = enuntiatio]).
89These conclusions are discussed both by Frede [1987b, p. 349] and by Long [1971, p. 105]; however, neither author agrees with them.
90cf. Rist [1969a], 159; Long [1971], 105; Frede [1987b], 347. For citations from the sources see SVF 2.449, 463; DL 7.134; Simplicius in cat. 209.10.
91Rist outlines this difficulty as follows:
Our problem is why the Stoics put these common qualities into the category of quality, that is, of material objects … rather than with other incorporeals like time, void, place and the lekta. The answer to this is not easy to find [Rist, 1969a, pp. 165–66].
It should be noted that the purported textual evidence adduced by Rist and others to show that common qualities are not corporeal, would not show, even if it were correct, that common qualities were classed with the incorporeals such as lekta. What would be shown, as we soon shall see, is that common qualities had no ontological status at all.
92Much of what we write on the notion of a syntax of lekta is drawn from two papers by Michael Frede, both of which appear in his Essays in Ancient Philosophy. These are: “The Principles of Stoic Grammar” (especially 323–32) and “The Origins of Traditional Grammar” (especially 353–57).
93These titles have been numbered as they are since they are second and third in a sequence of four to which we shall refer.
94A Stoic also known as Diogenes of Seleucia, but called The Babylonian because Seleucia is near Babylon (cf. DL 6.81).
95Andreas Graeser, for instance, asserts that “in Stoic semantics [the verb sēmainein] stands exclusively for a relation that holds between the linguistic sign and its sense” [Graeser, 1978b, p. 81]. Since he also takes sēmainomenon to be synonymous with lekton [Graeser, 1978b, p. 87], it is apparent that he would give preference to this reading. The Kneales, who argue that the Stoics “deliberately identified sēmainomena with lekta,” are of the opinion that “what is meant” is probably the most literal translation of lekton” [Kneale and Kneale, 1962a, p. 140]. According to Boche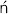 ski, “the λε
ski, “the λε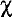 τóν corresponded to the intension or connotation of the words” [Boche
τóν corresponded to the intension or connotation of the words” [Boche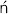 ski, 1963, p. 84].
ski, 1963, p. 84].
96For additional citations from the primary sources, see SVF 2.329–35; AM 10.234; AM 11.224; PH 2.223-25; Plutarch adv. colot. 1116b-c. For commentary on these notions by modern writers, see Long and Sedley [1990, pp. 162–66]; Long [1971, pp. 88–90]; Rist [1969a, pp. 152–54]; Watson [1966, pp. 92–96]; Sandbach [1975, p. 92].
97cf. Plutarch, adv. colot. 1116B.
98 (Plutarch comm. not. 1073e). cf. Aëtius plac. 1.11.4, 4.20 (SVF 2.340, 387); Stobaeus eclog. 1.336, 338; Cicero acad. 1.39; Seneca epist. 117.2, 106.4; DL 7.56.
(Plutarch comm. not. 1073e). cf. Aëtius plac. 1.11.4, 4.20 (SVF 2.340, 387); Stobaeus eclog. 1.336, 338; Cicero acad. 1.39; Seneca epist. 117.2, 106.4; DL 7.56.
99Note that the Stoic use of the expression ‘universal Man’ is as a synonym for the expression ‘the concept “Man”’ We should remind ourselves that such items belong to an ontological category different from that to which the common quality ‘Man’ belongs, the latter, according to the Stoics, being something corporeal.
10076 Cleomedes SVF 2.541; Proclus SVF 2.521; Stobaeus eclog. 1.106.19.
101For example, Sextus Empiricus: AM 8.10; 12; 73; 74; Diogenes Laërtius: 7.65; 68.
102Martha Kneale observes that “if we take  )102 here as equivalent to
)102 here as equivalent to 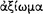 then Sextus is defining the truth of presentations in terms of the truth of axiōmata” [Kneale and Kneale, 1962a, p. 150]. Although admitting that “this identification is plausible” [Kneale and Kneale, 1962a, p. 150], she is hesitant however to apply it, her reason being that the term ‘katēgoria’ appears only this once in Sextus’ writings, and its meaning is nowhere mentioned by him [Kneale and Kneale, 1962a, p. 150]. But it seems that many commentators think that this identification is more than plausible (e.g., Mates [1953, p. 34]; Long and Sedley [1990, 1.240]; Long [1971, p. 92]; Graeser [1978a, p. 201]).
then Sextus is defining the truth of presentations in terms of the truth of axiōmata” [Kneale and Kneale, 1962a, p. 150]. Although admitting that “this identification is plausible” [Kneale and Kneale, 1962a, p. 150], she is hesitant however to apply it, her reason being that the term ‘katēgoria’ appears only this once in Sextus’ writings, and its meaning is nowhere mentioned by him [Kneale and Kneale, 1962a, p. 150]. But it seems that many commentators think that this identification is more than plausible (e.g., Mates [1953, p. 34]; Long and Sedley [1990, 1.240]; Long [1971, p. 92]; Graeser [1978a, p. 201]).
104examples of axiōmata which Sextus cites at AM 8.93–98 and which Diogenes Laërtius cites at 7.68-70 are all clearly signified by declarative sentences. The texts at AM 8.71 and DL 65–66 also indicate that axiōmata are signified by declarative sentences.
105Here we are translating “τò λεγòμενoν’, which literally means ‘that which is spoken’ as ‘lekton’. A.A. Long has said that “in sense lekton can hardly be distinguished from τò λεγóμενoν”) ([Long, 1971], 107n13).
106Graeser’s remarks on these differences between axiōmata and propositions [Graeser, 1978b, pp. 94–95].
107We have followed the translations of Long and Sedley ([1990], 1.205) to render these terms.
108Sextus Empiricus’ account of complex axiōmata is not so compact or concise as that of Diogenes, but it is perhaps more philosophically interesting. He talks about the conditional axiŌma at AM 8.108-12, and about the conjunctive axiōma at AM 8.124-29, but he does not seem to have an account of the disjunctive axiōma which is comparable to that of Diogenes.
109This doxography is attested by Chrysippus in his Dialectics and by Diogenes the Babylonian in his Art of Dialectic (DL 7.71).
110 .
.
111In the Theatetus Socrates says that “when the mind is thinking, it is simply talking to itself, asking questions and answering them, and saying yes or no” (190a). In a similar vein in the Sophist, the Eliatic Stranger says that “thinking and discourse are the same thing, except that what we call thinking is precisely, the inward dialogue carried on by the mind with itself without spoken sound” (263a). No doubt there are problems with the view that all thinking is like internal discourse; it seems, however, that something of this tradition was carried on by the Stoics, for according to Sextus Empiricus, they held that “it is not with respect to uttered speech 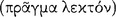 that man differs from the irrational animals (for crows and jays and parrots utter articulate sounds), but with respect to internal discourse
that man differs from the irrational animals (for crows and jays and parrots utter articulate sounds), but with respect to internal discourse 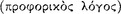 (AM 8.275). And according to Galen, the Stoics define the mental process which provides the means of converting sensory data to knowledge, that is, the process by means of which “we understand consequence and conflict, in which separation, synthesis, analysis and demonstration are involved” (SVF 2.135), as ‘internal discourse’ (endiathetos logos).
(AM 8.275). And according to Galen, the Stoics define the mental process which provides the means of converting sensory data to knowledge, that is, the process by means of which “we understand consequence and conflict, in which separation, synthesis, analysis and demonstration are involved” (SVF 2.135), as ‘internal discourse’ (endiathetos logos).
112Sextus notes that reversing the normal sentence order does not affect this rule. Thus, in each of the examples ‘If it is day, it is light’ and ‘It is light, if it is day’, the antecedent is the axiōma signified by the sentence ‘It is day’ (AM 8.110).
113At AM 8.104, Sextus implies that this definition was reserved only for the ‘indicative sign’
114The adjective ‘μεταβτι óζ’ is derived from the noun ‘μετιβασιζ’, the basic meaning of which is ‘a moving over’ or ‘a shifting’ or ‘a change of position’ (Liddell and Scott). This etymology is reflected in the use of the adjective in this context which seems to suggest the transition from one conception to another by the process of inferential or discursive thought
óζ’ is derived from the noun ‘μετιβασιζ’, the basic meaning of which is ‘a moving over’ or ‘a shifting’ or ‘a change of position’ (Liddell and Scott). This etymology is reflected in the use of the adjective in this context which seems to suggest the transition from one conception to another by the process of inferential or discursive thought
115See Section 4.2 for both of these references
116We are making two assumptions here which we have not made explicit but which seem plausible. These are (1) that a basic notion of causality would be recognised by the Stoics as a preconception 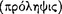 acquired by most people, and (2) that the Stoics would recognise the examples of commemorative signs listed above as cases in which there is a causal connection between the sign and what it indicates
acquired by most people, and (2) that the Stoics would recognise the examples of commemorative signs listed above as cases in which there is a causal connection between the sign and what it indicates
117The arrow will turn out to be the item at the level of lekta which is signified by the connective ‘if ‘
118cf. DL 7.78 where this conditional is featured as the major premiss of the argument ‘If Dion is walking, Dion is moving; but Dion is walking; therefore, Dion is moving’
119The arrow is the item at the level of lekta which is signified by the connective ‘if’ 
120Stoics characterise the relationship between these situations by saying that they ‘conflict’  with one another
with one another
121cf. Mueller [1978, p. 20]; Kneale and Kneale [1962a, p. 161]; Long and Sedley [1990, 1.211]. Note that the relationship between these situations could not be signified by the Stoic disjunction, since that connective indicates that exactly one of the disjuncts is true. But evidently it need not be the case that Dion be either at Athens or on the Isthmus.
122Zeller [1962, 119n2]; Mates [1953, p. 69] attests that both Prantl and Zeller held this view, and Kieffer [1964, p. 66] confirms that Prantl held it. He cites Volume 1, page 386 of Prantl’s Geschichte der Logik im Abendlande (Graz, 1955). (Photographic reprint of Leipzig, 1855, edition).
123Both Mates [1953, p. 69] and Kieffer [1964, p. 8] cite Boche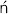 ski’s La Logique de Thu)opraste (Collectanea Friburgensia, N.S. fasc. xxxvii) (Fribourg: 1947). Mates cites pages 116–17 and chapter 7, note 5; while Kieffer cites page 103 ff.
ski’s La Logique de Thu)opraste (Collectanea Friburgensia, N.S. fasc. xxxvii) (Fribourg: 1947). Mates cites pages 116–17 and chapter 7, note 5; while Kieffer cites page 103 ff.
124Kieffer writes that Prantl “by a strained interpretation of certain passages in the later commentators on Aristotle … reached the unjustified conclusion that the traditional hypothetical syllogisms were the discovery or invention of Theoprastus” ([Kieffer, 1964], 66). It seems clear that Mates ([1953], 69) also rejects Prantl’s conclusion.
125This is the wording of Alexander of Aphrodisias (in an. pr. 389.31).
126See Mates [1953, p. 68] (Table II) for an extensive documentation of the evidence for the indemonstrables. Strictly speaking, I should be talking about the ‘conditional axiōma’, the ‘disjunctive axiōma’, and the ‘conjunctive axiōma’, but for the most part we shall refer to ‘conditionals’, ‘disjunctions,’ and ‘conjunctions’ in the sequel.
127This reference to the ‘dialecticians’ would seem to be one in which the term should be taken in the general sense of ‘one who practices dialectic’ or ‘logician’, rather than in the sense of denoting a member of the Dialectical School (cf. footnote 20, page 408).
128In his translation of Sextus Empiricus, R.G. Bury renders  as ‘hypothetical syllogism’; however, as Mates points out ([Mates, 1953], 43), this term always denotes an ‘if …, then … ’ proposition in the examples given by ancient commentators, never an argument or inference-schema.
as ‘hypothetical syllogism’; however, as Mates points out ([Mates, 1953], 43), this term always denotes an ‘if …, then … ’ proposition in the examples given by ancient commentators, never an argument or inference-schema.
The Stoics seem to use 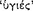 (sound) and
(sound) and 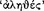 (true) interchangeably in these contexts. We shall argue in the sequel that we should understand ‘true’ in the sense of ‘sound’ when it so occurs, rather than the other way around.
(true) interchangeably in these contexts. We shall argue in the sequel that we should understand ‘true’ in the sense of ‘sound’ when it so occurs, rather than the other way around.
129The Greek is  . This term is often translated as ‘proposition’ but we have not committed ourselves to so translate it (see page 423). It would seem better for us to transliterate the term, since at least part of our thesis involves the question of its meaning.
. This term is often translated as ‘proposition’ but we have not committed ourselves to so translate it (see page 423). It would seem better for us to transliterate the term, since at least part of our thesis involves the question of its meaning.
130Similarly, Diogenes Laërtius relates that on the Stoics account, the axiöma ‘It is day’ is true  just in case it really is day, otherwise, it is false
just in case it really is day, otherwise, it is false  (DL 7.65).
(DL 7.65).
131According to the classification of invalid arguments reported by Sextus at PH 2.146 and AM 8.429, Gellius’ argument in its unaltered form is also an example of an argument invalid because of deficiency.
132 .
.
133In the passage AM 8.112–17 Sextus gives a more detailed account of the differences between Diodorus and Philo, but he does not include any mention of the other competing views.
134In his glossary, Mates points out the distinction between 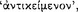 , which means the contradictory of a proposition, and
, which means the contradictory of a proposition, and  , which means a proposition with ‘not’ prefixed to it. His example makes the distinction clear: “The propositions
, which means a proposition with ‘not’ prefixed to it. His example makes the distinction clear: “The propositions  [It is day] and
[It is day] and  [It is not day] are both
[It is not day] are both  with respect to one another, but only the latter is
with respect to one another, but only the latter is  ([Mατεζ, 1953], 133).
([Mατεζ, 1953], 133).
135The name has been adopted in certain modern interpretations such as those of Storrs McCall (e.g., in Anderson and Belnap [c1975-, pp. 434–52] and in McCall [1966].
136In his discussions of conditionals, Sextus seems for the most part to use 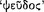 to contrast with both
to contrast with both  and
and 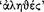 (cf. AM 8.112–17 and PH 2.110–12). On the other hand, he also uses
(cf. AM 8.112–17 and PH 2.110–12). On the other hand, he also uses  for this purpose (cf. PH 2.105, 111), but this latter term seems to be used more extensively to mean ‘invalid’ or ‘faulty’ in connection with arguments (PH 2.150; AM 8.433) or argument schemata (PH 2.146, 147; AM 8.429, 432).
for this purpose (cf. PH 2.105, 111), but this latter term seems to be used more extensively to mean ‘invalid’ or ‘faulty’ in connection with arguments (PH 2.150; AM 8.433) or argument schemata (PH 2.146, 147; AM 8.429, 432).
137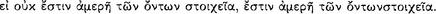 .
.
Bury translates this as: ‘If atomic elements of things do not exist, atomic elements exist’, whereas Martha Hurst has a reading similar to ours [Hurst, 1935, p. 489]. Mates appears to agree with Bury’s translation, and his argument for this reading is as follows: “[W]e are explicitly told that the denial of the consequent is not incompatible with the antecedent. Since the denial of the consequent is the antecedent, this implies that the antecedent is not incompatible with itself. But if the antecedent were the negation of an analytic statement, it would be incompatible with itself” [Mates, 1953, p. 50]. The problem with this argument is that Mates is assuming a ‘non-connexivist’ interpretation of ‘incompatible’. According to this view, any necessary proposition is incompatible with itself. But this is just the assumption that the connexivists wish to deny (cf. page 482).
It is perhaps worth mentioning that Hurst cites this example as evidence in her argument against a temporal reading of Diodorus’ definition of a sound conditional [Hurst, 1935, p. 489], the temporal interpretation being the one favoured by Mates. In doing so, however, we believe she errs in not taking seriously the possibility that this is a counter-example brought against the Diodorean criterion by the connexivists, and not necessarily an example which Diodorus would have put forward himself.
138Bury fails to translate the Greek word for ‘always’, thereby missing the point of the example.
139 . This account of the necessary is not specifically attributed to Chrysippus by Diogenes; however, as Mates points out, a passage of Plutarch (de Stoic repugn. 1055d-e) would seem to indicate that this view cited by Diogenes is that of Chrysippus.
. This account of the necessary is not specifically attributed to Chrysippus by Diogenes; however, as Mates points out, a passage of Plutarch (de Stoic repugn. 1055d-e) would seem to indicate that this view cited by Diogenes is that of Chrysippus.
Compare the view called ‘Stoic’ by Boethius (in de interp. 235): necessarium autem, quod cum verum sit falsam praedicationem nulla ratione suscipiat (The necessary is that which when it is true, by no account will admit of a false affirmation). According to Martha Kneale [1962a, p 123], this version “can safely be attributed to Chrysippus” since the context in which it occurs in Boethius is similar to that in which Cicero (de fato 12–20) contrasts the views on modality of Chrysippus and Diodorus.
140Another characteristic connexive property mentioned by McCall is ‘Boethius’ Thesis’, represented as: CCqrNCqNr ([McCall, 1966], 416). In De syllogismo hypothetico, Boethius presents an inference schema which McCall takes to require the assumption of the connexivist principle for a sound conditional. The schema is this: If p, then if q then r; if q then not-r; therefore, not-p [McCall, 1966, p. 415]. If we take Cpq and CpNq as connexivist conditionals, then p is in conflict with both Nq and NNq. Hence, it seems reasonable on connexivist grounds to say that Cpq and CpNq are in conflict, and by the connexivist definition for a sound conditional, we get CCqrNCqNr, i.e., Boethius’ Thesis. Presumably, then, Boethius’ argument proceeded as follows (cf. McCall [1966, p. 416]):
| (1) | p → (q → r) | Assumption |
| (2) | q → ¬r | Assumption |
| (3) | (q → r) → ¬(q → ¬r) | Boethius |
| (4) | ¬¬(q → ¬r) | 2 Double Negation |
| (5) | ¬(q → r) | 3,4 Modus Tollens |
| (6) | ¬p | 1,5 Modus Tollens |
141Commenting on Sextus’ statement that the inclusion definition would reject a conditional of the form ‘If p, then p’, Michael Frede says that “Sextus Empiricus himself makes it very clear his comment is merely his own interpretation of the definition” [Frede, 1974, p. 90].
142See pages 407 and 479 for references. Long and Sedley take it that the ‘cohesion’ criterion is the standard Stoic doctrine for a sound conditional; moreover, they think that “it probably had the approval of Chrysippus” [Long and Sedley, 1990, 1.211].
143Sextus claims not to reject altogether the existence of signs, but only those signs which the ‘dogmatic philosophers’ and ‘logical physicians’ call ‘indicative’  (AM 8.156). On the other hand, those signs called ‘commemorative’
(AM 8.156). On the other hand, those signs called ‘commemorative’ 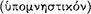 are accepted by Sextus, since he takes them to be among the ‘common preconceptions of mankind’
are accepted by Sextus, since he takes them to be among the ‘common preconceptions of mankind’  (8.157). Thus, Sextus is apparently attacking the conception as well as the Stoic theory of indicative signs in these passages, but not the Stoic theory of commemorative signs.
(8.157). Thus, Sextus is apparently attacking the conception as well as the Stoic theory of indicative signs in these passages, but not the Stoic theory of commemorative signs.
144Note that on each of the four accounts, not just on the Philonian definition, a conditional with a true antecedent and false consequent will not be sound; moreover, on each account a sound conditional may have either a true antecedent and true consequent, or a false antecedent and false consequent, or a false antecedent and true consequent.
145i.e., an argument with the schema ‘If p, then q; p; therefore q.
146We are not unaware that Diogenes’ definition refers to a true  conditional, not a sound
conditional, not a sound  conditional. We have already argued, however, that in these contexts both
conditional. We have already argued, however, that in these contexts both 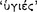 and
and  should be understood as ‘proper’ or ‘genuine’ (See page 477).
should be understood as ‘proper’ or ‘genuine’ (See page 477).
147Consider, for example, Gould’s comment that “it may be the case that [the] distinction [between empirical impossibility and logical impossibility] had not, as a matter of fact, been discerned in the Hellenistic age” [Gould, 1970, p. 81].
148See, for example, E.J. Nelson [1930, esp. pp. 440–43]; and R.M. Stopper, [1983, pp. 281–86].
149M.R. Stopper quoting from a paper by Mauro Nasti de Vincenti (“Logica scettica e implicazione stoica,” in Lo scetticismo antico, ed. G. Giannantoni, Naples, 1981.), writes that “P” conflicts with ‘Q’ just in case ‘P’ and ‘Q’ are not compossible,” and he symbolises this definition thus [Stopper, 1983, p. 284]:
He goes on to say that (A3) has “some strange consequences.” For example, “any impossible proposition is incompossible with any other proposition whatsoever” [Stopper, 1983, p. 285].
150e.g., AM 8.415; PH 2.113, 137. See Mates ([1953], 74–77) for a discussion of this principle. As Mates points out, this principle need not be taken as defining the Stoic conditional, but merely as a characterising a property common to all valid arguments.
151In some places (e.g., PH 2.137, 146) Sextus uses 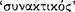 and
and 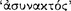 for ‘conclusive’ and ‘inconclusive’ (or ‘valid’ and ‘invalid’), whereas at other places (e.g., AM 8.429) he uses
for ‘conclusive’ and ‘inconclusive’ (or ‘valid’ and ‘invalid’), whereas at other places (e.g., AM 8.429) he uses 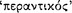 and
and 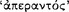 . Hence, as Mates indicates in his glossary [Mates, 1953, pp. 132–36], these terms appear to be interchangeable.
. Hence, as Mates indicates in his glossary [Mates, 1953, pp. 132–36], these terms appear to be interchangeable.
152 .
.
153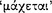
The question concerning the interpretation of the Greek term 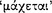 , which we have rendered as ‘conflicts’, has already been discussed (see page 489). We have argued that the notion of conflict which the Stoics had in mind requires some degree of common content between the axiōmata in this relationship.
, which we have rendered as ‘conflicts’, has already been discussed (see page 489). We have argued that the notion of conflict which the Stoics had in mind requires some degree of common content between the axiōmata in this relationship.
154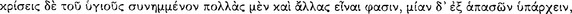
 (AM 8. 245).
(AM 8. 245).
155It should be noted here that although  would normally be classed as a demonstrative pronoun, it seems evident that in constructions such as this where it serves as a relative pronoun with anaphoric reference to an indefinite pronoun, it must be taken as an indefinite relative pronoun.
would normally be classed as a demonstrative pronoun, it seems evident that in constructions such as this where it serves as a relative pronoun with anaphoric reference to an indefinite pronoun, it must be taken as an indefinite relative pronoun.
156Mates has pointed out that “nowhere in the rather elaborate classification [of propositions] is any provision made for universal affirmative propositions, that is, for propositions beginning with ‘all’” [Mates, 1953, p. 32].
157Topica, 14.56–7. Reliqui dialecticorum modi plures sunt, qui ex disiunctionibus constant: aut hoc aut illud; hoc autem; non igitur illud. Itemque: aut hoc aut illud; non autem hoc; illud igitur. Quae conclusiones idcirco ratae sunt quod in disiunctione plusuno verum esse non potest.
158Noctes Atticae, 16.8. Est item aliud, quod Graeci 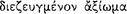 nos ‘disiunctum’ dicimus. Id huiuscemodi est: ‘aut malum est voluptas aut bonum neque malum est’. Omnia autem, quae disiunguntur, pugnantia esse inter sese oportet, eorumque opposita, quae
nos ‘disiunctum’ dicimus. Id huiuscemodi est: ‘aut malum est voluptas aut bonum neque malum est’. Omnia autem, quae disiunguntur, pugnantia esse inter sese oportet, eorumque opposita, quae  Graeci dicunt, ea quoque ipsa inter se adversa esse. Ex omnibus, quae disiunguntur, unum esse verum debet, falsa cetera.
Graeci dicunt, ea quoque ipsa inter se adversa esse. Ex omnibus, quae disiunguntur, unum esse verum debet, falsa cetera.
159Inst. Log., 5.1. 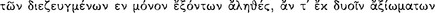
 . (The translation is that of Kieffer [1964].)
. (The translation is that of Kieffer [1964].)
160PH 2.191. 
 .
.
162For a detailed authoritative discussion, see Denniston [1954].
163The Kneales are a notable exception, and offer a plausible and detailed alternative account. Boche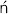 ski has remarked (in conversation) that to ask Cicero about logic is about as sensible as to enquire of Sartre about the writings of Carnap. Calvin Normore has offered that the error may be imputed to Cicero’s well known insomnia. Both may well have some bearing.
ski has remarked (in conversation) that to ask Cicero about logic is about as sensible as to enquire of Sartre about the writings of Carnap. Calvin Normore has offered that the error may be imputed to Cicero’s well known insomnia. Both may well have some bearing.
164Particularly bearing in mind that the account in the Topica is a reconstruction written, not in a library, but during a journey.
165Ammonius in an. pr. Praefatio xi. The translation is Mates’s [1953, p. 131].
166SE AM 8.434
167See [Barnes, 1985] for a discussion of the evidence suggesting that Theophrastus was one Peripatetic source.
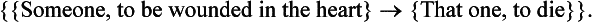

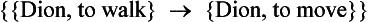
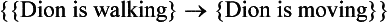


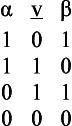






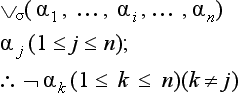
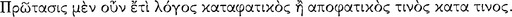
 (Prior Analytic 24a 16).
(Prior Analytic 24a 16). (46b 31).
(46b 31). (… every mortal animal is either footed or footless)
(… every mortal animal is either footed or footless) (Categories 12a 13).
(Categories 12a 13).
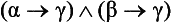
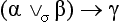



 (SE PH 8.191).
(SE PH 8.191).