6 Concluding Remarks
These concluding remarks are, strictly speaking, more of an apology for the narrow focus and relentlessly historical emphasis of this chapter, and for the tentative nature of its claims. To trace a set of logical discussions from fragments written in Abbasid times through to the introductory madrasa texts of the late thirteenth century entails finding a topic common to all the texts. That common topic, the syllogistic, is apt for study due to the existing scholarship. I further think (to repeat my introductory comments) that tracing such a common topic is worthwhile above all because it begins the process of delineating the framework of logical traditions which in turn determine the system that is the primary object of discussion and dispute for any given logician. The very first thing to do when setting out to study an Arabic logical work is to assign the work to its proper systematic context, that is, the texts it addresses and the methods by which it engages with those texts. I cannot say that Muslim scholars adhered to the traditions apparent in the syllogistic when they contributed to other areas of logic, but I think it is likely that they did, and that the historical account put forward in this chapter may serve provisionally for the study of other debates.
Here then is a summary of the points made in this chapter regarding the syllogistic traditions. The account differs most significantly from Rescher’s in speculating that Avicenna belonged to an existing tradition already fundamentally different from Alfarabi’s, and in rejecting his claims regarding a ‘Western’ school of logic [Rescher, 1964, chapters five and six].
Syllogistic traditions Alfarabi was the first truly independent logician writing in Arabic. We may discern three factors in his writings. Above all, he was a product of late Alexandrian Aristotelianism, and drew, however remotely, on the texts and techniques of that tradition. These he modified in response to the fact that he was a Muslim scholar working on a foreign and pagan intellectual tradition. Lastly, Alfarabi came to be conscious of how badly the Aristotelian corpus was served by the interpretations in the existing Alexandrian and Syriac works. This led Alfarabi to try to revive a true Aristotelianism after a period of rupture, which he did by writing commentaries on Aristotelian texts. Though we no longer have the commentary on the first part of the Prior Analytics, we can reconstruct his treatment of the conversion of contingent propositions from references in the works of Avicenna and Averroes. In this treatment, Alfarabi tried to let the Aristotelian text stand by finding an appropriate stratagem (in this case, a distinction prefiguring the Averroist distinction between reading a term per se or per accidens). Alfarabi in his moments of exegetical exertion was fairly dismissive of the ‘commentators’, presumably members of the Syriac tradition from which he distanced himself.
Avicenna had, broadly speaking, the same philosophical ancestry as Alfarabi, and claimed Alfarabi as his most eminent forebear after Aristotle. Avicenna’s prominence among logicians in Iran and further east roughly parallels that of Alfarabi among the Baghdad logicians. Many of his doctrines which seem idiosyncratic to us are not in the writings of the Baghdad scholars, and are presented as though they are already known to his readers. This procedure may indicate that he was simply modifying an existing tradition, different from that of Baghdad. In any event, Avicenna’s syllogistic differed radically from Alfarabi’s, and he set out some important points in his system by explicitly stating what was wrong with Alfarabi’s corresponding doctrine. The single most important factor determining these differences was the fact that whereas Alfarabi thought that the Aristotelian text would, with sufficient attention, yield a coherent system, Avicenna thought that he already knew the coherent system, and used it to identify obscure parts of the text. Alfarabi bent his system to the text, Avicenna bent the text to his system.
In his logical writings, Avicenna covered the same territory as Alfarabi’s Aristotelian commentaries. Avicenna did not go on, however, to deal to the same extent that Alfarabi had with the problems of relating logic to the Islamic disciplines. That strand in Alfarabi’s logical writings was taken up by various Andalusian logicians, and by Ġaz lī. Ġaz
lī. Ġaz lī prepared the ground for the institutional acceptance of logic, a Farabian task, but he did it by basing his formal treatment on the elementary section of Avicenna’s Philosophy for ‘Al
lī prepared the ground for the institutional acceptance of logic, a Farabian task, but he did it by basing his formal treatment on the elementary section of Avicenna’s Philosophy for ‘Al ’addawla. Ġaz
’addawla. Ġaz lī’s work on the syllogistic, however, was so superficial as to be negligible.
lī’s work on the syllogistic, however, was so superficial as to be negligible.
Ġaz lī is a special case, because he wrote primarily as a jurist and a theologian. But by his death in the twelfth century, two logical traditions had emerged, one Farabian, the other Avicennan. The finest representative of the Farabian tradition was the Andalusian Averroes, who in his syllogistic developed doctrines found in Alfarabi’s writings. In fact, Averroes tells us he took from Alfarabi the distinction between the per se and per accidens. But Averroes’ relation to Alfarabi is complex. As Averroes developed the incipient Aristotelianism of Alfarabi, he became increasingly less satisfied with the Farabian answers to exegetical problems, and sought more global solutions which gave every part of the Aristotelian text due weight. This is an extension of the Farabian attitude to the Aristotelian text, in which every position adopted is intrinsically defeasible in the face of a better stratagem. The other scholar to whom Averroes made constant reference, aside from Aristotle, is Avicenna: Avicenna had problematized the Aristotelian system, and thereby determined those points on which Averroes had to dwell longest.
lī is a special case, because he wrote primarily as a jurist and a theologian. But by his death in the twelfth century, two logical traditions had emerged, one Farabian, the other Avicennan. The finest representative of the Farabian tradition was the Andalusian Averroes, who in his syllogistic developed doctrines found in Alfarabi’s writings. In fact, Averroes tells us he took from Alfarabi the distinction between the per se and per accidens. But Averroes’ relation to Alfarabi is complex. As Averroes developed the incipient Aristotelianism of Alfarabi, he became increasingly less satisfied with the Farabian answers to exegetical problems, and sought more global solutions which gave every part of the Aristotelian text due weight. This is an extension of the Farabian attitude to the Aristotelian text, in which every position adopted is intrinsically defeasible in the face of a better stratagem. The other scholar to whom Averroes made constant reference, aside from Aristotle, is Avicenna: Avicenna had problematized the Aristotelian system, and thereby determined those points on which Averroes had to dwell longest.
The other logical tradition, the Avicennan, had by the early twelfth century at the latest come to identify problems and cruces in Avicenna’s syllogistic which were to occupy the tradition thereafter. Avicennan logicians ceased to consider anything other than the system Avicenna had used in judging Aristotle’s logic and, though referring to Avicenna generally as ‘the most eminent of the later scholars’, never treated his texts or doctrines as immune to criticism and modification. Some representatives of the tradition, such as R zī, were even fairly scathing about Avicenna’s expositions, though in the late thirteenth century others began to refer reverentially to Avicenna and find ways to explain away his logical errors. This did not, however, prevent them from modifying his logical system exactly the same way as the earlier Avicennan scholars.
zī, were even fairly scathing about Avicenna’s expositions, though in the late thirteenth century others began to refer reverentially to Avicenna and find ways to explain away his logical errors. This did not, however, prevent them from modifying his logical system exactly the same way as the earlier Avicennan scholars.
The twelfth century saw the clear delineation of the Farabian and Avicennan traditions, each of which paid attention to the other’s founder, but rarely to his epigones. The twelfth century also saw other writers referring to Alfarabi, Avicenna and Aristotle. These writers in some cases tended more to an Avicennan systematic, such as Abū-l-Barak t al-Baġd
t al-Baġd dī, in other cases, to a more Farabian, such as ‘Abdalla
dī, in other cases, to a more Farabian, such as ‘Abdalla īf al-Baġd
īf al-Baġd dī. At least in the case of the former, however, there is no evidence that his syllogistic was developed further by his students, and it really speaks past the interests of the mainstream Avicennan tradition. Neither scholar enjoyed a posterity. Even the Farabian tradition guttered, and after the middle of the thirteenth century, the Avicennan tradition had come to predominate in the Muslim world. The Farabian tradition had been weakened by its continued fixation on the non-Muslim Aristotle; although Avicenna worked in conversation with Aristotle and the later peripatetics, logicians after him worked directly on the system against which he had measured Aristotle.
dī. At least in the case of the former, however, there is no evidence that his syllogistic was developed further by his students, and it really speaks past the interests of the mainstream Avicennan tradition. Neither scholar enjoyed a posterity. Even the Farabian tradition guttered, and after the middle of the thirteenth century, the Avicennan tradition had come to predominate in the Muslim world. The Farabian tradition had been weakened by its continued fixation on the non-Muslim Aristotle; although Avicenna worked in conversation with Aristotle and the later peripatetics, logicians after him worked directly on the system against which he had measured Aristotle.
Avicenna was in one respect too successful in naturalizing the study of Aristotelian logic. Though the Averroist approach was intrinsically less stable and mired in a Greek past, it turned out to be transportable, because it spoke directly to the problematic of Latin writers after the coming of the logica moderna. Avicennan logics by contrast were only translated much later (see e.g. [Brockelmann, 1936-1949, Sup. vol. I, page 845]), and aroused no interest. The problem was that it was no longer obvious which parts of the Avicennan system were commensurable with the Aristotelian. It is a problem which still plagues the study of his logic, and research needs to be directed to clearing the ground preparatory to making such assessments.
The work ahead I hope that I have conveyed some sense of how many tasks await attention in the study of medieval Arabic logic. Even in the narrow range of material examined in this chapter, there is much to be done. There has been no sustained effort to reconstruct Alfarabi’s modal syllogistic (though Lameer has announced he is preparing such a study); there has been no plausible interpretation given of Avicenna’s modal syllogistic, and there are still many problems in understanding his hypothetical syllogistic; we have no overall picture of what Averroes was doing; and the other post-Avicennan logicians are, with two exceptions among writers on the syllogistic, largely uncharted territory. And this is in the syllogistic, one of the logical disciplines which has been relatively well treated in the scholarly literature. This is not to say that there are not valuable studies in the other logical disciplines; there are (see appendix three for lists of such work), but they suffer from even worse gaps in coverage.
Of the many, many logical issues left out of consideration in this chapter, one is particularly noticeable by its absence, and a few words are in order as to why. I have made no attempt to identify the modal notions which lie behind the syllogistic systems of the various authors. Averroes’ modal notions have been compared with the broader range of options explored in the middle ages [Knuuttila, 1982, pages 352–353], and a lengthy study has been made of Avicenna’s conception of the modalities [Bäck, 1992]. These are valuable contributions. As a matter of procedure, however, I think the preliminary task should be to lay out as precisely as possible the syntactic outline of any given system, and only then investigate its underlying conceptions of modality.
The most unfortunate consequence of concentrating on the syllogistic, however, is that it leads to minimizing consideration of how Islam influenced the constitution of logic in its realms. It has been noted in the course of this chapter how apologetic tendencies drove early logicians like Alfarabi to argue for logic’s utility for and complementarity with the Islamic disciplines of grammar, theology and jurisprudence, and how later theologians and jurists like Ġaz lī came to accept these arguments. But there are many more, and more complex, issues to take into account in studying the relation between Islam and logic. The great historical task is working out the precise clashes between the Islamic disciplines and philosophy which left the logical treatises as narrowly focussed as they are, and finding the genres which took over treatment of these previously logical topics. This is really the key point for future research, because as each book of the Organon gave way to a competing Islamic discipline (as for example topics gave way to
lī came to accept these arguments. But there are many more, and more complex, issues to take into account in studying the relation between Islam and logic. The great historical task is working out the precise clashes between the Islamic disciplines and philosophy which left the logical treatises as narrowly focussed as they are, and finding the genres which took over treatment of these previously logical topics. This is really the key point for future research, because as each book of the Organon gave way to a competing Islamic discipline (as for example topics gave way to  d
d b al-ba
b al-ba t, and rhetoric to ‘ilm al-ma‘
t, and rhetoric to ‘ilm al-ma‘ nī), aspects of the original Aristotelian discipline either transmuted or decomposed into other disciplines. And if ever we can appreciate those changes, we can speak not only of the contributions of Muslim scholars to logic, but also of the contributions of logic to Islamic culture.
nī), aspects of the original Aristotelian discipline either transmuted or decomposed into other disciplines. And if ever we can appreciate those changes, we can speak not only of the contributions of Muslim scholars to logic, but also of the contributions of logic to Islamic culture.
Acknowledgements
I have incurred a number of debts in writing this chapter, and it is a pleasant duty to acknowledge them here. Most of all, I am indebted to Dimitri Gutas, who kindly read and commented on an earlier version of this chapter. His suggestions have saved me from numerous mistakes and omissions. Henrik Lagerlund and Christopher Martin also read an earlier version of this chapter, and I am grateful to them for their suggestions. I regret that I was not able to deal comprehensively with a number of the points they raised, and can only hope that future research will make studies on Arabic logic more satisfying for those who work on Western logic. There are a number of other people who, though not having read the chapter, have helped in its construction in one way or another. They did so generally in the course of looking at earlier attempts I have made to study Arabic logic, and making me aware of relevant manuscripts, studies I had overlooked, or various mistaken conceptions. So, thanks to: Ahmad Hasnawi, Dominic Hyde, James Montgomery, Ahmed al-Rahim, and David Reisman. Lastly, as with all who work in the field of Arabic logic, I owe a vote of thanks to Nicholas Rescher, both for his pioneering work, and for his generous words of encouragement.
A Avicenna’s Modals
Modalized propositions are represented (from left to right) by a modal operator, followed by the predicate, the subject, and a superscripted letter indicating quantity and quality. The modal operators are as follows: X stands for an absolute (mu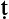 laqa) proposition, A for a perpetual (d
laqa) proposition, A for a perpetual (d ’ima), M for a possible (mumkina) and L for a necessary (
’ima), M for a possible (mumkina) and L for a necessary (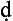 arūriyya). The default reading is d
arūriyya). The default reading is d tī; wa
tī; wa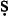 fī readings are indicated by a superscripted w to the right of the modal operator. Premise-sets are given in order of major, minor and conclusion (if applicable). All references to Pointers may be checked in [Inati, 1981], which gives the Arabic page numbers in the margin.
fī readings are indicated by a superscripted w to the right of the modal operator. Premise-sets are given in order of major, minor and conclusion (if applicable). All references to Pointers may be checked in [Inati, 1981], which gives the Arabic page numbers in the margin.
Purely d tī premises
tī premises
X1A contradictories See [Avicenna, 19712, pages 307–308].
(Square for M1L is isomorphic; see [Avicenna, 19712, pages 318–319].)
X2A contradictories See [Avicenna, 19712, pages 309–311]
(Square for M2L is isomorphic; see [Avicenna, 19712, pages 319–320].)
Perfect first figure mixes XXX, XLX, LXL, LLL, MMM, MXM, MLM. Proofs for some second-figure moods also assume AXA and ALA. See [Avicenna, 19712, pages 387–397].
X conversions X e-conversion fails. X1 a- and i-propositions convert as X1 i-propositions. X2 a- and i-propositions convert as X1 i-propositions. See [Avicenna, 19712, pages 321–333]
Substituting M1 for X1 and M2 for X2 gives all M conversions; see [Avicenna, 19712, pages 338–340]
L conversions L e-proposition converts as L e-proposition. L a- and i-propositions convert as M i-propositions. See [Avicenna, 19712, pages 334–337]
Further development In the first figure, there are two imperfect mixes: LML, XMM. See [Avicenna, 19712, pages 391–395].
In the second figure, the following are proved: LLL, XLL, LXL, MLL, LML. Premise pairs XX, MM, XM and MX all fail to produce. See [Avicenna, 19712, pages 403–407]
In the third figure, the following are proved: XXX, LLL, LXL, XLX, MMM, XMM, MXM, LML, MLM. See [Avicenna, 19712, pages 423–426]
Wa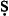 fī premises
fī premises
Avicenna introduces the wa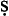 fī as one of his stratagems (along with the temporal) to find a proposition which will have a contradictory and a converse “in its own kind”. (The temporal is only considered for contradiction and conversion, and for nothing else.) He takes the wa
fī as one of his stratagems (along with the temporal) to find a proposition which will have a contradictory and a converse “in its own kind”. (The temporal is only considered for contradiction and conversion, and for nothing else.) He takes the wa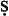 fī e-proposition (say) to convert as a wa
fī e-proposition (say) to convert as a wa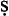 fī e-proposition, and to be contradicted by a wa
fī e-proposition, and to be contradicted by a wa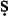 fī i-proposition. He makes no mention of the temporality being different between the contradictories, and refers to these wa
fī i-proposition. He makes no mention of the temporality being different between the contradictories, and refers to these wa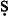 fī propositions as ‘absolutes’. Pure wa
fī propositions as ‘absolutes’. Pure wa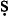 fī premises will produce all fourteen moods in the three figures.
fī premises will produce all fourteen moods in the three figures.
In Pointers, Avicenna also investigates d tī-wa
tī-wa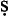 fī mixes, proceeding from Barbara LwLL.
fī mixes, proceeding from Barbara LwLL.
If the major is absolute, and the time of its assertion is as long as the subject remains described by whatever it is described by, then the conclusion will be necessary, because J is B always, and it has been posited that B, as long as it is B, is A; so J is always A—so here the conclusion is necessary and the major absolute. [Avicenna, 13312 A.H., pages 57–58]
B Later Modal Logic
There is no purely d tī logic among the later logicians, in that d
tī logic among the later logicians, in that d tī premises in some cases convert as wa
tī premises in some cases convert as wa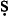 fī propositions. XA contradictories are all as in Avicenna, and are still isomorphic with the tables for ML propositions. Perfect first-figure mixes differ most significantly in that all syllogisms with possible minors fail. X conversions are the same as according to Avicenna, but M propositions all fail to convert. L conversions are all different; an L e-proposition converts as A e-proposition, and L a- and i-propositions convert as Aw i-propositions. Temporals are treated extensively, but none matches Avicenna’s use, nor do they work as assertorics.
fī propositions. XA contradictories are all as in Avicenna, and are still isomorphic with the tables for ML propositions. Perfect first-figure mixes differ most significantly in that all syllogisms with possible minors fail. X conversions are the same as according to Avicenna, but M propositions all fail to convert. L conversions are all different; an L e-proposition converts as A e-proposition, and L a- and i-propositions convert as Aw i-propositions. Temporals are treated extensively, but none matches Avicenna’s use, nor do they work as assertorics.
The wa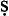 fī propositions are differentiated fully as to modality and temporality.
fī propositions are differentiated fully as to modality and temporality.
Absolute wa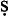 fī conversions Awbje converts to Awjbe; Awbja and Awbji convert to Xwjbi.
fī conversions Awbje converts to Awjbe; Awbja and Awbji convert to Xwjbi.
Syllogisms The rule for productivity in the first figure is given as follows; note that it includes the wa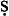 fī propositions:
fī propositions:
(1) The minor premise must be one of the seventeen actuals.
(2) If the major is not one of (
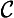 ), (∀
), (∀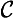 ), (
), (
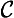 & ∼ ∀
& ∼ ∀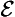 ), then the mode of the conclusion is that of the major.
), then the mode of the conclusion is that of the major.
(3) If the major is one of these four, then the mode of the conclusion is like that of the minor except that
(a) the restriction of the conclusion is same as the restriction of the major [and]
(b) the conclusion is necessitated if and only if both the minor and the major are.
(4) All other moods are non-productive. [Rescher and vander Nat, 1974, page 36]
Rescher’s semantics
I give here the names of the propositions, with examples and symbolic rendition, due to Rescher and vander Nat. It may prove a helpful reference for the propositions referred to throughout the text. Note that we cannot be sure that all Avicennan logicians meant the same thing by a given proposition. It is certain that Avicenna did not mean his propositions to be taken this way.
Rescher and vander Nat begin their representation by putting forward Rt as the basic operator for realization-at-time-t (which is described more fully in N. Rescher and A. Urquhart Temporal logic (New York and Vienna, 1971) at pages 31–32), and then use it to make the following abbreviations:
They go on to say:
In our symbolizations of modal propositions, we shall systematically suppress the temporality condition (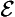 ) relation to the existence of the subject.
) relation to the existence of the subject.
Concerning the symbolic rendition of modes, we take notice of the following points. First, in adopting the symbolic machinery we have, we assume that all the usual quantificational and modal rules hold. Secondly, in the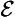 -modes the existence condition has been suppressed; fully stated, (
-modes the existence condition has been suppressed; fully stated, (
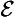 ) (All A is B), for example, would be (∀x)[(∃t)RtAx ⊃ (∀t)
) (All A is B), for example, would be (∀x)[(∃t)RtAx ⊃ (∀t) Rt(Ax ⊃ Bx)]. Thirdly, the modes
Rt(Ax ⊃ Bx)]. Thirdly, the modes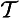 and
and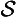 are special time-instantiations, with regard to the existence of the subject, and accordingly, we here use ‘
are special time-instantiations, with regard to the existence of the subject, and accordingly, we here use ‘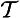 ’ and ‘
’ and ‘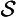 ’ as time-constants. [Rescher and vander Nat, 1974, page 32]
’ as time-constants. [Rescher and vander Nat, 1974, page 32]
With these preliminaries in hand, they then go on to offer symbolic renditions of the various a-propositions as presented in a late text [Širw nī,] as follows ([Street, 2000] gives all Arabic terms used to present and define these propositions, and in the order here presented, though note that the translation there of wa
nī,] as follows ([Street, 2000] gives all Arabic terms used to present and define these propositions, and in the order here presented, though note that the translation there of wa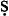 fī as ‘composite’ is wrong, and I would now adopt the Sprenger/Rescher terms for the propositions):
fī as ‘composite’ is wrong, and I would now adopt the Sprenger/Rescher terms for the propositions):
The propositions
All men are rational of necessity (as long as they exist).
2. Lw: General conditional (
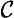 ):
):
All writers move their fingers of necessity as long as they write.
The moon is eclipsed of necessity at the time when the earth is between it and the sun.
All men breathe of necessity at some times.
All men are rational perpetually (as long as they exist).
6. Aw: General conventional (∀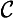 ):
):
All writers move as long as they write.
7. Xw: Absolute continuing (∃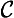 ):
):
All writers move while they are writing.
All writers move at the time they are writing.
All men breathe at certain times.
All men breathe (at some times).
All writers move with a possibility while they are writing.
The moon is eclipsed with a possibility at the time when the earth is between it and the sun.
All writers move with a possibility (at some time).
All men breathe with a possibility at all times.
15. Non-perpetual necessary (
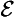 & ∼ ∀
& ∼ ∀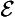 ):
):
16. Special conditional (
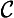 & ∼ ∀
& ∼ ∀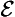 ):
):
19. Non-perpetual perpetual (∀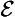 & ∼ ∀
& ∼ ∀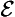 ):
):
20. Special conventional (∀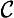 & ∼ ∀
& ∼ ∀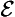 ):
):
21. Non-perpetual continuing absolute (∃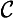 & ∼ ∀
& ∼ ∀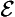 ):
):
22. Non-perpetual temporal absolute (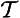 & ∼ ∀
& ∼ ∀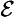 ):
):
23. Non-perpetual spread absolute (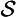 & ∼ ∀
& ∼ ∀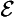 ):
):
24. X2: Non-perpetual existential (∃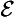 & ∼ ∀
& ∼ ∀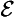 ):
):
25. Non-necessary existential (∃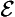 & ∼
& ∼ 
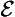 ):
):
C Bibliographical Notes
The best general introduction to the history of Arabic logic is still, sadly (given its age), [Rescher, 1964]. All of the individual logicians listed in its concluding register demand serious further study.
General bibliographical resources The best place to start for a comprehensive list of logical studies is now [Daiber, 1999], updated against Index Islamicus and Bulletin de philosophie médiévale. The bibliographies of major medieval scholars are listed in [Daiber, 1999], but note on Avicenna especially [Janssens, 1991]. A new bibliography covering the articles, books and editions of more recent years is under preparation.
Terminology There is as yet no sure guide to the technical terms used by logicians writing in Arabic; [Jabre et al., 1996] is extremely helpful, though has some limitations, especially for terms relating to the modal syllogistic. [Endress and Gutas, 1992–] will ultimately provide the most important materials for a complete lexicon. Each sub-discipline within logic has its own set of technical terms. The following works include valuable glossaries: [Black, 1990; Shehaby, 1973b; Zimmermann, 1981]. [Street, 2000] is wrong in translating wa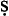 fī as ‘composite’, but still gives important references that need to be worked into any putative future lexicon for post-Avicennan usage. [Street,] presents the consecrated phrases by which logicians put forward propositions, proofs and so forth. Individual logicians occasionally have contingent or idiosyncratic usage. Thus especially the early logicians tend to change terminology fairly readily [Lameer, 1994]. The išr
fī as ‘composite’, but still gives important references that need to be worked into any putative future lexicon for post-Avicennan usage. [Street,] presents the consecrated phrases by which logicians put forward propositions, proofs and so forth. Individual logicians occasionally have contingent or idiosyncratic usage. Thus especially the early logicians tend to change terminology fairly readily [Lameer, 1994]. The išr qī logicians (who worked in the tradition founded by the twelfth-century logician and metaphysician, Suhrawardī) had their own terms, a number of which are decoded in [Ziai, 1990].
qī logicians (who worked in the tradition founded by the twelfth-century logician and metaphysician, Suhrawardī) had their own terms, a number of which are decoded in [Ziai, 1990].
Translation movement, and genres The translation of each work within the Organon is treated in [Goulet, 1989–], though note the following important works which have come out since its publication: [Black, 1991] for On Interpretation, [Hugonnard-Roche, 1999] for demonstration, and [Aouad and Rashed, 1999] for the rhetoric.
The genres in which the logicians wrote have been studied in [Gutas, 1993], but this study really stops at the fourteenth century, and many genres which should properly should be thought logical have yet to be examined.
Short treatments (as for example on the heap and the liar paradox) have yet even to be listed as they occur through the literature.
Leiden Afnan, S., Philosophical terminology in Arabic and Persian, 1964.
Beirut Alexander, FT n’ik s al-muqaddam
s al-muqaddam t. 1971:55–80.
t. 1971:55–80.
Ankara Alfarabi, Kit b al-Qiy
b al-Qiy s as-saġīr. Türker, M., eds. Revue de la Faculté de Langues, d´Histoire, et de Géographic de L’Université d’Ankara. 1958:214–286.
s as-saġīr. Türker, M., eds. Revue de la Faculté de Langues, d´Histoire, et de Géographic de L’Université d’Ankara. 1958:214–286.
Beirut Alfarabi, al-Mantiq ‘inda l-F r
r bī: Kit al-Burh
bī: Kit al-Burh n wa-Kit
n wa-Kit b Sar
b Sar ’it al-yaqīn; ma’a ta’
’it al-yaqīn; ma’a ta’ līq ibn-B
līq ibn-B a ‘ai
a ‘ai l-Burh
l-Burh n. Fakhry, M., eds. 1986.
n. Fakhry, M., eds. 1986.
Beirut Alfarabi, Kit b al-Qiy
b al-Qiy s as-saġīr [in three volumes] al-’Ajam, R., eds. al-Mantiq ‘inda 1-F
s as-saġīr [in three volumes] al-’Ajam, R., eds. al-Mantiq ‘inda 1-F r
r bī, vol 1986;2:65–93.
bī, vol 1986;2:65–93.
Aouad, M., Rashed, M., Commentateurs “satisfaisants” et “non satisfaisants” de la Rhétorique selon Averroes. Endress, Aertsen, eds. 1999:83–124.
Leiden Arnaldez Mantik, R. 2nd edition. Encyclopedia of Islam, volume 1960;6:442–452.
Cairo Averroes, Commentarium medium in Aristotelis Priorum Analiticorum libros recensum textis Arabicis initiavit M. Kassem, complevit, revidit et adnotationibus illustravit, 1983.
Casablanca Averroes, Ras ’il falsafiyya. Maq
’il falsafiyya. Maq l
l t ft l-mantiq wal-’ilm at-tabīī li-abī l-walīd ibn-Rušd. ‘Alawī, J., eds. 1983.
t ft l-mantiq wal-’ilm at-tabīī li-abī l-walīd ibn-Rušd. ‘Alawī, J., eds. 1983.
Avicenna. Kit b an-Na
b an-Na t, Cairo, M. Kurdī, 1331
t, Cairo, M. Kurdī, 1331
Cairo Avicenna, Kit b aš-Šif
b aš-Šif ’: al-Madhal. el-Khodeiri, M., Anawati, G., el-Ahwani, F., eds. 1952.
’: al-Madhal. el-Khodeiri, M., Anawati, G., el-Ahwani, F., eds. 1952.
Cairo Avicenna, Kit b aš-Šif
b aš-Šif ’: al-Maqūl
’: al-Maqūl t. el-Khodeiri, M., Anawati, G., et al. 1959.
t. el-Khodeiri, M., Anawati, G., et al. 1959.
Cairo Avicenna, Kit b aš-Šif
b aš-Šif ’: al-Qiy
’: al-Qiy s. Zayed, S., Madkour, I., eds. 1964.
s. Zayed, S., Madkour, I., eds. 1964.
The Hague Avicenna, Treatise on logic [Translation of] Zabeeh F., ed. D niš-N
niš-N ma. 1971.
ma. 1971.
Cairo Avicenna, al-Iš r
r t wat-tanbīh
t wat-tanbīh t [Edited by S. Duny
t [Edited by S. Duny , in four volumes, with Tūsī’s commentary at the bottom of page] 1971.
, in four volumes, with Tūsī’s commentary at the bottom of page] 1971.
Bäck, A. Avicenna’s conception of the modalities. Vivarium. 1992;30:217–255.
Cairo Badawī, A.R., Aristū ‘inda l-’arab, 1948.
Cairo Badawī, A.R., Mantiq Aristū [3 volumes] 1948/52.
Hyderabad, Baġd dī, al-Kit
dī, al-Kit b al-Mu’tabar ft l-hikma, S. Yaltakaya, 1357
b al-Mu’tabar ft l-hikma, S. Yaltakaya, 1357
New Brunswick and Oxford Barnes, J., Theophrastus and hypothetical syllogistic. Fortenbaugh W., Huby P., Long A., eds., eds. Theophrastus of Eresus. 1985:125–141.
Leipzig Bergsträsser, G., Hunain Ibn Ishdq über die syrischen und arabischen Galen-Übersetzungen. Abhandlungen für die Kunde des Morgenlandes, xvii, Band 1925;2.
Leiden Black, D.L., Logic and Aristotle’s Rhetoric and Poetics in medieval Arabic philosophy, 1990.
Supplementary volume Black, D.L. Aristotle’s ‘Peri hermeneias’ in medieval Latin and Arabic philosophy: logic and the linguistic arts. Canadian Journal of Philosophy. 1991;17:25–83.
London Black, D.L., Logic in Islamic philosophy. Routledge Encyclopedia of Philosophy, volume 1998;5:706–713.
Lahore Brewster, D.P., The Just Balance [Translation of Ġaz lī’s al-Qist
lī’s al-Qist s al-mustaqīm] 1978.
s al-mustaqīm] 1978.
Brock, S., The Syriac commentary tradition. Burnett, eds. 1993:3–18.
Berlin Brockelmann, C., Geschichte der arabischen Litteratur [Two volumes, and three supplementary volumes] 1936, 1949.
Burnett C., ed., eds. Glosses and Commentaries on Aristotelian Logical Texts. 1993.
Burnett, C., The “sons of Averroes with the emperor Frederick” and the transmission of the philosophical works of Ibn Rushd. Endress, Aertsen, eds. 1999:259–299.
Princeton Calverley, E.E., Al-Abharīs “Īs ghūjī fī ‘l-mantiq”. The Macdonald presentation volume. 1933:75–85.
ghūjī fī ‘l-mantiq”. The Macdonald presentation volume. 1933:75–85.
Chejne, A.G. Ibn Hazm of Cordova on logic. Journal of the American Oriental Society. 1984;104:57–72.
Tehran Chittick, W., B b
b Afal. Encyclopaedia Iranica, volume 1982;3:285–291.
Afal. Encyclopaedia Iranica, volume 1982;3:285–291.
Leiden Daiber, H., Bibliography of Islamic philosophy [2 volumes] 1999.
Tehran D nišpažuh, M.T., al-Mantiq libni l-Muqajfa’. Hudūd al-mantiq libn Bihrīz, 1978.
nišpažuh, M.T., al-Mantiq libni l-Muqajfa’. Hudūd al-mantiq libn Bihrīz, 1978.
Qum D nišpažūh, M.T., al-Mantiqiyy
nišpažūh, M.T., al-Mantiqiyy t lil-F
t lil-F r
r bī [3 volumes] 1989.
bī [3 volumes] 1989.
Dunlop, D.M. Philosophical predecessors and contemporaries of Ibn B jjah. The Islamic Quarterly. 1955;2:100–116.
jjah. The Islamic Quarterly. 1955;2:100–116.
Edition and translation of Alfarabi’s Ris la suddira bih
la suddira bih l-kit
l-kit b Dunlop, D.M. Al-F
b Dunlop, D.M. Al-F r
r bī’s introductory ris
bī’s introductory ris la on logic. Islamic Quarterly. 1956;3:224–235.
la on logic. Islamic Quarterly. 1956;3:224–235.
El-Ghannouchi, A. “Des propositions modals”,épitre d’Ibn Malīh al-Raqq d. Arabica. 1971;18:202–210.
d. Arabica. 1971;18:202–210.
Paris Elamrani-Jamal, A., Logique aristotelicienne et grammaire arabe (étude et documents), 1983.
Elamrani-Jamal, A., Alīnūs. Goulet, eds. 1989:151–152.
END Elamrani-Jamal, A. Ibn Rušd et les Premiers Analytiques d’Aristote: aperçu sur un problème de syllogistique modale. Arabic Sciences and Philosophy. 1995;5:51–74.
Endress G., Aertsen J.A., eds., eds. Averroes and the Aristotelian tradition. 1999.
Leiden Endress, G., Gutas, D., A Greek and Arabic lexicon: materials for a dictionary of the medieval translations from Greek into Arabic, 1992.
Wiesbaden Endress, G., The works of Yahy ibn ‘Adī, 1977.
ibn ‘Adī, 1977.
Amsterdam Endress, G., Grammatik und Logik. Arabische Philologie und griechische Philosophic im Widerstreit. Mojsisch B., ed., eds. Sprachphilosophie in Antike und Mittlealter. 1986:163–299.
New York Fakhry, M., A History of Islamic philosophy, 1983.
Leiden Fortenbaugh, W., et al. Theophrastus of Eresus. Sources for his life, writings, thought and influence. Volume 1, 1992.
Frank, R.M. Review of B. Mojsisch, Sprachphilosophie in Antike und Mittelalter (Amsterdam, 1986). Journal of the American Oriental Society. 1991;109:356–360.
Cairo Ġaz lī, al-Mustasf
lī, al-Mustasf min ‘ilm al-usūl, 1938.
min ‘ilm al-usūl, 1938.
Beirut Ġaz lī, al-Qist
lī, al-Qist s al-mustaqīm. Chelhot, V., eds. 1959.
s al-mustaqīm. Chelhot, V., eds. 1959.
Cairo Ġaz lī, Maq
lī, Maq sid al-fal
sid al-fal sifa. Duny
sifa. Duny , S., eds. 1961.
, S., eds. 1961.
Cairo Ġaz lī, Mi’y
lī, Mi’y r al-’ilm. Duny
r al-’ilm. Duny S., ed. Mantiq tah
S., ed. Mantiq tah fut al-fal
fut al-fal sifa. 1961.
sifa. 1961.
Beirut Ġaz lī, Mihakk an-nazar. Na’s
lī, Mihakk an-nazar. Na’s nī, M., eds. 1966.
nī, M., eds. 1966.
Paris Goichon, A.-M., Livre des directives et remarques, 1951.
Oxford Goldziher, I., The attitude of orthodox Islam toward the “ancient sciences”. Swartz M.L., ed., eds. In Studies on Islam. 1981:185–215.
Madrid González Palencia, C.A., Rectificación de la mente. Salt’s Abū-s, ed., eds. Taqwīm ad-dihn. 1915.
Goulet R., ed., eds. Dictionnaire des Philosophes Antiques. 1989.
Tehran Gutas, D., F r
r bī and Greek philosophy. Encyclopaedia Iranica, volume 1982;8:219–223.
bī and Greek philosophy. Encyclopaedia Iranica, volume 1982;8:219–223.
Tehran Gutas, D., F r
r bī: Biography. Encyclopedia Iranica, volume 1982;8:208–213.
bī: Biography. Encyclopedia Iranica, volume 1982;8:208–213.
Gutas, D. Paul the Persian on the classification of the parts of Aristotle’s philosophy: a milestone between Alexandria and Bagdad. Der Islam. 1983;60:231–267.
With an appendix on the question of his date of birth Gutas, D. Avicenna’s madhab. 1988. Quaderni di Studi Arabi. 1987;5–6:323–336.
Leiden Gutas, D., Avicenna and the Aristotelian tradition, 1988.
Gutas, D., Aspects of literary form and genre in Arabic logical works. Burnett, eds. 1993:29–76.
“Berlin and New York” Gutas, D., Pre-Plotinian philosophy in Arabic (other than Platonism and Aristotelianism): a review of the sources. Haase W., Temporini H., eds., eds. Aufstieg und Niedergang der Römischen Welt. 1994:4939–4973.
London and New York Gutas, D., Greek thought, Arabic culture, 1998.
Gutas, D., The ‘Alexandria to Baghdad’ complex of narratives. A contribution to the study of philosophical and medical historiography among the Arabs. Documenti e studi sulla tradizione filosofica medievale. 1999:155–193.
Gyekye, K. The term istithn ’ in Arabic logic. Journal of the American Oriental Society. 1972;92:88–92.
’ in Arabic logic. Journal of the American Oriental Society. 1972;92:88–92.
Hallaq, W.B. Logic, formal arguments and formalization of arguments in Sunnī jurisprudence. Arabica. 1990;87:315–358.
Oxford Hallaq, W.B., Ibn Taymiyya against the Greek logicians, 1993.
Hasnawi, A. F r
r bī et la pratique de l’exégèse philosophique. Revue de synthèse. 1985;117:27–59.
bī et la pratique de l’exégèse philosophique. Revue de synthèse. 1985;117:27–59.
London Hourani, G., Averroes on the harmony of religion and philosophy [A translation of Ibn Rushd’s Kit b fasl al-maq
b fasl al-maq l] 1961.
l] 1961.
Hugonnard-Roche, H., Remarques sur la tradition arabe de l’Organon d’après le manuscrit paris, Bibliothèque nationale, ar. 2346. Burnett, eds. 1993:19–28.
Hugonnard-Roche, H., Averroes et la tradition des Seconds Analytiques. Endress, Aertsen, eds. 1999:172–187.
British Library codex Add. 9624, Hūnaī, al-umal, 73b-80a
Cairo Ibn-Abī-Usaybi’a, Uyūn al-anb [2 volumes bound as one] Müller, A., eds. 1882.
[2 volumes bound as one] Müller, A., eds. 1882.
Paris Ibn-Haldūn, Prolégomènes d’Ebn-Khaldoun: texte arabe (troisième partie). Quatremère, M., eds. 1858.
London Ibn-Haldūn, The Muqaddimah of Ibn Khaldūn [3 volumes translated by F.Rosenthal] 1958.
Leipzig Ibn-Nadīm, al-Fihrist [1872] Flügel, G., Rodiger, J., Müller, A., eds. 1871.
Toronto Inati, S.D., Ibn Sīn . Remarks and admonitions. Part one: logic, 1981.
. Remarks and admonitions. Part one: logic, 1981.
Inati, S.D., Logic. Nasr, S.H., Leaman, O., eds. History of Islamic Philosophy, volume 1996;2:802–823. London
Beirut Jabre, F., al Ajam, R., Dgheim, S., Gihamy, G., Encyclopedia of Arabic terminology of logic (Mawsū’a mustalah t ‘ilm al-mantiq ‘inda l-’arab), 1996.
t ‘ilm al-mantiq ‘inda l-’arab), 1996.
Beirut Jabre, F., al-Nass al-k mil li-mantiq Aristū [2 volumes] 1999.
mil li-mantiq Aristū [2 volumes] 1999.
Liège Jannssens, H., L’entretien de la sagesse. Introduction aux Oeuvres Philosophiques de Bar Hebraeus, 1937.
Louvain Janssens, J., An annotated bibliography on Ibn Sīn , 1991.
, 1991.
Calcutta K tibī, ar-Ris
tibī, ar-Ris la aš-Šamsiyya. Sprenger A., ed., eds. Bibliotheca Indica; a collection of Oriental works. No. 88. First appendix to the Dictionary of the Technical Terms used in the Sciences of the Mussulmans, co. 1854.
la aš-Šamsiyya. Sprenger A., ed., eds. Bibliotheca Indica; a collection of Oriental works. No. 88. First appendix to the Dictionary of the Technical Terms used in the Sciences of the Mussulmans, co. 1854.
Cambridge University Library, MS Browne D.19(10); Persian text is published in M. Minuvi and Y. Mahdawi, K šī, al-Minh
šī, al-Minh al-mubīn, (Tehran 1337 AH solar), logic, Musannaf
al-mubīn, (Tehran 1337 AH solar), logic, Musannaf t Afdal al-Dīn K
t Afdal al-Dīn K sh
sh nī, 477-582
nī, 477-582
Cairo Kindī, Kammiyya kutub Aristūt lis [3 volumes] Rīda, Abū, eds. Ras
lis [3 volumes] Rīda, Abū, eds. Ras ’il al-Kindī al-falsafiyya, volume 1950;1:181–191.
’il al-Kindī al-falsafiyya, volume 1950;1:181–191.
Eine Ableitung der Logik aus dem Koran Kleinknecht, A., Al-Qist s al-Mustaqīm. Stern, et al. 1972:159–188.
s al-Mustaqīm. Stern, et al. 1972:159–188.
Oxford Kneale, W.C., Kneale, M., The development of logic, 1962.
Cambridge Knuuttila, S., Modal logic. Kenny A., Kretzmann N., Pinborg J., eds., eds. Cambridge history of later medieval philosophy. 1982:342–357.
Leiden Lagerlund, H., Modal syllogistics in the Middle Ages, 2000.
L no. Lameer, J. Aristotelian rhetoric and poetics as logical arts in medieval Islamic philosophy. A review article of Black, Logic and Aristotle’s Rhetoric and Poetics in medieval Arabic philosophy. Bibliotheca Orientalis. 1993;5/6:563–582.
Leiden Lameer, J., Al-F r
r bī and Aristotelian syllogistics: Greek theory and Islamic practice, 1994.
bī and Aristotelian syllogistics: Greek theory and Islamic practice, 1994.
Lameer, J. The Organon of Aristotle in the medieval oriental and occidental traditions. Journal of the American Oriental Society. 1996;116:90–98.
Paris Madkour, I., L’Organon d’Aristote dans le monde arabe, 1969.
Mahdi, M. Review of Reseller’s Development of Arabic logic. Islamic Studies. 1965;4:449–450.
Mahdi, M., Language and logic in classical Islam. von Grunebaum, eds. 1970:51–83.
, Moses Maimonides. Maimonides’ treatise on logic (Maq lah fi-sin
lah fi-sin ’at al-mantik): The original Arabic and three Hebrew translations. Efros, I., eds. Proceedings of the American Academy for Jewish Research, 1937;8, 1938:1–65.
’at al-mantik): The original Arabic and three Hebrew translations. Efros, I., eds. Proceedings of the American Academy for Jewish Research, 1937;8, 1938:1–65.
Dordrecht Manekin, C.H., The Logic of Gersonides, 1992.
Manekin, C.H. Modal logic and the theory of modality in Gersonides. Iyyun, The Jerusalem Philosophical Quarterly. 1993;42:347–381.
Margoliouth, D.S. The discussion between Abu Bishr Matta and Abu Sa’id al-Sirafi on the merits of logic and grammar. Journal of the Royal Asiatic Society. 1905:79–129.
Albany Marmura, M., Ghaz lī’s attitude to the secular sciences and logic. Hourani G., ed., eds. Essays on Islamic Philosophy and Science. 1975:100–111.
lī’s attitude to the secular sciences and logic. Hourani G., ed., eds. Essays on Islamic Philosophy and Science. 1975:100–111.
Marmura, M. Review of Zimmermann’s Al-Farabi’s Commentary and Short Treatise on Aristotle’s De Interpretatione. Journal of the American Oriental Society. 1983;103.4:763–764.
Leiden Maróth, M., Ibn Sīn und die peripatetische “Aussagenlogik”, 1989.
und die peripatetische “Aussagenlogik”, 1989.
Boston McCarthy, R.J., Freedom and fulfillment: An annotated translation of al-Ghaz lī’s Al-Munqidh min al-Dal
lī’s Al-Munqidh min al-Dal l and other relevant works of al-Ghaz
l and other relevant works of al-Ghaz lī, 1980.
lī, 1980.
Mohaghegh M., Izutsu T., eds., eds. Collected texts and papers on logic and language. 1974.
Leiden Peters, F.E., Aristoteles Arabus, 1968.
Leiden Pines, S., Abu ‘1-Barak t, 2nd edition. Encyclopedia of Islam, volume 1960;1:111–113.
t, 2nd edition. Encyclopedia of Islam, volume 1960;1:111–113.
Jerusalem Pines, S. A parallel in the east to the “logica vetus”. The Collected Works of Shlomo Pines. 1996;volume 3:262–266.
British Library codex Or. 2360, R zī, al-Mulahhas fi l-hikma wal-mantiq
zī, al-Mulahhas fi l-hikma wal-mantiq
Cambridge University Library codex Or. 746(10), R zī, Šarh al-Iš
zī, Šarh al-Iš r
r t
t
Cairo, R zī, Lub
zī, Lub b al-Iš
b al-Iš r
r t, A. ‘Atiyya, 13552
t, A. ‘Atiyya, 13552
Oxford Rescher, N., vander Nat, A., The theory of modal syllogistic in medieval Arabic philosophy. Rescher N., Manor R., et al, eds., eds. Studies in modality. 1974:17–56.
Rescher, N., Abū-’l-Salt of Denia on modal syllogisms. 1963:87–90.
Rescher, N., al-Kindī’s sketch of Aristotle’s Organon. 1963:28–38.
Rescher, N., Arabic logic: a brief account. 1963:13–20.
Rescher, N., Avicenna on the logic of ‘conditional’ propositions. 1963:76–86.
Pittsburgh Rescher, N., Studies in the History of Arabic Logic, 1963.
Rescher, N., A tenth-century Arab-Christian apologia for logic. 1963:55–63.
Pittsburgh Rescher, N., The Development of Arabic Logic, 1964.
New York Rescher, N. Arabic logic. The Encyclopedia of Philosophy. 1967;volume 4:525–527.
Dordrecht Rescher, N., Temporal modalities in Arabic logic, 1967.
Sabra, A.I. Review of Rescher’s Al-F r
r bī’s Short Commentary on Aristotle’s Prior Analytics (Pittsburgh 1963). Journal of the American Oriental Society. 1965;85:241–243.
bī’s Short Commentary on Aristotle’s Prior Analytics (Pittsburgh 1963). Journal of the American Oriental Society. 1965;85:241–243.
Sabra, A.I. Avicenna on the subject matter of logic. Journal of Philosophy. 1980;77:746–764.
[S wī, 1898] S
wī, 1898] S wī al-Bas
wī al-Bas ’ir an-nasīriyya fl ‘ilm al-mantiq. Cairo, 1898. Edited by M. ‘Abduh.
’ir an-nasīriyya fl ‘ilm al-mantiq. Cairo, 1898. Edited by M. ‘Abduh.
Dordrecht Shehaby, N., The influence of Stoic logic on al-Jass s’s legal theory. 1973:61–85.
s’s legal theory. 1973:61–85.
Dordrecht Shehaby, N., The propositional logic of Avicenna; a translation from al-Shif ’: al-Qiy
’: al-Qiy s with introduction, commentary and glossary, 1973.
s with introduction, commentary and glossary, 1973.
British Library codex Or. 12405, Širw nī, Šarh at-takmīl fi l-mantiq
nī, Šarh at-takmīl fi l-mantiq
Stern S.M., Brown H.V., et al, eds., eds. Islamic Philosophy and the Classical Tradition. 1972.
Stern, S.M. A collection of treatises by ‘Abd al-Latīf al-Baghd dī. Islamic Studies. 1962;1:53–70.
dī. Islamic Studies. 1962;1:53–70.
Forthcoming, T. Street, An outline of Avicenna’s syllogistic, Archiv für Geschichte der Philosophic
Street, T. Toward a history of syllogistic after Avicenna: notes on Rescher’s studies on Arabic modal logic. Journal of Islamic Studies. 2000;11(2):209–228.
Street, T. ‘The eminent later scholar’ in Avicenna’s Book of the Syllogism. Arabic Sciences and Philosophy. 2001;11:205–218.
al-Iš r
r t wat-tanbīh
t wat-tanbīh t with two commentaries. Qum, 1375 AH solar. 3 volumes, Taht
t with two commentaries. Qum, 1375 AH solar. 3 volumes, Taht nī
nī
Paper delivered at the Thorn, P., An Avicennan extension of Aristotle’s modal syllogistic. Ist international conference of SIPRIn. Tehran, 1999. 1999.
Dordrecht Thorn, P., The logic of essentialism, 1996.
Cairo Tūsī, Šarh al-Iš r
r t [Published with Avicenna’s al-Iš
t [Published with Avicenna’s al-Iš r
r t] 1971.
t] 1971.
van Ess, J., The logical structure of Islamic theology. von Grunebaum, eds. 1970:21–50.
von Grunebaum G.E., ed., eds. Logic in classical Islamic culture. 1970.
Oxford Walzer, R., New light on the Arabic translations of Aristotle. 1962:60–113.
Atlanta Ziai, H., Knowledge and Illumination: A study of Suhrawardī’sHikmat al-Ishr q, 1990.
q, 1990.
Zimmermann, F.W., Some observations on al-F r
r bī and logical tradition. Stern, et al. 1972:517–546.
bī and logical tradition. Stern, et al. 1972:517–546.
Interpretatione. Oxford Zimmermann, F.W., Al-Farabi’s Commentary and Short Treatise on Aristotle’s De, 1981.
London Zimmermann, F., The origins of the so-called Theology of Aristotle. Kraye J., Ryan W.F., Schmitt C.B., eds., eds. Pseudo-Aristotle in the Middle Ages. 1986:110–240.
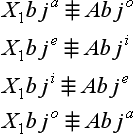
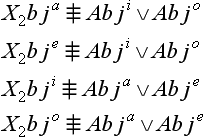
 fī contradictories
fī contradictories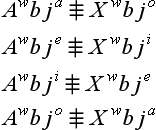
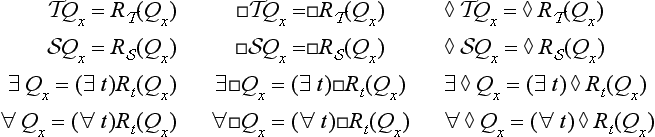
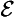 ):
):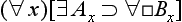
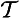 ):
):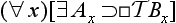
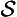 ):
):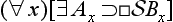
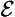 ):
):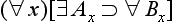
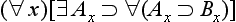
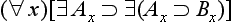
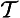 ):
):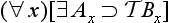
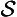 ):
):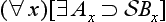
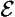 ):
):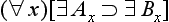

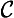 ):
):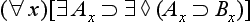
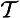 ):
):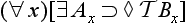
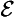 ):
):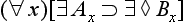
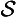 ):
):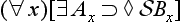
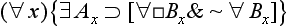
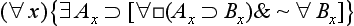
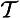 & ∼ ∀
& ∼ ∀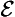 ):
):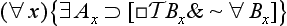
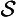 & ∼ ∀
& ∼ ∀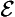 ):
):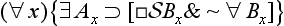
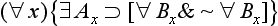
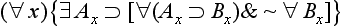
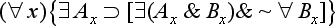
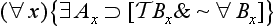
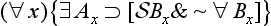

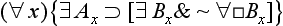
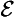 & ∼
& ∼ 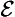 ):
):