2 Density and density flows
The density of an object or a parcel of fluid is equal to its mass divided by its volume. The density of seawater is an important concept in oceanography because dense water sinks below less dense water, creating currents and layering in the ocean.
The density of fresh water depends on temperature, and at 15 °C is approximately 1000 kg m–3. Seawater is a little denser than fresh water at the same temperature, as we shall see. The human body is made mostly of water, so we would expect the density of our bodies to be about the same. In fact, the average density of the human body is about 950 kg m–3, and so most humans float on water (are buoyant) because they are less dense than seawater.
2.1 Archimedes’ Principle
Archimedes’ Principle deals with the buoyancy objects experience when they are immersed in water. Things weigh less in water than they do in air. This is because they experience an upthrust equal to the weight of water they have displaced (they are supported by the surrounding water in just the same way that the water they have replaced was). This is a statement of Archimedes’ Principle. If a body has a mass m, it has a weight in air equal to mg, where g is the acceleration of gravity (equal to 9.81 m s–2). The same object in water will weigh mg where g is called the reduced gravity (Figure 2.1). We can calculate the reduced gravity g with the formula:

where d2 is the density of the submerged object and d1 is the density of water. For example, a grain of sand which is three times as dense as water will feel a reduced gravity (⅔)g when it is suspended in seawater. Its weight in water will therefore be ⅔ of its weight in air.

Figure 2.1 Illustration of reduced gravity. An object of mass m and density d2, surrounded by water of density d1 has a weight mg′ where g′ (defined by equation above) is called the reduced gravity.
A special case of Archimedes’ principle applies to floating bodies, when the principle states: ‘a floating body displaces its own weight of water’. By ‘displaces’ we mean ‘pushes out of the way’. So if you float an object on the surface of water, it pushes out of the way a volume of water that has the same weight as the floating object.
An iceberg weighing, say, 1 tonne (1000 kg), will have a volume of 1087 m3 (the density of ice is about 920 kg m–3, and since density = mass/volume it follows that volume = mass/density). If you place this iceberg in the sea, it will float because it is less dense than water, and it will displace 1000 kg of water exactly (its own weight). 1000 kg of seawater occupies about 976 m3, so some of the iceberg will stick out above the water surface. 976 m3 (about 90%) of the iceberg will be under water, and the remaining 111 m3 (about 10%) will stick above the water. When you see floating ice (not pack ice or frozen seawater) at sea, you only see ‘the tip of the iceberg’ (Figure 2.2).
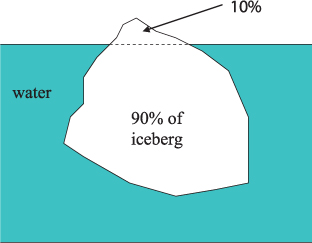

Figure 2.2 A floating iceberg displaces its own weight of water. The volume of the displaced water is about 90% of the volume of the iceberg; the remaining 1/10th of the volume of the iceberg is visible above the ocean surface. The photograph shows the tip of a floating iceberg.
What would happen if all the icebergs at sea were to melt? If we consider the 1 tonne iceberg, it has pushed 1000 kg of water out of the way, so it will cause sea level to rise by the equivalent of 1000 kg of water. When the iceberg melts, it will no longer displace any water but it will add 1000 kg of water to the sea (the mass will stay the same on melting). This is illustrated with the three photographs of a simple laboratory experiment shown in Figure 2.3. The first photograph (a) shows a tank containing some fresh water. The second photograph (b) shows the same tank with some small pieces of ice added. The water level rises as the floating ice displaces its own weight of water. Note that only a small part of the ice lies above the water surface. In the third photograph (c), the ice has melted and the water level is the same as in (b) because the mass of water added by the melting ice is the same as that which has been displaced by the floating ice.

Figure 2.3 Ice added to water in a flask raises the water level as water is displaced to support the floating ice (a and b). When the ice melts (c) there is little change in water level because the mass of melted ice water is the same as the mass of displaced water.
A consequence is that the melting of floating icebergs produced by global warming will not have a big impact on sea level. The melting of land-based glaciers is a different matter altogether. Land-based glaciers such as those on Greenland and the Antarctic continent are not currently displacing any seawater, so when they melt they will add a new mass of water to the ocean. It is estimated that the rise in sea level produced by the melting of all the landbased ice will be 80 m.
2.2 The density of water
Water is heavy. Its density is approximately 1000 kg m–3 and varies with temperature, salinity and (to a small extent) pressure. Fresh water has a maximum density at 4 °C and this fact is important in preventing ponds and lakes from freezing solid in winter. When surface water cools to 4 °C it sinks to the bottom of the lake. Further surface cooling produces water that is less dense, and this water therefore floats on top of the 4 °C water at the bottom of the lake. The surface water may eventually cool to the point where ice forms, but the fact that there is liquid water at the bottom means that animals and plants can survive the winter in freshwater lakes.
No such phenomenon occurs in the ocean. The density of seawater continues to increase as the temperature decreases. Salinity is also an important control on seawater density, which increases with increasing salinity. Mostly because of the salt content, the density of seawater is somewhat greater than that of fresh water. Typically, the density of seawater is a little greater than 1000 kg m–3. Oceanographers call the difference between the density of a sample of seawater and 1000 kg m–3 ‘sigma-t’, given the symbol σt. So, for example, seawater that has a density 1022.5 kg m–3 has a σt value of 22.5.
2.3 ‘Sigma-t’ on temperature salinity diagrams
Because the density of seawater depends mostly on temperature and salinity, lines of constant density can be marked on T/S diagrams. Figure 2.4 show how these look. For example, water which has a temperature of 6 °C and a salinity of 35 has a σt of 27.5 and therefore a density of 1027.5 kg m–3. Note that the σt contours become quite curved at low temperature. This can lead to an effect called caballing, which is thought to be important in the production of dense water at high latitude. In Figure 2.4, the two water masses A and B have the same density. If they mix, the mixture will lie on the line joining them. The density of the mixture will therefore be greater than either A or B and therefore the mixture will sink below the two water masses out of which it has formed.

Figure 2.4 Temperature/Salinity diagram with lines of σt added. Note the curvature of the constant density lines at low temperature. If two water masses A and B with the same density are mixed, the mixture will have a greater density. This effect, called caballing, is thought to be important in the formation of the densest bottom waters of the oceans.
2.4 Layering of water
All water, including seawater, likes to find its own level with the densest water on the bottom. This layering is called stratification and is a physical property of seawater that has important biological and chemical consequences.
We have already come across one important form of layering in the ocean, the main thermocline, which can be several kilometres thick and which separates the sun-warmed surface layers from the deep cold waters. Another form of stratification is found in estuaries and coastal waters, where a layer of relatively low salinity water, produced by rivers flowing into the sea, lies on top of a layer of salty water. The interface between the low and high salinity water is called a halocline. Stratification can therefore be produced by salinity and temperature, and sometimes by both acting together. For stable stratification to exist, the densest water will always be on the bottom. The interface between waters of different density is called a pycnocline.
When water is strongly stratified, it is possible for waves, called internal waves, to form on the interface between the different layers. We cannot normally see these waves from above the surface, but their effects can be measured with instruments recording temperature and salinity at a given depth. The vertical movement associated with the internal waves can be tens of metres – much bigger (and also slower) than surface waves. Submarines that have set their buoyancy to cruise at a particular depth (and therefore density level) are carried up and down with this movement. In highly stratified regions such as fjords, surface motor vessels can experience a phenomenon called ‘dead water’. The energy from their propeller goes into creating internal waves instead of driving the boat forward (Figure 2.5).

Figure 2.5 Illustration of the ‘dead water’ effect. The propeller of a motor boat in a sea with light surface water separated from denser deeper water by a pycnocline makes internal waves on the pycnocline. The energy from the motor goes into creating these waves instead of propelling the boat forward.
2.5 Density currents
When two water masses of different density lie adjacent to each other, there is a tendency for the denser of the two to flow under the less dense (and vice versa) to create a circulation known as a density current. Density currents (also called gravity currents) occur in may forms in the ocean. For example, the thermohaline circulation discussed in Chapter 1 is essentially a large-scale density current. In estuaries, salty ocean water can flow under the less dense river water. Other forms of density current include turbidity currents in which particles suspended in water increase the density. In the atmosphere, avalanches are also a form of density current in which suspended snow has increased the density of the air.
Density currents can be created and studied in a laboratory tank experiment known as the lock gate experiment (Figure 2.6). A perspex tank is set up with salt water at one end, divided by a removable lock gate from fresh water at the other. The water can be coloured with a dye to make the subsequent flow easy to see. When the lock gate is withdrawn, the salty water flows under the fresh water along the bottom of the tank and the fresh water flows over the salt water in the opposite direction. With salinities typical of seawater, the flow is quite slow – typically just a few cm s–1 for a tank 20 cm deep. Physically, the sinking of the salt water below the fresh produces a reduction in potential energy, and the kinetic energy of the resulting flow is derived from this. By matching the loss in potential energy to the gain in kinetic energy, it can be shown that the speed of the resulting density current depends on just two things: the density difference between the salt and fresh water and the depth of water in the tank. We can write an equation for the speed, S, of the current as follows:


Figure 2.6 The lock gate experiment. Salt water (coloured blue) is separated from fresh water by a lock gate. When the lock gate is removed, the salt water flows underneath the fresh in a current called a density current. Friction at the interface between the flowing salt water and the overlying fresh water causes internal waves to form on the interface.

Here, g′ is the reduced gravity (see section 2.1) and h is the thickness of the current. The factor C depends on the geometry of the tank: it is about 1 but in general must be determined exactly by experiment. In section 2.1 we defined reduced gravity in terms of an object immersed in water, but it can also be applied to two liquids of different density. For example, for the experiment shown in Figure 2.6, the density of the salt water was 1020 kg m–3 and that of the fresh water was 1000 kg m–3, giving g′ = 9.81 x (1020–1000)/1020 = 0.19 m s–2. The depth of the current in Figure 2.6 is 5 cm (0.05 m) and its speed was measured as 0.07 m s–1. Substituting these values into the equation above gives C = 0.5.
2.6 Density and pressure
The pressure at a surface in the ocean is equal to the weight of water above that surface (expressed as a force per unit area). The weight of water will equal the average density of the water times its volume times the acceleration of gravity. Because seawater is heavy compared to air (it is about 1000 times denser than air) the pressure in the ocean is much greater than the pressure in the atmosphere. As a rule of thumb, the pressure in the ocean increases by 1 atmosphere for every 10 m increase in depth (1 atmosphere is equal to the atmospheric pressure at sea level, also called 1 bar). The pressure in the ocean at a depth of 1000 m, therefore, will be 101 atmospheres compared to 1 atmosphere at the sea surface. An increase in depth by 1 m creates an increase in pressure of 1/10th of a bar, or 1 decibar.
It is a feature of pressure in a fluid that the pressure at a point acts equally in all directions. If we put a pipe down into the ocean, say to a depth of 1000 m, the pressure at the bottom of the pipe will be 101 bars compared to 1 bar at the top of the pipe. This difference in pressure just balances the weight of the water in the pipe. Now imagine that we displace the water in the pipe upwards (perhaps by applying suction at the top of the pipe). Imagine we are at a place where temperature decreases with depth (which is normal) and where salinity also decreases with depth (as it does in the Atlantic). In that case, we will suck cold, fresh (and dense) water into the pipe, compared to the water outside the pipe (see Figure 2.7). Before the water can sink back down again, it is possible that heat will flow into the pipe and the temperature will equilibrate with that outside. But the water in the pipe will still be fresh compared to that outside (salt can’t flow through the pipe). Because fresher water is less dense, the water in the pipe will weigh less than that outside, and it will no longer balance the pressure difference between the ends of the pipe. As a result it will be forced upwards, the cycle will repeat, and a continuous flow will be produced. This ‘salt fountain’ (first proposed by the American oceanographer Henry Stommel) is a potential way of generating energy from the ocean.

Figure 2.7 The salt fountain. An initial suck on the pipe creates a continuous upwards flow of water, which derives its energy from the vertical temperature and salinity gradients in the ocean.
A smaller scale version of the salt fountain can be created in a laboratory tank. A tank is set up with warm salty water overlying cold fresher water. The difference in temperature is sufficient to make the lower layer denser, and so the layering is initially stable. At the interface between the two layers, the salt and heat diffuse by molecular processes. The molecular diffusion of heat is faster than it is for salt, and so the upper layer cools more quickly than it freshens. Similarly the lower layer warms more quickly than it becomes saltier. This creates local instabilities, with denser water lying on top of less dense water. As a result, water movements occur in small columns (called salt fingers) extending both upwards and downwards. The salt fingers penetrate only so far before lateral diffusion of salt destroys the density difference. It is thought that this process may create layers in the ocean with sharply defined interfaces of temperature and salinity. Sometimes temperature staircases (in which the temperature varies with depth in a series of steps) are observed in the ocean and are thought to be produced by this mechanism.